对称分量法基本概念和简单计算[1]

对称分量法(零序,正序,负序)的理解与计算对称分量法（零序，正序，负序）的理解与计算1）求零序分量：把三个向量相加求和。

即A相不动，B相的原点平移到A相的顶端（箭头处），注意B相只是平移，不能转动。

同方法把C相的平移到B相的顶端。

此时作A相原点到C相顶端的向量（些时是箭头对箭头），这个向量就是三相向量之和。

最后取此向量幅值的三分一，这就是零序分量的幅值，方向与此向量是一样的。

2）求正序分量：对原来三相向量图先作下面的处理：A相的不动，B相逆时针转120度，C相顺时针转120度，因此得到新的向量图。

按上述方法把此向量图三相相加及取三分一，这就得到正序的A相，用A相向量的幅值按相差120度的方法分别画出B、C两相。

这就得出了正序分量。

3）求负序分量：注意原向量图的处理方法与求正序时不一样。

A相的不动，B 相顺时针转120度，C相逆时针转120度，因此得到新的向量图。

下面的方法就与正序时一样了。

对电机回路来说是三相三线线制，Ia+Ib+Ic=0，三相不对称时也成立；当Ia+Ib+Ic≠0时必有一相接地，对地有有漏电流；对三相四线制则为Ia+Ib+Ic+Io=0成立，只要无漏电，三相不对称时也成立；因此，零序电流通常作为漏电故障判断的参数。

负序电流则不同，其主要应用于三相三线的电机回路；在没有漏电的情况下（即Ia+Ib+Ic=0），三相不对称时也会产生负序电流；负序电流常作为电机故障判断；注意了：Ia+Ib+Ic=0与三相对称不是一回事；Ia+Ib+Ic=0时，三相仍可能不对称。

注意了：三相不平衡与零序电流不可混淆呀！三相不平衡时，不一定会有零序电流的；同样有零序电流时，三相仍可能为对称的。

（这句话对吗?）前面好几位把两者混淆了吧！正序、负序、零序的出现是为了分析在系统电压、电流出现不对称现象时，把三相的不对称分量分解成对称分量（正、负序）及同向的零序分量。

只要是三相系统，一般针对三相三线制的电机回路，就能分解出上述三个分量（有点象力的合成与分解，但很多情况下某个分量的数值为零）。

对称分量法正序：A相领先B相120度，B相领先C相120度，C相领先A相120度。

负序：A相落后B相120度，B相落后C相120度，C相落后A相120度。

零序：ABC三相相位相同，哪一相也不领先，也不落后。

三相短路故障和正常运行时，系统里面是正序。

单相接地故障时候，系统有正序、负序和零序分量。

两相短路故障时候，系统有正序和负序分量。

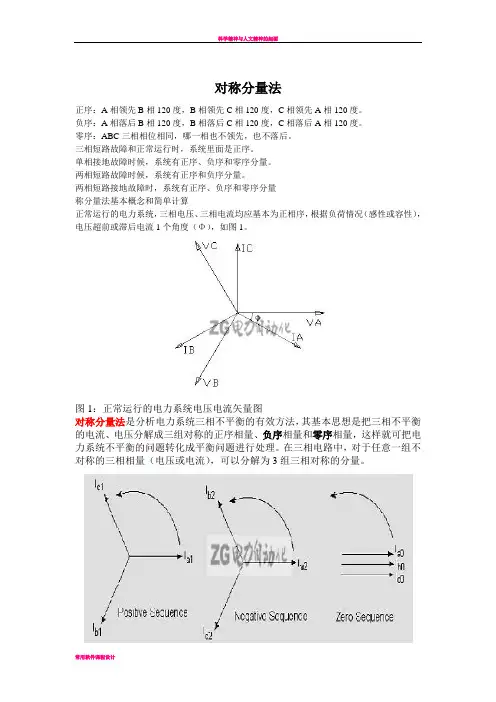
两相短路接地故障时，系统有正序、负序和零序分量称分量法基本概念和简单计算正常运行的电力系统，三相电压、三相电流均应基本为正相序，根据负荷情况（感性或容性），电压超前或滞后电流1个角度（Φ），如图1。

图1：正常运行的电力系统电压电流矢量图对称分量法是分析电力系统三相不平衡的有效方法，其基本思想是把三相不平衡的电流、电压分解成三组对称的正序相量、负序相量和零序相量，这样就可把电力系统不平衡的问题转化成平衡问题进行处理。

在三相电路中，对于任意一组不对称的三相相量（电压或电流），可以分解为3组三相对称的分量。

图2：正序相量、负序相量和零序相量（以电流为例）当选择A相作为基准相时，三相相量与其对称分量之间的关系（如电流）为：IA=Ia1+Ia2+Ia0――――――――――――――――――――――――――○1IB=Ib1+Ib2+Ib0=α2Ia1+αIa2 + Ia0――――――――――○2IC=Ic1+Ic2+Ic0=α Ia1+α2Ia2+Ia0―――――――――――○3对于正序分量：Ib1=α2 Ia1 ，Ic1=αIa1对于负序分量：Ib2=αIa2 ，Ic2=α2Ia2对于零序分量：Ia0= Ib0 = Ic0式中，α为运算子，α=1∠120°有α2＝1∠240°, α3＝1, α+α2+1=0由各相电流求电流序分量：I1=Ia1= 1/3(IA +αIB +α2 IC)I2=Ia2= 1/3(IA +α2IB +αIC)I0=Ia0= 1/3(IA +IB +IC)以上3个等式可以通过代数方法或物理意义（方法）求解。

对称分量法对称分量法（method of symmetrical components）电工中分析对称系统不对称运行状态的一种基本方法。

广泛应用于三相交流系统参数对称、运行工况不对称的电气量计算。

电力系统正常运行时可认为是对称的，即各元件三相阻抗相同，各自三相电压、电流大小相等，具有正常相序。

电力系统正常运行方式的破坏主要与不对称故障或者断路器的不对称操作有关。

由于整个电力系统中只有个别点是三相阻抗不相等，所以一般不使用直接求解复杂的三相不对称电路的方法，而采用更简单的对称分量法进行分析。

任何不对称的三相相量A，B，C 可以分解为三组相序不同的对称分量：①正序分量A1，B1，C1，②负序分量A2，B2，C2，③零序分量A，B，C。

即存在如下关系：（1）每一组对称分量之间的关系为（2）式中，复数算符．．．．a＝e j120。

将（２）代入（１）可得；（3）式中系数矩阵是非奇异的，其逆矩阵存在，所以有（4）任意不对称的电压、电流都可以用式（4）求出它们的正序、负序和零序电压、电流分量。

已知三序分量时，又可用式（3）合成三相向量。

在计算电力系统不平衡情况下引用了对称分量法，即任何三相不平衡的电流、电压或阻抗都可以分解成为三个平衡的相量成分即正相序（UA1、UB1、UC1）、负相序（UA2、UB2、UC2）和零相序（UA0、UB0、UC0），即有：UA=UA1+UA2+UA0，UB=UB1+UB2+UB0，UC=UC1+UC2+UC0，其正相序的相序（顺时方向）依次为UA1、UB1、UC1，大小相等，互隔120度；负相序的相序（逆时方向）依次为UA2、UB2、UC2，大小相等，互隔120度；零相序大小相等且同相，各相序都是按逆时针方向旋转。

在对称分量法中引用算子a ，其定义是单位相量依逆时针方向旋转120度，则有：UA0=1/3（UA+UB+UC ），UA1=1/3（UA+aUB+aaUC ），UA2=1/3（UA+aaUB+aUC ）注意以上都是以A 相为基准，都是矢量计算。

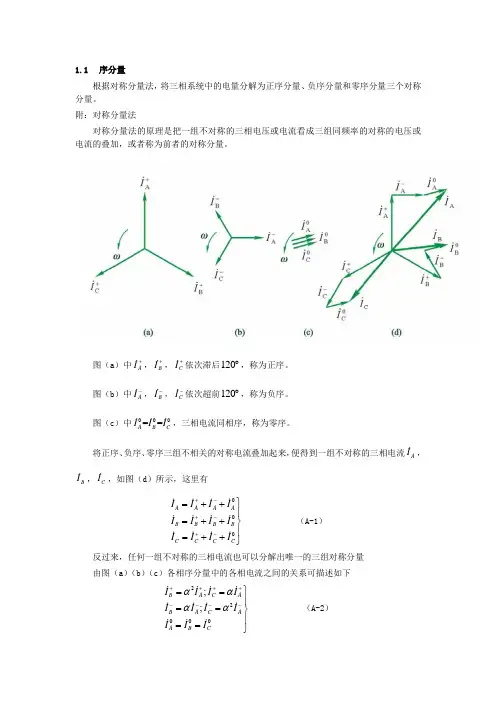
1.1 序分量根据对称分量法，将三相系统中的电量分解为正序分量、负序分量和零序分量三个对称分量。

附：对称分量法对称分量法的原理是把一组不对称的三相电压或电流看成三组同频率的对称的电压或电流的叠加，或者称为前者的对称分量。

图（a ）中A I +，B I +，C I +依次滞后120︒，称为正序。

图（b ）中A I -，B I -，C I -依次超前120︒，称为负序。

图（c ）中000==A B C I I I ，三相电流同相序，称为零序。

将正序、负序、零序三组不相关的对称电流叠加起来，便得到一组不对称的三相电流A I ，B I ，C I ，如图（d ）所示，这里有000A A A A B B B B C C C C I I I I I I I I I I I I +-+-+-⎫=++⎪=++⎬⎪=++⎭（A-1）反过来，任何一组不对称的三相电流也可以分解出唯一的三组对称分量由图（a ）（b ）（c ）各相序分量中的各相电流之间的关系可描述如下22000;;B A C A B A C A A B C I I I I I I I I I I I αααα++++----⎫==⎪==⎬⎪==⎭（A-2）式中，复数运算符号2/312j e πα==-+，其作用是使一个相量正转120︒。

将式（A-2）代入式（A-1），得02020A A A A B A A A C A A A I I I I I I I I I I I I αααα+-+-+-⎫=++⎪=++⎬⎪=++⎭（A-3）由式（A-3）可从不对称的三相电流A I ，B I ，C I 中求出A 相的各相序的分量，即 ()()()220131313A A B C A A B C A A B C I I I I I I I I I I I I αααα+-⎫=++⎪⎪⎪=++⎬⎪⎪=++⎪⎭ （A-4） 由于各相序分量都是对称的，找出A 相分量以后，B 、C 相分量就可以根据式（A-2）确定。

对称分量法（零序，正序，负序）的理解与计算1）求零序分量：把三个向量相加求和。

即A相不动，B相的原点平移到A相的顶端（箭头处），注意B相只是平移，不能转动。

同方法把C相的平移到B相的顶端。

此时作A相原点到C相顶端的向量（些时是箭头对箭头），这个向量就是三相向量之和。

最后取此向量幅值的三分一，这就是零序分量的幅值，方向与此向量是一样的。

2）求正序分量：对原来三相向量图先作下面的处理：A相的不动，B相逆时针转120度，C 相顺时针转120度，因此得到新的向量图。

按上述方法把此向量图三相相加及取三分一，这就得到正序的A相，用A相向量的幅值按相差120度的方法分别画出B、C两相。

这就得出了正序分量。

3）求负序分量：注意原向量图的处理方法与求正序时不一样。

A相的不动，B相顺时针转120度，C相逆时针转120度，因此得到新的向量图。

下面的方法就与正序时一样了。

对电机回路来说是三相三线线制，Ia+Ib+Ic=0，三相不对称时也成立；当Ia+Ib+Ic≠0时必有一相接地，对地有有漏电流；对三相四线制则为Ia+Ib+Ic+Io=0成立，只要无漏电，三相不对称时也成立；因此，零序电流通常作为漏电故障判断的参数。

负序电流则不同，其主要应用于三相三线的电机回路；在没有漏电的情况下（即Ia+Ib+Ic=0），三相不对称时也会产生负序电流；负序电流常作为电机故障判断；注意了：Ia+Ib+Ic=0与三相对称不是一回事；Ia+Ib+Ic=0时，三相仍可能不对称。

注意了：三相不平衡与零序电流不可混淆呀！三相不平衡时，不一定会有零序电流的；同样有零序电流时，三相仍可能为对称的。

（这句话对吗）前面好几位把两者混淆了吧！正序、负序、零序的出现是为了分析在系统电压、电流出现不对称现象时，把三相的不对称分量分解成对称分量（正、负序）及同向的零序分量。

只要是三相系统，一般针对三相三线制的电机回路，就能分解出上述三个分量（有点象力的合成与分解，但很多情况下某个分量的数值为零）。

对称分量法的变量矩阵
摘要：
1.对称分量法的概念和应用背景
2.变量矩阵的定义及其在对称分量法中的作用
3.对称分量法中的变量矩阵的构建方法
4.变量矩阵在对称分量法中的应用案例
5.对称分量法在电气领域的重要性
正文：
对称分量法是电工中分析对称系统不对称运行状态的一种基本方法，广泛应用于三相交流系统参数对称、运行工况不对称的电气量计算。

在实际应用中，由于系统的复杂性和多样性，对称分量法需要借助变量矩阵来描述和分析系统的不对称性。

变量矩阵是一个数学概念，它是一个矩阵，由一组变量组成。

在对称分量法中，变量矩阵用于描述电气系统的不对称性，包括电气量的幅值和相位。

变量矩阵的构建方法是根据电气系统的参数和运行工况，通过数学计算和推导得出。

在对称分量法中，变量矩阵的构建方法主要有两种：一种是基于电气系统的参数对称，另一种是基于电气系统的运行工况不对称。

基于参数对称的变量矩阵构建方法主要应用于三相交流系统的参数对称计算；基于运行工况不对称的变量矩阵构建方法主要应用于三相交流系统的运行工况不对称计算。

变量矩阵在对称分量法中的应用案例非常广泛。

例如，在三相交流系统的
参数对称计算中，可以通过变量矩阵来计算系统的幅值和相位；在三相交流系统的运行工况不对称计算中，可以通过变量矩阵来计算系统的不对称性和电气量的幅值和相位。

对称分量法在电气领域具有重要的应用价值。

它可以有效地分析和计算电气系统的不对称性，为电气系统的运行和管理提供科学依据。