七年级上册数学行程问题-相遇与追及问题-教学设计--上课用

学生活动
教师活动
教学目标
教学说明
预习相关概念及定理。
思考并回答。
学生同步回答
学生以小组形式进行讨论
小组讨论完成后请小组代表起来公布各个小组的答案。
学生观察并思考。
学生运用直尺进行绘图。
画完的学生举手，等待老师的提问。
学生观察黑板上两位同学的线段图，并以小组形式进行讨论。
学生观察思考，以小组形式谈论。
先让学生理解题意。
先让学生自己动手操作把复杂的题目用简单的图形来表达。
关注不同成绩和层次学生的思考能力。然后再进行总结，使得掌握各个层次学生的思考能力。
学生能更容易接受新知识。
先让学生掌握解应用题中审题的步骤。
让学生体会合作和竞争的关系。
让学生掌握怎么列相遇问题的方程和解方程。
解一道应用题前首先能够判断这题属于‘相遇’还是‘追及’？
初中数学双语教学设计数学应用题“相遇，追及问题”
西藏日喀则市桑珠孜区第二中学格桑德吉
课型：新授课
日期：2017
教材分析：
1、数学应用题“相遇，追及问题”在初中六本书中没有单独的列出一章。但是在方程与不等式的应用题中经常出现“相遇，追及问题”。
2、由于这类问题与实际问题紧密相联，所以考试中出现次数很多。
准备工作：1、制作讲学稿，上课之前发给每一位学生。
2、学生课前分小组预习，上课时按小组落座。
3、学生准备好直尺，为了方便画图。
教学设计策略：依据教学目标和学生的特点，依据教学时间和效率的要求，在此课教学方法和教学模式的设计中我主要体现了以下的设计思想和策略：
1、回归学生主体，一切围绕着学生的学习活动和当堂的反馈程度安排教学过程。
学生观察体验，领会怎么列方程，解方程。

七年级上数学方程解决问题的追及问题和相遇问题教学设计西安市蓝田县三里镇文姬中学张增涛课题：能追上小明吗？教材:北师版七年级5.7教学目的：借助“线段图”分析复杂问题中的数量关系，把问题由复杂变为简单。

能用一元一次方程解决实际生活中的相遇、追及问题。

培养学生的分析、解决问题能力。

转变学生的思维。

教学重点：运用方程解决追及和相遇的实际问题。

教学难点：能画出“线段图”分析行程中的等量关系。

教学过程：导入：同学们！你家离学校大约几米？平时上学你需要几分钟？（点名学生回答并板书），那么你平时上学的速度是多少？（目的：让学生从生活中的实际问题向数学问题转化）提问1：同学们能说出路程、时间、速度三个量之间的关系吗？（能说出：路程＝速度×时间）（板书）提问2：速度的单位如何表示？今天我们就这个等量关系运用在实际问题中，看如何解决？新课：1、A、B两地相距40千米，甲、乙分别在A、B两地相向同时出发。

已知甲的速度为20千米/小时，乙的速度为15千米/小时，那么多少小时后甲、乙两人相遇？（投影）提问1：你理解“相向走”吗？演示：让两名学生到讲台前来情景演示，并且要求学生带着问题：你能根据演示，画出线段图吗？提问2：两名同学演示过程中，你能找出当中的等量关系吗（甲走路程＋乙走路程＝相距路程）（甲走用的时间＝乙走用的时间）提问3：你能根据等量关系设出未知量列出方程吗？2、A、B两地相距40千米，甲、乙分别在A、B两地同向同时出发。

已知甲的速度为20千米/小时，乙的速度为15千米/小时，那么多少小时后甲能追上乙？（投影）提问1：你理解“同向走”吗？演示：让两名学生到讲台前来情景演示，并且要求学生带着问题:你能根据演示，画出线段图吗？提问2：两名同学演示过程中，你能找出当中的等量关系吗乙相距路程＋乙走路程＝甲追的路程）（甲追乙用的时间＝乙走用的时间）提问3：你能根据等量关系设出未知量列出方程吗？巩固练习：学生自学书中的情景例题，然后六人小组讨论，教师巡视发现问题。

一元一次方程模型相遇问题教学目标知识与技能：培养学生分析问题、解决实际问题、归纳整合的能力。

过程与方法：经历活动与思考、交流与讨论。

分析问题解决问题。

情感与态度、价值观：经历问题情境——建立数学模型——体会数学应用，感悟数学建模思想。

教学重点：找出等量关系建立数学模型教学难点：分析实例快捷寻找等量关系建立数学模型教学方法：指导探究角色表演合作交流教学资源：多媒体课件教学过程一知识回顾通过多媒体向学生展示本章前面所学的知识1、解一元一次方程的步骤⑴去分母⑵去括号⑶移项⑷合并同类项⑸未知数系数化为一⑹检验2、生活中的行程问题中的路程、速度、时间之间的关系路程＝速度×时间速度＝路程／时间时间＝路程／速度二情境引入多媒体展示课题揭示目标例1小明与小红的家相距20㎞，小明从家里出发骑自行车去小红家，两人商定小红到时候从家里出发骑自行车去接小明。

已知小明骑车的速度是13㎞∕h,小红的速度是12㎞∕h。

若两人同时出发，那么他们经过多长时间相遇？角色扮演：由两位学生一人扮演小红一人扮演小明，分别站在教室一前一后。

根据题意。

准确把握。

问题1小红与小明所走路程之和有什么关系？问题2小红与小明二人所用时间有什么关系？若设他们经过x小时相遇，则小明所走路程为（）小红所走路程为（）根据问题1中的等量关系可列出方程（）。

解得（）检验作答1、P102 练习1问题1甲、乙两车所行路程之和有什么关系？问题2甲、乙两车所用时间有什么关系？若设乙车的行驶速度是x㎞∕h根据问题1中的等量关系可列方程（）2、在例1中问题换做：如果小明先走30分钟，那么小红骑车要多长时间才能与小明相遇？问题1小红与小明所走路程之和有什么关系？问题2小红与小明二人所用时间有什么关系？若设他们经过x小时相遇，则小红所用时间为（）小明所用时间为（）小明所走路程为（）小红所走路程为（）根据问题1中的等量关系可列出方程（）。

解得（）检验作答。

三、合作交流多媒体出示相关练习，同桌之间分角色扮演并依照例1提出探究问题四、拓展延伸五、课堂小结六、作业七、学后反思在我们生活中你遇到过哪些涉及到行程中的相遇问题呢？能谈谈你的发现吗？在我们生活中对于相遇问题的求解对我们的日常安排有哪些帮助，谈谈你的想法。

一元一次方程的应用（相遇、追及问题）教学设计东莞市XX实验学校梁XX 【教学内容】人教版七年级数学上册P94页例2延伸【教材分析】本课是在解一元一次方程的基础上，讲述一元一次方程的应用，是本节的重点和难点，同时也是在学生学习了一元一次方程及其解法后的延伸，是一元一次方程的应用问题中的相遇、追及问题。

通过本节课的学习要求学生能借助“线段图”分析复杂问题中的数量关系，并利用方程解决此类问题，帮助学生从数量关系的角度更准确、清晰地描述和把握现实世界，让学生从具体的问题情境中抽象出数量关系，归纳出变化规律，并能用数学符号表示，最终解决实际问题。

体现数学知识的形成与应用过程，使学生明确方程是研究现实世界数量关系的重要数学模型，为以后学习列方程解应用题打下基础，这也正体现了数学教学前后的联系，由浅入深，由知识的掌握到能力的提升的规律。

【学情分析】本节课教学的对象是七年级4班学生，他们思想活跃，兴趣广泛，善于思考，在进行教学设计时，力争从教学内容、教学形式、教学评价中体现出趣味性和切近生活的原则。

通过教学活动，让学生自主探究、分组讨论，引导他们由浅入深、步步推进，从广度、高度和深度上开拓学生的思维，也有助于学生形成完整的知识体系。

通过微课+自学单的课前预习，从批改的情况来看，本班学生列方程的能力较弱。

在这里我根据学生的实际学情做了处理，在课件中制作了会运动的元素。

学生初学列方程解决相遇、追及问题时，可能存在以下几个方面的困难：（1）抓不准相等关系；（2）把相遇、追及关系中的数量弄反，而导致列错了方程。

还可能存在分析问题思路不同，列出方程不同，这样一来部分学生可能认为存在错误，实际不是，作为教师应鼓励学生开拓思路，只要思路正确，所列方程合理，都是正确的，让学生选择合理的思路，使得方程尽可能简单明了。

【教学目标】知识与技能：利用路程、时间、速度三者之间的关系，借助画示意图列一元一次以现实为背景的应用题。

过程与方法：运用画图直观分析。

新课标人教版七年级数学上册《一元一次方程行程问题——相遇与追及问题》教学设计一（学习版）编制人：__________________审核人：__________________审批人：__________________编制学校：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的教育资料，如教案大全、计划总结、说课评课、观察记录、特殊课程、毕业课件、班务材料、主题资料、作文大全、其他资料等等，想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this store provides various types of educational materials for everyone, such as lesson plans, plan summaries, lesson commentary, observation records, special courses, graduation coursewares, class management materials, theme materials, essay summaries, and other materials. If you want to learn about different data formats and writing methods, please pay attention!新课标人教版七年级数学上册《一元一次方程行程问题——相遇与追及问题》教学设计一学习目标：1、会用一元一次方程解决行程问题。

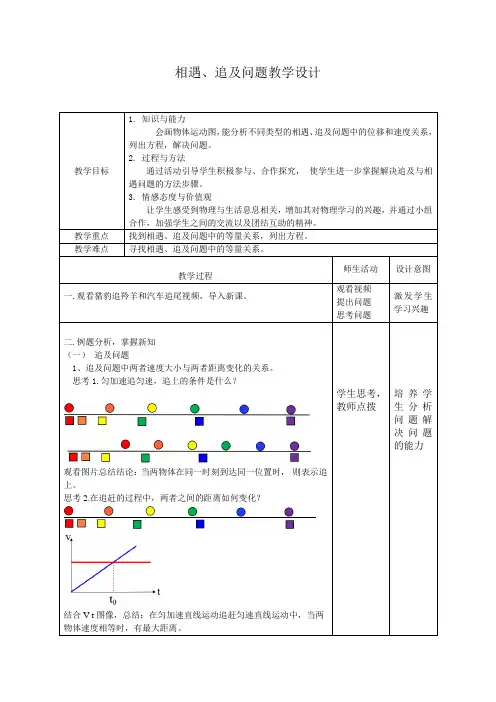
相遇、追及问题教学设计教学目标1.知识与能力会画物体运动图，能分析不同类型的相遇、追及问题中的位移和速度关系，列出方程，解决问题。

2.过程与方法通过活动引导学生积极参与、合作探究，使学生进一步掌握解决追及与相遇问题的方法步骤。

3.情感态度与价值观让学生感受到物理与生活息息相关，增加其对物理学习的兴趣，并通过小组合作，加强学生之间的交流以及团结互助的精神。

教学重点找到相遇、追及问题中的等量关系，列出方程。

教学难点寻找相遇、追及问题中的等量关系。

教学过程师生活动设计意图一.观看猎豹追羚羊和汽车追尾视频，导入新课。

观看视频提出问题思考问题激发学生学习兴趣二.例题分析，掌握新知（一）追及问题1、追及问题中两者速度大小与两者距离变化的关系。

思考1.匀加速追匀速，追上的条件是什么？观看图片总结结论：当两物体在同一时刻到达同一位置时，则表示追上。

思考2.在追赶的过程中，两者之间的距离如何变化？结合V-t图像，总结：在匀加速直线运动追赶匀速直线运动中，当两物体速度相等时，有最大距离。

学生思考，教师点拨培养学生分析问题解决问题的能力例1：一辆执勤的警车停在公路边。

当警员发现从他旁边以v0=8m/s的速度匀速行驶的货车有违章行为时，立即前去追赶。

警车以加速度a=2m/s2做匀加速运动。

试问：（1）警车要多长时间才能追上违章的货车？（2）在警车追上货车之前，两车间的最大距离是多大？总结解追及、相遇问题的思路：1.根据对两物体运动过程的分析，画出两物体运动的示意图；2.根据两物体的运动性质，分别列出两个物体的速度和位移方程，注意要将两物体运动时间的关系反映在方程中；3.由运动示意图找出两物体位移间的关联方程，这是关键；4.联立方程求解，并对结果进行简单分析．三、变式练习，巩固新知1.一辆值勤的警车停在公路边，当警员发现从他旁边以v0＝8 m/s的速度匀速行驶的货车有违章行为时，决定前去追赶，经t0＝2.5 s，警车发动起来，以加速度a＝2 m/s2做匀加速运动．试问：(1)警车要多长时间才能追上违章的货车？(2)在警车追上货车之前，两车间的最大距离是多大？（二）避免相撞问题思考1：在躲避的过程中，两者之间的距离如何变化？思考2：在躲避的过程中，如何保证两者不相撞？安排学生讲解教师总结点拨。

七年级一元一次方程行程问题的教学设计全文共四篇示例，供读者参考第一篇示例：教学设计：七年级一元一次方程行程问题一、教学目标：1. 知识与技能：学生能够掌握一元一次方程的基本概念，并能够运用这些知识解决实际问题。

2. 过程与方法：通过引导学生解决行程问题，培养学生的逻辑思维能力和数学应用能力。

3. 情感态度与价值观：激发学生对数学的兴趣和好奇心，使学生认识到数学在日常生活中的重要性，培养学生坚持不懈、勇于探索的学习态度。

二、教学内容：1. 一元一次方程的基本概念2. 一元一次方程的解法3. 行程问题的建模和解决方法三、教学过程设计：1. 导入（5分钟）教师引导学生回顾一元一次方程的概念和解法，通过简单的例子让学生了解方程的基本形式和解题步骤。

教师出示一组关于行程问题的案例，让学生分组讨论并尝试解决。

案例可以包括：小明开车去迎接朋友，两点之间距离为100公里，小明的车速是60km/h，那么小明开了几个小时？学生通过建立方程解决问题，并尝试用多种方法求解。

教师根据学生的解答情况指导学生分析问题、建立方程，并用代入、消元等方法求解方程。

教师引导学生总结解题方法和技巧。

教师出示几道类似的行程问题，让学生独立解决并进行讨论，巩固学习成果。

教师引导学生思考更复杂的行程问题，并鼓励学生用所学知识解决实际生活中的问题，如：如果小明的车速不是一定的，而是根据道路情况变化的，那么要怎么建立方程求解小明开车的时间？教师引导学生总结本节课的重点内容，并让学生展示他们的解题方法和答案。

鼓励学生对自己的学习过程进行反思，提出问题和建议。

四、教学手段：1. PPT，案例分析2. 小组讨论，合作解决问题3. 教师指导，激发学生思考4. 课堂练习，拓展应用5. 反思总结，巩固学习成果五、教学评价：1. 学生的课堂表现和解题能力2. 学生对于行程问题解决方法和建模能力的掌握情况3. 学生的自主学习能力和团队协作能力通过本节课的教学设计，希望能够激发学生的学习兴趣，加深对于一元一次方程和行程问题的理解，培养学生的数学思维能力和实际问题解决能力，为他们的数学学习打下坚实的基础。

相遇与追及问题一、学习目标1.理解相遇与追及的运动模型，掌握相遇与追及这两种情况下路程、时间、速度这三个基本量之间的关系.会利用这个关系来解决一些简单的行程问题.2.体会数形结合的数学思想方法.二、主要内容1.行程问题的基本数量关系式：路程二时间X速度；速度二路程F时间；时间二路程F速度.2．相遇问题的数量关系式：相遇路程二相遇时间X速度和；速度和二相遇路程F相遇时间；相遇时间二相遇路程F速度和.3.追及问题的数量关系式：追及距离二追及时间X速度差；速度差二追及距离F追及时间；追及时间二追及距离F速度差.4.能熟练运用路程、时间、速度这三个基本量的关系，结合图形分析，解决一些简单的行程问题.三、例题选讲例1两辆汽车同时分别从相距500千米的A,B两地出发，相向而行，速度分别为每小时40千米和每小时60千米.求几小时后两车相遇.例2甲车在乙车前200千米，同时出发，速度分别为每小时40千米与60千米.问多少小时后，乙车追上甲车.例3一辆公共汽车和一辆小轿车同时从相距598千米的两地相向而行.公共汽车每小时行40千米，小轿车每小时行52千米，问几小时后两车相距138千米？例4甲、乙两辆汽车同时从东、西两地相向开出，甲车每小时行56千米，乙车每小时行48千米，两车在离中点32千米处相遇.求东、西两地相距多少千米？例6一辆卡车和一辆摩托车同时从A、B两地相对开出，两车在途中距A地60千米处第一次相遇•然后，两车继续前进，卡车到达B地，摩托车到达A地后都立即返回，两车又在途中距B地30千米处第二次相遇.求A、B两地相距多少千米？例7甲、乙、丙三人进行100米赛跑•当甲到达终点时，乙离终点还有20米，丙离终点还有40米.如果甲、乙、丙赛跑的速度都不变，那么当乙到达终点时，丙离终点还有多远？例8小明步行上学，每分行75米，小明离家12分后，爸爸骑单车去追，每分行375米.问爸爸出发多少分后能追上小明？例9解放军某部快艇追击敌舰，追到A岛时，敌舰已逃离该岛15分钟，已测出敌舰每分钟行驶1000米，解放军快艇每分钟行驶1360米，在距离敌舰600米处可开炮射击.问解放军快艇从A岛出发经过多少分钟就可以开炮射击敌舰？例10甲、乙两人在环形跑道上以各自的不变速度跑步，如果两人同时从同地相背而行乙跑4分钟后两人第一次相遇，已知甲跑一周需6分钟，那么乙跑一周需要多少分钟？例11两名运动员在湖周围环形道上练习长跑，甲每分跑250米，乙每分跑200米，两人同时从两地同向出发，经过45分甲追上乙，如果两人同时同地反向出发，经过多少分两人相遇？例12甲、乙两人在相距90米的直路上来回跑步，甲的速度是每秒3米，乙的速度是每秒2米，如果她们同时分别从直路两端点出发，跑了6分，那么，这段时间内，两人共迎面相遇了多少次？巩固练习:1、甲、乙两站相距980千米，两列火车由两站相对开出，快车每小时行50千米，慢车每小时行多少千米，两车经10小时能相遇？2、甲车每小时行60千米，1小时后，乙车紧紧追赶，速度为每小时80千米，几小时后乙车可追上甲车？3、早晨6时，有一列货车和一列客车同时从相距360千米的甲、乙两城相对开出，中途相遇，这期间，货车停车一次60分钟，客车停车两次各30分钟，已知货车每小时行42千米，客车每小时行78千米，问两车在几点钟相遇？4、东、西两镇相距240千米，一辆客车从上午8时从东镇开往西镇，一辆货车在上午9时从西镇开往东镇，到正午12点，两车恰好在两镇间的中点相遇，如果两车都从上午8时由两地相向开出，速度不变，到上午10时，两车还相距多少千米？5、骑单车从甲地到乙地，以每小时10千米的速度行进，下午1点到，以每小时15千米的速度行进，上午11点到.如果希望中午12点到，那么应以怎样的速度行进呢？6、某人由甲地去乙地，如果他从甲地先骑摩托车行了12小时，再换骑自行车行9小时，恰好到达乙地.如果他从甲地先骑自行车行了21小时，再换骑摩托车行8小时，也恰好到达乙地.问：全程骑摩托车需要多少小时才能到达乙地？7、兄妹两人同时由家上学，哥哥每分钟走90米，妹妹每分钟走60米，哥哥到校门口时，发现忘了带课本，立即沿原路返回去取，行至离校门口180米处与妹妹相遇，他们家离学校多少米？8、兄妹两人在周长300米的圆形水池边玩.从同一地点同时背向饶水池而行.哥哥每分钟走13米，妹妹每分钟走12米.他们第5次相遇时，哥哥共走了多长的路？课后作业:1.甲以每小时4千米的速度步行去学校,乙比甲晚4小时骑自行车从同一地点出发去追甲,乙每小时行12千米,乙多少小时可追上甲？2.小张从家到公园,原打算每分钟走50米,为了提早10分钟到,他把速度加快,每分钟走75米.小张家到公园有多少米？3.父亲和儿子都在某厂工作,他们从家里出发步行到工厂,父亲用40分钟,儿子用30分钟.如果父亲比儿子早5分钟离家,问儿子用多少分钟可赶上父亲?4.解放军某部小分队,以每小时6千米的速度到某地执行任务,途中休息30分后继续前进,在出发5.5小时后,通讯员骑摩托车以56千米的速度追赶他们。

初中数学相遇追及问题教案教学目标：1. 理解相遇问题和追及问题的概念及其数学模型。

2. 学会运用一元一次方程解决相遇追及问题。

3. 提高学生分析问题、解决问题的能力。

教学重点：1. 相遇问题和追及问题的概念。

2. 一元一次方程在相遇追及问题中的应用。

教学难点：1. 相遇追及问题的数学模型的建立。

2. 灵活运用一元一次方程解决问题。

教学准备：1. 教师准备相关案例和练习题。

2. 学生准备笔记本和文具。

教学过程：Step 1：导入新课1. 教师通过生活中的实例引入相遇问题和追及问题的概念。

2. 引导学生思考如何用数学模型来描述相遇问题和追及问题。

Step 2：讲解相遇问题1. 教师讲解相遇问题的概念，如图甲乙两人从A、B两地同时出发，相向而行，在某一点C相遇。

2. 引导学生建立相遇问题的数学模型，如图甲乙两人的速度分别为v1和v2，相遇时的时间为t，A、B两地的距离为S。

Step 3：讲解追及问题1. 教师讲解追及问题的概念，如图甲乙两人从同一地点出发，甲以速度v1，乙以速度v2，甲追上乙的时间为t，甲乙之间的距离为S。

2. 引导学生建立追及问题的数学模型，如图甲乙两人的速度分别为v1和v2，追上乙的时间为t，甲乙之间的距离为S。

Step 4：运用一元一次方程解决问题1. 教师引导学生分析相遇追及问题中已知量和未知量。

2. 引导学生运用一元一次方程解决问题，如图甲乙两人相遇问题中，已知A、B两地的距离S，甲乙两人的速度v1和v2，求相遇时间t。

Step 5：巩固练习1. 教师出示练习题，让学生独立解决。

2. 教师选取部分学生的答案进行讲解和分析。

Step 6：课堂小结1. 教师引导学生总结相遇问题和追及问题的解题步骤。

2. 强调灵活运用一元一次方程解决问题的重要性。

Step 7：作业布置1. 教师布置课后作业，让学生巩固所学知识。

教学反思：本节课通过实例引入相遇问题和追及问题的概念，引导学生建立数学模型，运用一元一次方程解决问题。

相遇、追及问题教学设计教学目标 1.知识与能力: 会画线段图，能分析不同类型的相遇、追及问题中的相等关系，列出一元一次方程解应用题。

2.过程与方法:通过数学活动引导学生积极参与、合作探究， 使学生进一步掌握用一元一次方程解决实际问题的方法步骤。

3.情感态度与价值观: 让学生感受到数学与生活息息相关，增加其对数学学习的兴趣，并通过小组合作，加强学生之间的交流以及团结互助的精神。

教学重点 找到相遇、追及问题中的等量关系，列出一元一次方程。

教学难点寻找相遇、追及问题中的等量关系。

教学过程（师生活动）一.创设情境，导入新课。

1、A 、B 两车分别从相距S 千米的甲、乙两地同时出发，相向而行，两车会相遇吗？2、如果两车相遇，则相遇时两车所走的路程与A 、B 两地的距离有什么关系？3、如果两车同向而行，B 车先出发a 小时，在什么情况下两车能相遇？为什么？4、如果A 车能追上B 车，你能画出线段图吗？二.例题分析，掌握新知例1、、A 、B 两车分别停靠在相距240千米的甲、乙两地，甲车每小时行50千米，乙车每小时行30千米。

（1）若两车同时相向而行，请问B 车行了多长时间后与A 车相遇？A 的路程＋B 的路程=相距路程解：设B 走x 小时后与A 车相遇，根据题意列方程得50x+30x=240解得 x=3答：行走3小时后两车相遇。

（2） 若两车同时出发，相向而行，请问行走多长时间后两车相距80米？A 的路程＋B 的路程＋80米=相距路程 A 的路程＋B 的路程-80米=相距路程解：设行走x 小时后两车相距80米，①相遇前相距80米50x+30x+80=240解得 x=2 A B 体育馆教学楼 A B 甲 乙 80米 A B 80米甲乙②相遇后相距80米50x+30x-80=240解得 x=4答：行走2小时/4小时后两人相距80千米。

（1）若两车同时出发，同向而行，请问行走多长时间后A追上B？A B甲乙A的路程-B的路程=相距路程解：设行走x小时后A追上B，根据题意列方程得50x-30x=240解得 x=12答：行走12小时后A追上B。

用一元一次方程解行程问题一、教学目标1、在解决行程问题的过程中，进一步掌握列一元一次方程解简单应用题的方法和步骤。

2、能正确的分析问题，从问题中寻找已知量和未知量之间的数量关系。

3、提高分析问题和解决问题的能力。

4．初步养成正确思考问题的良好习惯。

二、重点：能正确的分析问题。

难点：从问题中寻找已知量和未知量之间的数量关系。

三、教学过程课前预习1、还记得小学学过的行程问题中的路程、时间和速度三个量之间关系吗？2、若小明每秒跑4米，那么他5秒能跑_____米。

3、、小明用4分钟绕学校操场跑了两圈(每圈400米)，那么他的速度为_____米/分。

4、已知小明家距离火车站1500米，他以4米/秒的速度骑车到达车站需要_____分钟。

5、汽车每小时行驶m千米，则n小时行驶了千米。

6、汽车匀速行驶，x小时行驶了m千米，则汽车的平均速度为千米/时。

例1、小明每天早上要在7：50之前赶到距家1000米的学校上学。

小明以80米/分的速度出发，5分后，小明的爸爸发现他忘了带语文书。

于是，爸爸立即以180米/分的速度去追小明，并且在途中追上了他。

（1）爸爸追上小明用了多长时间？（2）追上小明时，距离学校还有多远？2、两匹马赛跑，黄色马的速度是6m/s，棕色马的速度是7m/s，如果让黄马先跑5m，棕色马再开始跑，几秒后可以追上黄色马？追及问题的基本题型1、不同地点同时出发2、同地点不同时出发追及问题的等量关系1、追及时快者行驶的路程－慢者行驶的路程＝相距的路程2、追及时快者行驶的路程＝慢者行驶的路程或慢者所用时间=快者所用时间+多用时间随堂练习1、小彬和小明每天早晨坚持跑步，小彬每秒跑4米，小明每秒跑6米.如果小明站在百米跑道的起点处，小彬站在他前面10米处，两人同时同向起跑，几秒后小明能追上小彬？2、小王、叔叔在400米长的环形跑道上练习跑步，小王每秒跑5米，叔叔每秒跑7.5米。

（1）若两人同时同地同向出发，多长时间两人首次相遇？等量关系甲行的路程-乙行的路程=400米（2）若两人同时同地反向出发，多长时间两人首次相遇？等量关系甲行的路程+乙行的路程=400米课堂小结列一元一次方程解实际问题的一般步骤1、审：审题，分析题中已知什么、求什么，明确各数量之间的关系2、设：设未知数（直接设法、间接设法）3、找：找出能够表示题中全部含义的一个等量关系4、列：根据等量关系列出方程5、解：解所列出的方程，求出未知数的值6、验：是否所列方程的解，是否符合实际意义7、答：检验所求的解是否符合题意，在写出答案课堂检测甲，乙两地相距162千米，甲地有一辆货车，速度为每小时48千米，乙地有一辆客车，速度为每小时60千米，若两车同时相向而行，货车在路上耽误了半小时，多长时间客车可以追上货车？作业P125 练习3题（2）。

七年级上册数学行程问题教案
一、教学目标
1. 让学生理解行程问题的基本结构，掌握速度、时间和距离之间的关系。

2. 学生能够运用基本关系解决简单的行程问题。

3. 培养学生的逻辑思维和问题解决能力。

4. 激发学生的数学兴趣，培养他们良好的数学学习习惯。

二、教学内容
1. 行程问题的基本概念：速度、时间、距离。

2. 速度、时间、距离之间的关系：速度 = 距离 / 时间，距离 = 速度× 时间，时间 = 距离 / 速度。

3. 简单的行程问题：相遇问题、追及问题、过桥问题等。

三、教学难点与重点
1. 重点：速度、时间、距离之间的关系。

2. 难点：如何运用这些关系解决复杂的行程问题。

四、教具和多媒体资源
1. 黑板
2. 投影仪与PPT课件
3. 教学软件：几何画板等动态演示工具
五、教学方法
1. 激活学生的前知：回顾速度、时间、距离的基本概念。

2. 教学策略：采用讲解与示范相结合的方法，配合实例和练习题进行讲解，引导学生观察、思考和讨论。

3. 学生活动：小组讨论，解答练习题，分享解题思路。

六、教学过程
1. 导入：故事导入，讲述一个与行程问题有关的有趣故事，激发学生的兴趣。

2. 讲授新课：通过实例和图示，详细讲解速度、时间、距离的关系，以及各种行程问题的解决方法。

3. 巩固练习：提供几道典型的行程问题，让学生运用所学知识进行解答，并引导他们分享解题思路。

4. 归纳小结：总结本节课的重点内容，强调行程问题的解决方法。

七年级上册数学行程问题-相遇与追及问
题-教学设计--上课用
一元一次方程模型在行程问题中的应用
本文将介绍一元一次方程模型在行程问题中的应用，重点是相遇和追及问题的解决方法。

通过“线段图”分析数量关系，建立方程解决问题。

教学目标是让学生进一步领会代数方法解应用题的优越性，培养实事求是的态度及与人合作交流的能力，逐步树立客服困难的信心、意志力，培养学生研究数学的热情和良好的人格品质。

在教学过程中，教师采用引导法、分析法、小组讨论法等教学方法，多媒体辅助教学手段。

首先，回顾速度、路程、时间之间的关系，让学生复基础知识。

接着，通过实例演示相遇问题和追及问题的解决方法，引导学生找到等量关系，建立方程解决问题。

同时，教师鼓励学生自主思考，提高观察、思考和归纳总结的能力。

在相遇问题中，教师通过动画演示两车相遇情况，让学生自己找出等量关系解决问题，培养学生的观察、思考能力。

在追及问题中，教师引导学生找到快车和慢车之间的关系式，让学生自己解决问题，提高学生的自主研究能力。

通过本教学设计，学生能够掌握相遇、追及问题的解题规律，学会解决环形跑道问题。

同时，培养学生实事求是的态度及与人合作交流的能力，逐步树立客服困难的信心、意志力，培养学生研究数学的热情和良好的人格品质。

初中数学行程问题说课教案1. 让学生掌握行程问题的基本概念和公式，包括路程、速度、时间的关系。

2. 培养学生解决行程问题的能力，提高学生的逻辑思维和数学应用能力。

3. 培养学生合作学习、讨论问题的良好习惯，提高学生的沟通表达能力。

二、教学内容1. 行程问题的基本概念：路程、速度、时间。

2. 行程问题的基本公式：路程=速度×时间，速度=路程÷时间，时间=路程÷速度。

3. 行程问题的类型及解决方法：单人单程、单人往返、多人相遇、追及等问题。

4. 典型例题解析及练习。

三、教学过程1. 导入：通过生活中的实际例子，如上学、旅游等，引发学生对行程问题的关注，激发学生的学习兴趣。

2. 基本概念和公式：介绍路程、速度、时间的定义及它们之间的关系，引导学生理解和记忆行程问题的基本公式。

3. 行程问题的类型及解决方法：讲解单人单程、单人往返、多人相遇、追及等类型的行程问题，引导学生掌握解决行程问题的方法。

4. 典型例题解析：选取具有代表性的例题，引导学生分析问题、列方程、解方程，最后得出答案。

过程中注意引导学生思考、讨论，培养学生的逻辑思维和数学应用能力。

5. 练习：布置一些类似的练习题，让学生独立完成，检验学生对行程问题的掌握程度。

6. 总结：对本节课的内容进行总结，强调行程问题的解决方法及注意事项。

7. 拓展：引导学生思考行程问题在现实生活中的应用，激发学生学习兴趣，提高学生的数学应用能力。

四、教学策略1. 采用讲解、示范、练习、讨论等多种教学方法，激发学生的学习兴趣，提高学生的参与度。

2. 注重学生的主体地位，鼓励学生提问、思考、讨论，培养学生的逻辑思维和数学应用能力。

3. 针对不同学生的学习情况，给予个性化的指导，帮助学生克服困难，提高学生的学习效果。

4. 及时反馈，鼓励学生自主检查，培养学生的自我管理能力。

五、教学评价1. 学生对行程问题的基本概念和公式的掌握程度。

2. 学生解决行程问题的能力，包括逻辑思维、数学应用能力。

《3.3.3追及问题》教学设计教学目标：知识方面：1、能通过分析题意理解追击问题中存在的等量关系,2、会利用一元一次方程的知识解决行程问题中的----追及问题.过程与方法：根据行程问题的特点，借助线段图将问题中研究对象的行进过程以图示的形式呈现出来，培养学生的逻辑思维能力和综合运用知识解决实际问题的能力情感态度与价值观：通过学生积极参与，激发学生学习数学的兴趣，体验数学的探索与创造的快乐，养成动手、动脑的好习惯。

教学重点：一元一次方程追及问题；教学难点：发现并理解追及问题中的等量关系。

教学过程：一、情景引入教师课件展示动画视频出示问题：光头强带着嘟嘟在飞艇前方5400米的地方,发现有歹徒追来,马上以220米/秒的速度快速逃离,歹徒以340米/秒的速度紧紧追赶.你能帮忙算算熊大熊二至少需要在多长时间内拦截到歹徒才能帮助光头强吗?引出本节课的课题及学习目标。

二、教学过程（一）复习回顾提问：行程问题中路程、时间、速度三者之间的关系学生回答：路程=速度×时间（二）学习追击问题类型一：同地出发不同时1、出示问题：小明每天早上要在7:30分之前到校上学.一天,小明以80米/分的速度出发去上学,5分钟后,小明的爸爸发现他忘了带数学书.于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他,问爸爸追上小明用了多长时间?教师依次提出问题：1、这个问题中有哪些已知条件？2、这个题目中存在哪些等量关系？3、如何设未知数？怎么样列方程？学生回答后，教师展示课件进行点拨明确等量关系：1）小明走的路程= 爸爸走的路程2）小明被追所用时间= 爸爸追赶所用时间（学生尝试列出方程，解决问题）2、小试牛刀:甲乙两人登一座山，甲每分登高10米，并且先出发30分。

乙每分登高15米，两人同时登上山顶。

甲用多少时间登山？这山有多高？(学生独立完成，教师巡视，一名学生板演，教师讲解点评)3、能力挑战周末,家住设计院的小兵和他的爸爸一起,去盛世龙城看姥姥。

选自行车为参照物，则从开始运动到两车相距最远过程中，以汽
车相对地面的运动方向为正方向，汽车相对此参照物的各个物理
量的分别为：v0=-6m/s，a=3m/s2，v=0
对汽车由公式 vv0 at
tvv0 0(6)2s
a
3
由v2 v02 2ax
xv2v0 20(6)2m6m 2a 23
以自行车为参照物, 公式中的各个量都 应是相对于自行车 的.注意：物理量的 正负号.
当t=t0两物体速度相等时： ①若Δx=x0，则恰能追及,且两 物体只能相遇一次。
这也是甲乙避碰的临界条件。
②若Δx<x0,则不能追及。 此时两物体最小距离为x0-Δx ③若Δx>x0,则相遇两次。 其中相遇时刻t1和t2由下列方程 求出：
x甲=x0+x乙
练习两辆完全相同的汽车，沿水平直路一前一后以相
2a1 21.5
x2=
v2 2
102
m =100 m
2a2 20.5
x=x1+x2=175 m 两车需在相隔175 m处刹车才不相碰.
2、考虑反应时间的避碰
例5.为了安全,在公路上行驶的汽车之间应保持必要的距离. 已知某高速公路的最高限速为120 km/h。假设前方车辆突 然停止,后车司机从发现这一情况开始，经操纵刹车到汽车 开始减速所经历的时间为(即反应时间)t=0.5 s,刹车时汽车加 速度为4 m/s2.则该段高速公路上汽车间应保持的最小距离 是多少
①t=t0以前,两物体间距离增 大
②t=t0时,两物体相距最 远为x0+Δx ③t=t0以后,甲物体比乙物体 快，两者间距减小
④只能相遇一次，相遇时刻 由方程求出：
x甲=x乙+x0

4.针对本节课所学内容，每位学生撰写一篇学习心得，总结自己在解决行程问题方面的收获和不足，并提出改进措施。
5.预习下一节课内容，了解速度、时间和路程在几何图形中的应用，为课堂学习做好准备。
作业要求：
1.作业应在规定时间内完成，确保作业质量。
2.学生应独立思考，尽量自己解决问题，遇到困难时可向同学和老师请教。
4.各小组汇报讨论成果，分享解题过程和经验，互相学习，共同提高。
5.教师点评各小组的表现，总结讨论过程中的优点和不足，为后续学习提供指导。
（四）课堂练习，500字
1.教师设计具有代表性的练习题，涵盖不同难度的行程问题，让学生独立完成。
2.学生在规定时间内完成练习题，教师巡回检查，了解学生的掌握情况。
4.小组合作，交流分享
-组织学生进行小组合作，共同探讨行程生分享解题思路和经验，互相学习，共同进步。
5.课堂小结，巩固提升
-通过课堂小结，帮助学生梳理所学知识，巩固重点，提高学习效果。
-设计富有挑战性的课后作业，激发学生的探究欲望，培养他们的自主学习能力。
4.翻转课堂：利用信息技术手段，将课堂变为学生展示、讨论和解决问题的场所，提高学生的学习积极性和自主性。
5.素质评价：注重过程性评价，关注学生在学习过程中的表现，激发他们的内在学习动机。
（三）情感态度与价值观
1.培养学生对数学学习的兴趣，使他们体会到数学在生活中的重要性。
2.培养学生勇于面对困难、敢于挑战的精神，使他们具备解决问题的信心和能力。
2.强调行程问题在实际生活中的应用，激发学生学习数学的兴趣。
3.鼓励学生提出疑问，解答他们的困惑，巩固所学知识。
4.布置课后作业，要求学生运用所学知识解决实际问题，提高他们的自主学习能力。