05第5讲 图论模型

图论模型此模型解决的是垃圾清运路线的最佳方案。

1、收集路线方案：用中国邮递员问题解决达到最佳经济效益和环保效果的垃圾清运路线问题是在车辆限载约束条件下的最优路径选择的问题，同时本项目涉及到深圳市南山区38个垃圾中转站，而每个中转站所覆盖的收集区域的选取需要满足最大覆盖域（即总体能够消耗最少资源来覆盖整片区域），收集区域的划分又要同时考虑实地情况（地形、路线、用地性质、人流量、垃圾量等）。

1.1模型建立：为简化问题讨论，在转运站覆盖区域的划分的问题上，需要运用“最大覆盖”及“模糊划分”的思想，具体划分出每个转运站所对应 的片区的近似最优划分。

将问题简化后，所要求解的问题就是每个垃圾中转站所对应的每个小分区的街道所构成的收集网络的垃圾收运车辆优化路线的问题，也就是要求每一条街道至少有一辆垃圾收运车经过并且车辆重复走过的街道的总长度最小化的问题。

对于这个问题，我们采用图论模型，将每个小分区的街道及收集点简化成网络图（也叫赋权图）。

对于网络图中的圈用圈点来表示，计算各个圈点的垃圾量（也即围成圈的街道上的垃圾量的和），将相邻（有公共顶点）的圈点用线连接起来，这就构成了圈点图。

遵循以垃圾中转站为圆心沿径向发散求最小生成树的原则将圈点图中相邻的圈点组块，使得每块的垃圾量近似于垃圾收运车载限，对应于圈点分块，网络图分开成了各个子网络图，对于每一个子网络图即可利用欧拉回路求得其最小路径线路。

现在给出最短欧拉回路求解举例：图代表的是其中一个收集子网络图，其中直线表示车辆需要经过的街道，线上的数字表示该街道的长度，该子网络图各条街道的垃圾量之和近似于收集车辆的载限。

现要求的是车辆经过每一条街道至少一次的最短回路，现在对这个问题分步求解：第一步：找出图中的奇点，如图中橙色小圆点所在处为奇点。

第二步：将各对奇点沿街道连接起来，使得连接奇点的所有街道总长度最小。

如下图绿色线条：第三步：得出经过每条街道至少一次的最短路径长度为所有街道的总长加上连接奇点的街道的长度。

各种图论模型及其解答摘要：本文用另一种思路重新组织《图论及其应用》相关知识。

首先，用通俗化语言阐述了如何对事物间联系的问题进行图论建模；接着从现实例子出发，给出各种典型图论模型，每种图论模型对应于图论一个重要内容；再者，介绍相关知识对上述提到的图论模型涉及的问题进行解答；最后，补充一些图论其他知识，包括图论分支、易混概念。

符号约定：Q(Question)表示对问题描述，M(Modeling)表示数学建模过程，A(Answer)表示原问题转化为何种图论问题。

一、引言图论是研究点、线间关系的一门学科，属于应用数学的一部分。

现实生活中，凡是涉及到事物间的关系，都可以抽象为图论模型。

点表示事物，连线表示事物间的联系。

整个求解过程如下：原问题——>图论建模——>运用图论相关理论求解——>转化为原问题的解整个过程关键在于图论建模，所谓图论建模，就是明确点表示什么，连线表示什么，原问题转化为图论中的什么问题。

存在以下两种情况：①若事物间联系是可逆的(比如双行道，朋友)，则抽象成无向图②若事物间联系是不可逆的(比如单行道，状态转化不可逆)，则抽象成有向图如果需要进一步刻画事物间的联系（比如城市间的距离），就给连线赋一个权值，从而抽象成赋值图。

综上，根据实际问题，可建模成下列图论模型的一种：无向赋权图、有向赋权图、无向非赋权图、有向非赋权图。

例1.宴会定理：任何一宴会中，一定存在两个人有相同的数量朋友M：点表示人，连线表示当且仅当该两个人是朋友A：问题转化为任何一个图一定存在两个顶点的度相等二、图论模型接下来介绍若干典型的图论模型，每种模型几乎对应于图论的一个重要内容，这些内容将在第三章进行讨论，也就给出了这些模型的解答思路。

2.1 偶图模型凡涉及两类事物间的联系（即只考虑两类事物间的联系，而不考虑同类事物间的联系），均可抽象成偶图模型。

作图时，将两类事物分成两行或者两列。

这类模型通常被包含在后续的模型中，但因许多现实问题可抽象成该模型，所以单列出来讨论。

图论模型图是为了解决一些具体问题而产生的模型，这可以从它的发源“哥尼斯堡的七桥问题”看到。

一个图表示了某些对象集合元素之间的关系，所以它被广泛用来作为许多与对象的离散安排有关问题的模型。

它已在物理、化学、经济、管理、信息、控制等所有离散系统中应用。

本章仅介绍几类图论模型。

9.1 连线问题一、问题的背景与提出现实社会中，我们可以看到，公路、铁路、通信、输电线路等的建设中，都涉及到“如何设计建造一个既能畅通无阻又造价小的网络”问题，即连线问题。

二、模型假设与符号说明假设要建造一个连接若干城镇的通信网络，第i个城镇与第j个城镇之间直通线路的造价为cij。

三、模型的建立与求解把每个城镇看作是一个点v；两个城镇直通线路看作边e；城镇vi与城镇vj之间直通线路的造价看作边vivj的权w(vivj)=cij，这样我们得到了一个赋权图G。

设计一个总造价最小的通信网络，就转化为：在赋权图G，找出具有最小权的连通生成子图，即寻找赋权图的最小权的生成树（最优数）。

1956年Kruskal给出了一种求最优树的算法，称为避圈法，算法如下： 10 选择边e1，使得w(e1)尽可能小；20 若已选定边e1, e2, …, ei, 则从边集E\{e1, e2, …, ei}中选取ei+1，使（ⅰ）G[{e1, e2, …, ei+1}]为无圈图；（ⅱ）w(ei+1)是满足（ⅰ）的尽可能小的权， 30 当20不能继续执行时停止。

对于p个点ε条的赋权图G，该算法就是先将赋权图的边按权的递增顺序排列：a1, a2, …, aε设e1=a1, e2=a2, 检查a3，如果a3与e1, e2不构成圈，则令e3=a3，否则放弃a3，检查a4，1。

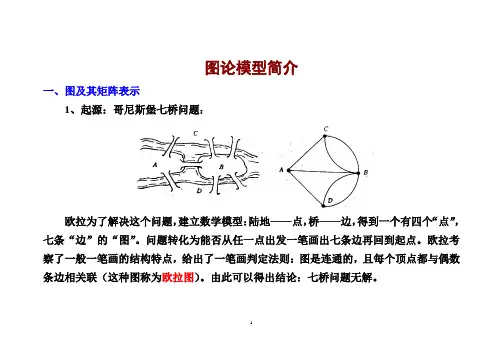
图论模型简介一、图及其矩阵表示1、起源：哥尼斯堡七桥问题：欧拉为了解决这个问题，建立数学模型：陆地——点，桥——边，得到一个有四个“点”，七条“边”的“图”。

问题转化为能否从任一点出发一笔画出七条边再回到起点。

欧拉考察了一般一笔画的结构特点，给出了一笔画判定法则：图是连通的，且每个顶点都与偶数条边相关联（这种图称为欧拉图）。

由此可以得出结论：七桥问题无解。

2、基本概念：图（graph）：由顶点和边（又称线，边的两端必须是顶点）组成的一个结构。

邻接：一条边的两个端点称是邻接的；关联：边与其两端的顶点称是关联的。

无向图（graph）：边无方向的图；有向图（digraph）：边有方向的图。

路(path)：由相邻边组成的序列，其中中间顶点互不相同。

圈(cycle)：首、尾顶点相同的路，即闭路。

连通图（connected graph）：图中任意两顶点间都存在路的图。

树（tree）：无圈连通图完全图（complete graph）：任意两个顶点之间都有边相连的无向图，记为K n。

竞赛图（tournament）：由完全图给每条边定向而得到的有向图。

二部图（bipartite graph）：图的顶点分成两部分，只有不同部分顶点之间才有边相连。

图G的子图H（subgraph）：H是一个图，H的顶点（边）是图G的顶点（边）。

网络（Network）：边上赋了权的有向图。

3、图的矩阵表示无向图 有向图01000101100101101100010⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦ ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡011101000001001000001104、著名的图论问题例1 最短路问题（shortest path problem）出租车司机要从城市甲地到乙地，在纵横交错的路中如何选择一条最短的路线？例2 最小生成树问题（minimum-weight spanning tree problem）为了给小山村的居民送电，每户立了一根电杆，怎样连接可使连线最短？例3 中国邮递员问题（chinese postman problem）一名邮递员负责投递某个街区的邮件。

第七部分图论方法第十六章图论模型图论是应用数学的一个分支，它的概念和结果来源非常广泛，最早起源于一些数学游戏的难题研究，如欧拉所解决的哥尼斯堡七桥问题，以及在民间广泛流传的一些游戏难题，如迷宫问题、博弈问题、棋盘上马的行走路线问题等．这些古老的难题，当时吸引了很多学者的注意．在这些问题研究的基础上又继续提出了著名的四色猜想和汉米尔顿（环游世界）数学难题．1847年，图论应用于分析电路网络，这是它最早应用于工程科学，以后随着科学的发展，图论在解决运筹学，网络理论，信息论，控制论，博弈论以及计算机科学等各个领域的问题时，发挥出越来越大的作用．在实践中，图论已成为解决自然科学、工程技术、社会科学、军事等领域中许多问题的有力工具之一，图论模型属于离散类数学模型，是数学模型中比较容易为学生接受的一类模型，具有直观性、趣味性和简洁性，深得大学生的青睐。

另外，图论模型属于较为近代的前沿性数学知识，又具有强烈的，易于为学生接受的数学建模味道，对于培养学生通过建模解决实际问题的能力与学习兴趣都是不可多得的知识内容，因此越来越受到数学家和建模工作者的喜爱．我们所学的这一章只是介绍一些基本概念、原理以及一些典型的应用实例，目的是在今后的学习研究时，可以把图论的基本知识、方法作为工具．本章先介绍图论的基本概念，然后通过哥尼斯堡七桥问题、最短路径问题、中国邮递员问题、人员分派问题、稳定匹配问题、竞赛图等例子介绍图论的具体应用。

16.1 图的基本概念图是一个有序对<V，E>，V是结点集，E是边集，以表示结点数目，表示边的数目，则当∣V∣和∣E∣有限时，<V,E>称为有限图；否则称无限图.无向边, 与无序结点对(v, u)相关联的边；有向边，与有序结点对<v, u>相关联的边；无向图，每条边都是无向边的图，记作G＝<V,E>; 有向图，每条边都是有向边的图，记作D＝<V,E>.混合图，既有有向边，也有无向边的图.平凡图，仅有一个结点的图；零图，边集为空集的图<V, ∅>，即仅有结点的图.自回路(环)，关联于同一个结点的边.无向平行边，联结相同两个结点的多于1条的无向边；有向平行边，联结两个结点之间的多于1条且方向相同的有向边.简单图，不含平行边和自回路的图.在有向图D＝<V,E>中，以v(∈V)为起点的边之条数为出度deg＋(v)；以v(∈V)为终点的边之条数为入度deg－(v).在无向图G＝<V,E>中，与结点v(∈V)关联的边数，即为结点度数deg(v)或d(v).；在有向图中，结点v的出度和入度之和为度数.最大度数，∆(G)＝max{deg(v)∣v∈V}；最小度数，δ(G)=min{deg(v)∣v∈V}有n个结点的且每对结点都有边相连的无向简单图，称为无向完全图.此时有)1(21-=n n E ；有n 个结点的且每对结点之间都有两条方向相反的边相连的有向简单图为有向完全图. 此时有)1(-=n n E 。

图论模型图论是运筹学的一个经典和重要分支，专门研究图与网络模型的特点、性质以及求解方法。

许多优化问题，可以利用图与网络的固有特性而形成的特定方法来解决，比用数学规划等其他模型来求解往往要简单且有效得多。

图论起源于1736年欧拉对柯尼斯堡七桥问题的抽象和论证。

1936年，匈牙利数学家柯尼希（D. Kӧnig ）出版的第一部图论专著《有限图与无限图理论》，树立了图论发展的第一座里程碑。

近几十年来，计算机科学和技术的飞速发展，大大地促进了图论研究和应用，其理论和方法已经渗透到物理、化学、计算机科学、通信科学、建筑学、生物遗传学、心理学、经济学、社会学各个学科中。

9.1 图的基础理论9.1.1 图的基本概念所谓图，概括地讲就是由一些点和这些点之间的连线组成的。

定义为(,)G V E =，V 是顶点的非空有限集合，称为顶点集。

E 是边的集合，称为边集。

边一般用(,)i j v v 表示，其中,i j v v 属于顶点集V 。

以下用V 表示图(,)G V E =中顶点的个数，E 表示边的条数。

如图9.1是几个图的示例，其中图9.1 (a)共有3个顶点、2条边，将其表示为(,)G V E =，123{,,}V v v v =，1213{(,),(,)}E v v v v =.23v 45v 34(a)(c)图9.1 图的示意图1.无向图和有向图如果图的边是没有方向的，则称此图为无向图（简称为图），无向图的边称为无向边（简称边）。

如图9.1 (a)和(b)都是无向图。

连接两顶点i v 和j v 的无向边记为(,)i j v v 或(,)j i v v 。

如果图的边是有方向（带箭头）的，则称此图为有向图，有向图的边称为弧（或有向边），如图9.1 (c)是一个有向图。

连接两顶点i v 和j v 的弧记为,i j v v 〈〉，其中i v 称为起点，j v 称为终点。

显然此时弧,i j v v 〈〉与弧,j i v v 〈〉是不同的两条有向边。