chapt5-2-清华大学半导体物理

极低温时，杂质基本没电离，到NC >0.11N D，p D=N D/3，进入中等电离区。

（图3.3N复习：分析只含受主杂质的型半导体的p 和E 随温度的变化。

iF E E =多重电杂质的统计与补偿通常，多重电杂质一般在半导体中形成深能级，它们对半导体导电能力的影响表现在对相反类型的浅能级杂质的补偿上。

多重电杂质的统计多重电杂质——不仅能量相同的不同状态的电子态不独立，而且引入的多重能级也不是独立的。

杂质处于某种荷电状态，起作用的是某一、二个相关能级。

随着杂质荷电状态改变，起作用的能级发生变化。

电子在杂质能级上的占据几率采用吉布斯统计。

Au在Ge中的施主能级E D的电离能很大，是深施主。

起施主作用的温度高，本征激发已不可忽略（不仅如此…….）。

因此不能直接测量，需要采用掺入浅受主补偿的办法。

N D；N AAu 在Ge 中的其它能级：E A1位于E i 之下，视为浅受主，由ln p 0～1/T 关系求ΔE A1E A2 和E A3是深受主能级，电离能采用掺入浅施主杂质的办法求出（n 型导电）。

请同学自己分析如何得到E A2 和E A3⎠⎝，发生简并（确定的掺杂浓度）的温度上、下限的含义：下限：温度低，载流子浓度不够大；上限：温度过高，态密度升高更快。

泡利原理不起作用，仍然可以用玻尔兹曼分布。

以χ=0为简并化条件Si：m dn=0.1m0，ΔE D =0.04eV，N dmin∼1020/cm3Ge：m dn=0.55m0，ΔE D =0.01eV，N dmin∼1018/cm3 GaAs：m dn=0.068m0，ΔE D =0.01eV，N dmin∼1016/cm3InSb：窄E g，m dn/m dp∼32，E i接近E C(如400K，E i≈E C，较低温度下，本征InSb也会发生简并。

总结态密度费米分布和玻尔兹曼分布非简并半导体的载流子浓度本征载流子浓度只含一种杂质的情形杂质补偿情况简并半导体(掺杂浓度很高时)练习题:一块补偿的p型Si，1，低温弱电离时的电中性条件是_________________；2，杂质强电离、本征激发可以忽略时的电中性条件是__________________；3，温度升高，本征激发不可忽略时，电中性条件是__________________；4，温度进一步升高，Si处于本征时，电中性条件是__________________；作业：3.13.2（低温弱电离）3.3（强电离）3.43.5说明：为什么Si器件比Ge器件的工作温度高？。

清华大学831半导体物理、器件及集成电路考研参考书目、考研真题、复试分数线831半导体物理、器件及集成电路课程介绍研究半导体原子状态和电子状态以及各种半导体器件内部电子过程的学科。

是固体物理学的一个分支。

研究半导体中的原子状态是以晶体结构学和点阵动力学为基础，主要研究半导体的晶体结构、晶体生长，以及晶体中的杂质和各种类型的缺陷。

研究半导体中的电子状态是以固体电子论和能带理论为基础，主要研究半导体的电子状态，半导体的光电和热电效应、半导体的表面结构和性质、半导体与金属或不同类型半导体接触时界面的性质和所发生的过程、各种半导体器件的作用机理和制造工艺等。

半导体物理学的发展不仅使人们对半导体有了深入的了解，而且由此而产生的各种半导体器件、集成电路和半导体激光器等已得到广泛的应用。

典型的半导体主要是由共价键结合的晶体。

如硅、锗的晶体具有半导体物理学金刚石结构（图1），Ⅲ-Ⅴ化合物以及一些Ⅲ-Ⅵ化合物具有闪锌矿结构（图2）或纤锌矿结构（图3）。

这些都是最典型的共价键结合的晶体结构，其中每个原子由四个共价键与近邻原子相结合。

能带的概念组成共价键的价电子呈现出相对集中于近邻原子之间的空间分布，它们同时又是运动于晶体中的共有电子，具有典型的连续能量分布（图4）就是由X射线电子谱所测的硅中价电子的能量分布）。

按照固体的能带理论，晶体中的电子态分属于若干能带，每个能带包含能量连续分布的2N个电子态（计入自旋），N代表晶体包含的元胞总数。

上述价电子的能量分布实际上包含着几个部分相互重叠的能带，它们正好被晶体中的价电子所填满，统称为价带。

原理能带中的电子态是用一个波数矢k标志的，它的意义近似于一个自由电子的德布罗意波的波数。

为了展示能带中的电子态，往往采用以k为坐标的“k空间”，k空间中的一点表示一个电子态(不计自旋),k的取值限于环绕原点的一个具有晶体对称性的多面体区域，称为布里渊区。

图5表示半导体物理学金刚石(或闪锌矿)晶体的布里渊区。

第一章习题1．设晶格常数为a 的一维晶格，导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为：E c =0220122021202236)(,)(3m k h m k h k E m k k h m k h V -=-+ 0m 。

试求：为电子惯性质量，nm a ak 314.0,1==π（1）禁带宽度;（2） 导带底电子有效质量; （3）价带顶电子有效质量;（4）价带顶电子跃迁到导带底时准动量的变化 解：（1）eV m k E k E E E k m dk E d k m kdk dE Ec k k m m m dk E d k k m k k m k V C g V V V c 64.012)0()43(0,060064338232430)(2320212102220202020222101202==-==<-===-==>=+===-+ 因此：取极大值处，所以又因为得价带：取极小值处，所以：在又因为：得：由导带：043222*83)2(1m dk E d mk k C nC===sN k k k p k p m dk E d mk k k k V nV/1095.7043)()()4(6)3(25104300222*11-===⨯=-=-=∆=-== 所以：准动量的定义：2. 晶格常数为0.25nm 的一维晶格，当外加102V/m ，107 V/m 的电场时，试分别计算电子自能带底运动到能带顶所需的时间。

解：根据：tkhqE f ∆∆== 得qE k t -∆=∆sat sat 137192821911027.810106.1)0(1027.810106.1)0(----⨯=⨯⨯--=∆⨯=⨯⨯--=∆ππ第三章习题和答案1. 计算能量在E=E c 到2*n 2C L 2m 100E E π+= 之间单位体积中的量子态数。

解322233*28100E 21233*22100E 0021233*231000L 8100)(3222)(22)(1Z VZZ )(Z )(22)(2322C 22C L E m h E E E m V dE E E m V dE E g V d dEE g d E E m V E g c nc C n l m h E C n l m E C n n c n c πππππ=+-=-====-=*++⎰⎰**）（）（单位体积内的量子态数）（2. 试证明实际硅、锗中导带底附近状态密度公式为式（3-6）。

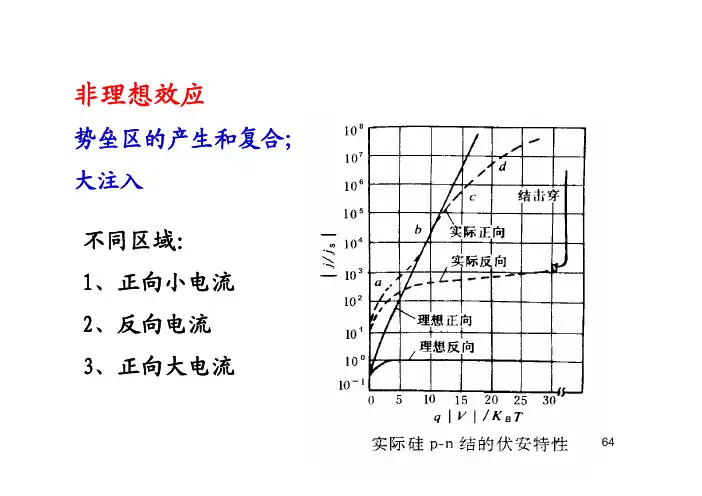
64非理想效应势垒区的产生和复合；大注入不同区域：1、正向小电流2、反向电流3、正向大电流66势垒区中的复合、产生电流与扩散区中的复合、产生电流性质相同，只是地点不同。

pn 结正向电流= 少子扩散流+ 势垒区复合电流。

pn 结反向电流= 少子扩散流+ 势垒区产生电流。

73§6.2.3 大注入下的正向伏安特性大注入：注入的少子浓度≥被注入区的多子浓度。

以p +n 结为例，（p +n 结只讨论p +区向n 区的注入） n 区L p 内，Δp >0，p (x )有一个分布，电中性要求n (x )也有相应的分布。

电子的浓度梯度引起电子向n 区体内的扩散，产生自建电场E 自建，其方向指向n 区体内。

E 自建稳态：j n = 0（E 自建引起的电子漂移流抵消电子扩散流）j p = j F （E 自建引起的空穴漂移流+ 空穴扩散流）74自建电场引起附加电势V p （界面高，体内低）。

附加电势V p 引起附加电子能量−qV p ，能带弯曲。

V F =V j (势垒区)+ V p (扩散区)77稳态连续性方程022*=Δ−∂Δ∂τp xp Dτ*)(0])([)(D x x n Tn Tn ep x p x p −−=Δτ*0)()()(D p x p dx x p d dx x dp n Tn x x x x Tn Tn −−=Δ===解为：?)(=Tn x p (6.78)假设大注入下玻尔兹曼分布仍然成立，TK qV n TK V V q p Tn B jB j D ep ep x p 0)(0)(==−−TK qV n Tn B p en x n 0)(=(6.77)TK qV iTn Tn B F en x n x p 2)()(=⋅由(6.77)：半导体中的体电阻不能忽略，V F中有80§6.3 pn结电容现象：高频下pn结整流特性变差外加偏压变化引起pn结中电荷变化——电容效应pn结电容有两类：势垒电容CT势垒区中的电荷随外加偏压变化。

《半导体物理与器件》课程教学大纲一、课程名称（中英文）中文名称：半导体物理与器件英文名称：Semiconductor Physics and Devices二、课程代码及性质专业选修课程三、学时与学分总学时：40学分：2.5四、先修课程《量子力学》、《统计物理》、《固体物理》、《电路原理》五、授课对象本课程面向功能材料专业学生开设六、课程教学目的（对学生知识、能力、素质培养的贡献和作用）本课程是功能材料专业的选修课之一，其教学目的包括：1、能够应用物理、化学基本原理，识别、表达、并通过文献研究分析复杂半导体物理与器件相关工程问题，获得有效结论。

2、掌握半导体物理与器件相关问题的特征，以及解决复杂工程问题的方法。

3、掌握文献检索、资料查询、现代网络搜索工具的使用方法；具备应用各类文献、信息及资料进行半导体物理与器件领域工程实践的能力。

4、了解半导体物理与器件的专业特征、学科前沿和发展趋势，正确认识本专业对于社会发展的重要性。

5、了解半导体物理与器件领域及其相关行业的国内外的技术现状，具有较强的业务沟通能力与竞争能力。

表1 课程目标对毕业要求的支撑关系七、教学重点与难点课程重点：（1）掌握能带理论以及从能带理论的角度分析半导体的导电机制；熟悉半导体中电子的状态及其运动规律；熟悉实际半导体中的杂质和缺陷的种类、性质及其作用；掌握并且会计算热平衡状态下载流子的浓度问题以及非平衡载流子的概念、产生及其随时间的演化规律（寿命问题）；掌握载流子的几种输运机制。

（2）理解和熟悉PN结及其能带图；掌握PN结的电流-电压特性以及电容-电压特性；熟悉PN结的三种击穿机理；理解和掌握PN结二极管的工作原理。

（3）在对PN结二极管工作原理分析的基础上，学会将此分析进行合理的拓宽，即从单结/两端二极管发展到双结/三端晶体管；掌握双极型晶体管（BJT）的基本概念、符号的定义、工作原理的定性分析以及关键的关系表达式等。

（4）系统地了解和掌握MOSFET的基本工作原理与物理机制；掌握MOSFET器件的主要结构形式、工作特性和有关的物理概念；熟悉MOSFET的电容-电压特性、伏-安特性及其交流效应，并能掌握主要参数和特性的分析与计算方法；了解半导体器件制备的方法、过程及几个器件制备的实例。

半导体物理 SEMICONDUCTOR PHYSICS 编写：刘诺独立制作：刘诺电子科技大学微电子与固体电子学院微电子科学与工程系刘诺第五篇非平衡载流子 §5.1 非平衡载流子的注入与复合一、非平衡载流子及其产生非平衡态：系统对平衡态的偏离。

相应的：n=n0+ ⊿n p=p0+ ⊿p 且⊿n= ⊿p 非平衡载流子：⊿n 和⊿p（过剩载流子）刘诺当非平衡载流子的浓度△n和△p《多子浓度时，这就是小注入条件。

结论⇒小注入条件下非平衡少子∆p对平衡少子p0的影响大非平衡载流子⇐非平衡少子刘诺二、产生过剩载流子的方法光注入电注入高能粒子辐照… 刘诺注入的结果产生附加光电导σ = nq µ n + pq µ p = (n0 qµn + p0 qµ p + (∆nqµn + ∆pqµ p = (n0 + ∆n qµn + ( p0 + ∆p qµ p = σ 0 + ∆σ 故附加光电导∆σ 0 = ∆nqµ n +∆pqµ p = ∆nq (µ n + µ p 刘诺三、非平衡载流子的复合光照停止，即停止注入，系统从非平衡态回到平衡态，电子空穴对逐渐消失的过程。

即：△n=△p 0 刘诺§5.2 非平衡载流子的寿命 1、非平衡载流子的寿命寿命τ ⇐非平衡载流子的平均生存时间1 τ ⇐单位时间内非平衡载流子的复合几率⎧1 ⎯→ ⎪τ ⎯单位时间内非平衡电子的复合几率⎪ n ⎨ 1 ⎪⎯单位时间内非平衡空穴的复合几率⎯→⎪τ p 刘诺⎩例如d [∆p (t ] 则在单位时间内非平衡载流子的减少数= − dt ∆p 而在单位时间内复合的非平衡载流子数= τp 如果在t = 0时刻撤除光照在小注入条件下，τ为常数.解方程(1得到则d [∆p (t ] ∆p − = ⎯ (1 ⎯→ dt τp − t ∆p(t = ∆p(0e − t τp ⎯ (2 ⎯→ 同理也有∆n(t = ∆n(0 e 刘诺τn ⎯ (3 ⎯→对 (2 式求导 2、寿命的意义∆p (t d [∆ p (t ] = − τp ∞ dt ⇒衰减过程中从 t到 t + dt 内复合掉的过剩空穴因此⇐(∆p 0 个过剩载流子的平均可生存时间为∫ td [∆p(t ]= τ t= ∫ d [∆p(t ] − 0 ∞ 0 p ⎯ (3 同理⎯→∫ td [∆n(t ] = τ t= ∫ d [∆n(t ] ∞ − 0 ∞ 0 n ⎯ (4 ⎯→τ − ⎧ 1 τ ⎯→ ⎪ ∆ p (τ = (∆ p 0 e = (∆ p 0 ⎯ (5 ⎪ e 可见⎨τ − ⎪ ∆ n (τ = (∆ n e τ = 1 (∆ n ⎯ (6 0 0 ⎯→ ⎪ e ⎩ 1 ⇒ τ就是∆p (t 衰减到(∆p 0的所需的时间刘诺 e§5.3 准费米能级非平衡态的电子与空穴各自处于热平衡态准平衡态，但具有相同的晶格温度： 1 ⎧⎯⎯→ (1 E−E ⎪ f n (E = ⎪⎪ 1 + e k 0T ⎨ 1 ⎪ f p (E = ⎯⎯→(2 p EF −E ⎪⎪ 1 + e k 0T ⎩ n EF ⎯电子准费米能级⎯→ p 刘诺 EF ⎯空穴准费米能级⎯→ n F刘诺§5.4 复合理论（2）间接复合 Ec 1、载流子的复合形式：（1）直接复合刘诺 Ev复合率 R=rnp 2、带间直接复合：（1）其中，r是电子空穴的复合几率，与n 和p无关。

Bipolar JunctionTransistors双极型晶体管14集成电路中的npn-BJT杂质分布特点：•两头大，中间小•发射区掺杂浓度比基区高很多•四层结构•A E < A C本征晶体管非本征晶体管•埋层•隔离：采用pn 结5双极晶体管的四个工作区9正向有源区（正向放大模式，有源模式）——发射结正偏，集电结反偏9反向有源区（反向放大模式）——发射结反偏，集电结正偏SaturationCutoffActive InvertedV CB (pnp )V BC (npn )V EB (pnp ) V BE (npn )9截止区——两个结都反偏9饱和区——两个结都正偏双极型晶体管使用时，有共基极、共发射极和共集电极三种接法。

BJT的电流方向67理想npn-BJT ( 原型BJT )8•发射结正偏•集电结反偏910处于正向有源区BJT 的内部少子分布示意图162. 杂质任意分布的晶体管理论BJT 的晶体管作用主要发生在基区，研究基区的特性是获得BJT 电流电压关系的关键。

•缓变基区——基区杂质分布为任意形式•通过缓变基区的研究，将获得BJT 的基区电场分布、载流子分布以及电流分布的公式•介绍BJT 的一个重要的参数——基区渡越时间常数182.1 基区电流求基区非平衡少子(电子) 分布及电流密度分布——Moll-Ross方法推导前提是6个基本假定：1)少子在基区中的运动是一维的2)基区宽度大于载流子的平均自由程3)基区中准中性近似成立4)载流子的迁移率等于常数（可以引入平均迁移率）5)基区处于小注入状态6)忽略基区复合（对于现代高β-BJT是成立的）1922问题：分析基区电流的漂移流成分与扩散流成分归一化基区非平衡少子浓度分布2.3 重掺杂发射区为了获得高增益，发射结要求高注入比，即I pE(–x E) << I nB(0) ，因此发射区要求重掺杂1) 禁带变窄•重掺杂会导致电子在杂质原子之间进行共有化运动。