控制器极点配置方法

一、简介在控制系统设计中，rst结构控制器是一种常用的控制器结构，其极点配置是控制系统设计中重要的一环。

极点配置方法可以有效地影响控制系统的性能指标，如稳定性、快速响应性等。

本文将介绍rst结构控制器的极点配置方法，帮助读者更好地理解和应用该方法。

二、rst结构控制器的基本原理1. rst结构控制器概述rst结构控制器是由一个比例环节、一个复式滤波器和一个时延环节组成的控制器结构。

其闭环传递函数可以表示为：G(s) = K * (1 + Ts) / (1 + Ts + Td*s)其中，K为比例增益，T为复式滤波器的时间常数，Td为时延环节的时间常数。

rst结构控制器既可以用于离散系统，也可以用于连续系统。

2. rst结构控制器的特点- rst结构控制器可以在保证系统稳定性的前提下，实现对系统性能的灵活调节。

- 通过合理配置比例环节、复式滤波器和时延环节的参数，可以使系统在满足动态响应指标的前提下，获得较好的抗干扰性能和鲁棒性能。

三、rst结构控制器极点配置方法1. 极点配置的基本原理极点配置方法是一种通过选取控制系统闭环传递函数的极点来调节系统的性能指标的方法。

rst结构控制器的极点配置方法主要包括两种：位置型极点配置和动态可调型极点配置。

2. 位置型极点配置方法- 位置型极点配置方法是指通过直接选取所需的闭环极点位置来调节系统的性能指标。

这种方法需要事先确定所需的阶跃响应特性，并根据特性要求来确定控制系统的极点位置，然后通过计算得到对应的rst结构控制器参数。

- 位置型极点配置方法适用于要求系统快速响应和较好抗干扰性能的场合，但对稳定性的要求不是很高。

3. 动态可调型极点配置方法- 动态可调型极点配置方法是指在闭环极点位置一定的情况下，通过调节rst结构控制器的参数来实现对系统性能指标的调节。

这种方法通常需要通过迭代计算或数值优化方法来确定合适的参数值。

- 动态可调型极点配置方法适用于对系统性能指标要求较为严格的场合，需要兼顾稳定性、快速响应性、抗干扰性等多个方面。

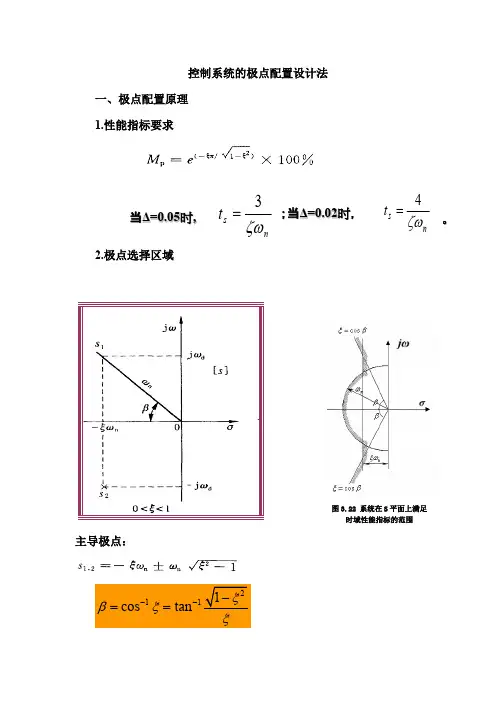
控制系统的极点配置设计法一、极点配置原理1.性能指标要求n s t ζω4=；当Δ=0.02时，。

ns t ζω3= 当Δ=0.05时,2.极点选择区域主导极点：2111cos tan ξβξξ---==3.其它极点配置原则系统传递函数极点在s 平面上的分布如图（a ）所示。

极点s 3距虚轴距离不小于共轭复数极点s 1、s 2距虚轴距离的5倍，即（此处，对应于极点s 1、s 2）；同时，极点n s s ξω5Re 5Re 13=≥ξn ωs 1、s 2的附近不存在系统的零点。

由以上条件可算出与极点s 3所对应的过渡过程分量的调整时间为1351451s n s t t =⨯≤ξω式中是极点s 1、s 2所对应过渡过程的调整时间。

1s tn x o (t)（a ）（b系统极点的位置与阶跃响应的关系图（b ）表示图（a ）所示的单位阶跃响应函数的分量。

由图可知，由共轭复数极点s 1、s 2确定的分量在该系统的单位阶跃响应函数中起主导作用，即主导极点。

因为它衰减得最慢。

其它远离虚轴的极点s 3、s 4、s 5所对应的单位阶跃响应衰减较快，它们仅在极短时间内产生一定的影响。

因此，对系统过渡过程进行近似分析时。

可以忽略这些分量对系统过渡过程的影响。

二、极点配置实例磁悬浮轴承控制系统设计1.1磁悬浮轴承系统工作原理图1是一个主动控制的磁悬浮轴承系统原理图。

主要由被悬浮转子、传感器、控制器和执行器(包括电磁铁和功率放大器)四大部分组成。

设电磁铁绕组上的电流为I0，它对转子产生的吸力F和转子的重力mg相平衡，转子处于悬浮的平衡位置，这个位置称为参考位置。

（a）（b）图1 磁悬浮轴承系统的工作原理Fig.1 The magnetic suspension bearing system principledrawing假设在参考位置上，转子受到一个向下的扰动，转子就会偏离其参考位置向下运动，此时传感器检测出转子偏离其参考位置的位移，控制器将这一位移信号变换成控制信号，功率放大器又将该控制信号变换成控制电流I0+i，控制电流由I0增加到I0+i，因此，电磁铁的吸力变大了，从而驱动转子返回到原来的平衡位置。

线性系统的状态反馈及极点配置1.前言随着现代控制理论的不断发展和成熟，线性系统的状态反馈控制在控制理论中得到了广泛的应用，并成为了控制领域中重要的一种控制方法。

状态反馈控制能够将系统的状态进行反馈，并利用反馈得到的信息对系统进行控制，从而达到使系统达到预期控制目标的目的。

本文将从状态反馈控制的原理和实现方法两方面介绍线性系统的状态反馈及极点配置。

2.状态反馈控制的原理状态反馈控制是建立在现代控制理论的基础上的一种高级控制方法。

状态反馈控制的基本思想是在系统中引入反馈环节，设计一个反馈控制器，将系统的状态量反馈给控制器，控制器再根据反馈信号输出控制量，以期望控制系统按照预期的运动轨迹运行。

因此，状态反馈控制要实现以下两个步骤：- 系统状态量的测量：首先要在系统中安装测量传感器，实时地测量系统状态量，使得状态量可以被反馈到控制器中。

- 反馈控制器的设计：设计一个反馈控制器，将系统的状态量反馈给控制器，控制器再根据反馈信号输出控制量，实现对系统的精确控制。

因此，状态反馈控制的基本原理就是将系统状态量反馈到控制器中，以期望控制系统按照预期的运动轨迹运行。

2.2 状态空间模型与状态反馈控制状态空间模型是状态反馈控制的基础。

状态空间模型是一种方便描述线性系统动态行为和控制器的模型。

对于线性时不变系统，我们可以用如下的状态变量描述：x(t) = [x1(t),x2(t),...,xn(t)]T其中，x(t) 是系统在时刻 t 的状态量，n 是状态量的数量，x1(t),x2(t),...,xn(t) 分别是系统的每个状态量。

状态空间模型可以用一组线性常微分方程描述：dx/dt = Ax + Bu其中，A 是系统的状态方程矩阵，B 是输入矩阵，C 是输出矩阵，D 是直接耦合矩阵。

系统的状态反馈控制可以表示为：u(t) = -Kx(t)其中，K 是状态反馈矩阵。

将状态反馈控制引入到状态空间模型中，可以得到控制器的状态空间模型为：y = Cx上述控制器的状态空间模型就是一个闭环系统，通过反馈控制器将系统状态返回到系统，形成了一个反馈环。

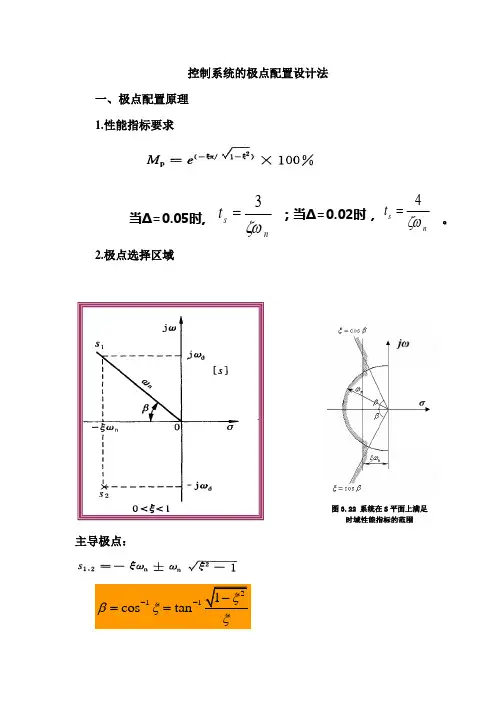
控制系统的极点配置设计法一、极点配置原理1.性能指标要求2.极点选择区域主导极点：2111cos tanξβξξ---==图3.22 系统在S平面上满足时域性能指标的范围nstζω4=；当Δ=0.02时，。

nstζω3=当Δ=0.05时,3.其它极点配置原则系统传递函数极点在s 平面上的分布如图（a ）所示。

极点s 3距虚轴距离不小于共轭复数极点s 1、s 2距虚轴距离的5倍，即n s s ξω5Re 5Re 13=≥（此处ξ，n ω对应于极点s 1、s 2）；同时，极点s 1、s 2的附近不存在系统的零点。

由以上条件可算出与极点s 3所对应的过渡过程分量的调整时间为1351451s n s t t =⨯≤ξω 式中1s t 是极点s 1、s 2所对应过渡过程的调整时间。

图（b ）表示图（a ）所示的单位阶跃响应函数的分量。

由图可知，由共轭复数极点s 1、s 2确定的分量在该系统的单位阶跃响应函数中起主导作用，即主导极点。

因为它衰减得最慢。

其它远离虚轴的极点s 3、s 4、s 5 所对应的单位阶跃响应衰减较快，它们仅在极短时间内产生一定的影响。

因此，对系统过渡过程进行近似分析时。

可以忽略这些分量对系统过渡过程的影响。

n x o (t)（a ）（b ）系统极点的位置与阶跃响应的关系二、极点配置实例磁悬浮轴承控制系统设计1.1磁悬浮轴承系统工作原理图1是一个主动控制的磁悬浮轴承系统原理图。

主要由被悬浮转子、传感器、控制器和执行器(包括电磁铁和功率放大器)四大部分组成。

设电磁铁绕组上的电流为I0，它对转子产生的吸力F和转子的重力mg相平衡，转子处于悬浮的平衡位置，这个位置称为参考位置。

（a）（b）图1 磁悬浮轴承系统的工作原理Fig.1 The magnetic suspension bearing system principledrawing假设在参考位置上，转子受到一个向下的扰动，转子就会偏离其参考位置向下运动，此时传感器检测出转子偏离其参考位置的位移，控制器将这一位移信号变换成控制信号，功率放大器又将该控制信号变换成控制电流I0+i，控制电流由I0增加到I0+i，因此，电磁铁的吸力变大了，从而驱动转子返回到原来的平衡位置。

极点配置的原理今天来聊聊极点配置的原理。

我不是一开始就接触到极点配置这个概念的，之前做项目的时候遇到了控制系统的性能优化问题，就开始研究起它来了。

极点配置就像是给控制系统这个大机器调音一样。

咱们先从生活现象说起，想象一下开车。

汽车有个速度控制系统，我们想要汽车的速度按照我们期望的方式变化，比如说快速稳定地达到一个设定速度，并且在遇到一些小干扰（像路面有点小坡度）的时候还能保持稳定。

这个时候极点配置就像调整汽车的“脾气秉性”的工具一样。

在控制系统里，系统的特性跟极点的位置密切相关。

从原理上讲呢，极点就是系统传递函数分母等于零的根。

我记得第一次接触这个理论公式的时候，觉得满脑袋都是浆糊。

比如说一个简单的二阶系统，它的极点会影响系统的响应速度和稳定性，就像一个跷跷板，两个极点要处于一个合适的位置，系统才会又快又稳。

这可是我琢磨了好久才有点理解的地方。

说到这里，你可能会问，这个极点怎么才能配置到我们想要的位置呢？这就要用到反馈控制理论了。

就像我们在训练宠物一样，通过反馈（知道宠物做的好不好，然后奖惩）来让系统的特性符合我们的要求。

比如说，通过调整反馈增益，就可以改变极点的位置。

老实说，我一开始也不明白极点配置到底为啥这么重要。

后来遇到好多实际例子才恍然大悟。

实际在航空航天领域，飞行器的姿态控制系统要很精确才行，极点配置就大有用武之地。

合理的极点配置能让飞行器快速准确地调整姿态且保持稳定，就像杂技演员总能在高空钢丝上保持平衡一样。

再讲讲相关的注意事项吧。

极点配置虽然很强大，但并不是随心所欲的，要考虑系统的物理可实现性以及对于外部干扰和不确定性的鲁棒性。

比如说，不能要求汽车做到像火箭那样的加速能力，因为汽车有它的物理限制。

这就像我们人一样，虽然有潜力可以挖掘，但是也有自身的极限。

我觉得极点配置这个原理还有很多可以延伸思考的地方。

比如如何在更加复杂多变的环境下进行适当地极点配置，这就像在不断变化的天气下管理一个大农场，要根据不同情况调整策略。

极点配置状态反馈控制器的设计王俊伟于新海(河套学院机电工程系)摘要围绕双级倒立摆案例，对极点配置状态反馈控制器的设计方法展开讨论，对最终的计算结果进行仿真,并通过仿真结果分析了系统的稳定性、动态性能和稳态误差情况。

倒立摆的开环系统状态空间模型状态不稳定且动态性能较差，通过引进极点配置状态反馈控制器，倒立摆的闭环系统状态达到稳定，而且动态性能得到改善。

关键词状态反馈控制器双级倒立摆极点配置能控标准型爱克曼公式动态特性稳态误差中图分类号TH865文献标识码B文章编号1000-3932(2021)01-0015-05极点配置状态反馈控制器设计得好坏直接决定了控制系统动态性能的优劣！配置极点的目的不仅是使系统稳定还要使系统的动态性能满足控制要求[1]!在配置状态反馈控制器时，根据被控制对象的要求，可以采用3种方法实现:极点配置状态反馈控制器的直接法、极点配置状态反馈控制器的变换法和爱克曼公式[2]'这3种方法仅适用于单输入系统，优点是只要系统能控，就可以实现极点配置的状态反馈，缺点是不能用于多输入系统的极点配置状态反馈控制器。

对于单输入系统，如果系统能控可以实现极点的任意配置,改善动态性能，但有可能使闭环控制系统的稳态误差变大[3]!1极点配置状态反馈控制器的直接法线性时不变系统如下:x=Ax+Bu(])'=Cx其中,X是系统的*维状态向量;*是状态向量对时间的导数;u是状态反馈控制律；#、B和C是适当维数的已知常数矩阵;'是系统的输出。

采用的状态反馈控制律是:u=-kx+v(2)其中，-是一维外部输入;k是反馈增益矩阵。

将式(2)代入式(1)得到闭环系统状态方程：*二(.-Bk)x+B-(3)极点配置状态反馈控制器的直接法分5步实现⑷。

第1步,检验系统(1)的能控性,如果系统能控,进行第2步。

第2步，计算闭环系统特征多项式：)et[!0—(#—Bk)]二！*+(3*_]+k*_14!*i1--------(3]+k])!+30+,0(4)其中，！是闭环极点。

网络控制系统的增广状态极点配置设计法网络控制系统的增广状态极点配置设计方法是一种针对网络控制系统稳定性和性能优化的设计方法。

该方法通过优化极点的位置来改变系统的特性，从而实现系统的稳定性和响应性能的优化。

这种方法可以用于解决一般的网络控制系统设计中遇到的性能问题，如抖动、不稳定等。

在网络控制系统中，增广状态极点通常是指将控制器引入系统后，系统的特征方程中新增的极点。

这些极点可以通过调整控制器参数来改变，从而实现对系统的优化。

增广状态极点配置设计方法的目标是将新增的极点配置到合适的位置，使得系统的稳定性和响应性能达到最佳状态。

增广状态极点配置设计方法通常分为两个步骤：极点配置和参数优化。

首先，进行极点配置。

极点配置的目标是将控制器引入系统后的增广状态极点配置到合适的位置。

一般来说，对于网络控制系统，我们希望系统的极点分布在左半平面，这样系统就能保持稳定。

同时，我们还可以根据系统的响应速度要求，将极点配置在合适的位置，从而获得更好的响应性能。

常用的极点配置方法有根轨迹法、随机法、模拟退火法等。

其次，进行参数优化。

参数优化的目标是确定控制器的参数，使得系统的增广状态极点配置到合适的位置。

参数优化可以使用各种优化算法，如遗传算法、粒子群算法、模拟退火算法等。

通过优化算法最优参数，使得控制器的增广状态极点配置到合适的位置，并且使得系统的指标函数最小化。

在进行增广状态极点配置设计时，需要考虑一些因素。

首先是系统的稳定性，即极点的位置应该在左半平面，以保持系统的稳定。

其次是系统的性能要求，即我们希望系统的响应速度和稳态误差达到一定的要求。

另外，还需要考虑控制器的结构和计算复杂度，以及系统的可行性和可实现性。

总结起来，增广状态极点配置设计方法是一种针对网络控制系统稳定性和性能优化的设计方法。

通过优化控制器的参数和极点位置，可以实现系统的稳定性和响应性能的优化。

该方法可以应用于一般的网络控制系统设计中，提供一种解决性能问题的有效方法。

极点配置状态反馈控制器设计方法
嘿，朋友们！今天咱来聊聊极点配置状态反馈控制器设计方法。

这玩意儿啊，就像是给一个系统装上了精准的导航仪，能让它乖乖地按照咱的想法走。

你看啊，一个系统就好比是一辆汽车，而极点配置状态反馈控制器就是那个掌握方向盘的司机。

咱得通过巧妙的设计，让这个司机能精准地操控汽车，该加速的时候加速，该转弯的时候转弯，不能有一点儿含糊。

设计这个控制器就像是搭积木，一块一块地拼凑起来。

咱得先了解系统的特性，就像了解汽车的性能一样。

然后呢，根据这些特性来选择合适的参数，这可不能马虎，得仔细琢磨。

比如说，要是参数没选好，那可就糟糕啦！就像司机开车老是开歪一样，系统也会变得不稳定，那可不行！咱得让系统稳稳当当的，该干啥干啥。

这其中的学问可大着呢！就好像做菜一样，各种调料得搭配得恰到好处，才能做出美味的菜肴。

极点配置状态反馈控制器的设计也是如此，每个环节都得精心处理。

而且哦，这个设计方法可不是一成不变的。

不同的系统就像不同口味的人，得用不同的方法去对待。

有时候得灵活一点，不能太死板啦。

想想看，如果所有系统都用一种方法去设计控制器，那多无趣啊！就像所有人都穿一样的衣服，那还有啥意思呢？咱得根据实际情况来调整，找到最适合的方案。

在实际应用中，这可真是帮了大忙啦！它能让那些复杂的系统乖乖听话，按照我们的要求运行。

这多厉害呀！难道不是吗？
所以啊，极点配置状态反馈控制器设计方法可真是个宝贝！咱可得好好研究，好好利用。

让它为我们的各种系统服务，让它们变得更智能、更高效。

怎么样，是不是觉得很有意思呢？别犹豫啦，赶紧去试试吧！。

课程名称：控制理论乙指导老师：姚唯成绩：实验名称：控制系统的极点配置实验类型：同组学生姓名：郁明非一、实验目的和要求（必填）二、实验内容和原理（必填）三、主要仪器设备（必填）四、操作方法和实验步骤五、实验数据记录和处理六、实验结果与分析（必填）七、讨论、心得一、实验目的和要求1．掌握全状态反馈系统的极点配置方法2．在 Simulink 仿真环境中，研究极点配置对系统特性的影响二、实验内容和原理（一）实验内容1．一被控对象，其传递函数为10G ( s )( s 1)( s 2 )( s 3 )设计反馈控制器u=-kx ，使闭环系统的极点为12j 23，2 2 j 2 3 ，310 。

2．在 Simulink仿真环境下，用基本环节组成经过极点配置后的系统，通过图形观察环节，观察系统的各点响应。

（二）实验原理对一给定控制系统如果其状态完全可控，则可进行任意极点配置即通过设计反馈増益 K 使闭环系统具有期望的极点。

极点配置有二种方法：第一种方法是采用变换矩阵T，使系统具有期望的极点，从而求出矩阵K ；第二种方法基于 Caylay-Hamilton 理论，通过矩阵多项式φ（a），可求出 K（这种方法称为 Ackermann 公式）。

在 MATLAB 中，利用控制系统工具箱函数 place 和 acker 进行极点配置设计。

三、主要仪器设备一台 PC 电脑， matlab 仿真软件， simulink 仿真环境四、实验源代码及实验结果function jidianpeizhinum=[10];den=[1,6,11,6];[A,B,C,D]=tf2ss(num,den);J=[-2-j*2*sqrt(3),-2+j*2*sqrt(3),-10];K=place(A,B,J);Ksys=ss(A-B*K,[0;0;0],eye(3),0);t=0:0.01:4;X=initial(sys,[1;0;0],t);x1=[1,0,0]*X';x2=[0,1,0]*X';x3=[0,0,1]*X';subplot(3,1,1);plot(t,x2);grid on ;title('Reponse to initial condition'); ylabel('x1');subplot(3,1,2);plot(t,x2);grid on ;ylabel('x2');subplot(3,1,3);plot(t,x3);grid on ;ylabel('x3');xlabel('t(sec)');实验结果K =8.000045.0000 154.0000实验验证：>>num=[10];>>den=[1 6 11 6];>>[A,B,C,D]=tf2ss(num,den);>>J=[-2-j*2*sqrt(3),-2+j*2*sqrt(3),-10];>>K=place(A,B,J)K =8.000045.0000 154.0000>>A1=A-B*K;>>sys=ss(A1,B,C,D);>>G1=zpk(sys);>>G1=zpk(sys)G1 =10----------------------(s+10) (s^2 + 4s + 16)Continuous-time zero/pole/gain model.五、 simulink 仿真1.简单环节叠加仿真2.状态函数仿真六、心得、体会1.通过本次实验，掌握了状态反馈的概念，并且掌握了利用状态反馈进行极点配置的方法，学会了用MATLAB求解状态反馈矩阵。

控制系统的极点配置设计法一、极点配置原理1.性能指标要求2.极点选择区域主导极点：nstζω4=；当Δ=0.02时，。

nstζω3=当Δ=0.05时,3.其它极点配置原则系统传递函数极点在s 平面上的分布如图（a ）所示。

极点s 3距虚轴距离不小于共轭复数极点s 1、s 2距虚轴距离的5倍，即n s s ξω5Re 5Re 13=≥（此处ξ，n ω对应于极点s 1、s 2）；同时，极点s 1、s 2的附近不存在系统的零点。

由以上条件可算出与极点s 3所对应的过渡过程分量的调整时间为1351451s n s t t =⨯≤ξω式中1s t 是极点s 1、s 2所对应过渡过程的调整时间。

图（b ）表示图（a ）所示的单位阶跃响应函数的分量。

由图可知，由共轭复数极点s 1、s 2确定的分量在该系统的单位阶跃响应函数中起主导作用，即主导极点。

因为它衰减得最慢。

其它远离虚轴的极点s 3、s 4、s 5 所对应的单位阶跃响应衰减较快，它们仅在极短时间内产生一定的影响。

因此，对系统过渡过程进行近似分析时。

可以忽略这些分量对系统过渡过程的影响。

n x o (t)（a ）（b ）系统极点的位置与阶跃响应的关系二、极点配置实例磁悬浮轴承控制系统设计1.1磁悬浮轴承系统工作原理图1是一个主动控制的磁悬浮轴承系统原理图。

主要由被悬浮转子、传感器、控制器和执行器(包括电磁铁和功率放大器)四大部分组成。

设电磁铁绕组上的电流为I0，它对转子产生的吸力F和转子的重力mg相平衡，转子处于悬浮的平衡位置，这个位置称为参考位置。

（a）（b）图1 磁悬浮轴承系统的工作原理Fig.1 The magnetic suspension bearing system principledrawing假设在参考位置上，转子受到一个向下的扰动，转子就会偏离其参考位置向下运动，此时传感器检测出转子偏离其参考位置的位移，控制器将这一位移信号变换成控制信号，功率放大器又将该控制信号变换成控制电流I0+i，控制电流由I0增加到I0+i，因此，电磁铁的吸力变大了，从而驱动转子返回到原来的平衡位置。

零极点配置控制器及其在随机参数液压系统中的应用零极点配置控制器是一种常用的控制器设计方法，它通过将系统的极点和零点进行配置，来实现对系统的控制。

在随机参数液压系统中，零极点配置控制器也被广泛应用。

本文将从零极点配置控制器的基本原理、设计方法和在随机参数液压系统中的应用等方面进行探讨。

一、零极点配置控制器的基本原理零极点配置控制器是一种基于系统的极点和零点进行配置的控制器设计方法。

在控制系统中，极点和零点是决定系统动态响应的重要因素。

极点是系统传递函数的分母根，它决定了系统的稳定性和响应速度；零点是系统传递函数的分子根，它决定了系统的响应特性。

通过对系统的极点和零点进行配置，可以实现对系统的控制。

二、零极点配置控制器的设计方法零极点配置控制器的设计方法主要包括以下几个步骤：1. 确定系统的传递函数首先需要确定系统的传递函数，即系统的输入与输出之间的关系。

在液压系统中，系统的传递函数可以通过建立系统的数学模型来得到。

2. 分析系统的极点和零点通过对系统的传递函数进行分析，可以得到系统的极点和零点。

极点和零点的位置决定了系统的响应特性。

3. 配置系统的极点和零点根据系统的控制要求，可以对系统的极点和零点进行配置。

通过配置极点和零点的位置，可以实现对系统的控制。

4. 设计控制器根据配置后的系统传递函数，可以设计出相应的控制器。

控制器的设计方法可以采用经典控制理论或现代控制理论。

5. 仿真验证通过仿真验证，可以验证控制器的设计是否符合系统的控制要求。

如果不符合要求，需要重新进行设计。

三、零极点配置控制器在随机参数液压系统中的应用随机参数液压系统是一种具有不确定性的系统，其参数值可能会随着时间和环境的变化而发生变化。

在这种情况下，传统的控制方法可能会失效。

零极点配置控制器可以通过对系统的极点和零点进行配置，来适应随机参数液压系统的变化。

在随机参数液压系统中，零极点配置控制器可以通过对系统的极点和零点进行在线调整，来实现对系统的控制。

实验3 控制系统极点的任意配置一、实验目的1. 掌握用全状态反馈的设计方法实现控制系统极点的任意配置2. 用电路模拟的方法，研究参数的变化对系统性能的影响二、实验设备1.THSSC-4型信号与系统·控制理论·计算机控制技术实验箱2.PC机一台(含上位机软件)、USB数据采集卡、37针通信线1根、16芯数据排线、USB接口线三、实验内容1. 用全状态反馈实现二阶系统极点的任意配置，并用电路模拟的方法予以实现2. 用全状态反馈实现三阶系统极点的任意配置，并通过电路模拟的方法予以实现四、实验原理由于控制系统的动态性能主要取决于它的闭环极点在S平面上的位置，因而人们常把对系统动态性能的要求转化为一组希望的闭环极点。

一个单输入单输出的N阶系统，如果仅靠系统的输出量进行反馈，显然不能使系统的n个极点位于所希望的位置。

基于一个N阶系统有N个状态变量，如果把它们作为系统的反馈信号，则在满足一定的条件下就能实现对系统极点任意配置，这个条件就是系统能控。

理论证明，通过状态反馈的系统，其动态性能一定会优于只有输出反馈的系统。

设系统受控系统的动态方程为=Axbux+y=cx图3-1为其状态变量图。

图3-1 状态变量图令Kx r u -=，其中]...[21n k k k K =，r 为系统的给定量，x 为1⨯n 系统状态变量，u 为1×1控制量。

则引入状态反馈后系统的状态方程变为bu x bK A x+-=)( 相应的特征多项式为)](det[bK A SI --，调节状态反馈阵K 的元素]...[21n k k k ，就能实现闭环系统极点的任意配置。

图3-2为引入状态反馈后系统的方框图。

图3-2 引入状态变量后系统的方框图1. 典型二阶系统全状态反馈的极点配置二阶系统方框图如3-3所示。

图3-3 二阶系统的方框图1.1 由图得)15.0(10)(+=S S S G ，然后求得：223.0=ξ，%48≈p δ同时由框图可得：2115.01)(X S X R =+- ，2110X X = 所以：R X X X 222212+--= R X X ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=2022100[]X X y 011==1.2 系统能控性[]242200=⎥⎦⎤⎢⎣⎡-=rank Ab b rank 所以系统完全能控，即能实现极点任意配置。