等额本金与等额本息按揭贷款还款方式比较(excel表格自动套用格式计算)
- 格式:xls
- 大小:250.00 KB
- 文档页数:14

等额本金和等额本息的区别与选择大家好,我是一名金融行业的专家,今天我们来聊聊等额本金和等额本息这两种贷款方式的区别与选择。
我们要明白什么是等额本金,什么是等额本息。
简单来说,等额本金就是每月还款金额相同,但每月还款中的本金部分逐月递减;等额本息则是每月还款金额相同,但每月还款中的本金和利息部分逐月递增。
接下来,我们将从三个方面来详细分析这两种贷款方式的区别与选择。
一、计算公式对比1.1 等额本金等额本金的计算公式为:每月还款金额 = (本金 / 还款月数) + (本金已归还本金累计) × 利率其中,本金是指贷款总额,还款月数是指贷款期限,利率是年化利率除以12。
从这个公式我们可以看出,等额本金的每月还款金额是逐月递减的,而且每月的利息部分也是逐月递减的。
1.2 等额本息等额本息的计算公式为:每月还款金额 = (本金× 月利率× (1 + 月利率)^还款月数) ÷ ((1 + 月利率)^还款月数 1)其中,本金是指贷款总额,月利率是年化利率除以12,还款月数是指贷款期限。
从这个公式我们可以看出,等额本息的每月还款金额是相同的,但是每月的本金和利息部分是逐月递增的。
二、实际支出对比2.1 等额本金由于等额本金的每月还款金额逐月递减,所以在贷款初期,每月的还款金额会相对较高。
但是随着时间的推移,每月的还款金额会越来越低。
这意味着在整个贷款期限内,等额本金的总利息支出会逐渐减少。
因此,从实际支出的角度来看,等额本金的总支出会比等额本息要少。
2.2 等额本息由于等额本息的每月还款金额相同,所以在整个贷款期限内,每月的还款金额都是固定的。
这意味着在整个贷款期限内,等额本息的总利息支出是固定的。
因此,从实际支出的角度来看,等额本息的总支出会比等额本金要高。
三、选择建议3.1 如果您希望在整个贷款期限内总支出较少,那么等额本金是一个更好的选择。
因为它可以让您在贷款初期分摊更多的利息支出,从而降低整个贷款期限的总利息支出。

等额本金和等额本息的区别(含计算公式)对于大多数人来说,买房都需要向银行借贷,这里面就牵扯到一个重要问题,一般向银行贷款有两种方式:等额本金法和等额本息法。
许多人对这两种方法不甚了解,以至于在贷款方面吃了大亏,今天笔者就详细的向大家讲述等额本金和等额本息的区别和各自适用的人群。
等额本息法等额本息法最重要的一个特点是每月的还款额相同,从本质上来说是本金所占比例逐月递增,利息所占比例逐月递减,月还款数不变,即在月供“本金与利息”的分配比例中,前半段时期所还的利息比例大、本金比例小,还款期限过半后逐步转为本金比例大、利息比例小,其计算公式为:每月还本付息金额 =[ 本金 x 月利率 x(1+月利率)贷款月数 ] / [(1+月利率)还款月数 - 1]每月利息 = 剩余本金x贷款月利率还款总利息=贷款额*贷款月数*月利率*(1+月利率)贷款月数/【(1+月利率)还款月数 - 1】-贷款额还款总额=还款月数*贷款额*月利率*(1+月利率)贷款月数/【(1+月利率)还款月数 - 1】注意:在等额本息法中,银行一般先收剩余本金利息,后收本金,所以利息在月供款中的比例会随本金的减少而降低,本金在月供款中的比例因而升高,但月供总额保持不变。
等额本金法等额本金法最大的特点是每月的还款额不同,呈现逐月递减的状态;它是将贷款本金按还款的总月数均分,再加上上期剩余本金的利息,这样就形成月还款额,所以等额本金法第一个月的还款额最多,然后逐月减少,越还越少,计算公式为:每月还本付息金额=(本金/还款月数)+(本金-累计已还本金)×月利率每月本金=总本金/还款月数每月利息=(本金-累计已还本金)×月利率还款总利息=(还款月数+1)*贷款额*月利率/2还款总额=(还款月数+1)*贷款额*月利率/2+贷款额注意:在等额本金法中,人们每月归还的本金额始终不变,利息随剩余本金的减少而减少,因而其每月还款额逐渐减少。

Excel计算房贷中的等额本息,⽤等额本息公式计算在 Excel 中,计算房贷中的等额本息可以⽤PMT函数,不需⽤等额本息计算公式,这样既⽅便⼜快速;但计算等额本⾦没有直接的函数,需要⽤等额本⾦计算公式⼀项项计算;下就是它们⽤ Excel 计算的具体操作⽅法,操作中所⽤版本均为 Excel 2016。
⼀、⽤Excel计算房贷中的等额本息假如购房贷款 820000 元,商业贷款年利率为 4.9%,贷款时间 25 年,还款⽅式为等额本息;现在要求⽤ Excel 计算每⽉应该还款数额和需还总贷款数额。
(⼀)⽤PMT函数计算1、计算每⽉应该还款数额。
采⽤等额本息还款每⽉还款数额⼀样,所以只需计算⼀次;双击D3 单元格,把公式 =PMT(B3/12,C3*12,A3) 复制到 D3,按回车,返回 -4,745.98,负号表⽰需还款。
2、计算需还总贷款数额。
双击 E3,输⼊公式 =D3*12*C3,按回车,返回 -1,423,795.38;操作过程步骤,如图1所⽰:图13、公式 =PMT(B3/12,C3*12,A3) 说明:A、Pmt函数的表达式为 PMT(Rate, Nper, Pv, [Fv], [Type]);Rate 表⽰贷款⽉利率,Nper 表⽰贷款总期数(⽉数),Pv 表⽰本⾦;Fv 为可选项,表⽰未来值,若省略,默认取 0;Type 也为可选项,表⽰⽀付时间,0 或省略表⽰期末,1 表⽰期初。
B、公式中的 B3/12 ⽤于计算⽉利率,12 表⽰⼀年 12 个⽉;C3*12 计算总期数,A3 是本⾦,公式省略了后两个参数。
(⼆)⽤等额本息公式计算1、等额本息计算⽉还款公式为:(贷款本⾦×⽉利率×(1+⽉利率)^还款⽉数)/((1+⽉利率)^还款⽉数-1),把数值代⼊此公式变 =(A3*B3/12*(1+B3/12)^(C3*12))/((1+B3/12)^(C3*12)-1),双击 D5 单元格,把公式复制到 D5,按回车,返回 4,745.98,跟⽤PMT函数计算结果⼀致;确保当前选项卡为“开始”,单击“常规”下拉列表框,在弹出的选项中选择“货币”,则数字前⾃动加上元符号;再单击“字体颜⾊”图⽰,选择“浅蓝⾊”,则⽂字变为所选颜⾊;操作过程步骤,如图2所⽰:图22、计算需还总贷款⽅法跟上⾯⼀样,⽤已计算出的每⽉还款数额乘上贷款年数再乘每年12个⽉即可。
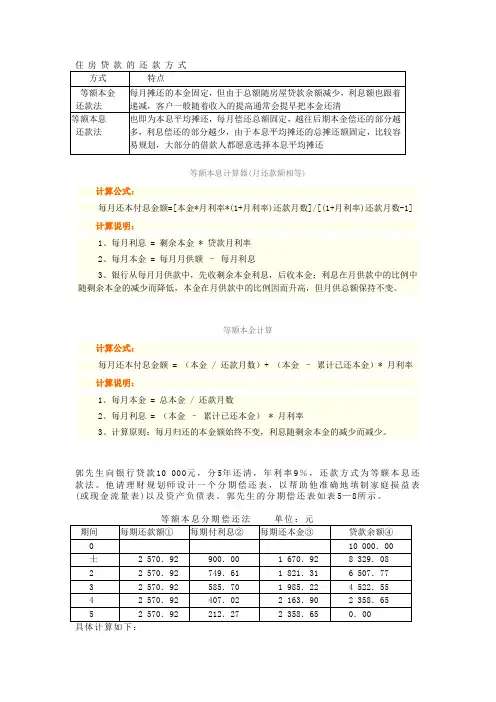
等额本息计算器(月还款额相等)计算公式:每月还本付息金额=[本金*月利率*(1+月利率)还款月数]/[(1+月利率)还款月数-1] 计算说明:1、每月利息 = 剩余本金 * 贷款月利率2、每月本金 = 每月月供额–每月利息3、银行从每月月供款中,先收剩余本金利息,后收本金;利息在月供款中的比例中随剩余本金的减少而降低,本金在月供款中的比例因而升高,但月供总额保持不变。
等额本金计算计算公式:每月还本付息金额 = (本金 / 还款月数)+ (本金–累计已还本金)* 月利率计算说明:1、每月本金 = 总本金 / 还款月数2、每月利息 = (本金–累计已还本金) * 月利率3、计算原则:每月归还的本金额始终不变,利息随剩余本金的减少而减少。
郭先生向银行贷款10 000元,分5年还清,年利率9%,还款方式为等额本息还款法。
他请理财规划师设计一个分期偿还表,以帮助他准确地填制家庭损益表(或现金流量表)以及资产负债表。
郭先生的分期偿还表如表5—8所示。
①=10 000/(P/A,9%,5)=2 570.92(元)②=上期④×9%(即:749.61=8 329.08×9%)③=①一②(即:1 821.31=2 570.92-749.61)④=上期④—③(即:8 329.08=10 000.00-l 670.92)案例等额本金还贷法和等额本息还款法的比较小李近期办理购房贷款,计算下来需要贷款50万元,并需要在20年内还清。
目前银行的贷款年利率为5.04%,具体还款方式有等额本息还款法、等额本金还款法可供选择。
小李陷入了困惑,以下我们分别计算两种方式下的月还款额和到期合计利息以帮助小李作出决策。
(1)等额本息还款法:月利率=年利率/12=5.04%/12=0.42%每月还款额=500 000/(P/A,0.42%,20×12)=3 310.84(元)到期合计本息总额=3 310.84×240=794 601.60(元)到期合计利息总额=794 601.60—500 000=294 601.60(元)(2)等额本金还款法:月利率=年利率/12=5.04%/12=0.42%每月归还本金=500 000/240=2 083.33(元)第一个月利息=500 000×0.42%=2 100(元) ’以后每月利息减少额=2 083.33×0.42%=8.75(元)每月利息是以等差数列减少,所以到期合计支付的利息总额:Sn=(a1+an) ×n÷2=(2 100+8.75) ×120=253 050(元)到期合计本息总额:253 050+500 000=753 050(元)经过计算,很容易看出这两种还款方式的区别,小李完全可以根据自己的实际情况选择合适的还款方式。

等额本息还贷方式与等额本金还贷方式有什么区别等额本息还贷方式与等额本金还贷方式有什么区别?等额本息还贷方式和等额本金还贷方式的主要区别有如下:1、每月还款额不同。
等额本息还贷方式每月按相同金额还贷款本息,月还款中利息逐月递减,本金逐月递增;等额本金还贷方式还款金额递减,月还款中本金保持相同金额,利息逐月递减。
贷款金额、年限相同情况下,等额本息还贷方式的月还款额约等于等额本金还贷方式贷款期限接近一半时的月还款额。
2、贷款利息不同。
虽然等额本息还贷方式和等额本金还贷方式执行相同的贷款利率,都是每月按剩余贷款本金计息,每月还款的金额除还当月利息外剩余部分还贷款本金,但由于一种是等额还款,另一种是递减还款,所以两者的计息不同。
除贷款首月利息相同外,其余月份利息都不同,贷款总利息也不同。
3、借款人可选择的最短贷款期限不同。
贷款金额确定以后,可选择的最短贷款期限由借款人每月可用于还款的金额确定。
每月可用于还款的金额相同的情况下,等额本金还贷方式下的最短贷款期限要长于等额本息还贷方式下的最短贷款期限。
4、适用的对象不同。
一般而言,等额本息还款方式适用于绝大多数可还款金额比较稳的借款人,等额本金还贷方式适用于预期未来(贷款期限内)可还款金额会降低或希望采用递减还款的借款人。
在贷款方个贷程序具备的前提下,借款人可根据自己的经济状况和还款意愿自主选择还贷方式。
“等额本金”与“等额本息”还款方式相比,前者比后者要少付利息,但是———个人住房按揭贷款已经成为消费者实现安家置业的重要手段。
如何选择合适的还款方式,对借款人来说是值得考虑的问题。
谁都知道,通过计算“等额本金”与“等额本息”还款方式的应付利息,前者比后者要少付利息。
那么借款人选择等额本息还款法是不是一定就吃亏了呢?回答是否定的。
依笔者在银行的工作实践及对购房户的调查来看,大多数按揭客户都有提前还款、缩短借款期限的记录或计划。
事实上,借款人通过提前还款、缩短借款期限,可以取得与等额本金还款法大致相同,甚至比等额本金还款法还要少付利息的效果。

用Excel制作等额本金和等额本息两种还贷表Excel里计算还贷明细非常简单,我们来看针对等额本息、等额本金两种不同方式如何计算每月应还款额。
例:同事小张为了买新房准备到银行贷款30万元,商定20年还清。
如果用等额本息法,会把贷款总额的本息之和平均分摊到整个还款期,按月等额还款;如果用等额本金法,针将贷款额的本金平均分摊到整个还款期限内每月归还,同时付清上一交易日到本次还款日之间的贷款利息。
到底哪种还款方式对自己更有利一些?先算第一种方案,月还款额的计算在Excel中有专门的函数PMT。
其用法是PMT(月利率,还款期限,贷款总额),非常简单。
所以,我们只要如图1所示表格的B5单元格中,输入公式“=PMT(B2/12,B3,B4)”,回车后就可以得到按等额本息法计算的每月还款额,其中第一个参数“B2/12”是为了得到月贷款利率。
再在B6单元格输入公式“=B5*B3”,回车就可以轻松得到20年的还款总额了。
用第二种方案稍显麻烦一些。
按照规则,我们可以先将本金300000元分摊到每个月中,再计算每个月应支付的利息,显然,每个月应付利息数值是不同的。
因此,我们可以建立一个如图2所示的表格。
表格直至E244单元格,正好表示240个月。
在E2单元格输入公式“=300000/240”,回车后即可得到每月平均分摊的贷款本金。
在利息计算上,我们可以很容易地推想:每交完一次款后,那么下月付款时就会少交相应部分的利息。
因此,我们在表格的E5单元格输入公式“=(300000-($D5-1)*$E$2)*($B$2/12)”,回车后就可以得到第一次交款时所应付的利息部分。
其中“$B$2/12”仍然是根据年利率计算月利率。
拖动E5单元格的填充句柄向下直至E244单元格填充公式,那么每月应付的利息数就都有了。
我们每个月应付款为每月分摊的本金及应付利息数。
所以,找个空白单元格,输入公式“=SUM(E5:E244)+300000”,回车,就可以得到这20年中我们一共向银行交纳的钱数“519611.25”(真够恐怖的)。

基于Excel的等额还款与等本还款计算模型[摘要]等额还款与等本还款是按揭贷款中两种最常见的还款方式,笔者构建了基于Excel的等额还款与等本还款计算模型,模型由贷款参数与数据区域两部分组成。
通过该模型可以非常容易得到贷款周期内各期需要偿还的本金、利息,总还款额,提前还贷时的还款额,贷款利率变动时的还款额等重要信息,有助于事前制定合理的按揭贷款计划。
[关键词]等额还款;等本还款;计算模型;Excel1 引言在现代社会中,随着居民收入水平的提高以及消费观念的转变,按揭贷款购房、购车应运而生。
按揭贷款的还款方式有两种——等额还款法与等本还款法。
二者的主要区别在于等本还款法在整个贷款周期内支付的利息总和相对较少,提前还贷时“合算”,但主要缺点是前期还贷压力很大。
对于按揭者而言,不仅需要知道上述区别,还要把它们的区别量化。
况且我国目前正处于一个加息周期中,有比较明确的加息预期,按揭者希望在贷款前进行敏感性分析以了解利率在目前基础上每上升若干基点,还款额将增加多少,这样有利于做出合适的贷款计划。
面对诸如此类的问题,笔者构建了基于Excel的等额还款与等本还款模型,能提供按揭者需要的各种数据,比如:每期的还贷额,每期偿还的本金、利息,在某一期提前还贷时需要偿还的金额等。
当贷款利率等因素发生变动时,只需在模型中的贷款参数栏填入变动后的数值,上述各种按揭者需要的数据将自动更新,使用起来非常便利。
2 模型的构建2. 1等额还款模型等额还款模型包括两部分,一是贷款参数部分,由贷款年利率、贷款月利率、贷款期限、贷款金额4个参数组成。
其中贷款月利率等于贷款年利率除以12,由系统以公式的方式产生计算值,勿以人工方式填入,以防在除不尽时产生比较大的计算误差,其余的三要素则以手工填入。
二是各种还款数据区域,包括实际期次、计算期次、期初尚欠的贷款本金、本期需偿还的利息、截至本期末累计偿还的利息,本期需偿还的本金,截至本期末累计偿还的本金、本期还款之和、本期末尚欠的贷款本金等9个要素。
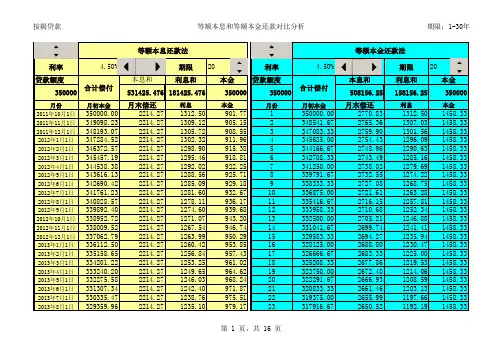
3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金350000531425.476181425.476350000350000508156.25158156.25350000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金2011年10月1日350000.002214.271312.50901.771350000.002770.831312.501458.332011年11月1日349098.232214.271309.12905.152348541.672765.361307.031458.332011年12月1日348193.072214.271305.72908.553347083.332759.901301.561458.332012年1月1日347284.522214.271302.32911.964345625.002754.431296.091458.332012年2月1日346372.572214.271298.90915.385344166.672748.961290.631458.332012年3月1日345457.192214.271295.46918.816342708.332743.491285.161458.332012年4月1日344538.382214.271292.02922.257341250.002738.021279.691458.332012年5月1日343616.132214.271288.56925.718339791.672732.551274.221458.332012年6月1日342690.422214.271285.09929.189338333.332727.081268.751458.332012年7月1日341761.232214.271281.60932.6710336875.002721.611263.281458.332012年8月1日340828.572214.271278.11936.1711335416.672716.151257.811458.332012年9月1日339892.402214.271274.60939.6812333958.332710.681252.341458.332012年10月1日338952.722214.271271.07943.2013332500.002705.211246.881458.332012年11月1日338009.522214.271267.54946.7414331041.672699.741241.411458.332012年12月1日337062.792214.271263.99950.2915329583.332694.271235.941458.332013年1月1日336112.502214.271260.42953.8516328125.002688.801230.471458.332013年2月1日335158.652214.271256.84957.4317326666.672683.331225.001458.332013年3月1日334201.222214.271253.25961.021*******.332677.861219.531458.332013年4月1日333240.202214.271249.65964.6219323750.002672.401214.061458.332013年5月1日332275.582214.271246.03968.2420322291.672666.931208.591458.332013年6月1日331307.342214.271242.40971.8721320833.332661.461203.131458.332013年7月1日330335.472214.271238.76975.5122319375.002655.991197.661458.332013年8月1日329359.962214.271235.10979.1723317916.672650.521192.191458.33合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金350000531425.476181425.476350000350000508156.25158156.25350000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金350000531425.476181425.476350000350000508156.25158156.25350000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金350000531425.476181425.476350000350000508156.25158156.25350000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金350000531425.476181425.476350000350000508156.25158156.25350000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金350000531425.476181425.476350000350000508156.25158156.25350000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金350000531425.476181425.476350000350000508156.25158156.25350000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金350000531425.476181425.476350000350000508156.25158156.25350000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金350000531425.476181425.476350000350000508156.25158156.25350000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金350000531425.476181425.476350000350000508156.25158156.25350000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金350000531425.476181425.476350000350000508156.25158156.25350000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金350000531425.476181425.476350000350000508156.25158156.25350000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金350000531425.476181425.476350000350000508156.25158156.25350000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金350000531425.476181425.476350000350000508156.25158156.25350000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金350000531425.476181425.476350000350000508156.25158156.25350000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金350000531425.476181425.476350000350000508156.25158156.25350000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法。

等额本息与等额本金还款方式的计算、比较及选择近日有朋友问起等额本息与等额本金还款的计算方法、区别以及如何选择,我到网上搜了搜,发现确实有很多人在询问这个问题,同时也有很多回答版本,但是没有一个版本是让我感到满意的,很多都是从很不严谨甚至很片面的角度来解答问题,给人一种盲人摸象的感觉,于是我才有了写这篇博客的想法。
第一:我们先来看看不同还款方式是如何计算的。
首先,我们先举一个极端的例子,如果贷款1,000,000元,贷款期限25年(300个月),当前银行的年贷款利率为5.94%(这里银行给的年贷款利率为年名义利率,转换为月实际利率为5.94%/12,以下用r表示),还款方式为到期一次性还本付息,那么25年后我们应该还银行多少钱呢?通常我们借助“时间图”工具来理解这个问题。
所谓“时间图”是一个一维的图形,其中时间单位沿一维正方向度量,支付和回收的款项则置于图上的对应时间点上,同一类型的款项(如同为支付款)位于图的下部,而另一类型的款项(如同为回收款)位于图的上部。
如下图所示:25年后一次还本付息的钱其实计算起来很简单,就是逐月复利累计生息的本利和:第1个月的本利和为:1000000*(1+r)第2个月的本利和为:1000000*(1+r)^2...第300个月的本利和为:1000000*(1+r)^300=4,398,821.70另,也可以通过excel里插入财务公式FV(0.0594/12,300,0,1000000,0)直接得到4,398,821.70然后,我们再来看看最常用的等额本息还款方式,同样贷款1,000,000元,贷款期限25年(300个月),当前银行的年贷款利率为5.94%,那么每个月需要还银行多少钱呢?25年中每个月要还的钱计算起来也不难,先假设每个月还款额为a,逐月计算贷款余额,令第300个月的贷款余额为零,这样就很容易求出这个还款额a了:第1个月:月还款利息1000000*r月还款本金a-1000000*r贷款余额1000000-(a-1000000*r)=1000000*(1+r)-a第2个月:月还款利息(1000000*(1+r)-a) *r月还款本金a- (1000000*(1+r)-a) *r贷款余额1000000*(1+r)-a-a+ (1000000*(1+r)-a) *r =1000000*(1+r)^2-a(1+(1+r)) ...第300个月:月还款利息(1000000*(1+r)^299-a(1+(1+r)+…+(1+r)^298) )*r月还款本金a-(1000000*(1+r)^299-a(1+(1+r)+…+(1+r)^298) )*r贷款余额1000000*(1+r)^299-a(1+(1+r)+…+(1+r)^298) -a+(1000000*(1+r)^299-a(1+(1+r)+…+(1+r)^298) )*r=1000000*(1+r)^300-a(1+(1+r)+…+(1+r)^299)=1000000*(1+r)^300-a*((1+r)^300-1)/r令1000000*(1+r)^300-a*r*((1+r)^300-1)/r=0 得月还款额a=6,406.39另,通过excel里插入财务公式PMT(0.0594/12,300,1000000,0,0)直接得到6,406.39 最后,我们来看看平时大家选择比较少的等额本金还款方式,同样是贷款1,000,000元,贷款期限25年(300个月),当前银行的年贷款利率为5.94%,那么每个月需要还银行多少钱呢?25年中每个月要还的钱计算起来最简单,既然是等额本金,那么首先可以计算出每个月应还银行的本金,即为1,000,000/300=3,333.33,接下来逐月计算每个月应还银行的钱:第1个月:月还款利息1000000*r=4,950.00月还款额3333.33+4950.00=8,283.33第2个月:月还款利息(1000000-3333.33)*r=4,933.50月还款额3333.33+4933.50=8,266.33...第300个月:月还款利息(1000000-299*3333.33)*r=16.5月还款额3333.33+16.5=3,349.83第二,各种不同还款方式下计算方法已经弄明白了,现在需要回答另外两个问题——不同还款方式有本质区别吗?我们该如何选择呢?“一次性还本利和方式”25年下来一共还了3,398,821.70的利息:4,398,821.70-1,000,000=3,398,821.70;“等额本息方式”25年下来一共还了921,917.00的利息:6,406.39*300-1,000,000=921,917.00;“等额本金方式”25年下来一共还了744,975.74的利息:8,283.33+8,266.33+…+3,349.83-1,000,000=744,975.74;为什么三种还款方式的利息会有如此大的差别呢?我们从excel表中三种还款方式还款额计算工作表中贷款余额一列可以清晰看到,任何时点(除最后一期),都存在“一次还本付息方式的贷款余额>等额本息还款方式的贷款余额>等额本金还款方式的贷款余额”。

吐血推荐详细说明等额本金和等额本息的计算方式与利弊关于利率表请查看以下的帖子,这里只给举出例子,相信大家看后都可以自己计算了。
注:1.贷款年限5年以上的年利率一律为5.4%。
2.月利率等额本金与等额本息的都一样为0.0042。
3.以贷款20万20年为例。
一、等额本金贷款利率计算1.20年应付利息:200000(元~贷款额)*5.04%(年利率)*20(年限)=201600(元)2.20年应付本息总计:200000(元~贷款额)+201600(元)=401600(元)3.首月还款:401600(元)÷240(月~期数)=1673.333(元)注:月还款额至此依次递减,绝对不会再超过这个数目。
4.首月利息:200000(元~贷款额)*0.0042(月利率)=840(元)5.首月本金:1673.333(元)-840(元)=833.333(元)注:一直到偿还全部贷款,每月本金保持833.333元不变,这也就是等额本金的命名来源。
6.第二月利息:200000(元~贷款额)-833.333(元)=199166.667(元)(贷款额减去已还本金)199166.667*0.0042(月利率)=836.500(元)7.第二月还款:833.333(元~本金)+836.500(元)=1669.833(元)8.第三月利息:199166.667(元~剩余贷款额)-833.333(元)=198333.334(元)198333.334(元)*0.0042(月利率)=833.000(元)9.第三月还款:833.333(元~本金)+833.000=1666.333(元)10.依次类推。
注:请注意每月还款额依次递减3.5元,和等额本息相比等额本金仍然是在先还利息,只不过在每月还款中利息与本金的比例降低了。
换句话说就是让你每月多还些本金且固定本金数额,这样逐月所付利息相应减少,这也就是等额本金还贷的前期压力较大的原因。
二、等额本息贷款利率计算1.首月还款:200000(元)*66.217(速算表系数)=1324.340(元)注:月还款额至还贷结束保持不变。

等额本息PK等额本金房贷还款哪种划算一、还款方式等额本金与等额本息哪个好一、还款方式等额本金与等额本息哪个好相较而言,等额本金的信贷方式较为划算。
由于借贷金额以及期限相同,采用等额本金偿还方式的总利息将明显低于等额本息。
无论是等额本金还是等额本息都具有各自的优势和劣势。
1.等额本金。
此种方法是每月还款额中的本金保持固定数值,利息则在每月逐渐减少。
在还款初期阶段,等额本金的月供应较之于等额本息较大,随后每个月都会逐步降低。
如此的还款模式虽然较初造成的费用压力大于等额本息,但总体的偿债利息却显著少于等额本息。
若用户有提前还款的计划,则建议选用等额本金的偿还方式。
2.等额本息。
该方式要求每月的还款金额保持稳定,因此在还款初期,每月的月供应便小于等额本金。
当购买者手中资金并不充裕,并寄希望于减轻经济压力时,等额本息作为一项可选方案也是值得考虑的。
《个人贷款管理暂行办法》第十四条贷款调查包括但不限于以下内容:(一)借款人基本情况;(二)借款人收入情况;(三)借款用途;(四)借款人还款来源、还款能力及还款方式;(五)保证人担保意愿、担保能力或抵(质)押物价值及变现能力。
二、信用卡还款后几个小时可以刷在完成信用卡还款之后,我们强烈建议您等候至少30分钟至2个小时以后再对同一张卡片进行进一步的消费行为。
此举的主要目的在于有效规避可能因此而触动的银行风险控制机制,从而有助于确保您的信用纪录始终保持在良好水平上。
当然,若如您在某些特殊情况下需立即使用到这张信用卡的话,稍微提前开始刷卡也是完全可以接受的选择。
但是,请格外留意不要过于频繁或大幅度的挥霍此卡的金融额度,避免因为支付动作过于异常而让银行反应过来将其视为一种潜在风险操作。
二、等额本金与等额本息哪个还贷方式更划算【等额本金】与【等额本息】的概念等额本金:每个月还款本金一样,利息递减,也就是一个月月还款总额较高,以后依次递减。
计算公式为:每月还款金额=(贷款本金/还款月数)+(本金—已归还本金累计额)×每月利率。
等额本息和等额本金哪个划算一、背景在购买房屋、购车等大额支出时,许多人会选择贷款来分期偿还。
等额本息和等额本金是两种常见的贷款还款方式。
那么,在选择贷款方式时,应该选择哪一种方式呢?本文将从利息计算、月供变化和总还款额等方面对比等额本息和等额本金,分析哪一种方式更划算。
二、等额本息等额本息是一种贷款还款方式,在还款期限内每月还款金额相等,包括本金和利息。
在贷款初期,由于贷款本金较高,利息占比较大,因此每月还款额较高。
随着贷款期限的推移,贷款本金逐渐减少,利息逐渐减少,每月还款额也逐渐减少。
具体计算公式如下:月还款额 = (贷款本金 × 月利率 × (1 + 月利率) ^ 还款月数) / ((1 + 月利率) ^ 还款月数 - 1)三、等额本金等额本金是另一种贷款还款方式,每月还款本金相等,而利息则随着贷款本金的减少而逐渐减少。
在还款期限内,每月还款金额逐渐减少。
具体计算公式如下:月还款额 = 贷款本金 / 还款月数 + (贷款本金 - 当前已还本金累计额) × 月利率四、对比分析1. 利息计算在等额本息方式下,由于每月还款金额固定,利息计算相对简单明确。
在还款期限内,每月利息逐渐减少。
而在等额本金方式下,由于每月还款本金相等,每月还款利息是按照剩余贷款本金计算的,因此每月还款利息会逐渐减少。
综合来看,等额本金方式的贷款利息较低,相比等额本息方式更加划算。
2. 月供变化在等额本息方式下,每月还款额固定,无论是贷款初期还是还款末期,还款金额都一样。
这对于月收入较固定的人来说,可能比较合适。
而在等额本金方式下,由于每月还款本金相等,每月还款金额会逐渐减少。
即一开始每月还款较高,后期每月还款较低。
这对于一些月收入会逐渐增加的人来说,可能更加适合。
3. 总还款额总还款额是选择贷款方式时一个重要的考虑因素。
在等额本息方式下,由于每月还款额固定,因此总还款额较等额本金方式要高。
因为在等额本金方式下,贷款本金逐渐减少,因此要还的利息也相应减少。
3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金319000484356.3624165356.362319000319000463148.13144148.13319000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金2011年10月1日319000.002018.151196.25821.901319000.002525.421196.251329.172011年11月1日318178.102018.151193.17824.982317670.832520.431191.271329.172011年12月1日317353.112018.151190.07828.083316341.672515.451186.281329.172012年1月1日316525.042018.151186.97831.184315012.502510.461181.301329.172012年2月1日315693.852018.151183.85834.305313683.332505.481176.311329.172012年3月1日314859.562018.151180.72837.436312354.172500.491171.331329.172012年4月1日314022.132018.151177.58840.577311025.002495.511166.341329.172012年5月1日313181.562018.151174.43843.728309695.832490.531161.361329.172012年6月1日312337.842018.151171.27846.889308366.672485.541156.381329.172012年7月1日311490.952018.151168.09850.0610307037.502480.561151.391329.172012年8月1日310640.892018.151164.90853.2511305708.332475.571146.411329.172012年9月1日309787.642018.151161.70856.4512304379.172470.591141.421329.172012年10月1日308931.202018.151158.49859.6613303050.002465.601136.441329.172012年11月1日308071.542018.151155.27862.8814301720.832460.621131.451329.172012年12月1日307208.652018.151152.03866.1215300391.672455.641126.471329.172013年1月1日306342.542018.151148.78869.3716299062.502450.651121.481329.172013年2月1日305473.172018.151145.52872.6317297733.332445.671116.501329.172013年3月1日304600.542018.151142.25875.9018296404.172440.681111.521329.172013年4月1日303724.642018.151138.97879.1819295075.002435.701106.531329.172013年5月1日302845.462018.151135.67882.4820293745.832430.711101.551329.172013年6月1日301962.982018.151132.36885.7921292416.672425.731096.561329.172013年7月1日301077.192018.151129.04889.1122291087.502420.741091.581329.172013年8月1日300188.072018.151125.71892.4523289758.332415.761086.591329.17合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金319000484356.3624165356.362319000319000463148.13144148.13319000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金319000484356.3624165356.362319000319000463148.13144148.13319000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金319000484356.3624165356.362319000319000463148.13144148.13319000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金319000484356.3624165356.362319000319000463148.13144148.13319000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金319000484356.3624165356.362319000319000463148.13144148.13319000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金319000484356.3624165356.362319000319000463148.13144148.13319000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金319000484356.3624165356.362319000319000463148.13144148.13319000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金319000484356.3624165356.362319000319000463148.13144148.13319000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金319000484356.3624165356.362319000319000463148.13144148.13319000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法按揭贷款等额本息和等额本金还款对比分析期限:1-30年3535利率 4.50%450.00期限20利率 4.50%期限20贷款额度本息和利息和本金贷款额度本息和利息和本金319000484356.3624165356.362319000319000463148.13144148.13319000月份月初本金月末偿还利息本金月份月初本金月末偿还利息本金合计偿付合计偿付等额本息还款法等额本金还款法第 11 页,共 11 页。
用excel编制等额本金与等额本息还款表用excel编制等额本金与等额本息还款表目前,银行的个人按揭贷款的还款方式主要有以下2种方式:等额本金与等额本息。
借贷者往往十分纠结于是选用等额本金,还是等额本息实惠,还有提前还款是否要吃亏等问题,下面通过excel计算,一方面给出了两种方式的还款明细表,另一面通过对计算过程的理解,让大家知道其实无论选用哪一种方式都是一样的,无所谓吃亏与否。
一、等额本金设借贷金额500000元,贷款年限5年,贷款期数60期,首次还贷日期2016年1月20日,按如下图所示设计等额本金贷款还款计划书。
在单元格A6键入公式:=IF(ROW()-5>$F$3,"",ROW()-5),然后向下引用。
在单元格B6键入公式:=H3&"/"&J3&"/"&L3在单元格C6键入年利率百分点p=4.25,在单元格F6键入公式:=ROUND(B3/F3,2)在单元格G6键入公式:=ROUND(B3*C6/100/12,2)在单元格E6键入公式:=F6+G,然后向下引用。
在单元格H6键入公式:=B3-F6在单元格J6键入公式:=E6在单元格B7键入公式:=IF(A7<>"",$H$3+INT(($J$3-2+A7)/12)&"/"&(($ J$3-1+A7)-12*INT(($J$3-2+A 7)/12))&"/"&$L$3,""),然后向下引用。
在单元格C7键入公式:=IF(A7<>"",C6,""),然后向下引用。
在单元格F7键入公式:=IF(A7<>"",H6/($F$3-A6),""),然后向下引用。