26.1二次函数水平测试(含答案)

二次函数测试题及答案一、选择题（每题3分，共30分）1. 以下哪个选项是二次函数的一般形式？A. y = 2x + 1B. y = x^2 + 3x + 2C. y = 3x^3 - 5D. y = 4/x答案：B2. 二次函数y = ax^2 + bx + c的顶点坐标为（h, k），那么h的值为：A. -b/2aB. -b/aC. b/2aD. b/a答案：C3. 二次函数y = 2x^2 - 4x + 3的对称轴方程是：A. x = 1B. x = -1C. x = 2D. x = -2答案：A4. 如果二次函数y = ax^2 + bx + c的图象开口向上，那么a的值：A. 大于0B. 小于0C. 等于0D. 可以是任意实数答案：A5. 二次函数y = -x^2 + 4x - 3的顶点坐标是：A. (1, 2)B. (2, 1)C. (3, 0)D. (3, 4)答案：C6. 二次函数y = 3x^2 - 6x + 5的图象与x轴的交点个数是：A. 0个B. 1个C. 2个D. 3个答案：C7. 二次函数y = x^2 - 4x + 4的最小值是：A. 0B. 4C. -4D. 1答案：A8. 二次函数y = 2x^2 - 4x + 3的图象开口方向是：A. 向上B. 向下C. 向左D. 向右答案：A9. 二次函数y = -x^2 + 2x + 3的图象与y轴的交点坐标是：A. (0, 3)B. (0, -3)C. (0, 5)D. (0, -5)答案：A10. 二次函数y = 5x^2 - 10x + 8的图象与x轴的交点坐标是：A. (2, 0)B. (-2, 0)C. (1, 0)D. (-1, 0)答案：A二、填空题（每题4分，共20分）1. 二次函数y = ax^2 + bx + c的图象开口向上，且经过点（2, 0），则a的值至少为______。

答案：02. 二次函数y = 2x^2 - 4x + 3的顶点坐标是（______, ______）。

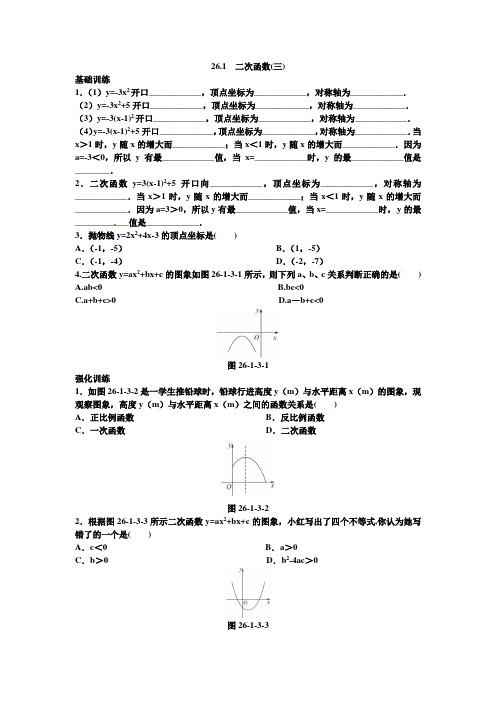
26.1 二次函数(三)基础训练1．（1）y=-3x2开口____________，顶点坐标为____________，对称轴为____________．（2）y=-3x2+5开口____________，顶点坐标为____________，对称轴为____________．（3）y=-3(x-1)2开口____________，顶点坐标为____________，对称轴为____________．（4）y=-3(x-1)2+5开口____________，顶点坐标为____________，对称轴为____________．当x＞1时，y随x的增大而____________；当x＜1时，y随x的增大而____________．因为a=-3＜0，所以y有最____________值，当x=____________时，y的最____________值是________．2．二次函数y=3(x-1)2+5开口向____________，顶点坐标为____________，对称轴为____________．当x＞1时，y随x的增大而____________；当x＜1时，y随x的增大而____________．因为a=3＞0，所以y有最____________值，当x=____________时，y的最____________值是____________．3．抛物线y=2x2+4x-3的顶点坐标是( )A．（-1，-5）B．（1，-5）C．（-1，-4）D．（-2，-7）4.二次函数y=ax2+bx+c的图象如图26-1-3-1所示，则下列a、b、c关系判断正确的是( )A.ab<0B.bc<0C.a+b+c>0D.a－b+c<0图26-1-3-1强化训练1．如图26-1-3-2是一学生推铅球时，铅球行进高度y（m）与水平距离x（m）的图象，现观察图象，高度y（m）与水平距离x（m）之间的函数关系是( )A．正比例函数B．反比例函数C．一次函数D．二次函数图26-1-3-22．根据图26-1-3-3所示二次函数y=ax2+bx+c的图象，小红写出了四个不等式,你认为她写错了的一个是( )A．c＜0 B．a＞0C．b＞0 D．b2-4ac＞0图26-1-3-33．二次函数y=21x 2+3x+25的图象是由函数y=21x 2的图象先向_________（左、右）平移个_________单位，再向_________（上、下）平移_________个单位得到的．4．(甘肃兰州模拟)一条抛物线的对称轴是x=1且与x 轴有唯一的公共点，并且开口方向向下，则这条抛物线的解析式是_________（任写一个）．5．如图26-1-3-4，AC ⊥CD ，甲、乙两船分别从A 地和C 地同时开出，各沿箭头所指方向航行，AC=10海里，甲、乙两船的速度分别为16海里/时和12海里/时，问多长时间后两船相距最近，最近距离为多少？（甲船到C 地后不再行驶）图26-1-3-4巩固训练1．若二次函数y=ax 2+ax-1的最小值为47，则a 的值是( ) A ．-1 B ．0 C ．3 D ．3或02．如图26-1-3-5,关于x 的两个函数y=x 2+2mx+m 2和y=mx-m(m≠0)在同一坐标系中的图象可能是( )图26-1-3-53．由于被墨水污染，一道数学题仅能见到如下文字：“已知二次函数y=x 2+bx+c 的图象过点(1，0)……求证：这个二次函数的图象关于直线x=2对称．”根据现有信息，题中的二次函数图象不具有的性质是( ) A ．过点（3，0） B ．顶点是（2，-2） C.b ＜0 D.c=34．已知A(a+1,a 2)在函数y=x 2+2x 的图象上，则a=______________．5．若抛物线y=x 2+4x+c 的顶点在x 轴上，则c=______________；若抛物线y=x 2+2bx+3的对称轴是y 轴，则b=______________；若抛物线y=x 2+2mx+m 2-3m+6的顶点在x 轴下方，则m 的取值范围是______________．6．已知抛物线y=x 2+4x-k-1与x 轴有两个交点，且这两个交点分别在直线x=1的两侧，则k 的取值范围为______________．7．通过配方，确定抛物线y=-2x 2+4x+6的开口方向、对称轴、顶点坐标，再描点画图． 8．已知两数和为20，当这两个数各为多少时，这两个数的积最大？9．老师给出一个函数y=f（x），甲、乙、丙、丁四位同学各指出这个函数的一个性质：甲：函数图象不经过第三象限；乙：函数图象经过第一象限；丙：当x＜2时，y随x的增大而减小；丁：当x＜2时，y＞0．已知这四位同学的叙述都正确，请你构造满足上述所有性质的一个二次函数．10．如图26-1-3-6，已知等腰梯形ABCD的边BC在x轴上，点A在y轴的正方向上，A(0,6)、2．D(4，6），且AB＝10图26-1-3-6（1）求点B的坐标；（2）求经过A、B、D三点的抛物线的解析式.11．(2010江苏盐城模拟，26)已知抛物线y=-x2+4x-3与x轴相交于A、B两点(A点在B点的左侧)，顶点为P．图26-1-3-7(1)求A、B、P三点坐标；(2)在右面的直角坐标系内画出此抛物线的简图，并根据简图写出当x取何值时，函数值y 大于零；(3)确定此抛物线与直线y=-2x+6公共点的个数，并说明理由．26.1 二次函数(三)5分钟训练(预习类训练，可用于课前) 1．（1）y=-3x 2开口____________，顶点坐标为____________，对称轴为____________． （2）y=-3x 2+5开口____________，顶点坐标为____________，对称轴为____________． （3）y=-3(x-1)2开口____________，顶点坐标为____________，对称轴为____________． （4）y=-3(x-1)2+5开口____________，顶点坐标为____________，对称轴为____________．当x ＞1时，y 随x 的增大而____________；当x ＜1时，y 随x 的增大而____________．因为a=-3＜0，所以y 有最____________值，当x=____________时，y 的最____________值是________．解析：二次函数y=ax 2＋bx ＋c 的对称轴是x=a b 2-，顶点坐标为（ab ac a b 44,22--），由a＜0开口向下，有最大值，a ＞0开口向上，有最小值．再由对称轴两侧看变化．答案：（1）向下 （0，0） x=0 （2）向下 （0，5） x=0 （3）向下 （1，0） x=1 [来源:Z*xx*]（4）向下 （1，5） x=1 减小 增大 大 1 大 52．二次函数y=3(x-1)2+5开口向____________，顶点坐标为____________，对称轴为____________．当x ＞1时，y 随x 的增大而____________；当x ＜1时，y 随x 的增大而____________．因为a=3＞0，所以y 有最____________值，当x=____________时，y 的最____________值是____________．解析：在二次函数中，当二次项系数大于0时，开口向上，有最低点，最小值，在对称轴左侧，函数值y 随着x 的增大而减小；在对称轴右侧，函数值y 随着x 的增大而减小． 答案：上 （1，5） x=1 增大 减小 小 1 小 5 3．抛物线y=2x 2+4x-3的顶点坐标是( ) A ．（-1，-5） B ．（1，-5） C ．（-1，-4） D ．（-2，-7） 解析：方法一（配方法）：y=2x 2+4x-3=2(x 2+2x-23)＝2（x 2+2x+1-1-23）=2(x+1)2-5，∴顶点坐标为（-1，-5）． 方法二（公式法）：∵a=2，b=4， c=-3， ∴2242⨯-=-a b =-1， 2416)3(24442⨯--⨯⨯=-a b ac =-5． ∴顶点坐标为（-1，-5）. 答案：A4.二次函数y=ax 2+bx+c 的图象如图26-1-3-1所示，则下列a 、b 、c 关系判断正确的是( ) A.ab<0 B.bc<0C.a+b+c>0D.a －b+c<0图26-1-3-1解析：抛物线开口向下，a ＜0,对称轴为直线x=ab2-＜0,得b ＜0，由与 y 轴交点知c<0，所以ab>0，bc>0．当x=1时得a+b+c<0，当x=-1时得a-b+c<0. 答案：D10分钟训练(强化类训练，可用于课中)[来源:学科网ZXXK]1．如图26-1-3-2是一学生推铅球时，铅球行进高度y （m ）与水平距离x （m ）的图象，现观察图象，高度y （m ）与水平距离x （m ）之间的函数关系是( ) A ．正比例函数 B ．反比例函数 C ．一次函数 D ．二次函数图26-1-3-2解析：由图形可知，图中函数图象是一抛物线,是二次函数，而一次函数的图象是直线，反比例函数的图象是双曲线，反之亦成立． 答案：D[来源:学_科_网]2．根据图26-1-3-3所示二次函数y=ax 2+bx+c 的图象，小红写出了四个不等式,你认为她写错了的一个是( )A ．c ＜0B ．a ＞0C ．b ＞0D ．b 2-4ac ＞0[来源:Z+xx+] 图26-1-3-3解析：观察图形知，对称轴x=ab2-＞0,又开口向上a ＞0,所以b ＜0． 答案：C 3．二次函数y=21x 2+3x+25的图象是由函数y=21x 2的图象先向_________（左、右）平移个_________单位，再向_________（上、下）平移_________个单位得到的．解析：一般先将二次函数由一般式化成顶点式，再确定上下左右平移的单位，但是，在化为顶点式时，常常会出现下列错误，应引以为戒． 错解一：y=21x 2+3x+25=21（x 2+23x+45)=21x 2+23x+169-169+45)=21(x+43)2+811，∴y=21x 2+3x+25是由y=21x 2向左平移43个单位，再向上平移811个单位得到的．错解二：y=21x 2+3x+25=21x 2+6x+5)=21(x 2+6x+9-9+5)=21(x+3)2-4．正确解法：y=21x 2+3x+25=21（x 2+6x+5）=21(x 2+6x+9-9+5)=21(x+3)2-2．∴抛物线y=21x 2+3x+25是由y=21x 2向左平移3个单位，再向下平移2个单位得到的．答案：左 3 下 24．(甘肃兰州模拟)一条抛物线的对称轴是x=1且与x 轴有唯一的公共点，并且开口方向向下，则这条抛物线的解析式是_________（任写一个）．解析：由与x 轴有唯一交点知该抛物线顶点在x 轴上，所以可写为y= -2(x-1)2等．[来源:Z_xx_]答案：y=-2(x-1)25．如图26-1-3-4，AC ⊥CD ，甲、乙两船分别从A 地和C 地同时开出，各沿箭头所指方向航行，AC=10海里，甲、乙两船的速度分别为16海里/时和12海里/时，问多长时间后两船相距最近，最近距离为多少？（甲船到C 地后不再行驶）图26-1-3-4解：设BD=y 海里，两船行驶的时间为x 小时，BC=10-16x ，CD=12x ，根据题意，得y=100320400)12()1610(222+-=+-x x x x=36)52(400)100925454(400)4154(400222+-=++-=+-x x x x x ∴当x=52时，y 有最小值为6（海里）． 答：经过0．4小时后，两船距离最近，距离最近为6海里． 30分钟训练(巩固类训练，可用于课后) 1．若二次函数y=ax 2+a-1的最小值为47-，则a 的值是( ) A ．-1 B ．0 C ．3 D ．3或0解析:可直接写出顶点的纵坐标，即函数的最小值，但解题时易忘记隐含条件a ＞0．错解：∵二次函数y=ax 2+a-1有最小值47-，∴47442-=--a a a ．两边同乘以4a ，整理得a 2-3a=0．解得a 1=0，a 2=3．故选D ．正确解法：∵二次函数有最小值，∴a>0．∴a=3． 答案：C[来源:]2．如图26-1-3-5,关于x 的两个函数y=x 2+2mx+m 2和y=mx-m(m≠0)在同一坐标系中的图象可能是( )图26-1-3-5解析:应分两种情况，m>0时,抛物线开口向上，直线过一、四、三象限和m<0时,抛物线开口向上，直线过二、一、四象限，顶点坐标为（－m,0）． 答案：C3．由于被墨水污染，一道数学题仅能见到如下文字：“已知二次函数y=x 2+bx+c 的图象过点(1，0)……求证：这个二次函数的图象关于直线x=2对称．”根据现有信息，题中的二次函数图象不具有的性质是( ) A ．过点（3，0） B ．顶点是（2，-2） C.b ＜0 D.c=3解析:由题意知二次函数y=x 2+bx+c 的图象过点(1，0)，且这个二次函数的图象关于直线x=2对称,故A 、C 都正确.由2b-=2，b=-4,把点(1，0)代入得c=3，D 也正确．当x=2时，y=-1，所以顶点坐标为（2，-1）． 答案：B4．已知A(a+1,a 2)在函数y=x 2+2x 的图象上，则a=______________． 解析:把x=a+1，y=a 2代入y=x 2+2x ，得a 2=(a+1)2+2(a+1)．解得a=43-．[来源:学,科,网] 答案：43-5．若抛物线y=x 2+4x+c 的顶点在x 轴上，则c=______________；若抛物线y=x 2+2bx+3的对称轴是y 轴，则b=______________；若抛物线y=x 2+2mx+m 2-3m+6的顶点在x 轴下方，则m 的取值范围是______________．解析:抛物线y=x 2+4x+c 的顶点在x 轴上，则42-4c=0，∴c=4．抛物线y=x 2+2bx+3的对称轴为y 轴，则b=0；抛物线y=x 2+2mx+m 2-3m+6开口向上，若顶点在x 轴下方，则需Δ>0，即4m 2-4(m 2-3m+6)>0．∴m>2．答案：4 0 m>2[来源:Z§xx§]6．已知抛物线y=x 2+4x-k-1与x 轴有两个交点，且这两个交点分别在直线x=1的两侧，则k 的取值范围为______________． 解析:设抛物线与x 轴交于（x 1，0）、（x 2，0），则（x 1-1）（x 2-1）<0． ∴x 1x 2-(x 1+x 2)+1<0.∴⎩⎨⎧<+++->---.014)1(,0)1(442k k 解这个不等式组，得⎩⎨⎧>->.4,5k k ∴k ＞４答案：k>47．通过配方，确定抛物线y=-2x 2+4x+6的开口方向、对称轴、顶点坐标，再描点画图．解析:配方为y=-2x 2+4x+6=-2(x 2-2x-3)=-2(x 2-2x+1-4)=-2（x-1）2+8．所以开口向下，对称轴为直线x=1，顶点坐标为（1，8）.描点画图略．答案：y=-2（x-1）2+8，抛物线开口向下，对称轴为直线x=1，顶点坐标为（1，8），图略. 8．已知两数和为20，当这两个数各为多少时，这两个数的积最大？ 解：设其中一个为x,另一个为20-x,根据题意得，y=x(20-x)=-x 2+20x=-(x-10)2+100， 当x=10时,y 最大值=100，所以当两个数分别为10，10时，积最大为100． 9．老师给出一个函数y=f （x ），甲、乙、丙、丁四位同学各指出这个函数的一个性质： 甲：函数图象不经过第三象限； 乙：函数图象经过第一象限；丙：当x ＜2时，y 随x 的增大而减小； 丁：当x ＜2时，y ＞0．已知这四位同学的叙述都正确，请你构造满足上述所有性质的一个二次函数．解析:设所求函数为二次函数，开口向上，对称轴为直线x=2，顶点在第一象限，不妨设为（2，3），即可求出关系式．（写出一个即可）答案：y=x 2-4x+7． 10．如图26-1-3-6，已知等腰梯形ABCD 的边BC 在x 轴上，点A 在y 轴的正方向上，A(0,6)、D(4，6），且AB ＝102．图26-1-3-6[来源:学科网ZXXK]（1）求点B 的坐标；（2）求经过A 、B 、D 三点的抛物线的解析式.解：（1）在Rt △ABC 中，OB 2=AB 2-OA 2，所以OB=2，又因为点B 在x 轴的负半轴上，所以B （－2，0）．（2）设过A 、B 、D 三点的抛物线的解析式为y=ax 2+bx+c ，将A （0，6），B （－2，0），D （4，6）三点的坐标代入得⎪⎪⎩⎪⎪⎨⎧==-=⎪⎩⎪⎨⎧=+-=++=.6,2,21,024,6416,6c b a c b a c b a c 解得所以y=-21x 2+2x+6． 11．(2010江苏盐城模拟，26)已知抛物线y=-x 2+4x-3与x 轴相交于A 、B 两点(A 点在B 点的左侧)，顶点为P ．图26-1-3-7(1)求A 、B 、P 三点坐标；(2)在右面的直角坐标系内画出此抛物线的简图，并根据简图写出当x 取何值时，函数值y 大于零；(3)确定此抛物线与直线y=-2x+6公共点的个数，并说明理由．解:(1)令y=0,解方程-x 2+4x-3=0则x 1=1,x 2=2,则A(1,0),B(3,0).将y=-x 2+4x-3配方得y=-(x-2)2+1,得顶点P(2,1). (2)作图,当1<x<3时,y>0.(3)由题意列方程组得⎩⎨⎧+-=-+-=.62,342x y x x y转化得x 2-6x+9=0,Δ=0,∴方程的两根相等,方程只有一组解.[来源:学科网] ∴此抛物线与直线有唯一的公共点.。

第二十六章二次函数26.1 二次函数(一)1.矩形周长是20cm,一边长是x㎝,面积是y㎝2,则y与x的函数关系式是,这个函数称作次函数.2.下列函数y=0.5x-1,y=3x2,y=0.5x2-4x+1,y=x(x-2),y=(x-1)2-x2中,二次函数的个数为( )(A)2个(B)3个(C)4个(D)5个3.k取哪些值时,函数y=(k2-k)x2+kx+(k+1)是以x为自变量是一次函数?二次函数?4.已知等腰直角三角形的斜边长为xcm,面积为ycm2,请写出y与x的函数关系式,并判断它是什么函数?5.如图,正方形ABCD边长是4,E､F分别在BC､CD上,设ΔAEF面积是y,EC=x,如果CE=CF,试求出y与x的函数关系及自变量取值范围,并判定y是x的什么函数?6.已知二次函数y=ax2+c,当x=0时，y=-3;当x=1时，y=-1,求当x=-2时，y的值.7.一块矩形耕地大小尺寸如下图,要在这块地上沿东西方向挖一条水渠,沿南北方向挖两条水渠,水渠宽为xm,余下的可耕地面积为ym2,(1)请你写出y与x之间的函数关系式.(2)根据你写出的函数关系式,求出水渠宽为1m时,余下的可耕地面积为多少?(3)若耕除去水渠剩余部分面积为4408m2,求此时水渠的宽度.26.1二次函数(二)1.已知函数y=ax2的图象过点(2,-4),则a=,对称轴是,顶点坐标是,抛物线的开口方向,抛物线的顶点是最点.2.下列关于函数y=-0.5x2的图象说法( )①图象是一条抛物线;②开口向下;③对称轴是y轴;④顶点(0,0).其中正确的有( )(A)1个(B)2个(C)3个(D)4个3.已知函数y=x2的图象过点(a,b),则它必通过的另一点是( )(A)(a,-b) (B)(-a,b)(C)(-a,-b) (D)(b,a)4.抛物线y=ax2过A(-1,2),试判断B(-2,-3),C(,)是否在抛物线上.5､已知正方形的对角线长为x,面积为y.(1)写出y与x的函数关系;(2)画出这个函数的图象草图.6.抛物线y=ax2(a≠0)与直线y=4x-3交于点A(m,1),求:(1)点A的坐标及抛物线顶点C的坐标和对称轴;(2)抛物线y=ax2与直线y=4x-3是否还有其他交点?若有,请求出这个交点B的坐标,若没有,请说明理由. 并求点A､B､C三点构成的三角形的面积.2.6.1二次函数(三)1.函数y=-1.5x2+2的图象开口方向,对称轴是,顶点坐标是,当x=时,y最大.2.把抛物线y=-x2向上平移4个单位后,得到的抛物线的函数解析式为,平移后的抛物线的顶点坐标是,对称轴是,与y轴的交点坐标是,与x轴的交点坐标是.3.将抛物线y=2x2-3通过下列( )平移后得到抛物线y=2x2,(A)向下平移3个单位(B)向上平移3个单位(C)向下平移2个单位(D)向上平移2个单位4.已知抛物线的对称轴是y轴,顶点的纵坐标为5,且过点(1,2)求这条抛物线的解析式.5.抛物线y=ax2+c顶点是(0,2),且形状及开口方向与y=-0.5x2相同.(1)确定a､c的值;(2)画出这个函数的图象.6.在同一坐标系中,画出函数y=-x2+2与y=x2-2的图像请分别说出图象的顶点坐标､对称轴及开口方向,并比较两个图像之间有何联系?26.1二次函数(四)1.抛物线y=3(x-2)2的对称轴是( )(A)直线x=2 (B)直线x=-2 (C)y 轴 (D)x 轴2.将抛物线y=3x 2向左平移3个单位所得的抛物线的函数关系式为( )A ､332-=x y B ､2)3(3-=x y C ､332+=x y D ､2)3(3+=x y3.抛物线2)1(--=x y 是由抛物线向平移个单位得到的,平称后的抛物线对称轴是,顶点坐标是,当x=时,y 有最值,其值是.4.用配方法把下列函数化成y=a(x-h)2的形式,并指出开口方向,顶点坐标和对称轴.(1)y=x 2+4x+4(2)y=- x 2+3x-(3)y=2x 2-4x5､已知二次函数图像的顶点在x 轴上,且图像经过点(2,-2)与(-1,-8)求此函数解析式.6.抛物线2)2(-=x a y 经过(1,-1).(1)确定a 的值;(2)画出这个函数图象; (3)求出抛物线与坐标轴的交点坐标.2.6.1 二次函数(五) 1､填表2､下列抛物线顶点是(2,1)的是( )A.1)2(22--=x yB.2)1(32+-=x y C.1)2(22+-=x y D.2)1(42+-=x y 3､抛物线23x y =先向上平移2个单位,后向右平移3个单位,所得抛物线是( )A.2)3(32-+=x y B.2)3(32++=x y C.2)3(32--=x y D.2)3(32+-=x y 4､抛物线的顶点在(-1,-2)且又过(-2,-1). (1)确定抛物线的解析式; (2)画出这个函数的图象.综合与运用5､如图所示,求:(1)抛物线的解析式,(2)抛物线与x 轴的交点坐标.6.某同学在推铅球时,推球经过的路线是抛物线的一部分(如图),出手处A 点坐标是(0,2),最高点B 坐标是(6,5),(1)求此抛物线的函数表达式.(2)你能算出这位学生推出的铅球有多远吗?拓展与探索7.如图,在一幢建筑物里,从10m 高的窗户处用水管斜着向外喷水,喷出的水,在垂直于墙壁的平面内画出一条抛物线,其顶点离墙1m,并且在离墙3m 处落到地面上,问抛物线的顶点比喷出的水高出多少?26.1二次函数(六)1､二次函数322+-=x x y 的顶点坐标是( ) A ､(1,0) B ､(1,2) C ､(2,1) D ､(―1,―2)2､二次函数y= x 2+x-1的图像是由函数y=x 2的图像先向平移个单位,再向平移个单位得到的. 3､用配方法求下列抛物线的顶点坐标和对称轴(1)x x y -=2(2)122+--=x x y4､写出下列抛物线的开口方向､对称轴､顶点坐标,当x 为何值时,y 有最大(小)值?并求其值. (1)y=-x 2+3x-2 (2))12)(2(--=x x y综合与运用5､有一矩形的苗圃,其四周是总长为40m 篱笆,假设它的一边长为xm ,面积为2ym . (1)y 随x 的变化的规律是什么?请分别用函数的表达式､表格､函数的图象表示出; (2)由函数的图象指出当x 取何值时,苗圃的面积最大?最大面积是多少?6､有一条长为7.2m 的木料,做成如图所示的“日”字形的窗柜,窗柜的宽和高各取多少时,这个窗的面积S 最大?最大面积是多少?(不考虑木料加工时的损耗和中间木柜所占的面积)7､心理学家发现,学生对概念的接受能力y 与提出概念所用的时间x (单位:min)之间满足函数关系y=-0.1x 2+2.6x+43 (0≤x ≤30),y 值越大,表示接受能力越强.(1)x 在什么范围内,学生的接受能力逐步增强?x 在什么范围内,学生的接受能力逐步降低? (2)第10min 时,学生的接受能力是多少? (3)多长时间内,学生的接受能力最强? 复习巩固1､下列函数中,是二次函数的是( )A ､y=0.5(x-3)xB ､y=(x+2)(x-2)-x 2C ､y=-0.75xD ､y=2､抛物线1)1(22+-=x y 的顶点是( ) A ､(1,1) B ､(-1,1) C ､(1,-1) D ､(-1,-1)3､顶点是(-2,0),开口方向､形状与抛物线y=0.5x 2相同的抛物线是( )A ､y=0.5(x-2)2B ､y=0.5(x+2)2C ､y=-0.5(x-2)2D ､y=-0.5(x+2)2 4､抛物线32+=x y 向右平移2个单位,再向上平移3个单位,所得新的抛物线是. 5､写出一个开口向下且对称轴是x=-2的二次函数解析式 6､将二次函数222---=x x y 经配方后得( )A ､3)1(2---=x y B ､3)1(2-+-=x yC ､1)1(2---=x yD ､1)1(2-+-=x y 7､二次函数42-=x y 与x 轴的交点坐标为,8､二次函数a x ax y ++=42的最大值是3,则=a9､将一根铁丝长为x,围成一个等边三角形,则面积S 与周长x 的关系式为. 10､ 根据下列条件,分别确定二次函数中字母系数的值:(1)抛物线c x x y ++=42的顶点在x 轴上;c= (2)抛物线232+-=x ax y 的图像经过点(-1,3)a= (3)抛物线52+-=bx x y 的对称轴是直线x=-2,b=综合与运用11､如图,有一直角梯形的苗圃,它的两邻边借用夹角是135°的两围墙,另外两边用总长为30m的篱笆,问篱笆的两边各是多少米时,苗圃的面积最大?最大面积是多少?12､某商场将进价为30元的台灯以40元售出,平均每月能售出600个,调查表明:这种台灯的售价每上涨1元,其销售量就减少10个.(1)为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少?这时应进台灯多少个?(2)如果商场要想每月的销售利润最多,这种台灯的售价又将定为多少?这时应进台灯多少个?13.某瓜果基地市场部为指导该基地某种蔬菜的生产和销售,在对历年市场行情和生产情况进行了调查的基础上,对今年这种蔬菜上市后的市场售价和生产成本进行了预测,提供了两个方面的信息,如图甲､乙两图请你根据图象提供的信息说明:(1)在3月份出售这种蔬菜,每千克的收益是多少元?(收益=售价-成本)(2)哪个月出售这种蔬菜每千克的收益最大?说明理由.拓展与探索14､已知二次函数y=-0.5x 2+x+1.5 (1)用配方法求它的顶点坐标和对称轴; (2)画出这个函数的图象;(3)根据图象回答:当x 取哪些值时,y =0,y >0,y <0第二十六章答案 26.1二次函数(一)1､x x y 102+-=,二. 2､B 3､k=1,k ≠0且k ≠1.4､241x y =它是二次函数 5､x x y 4212+-= 0<x<4,二次 6､5 7(1)480020022+-=x x y , (2)4602m 2, (3)此时水渠的宽度是2m.26､1二次函数(二)1､-1 y 轴 (0,0) 向下 高 2､D 3､B 4､点B 不在,点C 在 5､(1)221x y = (2)略 6､A 7(1)A(1,1) 顶点C(0,0)对称轴是y 轴.(2)(3,9)3 26､1二次函数(三)1、 下､y 轴､(0,2),1,2 2､42+-=x y (0,4) y 轴 (0,4) (2,0)(-2,0) 3､B 4､532+-=x y 5､(1)2,21=-=c a (2)略 6､顶点坐标分别是(0,2)(0,-2) 对称轴都是y 轴,开口方向向下与向上,两个图象关于x 轴对称, 6､ 26.1二次函数(四)1､A 2､D 3､2x y -= 右 1 直线x=1 1 大草原0 4､(1)2)2(+=x y 开口向上, 顶点(-2,0)对称轴是直线x=-2 (2)2)3(21--=x y 开口向下,顶点(3,0)对称轴是直线x=3 5､2)5(92--=x y 或2)1(2--=x y ,6､(1)-1,(2)略(3) (0,-4)(2,0) 26.1二次函数(五)1､略 2､C 3､D 4､(1)2)1(2-+=x y (2)略5､(1)3)2(432+--=x y (2)(0,0) (4,0 ) 6､(1)5)6(1212+--=x y (2)1526+ 7､310 26.1二次函数(六)1､B 2､左 2 下 2 3､(1)41)21(2--=x y 顶点()41,21- 对称轴是直线21=x (2)2)1(2++-=x y 顶点(-1,2)对称轴是直线x=-1, 4､(1)25)3(212+--=x y 开口向下,顶点(3,)25对称轴是直线x=3,当x=3时,y 有最大值是35 (2)87)45(22--=x y 开口向上,顶点()87,45- 对称轴是直线x=45,当x= 45时,y 有最小值87- 5､(1)变化规律是二次函数､x x y 202+-= 表格与图象略,(2)当x=10m 时,y 的最大值是100m 2,6､宽为,21m ⋅高为m 8.1,最大面积为216.2m . 7､(1) 0≤x ≤13 13<x ≤30 (3)x=13复习题1､A 2､A 3､B 4､6)2(2+-=x y 5､不唯一如2)2(+-=x y 6､D 7､(2,0) (-2,0)8､4或-1 9､2363x y = 10､(1)4 (2)-2 (3)-4 11､直角腰为10m,下底边为20m,最大面积为150m 2.12､(1)当售价定为50元时,销售量为500个,当售价定为80元时,销售量为200个,(2)当售价定为65元时,销售量为350个,获利最大是1225元.13､(1)1元,(2)每千克售价关于月份的函数关系式为7321+-=x y ,每千克成本关于月份的函数关系式1)6(3122+-=x y ,每千克的收益21y y y -=,故37)5(312+--=x y ,当x=5时,y 最大值37, 14､(1)2)1(212+--=x y 顶点点坐标(1,2) 对称轴是直线x=1,(2)略 (3)当x=-1或x=3时,y=0,当-1<x<3时y>0,当x<-1或x>3时,y<0.。

新华师大版九年级下册数学摸底试卷（四）第26章二次函数测试卷 A 卷姓名____________ 时间: 90分钟 满分:120分 总分____________一、选择题（每小题4分,共60分）1. 如图是二次函数c bx ax y ++=2图象的一部分,且过点A （3 , 0）,二次函数图象的对称轴是直线1=x ,下列结论正确的是 【 】（A ）ac b 42< （B ）0>ac （C ）02=-b a（D ）0=+-c b a2. 如图所示,抛物线c bx ax y ++=2与两坐标轴的交点分别为A 、B 、C ,且1==OC OA ,则下列关系中正确的是 【 】（A ）1-=+b a （B ）1-=-b a （C ）a b 2<（D ）0<ac 3. 如图,在二次函数c bx ax y ++=2的图象中,刘星同学观察得出了下面四个结论:①042>-ac b ; ②1>c ; ③02<-b a ; ④0<++c b a .你认为错误的有 【 】（A ）2个（B ）3个（C ）4个（D ）1个4. 如图,已知抛物线c bx ax y ++=2,则下列结论:①0<abc ;②02>+b a ;③02<-b a ;④0>++c b a ;⑤0<+-c b a .其中正确的有【 】（A ）1个（B ）2个（C ）3个（D ）4个第 1 题图第 2 题图5. 若抛物线c ax ax y +-=22经过点()0,1-,则方程022=+-c ax ax 的解为 【 】（A ）1,321-=-=x x （B ）3,121==x x （C ）3,121=-=x x（D ）1,321=-=x x 6. 抛物线c bx ax y ++=2的对称轴为直线1=x ,与x 轴的一个交点坐标为()0,1-,抛物线的一部分如图所示,下列结论:①24b ac <; ②方程02=++c bx ax 的两个根是3,121=-=x x ;③03>+c a ; ④当0>y 时,x 的取值范围是1-≤3<x ;⑤当0<x 时,y 随x 的增大而增大.其中正确结论的个数是 【 】（A ）4个（B ）3个（C ）2个（D ）1个7. 如图,抛物线x x y 421+-=和直线x y 22=,当21y y >时,x 的取值范围是 【 】（A ）20<<x （B ）0<x 或4>x （C ）0<x 或2>x（D ）40<<x第 3 题图第 4 题图第 6题图8. 函数c bx x y ++=2与函数x y =的图象如图所示,有以下结论:①042>-c b ; ②0=+c b ; ③0<b ; ④方程组⎩⎨⎧=++=x y c bx x y 2的解为⎩⎨⎧==1111y x ,⎩⎨⎧==3322y x ; ⑤当31<<x 时,()012>+-+c x b x .其中正确的是 【 】（A ）①②③ （B ）②③④（C ）③④⑤（D ）②③⑤9. 将如图所示的抛物线先向右平移1个单位,再向下平移2个单位,经此变换后的抛物线的解析式为【 】（A ）()23432+--=x y （B ）()21432+--=x y （C ）()23322+--=x y（D ）()21322+--=x y 10. 已知二次函数c bx ax y ++=2的图象如图所示,若方程()02≠=++k k c bx ax 有两个不相等的实数根,则k 的取值范围是 【 】（A ）3-<k（B ）3->k（C ）3<k （D ）3>k 11. 抛物线c bx ax y ++=2的对称轴为直线1-=x ,其一部分图象如图所示,下列判断中:①0>abc ; ②042>-ac b ; ③039=+-c b a ; ④025=+-c b a ;⑤若点()1,5.0y -,()2,2y -均在抛物线上,则21y y >.其中正确的个数为【 】第 8 题图第 9 题图（A ）2 （B ）3（C ）4 （D ）512. 如图,已知二次函数c bx ax y ++=2()0≠a 的图象与x 轴交于A 、B 两点,对称轴为直线2=x ,下列结论:①0>abc ;②04=+b a ;③若点A 的坐标为()0,1-,则线段5=AB ;④若点()11,y x M ,()22,y x N 在该函数的图象上,且满足32,101<<<<x x ,则21y y <.其中正确结论的序号为 【 】（A ）①②（B ）②③（C ）③④（D ）②④13. 如图所示的是二次函数c bx ax y ++=2的图象,下列结论:①二次三项式c bx ax ++2的最小值为4; ②024<++c b a ;③一元二次方程12=++c bx ax 的两根之和为1-;④使y ≤3成立的x 的取值范围是x ≥0.其中正确结论的个数为 【 】（A ）1（B ）2（C ）3（D ）414. 如图,抛物线c bx ax y ++=2经过点()0,1-,对称轴为l ,则下列结论:①0>abc ;②0=+-c b a ;③02<+c a ;④0<+b a .其中正确的结论【 】（A ）①③（B ）②③（C ）②④ （D ）②③④第 11 题图第 12 题图第 13 题图第 14 题图15. 如图,抛物线12+=x y 与双曲线xky =的交点A 的横坐标是1,则关于x 的不等式012<++x xk的解集是 【 】（A ）1>x（B ）1-<x（C ）10<<x（D ）01<<-x二、填空题（每小题4分,共 60分）16. 已知二次函数132+-=x x y ,当x ≥6时,它的最小值为_________.17. 已知抛物线42-=x y 与x 轴交于B 、C 两点,顶点为A ,则△ABC 的周长为_________.18. 已知抛物线c bx ax y ++=2与x 轴的交点是()0,4-,（2 , 0）,则这条抛物线的对称轴是直线_________.19. 已知抛物线12+-+-=k kx x y 的顶点在x 轴上,则=k _________.20. 若二次函数在23=x 时,有最小值41-,且函数的图象经过点（0 , 2）,则此函数的表达式为________________.21. 若抛物线122-+=x ax y 与x 轴有交点,则a 的取值范围是_________.22. 如图,点P 是第一象限内抛物线1412-=x y 上的任意一点,x PA ⊥轴于点A ,则=-PA OP _________.23. 点()a P ,1,()b Q ,1-都在抛物线12+-=x y 上,则PQ 的长为_________.24. 将抛物线()5322+--=x y 绕顶点旋转︒180后的抛物线的表达式为________________.25. 若抛物线122-++=m x x y 与x 轴有两个不同的交点,则m 的取值范围是__________.26. 若二次函数mx x y +=2图象的对称轴是直线3=x ,则关于x 的方程72=+mx x 的解为____________.第 23 题图27. 已知二次函数m x x y +-=32的图象与x 轴的一个交点为（1 , 0）,则关于x 的一元二次方程032=+-m x x 的两实数根是____________.28. 若抛物线2222+++=a ax ax y 与x 轴的一个交点为()0,3-,则另一个交点为_________.29. 如图,抛物线c bx ax y ++=2的顶点为()3,2-,若k c bx ax =++2有三个不相等的实数根,则k 的值是_________.30. 如图,抛物线c bx x y ++-=221与x 轴交于A 、B 两点,与y 轴交于点C ,且3,2==OC OA ,点D （2 , 2）在抛物线上,点P 是抛物线的对称轴上一动点,当△BDP 的周长最小时,点P 的坐标为__________.第 29 题图第 30 题图新华师大版九年级下册数学摸底试卷（四）第26章 二次函数测试卷 A 卷参考答案一、选择题（每小题3分,共30分）题号12345答案DBDDC题号678910答案BABAD题号1112131415答案ADADD二、填空题（每小题3分,共15分）16. 1917. 454+18. 1-=x19. 220. 41232-⎪⎭⎫ ⎝⎛-=x y 21. a ≥1-且0≠a 22. 2 23. 224. ()5322+-=x y25. 2<m 26. 7,121=-=x x 27. 2,121==x x28. ()0,129. 330. ⎪⎭⎫ ⎝⎛45,21部分选择题、填空题答案提示4. 如图,已知抛物线c bx ax y ++=2,则下列结论:①0<abc ;②02>+b a ;③02<-b a ;④0>++c b a ;⑤0<+-c b a .其中正确的有 【 】（A ）1个 （B ）2个（C ）3个（D ）4个解析 对于结论①,由0,0,0<>>c b a得第 4 题图0<abc ,故结论①正确;对于结论②,由0,0>>b a ,知02>+b a ,故结论②正确;对于结论③,由12->-ab得12<a b ,因为0>a ,所以a b 2<,02>-b a ,故结论③错误;对于结论④,因为点()c b a ++,1在第一象限,所以0>++c b a ,故结论④正确;对于结论⑤,因为点()c b a +--,1在第三象限,所以0<+-c b a ,故结论⑤正确.综上所述,正确的结论是①②④⑤,共4个.∴选择答案【 D 】.5.若抛物线c ax ax y +-=22经过点()0,1-,则方程022=+-c ax ax 的解为【 】（A ）1,321-=-=x x （B ）3,121==x x （C ）3,121=-=x x （D ）1,321=-=x x 解析 该抛物线的对称轴为:直线122=--=aax 设抛物线与x 轴的另一个交点为()0,2x ,则有1212=+-x ,解之得:32=x ∴抛物线与x 轴的另一个交点为()0,3∴022=+-c ax ax 的解为3,121=-=x x ∴选择答案【 C 】.6. 抛物线c bx ax y ++=2的对称轴为直线1=x ,与x 轴的一个交点坐标为()0,1-,抛物线的一部分如图所示,下列结论:①24b ac <; ②方程02=++c bx ax 的两个根是3,121=-=x x ;③03>+c a ; ④当0>y 时,x 的取值范围是1-≤3<x ;⑤当0<x 时,y 随x 的增大而增大.其中正确结论的个数是 【 】（A ）4个 （B ）3个（C ）2个（D ）1个解析 对于结论①,因为抛物线与x 轴有两个不同的交点,所以042>-=∆ac b ∴24b ac <,故结论①正确;对于结论②,抛物线与x 轴的一个交点为()0,1-,设另一个交点为()0,2x ,则有1212=+-x ,解之得:32=x ∴抛物线与x 轴的另一个交点为()0,3∴02=++c bx ax 的解是3,121=-=x x ;故结论②正确;对于结论③,∵抛物线的对称轴为直线1=x ∴ab 2-=第 6 题图∵抛物线经过点()0,1-∴0=+-c b a ∴bc a =+∴023=-=++=+b b a c a c a 故结论③错误;对于结论④,当0>y 时,x 的取值范围是31<<-x ,故结论④错误;对于结论⑤,当1<x 时,y 随x 的增大而增大∴当0<x 时,y 随x 的增大而增大故结论⑤正确.综上所述,正确的结论是①②⑤,共3个.∴选择答案【 B 】.8. 函数c bx x y ++=2与函数x y =的图象如图所示,有以下结论:①042>-c b ; ②0=+c b ;③0<b ; ④方程组⎩⎨⎧=++=x y cbx x y 2的解为⎩⎨⎧==1111y x ,⎩⎨⎧==3322y x ;⑤当31<<x 时,()012>+-+c x b x .其中正确的是 【 】（A ）①②③ （B ）②③④（C ）③④⑤（D ）②③⑤解析 对于结论①,因为抛物线与x 轴无交点∴042<-=∆c b 故结论①错误;对于结论②,因为抛物线c bx x y ++=2经过点()1,1∴11=++c b ∴0=+c b 故结论②正确;对于结论③,因为抛物线的对称轴在y 轴右侧,所以二次项系数与一次项系数异号∵01>∴0<b 故结论③正确;对于结论④,因为抛物线c bx x y ++=2与直线x y =的交点为()1,1和()3,3∴方程组⎩⎨⎧=++=x y cbx x y 2的解为⎩⎨⎧==1111y x ,⎩⎨⎧==3322y x ;故结论④正确;对于结论⑤,当31<<x 时,x c bx x <++2∴()012<+-+c x b x 故结论⑤正确.综上所述,正确的结论是②③④.∴选择答案【 B 】.10. 已知二次函数c bx ax y ++=2的图象如第 8 题图图所示,若方程()02≠=++k k c bx ax 有两个不相等的实数根,则k 的取值范围是 【 】（A ）3-<k （B ）3->k （C ）3<k（D ）3>k 解析 构造函数c bx ax y ++=2,其图象为:保留函数c bx ax y ++=2的图象位于x 轴上及其上方的图象不变,把x 轴下方的图象翻折到x 轴上方,如图所示.∵0≠k ∴当3>k 时,函数c bx ax y ++=2的图象与直线k y =有两个不同的交点,即方程()02≠=++k k c bx ax 有两个不相等的实数根.∴选择答案【 D 】.变式 已知二次函数c bx ax y ++=2的图象如图所示,若方程k c bx ax =++2有两个不相等的实数根,则k 的取值范围是______.（A ）3-<k （B ）3->k （C ）3<k（D ）3>k 11. 抛物线c bx ax y ++=2的对称轴为直线1-=x ,其一部分图象如图所示,下列判断中:①0>abc ; ②042>-ac b ;③039=+-c b a ; ④025=+-c b a ;⑤若点()1,5.0y -,()2,2y -均在抛物线上,则21y y >.其中正确的个数为 【 】（A ）2（B ）3（C ）4（D ）5解析 对于结论①,因为0,0,0<>>c b a ,所以0<abc ,故结论①错误;第 11 题图对于结论②,因为抛物线c bx ax y ++=2与x 轴有两个不同的交点,所以042>-ac b 故结论②正确;对于结论③,设抛物线与x 轴的另一个交点为()0,2x ,则有1212-=+x ,解之得:3-=x ∴抛物线与x 轴的另一个交点为()0,3-∴039=+-c b a 故结论③正确;对于结论④,∵抛物线的对称轴为直线1-=x ∴12-=-ab∴ab 2=∵抛物线经过点()0,1∴0=++c b a ∴0<-=+b c a ∴04525<+=+-=+-c a c a a c b a 故结论④错误;对于结论⑤,∵抛物线开口向上,点()2,2y -离对称轴较远∴21y y <故结论⑤错误.综上所述,正确的结论是②③,共2个.∴选择答案【 A 】.14. 如图,抛物线c bx ax y ++=2经过点()0,1-,对称轴为l ,则下列结论:①0>abc ;②0=+-c b a ;③02<+c a ;④0<+b a .其中正确的结论 【 】（A ）①③ （B ）②③ （C ）②④（D ）②③④解析 对于结论①,因为0,0,0>><c b a ,所以0<abc ,故结论①错误;对于结论②,因为抛物线经过点()0,1-,所以0=+-c b a ,故结论②正确;对于结论③,∵0=+-c b a ∴bc a =+∵点()c b a ++24,2在第四象限∴0)(2424<+++=++c c a a c b a ∴0236<+=+c a c a 故结论③正确;对于结论④,∵02<+c a ,b c a =+∴0<+=++b a c a a 故结论④正确.综上所述,正确的结论是②③④.∴选择答案【 D 】.19. 已知抛物线12+-+-=k kx x y 的顶点在x 轴上,则=k _________.解析 若抛物线的顶点在x 轴上,则抛物线第 14 题图与x 轴只有一个交点∴()()021422=-=--=∆k k k ∴221==k k ∴2=k .21. 若抛物线122-+=x ax y 与x 轴有交点,则a 的取值范围是_________.解析 本题为易错题,许多学生忽视0≠a 这个约束条件.由题意可得:⎩⎨⎧≥+=∆≠0440a a 解之得:a ≥1-且0≠a 学生整理用图。

二次函数经典测试题附答案二次函数经典测试题附答案一、选择题1.小明从如图所示的二次函数 $y=ax^2+bx+c$ 的图像中，观察得出了下面五条信息：①$c0$，③$a-b+c>0$，④$b^2>4ac$，⑤$2a=-2b$，其中正确结论是（）．A。

①②④B。

②③④C。

③④⑤D。

①③⑤解析】本题考查了二次函数图像与系数关系，观察图像判断图像开口方向、对称轴所在位置、与 $x$ 轴交点个数即可得出二次函数系数满足条件。

由抛物线的开口方向判断 $a$ 的符号，由抛物线与 $y$ 轴的交点判断 $c$ 的符号，然后根据对称轴及抛物线与 $x$ 轴交点情况进行推理，进而对所得结论进行判断。

详解】①由抛物线交 $y$ 轴于负半轴，则 $c0$；由对称轴在 $y$ 轴右侧，对称轴为 $x=-\frac{b}{2a}$，又 $a>0$，故$b0$，故②错误；③结合图像得出 $x=-1$ 时，对应 $y$ 的值在 $x$ 轴上方，故 $y>0$，即 $a-b+c>0$，故③正确；④由抛物线与 $x$ 轴有两个交点可以推出 $b^2-4ac>0$，故④正确；⑤由图像可知：对称轴为 $x=-\frac{b}{2a}$，则 $2a=-2b$，故⑤正确；故正确的有：③④⑤。

故选：C。

点睛】本题考查了二次函数图像与系数关系，观察图像判断图像开口方向、对称轴所在位置、与 $x$ 轴交点个数即可得出二次函数系数满足条件。

2.二次函数 $y=ax^2+bx+c$（$a\neq0$）图像如图所示，下列结论：①$abc>0$；②$2a+b^2=2$；③当 $m\neq1$ 时，$a+b>am^2+bm$；④$a-b+c>0$；⑤若$ax_1+bx_1=ax_2+bx_2$，且 $x_1\neq x_2$，则 $x_1+x_2=2$。

其中正确的有（）A。

①②③B。

②④C。

②⑤D。

第二十六章二次函数26．1二次函数（第一课时）一、课前小测1．已知函数y=(k+2)x+3是关于x的一次函数,则k_______.2．已知正方形的周长是ccm,面积为Scm2,则S与c之间的函数关系式为__ ___. 3．填表:4．在边长为4m的正方形中间挖去一个长为xm的小正方形, 剩下的四方框形的面积为y,则y与x间的函数关系式为_________.5．用一根长为8m的木条,做一个长方形的窗框,若宽为xm,则该窗户的面积y(m2)与x(m)之间的函数关系式为________.二、基础训练121．形如_______ ________的函数叫做二次函数.2．扇形周长为10，半径为x ，面积为y ，则y 与x 的函数关系式为_______________。

3．下列函数中,不是二次函数的是( )x 2 B.y=2(x-1)2+4 C.y=12(x-1)(x+4) D.y=(x-2)2-x 2 4．在半径为4cm 的圆中, 挖去一个半径为xcm 的圆面, 剩下一个圆环的面积为ycm 2,则y与x 的函数关系式为( )A.y=πx 2-4 B.y=π(2-x)2; C.y=-(x 2+4) D.y=-πx 2+16π 5．若y=(2-m)22m x -是二次函数,则m 等于( )A.±2 B.2 C.-2 D.不能确定三、综合训练1．已知y 与x 2成正比例,并且当x=1时,y=2,求函数y 与x 的函数关系式,并求当x=-3时,y的值.当y=8时,求x 的值.2．已知函数y =(m 2－m )x 2+(m －1)x +m +1.(1)若这个函数是一次函数，求m 的值;(2)若这个函数是二次函数，则m 的值应怎样？326．1二次函数（第二课时）一、课前小测1．函数y =ax 2+bx +c (a ，b ，c 是常数)是二次函数的条件是（ ）A.a ≠0，b ≠0，c ≠0B.a <0，b ≠0，c ≠0C.a >0，b ≠0，c ≠0D.a ≠02．下列函数中：①y =－x 2；②y =2x ；③y =22+x 2－x 3；④m =3－t －t 2是二次函数的是__ __(其中x 、t 为自变量).3．当k=__ ___时，27(3)k y k x -=+是二次函数。

26.1二次函数 (B2卷) (50分钟，共100分)班级：_______ 姓名：_______ 得分：_______ 一、请准确填空(每小题3分，共24分)1.已知抛物线y =ax 2+bx +c 的图象顶点为(－2，3)，且过(－1，5)，则抛物线的表达式为______.2.二次函数y =x 2+kx +1与y =x 2－x －k 的图象有一个公共点在x 轴上，则k =______.3.已知抛物线y =ax 2+bx +c ，其中a <0，b >0，c >0，则抛物线的开口方向______；抛物线与x 轴的交点是在原点的______；抛物线的对称轴在y 轴的______.4.如图1中的抛物线关于x 轴对称的抛物线的表达式为______.5.函数y =mx 2+x －2m (m 是常数)，图象与x 轴的交点有_____个.图1图26.当m =_____时，抛物线y =mx 2+2(m +2)x +m +3的对称轴是y 轴；当m =_____时，图象与y 轴交点的纵坐标是1；当m =_____时，函数的最小值是－2.7.若二次函数y =ax 2+bx +c 的图象如图2所示，则直线y =abx +c 不经过_____象限.8.二次函数y =mx 2+2x +m －4m 2的图象过原点，则此抛物线的顶点坐标是______.二、相信你的选择(每小题3分，共24分)9.二次函数y =x 2+p x +q 中，若p+q=0，则它的图象必经过下列四点中（ ）A.(－1，1)B.(1，－1)C.(－1，－1)D.(1，1)10.函数y =ax +b 的图象经过一、二、三象限，则二次函数y =ax 2+bx 的大致图象是（）B11.下列说法错误的是（ ）A.二次函数y =－2x 2中，当x =0时，y 有最大值是0B.二次函数y =4x 2中，当x >0时，y 随x 的增大而增大C.在三条抛物线y =2x 2，y =－0.5x 2，y =－x 2中，y =2x 2的图象开口最大，y =－x 2的图象开口最小D.不论a 是正数还是负数，抛物线y =ax 2(a ≠0)的顶点一定是坐标原点 12.小颖在二次函数y =2x 2+4x +5的图象上，依横坐标找到三点(－1，y 1)，(21，y 2)， (－321，y 3)，则你认为y 1，y 2，y 3的大小关系应为（ ）A.y 1>y 2>y 3B.y 2>y 3>y 1C.y 3>y 1>y 2D.y 3>y 2>y 113.若二次函数y =ax 2+bx +c 的图象如图4，则点(a +b ，ac )在（ ） A.第一象限B.第二象限C.第三象限D.第四象限图414.已知二次函数y =x 2+(2k +1)x +k 2－1的最小值是0，则k 的值是（ ）A.43 B.－43 C.45 D.－4515.若二次函数y =x 2－2x +c 图象的顶点在x 轴上，则c 等于（ ） A.－1 B.1 C.21 D.216.物体在地球的引力作用下做自由下落运动，它的运动规律可以表示为：s =21gt 2.其中s 表示自某一高度下落的距离，t 表示下落的时间，g 是重力加速度.若某一物体从一固定高度自由下落，其运动过程中下落的距离s 和时间t 函数图象大致为（ ）ABCD图5三、考查你的基本功(共18分)17.(8分)请写出一个二次函数，此二次函数具备顶点在x 轴上，且过点(0，1)两个条件，并说明你的理由.18.(10分)把抛物线y =－3(x －1)2向上平移k 个单位，所得的抛物线与x 轴交于点A (x 1，0)，B (x 2，0)，若x 12+x 22=926，请你求出k 的值.四、生活中的数学(共22分)19.(10分)如图6是把一个抛物线形桥拱，量得两个数据，画在纸上的情形.小明说只要建立适当的坐标系，就能求出此抛物线的表达式.你认为他的说法正确吗？如果不正确，请说明理由；如果正确，请你帮小明求出该抛物线的表达式.图620.(12分)心理学家发现，学生对概念的接受能力y与提出概念所用的时间x(分钟)之间满足函数关系：y=－0.1x2+2.6x+43(0≤x≤30)，y值越大表示接受能力越强.(1)x在什么范围内，学生的接受能力逐步增加？x在什么范围内，学生的接受能力逐步降低？(2)第10 分钟时，学生的接受能力是多少？几分钟时，学生的接受能力最强？(3)结合本题针对自己的学习情况有何感受？五、探究拓展与应用(共12分)21.(12分)有这样一道题：“已知二次函数y=ax2+bx+c图象过P(1，－4)，且有c=－3a，……求证这个二次函数的图象必过定点A(－1，0).”题中“……”部分是一段被墨水污染了无法辨认的文字.(1)你能根据题中信息求这个二次函数表达式吗？若能，请求出；若不能，请说明理由.(2)请你根据已有信息，在原题“……”处添上一个适当的条件，把原题补充完整.参考答案一、1.y =2x 2+8x +11 2. 2 3.向下 两侧 右侧 4.y =－45x 25.26.－2 －2 47.第四8.(－4，－4)二、9.D 10.B 11.C 12.D 13.D 14.B 15.D 16.B 三、17.y =x 2+2x +1(不唯一). ∵1421144422⨯-⨯⨯=-ab ac =0,∴抛物线顶点的纵坐标为0.当x =0，y =1时符合要求.18.解：把抛物线y =－3(x －1)2向上平移k 个单位，所得的抛物线为y =－3(x －1)2+k.当y =0即－3x 2+6x －3+k=0时，∵x 1+x 2=2，x 1·x 2=,33-+-k ∴x 12+x 22=(x 1+x 2)2－2x 1x 2=4+.926362=-k解得k=34.四、19.解：正确.抛物线依坐标系所建不同而各异，如下图.(仅举两例)22003x y =620032+-=x y20.解：(1)y =－0.1x 2+2.6x +43=－0.1(x －13)2+59.9.∴当0≤x ≤13时，学生的接受能力逐步增强. 当13<x ≤30时，学生的接受能力逐步下降. (2)当x =10时，y =59,x =13时，y 取最大值. ∴第13分钟时，学生的接受能力最强.(3)前13分钟尽快进入状态，集中注意力，提高学习效率，13分钟后要注意调解.五、21.解：(1)依题意，能求出. ∴⎪⎩⎪⎨⎧-=-==⎪⎩⎪⎨⎧+-=-=++=-.3,2,1,0,3,4c b a c b a a c c b a 解得 y =x 2－2x －3.(2)添加条件：对称轴x =1(不唯一).。

二次函数测试题及答案一、选择题1. 下列哪个选项不是二次函数的一般形式？A. y = ax^2 + bx + cB. y = 3x^2 - 2x + 1C. y = 5x^2 + 3D. y = 2x答案：D2. 二次函数y = ax^2 + bx + c的顶点坐标是：A. (-b, c)B. (-b/2a, c)C. (-b/2a, 4ac - b^2 / 4a)D. (-b/a, 4ac - b^2 / 4a)答案：C3. 若二次函数y = ax^2 + bx + c的图象开口向上，则a的取值范围是：A. a > 0B. a < 0C. a = 0D. a ≠ 0答案：A二、填空题4. 二次函数y = x^2 - 2x + 1的顶点坐标是_________。

答案：(1, 0)5. 当a > 0时，二次函数y = ax^2 + bx + c的图象与x轴的交点个数最多为_______。

答案：2三、解答题6. 已知二次函数y = 2x^2 - 4x + 3，求其顶点坐标。

解：首先，我们可以将二次函数写成顶点形式：y = 2(x - 1)^2 + 1。

因此，顶点坐标为(1, 1)。

7. 某二次函数的图象经过点(1, 1)和(2, 4)，且对称轴为直线x = 2。

求该二次函数的解析式。

解：设二次函数的解析式为y = a(x - 2)^2 + k。

将点(1, 1)代入得：1 = a(1 - 2)^2 + k1 = a + k将点(2, 4)代入得：4 = a(2 - 2)^2 + k4 = k由上述两个方程组可得a = -3，k = 4。

因此，该二次函数的解析式为y = -3(x - 2)^2 + 4。

四、应用题8. 某工厂生产一种产品，其成本函数为C(x) = 0.5x^2 - 10x + 100，其中x表示产品数量。

求该工厂生产多少件产品时，平均成本最低。

解：平均成本为C(x)/x = 0.5x - 10 + 100/x。