26.1二次函数水平测试

26.1二次函数同步练习一、选择题 1.函数432-+=x xy ( )A ．一次函数B ．二次函数C ．正比例函数D ．反比例函数答案：B解析：解答：因为函数中二次项的系数03≠，函数形式符合二次函数． 故选：B ．分析：根据二次函数的定义形如c bx axy ++=2，()0≠a 判断函数是否是二次函数．2．在下列y 关于x 的函数中，一定是二次函数的是（ ） A ．2x y =B ．21xy =C ．2kx y =D ．x k y 2= 答案：A解析：解答：A.符合二次函数定义形式，是二次函数；B.是分式方程，故B 错误；C.当k =0时，不是函数，故C 错误；D.当k =0是常函数，故D 错误． 故选：A ．分析：根据二次函数的定义形如c bx axy ++=2，()0≠a 是二次函数．3.对于任意实数m ,下列函数一定是二次函数的是( ) A ．()221xm y -=B ．()221xm y +=C ．()221x m y +=D ．()221x my -=答案：C解析：解答：A.当m =1时，二次项系数等于0，不是二次函数，故错误；B.当m =-1时，二次项系数等于0，不是二次函数，故错误；C.无论m 取何值，12+m 总大于或等于1，即无论m 取何值，12+m 都不等于0，符合二次函数概念，是二次函数，故正确．故选：C ．分析：根据二次函数的定义形如c bx axy ++=2，()0≠a 是二次函数．4. 二次函数532+=x y 的二次项系数是( ) A.3 B.2 C.5 D.0 答案：A解析：解：二次函数532+=x y的二次项系数是3，一次项系数是0．故选：A ．分析：本题考查二次函数的定义，是基础题，熟记概念是解题的关键． 5．下列各式中，y 是x 的二次函数的是（ ） A ．22=+x xy B ．0222=+-y xC ．21xy =D ．02=-x y答案：B解析：解：A.整理为y=22x x x-+不是二次函数，故A 错误； B.0222=+-y x变形，得1212+=x y ，是二次函数，故B 正确；C.分母中含自变量，不是二次函数，故C 错误；D.y 的指数是2，y 不是x 的二次函数，故此选项错误． 故选：B ．分析：整理成一般形式后，根据二次函数的定义判定即可． 6．下列函数中，属于二次函数的是（ ）A ．x y 2=B ．()()312-+=x x yC ．23-=x yD ．xx y 12+=答案：B 解析：解：A.xy 2=是反比例函数，故本选项错误； B.()()6423122--=-+=x xx x y ，是二次函数，故本选项正确；C.23-=x y 是一次函数，故本选项错误；D.xx x x y 112+=+=，不是二次函数，故本选项错误．故选：B ．分析：根据反比例函数的定义，二次函数的定义，一次函数的定义对各选项分析判断后利用排除法求解． 7．已知函数()5621--+=m m xm y 是二次函数，则m 等于（ ）A ．7B ．-2或7C ．﹣1D ．以上都不对答案：A解析：解：∵()5621--+=m m xm y 是二次函数，∴2562=--m m ，∴m =7或m =﹣1（舍去）． 故选A ．分析：根据二次函数的定义列出关于m 的方程，求出m 的值即可． 8．下列函数是二次函数的是（ ） A ．12+=x y B ．12+-=x y C ．22+=x y D ．221-=x y 答案：C解析：解：A.12+=x y ，是一次函数，故此选项错误； B.12+-=x y ，也是一次函数，故此选项错误； C.22+=x y 是二次函数，故此选项正确；D.221-=x y ，是一次函数，故此选项错误． 故选：C ．分析：直接根据二次函数的定义判定即可． 9．下列函数中，属于二次函数的是（ ） A ．32-=x y B ．()221x x y -+= C ．x xy 722-= D ．22xy -= 答案：C解析：解：A.函数32-=x y 是一次函数，故本选项错误； B.由原方程化简，得12+=x y ，属于一次函数，故本选项错误； C.函数x x y 722-=符合二次函数的定义；故本选项正确；D.22xy -=不是整式；故本选项错误． 故选:C ．分析：二次函数是指未知数的最高次数为二次的多项式函数．二次函数可以表示为c bx ax y ++=2，()0≠a ．10．下列四个函数中，一定是二次函数的是（ ）A ．x xy +=21 B ．c bx ax y ++=2 C ．()227+-=x x y D ．()()121-+=x x y 答案：D解析：解答：解：A.x xy +=21中未知数的最高次数不是2，故本选项错误； B.c bx ax y ++=2二次项系数a =0时，c bx ax y ++=2不是二次函数，故本选项错误；C.∵()()4914121--=-+=x x x y ，即4914--=x y ，没有二次项，故本选项错误；D.由原方程得，122--=x x y ，符合二次函数的定义，故本选项正确．故选：D ．分析：根据二次函数的定义解答．11．已知函数①45-=x y ，②x x t 6322-=，③38223+-=x x y ，④1832-=x y ，⑤2132+-=xx y ，其中二次函数的个数为（ ）A ．1B ．2C ．3D ．4答案：B解析：解：①45-=x y ，③38223+-=x xy ，⑤2132+-=xx y 不符合二次函数解析式， ②x x t6322-=，④1832-=x y 符合二次函数解析式，有两个． 故选B ．分析：首先去掉不是整式的函数，再利用二次函数的定义条件判定即可． 12.下列函数关系中，可以看做二次函数c bx ax y++=2，()0≠a 模型的是（）A.在一定的距离内汽车的行驶速度与行驶时间的关系B.我国人口年自然增长率1%，这样我国人口总数随年份的关系C.竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系（不计空气阻力）D.圆的周长与圆的半径之间的关系 答案：C解析：解：A.距离一定，汽车行驶的速度与行驶的时间的积是常数，即距离，速度与时间成反比例关系；B.设原来的人口是a ，x 年后的人口数是y ，则()x a y%11+=，是正比例函数；C.竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系（不计空气阻力）是二次函数．D.设半径是r ，则周长r C π2=，是一次函数关系．故选C ．分析：根据实际问题中的数量关系及二次函数的模型，逐一判断． 13.若函数()1222--+=m m xm m y是二次函数,那么m 的值是( )A.2B.-1或3C.3D.1- 答案：C 解析：解：∵()1222--+=m m xm my 是二次函数，∴2122=--m m ，∴m =3或m =-1． 当m =-1时02=+m m ，所以m =3故选C ．分析：根据二次函数的定义列出关于m 的方程，求出m 的值即可． 14.下列函数中,是二次函数的是( ) A.182+=x yB.18+=x yC.x y 8=D.28xy =答案：A解析：解答：A 符合二次函数定义形式，是二次函数；B 一次函数，故B 错误；C 是反比例函数，故C 错误；D 不符合二次函数定义形式，故D 错误． 故选：A ．分析：根据二次函数的定义形如c bx ax y ++=2，()0≠a 是二次函数．15.若()222--=m xm y 是二次函数,则m 等于( ) A ．2B ．-2C ．±2D ．不能确定答案：B解析：解答：根据二次函数的定义,得222=-m ,解得m =2或m =-2,又2-m ≠0,即m ≠2,故当m =-2时,这个函数是二次函数.故选：B ．分析：根据二次函数的定义可得答案． 二、填空题 16. 关于x 的函数()()m x m x m y+-++=112,当m =0时,它是________函数;当m =-1时,它是________函数. 答案：二次|一次解析：解答：当m =0时,函数关系式可化为x x y -=2,是一个二次函数;当m =-1时,函数关系式可化为12--=x y,是一次函数．分析：将m =0和m =1分别代入等式中再进行判断． 17．已知()ax x a y++=21是二次函数，那么a 的取值范围是_________答案：a ≠﹣1解析：解答：根据二次函数的定义可得a +1≠0， 即a ≠﹣1．分析：根据二次函数的定义条件列出不等式求解即可． 18．已知()322-++=x x a y 是关于x 的二次函数，则常数a 应满足的条件是_________． 答案：a ≠﹣2 解析：解答：由()322-++=x x a y 是关于x 的二次函数，得02≠+a ．解得a ≠﹣2， 故答案为：a ≠﹣2． 分析：根据形如c bx ax y ++=2，()0≠a 是二次函数，可得答案．19．已知()kk xk y ++=22是二次函数，则k 的值为_________．答案：1解析：解答：∵()kk xk y ++=22是二次函数，∴22=+k k 且k +2≠0，解得k =1，故答案为：1．分析：利用二次函数的定义列方程求解即可． 20．已知方程02=++cy bx ax（0≠a ，b 、c 为常数），请你通过变形把它写成你所熟悉的一个函数表达式的形式．则函数表达式为_________，成立的条件是_________，是 _________函数． 答案：x cbx c a y --=2|a ≠0，c ≠0|二次． 解析：解答：整理得函数表达式为x cbx c a y --=2，成立的条件是a ≠0，c ≠0，是二次函数．故答案为：x cbx c a y --=2；a ≠0，c ≠0；二次． 分析：函数通常情况下是用x 表示y ．注意分母不为0，二次项的系数不为0． 三、解答题 21.已知函数()35112-+-=+x xm y m y 是二次函数，求m 的值． 答案：解答：()35112-+-=+x xm y m 是二次函数，得21012m m ì-?ïïíï+=ïî 解得m =﹣1．解析：本题考查了二次函数的定义，注意二次项的系数不等于零，二次项的次数是2． 分析：根据二次函数是c bx ax y ++=2的形式，可得答案．22. 已知函数()2222+-+=m m x m my ．(1)当函数是二次函数时,求m 的值． 答案：解答：(1)依题意,得2222=+-m m ,解得m =2或m =0; 又02≠+m m ,解得m ≠0且m ≠-1;因此m =2.(2)当函数是一次函数时,求m 的值． 答案：解答：依题意,得1222=+-m m ,解得m =1; 当m =1时,02≠+m m ,因此m =1.解析：本题考查了二次函数和一次函数的定义，注意二次项的系数不等于零，二次项的次数是2，所以令2222=+-m m 且02≠+m m 即可．同理第二问令1222=+-m m 即可求解.分析：根据二次函数是c bx ax y ++=2,()0≠a 的形式，可得答案．23．己知()m xm y m ++=21是关于x 的二次函数，且当x ＞0时，y 随x 的增大而减小．求：（1）m 的值． 答案：解答：（1）∵()m xm y m ++=21是关于x 的二次函数，∴22=m ，解得m =，∵当x ＞0时，y 随x 的增大而减小， ∴m+1＜0，m =﹣，m =（不符合题意，舍）；（2）求函数的最值．答案：解答：当x =0时，y 最大=m =﹣．解析：（1）根据()m xm y m ++=21是关于x 的二次函数，可得22=m ，再由当x ＞0时，y随x 的增大而减小，可得m +1＜0，从而得出m 的值； （2）根据顶点坐标即可得出函数的最值．分析：本题考查了二次函数的定义，利用了二次函数的定义，二次函数的性质． 24．已知()()212232m x m x m my m x +-+-=--是x 的二次函数，求出它的解析式．答案：解答：根据二次函数的定义可得：2122=--m m ，且02≠-m m ，解得 m =3或m =﹣1； 当m =3时，962+=xy ；当m =﹣1时，1422+-=x x y ；综上所述，该二次函数的解析式为：962+=x y 或1422+-=x x y ．解析：本题考查二次函数的定义．一般地，形如c bx axy ++=2,()0≠a 的函数，叫做二次函数．其中x 、y 是变量，a 、b 、c 是常量，a 是二次项系数，b 是一次项系数，c 是常数项．c bx axy ++=2,()0≠a 也叫做二次函数的一般形式．分析：根据二次函数的定义列出不等式求解即可． 25．函数()()31--=x kx y ，当k 为何值时，y 是x 的一次函数？当k 为何值时，y 是x 的二次函数？ 答案：解答：∵()()()313333122++-=+--=--=x k kx x kx kxx kx y ，∴k=0时，y是x的一次函数，k≠0时，y是x的二次函数．解析：利用一次函数与二次函数的定义分别分析得出即可．。

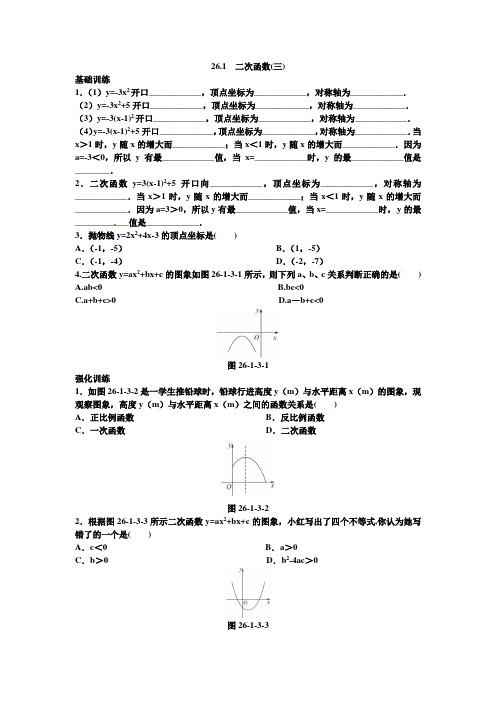
26.1 二次函数(三)基础训练1．（1）y=-3x2开口____________，顶点坐标为____________，对称轴为____________．（2）y=-3x2+5开口____________，顶点坐标为____________，对称轴为____________．（3）y=-3(x-1)2开口____________，顶点坐标为____________，对称轴为____________．（4）y=-3(x-1)2+5开口____________，顶点坐标为____________，对称轴为____________．当x＞1时，y随x的增大而____________；当x＜1时，y随x的增大而____________．因为a=-3＜0，所以y有最____________值，当x=____________时，y的最____________值是________．2．二次函数y=3(x-1)2+5开口向____________，顶点坐标为____________，对称轴为____________．当x＞1时，y随x的增大而____________；当x＜1时，y随x的增大而____________．因为a=3＞0，所以y有最____________值，当x=____________时，y的最____________值是____________．3．抛物线y=2x2+4x-3的顶点坐标是( )A．（-1，-5）B．（1，-5）C．（-1，-4）D．（-2，-7）4.二次函数y=ax2+bx+c的图象如图26-1-3-1所示，则下列a、b、c关系判断正确的是( )A.ab<0B.bc<0C.a+b+c>0D.a－b+c<0图26-1-3-1强化训练1．如图26-1-3-2是一学生推铅球时，铅球行进高度y（m）与水平距离x（m）的图象，现观察图象，高度y（m）与水平距离x（m）之间的函数关系是( )A．正比例函数B．反比例函数C．一次函数D．二次函数图26-1-3-22．根据图26-1-3-3所示二次函数y=ax2+bx+c的图象，小红写出了四个不等式,你认为她写错了的一个是( )A．c＜0 B．a＞0C．b＞0 D．b2-4ac＞0图26-1-3-33．二次函数y=21x 2+3x+25的图象是由函数y=21x 2的图象先向_________（左、右）平移个_________单位，再向_________（上、下）平移_________个单位得到的．4．(甘肃兰州模拟)一条抛物线的对称轴是x=1且与x 轴有唯一的公共点，并且开口方向向下，则这条抛物线的解析式是_________（任写一个）．5．如图26-1-3-4，AC ⊥CD ，甲、乙两船分别从A 地和C 地同时开出，各沿箭头所指方向航行，AC=10海里，甲、乙两船的速度分别为16海里/时和12海里/时，问多长时间后两船相距最近，最近距离为多少？（甲船到C 地后不再行驶）图26-1-3-4巩固训练1．若二次函数y=ax 2+ax-1的最小值为47，则a 的值是( ) A ．-1 B ．0 C ．3 D ．3或02．如图26-1-3-5,关于x 的两个函数y=x 2+2mx+m 2和y=mx-m(m≠0)在同一坐标系中的图象可能是( )图26-1-3-53．由于被墨水污染，一道数学题仅能见到如下文字：“已知二次函数y=x 2+bx+c 的图象过点(1，0)……求证：这个二次函数的图象关于直线x=2对称．”根据现有信息，题中的二次函数图象不具有的性质是( ) A ．过点（3，0） B ．顶点是（2，-2） C.b ＜0 D.c=34．已知A(a+1,a 2)在函数y=x 2+2x 的图象上，则a=______________．5．若抛物线y=x 2+4x+c 的顶点在x 轴上，则c=______________；若抛物线y=x 2+2bx+3的对称轴是y 轴，则b=______________；若抛物线y=x 2+2mx+m 2-3m+6的顶点在x 轴下方，则m 的取值范围是______________．6．已知抛物线y=x 2+4x-k-1与x 轴有两个交点，且这两个交点分别在直线x=1的两侧，则k 的取值范围为______________．7．通过配方，确定抛物线y=-2x 2+4x+6的开口方向、对称轴、顶点坐标，再描点画图． 8．已知两数和为20，当这两个数各为多少时，这两个数的积最大？9．老师给出一个函数y=f（x），甲、乙、丙、丁四位同学各指出这个函数的一个性质：甲：函数图象不经过第三象限；乙：函数图象经过第一象限；丙：当x＜2时，y随x的增大而减小；丁：当x＜2时，y＞0．已知这四位同学的叙述都正确，请你构造满足上述所有性质的一个二次函数．10．如图26-1-3-6，已知等腰梯形ABCD的边BC在x轴上，点A在y轴的正方向上，A(0,6)、2．D(4，6），且AB＝10图26-1-3-6（1）求点B的坐标；（2）求经过A、B、D三点的抛物线的解析式.11．(2010江苏盐城模拟，26)已知抛物线y=-x2+4x-3与x轴相交于A、B两点(A点在B点的左侧)，顶点为P．图26-1-3-7(1)求A、B、P三点坐标；(2)在右面的直角坐标系内画出此抛物线的简图，并根据简图写出当x取何值时，函数值y 大于零；(3)确定此抛物线与直线y=-2x+6公共点的个数，并说明理由．26.1 二次函数(三)5分钟训练(预习类训练，可用于课前) 1．（1）y=-3x 2开口____________，顶点坐标为____________，对称轴为____________． （2）y=-3x 2+5开口____________，顶点坐标为____________，对称轴为____________． （3）y=-3(x-1)2开口____________，顶点坐标为____________，对称轴为____________． （4）y=-3(x-1)2+5开口____________，顶点坐标为____________，对称轴为____________．当x ＞1时，y 随x 的增大而____________；当x ＜1时，y 随x 的增大而____________．因为a=-3＜0，所以y 有最____________值，当x=____________时，y 的最____________值是________．解析：二次函数y=ax 2＋bx ＋c 的对称轴是x=a b 2-，顶点坐标为（ab ac a b 44,22--），由a＜0开口向下，有最大值，a ＞0开口向上，有最小值．再由对称轴两侧看变化．答案：（1）向下 （0，0） x=0 （2）向下 （0，5） x=0 （3）向下 （1，0） x=1 [来源:Z*xx*]（4）向下 （1，5） x=1 减小 增大 大 1 大 52．二次函数y=3(x-1)2+5开口向____________，顶点坐标为____________，对称轴为____________．当x ＞1时，y 随x 的增大而____________；当x ＜1时，y 随x 的增大而____________．因为a=3＞0，所以y 有最____________值，当x=____________时，y 的最____________值是____________．解析：在二次函数中，当二次项系数大于0时，开口向上，有最低点，最小值，在对称轴左侧，函数值y 随着x 的增大而减小；在对称轴右侧，函数值y 随着x 的增大而减小． 答案：上 （1，5） x=1 增大 减小 小 1 小 5 3．抛物线y=2x 2+4x-3的顶点坐标是( ) A ．（-1，-5） B ．（1，-5） C ．（-1，-4） D ．（-2，-7） 解析：方法一（配方法）：y=2x 2+4x-3=2(x 2+2x-23)＝2（x 2+2x+1-1-23）=2(x+1)2-5，∴顶点坐标为（-1，-5）． 方法二（公式法）：∵a=2，b=4， c=-3， ∴2242⨯-=-a b =-1， 2416)3(24442⨯--⨯⨯=-a b ac =-5． ∴顶点坐标为（-1，-5）. 答案：A4.二次函数y=ax 2+bx+c 的图象如图26-1-3-1所示，则下列a 、b 、c 关系判断正确的是( ) A.ab<0 B.bc<0C.a+b+c>0D.a －b+c<0图26-1-3-1解析：抛物线开口向下，a ＜0,对称轴为直线x=ab2-＜0,得b ＜0，由与 y 轴交点知c<0，所以ab>0，bc>0．当x=1时得a+b+c<0，当x=-1时得a-b+c<0. 答案：D10分钟训练(强化类训练，可用于课中)[来源:学科网ZXXK]1．如图26-1-3-2是一学生推铅球时，铅球行进高度y （m ）与水平距离x （m ）的图象，现观察图象，高度y （m ）与水平距离x （m ）之间的函数关系是( ) A ．正比例函数 B ．反比例函数 C ．一次函数 D ．二次函数图26-1-3-2解析：由图形可知，图中函数图象是一抛物线,是二次函数，而一次函数的图象是直线，反比例函数的图象是双曲线，反之亦成立． 答案：D[来源:学_科_网]2．根据图26-1-3-3所示二次函数y=ax 2+bx+c 的图象，小红写出了四个不等式,你认为她写错了的一个是( )A ．c ＜0B ．a ＞0C ．b ＞0D ．b 2-4ac ＞0[来源:Z+xx+] 图26-1-3-3解析：观察图形知，对称轴x=ab2-＞0,又开口向上a ＞0,所以b ＜0． 答案：C 3．二次函数y=21x 2+3x+25的图象是由函数y=21x 2的图象先向_________（左、右）平移个_________单位，再向_________（上、下）平移_________个单位得到的．解析：一般先将二次函数由一般式化成顶点式，再确定上下左右平移的单位，但是，在化为顶点式时，常常会出现下列错误，应引以为戒． 错解一：y=21x 2+3x+25=21（x 2+23x+45)=21x 2+23x+169-169+45)=21(x+43)2+811，∴y=21x 2+3x+25是由y=21x 2向左平移43个单位，再向上平移811个单位得到的．错解二：y=21x 2+3x+25=21x 2+6x+5)=21(x 2+6x+9-9+5)=21(x+3)2-4．正确解法：y=21x 2+3x+25=21（x 2+6x+5）=21(x 2+6x+9-9+5)=21(x+3)2-2．∴抛物线y=21x 2+3x+25是由y=21x 2向左平移3个单位，再向下平移2个单位得到的．答案：左 3 下 24．(甘肃兰州模拟)一条抛物线的对称轴是x=1且与x 轴有唯一的公共点，并且开口方向向下，则这条抛物线的解析式是_________（任写一个）．解析：由与x 轴有唯一交点知该抛物线顶点在x 轴上，所以可写为y= -2(x-1)2等．[来源:Z_xx_]答案：y=-2(x-1)25．如图26-1-3-4，AC ⊥CD ，甲、乙两船分别从A 地和C 地同时开出，各沿箭头所指方向航行，AC=10海里，甲、乙两船的速度分别为16海里/时和12海里/时，问多长时间后两船相距最近，最近距离为多少？（甲船到C 地后不再行驶）图26-1-3-4解：设BD=y 海里，两船行驶的时间为x 小时，BC=10-16x ，CD=12x ，根据题意，得y=100320400)12()1610(222+-=+-x x x x=36)52(400)100925454(400)4154(400222+-=++-=+-x x x x x ∴当x=52时，y 有最小值为6（海里）． 答：经过0．4小时后，两船距离最近，距离最近为6海里． 30分钟训练(巩固类训练，可用于课后) 1．若二次函数y=ax 2+a-1的最小值为47-，则a 的值是( ) A ．-1 B ．0 C ．3 D ．3或0解析:可直接写出顶点的纵坐标，即函数的最小值，但解题时易忘记隐含条件a ＞0．错解：∵二次函数y=ax 2+a-1有最小值47-，∴47442-=--a a a ．两边同乘以4a ，整理得a 2-3a=0．解得a 1=0，a 2=3．故选D ．正确解法：∵二次函数有最小值，∴a>0．∴a=3． 答案：C[来源:]2．如图26-1-3-5,关于x 的两个函数y=x 2+2mx+m 2和y=mx-m(m≠0)在同一坐标系中的图象可能是( )图26-1-3-5解析:应分两种情况，m>0时,抛物线开口向上，直线过一、四、三象限和m<0时,抛物线开口向上，直线过二、一、四象限，顶点坐标为（－m,0）． 答案：C3．由于被墨水污染，一道数学题仅能见到如下文字：“已知二次函数y=x 2+bx+c 的图象过点(1，0)……求证：这个二次函数的图象关于直线x=2对称．”根据现有信息，题中的二次函数图象不具有的性质是( ) A ．过点（3，0） B ．顶点是（2，-2） C.b ＜0 D.c=3解析:由题意知二次函数y=x 2+bx+c 的图象过点(1，0)，且这个二次函数的图象关于直线x=2对称,故A 、C 都正确.由2b-=2，b=-4,把点(1，0)代入得c=3，D 也正确．当x=2时，y=-1，所以顶点坐标为（2，-1）． 答案：B4．已知A(a+1,a 2)在函数y=x 2+2x 的图象上，则a=______________． 解析:把x=a+1，y=a 2代入y=x 2+2x ，得a 2=(a+1)2+2(a+1)．解得a=43-．[来源:学,科,网] 答案：43-5．若抛物线y=x 2+4x+c 的顶点在x 轴上，则c=______________；若抛物线y=x 2+2bx+3的对称轴是y 轴，则b=______________；若抛物线y=x 2+2mx+m 2-3m+6的顶点在x 轴下方，则m 的取值范围是______________．解析:抛物线y=x 2+4x+c 的顶点在x 轴上，则42-4c=0，∴c=4．抛物线y=x 2+2bx+3的对称轴为y 轴，则b=0；抛物线y=x 2+2mx+m 2-3m+6开口向上，若顶点在x 轴下方，则需Δ>0，即4m 2-4(m 2-3m+6)>0．∴m>2．答案：4 0 m>2[来源:Z§xx§]6．已知抛物线y=x 2+4x-k-1与x 轴有两个交点，且这两个交点分别在直线x=1的两侧，则k 的取值范围为______________． 解析:设抛物线与x 轴交于（x 1，0）、（x 2，0），则（x 1-1）（x 2-1）<0． ∴x 1x 2-(x 1+x 2)+1<0.∴⎩⎨⎧<+++->---.014)1(,0)1(442k k 解这个不等式组，得⎩⎨⎧>->.4,5k k ∴k ＞４答案：k>47．通过配方，确定抛物线y=-2x 2+4x+6的开口方向、对称轴、顶点坐标，再描点画图．解析:配方为y=-2x 2+4x+6=-2(x 2-2x-3)=-2(x 2-2x+1-4)=-2（x-1）2+8．所以开口向下，对称轴为直线x=1，顶点坐标为（1，8）.描点画图略．答案：y=-2（x-1）2+8，抛物线开口向下，对称轴为直线x=1，顶点坐标为（1，8），图略. 8．已知两数和为20，当这两个数各为多少时，这两个数的积最大？ 解：设其中一个为x,另一个为20-x,根据题意得，y=x(20-x)=-x 2+20x=-(x-10)2+100， 当x=10时,y 最大值=100，所以当两个数分别为10，10时，积最大为100． 9．老师给出一个函数y=f （x ），甲、乙、丙、丁四位同学各指出这个函数的一个性质： 甲：函数图象不经过第三象限； 乙：函数图象经过第一象限；丙：当x ＜2时，y 随x 的增大而减小； 丁：当x ＜2时，y ＞0．已知这四位同学的叙述都正确，请你构造满足上述所有性质的一个二次函数．解析:设所求函数为二次函数，开口向上，对称轴为直线x=2，顶点在第一象限，不妨设为（2，3），即可求出关系式．（写出一个即可）答案：y=x 2-4x+7． 10．如图26-1-3-6，已知等腰梯形ABCD 的边BC 在x 轴上，点A 在y 轴的正方向上，A(0,6)、D(4，6），且AB ＝102．图26-1-3-6[来源:学科网ZXXK]（1）求点B 的坐标；（2）求经过A 、B 、D 三点的抛物线的解析式.解：（1）在Rt △ABC 中，OB 2=AB 2-OA 2，所以OB=2，又因为点B 在x 轴的负半轴上，所以B （－2，0）．（2）设过A 、B 、D 三点的抛物线的解析式为y=ax 2+bx+c ，将A （0，6），B （－2，0），D （4，6）三点的坐标代入得⎪⎪⎩⎪⎪⎨⎧==-=⎪⎩⎪⎨⎧=+-=++=.6,2,21,024,6416,6c b a c b a c b a c 解得所以y=-21x 2+2x+6． 11．(2010江苏盐城模拟，26)已知抛物线y=-x 2+4x-3与x 轴相交于A 、B 两点(A 点在B 点的左侧)，顶点为P ．图26-1-3-7(1)求A 、B 、P 三点坐标；(2)在右面的直角坐标系内画出此抛物线的简图，并根据简图写出当x 取何值时，函数值y 大于零；(3)确定此抛物线与直线y=-2x+6公共点的个数，并说明理由．解:(1)令y=0,解方程-x 2+4x-3=0则x 1=1,x 2=2,则A(1,0),B(3,0).将y=-x 2+4x-3配方得y=-(x-2)2+1,得顶点P(2,1). (2)作图,当1<x<3时,y>0.(3)由题意列方程组得⎩⎨⎧+-=-+-=.62,342x y x x y转化得x 2-6x+9=0,Δ=0,∴方程的两根相等,方程只有一组解.[来源:学科网] ∴此抛物线与直线有唯一的公共点.。

P B CQ A 练习26.1（一）1．一个圆柱的高等于底面半径，写出它的表面积S 与半径r 之间的关系式。

2.n 支球队参加比赛,每两队之间进行一场比赛.写出比赛的场次数m 与球队数n 之间的关系式.(二)在同一直角坐标系中,画出下列二次函数的图象:y=221x ,2212+=x y ,y=2212-x .观察三条抛物线的相互关系,并分别指出它们的开口方向、对称轴及顶点。

你能说出抛物线k x y +=221的开口方向、对称轴及顶点吗？它与抛物线221x y =有什么关系？ （三） 在同一直角坐标系中,画出下列二次函数的图象: 222)2(21,)2(21,21-=+==x y x y x y 观察三条抛物线的相互关系,并分别指出它们的开口方向、对称轴及顶点。

（四）说出下列抛物线的开口方向、对称轴及顶点：(1)y=2(x+3)2+5;(2)y =－3(x －1)2－2; (3)y=4(x －3)2+7;(4) y =－5(x+2)2－6(五)1.写出下列抛物线的开口方向、对称轴及顶点坐标.当x 为何值时y 的值最小(大)?(1)y=3x 2+2x;(2)y =－x 2－2x;(3)y=－2x 2+8x －8;(4)34212+-=x x y 2. 已知直角三角形两条直角边的和等于8,两条直角边各为多少时,这个直角三角形的面积最大,最大值是多少?习题26.1复习巩固1. 一个长方形的长是宽的2倍,写出这个长方形的面积与宽之间的函数关系式.2. 某种商品的价格是2元,准备进行两次降价.如果每次降价的百分率都是x,经过两次降价后的价格y(单位:元)随每次降价的百分率x 的变化而变化,y 与x 之间的关系可以用怎样的函数来表示?3. 在同一直角坐标系中画出下列函数的图象:y=3x 2,y =－3x 2,y=31x 2. 4. 分别写出抛物线y=4x 2与241x y -=的开口方向、对称轴及顶点. 5. 分别在同一直角坐标系内,描出下列二次函数的图象,并写出对称轴及顶点: (1)y=31x 2+3, y=31x 2－2;(2)2)2(41+-=x y ,2)1(41--=x y (3)y=21(x+2)2－2, y=21(x －1)2+2. 6. 先确定下列抛物线的开口方向、对称轴及顶点(用公式),再描点画图:(1)y=－3x 2+12x －3; (2)y=4x 2－24x+26; (3)y=2x 2+8x －6; (4)y=12212--x x 综合运用 7. 如图,在三角形ABC 中,∠B=90°,AB=1.2㎝,BC=2.4㎝,动点P 从点A 开始沿边AB 向B 以2㎜/s 的速度移动,动点Q 从点B 开始沿边BC 向C 以4㎜/s 的速度移动,如果P,Q 分别从A,B 同时出发,BDACDCAEF B那么△PBQ的面积S随出发时间t如何变化?写出函数关系式及t的取值范围.8.一辆汽车的行驶距离s(单位:m)与行驶时间t(单位:s)的函数关系式是s=9t+221t,经过12s汽车行驶了多远?行使380m需要多少时间?9.从地面竖直向上抛出一小球.小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系式是h=30t－5t2.小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?10.如图,四边形的两条对角线AC,BD互相垂直,AC+BD=10,当AC,BD的长是多少时,四边形ABCD的面积最大?拓广探索11.钢球从斜面顶端由静止开始沿斜面滚下,速度每秒增加1.5m/s.(1)写出滚动的距离s(单位:m)与滚动的时间t(单位:s)之间的关系式.(提示:本题中,距离=平均速度v×时间t, v=20tvv+,其中,v是开始时的速度,tv是t秒时的速度)(2)如果斜面的长是1.5m,从斜面顶端滚到底端用多长时间?12.填空:(1)已知函数y=2(x+1)2+1,当x<______时y随x的增大而减小, 当x>_____时y随x的增大而增大, 当x=_____时y最_____.(2)已知函数y=—2x2+x—4,当x<______时y随x的增大而增大, 当x>_____时y随x的增大而减小, 当x=_____时y最_____.习题26.2 复习巩固1.已知函数y=3x2—4x+1.(1)画出函数的图象;(2)观察图象,当x取哪些值时,函数值为0?2.用函数的图象求下列方程的解:(1)x2—3x+2=0 (2)—x2+6x—9=0(3)x2+x+2=0 (4)4—x—x2=0综合运用3.如图,一名男生推铅球,铅球行进高度y与水平距离x之间的关系是35321212++-=xxy(1)画出函数的图象;(2)观察图象,指出铅球推出的距离.4.抛物线与x轴的公共点是(-1,0),(3,0),求这条抛物线的对称轴.拓广探索5.画出函数y=x2-2x-3的图象,利用图象回答:(1)方程x2-2x-3=0的解是什么;(2)x取什么值时,函数值大于0;(3) x取什么值时,函数值小于0;6.下列情形时,如果a>0,抛物线y=ax2+bx+c的顶点在什么位置?(1)方程ax2+bx+c=0有两个不等的实数根;(2)方程ax2+bx+c=0有两个相等的实数根;(3)方程ax2+bx+c=0无实数根;如果a<0呢?习题26.3 复习巩固1．下列抛物线有最高点或最低点吗？如果有，写出这些点的坐标（用公式）：（1）y=－4x2+3x; (2)y=3x2+x+62.某种商品每件的进价为30元，在某段时间内若以每件x元出售，可卖出（200-x）件，应如何定价才能使利润最大？H E C B A E G F D 3．飞机着陆后滑行的距离s （单位：m ）与滑行的时间t(单位：s)的函数关系式是s=60t-1.5t 2.飞机着陆后滑行多远才能停下来？综合运用4．一块三角形废料如图所示，∠A=30°，∠C=90°，AB=12，用这快废料剪出一个长方形CDEF ，其中，点D ，E ，F 分别在AC ，AB ，BC 上，要使剪出的长方形CDEF 面积最大，点E 应选在何处？5．如图，点E 、F 、G 、H 分别位于正方形ABCD 的四条边上，四边形EFGH 也是正方形.当点E 位于何处时,正方形EFGH 的面积最小? 6.某宾馆有50个房间供游客居住,当每个房间的定价为每天180元时,房间会全部住满.当每个房间的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.房价定为多少时,宾馆利润最大?拓广探索7. 如图, 厂门的上方是一段抛物线,抛物线的顶点离地面的高度是3.8m,一辆装满货物的卡车,宽为1.6m,高为2.6m,要求卡车的上端与门的距离不小于0.2m,这辆卡车能否通过厂门?8. 分别用定长为L 的线段围成矩形和圆,哪种图形的面积大?为什么?复习题26 复习巩固 1.如图,正方形ABCD 的边长是4,E 是AB 上一点,F 是AD 的延长线上一点,BE=DF.四边形AEGF 是矩形,则矩形AEGF 的面积y 随BE 的长x 的变化而变化,y 与x 之间的函数关系式可以用怎样的函数来表示?2.某商场第1年销售计算机5000台,如果每年的销售量比上一年增加相同的百分率x,写出第3年的销售量y 与每年增加的百分率x 之间的函数关系式.3.选择题 在抛物线y=x 2-4x-4上的一个点是( )(A)(4,4) (B)(3,-1) (C)(-2,-8) (D)(47,21--) 4.先确定下列抛物线的开口方向、对称轴及顶点坐标(用公式),再描点画图:(1)y=x 2-2x-3 (2)y=1+6x-x 2 (3)y=12212+-x x (4)y=4412-+-x x 5.汽车刹车后行使的距离s(单位:m)与行使的时间t(单位:s)的函数关系式是s=15t-6t 2,汽车刹车后到停下来前进了多远?综合运用6.用一段长为30m 的篱笆围成一个一边靠墙的矩形菜园,墙长为18m,这个矩形的长,宽各为多少时,菜园的面积最大,最大限面积是多少?7.一个滑雪者从85m 长的山坡滑下,滑行的距离s(单位:m)与滑行时间t(单位:s)的函数关系式是s=1.8t+0.064t 2.他通过这段山坡需要多长时间?8.已知矩形的周长为36cm ,矩形绕它的一条边旋转形成一个圆柱,矩形的长,宽各为多少时,旋转形成的圆柱的侧面积最大?9.在周长为定植p 的扇形中,半径是多少时扇形的面积最大?10.对某条线路的长度进行n 次测量,得到n 个结果x 1x 2,…,x n .如果用x 作为这条线路长度的近似值,当x 取什么值时,(x-x 1)2+(x-x 2)2+,,…+(x-x n )2最小?。

第二十六章二次函数26.1 二次函数(一)1.矩形周长是20cm,一边长是x㎝,面积是y㎝2,则y与x的函数关系式是,这个函数称作次函数.2.下列函数y=0.5x-1,y=3x2,y=0.5x2-4x+1,y=x(x-2),y=(x-1)2-x2中,二次函数的个数为( )(A)2个(B)3个(C)4个(D)5个3.k取哪些值时,函数y=(k2-k)x2+kx+(k+1)是以x为自变量是一次函数?二次函数?4.已知等腰直角三角形的斜边长为xcm,面积为ycm2,请写出y与x的函数关系式,并判断它是什么函数?5.如图,正方形ABCD边长是4,E､F分别在BC､CD上,设ΔAEF面积是y,EC=x,如果CE=CF,试求出y与x的函数关系及自变量取值范围,并判定y是x的什么函数?6.已知二次函数y=ax2+c,当x=0时，y=-3;当x=1时，y=-1,求当x=-2时，y的值.7.一块矩形耕地大小尺寸如下图,要在这块地上沿东西方向挖一条水渠,沿南北方向挖两条水渠,水渠宽为xm,余下的可耕地面积为ym2,(1)请你写出y与x之间的函数关系式.(2)根据你写出的函数关系式,求出水渠宽为1m时,余下的可耕地面积为多少?(3)若耕除去水渠剩余部分面积为4408m2,求此时水渠的宽度.26.1二次函数(二)1.已知函数y=ax2的图象过点(2,-4),则a=,对称轴是,顶点坐标是,抛物线的开口方向,抛物线的顶点是最点.2.下列关于函数y=-0.5x2的图象说法( )①图象是一条抛物线;②开口向下;③对称轴是y轴;④顶点(0,0).其中正确的有( )(A)1个(B)2个(C)3个(D)4个3.已知函数y=x2的图象过点(a,b),则它必通过的另一点是( )(A)(a,-b) (B)(-a,b)(C)(-a,-b) (D)(b,a)4.抛物线y=ax2过A(-1,2),试判断B(-2,-3),C(,)是否在抛物线上.5､已知正方形的对角线长为x,面积为y.(1)写出y与x的函数关系;(2)画出这个函数的图象草图.6.抛物线y=ax2(a≠0)与直线y=4x-3交于点A(m,1),求:(1)点A的坐标及抛物线顶点C的坐标和对称轴;(2)抛物线y=ax2与直线y=4x-3是否还有其他交点?若有,请求出这个交点B的坐标,若没有,请说明理由. 并求点A､B､C三点构成的三角形的面积.2.6.1二次函数(三)1.函数y=-1.5x2+2的图象开口方向,对称轴是,顶点坐标是,当x=时,y最大.2.把抛物线y=-x2向上平移4个单位后,得到的抛物线的函数解析式为,平移后的抛物线的顶点坐标是,对称轴是,与y轴的交点坐标是,与x轴的交点坐标是.3.将抛物线y=2x2-3通过下列( )平移后得到抛物线y=2x2,(A)向下平移3个单位(B)向上平移3个单位(C)向下平移2个单位(D)向上平移2个单位4.已知抛物线的对称轴是y轴,顶点的纵坐标为5,且过点(1,2)求这条抛物线的解析式.5.抛物线y=ax2+c顶点是(0,2),且形状及开口方向与y=-0.5x2相同.(1)确定a､c的值;(2)画出这个函数的图象.6.在同一坐标系中,画出函数y=-x2+2与y=x2-2的图像请分别说出图象的顶点坐标､对称轴及开口方向,并比较两个图像之间有何联系?26.1二次函数(四)1.抛物线y=3(x-2)2的对称轴是( )(A)直线x=2 (B)直线x=-2 (C)y 轴 (D)x 轴2.将抛物线y=3x 2向左平移3个单位所得的抛物线的函数关系式为( )A ､332-=x y B ､2)3(3-=x y C ､332+=x y D ､2)3(3+=x y3.抛物线2)1(--=x y 是由抛物线向平移个单位得到的,平称后的抛物线对称轴是,顶点坐标是,当x=时,y 有最值,其值是.4.用配方法把下列函数化成y=a(x-h)2的形式,并指出开口方向,顶点坐标和对称轴.(1)y=x 2+4x+4(2)y=- x 2+3x-(3)y=2x 2-4x5､已知二次函数图像的顶点在x 轴上,且图像经过点(2,-2)与(-1,-8)求此函数解析式.6.抛物线2)2(-=x a y 经过(1,-1).(1)确定a 的值;(2)画出这个函数图象; (3)求出抛物线与坐标轴的交点坐标.2.6.1 二次函数(五) 1､填表2､下列抛物线顶点是(2,1)的是( )A.1)2(22--=x yB.2)1(32+-=x y C.1)2(22+-=x y D.2)1(42+-=x y 3､抛物线23x y =先向上平移2个单位,后向右平移3个单位,所得抛物线是( )A.2)3(32-+=x y B.2)3(32++=x y C.2)3(32--=x y D.2)3(32+-=x y 4､抛物线的顶点在(-1,-2)且又过(-2,-1). (1)确定抛物线的解析式; (2)画出这个函数的图象.综合与运用5､如图所示,求:(1)抛物线的解析式,(2)抛物线与x 轴的交点坐标.6.某同学在推铅球时,推球经过的路线是抛物线的一部分(如图),出手处A 点坐标是(0,2),最高点B 坐标是(6,5),(1)求此抛物线的函数表达式.(2)你能算出这位学生推出的铅球有多远吗?拓展与探索7.如图,在一幢建筑物里,从10m 高的窗户处用水管斜着向外喷水,喷出的水,在垂直于墙壁的平面内画出一条抛物线,其顶点离墙1m,并且在离墙3m 处落到地面上,问抛物线的顶点比喷出的水高出多少?26.1二次函数(六)1､二次函数322+-=x x y 的顶点坐标是( ) A ､(1,0) B ､(1,2) C ､(2,1) D ､(―1,―2)2､二次函数y= x 2+x-1的图像是由函数y=x 2的图像先向平移个单位,再向平移个单位得到的. 3､用配方法求下列抛物线的顶点坐标和对称轴(1)x x y -=2(2)122+--=x x y4､写出下列抛物线的开口方向､对称轴､顶点坐标,当x 为何值时,y 有最大(小)值?并求其值. (1)y=-x 2+3x-2 (2))12)(2(--=x x y综合与运用5､有一矩形的苗圃,其四周是总长为40m 篱笆,假设它的一边长为xm ,面积为2ym . (1)y 随x 的变化的规律是什么?请分别用函数的表达式､表格､函数的图象表示出; (2)由函数的图象指出当x 取何值时,苗圃的面积最大?最大面积是多少?6､有一条长为7.2m 的木料,做成如图所示的“日”字形的窗柜,窗柜的宽和高各取多少时,这个窗的面积S 最大?最大面积是多少?(不考虑木料加工时的损耗和中间木柜所占的面积)7､心理学家发现,学生对概念的接受能力y 与提出概念所用的时间x (单位:min)之间满足函数关系y=-0.1x 2+2.6x+43 (0≤x ≤30),y 值越大,表示接受能力越强.(1)x 在什么范围内,学生的接受能力逐步增强?x 在什么范围内,学生的接受能力逐步降低? (2)第10min 时,学生的接受能力是多少? (3)多长时间内,学生的接受能力最强? 复习巩固1､下列函数中,是二次函数的是( )A ､y=0.5(x-3)xB ､y=(x+2)(x-2)-x 2C ､y=-0.75xD ､y=2､抛物线1)1(22+-=x y 的顶点是( ) A ､(1,1) B ､(-1,1) C ､(1,-1) D ､(-1,-1)3､顶点是(-2,0),开口方向､形状与抛物线y=0.5x 2相同的抛物线是( )A ､y=0.5(x-2)2B ､y=0.5(x+2)2C ､y=-0.5(x-2)2D ､y=-0.5(x+2)2 4､抛物线32+=x y 向右平移2个单位,再向上平移3个单位,所得新的抛物线是. 5､写出一个开口向下且对称轴是x=-2的二次函数解析式 6､将二次函数222---=x x y 经配方后得( )A ､3)1(2---=x y B ､3)1(2-+-=x yC ､1)1(2---=x yD ､1)1(2-+-=x y 7､二次函数42-=x y 与x 轴的交点坐标为,8､二次函数a x ax y ++=42的最大值是3,则=a9､将一根铁丝长为x,围成一个等边三角形,则面积S 与周长x 的关系式为. 10､ 根据下列条件,分别确定二次函数中字母系数的值:(1)抛物线c x x y ++=42的顶点在x 轴上;c= (2)抛物线232+-=x ax y 的图像经过点(-1,3)a= (3)抛物线52+-=bx x y 的对称轴是直线x=-2,b=综合与运用11､如图,有一直角梯形的苗圃,它的两邻边借用夹角是135°的两围墙,另外两边用总长为30m的篱笆,问篱笆的两边各是多少米时,苗圃的面积最大?最大面积是多少?12､某商场将进价为30元的台灯以40元售出,平均每月能售出600个,调查表明:这种台灯的售价每上涨1元,其销售量就减少10个.(1)为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少?这时应进台灯多少个?(2)如果商场要想每月的销售利润最多,这种台灯的售价又将定为多少?这时应进台灯多少个?13.某瓜果基地市场部为指导该基地某种蔬菜的生产和销售,在对历年市场行情和生产情况进行了调查的基础上,对今年这种蔬菜上市后的市场售价和生产成本进行了预测,提供了两个方面的信息,如图甲､乙两图请你根据图象提供的信息说明:(1)在3月份出售这种蔬菜,每千克的收益是多少元?(收益=售价-成本)(2)哪个月出售这种蔬菜每千克的收益最大?说明理由.拓展与探索14､已知二次函数y=-0.5x 2+x+1.5 (1)用配方法求它的顶点坐标和对称轴; (2)画出这个函数的图象;(3)根据图象回答:当x 取哪些值时,y =0,y >0,y <0第二十六章答案 26.1二次函数(一)1､x x y 102+-=,二. 2､B 3､k=1,k ≠0且k ≠1.4､241x y =它是二次函数 5､x x y 4212+-= 0<x<4,二次 6､5 7(1)480020022+-=x x y , (2)4602m 2, (3)此时水渠的宽度是2m.26､1二次函数(二)1､-1 y 轴 (0,0) 向下 高 2､D 3､B 4､点B 不在,点C 在 5､(1)221x y = (2)略 6､A 7(1)A(1,1) 顶点C(0,0)对称轴是y 轴.(2)(3,9)3 26､1二次函数(三)1、 下､y 轴､(0,2),1,2 2､42+-=x y (0,4) y 轴 (0,4) (2,0)(-2,0) 3､B 4､532+-=x y 5､(1)2,21=-=c a (2)略 6､顶点坐标分别是(0,2)(0,-2) 对称轴都是y 轴,开口方向向下与向上,两个图象关于x 轴对称, 6､ 26.1二次函数(四)1､A 2､D 3､2x y -= 右 1 直线x=1 1 大草原0 4､(1)2)2(+=x y 开口向上, 顶点(-2,0)对称轴是直线x=-2 (2)2)3(21--=x y 开口向下,顶点(3,0)对称轴是直线x=3 5､2)5(92--=x y 或2)1(2--=x y ,6､(1)-1,(2)略(3) (0,-4)(2,0) 26.1二次函数(五)1､略 2､C 3､D 4､(1)2)1(2-+=x y (2)略5､(1)3)2(432+--=x y (2)(0,0) (4,0 ) 6､(1)5)6(1212+--=x y (2)1526+ 7､310 26.1二次函数(六)1､B 2､左 2 下 2 3､(1)41)21(2--=x y 顶点()41,21- 对称轴是直线21=x (2)2)1(2++-=x y 顶点(-1,2)对称轴是直线x=-1, 4､(1)25)3(212+--=x y 开口向下,顶点(3,)25对称轴是直线x=3,当x=3时,y 有最大值是35 (2)87)45(22--=x y 开口向上,顶点()87,45- 对称轴是直线x=45,当x= 45时,y 有最小值87- 5､(1)变化规律是二次函数､x x y 202+-= 表格与图象略,(2)当x=10m 时,y 的最大值是100m 2,6､宽为,21m ⋅高为m 8.1,最大面积为216.2m . 7､(1) 0≤x ≤13 13<x ≤30 (3)x=13复习题1､A 2､A 3､B 4､6)2(2+-=x y 5､不唯一如2)2(+-=x y 6､D 7､(2,0) (-2,0)8､4或-1 9､2363x y = 10､(1)4 (2)-2 (3)-4 11､直角腰为10m,下底边为20m,最大面积为150m 2.12､(1)当售价定为50元时,销售量为500个,当售价定为80元时,销售量为200个,(2)当售价定为65元时,销售量为350个,获利最大是1225元.13､(1)1元,(2)每千克售价关于月份的函数关系式为7321+-=x y ,每千克成本关于月份的函数关系式1)6(3122+-=x y ,每千克的收益21y y y -=,故37)5(312+--=x y ,当x=5时,y 最大值37, 14､(1)2)1(212+--=x y 顶点点坐标(1,2) 对称轴是直线x=1,(2)略 (3)当x=-1或x=3时,y=0,当-1<x<3时y>0,当x<-1或x>3时,y<0.。

九年级数学下册 26.1.1 二次函数（快乐预习+轻松尝试）导学案 新人教版学前温故1．函数的基本概念：在一个变化过程中，有______变量x 和y ，并且对于x 每一个确定的值，y 都有__________的值与其对应，那么我们就说y 是x 的______，也可以说x 是________，y 是________．2．一般地，形如y ＝kx ＋b (k ≠0，k ，b 均为常数)的函数，叫做__________，当b ＝0时称y 为x 的________函数，正比例函数是一次函数中的______情况，可表示为________．新课早知1．二次函数的概念：一般地，形如y ＝ax 2＋bx ＋c (其中a ，b ，c 是常数，a ≠0)的函数叫做二次函数，其中ax 2是二次项，______是一次项，c 是常数项，______是二次项系数，______是一次项系数．2．圆面积公式S ＝πR 2，S 与R 之间的关系是( )．A ．正比例函数B ．一次函数C ．二次函数D ．以上答案都不对3．二次函数的三个特征：(1)函数关系式必须是______；(2)化简后二次函数的最高次数必须是______次；(3)二次项系数必须不为______．4．函数y ＝(n －3)xn 2－7＋2x －1是二次函数，则n ＝__________.答案：学前温故1．两个 唯一确定 函数 自变量 因变量2．一次函数 正比例 特殊 y ＝kx新课早知1．bx a b2．C 因为系数是π≠0，次数是2次，所以为二次函数，故选C.3．(1)整式 (2)2 (3)04．－3 函数是二次函数应满足⎩⎪⎨⎪⎧n －3≠0，n 2－7＝2，解得n ＝－3，故填－3.1．二次函数的概念【例1】已知函数y ＝(m ＋2)xm 2＋m －4＋2x ＋6是关于x 的二次函数，求满足条件的m的值．分析：由二次函数的概念，可以得到m 2＋m －4＝2，且m ＋2≠0，解得m ＝－3，或m ＝2.解：根据题意可得，m 2＋m －4＝2，且m ＋2≠0，解得m ＝－3，或m ＝2.即满足条件的m 的值为m ＝－3，或m ＝2.点拨：判断一个函数是否为二次函数，应根据二次函数的三个特征作出判断，缺一不可．2．列二次函数关系式【例2】某果园有100棵橙子树，每一棵平均结600个橙子，现准备多种一些橙子树以提高产量．但是如果多种树，树之间的距离和每一棵树所接受的阳光就会减少，根据经验估计，每多种一棵树，平均每棵树就会少结5个橙子．(1)若设增种x 棵橙子树，果园橙子的总产量为y 个，那么请你写出y 与x 之间的关系式．(2)y 与x 的函数关系式是几次函数，自变量x 的取值范围有何限制？分析：根据题意得，增种x 棵橙子树，果园共有(100＋x )棵橙子树，平均每棵树结(600－5x )个橙子．解：(1)果园增种x 棵橙子树后，那么果园共有(100＋x )棵橙子树，这时平均每棵树结(600－5x )个橙子，所以y ＝(600－5x )(100＋x )．(2)由(1)y ＝(600－5x )(100＋x )＝－5x 2＋100x ＋60 000可知，y 是x 的二次函数，自变量x 的取值范围是0≤x <120，且x 为自然数．点拨：列与实际问题有关的二次函数，应认真理解题意，明确各个量之间的关系，同时要注意自变量的取值范围，即便题目中没有注明写出取值范围，也要根据题意写出，注意函数关系式最后要化成一般形式．1．下列函数是二次函数的是( )．A. y ＝8x 2B. y ＝8x ＋1C. y ＝8xD. y ＝8x2＋1 2．国家为了解决农民就医难，就医贵的问题，决定对某药品价格分两次降价，若设平均每次降价的百分率为x ，该药品原价为18元，降价后的价格为y 元，则y 与x 的函数关系式为( )．A ．y ＝18(1－x )B ．y ＝18(1＋x )C ．y ＝18(1－x )2D ．y ＝18(1＋x )23．对于任意实数m ，下列函数一定是二次函数的是( )．A ．y ＝(m －1)2x 2B ．y ＝(m ＋1)2x 2C ．y ＝(m 2＋1)x 2D ．y ＝(m 2－1)x 24．二次函数y ＝3x 2－5的二次项系数是__________，一次项系数是__________，常数项是__________．5．已知正三角形的边长为x cm ，面积为y cm 2，则y 与x 之间的函数关系式为__________，y __________x 的二次函数(填“是”或“不是”)．6.小明的爸爸拟建一个温室大棚，小明帮助爸爸画出了它的平面图形，如果温室外围是一个矩形，周长为120 m ，室内通道的尺寸如图所示，设一条边长为x (m)，种植面积为y (m 2)，为了能较容易计算出种植面积，请你帮助小明建立一个能反映种植面积y 与x 的函数关系式，当x ＝10时，种植面积是多少？答案：1．A 在判断是否是二次函数的问题中，应紧紧抓住三个要素：(1)含两个变量，符合函数的对应关系；(2)是整式；(3)某个变量次数最高为2.D 项的右边代数式8x2是关于自变量x 的分式，不是二次函数；B 为一次函数；C 为反比例函数，故选A.2．C3．C 二次函数的二次项系数不能为0，选项A 中当m ＝1时，m －1＝0；选项B 中当m＝－1时，m ＋1＝0；选项D 中当m ＝±1时，m 2－1＝0，所以都不能满足对于任意实数m 使二次项系数不为0；只有选项C 中当m 为任意数时，保证m 2＋1≠0，故选C.4．3 0 －5 二次函数y ＝ax 2＋bx ＋c (a ≠0)，其中a 叫做二次项系数，b 叫做一次项系数，c 叫做常数项．5．y ＝34x 2 是 根据勾股定理得正三角形一边上的高为32x cm ，所以正三角形的面积为y＝34x2，y是x的二次函数．6．分析：根据图形标出的尺寸得，种植面积的一边为(60－x－4) m，另一边为(x－2) m，根据矩形面积公式求出y与x的函数关系式．解：y＝(60－x－4)(x－2)＝－x2＋58x－112，把x＝10代入得y＝368(m2)．。