10(超)静定结构的影响线解析

2022-2023年注册结构工程师《结构专业基础考试一级》考前冲刺卷②（答案解析）全文为Word可编辑，若为PDF皆为盗版，请谨慎购买！第I卷一.综合考点题库(共70题)1.磁偏角和子午线收敛角分别是指磁子午线、中央子午线与下列哪项的夹角？（）A.坐标纵轴B.指北线C.坐标横轴D.真子午线正确答案：D本题解析：真子午线方向与过该点的坐标X轴方向的夹角称为子午线收敛角，规定东偏（X轴偏于真子午线方向东侧）为正，西偏为负。

磁偏角是指过该点的真子午线方向与磁子午线方向的夹角，规定东偏（磁子午线方向偏于真子午线方向以东）为正，西偏为负。

2.可以只做外观检查的焊缝质量等级是（）。

A.一级焊缝B.二级焊缝C.三级焊缝D.上述所有三种焊缝正确答案：C本题解析：根据《钢结构工程施工质量验收标准》（GB 50205—2020）第5.2.4条和5.2.5条规定，一级焊缝要求对每条焊缝长度的100%进行超声波探伤。

二级焊缝要求对每条焊缝长度的20%进行抽检，且不小于200mm 进行超声波探伤。

三级焊缝只需进行外观检测。

3.图示简支梁在所示移动荷载下截面K的最大弯矩值是（）。

A.90kN·mB.110kN·mC.120kN·mD.150kN·m正确答案：B本题解析：简支梁跨中弯矩影响线如题46解图所示，截面K处竖标yK＝12×4/（12＋4）＝3kN·m，或根据单位力作用下的受力平衡条件求解。

当右侧集中力作用于影响线峰值上时，截面K的弯矩值最大，此时左侧集中力所在截面的竖标y左＝10/12×3＝2.5kN·m，则MKmax＝20×3＋20×2.5＝110kN·m。

4.《建筑工程质量管理条例》规定，在正常使用条件下，电气管线、给排水管道、设备安装和装修工程的最低保修期为（）。

A.3年B.2年C.1年D.5年正确答案：B 本题解析：《建筑工程质量管理条例》第四十条规定，在正常使用条件下，建设工程的最低保修期限为：基础设施工程、房屋建筑的地基基础工程和主体结构工程，为设计文件规定的该工程的合理使用年限；屋面防水工程、有防水要求的卫生间、房间和外墙面的防渗漏，为5年；供热与供冷系统，为2个采暖期、供冷期；电气管线、给排水管道、设备安装和装修工程，为2年，其他项目的保修期限由发包方与承包方约定，建设工程的保修期，自竣工验收合格之日起计算。

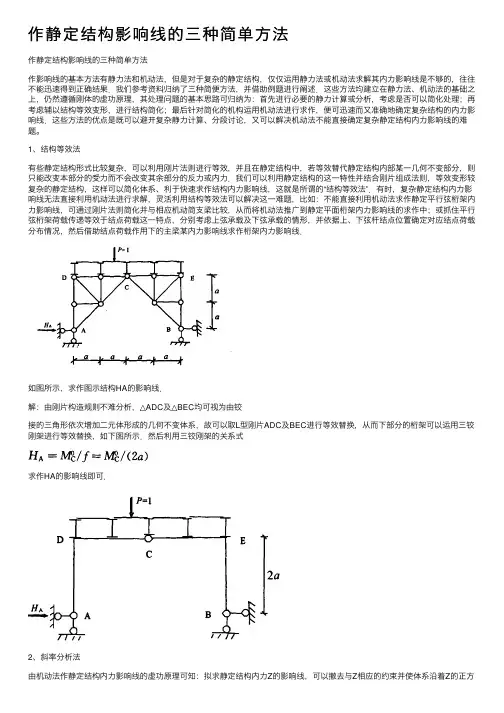
作静定结构影响线的三种简单⽅法作静定结构影响线的三种简单⽅法作影响线的基本⽅法有静⼒法和机动法，但是对于复杂的静定结构，仅仅运⽤静⼒法或机动法求解其内⼒影响线是不够的，往往不能迅速得到正确结果．我们参考资料归纳了三种简便⽅法，并借助例题进⾏阐述．这些⽅法均建⽴在静⼒法、机动法的基础之上，仍然遵循刚体的虚功原理，其处理问题的基本思路可归纳为：⾸先进⾏必要的静⼒计算或分析，考虑是否可以简化处理；再考虑辅以结构等效变形，进⾏结构简化；最后针对简化的机构运⽤机动法进⾏求作，便可迅速⽽⼜准确地确定复杂结构的内⼒影响线．这些⽅法的优点是既可以避开复杂静⼒计算、分段讨论，⼜可以解决机动法不能直接确定复杂静定结构内⼒影响线的难题。

1、结构等效法有些静定结构形式⽐较复杂，可以利⽤刚⽚法则进⾏等效，并且在静定结构中，若等效替代静定结构内部某⼀⼏何不变部分，则只能改变本部分的受⼒⽽不会改变其余部分的反⼒或内⼒．我们可以利⽤静定结构的这⼀特性并结合刚⽚组成法则，等效变形较复杂的静定结构，这样可以简化体系、利于快速求作结构内⼒影响线，这就是所谓的“结构等效法”．有时，复杂静定结构内⼒影响线⽆法直接利⽤机动法进⾏求解，灵活利⽤结构等效法可以解决这⼀难题，⽐如：不能直接利⽤机动法求作静定平⾏弦桁架内⼒影响线，可通过刚⽚法则简化并与相应机动简⽀梁⽐较，从⽽将机动法推⼴到静定平⾯桁架内⼒影响线的求作中；或抓住平⾏弦桁架荷载传递等效于结点荷载这⼀特点，分别考虑上弦承载及下弦承载的情形，并依据上、下弦杆结点位置确定对应结点荷载分布情况，然后借助结点荷载作⽤下的主梁某内⼒影响线求作桁架内⼒影响线．如图所⽰，求作图⽰结构HA的影响线．解：由刚⽚构造规则不难分析，△ADC及△BEC均可视为由铰接的三⾓形依次增加⼆元体形成的⼏何不变体系，故可以取L型刚⽚ADC及BEC进⾏等效替换，从⽽下部分的桁架可以运⽤三铰刚架进⾏等效替换，如下图所⽰．然后利⽤三铰刚架的关系式求作HA的影响线即可．2、斜率分析法由机动法作静定结构内⼒影响线的虚功原理可知：拟求静定结构内⼒Z的影响线，可以撤去与Z相应的约束并使体系沿着Z的正⽅向发⽣虚位移￡z=1，此时结构对应的荷载位移图为所求静定结构内⼒Z的影响线．也就是说，在竖向单位移动荷载P=1作⽤下，静定结构内⼒影响线取结构的竖向位移图；在⽔平单位移动荷载P=1作⽤下，静定结构内⼒影响线取结构的⽔平位移图；在单位移动⼒偶M=1作⽤下，静定结构内⼒影响线取结构的转⾓位移图，⽽当转⾓位移很⼩时，有等价关系，所以此时结构内⼒影响线可取竖向位移图的斜率．影响线竖距的正负号可规定如下：当结构转⾓位移⼝与单位移动⼒偶M=1⽅向⼀致时，取负号；反之，取正号．这就是所谓的“斜率法”，此种⽅法仅适⽤于求解静定结构在单位移动⼒偶M=1作⽤下的内⼒影响线．如图所⽰，试求作图⽰结构在单位移动⼒偶m=1作⽤下的Mc、Qc的影响线．解：分别撤去所⽰静定结构与Mc、Qc相应约束，并令结构分别沿其正⽅向发⽣的虚位移为“l”，然后分别作出结构的竖向位移图，如图所⽰，最后分别取结构竖向位移图的斜率即为所求图⽰结构Mc、Qc 的影响线，分别如图所⽰．3、联合分析法静定结构的内⼒影响线由分段的直线段组成，故可先运⽤机动法分析静定结构影响线的轮廓特征即影响线有⼏段及其相互位置关系(铰接或平⾏)，再利⽤静⼒法确定各直线段特征点竖标便可确定所求静定结构的内⼒影响线，这就是所谓的“联合分析法”。

第十章 影响线及其应用10．1 影响线的概念一、移动荷载对结构的作用1、移动荷载对结构的动力作用:启动、刹车、机械振动等.2、由于荷载位置变化，而引起的结构各处的反力、内力、位移等各量值的变化及产生最大量值时的荷载位置。

二、解决移动荷载作用的途径1、利用以前的方法解决移动荷载对结构的作用时，难度较大。

例如吊车在吊车梁上移动时，R B 、M C2、影响线是研究移动荷载作用问题的工具。

根据叠加原理，首先研究一系列荷载中的一个，而且该荷载取为方向不变的单位荷载。

10.2 用静力法绘制静定结构的影响线一、静力法把荷载Ｐ＝１放在结构的任意位置，以x 表示该荷载至所选坐标原点的距离，由静力平衡方程求出所研究的量值与x 之间的关系（影响线方程）。

根据该关系作出影响线。

二、简支梁的影响线1、支座反力的影响线∑M B =0：∑M A =0：2、弯矩影响线1M C影响线弯矩图（1）当P=1作用在AC段时，研究CB：∑M C=0：（2）当P=1作用在CB段时，研究CB：∑M C=0：3、剪力影响线（1）当P=1作用在AC段时，研究CB：（2）当P=1作用在CB段时，研究CB：三、影响线与量布图的关系1、影响线：表示当单位荷载沿结构移动时，结构某指定截面某一量值的变化情况（分析左图）。

2、量布图（内力图或位移图）：表示当荷载位置固定时，某量值在结构所有截面的分布情况（分析右图）。

四、伸臂梁的影响线例10−1 试作图10−4（a）所示外伸梁的反力R A、R B的影响线，C、D截面弯矩和剪力的影响线以及支座B截面的剪力影响线。

10.3 用机动法作影响线一、基本原理机动法是以虚位移原理为依据把作影响线的问题转化为作位移图的几何问题。

二、优点 不需要计算就能绘出影响线的轮廓。

以X 代替A 支座作用，结构仍能维 持平衡。

使其发生虚位移，依虚位移原理： X ·δX +P · δP =0 X=－P δP /δX =－ δP /δX 令 δX =1， 则 X=－δP 结论：为作某量值的影响线，只需将与该量值相应的联系去掉，并以未知量X 代替；Q C 影响线)而后令所得的机构沿X的正方向发生单位位移，则由此所得的虚位移图即为所求量值的影响线。

§9-5 超静定力的影响线1、影响线的特征与求解方法1）影响线的特征静定结构——反力、内力影响线均为直线；位移影响线为曲线。

超静定结构——各量值的影响线均为曲线。

2）影响线的求作方法静力法——利用静力平衡条件求影响线方程，进而绘制影响线。

但对超静定力的影响线须解超静定问题，复杂、少用。

机动法——利用影响线与移动载荷作用点位移（挠度）图的比拟关系，快速绘制影响线轮廓。

简便、实用。

2、机动法求作超静定力影响线以图9-14连续梁（超静定梁）M K的影响线为例，说明用机动法求作超静定力影响线的方法。

1）取基本结构（超静定、几何不变体系）图b——去掉与XK 相应的约束，代之以(暴露出)约束反力XK ；A B C D EF P=1K（a）原结构A B C D EF P=1X K(M K)(下拉为正)(b)基本结构图9-14§9-5 超静定力的影响线2）建立力法典型方程k kk kp X δδ+=1()kp k pk kk kkX x δδδδ∴=-=-⋅()()pk kp x x δδ=ABCD EF P =1K ABCD E F P =1X K (M K )(下拉为正)(b)基本结构§9-5 超静定力的影响线K 截面相对转角为0式中δkk ——常数,不随X 而变化。

δpk ——载荷F P =1位置参数X 的函数，即δPK =δPK (x)，其位移图如图9-14c 所示。

互等定理图9-14ABCDEX K (M K )(下拉为正)θB(c)挠度图⏹写成更明确的形式：()()1pk kkk x x X δδ=-ABCD EK+图9-15X k (M k )的影响线结论:X k 与δpk 成正比;挠度图即为影响线轮廓线图9-14ABCDEX K (M K )(下拉为正)θB(c)作用挠度图1kM=§9-5 超静定力的影响线X k 向上为正δpk 以向下为正(与p=1同向)X k 与δpk 反向3、求做超静定力影响线的步骤⏹1）撤去与所求约束力（或量值）相应的约束，代之以反力X K ；●2）使体系沿X K 正方向发生位移，作出移动载荷作用点的挠度δPK =δPK (x)（位移）图即为影响线X K (x)的形状；●3）将δPK 图除以常数δKK 使可确定影响线的具体数值；●4）横坐标以上图形为正号，横坐标以下图形为负号。