下载文档原格式
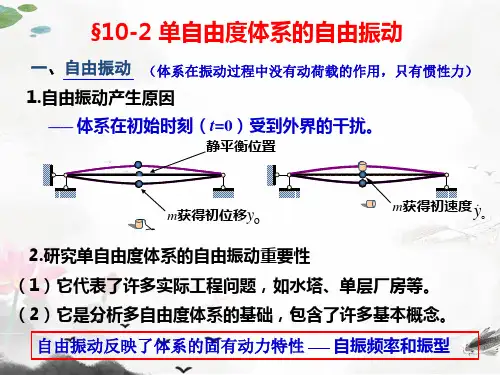
y sy(t)s=-k(y+y s )w=mg F(t)=-m y§1 单自由度体系的自由振动一、无阻尼的自由振动：如下图，以单自由度体系为例，设此梁上的集中质量为m ，其重量为W mg =，梁由于质量的重力引起的质量处的静力位移用s y 表示，与s y 相应的质量位置称为质量的静力平衡位置。
若此质量受到扰动离开了静力平衡位置，当扰动除去后，则体系将发生振动，这样的振动称为体系的自由振动。
由于振动的方向与梁轴垂直，故称为横向振动。
在此，只讨论微小振幅的振动，由振动引起的内力限于材料的弹性极限以内，用以表示质量运动的方程将为线性微分方程。
1、建立运动方程建立运动方程常用的基本原理是达朗伯原理（亦称惯性力法或动静法）。
今考虑在振动过程的某一瞬时t ，设质量在此瞬时离开其平衡位置的位移为y ，取质量为隔离体，则在质量上作用有三种力：质量的重量W ，杆件对质量的弹性恢复力S 和惯性力F(t)。
根据达朗伯原理，这三个力应成平衡，即 W+S+F(t)＝0 （1） 在弹性体系中，弹性恢复力S 为 ()s k y y s =-+上式中的K 为一常数，称为刚度系数，代表简支梁上使质量在运动方向产生单位位移时需要加在质量上的沿质量运动方向的集中力的量值。
式中负号表示s 的指向和位移的方向相反。
而 1y s W k=⋅ 即 y s W k =⋅因此，将()s k y y s =-+和y s W k =⋅代入式（1）得()0F t ky =-+ （2）上式表明，如果以静力平衡位置作为计算位移的起点，则建立体系的运动方程时，可以不考虑重力W 的影响。
这对其他体系的振动（包括受迫振动）也同样适用。
将22()d yF t m dt =-代入式（2）得：22()0d ym ky t dt+= 令2k m ω= dyy dt= （速度） 22d y y dt =（加速度） 则 22()0d ym ky t dt+= 可变为 20y y ω+= （3）此为单自由度体系无阻尼自由振动的运动方程，它反映了这种振动的一般规律。
