★卫生统计学专题九:方差分析
- 格式:doc
- 大小:141.00 KB
- 文档页数:4

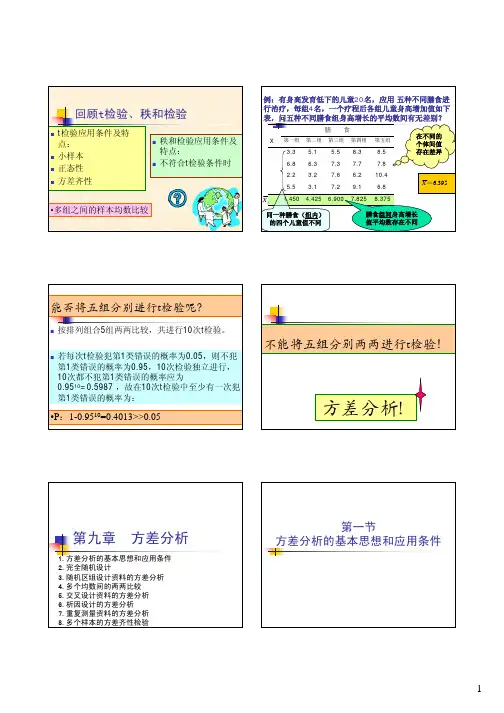
回顾t检验、秩和检验 t检验应用条件及特 点: 小样本 正态性 方差齐性 秩和检验应用条件及 特点: 不符合t检验条件时•多组之间的样本均数比较例:有身高发育低下的儿童20名,应用 五种不同膳食进 行治疗,每组4名,一个疗程后各组儿童身高增加值如下 表,问五种不同膳食组身高增长的平均数间有无差别?膳食 X 第一组 第二组 第三组 第四组 第五组3.3 5.1 5.5 8.3 8.5在不同的 个体间值 存在差异6.8 6.3 7.3 7.7 7.82.2 3.2 7.6 6.2 10.4 5.5 3.1 7.2 9.1 6.8X =6.395X i 4.450 4.425 6.900 7.825 8.375同一种膳食(组内) 的四个儿童值不同膳食组间身高增长 值平均数存在不同能否将五组分别进行t检验呢? 按排列组合5组两两比较,共进行10次t检验。
若每次t检验犯第1类错误的概率为0.05,则不犯 第1类错误的概率为0.95,10次检验独立进行, 10次都不犯第1类错误的概率应为 0.9510=0.5987 ,故在10次t检验中至少有一次犯 第1类错误的概率为:•P:1-0.9510=0.4013>>0.05不能将五组分别两两进行t检验!方差分析!第九章 方差分析1.方差分析的基本思想和应用条件 2.完全随机设计 3.随机区组设计资料的方差分析 4.多个均数间的两两比较 5.交叉设计资料的方差分析 6.析因设计的方差分析 7.重复测量资料的方差分析 8.多个样本的方差齐性检验第一节 方差分析的基本思想和应用条件1第一节 完全随机设计的方差分析1. 方差分析的概念 方差分析(ANOVA)又称变异数分析或F检验,其目的是推断两组或多组资料的总体均数是否相 同,检验两个或多个样本均数的差异是否有统计 学意义。
应用条件: • 各样本相互独立 • 均来自总体方差具有齐性的正态分布方差分析的基本思想 将全部观察值的总变异按影响实验结果的诸 因素分解为若干变异,构造出反映各部分变 异作用的统计量(SS),之后构造假设检验 统计量(F),实现对总体均数的推断。

方差分析是为了比较多个总体样本均数是否存在差别。
该方法有RA.Fisher首先提出,后来由GW.Snedecor完善,为了纪念Fisher,故称方差分析为F检验。
组间均方:MS组间=SS组间/ v组间,SS代表离均差平方和,v代表自由度,组间变异包括处理效应和随机误差。
组内均方:MS组内=SS组内/ v组内,组内差异包括随机误差。
F=MS组间/MS组内,F接近1,说明组间差异不大。
方差分析的基本思想,首先将总变异分为组间和组内变异,然后计算两者的F 值。
F值越大,说明组间差异大,处理起作用,反之,则不起作用,是由随机误差导致的。
方差分析应用条件:1)样本独立;2)来自正态总体;3)方差齐性。
方差分析包括完全随机设计(completely random design)的方差分析,又叫单向(one-way)方差分析和随机区组设计(radomized block design)的方差分析又叫双向(two-way)方差分析。
完全随机设计的方差分析是将受试对象随机化的分配到各个处理组或对照组的方法,未考虑干扰因素的影响,各个组的样本数可以不一样多。
随机区组设计的方差分析将受试对象按照性质相同或相近组成b个区组,每个区组有g个受试对象,分别随机分配到g个处理组,这样各个处理组不仅样本个数相同,生物学特性也比较均衡。
方差分析拒绝H0,接受H1,只说明g个总体均数不全相等,如果想要进一步了解那两个组均数不等,需要进行两两比较或称多重比较,即post-hoc检验。
ANOVA与T test的关系:.。
![卫生统计学_方差分析[新版]](https://uimg.taocdn.com/e9c41fb4804d2b160a4ec0dd.webp)
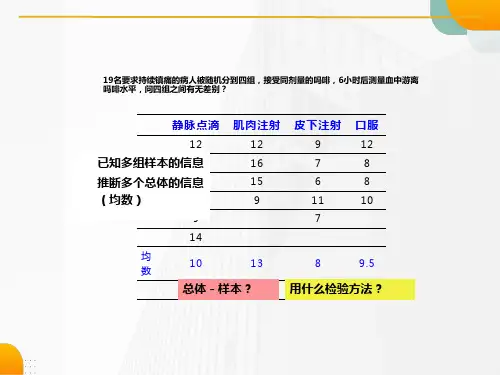





医学统计学方差分析方差分析是一种统计学方法,用于比较三个或三个以上的组之间的平均值是否存在显著差异。
在医学研究中,方差分析常用于比较不同治疗方法或不同个体群体之间的差异,以确定是否存在统计学上的显著差异。
方差分析的基本原理是比较组间离散程度与组内离散程度的比值,即组间均方与组内均方的比值。
组间方差表示不同组之间的差异性,组内方差表示同一组内个体之间的变异程度。
如果组间离散程度显著大于组内离散程度,即组间均方大于组内均方,就可以得出组间存在显著差异的结论。
在医学研究中,方差分析可以应用于很多不同的情况。
举例来说,我们可以使用方差分析来比较不同药物对同一疾病的治疗效果,或者比较不同药物剂量对同一疾病的治疗效果。
我们还可以使用方差分析比较不同年龄组、性别组或不同地区患者之间的其中一种疾病发病率。
方差分析的核心是比较组间差异与组内差异。
组间差异可以通过计算组间均方来得到。
组间均方的计算公式为组间平方和除以组间自由度。
组间平方和是每个组内数据与该组均值之差的平方的总和。
组间自由度等于组数减1、组内差异可以通过计算组内均方来得到。
组内均方的计算公式为组内平方和除以组内自由度。
组内平方和是每个组内数据与该组均值之差的平方的总和。
组内自由度等于总体样本量减去组数。
计算得到组间均方和组内均方之后,即可计算F值。
F值等于组间均方除以组内均方。
F值的计算结果可以与F分布的临界值进行比较,以判断组间均方是否显著大于组内均方。
如果F值大于F分布的临界值,就可以得出组间存在显著差异的结论。
除了F值,方差分析还可以计算一些其他的统计量。
例如,可以计算每个组的均值和标准差,以了解不同组之间的差异程度。
还可以计算方差分析表,其中包含了组间平方和、组间自由度、组间均方、组内平方和、总平方和、总自由度、组内自由度和组内均方等统计量。
需要注意的是,在进行方差分析之前,需要检验数据的正态性和方差齐性。
正态性检验可通过绘制正态概率图、Shapiro-Wilk检验或Kolmogorov-Smirnov检验进行。

专题九 方差分析方差分析(ANOV A ),又称F 检验,是一种以分析数据的变异为基础,以F 值为统计量的计量资料的假设检验方法。
用较不同变异来源的均方,借助F 分布做出统计推断。
⑴方差分析的应用条件:①各观察值相互独立,且每一水平下的观察值均服从正态分布。
②各总体方差相等,即具有方差齐性。
⑵对于不满足方差分析应用条件的资料,可采用以下两种方式进行处理:①变量变换,是指满足方差分析的基本假定。
②应用非参数统计分析方法。
⒉完全随机设计的ANOV A各组样本均数各不相等,这种差异可能由两种原因引起:①随机误差;②处理因素。
⑴完全随机设计的变异分解:完全随机设计(成组设计)资料的总变异可以分解为组间变异和组内变异。
①总变异:SS 总,用所有观察值与均数的离均差平方和表示。
SS 总=∑∑-ij2ijx x )(,υ总=N-1(N 为总例数)②组间变异:SS 组间,用各组均数与总均数的离均差平方和表示。
SS 组间=∑-i2ii x xn )(,υ组间=k-1(k 为处理组数)③组内变异:SS 组内,用各组内每个测量值xij 与该组均数得离均差平方和表示,仅反映随机误差,又称误差变异。
SS 组内=∑∑-ij2i ij x x )(,υ组内=N-k⑵三种变异及相关自由度的关系为:SS 总=SS 组间+SS 组内,υ总=υ组间+υ组内均方MS 组间=SS 组间/υ组间;MS 组内= SS 组内/υ组内⑶方差分析的统计量F :F=MS 组间/MS 组内⑷F 界值表:纵标目为组间自由度υ1,横标目为组内自由度υ2,表中给出了α=0.05和α=0.01时供方差分析用的单侧F 界值,用F α,(υ1,υ2)表示。
若F ≥F α,(υ1,υ2),则P ≤α,按α水准拒绝H 0,接受H 1,差别有统计学意义,可以认为总体均数不等或不全等(处理因素有效应);反之,则差别无统计学意义,尚不能认为总体均数不等或不全等(尚不能认为处理因素有效应)。
完全随机设计方差分析计算公式变异来源 SS υ MS F 组间变异(处理)∑-i2i i x x n )( k-11k SS -组间组内组间MS MS组内变异(误差)∑∑-ij2i ijx x )( N-kk-N SS 组内总变异∑2x -()Nx 2∑N-1【小结】①完全随即设计资料的总变异可分解为组间变异和组内变异两部分。
②方差分析常用于三个及以上均数的比较,当用于两个均数的比较时,同一资料所得结果与t 检验等价,即F=t 2③方差分析的结果若拒绝H0,而接受H1,只说明多个总体均数中至少有两个均数不同,不能说明任意两个总体均数都有差⑴随机区组设计的变异分解:SS 总=SS 处理+SS 区组+SS 误差,υ总=υ处理+υ区组+υ误差用k 表示处理组数,b 表示区组数,实验观察值x ij 下标i (i=1,2,…,k )表示组别,下标j (j=1,2,…,b )表示区组序号。
完全随机设计方差分析计算公式变异来源 SS υ MS F处理组()∑-i2i i xx nk-11k SS -处理误差处理MS MS区组()∑-j2j j xx nb-11b SS -区组误差区组MS MS误差 SS 总-SS 处理-SS 区组 N-k-b-1或(k-1)(b-1)1b k N SS +--误差总变异∑2x -()Nx 2∑N-11N SS -总⑵随机区组设计资料的ANOV A 的基本步骤: ①建立假设检验,确定检验水准:⑴对于处理组:H 0:μ1=μ2=μk ,即…相同;H 1:μ1、μ2、μk 不等或不全等,即…不同或不全同。
⑵对于区组:H 0:k 个区组的总体均数相等;H 1:k 个区组的总体均数不等或不全等。
②计算检验统计量:F= MS 处理/MS 误差;F= MS 区组/MS 误差 ③确定P 值,做出统计推断。
⑴对处理组:以υ1=k-1,υ2=N-k-b-1或(k-1)(b-1),查F 界值表,确定P 值,做出统计推断。
⑵对区组:以υ1=b-1,υ2= N-k-b-1或(k-1)(b-1),查F 界值表,确定P 值,做出统计推断。
【注意】①随机区组设计资料的总变异可以分解为处理组间变异、区组间变异和误差变异三个部分。
②随机区组设计与完全随机设计相比,由于利用区组控制了可能的混杂因素,并在进行方差分析时,将区组间变异从原组内变异中分离出来,当区组间变异有统计学意义时,由于减少了误差均方使处理间的F 值更容易出现显著性,从而提高了实验效率。
2多组均数假的两两比较不能用t 检验,会增大Ⅰ型错误。
两两比较的方法较多,常用的是多重比较,多重比较法有两种情况:①探索性研究,即事先没有计划的任意两个均数的事后比较:SNK-q 检验、Bonfferoni t 检验。
②证实性研究,即事先有明确假设,用于多组中某一对或某几对在专业上有特殊意义的均数间的比较:Dunnett-t 检验、LSD-t 检验、Bonfferoni t 检验等。
不能多种方法一起使用,然后选取“有利”的结果。
⒌交叉设计的ANOV A ⑴两阶段交叉设计的变异分解:二阶段交叉设计方差分析的总变异可以分解为处理间变异、阶段间变异、个体变异和误差变异四个部分。
SS 总=SS 处理+SS 阶段+SS 个体+SS 误差,υ总=υ处理+υ阶段+υ个体+υ误差⑵两阶段交叉设计的方差分析基本步骤: ①建立建设检验,确定检验水准。
②计算检验统计量F 值:MS 阶段/MS 误差、MS 个体/MS 误差、MS 处理/MS 误差; ③确定P 值,做出统计推断。
【说明】①交叉设计可以采用完全随机设计或配对设计方法来安排其受试对象。
②交叉实验的处理是单因素的,但影响实验结果的因素还有非人为控制的受试者之间的个体差异和试验阶段这两个因素。
因此交叉设计试验实际上是一个试验因素和两个重要的非实验因素的多因素实验。
⒍析因设计的ANOV A析因设计资料的方差分析包括主效应分析、交互效应分析和单独效应分析三个层次。
①单独效应:是指其他因素的水平固定时,同一因素不同水平间的差别。
②主效应:是指某一因素各水平间的平均差别。
③交互效应:是指当某一因素的各单独效应随某一因素水平的变化而变化时则称这两个因素间存在交互效应。
两因素析因设计即I ×J 析因设计,表示有两种处理因素,第一种处理因素有I 个水平,第二种因素有J 个水平,共有I ×J 种处理组合。
⑴析因设计的变异分解:SS 总=SS 处理+ SS 误差=(SSA+SSB+SSAB )+SSE ,υ总=υ处理+υ误差=(μA+μB+μAB )+μE若处理因素A 有a 个水平,处理因素B 有b 个水平,每个处理因素组含有n 个受试对象,则全部收拾对象的总数N=a ×b ×n 。
用x ijk 表示每个受试对象的观察值,其中i (i=1,2,…,a )表示A 因素的水平。
j (j=1,2,…,b )表示B 因素有b 个水平;k (k=1,2,…,n )表示A 、B 两因素不同水平组合下受试对象的序号。
析因设计方差分析计算表变异来源 SS υ MS F处理 ()∑∑-ij2ij ij xx nab-1A()∑-i2ii xxna-11a SS A- 误差MS MS AB()∑-j2j j xx nb-11-b SS B误差MS MS BAB SS 处理-SS A -SS B (a-1)(b-1)()()1b 1-a SS AB-误差MS MS AB误差 SS 误差=SS 总-SS 处理 N-ab 或ab (n-1)()1n ab SS -误差总变异()Nx x22∑∑-N-1或(abn-1)1N SS -总⑵两因素析因设计资料方差分析的基本步骤:①对于因素A 、B 、交互作用AB 分别建立假设检验,确定检验水准。
检验假设:⑴对于因素A :H 0:A 因素各水平总体均数相等;H 1:A 因素各水平总体均数不相等; ⑵对于因素B :H 0:B 因素各水平总体均数相等;H 1:B 因素各水平总体均数不相等; ⑶ 对于交互作用AB :H 0:A 、B 无交互作用;H 1:A 、B 有交互作用; ②计算检验统计量:列表计算各组均数及方差分析表。
③确定P 值,做出统计推断。
【说明】①析因设计是将两个或多个实验因素的各水平进行交叉分组、全面实验的方法。
因此析因设计的方差分析被广泛用于需要分析交互效应和选择最佳组合的实验研究中。
②析因设计不但可以分析主效应和交互效应,也可以分析单独效应,故效率较高,但当因素太多时,所需的样本含量会很大。
③对析因设计资料,应先分析交互效应,若交互效应有统计学意义,方进一步分析个因素的单独效应。
反之,若交互效应无统计学意义,则因素之间的作用相互独立,分析某一因素的作用只需考虑因素的主效应。
⒎重复测量设计的ANOV A重复测量设计是指给予一种或多种处理后,在多个时间点上从同一受试对象重复获得指标的观察值。
重复测量数据的两因素多水平设计,两因素是指处理因素和处理时间;多水平是指处理有k (≥1)个水平;测量时间有i (i ≥2)个水平(时间点),即每个观察对象有i 个重复测量数据。
⑴重复测量设计的变异分解:两因素重复测量设计的总变异包括两部分:受试对象间变异、受试对象内变异。
SS 总=SS 受试对象间+SS 受试对象内=(SS 处理+SS 个体间误差)+SS 时间+SS 处理与时间交互作用+SS 个体内误差 υ总=υ受试对象间+υ受试对象内=(υ处理+υ个体间误差)+υ时间+υ处理与时间交互作用+υ个体内误差⑵重复测量设计方差分析的基本步骤:①对于处理因素、时间因素、交互作用分别建立检验假设,确定检验水准; ②计算检验统计量:SPSS 软件 ③确定P 值,做出统计推断;⑶重复测量设计方差分析的前提条件: ①正态性和方差齐性;②协方差阵地球形性或复合对称性。
球对称性:Mauchly 检验。
【注意】①若资料不满足球对称性,则方差分析的F 值有偏,通常会增大Ⅰ型错误的概率。
②资料满足球对称性时,可采用重复测量设计资料的单变量方差分析方法;若资料不满足球对称性,可用Greenhouse-Geisser 、Huynh-Feldt 或Lower-bound 三种“球对称”系数对自由度进行校正或采用多变量方差分析的方法。
【小结】①完全随机设计资料的方差分析,若处理无作用,则F 值理论上应等于1。
②重复测量设计资料和随机区组设计资料的区别主要有两点:⑴重复测量设计资料中同一受试对象(看成区组)的数据高度相关。
⑵重复测量设计资料中的处理因素在受试对象间为随机分配,但受试对象内的个时间点却不能随机分配;随机区组设计资料中每个区组内的受试对象彼此独立,处理只在区组内随机分配,同一区组内的受试对象的处理各不相同。