第十八章多因素实验资料的方差分析
- 格式:docx
- 大小:18.86 KB
- 文档页数:4




多因素方差分析是对一个独立变量是否受一个或多个因素或变量影响而进行的方差分析。
SPSS调用“Univariate”过程,检验不同水平组合之间因变量均数,由于受不同因素影响是否有差异的问题。
在这个过程中可以分析每一个因素的作用,也可以分析因素之间的交互作用,以及分析协方差,以及各因素变量与协变量之间的交互作用。
该过程要求因变量是从多元正态总体随机采样得来,且总体中各单元的方差相同。
但也可以通过方差齐次性检验选择均值比较结果。
因变量和协变量必须是数值型变量,协变量与因变量不彼此独立。
因素变量是分类变量,可以是数值型也可以是长度不超过8的字符型变量。
固定因素变量(Fixed Factor)是反应处理的因素;随机因素是随机地从总体中抽取的因素。
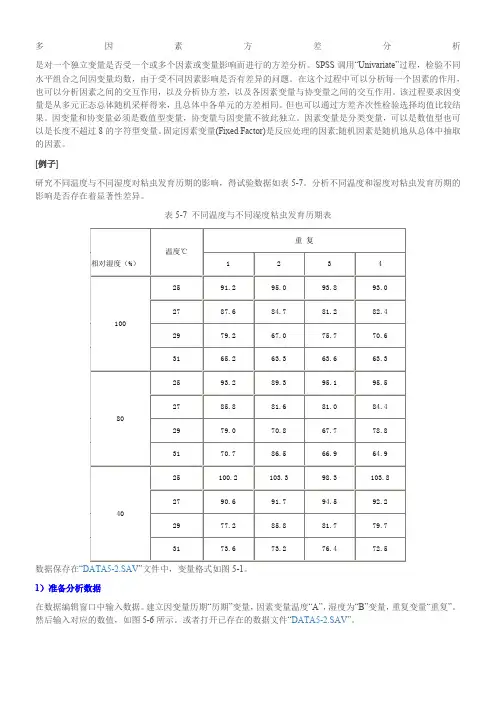
[例子]研究不同温度与不同湿度对粘虫发育历期的影响,得试验数据如表5-7。
分析不同温度和湿度对粘虫发育历期的影响是否存在着显著性差异。
表5-7 不同温度与不同湿度粘虫发育历期表图5-6 数据输入格式2)启动分析过程点击主菜单“Analyze”项,在下拉菜单中点击“General Linear Model”项,在右拉式菜单中点击“Univariate”项,系统打开单因变量多因素方差分析设置窗口如图5-7。
图5-7 多因素方差分析窗口3)设置分析变量设置因变量:在左边变量列表中选“历期”,用向右拉按钮选入到“Dependent Variable:”框中。
设置因素变量:在左边变量列表中选“a”和“b”变量,用向右拉按钮移到“Fixed Factor(s):”框中。
可以选择多个因素变量。
由于内存容量的限制,选择的因素水平组合数(单元数)应该尽量少。
设置随机因素变量:在左边变量列表中选“重复”变量,用向右拉按钮移到“到Random Factor(s)”框中。
可以选择多个随机变量。
设置协变量:如果需要去除某个变量对因素变量的影响,可将这个变量移到“Covariate(s)”框中。

第六讲 多因素试验资料的方差分析M ULTIFACTOR ANALYSIS OF V ARIANCE多因素试验是指同时研究n 个因素对试验指标的作用,以及它们的共同作用。
多因素试验的最大优点首先在于除了一次试验可以同时明确多个因素的效应,还可以分析出因素间的相互作用(互作),便于选定最优处理组合。
其次,多因素试验可增加误差项的自由度,降低试验误差。
因此比单因素试验精确度更高。
最后,多因素实验所得的结论确切、具体、论据充足。
如单独进行品种对比试验,结果只能粗略地明确品种间的优劣,如果与饲料水平、饲喂方式结合进行三因素试验,可具体明确用一定的饲喂方式在特定的饲料水平下,哪个品种优于哪个品种。
论据、内容都比单因素试验结果丰富。
田间试验中也常要考察哪个品种在何时播种以及在何种密度下的产量表现,同时还可以采用区组设计来安排重复,以便控制系统误差,提高试验的准确性。
现以三因素试验的资料介绍其方差分析方法。
第一节 线性模型与期望均方一、线性数学模型设A 、B 、C 三个因素各含a 、b 、c 个水平,共abc 个处理组合,每个处理组合重复数为r 。
则其任一观察值的线性数学模型为:kl j i l ijk jk ik j i k j i kl j i e y +++++++++=ραβγβγαγαβγβαμ)()()()(其中kl j i l ijk jk ik j i k j i e ,,)(,)(,)(,)(,,,,ραβγβγαγαβγβαμ依次表示总体平均数、A 、B 、C 主效应, A ×B 、A ×B 、B ×C 、A ×B ×C 互作效应,重复(区组)效应和随机误差。
在样本资料中依次分别由),(,x x x A -)(x x B -,)(x x C -,)(x x x x B A AB +--,)(x x x x C A AC +--,)(x x x x C B BC +--,)(x x x x x x x x BC AC AB C B A ABC ----+++,)(x x R -,)(x x x x R ABC ijkl +--进行估计。

多因素方差分析多因素方差分析是对一个独立变量是否受一个或多个因素或变量影响而进行的方差分析。
SPSS 调用“Univariate”过程,检验不同水平组合之间因变量均数,由于受不同因素影响是否有差异的问题。
在这个过程中可以分析每一个因素的作用,也可以分析因素之间的交互作用,以及分析协方差,以及各因素变量与协变量之间的交互作用。
该过程要求因变量是从多元正态总体随机采样得来,且总体中各单元的方差相同。
但也可以通过方差齐次性检验选择均值比较结果。
因变量和协变量必须是数值型变量,协变量与因变量不彼此独立。
因素变量是分类变量,可以是数值型也可以是长度不超过8的字符型变量。
固定因素变量(Fixed Factor )是反应处理的因素;随机因素是随机地从总体中抽取的因素。
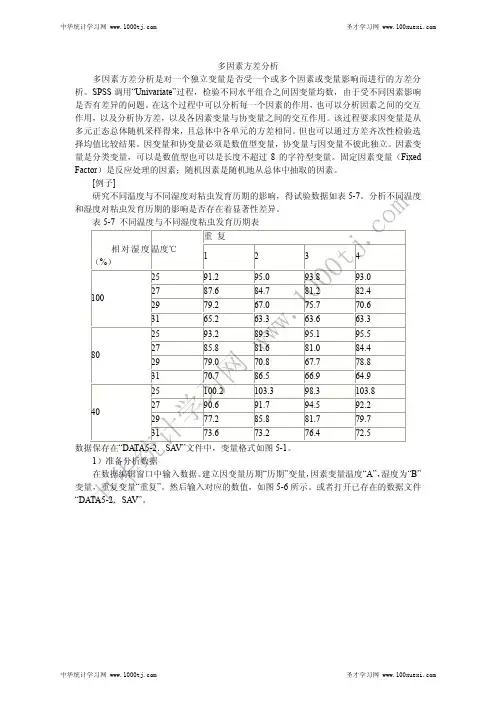
[例子]研究不同温度与不同湿度对粘虫发育历期的影响,得试验数据如表5-7。
分析不同温度和湿度对粘虫发育历期的影响是否存在着显著性差异。
表5-7 不同温度与不同湿度粘虫发育历期表重 复相对湿度(%)温度℃ 1 2 3 425 91.2 95.0 93.8 93.027 87.6 84.7 81.2 82.429 79.2 67.0 75.7 70.6 10031 65.2 63.3 63.6 63.325 93.2 89.3 95.1 95.527 85.8 81.6 81.0 84.4 29 79.0 70.8 67.7 78.8 8031 70.7 86.5 66.9 64.9 25 100.2 103.3 98.3 103.8 27 90.6 91.7 94.5 92.2 29 77.2 85.8 81.7 79.74031 73.6 73.2 76.4 72.5数据保存在“DATA5-2.SA V”文件中,变量格式如图5-1。
1)准备分析数据在数据编辑窗口中输入数据。
建立因变量历期“历期”变量,因素变量温度“A”,湿度为“B”变量,重复变量“重复”。


多因素方差分析是对一个独立变量是否受一个或多个因素或变量影响而进行的方差分析。
SPSS调用“Univariate”过程,检验不同水平组合之间因变量均数,由于受不同因素影响是否有差异的问题。
在这个过程中可以分析每一个因素的作用,也可以分析因素之间的交互作用,以及分析协方差,以及各因素变量与协变量之间的交互作用。
该过程要求因变量是从多元正态总体随机采样得来,且总体中各单元的方差相同。
但也可以通过方差齐次性检验选择均值比较结果。
因变量和协变量必须是数值型变量,协变量与因变量不彼此独立。
因素变量是分类变量,可以是数值型也可以是长度不超过8的字符型变量。
固定因素变量(Fixed Factor)是反应处理的因素;随机因素是随机地从总体中抽取的因素。
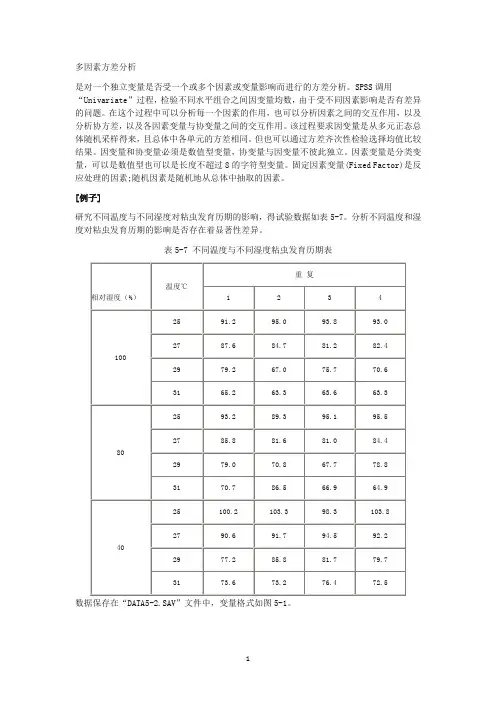
[例子]研究不同温度与不同湿度对粘虫发育历期的影响,得试验数据如表5-7。
分析不同温度和湿度对粘虫发育历期的影响是否存在着显著性差异。
表5-7 不同温度与不同湿度粘虫发育历期表1)准备分析数据在数据编辑窗口中输入数据。
建立因变量历期“历期”变量,因素变量温度“A”,湿度为“B”变量,重复变量“重复”。
然后输入对应的数值,如图5-6所示。
或者打开已存在的数据文件“DATA5-2.SAV”。
图5-6 数据输入格式2)启动分析过程点击主菜单“Analyze”项,在下拉菜单中点击“General Linear Model”项,在右拉式菜单中点击“Univariate”项,系统打开单因变量多因素方差分析设置窗口如图5-7。
图5-7 多因素方差分析窗口3)设置分析变量设置因变量:在左边变量列表中选“历期”,用向右拉按钮选入到“Dependent Variable:”框中。
设置因素变量:在左边变量列表中选“a”和“b”变量,用向右拉按钮移到“Fixed Factor(s):”框中。
可以选择多个因素变量。
由于内存容量的限制,选择的因素水平组合数(单元数)应该尽量少。
设置随机因素变量:在左边变量列表中选“重复”变量,用向右拉按钮移到“到Random Factor(s)”框中。
第十八章多因素实验资料的方差分析
第一节析因设计资料的方差分析
析因设计资料的方差分析被广泛用于需要分析交互效应和选择最佳组合的实验研究中。
一、2*2析因设计资料的方差分析
析因设计资料的方差分析包含主效应(main effect)分析、交互效应(interaction)分析和单独效应分析三个层次。
主效应和交互效应的方差分析又称析因分析(factorial analysis);
如果分析所有的主效应和交互效应,则为全因子模型;
如果只分析部分主效应和交互效应,称为非全因子模型。
1. 主效应和交互效应分析
交互项变异:由处理的总变异减去两个因素的主效应后得到。
误差项变异:误差项变异为总变异与各项主效应和交互效应之差。
用交互效应的轮廓图直观反映两个因素之间的关系:
(1)若两线近乎平行,提示无交互效应;反之,两线相交的锐角越大,交互效应越强。
(2)若两线近乎水平,提示B因素的两个水平相差不显著;反之,相差显著。
(3)若两线近乎重合,提示A因素的两个水平相差不显著;反之,相差显著。
2. 单独效应分析
上述析因分析给出了主效应和交互效应分析的结果,为了更细致地分析交互效应,还可以配合单独效应分析,即固定水平分析。
注意多次比较需要考虑α的调整问题,如使用Bonferroni方法进行调整。
二、2*3*2析因设计资料的方差分析
三、析因设计中的几个问题
1. 非平衡设计:对于非平衡的析因设计,仍然可以采用本节所介绍的方法,只是要注意自由度的分解和计算。
一般而言,如果所有的因素和水平的组合至少有1个观察值的话,主效应和交互效应的自由度与平衡设计一样,但误差项的自由度要根据总的自由度而变化。
如果某1个或几个因素和水平的组合缺如,则交互项的自由度要比平衡设计减少。
2. 全因子模型与非全因子模型:有的情形下,当某几个或某个交互项的F值小于1时,可以考虑将这些交互项并入误差项,这样可以
减少误差项的均方,同时还增大了误差项的自由度,使得分析的效率提高。
3. I*J析因设计与随机单位组设计的区别:两种设计都考虑了两种因素,但前者是两种处理因素,而后者是一个处理因素和一个配伍因素(非处理因素)。
前者可以分析交互效应,而后者却不能。
4. 多重比较:如果需要进行全部因素和水平组合间的多重比较,标准误根据析因分析的误差项计算即可。
5. 交互效应分析:当主效应水平间有统计差异时,分析交互效应可以获取更多有意义的信息。
6. 析因设计的局限:析因设计不但可以分析主效应和交互效应,也可以分析单独效应,故效率较高。
但是,当因素太多时,所需的样本量会很大。
此外,当因素较多时,因素间交互效应的分析和解释会变得越来越困难。
因此,析因设计安排的处理因素不要超过4个。
如果因素和水平数太多时,可以考虑用正交设计方法。
第二节二阶段交叉设计资料的方差分析
二阶段交叉设计(two-stage crossover design)是临床试验较常用的一种设计,主要有两大优点:
(1)经济:它比平行对照组设计节省一半受试对象,这对花费昂贵的药物临床试验显得尤为重要;
(2)可以消除个体差异的影响,从而达到减小随机误差的效果,因此,研究效率较高。
缺点:后效应相同或无后效应的要求限制了其应用,故不适于急性病研究或有明显延迟效应的药物研究。
第三节正交设计资料的方差分析
正交设计又称田口玄一方法,是研究多因素多水平的又一种设计方法,具有高效、快速、经济的特点,常用于配方筛选的研究。
对于正交设计资料的方差分析,通常不能像析因设计那样分析所有的交互效应。
到底哪些交互效应可以分析,哪些不能分析,有时根据正交设计表的表头也难以判断,为便于应用,我们可以通过统计软件的操作,在模型选择上进行尝试,从而选择最佳的方差分析结果。
相对于因素和水平数而言正交设计的样本量较小,用于估计误差项的例数也较少,当实验数据的变异较大时,误差项的变异也来得较大,不容易出现因素间的差异。
因此,正交设计通常不大适合实验数据变异较大的研究。
对正交实验数据的分析,有“直观分析”之说,即统计描述方法。
一般而言,统计分析应包含统计描述和统计推断两部分内容,缺一不可,仅用直观分析其可靠性较差,其结论缺乏普遍意义。