2020年常见几何体的特征

解析：建立如图所示的坐标系xOy′，△A′B′C′的顶点C′在y′轴上，A′B′边在x轴上，OC为△ABC的高．把y′轴绕原点逆时针旋转45°得y轴，则点C′变为点C，且OC＝2OC′，A、B点即为A′、B′点，长度不变．
已知A′B′＝A′C′＝a，在△OA′C′中，
由正弦定理得 ＝ ，
所以OC′＝ a＝ a，
A．圆柱
B．圆锥
C．球体
D．圆柱、圆锥、球体的组合体
解析：C[当用过高线的平面截圆柱和圆锥时，截面分别为矩形和三角形，只有球满足任意截面都是圆面．]
3．如图所示，观察四个几何体，其中判断正确的是( )
A．①是棱台B．②是圆台
C．③是棱锥D．④不是棱柱
解析：C[图①不是由棱锥截来的，所以①不是棱台；图②上、下两个面不平行，所以②不是圆台；图③是棱锥；图④前、后两个面平行，其他面是平行四边形，且每相邻两个四边形的公共边平行，所以④是棱柱．故选C.]
(2)原图形中平行于坐标轴的线段，直观图中仍分别平行于坐标轴．平行于x轴和z轴的线段在直观图中保持原长度不变，平行于y轴的线段长度在直观图中变为原来的一半.
斜二测画法中的“三变”与“三不变”
“三变”
“三不变”
[思考辨析]
判断下列说法是否正确，正确的在它后面的括号里打“√”，错误的打“×”．
(1)球的任何截面都是圆．( )
A. a2B. a2C. a2D. a2
[解析]D[如图所示为原图形和其直观图．
由图可知，A′B′＝AB＝a，O′C′＝ OC＝ a，
在图中作C′D′⊥A′B′于D′，则C′D′＝ O′C′
＝ a.∴S△A′B′C′＝ A′B′·C′D′＝ ×a× a＝ a2.故选D.]
[互动探究]

定理1. 平行六面体的对角线交于一点，并且
在交点处互相平分.
已知：平行六面体 ABCD-A`B`C`D` A`
D'
C'
B'
求证：对角线AC`、
BD`、CA`、DB`相
交于一点O，且在点
D
O处互相平分.
A
C B
练习：已知斜三棱柱的底面是边长为a的正三角 形，侧棱A1A与底面两边AB、AC都成450角.
棱台的性质
如果棱锥被平行于底面的平面所截，那么截面和底 面相似．
O`
O`
O O
动画
球的性质
• 球面被经过球心的平面截得的圆叫大圆, • 被不经过球心的平面截得的圆叫小圆.
球面上两点之间的最短连线的长度，就是经 过这两点的大圆在这两点的大圆在这两点间 的段劣弧的长度
球的性质
• 地球上的经度与纬度
棱柱的定义
（1）有两个面是互相平行的多边形
A B
E D
C
（2）其余各面都是四边平行
A
B
棱柱的有关概念、表示方法、分类
E D
C
侧棱与底面的公共点叫做棱柱的顶点． 侧棱和底面的边叫做棱柱的棱． 不在同一个面上的两个顶点的连线叫做棱柱 的对角线． 两底面间的距离叫做棱柱的高．
研究四棱柱的特殊情形 四棱柱 平行六面体 直平行六面体 长方体 正方体
棱锥的定义
有一个面是多边形，其余各面是一个有公共顶点的 三角形，这个多面体叫做棱锥．
棱锥的有关概念、表示方法、分类
正棱锥:如果一个棱锥的底面是正多边形，并
且顶点在底面内的射影是底面的中心，这样的 棱锥叫做正棱锥．
正棱锥的性质
棱柱的性质
（1）侧棱都相等，侧面是平行四边形； （2）两个底面与平行于底面的截面是全等的多边形； （3）过不相邻的两条侧棱的截面是平行四边形； 直棱柱性质： • （1）侧棱都相等，侧面是矩形． • （2）底面与平行于底面的截面是全等的多边形． • （3）对角面是矩形． • （4）侧棱长是棱柱的高． 正棱柱既有一般棱柱及直棱柱的性质，还有如下性质： • （1）底面与平行于底面的截面是全等的正多边形． • （2）侧面是全等的矩形．

正方体长方体圆柱和球的特点1.引言1.1 概述概述部分的内容：几何体是我们日常生活中经常接触到的物体，它们具有不同的形状和特点。

在本文中，我们将主要探讨正方体、长方体、圆柱和球这四种常见几何体的特点。

正方体是一种具有六个面都是正方形的立体物体。

它的每个面都是平整的，并且所有的面都相等，每个角都是直角。

正方体具有优秀的稳定性，常被用于建筑、立体拼图等领域。

长方体是一种具有六个面都是矩形的几何体。

它的长度、宽度和高度都不相同，因此可以根据需求进行调整。

长方体在日常生活中随处可见，如书桌、电视机、冰箱等。

圆柱是一种具有两个平行且相等的圆底的几何体。

底面上的圆与侧面成直角，它的形状特点使得它可以用来储存液体或者承载重物。

圆柱广泛应用于工业、建筑和交通运输等领域。

球是一种具有无限多个点到某一点的距离都相等的立体几何体。

它是三维空间中唯一完全对称的几何体，具有非常特殊的性质。

球体常用于运动、游戏和天体物理研究等领域。

通过分析正方体、长方体、圆柱和球的定义、形状特征和基本性质，我们可以更好地理解它们在不同领域的应用。

本文将进一步探讨这四种几何体的基本性质和应用领域，并通过对比分析，总结它们各自的特点。

通过本文的阅读，读者将更深入地了解这四种几何体的性质与特点。

1.2文章结构文章结构部分的内容：本文将按照以下顺序介绍正方体、长方体、圆柱和球的特点。

首先，在引言部分概述了整篇文章的主要内容和目的。

然后，文章将分别在第二、三、四和五部分详细探讨正方体、长方体、圆柱和球的定义、形状特征、基本性质和应用领域。

每个部分将先介绍几何体的定义和形状特征，然后讨论其基本性质和应用领域，以便读者能够全面了解并比较它们的特点。

最后，在结论部分总结了正方体、长方体、圆柱和球的特点，并进行了对比分析不同几何体之间的差异和相似之处。

通过这样的文章结构，读者可以逐步了解不同几何体的概念和形状特征，进而了解它们的基本性质和实际应用。

同时，通过对比分析不同几何体之间的特点，读者可以深入理解它们各自的独特性和相互关系。

几何体的分类方法几何体是指在三维空间中具有一定形状和大小的物体，通过对几何体的形状、结构和性质进行分类，可以更好地理解和研究几何学。

下面将介绍几何体的分类方法。

一、按照几何体的形状分类1. 点：点是几何体中最基本的概念，没有大小和形状。

2. 线：线由无数个点组成，是长度无限延伸的几何体。

3. 面：面是由无数个线组成的，它是二维的，有长度和宽度，但没有厚度。

4. 体：体是由无数个面组成的，它是三维的，有长度、宽度和厚度。

二、按照几何体的结构分类1. 凸体：凸体是指没有凹陷部分的三维物体，它的表面曲率都向外凸出。

2. 凹体：凹体是指存在凹陷部分的三维物体，它的表面曲率有凸出和凹陷的部分。

三、按照几何体的性质分类1. 对称性：几何体可以根据其对称性进行分类，如球体、立方体等都具有各种对称性。

2. 直线性：几何体可以根据其是否具有直线性进行分类，如长方体、圆柱体等就是具有直线性的几何体。

3. 曲线性：几何体可以根据其是否具有曲线性进行分类，如球体、圆锥体等就是具有曲线性的几何体。

4. 面性：几何体可以根据其是否具有面性进行分类，如立方体、四面体等就是具有面性的几何体。

5. 棱性：几何体可以根据其是否具有棱性进行分类，如立方体、八面体等就是具有棱性的几何体。

6. 角性：几何体可以根据其是否具有角性进行分类，如四面体、六面体等就是具有角性的几何体。

四、按照几何体的名称分类1. 球体：球体是一种具有曲面的几何体，其表面上的每一点到球心的距离都相同。

2. 圆柱体：圆柱体是一种具有直线面的几何体，其两个底面都是圆形，且底面上的每一点到轴线的距离都相同。

3. 圆锥体：圆锥体是一种具有直线面的几何体，其底面是圆形，且底面上的每一点到顶点的距离都相同。

4. 立方体：立方体是一种具有面性和棱性的几何体，其六个面都是正方形，且每个面都与相邻的面垂直。

5. 四面体：四面体是一种具有面性和角性的几何体，其四个面都是三角形，且每个面都与相邻的面共享一条边。

第八章立体几何初步复习课要点训练一空间几何体的结构特征1.紧扣结构特征是判断的关键,熟悉空间几何体的结构特征,依据条件构建几何模型,在条件不变的情况下,变换模型中的线面关系或增加线、面等基本元素,然后再依据题意判定.2.通过举反例对结构特征进行辨析,即要说明一个命题是错误的,只要举出一个反例即可.1.设有四个命题:①底面是矩形的平行六面体是长方体;②棱长都相等的直四棱柱是正方体;③侧棱垂直于底面两条边的平行六面体是直平行六面体;④对角线相等的平行六面体是直平行六面体.其中真命题的个数是()A.1B.2C.3D.4解析:底面是矩形的直平行六面体是长方体,①错误;棱长都相等的直四棱柱是正方体,②正确;侧棱垂直于底面两条相邻边的平行六面体是直平行六面体,③错误;任意侧面上两条对角线相等的平行六面体是直平行六面体,④错误.故命题正确的个数是1.答案:A2.在四棱锥的四个侧面中,直角三角形最多可有()A.1个B.2个C.3个D.4个解析:如图所示,在长方体ABCD-A1B1C1D1中,取四棱锥A1-ABCD,则此四棱锥的四个侧面都是直角三角形.答案:D要点训练二空间几何体的表面积与体积1.空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量.(2)多面体的表面积是各个面的面积之和;组合体的表面积问题注意衔接部分的处理.(3)旋转体的表面积问题,应注意其侧面展开图的应用.2.空间几何体体积问题的常见类型及解题策略(1)若所给定的几何体问题是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解.(2)若所给定的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等进行求解.(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,再根据条件求解.1.已知一个六棱锥的体积为2√3 ,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为12.解析:由题意可知,该六棱锥是正六棱锥.设该六棱锥的高为h ,则13×6×√34×22×h =2√3,解得h =1.由题意,得底面正六边形的中心到其边的距离为√3,所以侧面等腰三角形底边上的高为√(√3)2+1=2,所以该六棱锥的侧面积为6×12×2×2=12. 2.如图所示,三棱锥O -ABC 为长方体的一角,其中OA ,OB ,OC 两两垂直,三个侧面OAB ,OAC ,OBC 的面积分别为1.5 cm 2,1 cm 2,3 cm 2,求三棱锥O -ABC 的体积.解:设OA ,OB ,OC 的长依次为x cm,y cm,z cm,由已知可得12xy =1.5,12xz =1,12yz =3,解得x =1,y =3,z =2. 将三棱锥O -ABC 看成以C 为顶点,以OAB 为底面,易知OC 为三棱锥C -OAB 的高.故V 三棱锥O -ABC =V C -OAB =13S △OAB ·OC =13×1.5×2=1(cm 3). 3.如图所示,已知三棱柱ABC -A'B'C',侧面B'BCC'的面积是S ,点A'到侧面B'BCC'的距离是a ,求三棱柱ABC -A'B'C'的体积.解:连接A'B ,A'C ,如图所示,这样就把三棱柱ABC -A'B'C'分割成了两个棱锥,即三棱锥A'-ABC 和四棱锥A'-BCC'B'.设所求体积为V ,显然三棱锥A'-ABC 的体积是13V. 而四棱锥A'-BCC'B'的体积为13Sa , 故有13V +13Sa =V ,所以V =12Sa. 要点训练三 与球有关的切、接问题与球相关问题的解题策略(1)作适当的截面(如轴截面等)时,对于球内接长方体、正方体,则截面一要过球心, 二要过长方体或正方体的两条体对角线,才有利于解题.(2)对于“内切”和“外接”等问题,首先要弄清几何体之间的相互关系,主要是指特殊的点、线、面之间的关系,然后把相关的元素放到这些关系中来解决.1.正四棱锥的顶点都在同一球面上,若该棱锥的高为6,底面边长为4,则该球的表面积为( )A.443πB.4849πC.814πD.16π 解析:如图所示,设PE 为正四棱锥P -ABCD 的高,则正四棱锥P -ABCD 的外接球的球心O 必在其高PE 所在的直线上,延长PE 交球面于一点F ,连接AE ,AF.由球的性质可知△PAF 为直角三角形,且AE ⊥PF.因为该棱锥的高为6,底面边长为4,所以AE =2√2,PE =6,所以侧棱长PA =√PE 2+AE 2=√62+(2√2)2=√44=2√. 设球的半径为R ,则PF =2R. 由△PAE ∽△PFA ,得PA 2=PF ·PE ,即44=2R ×6,解得R =113,所以S =4πR 2=4π×(113)2=484π9.答案:B2.一个球与一个正三棱柱的三个侧面和两个底面都相切,如果这个球的体积是323π,那么这个正三棱柱的体积是( ) A.96√3 B.16√3 C.24√3 D.48√3解析:由球的体积公式可求得球的半径R =2. 设球的外切正三棱柱的底面边长为a ,高即侧棱长,为h ,则h =2R =4. 在底面正三角形中,由正三棱柱的内切球特征,得a 2×√33=R =2,解得a =4√3. 故这个正三棱柱的体积V =12×√32×(4√3)2×4=48√3.答案:D要点训练四 空间中的平行关系1.平行问题的转化关系2.直线与平面平行的主要判定方法(1)定义法;(2)判定定理;(3)面与面平行的性质.3.平面与平面平行的主要判定方法(1)定义法;(2)判定定理;(3)推论;(4)a ⊥α,a ⊥β⇒α∥β.1.如图所示,三棱柱ABC -A'B'C'中,M ,N 分别为BB',A'C'的中点.求证:MN ∥平面ABC'.证明:取B'C'的中点P ,连接MP ,NP (图略),则MP ∥BC',NP ∥A'B'. 因为A'B'∥AB ,所以NP ∥AB.因为AB ⊂平面ABC',NP ⊄平面ABC',所以NP ∥平面ABC'.同理MP∥平面ABC'.因为NP∩MP=P,所以平面MNP∥平面ABC'.因为MN⊂平面MNP,所以MN∥平面ABC'.2.两个全等的正方形ABCD和ABEF所在平面相交于AB, M∈AC,N∈FB,且AM=FN,过点M作MH⊥AB于点H.求证:平面MNH∥平面BCE.证明:因为正方形ABCD中,MH⊥AB,BC⊥AB,所以MH∥BC.因为BF=AC,AM=FN,所以FNBF =AM AC.因为MH∥BC,所以AMAC =AH AB,所以FNBF =AH AB,所以NH∥AF∥BE.因为MH⊂平面MNH,NH⊂平面MNH,MH∩NH=H, BC⊂平面BCE,BE⊂平面BCE,BC∩BE=B,所以平面MNH∥平面BCE.要点训练五空间中的垂直关系1.空间中垂直关系的相互转化2.判定线线垂直的方法(1)平面几何中证明线线垂直的方法.(2)线面垂直的性质:a⊥α,b⊂α⇒a⊥b;a⊥α,b∥α⇒a⊥b.3.判定线面垂直的常用方法(1)利用线面垂直的判定定理.(2)利用“两平行线中的一条与平面垂直,则另一条也与这个平面垂直”.(3)利用“一条直线垂直于两平行平面中的一个,则与另一个平面也垂直”.(4)利用面面垂直的性质.4.判定面面垂直的方法(1)利用定义:两个垂直平面相交,所成的二面角是直二面角.(2)判定定理:a⊂α,a⊥β⇒α⊥β.1.如图所示,Rt△AOC可以通过Rt△AOB以直角边AO所在直线为轴旋转得到,且二面角B-AO-C是直二面角,D是AB上任意一点.求证:平面COD⊥平面AOB.证明:由题意,得CO⊥AO,BO⊥AO,所以∠BOC是二面角B-AO-C 的平面角.因为二面角B-AO-C是直二面角,所以∠BOC=90°,所以CO⊥BO.因为AO∩BO=O,所以CO⊥平面AOB.因为CO⊂平面COD,所以平面COD⊥平面AOB.2.如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2, AD=CD=√7,PA=√3,∠ABC=120°,G为线段PC上的点,O为AC,BD交点.(1)证明:BD⊥平面APC;(2)若G满足PC⊥平面BGD,求PG的值.GC(1)证明:由AB=BC,AD=CD,得BD垂直平分线段AC.所以O为AC的中点,BD⊥AC.因为PA⊥平面ABCD,BD⊂平面ABCD,所以PA⊥BD.因为AC∩PA=A,AC⊂平面APC,PA⊂平面APC,所以BD⊥平面APC.(2)解:连接OG,如图所示.因为PC⊥平面BGD,OG⊂平面BGD,所以PC⊥OG.在△ABC中,由余弦定理,得AC=√22+22-2×2×2×cos120°=2√3.在Rt△PAC中,得PC=√AC2+PA2=√12+3=√所以由△GOC∽△APC可得GC=AC·OCPC =2√155.从而PG=3√155,所以PGGC=32.要点训练六空间角的求解方法1.找异面直线所成角的三种方法(1)利用图中已有的平行线平移.(2)利用特殊点(线段的端点或中点)作平行线平移.(3)补形平移.2.线面角求斜线与平面所成的角关键是找到斜线在平面内的射影,即确定过斜线上一点向平面所作垂线的垂足.通常是解由斜线段、垂线段、斜线在平面内的射影所组成的直角三角形.3.求二面角的两种常用方法(1)定义法:在二面角的棱上找一个特殊点,在两个半平面内分别过该点作垂直于棱的射线.(2)垂面法:过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条交线所成的角,即为二面角的平面角.1.如图所示,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°, AB≠AC,D,E分别是BC,AB的中点,AC>AD,设PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P-BC-A的平面角为γ,则α,β,γ的大小关系是α<β<γ.解析:因为D,E分别是BC,AB的中点,所以DE∥AC,所以PC与DE所成的角为∠PCA,即α.因为PA⊥平面ABC,所以PD与平面ABC所成的角为∠PDA,即β.如图所示,过点A作AH⊥BC,垂足为H,连接PH,易证BC⊥平面PAH,所以∠PHA是二面角P-BC-A的平面角,即γ.因为AB≠AC,所以AD>AH.因为AC >AD,所以AC >AD >AH,所以PAAC <PAAD<PAAH,所以tan α<tan β<tan γ,所以α<β<γ.2.如图所示,AB是☉O的一条直径,PA垂直于☉O所在的平面,C 是圆周上不同于A, B的一动点.(1)证明:△P BC是直角三角形;(2)若PA=AB=2,且当直线PC与平面ABC所成角的正切值为√2时,求直线AB与平面PBC所成角的正弦值.(1)证明:因为AB是☉O的一条直径, C是圆周上不同于A,B的一动点,所以BC⊥AC.因为PA⊥平面ABC,所以BC⊥PA.因为PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,所以BC⊥平面PAC,所以BC⊥PC,所以△BPC是直角三角形.(2)解:如图所示,过点A作AH⊥PC于点H,连接BH.因为BC⊥平面PAC,所以BC⊥AH.因为PC∩BC=C,PC⊂平面PBC,BC⊂平面PBC,所以AH⊥平面PBC,所以∠ABH是直线AB与平面PBC所成的角.因为PA⊥平面ABC,所以∠PCA即是PC与平面ABC所成的角.因为tan∠PCA=PAAC=√2,PA=2, 所以AC=√2.在Rt△PAC中,AH=√PA2+AC2=23√3,在Rt△ABH中,sin∠ABH=23√32=√33,即AB与平面PBC所成角的正弦值为√33.要点训练七转化思想转化思想是指在解决数学问题时,一个数学对象在一定条件下转化为另一种数学对象的思想.它包括从未知到已知的转化,从一般到特殊的转化等,折叠问题中体现了转化思想.解决折叠问题的关键在于认真分析折叠前后元素的位置变化情况,看看哪些元素的位置变了,哪些元素的位置没有变,基本思路是利用“不变求变”,一般步骤如下:(1)平面→空间:根据平面图形折出满足条件的空间图形,想象出空间图形,完成平面图形与空间图形在认识上的转化.(2)空间→平面:为解决空间图形问题,要回到平面上来,重点分析元素的变与不变.1.如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.若将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列结论正确的是()A.平面ABD⊥平面ABCB.平面ADC⊥平面BDCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC解析:因为在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°, ∠BAD=90°,所以BD⊥CD.因为平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,所以CD⊥平面ABD,所以CD⊥AB.因为AD⊥AB,AD∩CD=D,AD⊂平面ADC,CD⊂平面ADC,故AB⊥平面ADC.因为AB⊂平面ABC,所以平面ABC⊥平面ADC.答案:D2.如图所示,在矩形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABC.在平面ABD内过点D作DK⊥AB,垂足为K.设AK=t,则t的取值范围是(1,1).2→解析:如图所示,过点K作KM⊥AF于M点,连接DM,易得DM⊥AF,与折前的图形对比,可知在折前的图形中D,M,K三点共线,且DK⊥AF, 于是△DAK∽△FDA,所以AKAD =ADDF.所以t1=1DF.所以t=1DF.因为DF∈(1,2),所以t∈( 12,1).3.如图①所示,在等腰梯形CDEF中,DE=CD=√2,EF=2+√2,将它沿着两条高AD,CB折叠成四棱锥E-ABCD(E,F两点重合),如图②所示.①②(1)求证:BE⊥DE;(2)设M为线段AB的中点,试在线段CE上确定一点N,使得MN∥平面DAE.(1)证明:因为AD⊥EF,所以AD⊥AE,AD⊥AB.因为AB∩AE=A,AB⊂平面ABE,AE⊂平面ABE,所以AD⊥平面ABE,所以AD⊥BE.由题图①和题中所给条件知,AE=BE=1,AB=CD=√2,所以AE2+BE2=AB2,即AE⊥BE.因为AE∩AD=A,AE⊂平面ADE,AD⊂平面ADE,所以BE⊥平面ADE,所以BE⊥DE.(2)解:如图所示,取EC的中点G,BE的中点P,连接PM,PG,MG, 则MP∥AE,GP∥CB∥DA,所以MP∥平面DAE,GP∥平面DAE.因为MP∩GP=P,所以平面MPG∥平面DAE.因为MG⊂平面MPG,所以MG∥平面DAE,即存在点N与G重合满足条件,使得MN∥平面DAE.。

正方体、长方体、圆柱体、圆锥体的特征各是什么？1、长方体的特征：有12条棱，6个面，8个角，每个角都是90度。

2、正方体的特征：在长方体中，6个面都相等的长方体是正方体。

3、圆柱特征：1）上下面均为圆且相等、平行。

2）有一个侧面为曲面。

3）上下两面外加侧面（曲面）共三个面。

4、圆锥的特征：1）圆锥是由2个面围成。

2）一个底面是平面，一个侧面是曲面。

扩展资料：具体特征：一、长方形的特征1、长方体有6个面。

每组相对的面完全相同。

2、长方体有12条棱，相对的四条棱长度相等。

按长度可分为三组，每一组有4条棱。

3、长方体有8个顶点。

每个顶点连接三条棱。

三条棱分别叫做长方体的长，宽，高。

4、长方体相邻的两条棱互相垂直。

二、正方形的特征1、有一组邻边相等且一个角是直角的平行四边形叫做正方形。

2、四条边都相等、四个角都是直角的四边形是正方形。

3、正方形的两组对边分别平行，四条边都相等；四个角都是90°；对角线互相垂直、平分且相等，每条对角线都平分一组对角。

4、有一组邻边相等且一个角是直角的平行四边形叫做正方形。

有一组邻边相等的矩形叫做正方形，有一个角是90°的菱形叫做正方形。

正方形是矩形的特殊形式，也是菱形的特殊形式。

三、圆锥体的特征1、圆锥面和一个截它的平面（满足交线为圆）组成的空间几何图形叫圆锥。

2、以直角三角形的直角边所在直线为旋转轴，其余两边旋转而成的曲面所围成的几何体叫做圆锥。

四、圆柱体的特征1、旋转定义法：一个长方形以一边为轴顺时针或逆时针旋转一周，所经过的空间叫做圆柱体。

2、平移定义法：以一个圆为底面，上或下移动一定的距离，所经过的空间叫做圆柱体。

考点02 点、线、面、体1．粉刷墙壁时，粉刷工人用滚筒在墙上刷过几次后，墙壁马上换上了“新装”，在这个过程中，你认为下列判断正确的是（）A．点动成线B．线动成面C．面动成体D．面与面相交得到线【答案】B【分析】点动线，线动成面，将滚筒看做线，在运动过程中形成面．【详解】解：滚筒看成是线，滚动的过程成形成面，故选：B．【点睛】本题考查点、线、面的关系；理解点动成线，线动成面的过程是解题的关键．2．（福建省宁德福鼎市2020-2021学年七年级上学期期中数学试题）如图，将一个直角三角形绕它的一条直角边所在的直线旋转一周，得到的几何体是圆锥，这一现象能用以下哪个数学知识解释（）A．点动成线B．线动成面C．面动成体D．面面相交得线【答案】C【分析】根据一个直角三角形绕它的一条直角边所在的直线旋转一周得到圆锥即可解答．【详解】解：因为一个直角三角形绕它的一条直角边所在的直线旋转一周得到圆锥，所以体现了面动成体．故选：C．【点睛】本题主要考查了点线面体的关系，掌握点线面体的关系成为解答本题的关键．3．（甘肃省张掖市甘州区甘州中学2020-2021学年七年级上学期第一次月考数学试题）下面图形中，以直线l为轴旋转一周，可以得到圆柱体的是( )A．B．C．D．【答案】C【分析】直接根据旋转变换的性质即可解答．【详解】解：因为圆柱从正面看到的是一个长方形，所以以直线为轴旋转一周，可以形成圆柱的是长方形，故选：C．【点睛】此题主要考查图形的旋转变换，发挥空间想象是解题关键．4．（四川省实验外国语学校2020-2021学年七年级上学期期中数学试题）将下列各选项中的平面图形绕轴旋转一周，可得到如图所示的立体图形的是（）．A．B．C．D．【答案】B【分析】根据面动成体，平面图形旋转的特点逐项判断即可得．【详解】A、将平面图形绕轴旋转一周，得到的是上面大下面小中间凹，侧面是曲面的几何体，则此项不符题意；B、将平面图形绕轴旋转一周，得到的是上面小下面大中间凹，侧面是曲面的几何体，则此项符合题意；C、将平面图形绕轴旋转一周，得到的是上下底面等大，且中间凹的几何体，则此项不符题意；D、将平面图形绕轴旋转一周，得到的是一个圆台，则此项不符题意；故选：B．【点睛】本题考查了平面图形旋转后的几何体，熟练掌握平面图形旋转的特点是解题关键．5．（山西省2020-2021学年第一学期七年级期中质量评估试题）“十一黄金周”期间，小明和小亮相约去太原植物园游玩，中途两人口渴了，于是小明提议通过在地面旋转硬币的方法决定谁去买水，在旋转硬币时小明发现：当硬币在地面某位置快速旋转时，形成了一个几何体，请问这个几何体是（）A．圆锥B．圆柱C．球D．圆台【答案】C【分析】根据常见几何体的特征即可得．【详解】当硬币在地面某位置快速旋转时，形成的几何体是球，故选：C．【点睛】本题考查了常见几何体的特征，熟练掌握常见几何体的特征是解题关键．6．（湖北利川东城街道初中2020-2021学年七年级11月月考数学试题）“枪挑一条线，棍扫一大片”，从数学的角度解释为（）．A．点动成线，线动成面B．线动成面，面动成体C．点动成线，面动成体D．点动成面，面动成线【答案】A【分析】根据从运动的观点来看点动成线，线动成面进行解答即可．【详解】“枪挑”是用枪尖挑，枪尖可看作点，棍可看作线，故这句话从数学的角度解释为点动成线，线动成面．故选A．【点睛】本题考查了点、线、面得关系，难度不大，注意将生活中的实物抽象为数学上的模型．7．（山东昌乐一中初中部2020-2021学年七年级上学期数学10月月考数学试题）如图所示的平面图形绕轴旋转一周，可得到的立体图形是（)A．圆锥B．圆柱C．三棱锥D．棱柱【答案】A【分析】根据面动成体，所得图形是一个圆锥体．【详解】解：直角三角形绕其一条直角边旋转一周所得图形是一个圆锥体．故选：A．【点睛】本题考查了点、线、面、体，熟悉常见图形的旋转得到立体图形是解题的关键．8．（山西省2020-2021学年七年级上学期第一次大联考数学试题）将下面的平面图形绕轴旋转一周，可以得到的立体图形是（）A．B．C．D．【答案】B【分析】根据面动成体以及球体的特点进行分析判断即可.【详解】将题中图形绕轴旋转一周，可以得到一个球体，故选：B.【点睛】本题主要考查了面动成体的性质，熟练掌握相关概念是解题关键.9．（湖南省怀化市鹤城区2019-2020学年七年级上学期期末数学试题）如下图所示将三角形绕直线l旋转一周，可以得到图(e)所示的立体图形的是（）A．图(a)B．图(b)C．图(c)D．图(d)【答案】B【分析】由题意根据一个平面图形围绕一条边为中心对称轴旋转一周根据面动成体的原理进行分析即可．【详解】解：绕直角三角形一条直角边旋转可得到圆锥．本题要求得到两个圆锥的组合体，那么一定是两个直角三角形的组合体：两条直角边相对，绕另一直角边旋转而成的．故选：B．【点睛】本题考查面动成体，注意掌握可以把较复杂的体分解熟悉的立体图形来进行分析．10．（辽宁省沈阳市一二六中学2020-2021学年七年级上学期十月月考数学试题）如图所示的沙漏，可以看作是由下列所给的哪个平面图形绕虚线旋转一周而成的（）A．B．C．D．【答案】D【分析】根据点、线、面、体的关系，观察沙漏外观即可得出答案．【详解】解：根据沙漏的外观可直接得出绕虚线旋转一周而成为，故选D．【点睛】本题考查了平面图形旋转后所得的立体图形，解题的关键是观察平面图形的特征．11．如图，下列图形绕直线l旋转一周后，能得到圆锥体的是（）A．B．C．D．【答案】B【分析】根据点动成线，线动成面，面动成体，只有直角三角形绕直角边旋转一周，可以得到一个以旋转直角边为高，另一直角边为底面半径的圆锥．【详解】解：只有直角三角形绕直角边旋转一周，可以得到一个圆锥．故选：B．【点睛】本题考查了点、线、面、体之间的关系，抓住旋转的定义和圆锥的特征即可解决此类问题．12．（内蒙古自治区赤峰市林西县2019-2020学年七年级上学期期末数学试题）下边的立体图形是由哪个平面图形绕轴旋转一周得到的（）A．B．C．D．【答案】A【分析】根据面动成体逐项判断即得答案．【详解】解：A、直角梯形绕轴旋转一周得到圆台，故本选项符合题意；B、半圆绕轴旋转一周得到球，故本选项不符合题意；C、长方形绕轴旋转一周得到圆柱，故本选项不符合题意；D、直角三角形绕轴旋转一周得到圆锥，故本选项不符合题意．故选：A．【点睛】本题考查了点、线、面、体的相关知识，属于基本题型，熟练掌握面动成体是解题关键．13．（广东省中山市2019-2020学年七年级上学期期末数学试题）如图，将长方形ABCD绕CD边旋转一周，得到的几何体是（）A．棱柱B．圆锥C．圆柱D．棱锥【答案】C【分析】根据面动成体可得长方形ABCD绕CD边旋转所得的几何体．【详解】解：将长方形ABCD绕CD边旋转一周，得到的几何体是圆柱，故选：C．【点睛】此题考查了平面图形与立体图形的联系，培养学生的观察能力和空间想象能力．14．（新疆2019-2020学年七年级上学期期末数学试题）将下列平面图形绕轴旋转一周，可得到图中所示的立体图形的是（）A．B．C．D．【答案】B【分析】根据面动成体的原理即可解．【详解】A、是两个圆台，故A错误；B、上面小下面大，侧面是曲面，故B正确；C、是一个圆台，故C错误；D、上面下面一样大侧面是曲面，故D错误；故选：B．【点睛】本题考查了点线面体，熟记各种图形旋转的特征是解题关键．15．（山东省滨州市滨城区2019-2020学年七年级上学期期末数学试题）下列平面图形绕直线旋转一周，所得的图形与其名称对应不正确的是（）A．B．C．D．【答案】C【分析】根据面动成体，直角三角形绕直角边旋转是圆锥，矩形绕边旋转是圆柱，直角梯形绕直角边旋转是圆台，半圆案绕直径旋转是球，可得答案．【详解】直角三角形绕直角边旋转是圆锥，故A正确；矩形绕边旋转是圆柱，故B正确；三角形绕一边旋转是两个同底的圆锥，故C错误；半圆案绕直径旋转是球，故D正确；故选：C【点睛】本题考查了点线面体，熟记各种图形旋转得出的立体图形是解题关键．16．（江苏省无锡市2019-2020学年七年级上学期期末数学试题）长方形纸板绕它的一条边旋转1周形成的几何体为（）A．圆柱B．棱柱C．圆锥D．球【答案】A【分析】根据长方形纸板绕它的一条边旋转1周可以形成圆柱，即可得到答案.【详解】解：长方形纸板绕它的一条边旋转1周可以形成圆柱，故选：A.【点睛】此题主要考查了点线面体，关键是掌握点动成线，线动成面，面动成体，认识常见的立体图形．17．（福建省宁德市2019-2020学年七年级上学期期末数学试题）如图，将一个直角三角形绕它的一条直角边所在的直线旋转一周，得到的几何体是A．长方体B．球C．圆柱D．圆锥【答案】D【分析】根据旋转体的定义和几何体的侧面展开图即可得出答案.【详解】将一个直角三角形绕它的一条直角边所在的直线旋转一周，得到的几何体是圆锥故选D【点睛】本题主要考查了旋转体的定义和常见的几何体，掌握常见的几何体是解题的关键.18．下图中的几何体是由哪个平面图形旋转得到的（）A．B．C．D．【答案】A【分析】根据面动成体的原理即可解答.【详解】图中的几何体是圆锥和圆台的组合体，故应是三角形和梯形旋转得到，故选A.【点睛】此题主要考察旋转体的构成，简单构想图形即可解出.19．（甘肃省张掖市甘州区甘州中学2020-2021学年七年级上学期第一次月考数学试题）雨点从天空落下形成雨线，这个现象可帮助我们理解：_______________【答案】点动成线【分析】根据题目内容雨点从天空落下形成雨线，将雨点看作点，轨迹看作线，进而得出点动成线．【详解】解：由题意知：将雨点看作点，轨迹看作线，则从运动的角度得出：点动成线；故答案为：点动成线．【点睛】本题主要考查点、线的关系，掌握点动成线是解答此题的关键．20．长方体有________个面，有________条棱，有________个顶点；圆柱有________个面，其中有________个平面，有________个曲面．【答案】6128321【解析】长方体有6个面，有12条棱，有8个顶点；圆柱有3个面，其中有2个平面（上下底面），有1个曲面（侧面）．21．（山西省太原市知达常青藤中学2020-2021学年度第一学期七年级数学十月调研测试如图是一个五棱柱，用平面将其截成两个几何体，若其中一个几何体为三棱柱，则另一个几何体最少有______个面．【答案】6【分析】用一个平面将一个五棱柱截成两个几何体，其中有一个是三棱柱，根据截面位置的不同，另一个几何体有不同的情况，根据题意画出符合题意的图形，进行比较即可得答案．【详解】用一个平面去截五棱柱，其中一个为三棱柱，有以下几种截取方法，如图所示：图1中另一个几何体为四棱柱，有6个面，图2中另一个几何体为五棱柱，有7个面，图3中另一个几何体为六棱柱，有8个面，所以另一个几何体最少有6个面，故答案为：6．【点睛】本题考查了用一个平面截一个几何体，截取所得几何体的形状既与被截的几何体有关，还与截面的角度和方向有关．本题注意分情况讨论．22．（陕西西安雁塔区陕西师范大学附属中学2019~2020学年1七年级上学期2月月考数学试题）一个长方形纸片长和宽分别为4和3，将纸片绕它的一边旋转，则所形成的几何体的体积为___．（结果保留π）【答案】36π，48π【分析】由题意可分将纸片沿长为4的边进行旋转及沿长为3的边进行旋转，然后根据圆柱的体积计算公式进行求解即可．【详解】解：由题意得：当以边长为4的边进行旋转，则几何体的面积为：224348S r h πππ==⨯=；当以边长为3的边进行旋转时，则几何体的面积为：223436S r h πππ==⨯=；故答案为36π，48π．【点睛】本题主要考查几何初步认识，关键是根据题意得到所形成的几何体，然后进求解即可． 23．（河南省驻马店市驿城区2020-2021学年七年级上学期期中数学试题）下列几何体：①圆柱；②正方体；③棱柱；④球；⑤圆锥；在这些几何体中截面可能是圆的有_____________．【答案】①④⑤【分析】根据常见几何体的截面特点逐个判断即可得．【详解】圆柱和圆锥中，如果截面和底面平行是可以截出圆的，球的截面是圆，正方体和棱柱的截面不可能有弧度，所以一定不会截出圆，综上，在这些几何体中截面可能是圆的有①④⑤，故答案为：①④⑤．【点睛】本题考查了几何体的截面，熟练掌握常见几何体的截面特点是解题关键．24．如图的几何体有_______个面，________条棱，________个顶点，它是由简单的几何体________和________组成的．【答案】9 16 9 四棱锥 四棱柱【解析】观察这个几何体可知，它有9个面，16条棱，9个顶点，它是由简单的几何体四棱锥和四棱柱组成的．25．（河南省实验中学2020-2021学年七年级上学期期中数学试题）在朱自清的《春》中有描写春雨“像牛毛，像细丝，密密地斜织着”的语句，这里把雨看成了线，这说明_____________．【答案】点动成线．【分析】根据点动成线可得答案．【详解】解：“像牛毛，像细丝，密密地斜织着”的语句，这里把雨看成了线，这说明点动成线．故答案为：点动成线．【点睛】本题主要考查了点、线、面、体，从运动的观点来看：点动成线，线动成面，面动成体．26．（山东省济南市七贤中学2020-2021学年七年级上学期第一次月考数学试题）我们经常能看到车的雨刷把汽车玻璃上的雨水刷干净，说明了数学中的_________事实．【答案】线动成面【分析】汽车的雨刷实际上是一条线，通过运动把玻璃上的雨水刷干净，所以应是线动成面．【详解】汽车的雨刷把玻璃上的雨水刷干净，是运用了线动成面的原理，故答案为：线动成面．【点睛】此题主要考查了点、线、面、体，正确理解点线面体的概念是解题的关键．27．（陕西省西安黄河中学2020-2021学年七年级上学期第一次月考数学试题）数学老师用粉笔在黑板上快速滑动写出一个又一个数字，这说明______．【答案】点动成线【分析】利用点动成线，线动成面，面动成体，进而得出答案．【详解】解：笔尖在纸上快速滑动写出一个又一个数字，用数学知识解释为点动成线．故答案为：点动成线．【点睛】此题主要考查了点、线、面、体，正确把握它们之间的关系是解题关键．28．（山东省滕州市墨子中学、柴胡店中学、洪绪中学2020-2021学年七年级上学期第一次月考数学试题）夜晚的流星划过天空时留下一道明亮的光线，由此说明了________的数学事实．【答案】点动成线【解析】夜晚的流星划过天空时留下一道明亮的光线，由此说明了点动成线，故答案为点动成线．【点睛】本题主要考查了点、线、面、体，关键是掌握点动成线，线动成面，面动成体．29．（四川省渠县崇德实验学校2020-2021学年七年级上学期第一次月考数学试题）直角三角形绕它的直角边旋转一周，形成了一个圆锥体，这说明了_____．【答案】面动成体【分析】根据点动成线，线动成面，面动成体进行解答即可．【详解】解：直角三角形绕它的直角边旋转一周，形成了一个圆锥体，这说明了面动成体，故答案为：面动成体．【点睛】此题主要考查了点、线、面、体，关键是掌握点动成线，线动成面，面动成体．30．（河南省郑州市第七十九中学2020-2021学年七年级上学期第一次月考数学试题）将一枚硬币立在桌面上，当用力一转时，它形成的是一个__________体，说明的数学道理是__________．【答案】球面动成体【分析】这是面动成体的原理在现实中的具体表现．【详解】解：硬币立在桌面上用力一转，它形成的是一个球体；从运动的观点可知，这种现象说明面动成体．故答案为：球；面动成体．【点睛】此题主要考查了面与体的关系，关键把握点动成线，线动成面，面动成体．31．（山东省菏泽市郓城县高级学校2019-2020学年七年级上学期第一次质量检测数学试题）将弯曲的公路改直，可以缩短路程．这是依据___；“枪挑一条线，棍扫一大片”．用数学知识解释一下______．【答案】两点之间线段最短点动成线，线动成面【分析】根据线段的性质：两点之间线段最短和点动成线，线动成面进行解答即可．【详解】解：根据线段的性质：两点之间线段最短可得：把一条弯曲的公路改成直道，可以缩短路程，其道理用几何的知识解释应是两点之间线段最短．“枪挑一条线，棍扫一大片”，这句话说明点动成线，线动成面．故答案为：两点之间线段最短；点动成线，线动成面．【点睛】本题考查了线段的性质和点、线、面、体，属于基础题，比较简单．32．（四川省达州市渠县树德文武学校2020-2021学年七年级上学期iyici月考数学试题）笔尖在纸上快速滑动写出一个又一个字，用数学知识可以理解为___________.【答案】点动成线【分析】利用点动成线，线动成面，面动成体，进而得出答案．【详解】笔尖在纸上快速滑动写出一个又一个字，用数学知识解释为点动成线．故答案是：点动成线．【点睛】考查了点、线、面、体，正确把握它们之间的关系是解题关键．33．（黑龙江省绥化市青冈县2019-2020学年七年级上学期期末数学试题）长方形的长是20cm ，宽是10cm ．以长为轴旋转一周所得的几何体的体积是（___________）cm 3．（π≈3．14） 【答案】6280【分析】根据圆柱的体积公式即可得．【详解】由题意得：以长为轴旋转一周所得的几何体是圆柱， 则所求的体积为23102020006280()cm ππ⨯⨯=≈， 故答案为：6280．【点睛】本题考查了圆柱的体积公式，熟记公式是解题关键．34．（甘肃省酒泉市金塔县第三中学2020-2021学年七年级上学期期中数学试题）如图，直角三角形绕直线L 旋转一周，得到的立体图形是______．【答案】圆锥【分析】根据直角三角形绕直角边旋转是圆锥，可得答案． 【详解】解：直角三角形绕直角边旋转是圆锥．【点睛】本题考查了点线面体，熟记各种平面图形旋转得到的立体图形是解题关键．35．（四川省达州市渠县第三中学2020-2021学年七年级上学期期中数学测试题一个长方形的长AB 为5cm ，宽CD 为3cm ，则绕某一边旋转一周，得到一个圆柱体，则该圆柱体的体积是________cm 3．（保留π） 【答案】45π或75π【分析】根据圆柱体的体积=底面积×高求解，注意底面半径和高互换得圆柱体的两种情况． 【详解】解：分两种情况：①绕长AB 所在的直线旋转一周得到圆柱体积为：π×32×5=45π（cm 3）； ②绕宽CD 所在的直线旋转一周得到圆柱体积为：π×52×3=75π（cm 3）． 故它们的体积分别为45πcm 3或75πcm 3． 故答案为：45π或75π．【点睛】本题考查了点线面体，利用圆柱的体积公式是解题关键，要分类讨论，以防遗漏．36．（山东省济宁学院附属中学2020-2021学年七年级上学期月考数学试题）一个长方形绕着它的一条边所在的直线旋转一周后所得到的立体图形是圆柱．（_____） 【答案】对【分析】根据面动成体：一个长方形绕着它的一条边所在的直线旋转一周后所得到的立体图形是圆柱，据此判断即可．【详解】解：一个长方形绕着它的一条边所在的直线旋转一周后所得到的立体图形是圆柱，这一结论是对的． 故答案为：对．【点睛】本题考查了圆柱的概念和面动成体，属于应知应会题型，熟练掌握基础知识是解题关键． 37．（四川省铁路中学校2020~2021学年七年级上学期10月月考数学试题）如果长方形的长和宽分别为6和4，那么以长方形的一边为轴旋转一周所得的几何体的体积为______（结果保留π）． 【答案】96π或144π【分析】由题意易得可分两种情况进行求解，即①若以长方体的长为轴，旋转一周，则得到高为6，底面半径为4的圆柱，②若以长方体的宽4为轴，旋转一周，则得到高为4，底面半径为6的圆柱；然后进行求解即可．【详解】解：①若以长方体的长为轴，旋转一周，则得到高为6，底面半径为4的圆柱，其体积为24696ππ⨯⨯=； ②若以长方体的宽4为轴，旋转一周，则得到高为4，底面半径为6的圆柱，其体积为264144ππ⨯⨯=． 故答案为：96π或144π．【点睛】本题主要考查几何初步，关键是由平面图形得到几何体，进而求解即可．38．（重庆市缙云教育联盟2020-2021学年七年级10月月考数学试题）长方形的两条边长分别为3cm 和4cm ，以其中一条边所在的直线为轴旋转一周后得到几何体的底面积是_________________________． 【答案】9πcm 2或16πcm 2．【分析】根据长方形绕一边旋转一周，可得圆柱．分类讨论：3cm 是底面半径，4cm 是底面半径，根据圆的面积公式，可得圆柱的底面积，可得答案．【详解】这个长方形绕一边所在直线旋转一周后是圆柱． 当3cm 是底面半径时，圆柱的底面积是()222πr 3π9πcm==；当4cm 是底面半径时，圆柱的底面积是()222πr 4π16πcm ==． 故答案为29πcm 或216πcm ．【点睛】本题考查了点、线、面、体，利用了圆的面积公式，分类讨论是解题关键．39．（宁夏回族自治区银川景博学校2019-2020学年七年级上学期期中数学试题）我们曾学过圆柱的体积计算公式：2V sh R h π==（R 是圆柱底面半径，R 为圆柱的高），现有一个长方形，长为2cm ，宽为1cm ，以它的一边所在的直线为轴旋转一周，得到的几何体的体积是___________3cm ．（结果保留π）【答案】2π或4π.【分析】根据圆柱体的体积=底面积×高求解，注意底面半径和高互换得圆柱体的两种情况． 【详解】分两种情况：（1）绕长所在的直线旋转一周得到圆柱体积为：π×12×2=2π（cm 3）； （2）绕宽所在的直线旋转一周得到圆柱体积为：π×22×1=4π（cm 3）． 故它们的体积分别为2πcm 3或4πcm 3； 故答案为：2π或4π.【点睛】本题考查了点、线、面、体，圆柱体的体积的求法，注意分情况讨论，难度适中.40．小明学习了“面动成体”之后，他用一个边长为3cm 、4cm 和5cm 的直角三角形，绕其中一条边旋转一周，得到了一个几何体．(1)请画出可能得到的几何体简图．(2)分别计算出这些几何体的体积．（锥体体积=13底面积×高） 【答案】（1）画图见解析；（2）12πcm 2，16πcm 2，9.6πcm 2 【解析】【分析】（1）根据三角形旋转是圆锥，可得几何体； （2）根据圆锥的体积公式，可得答案． 【详解】（1）以4cm 为轴，得；以3cm 为轴，得；以5cm为轴，得；（2）以4cm为轴体积为13×π×32×4=12π，以3cm为轴的体积为13×π×42×3=16π，以5cm为轴的体积为13×π（125）2×5=9.6π．【点睛】本题考查了圆锥的体积公式的计算应用，抓住圆锥的展开图的特点，得出直角三角形绕直角边旋转一周得出的是圆锥体是解决本题是关键.41．（贵州省贵阳市清镇市贵阳清镇北大培文学校2020-2021学年七年级上学期9月月考数学试题）在七年级第一章的学习中，我们已经学习过：点动成，线动成，动成体．比如：（1）圆规在纸上划过会留下一个封闭的痕迹，这种现象说明．（2）一个人手里拿着一个绑在一根棍上的半圆面，当这个人把这个半圆面绕着这根棍飞快地旋转起来时就会看到一个球，这种现象说明．（3）聪明的你一定观察过生活中还有许多类似的现象，你能举出一个例子吗？并解释该现象．【答案】线，面，面；（1）点动成线；（2）面动成体；（3）见解析（答案不唯一）【分析】根据点、线、面、体的含义，结合运动观点可得答案；（1）由点的运动，可得点动成线，从而可得答案；（2）由线的运动，可得线动成面，从而可得答案；（3）．如：彗星从天空中划过一道明亮的弧线，是点动成线的实例，从而可得答案．【详解】解：（1）由点、线、面、体的含义知：点动成线，线动成面，面动成体．故答案为：线，面，面；（2）由点、线、面、体的关系得，点动成线，故答案为：点动成线；。

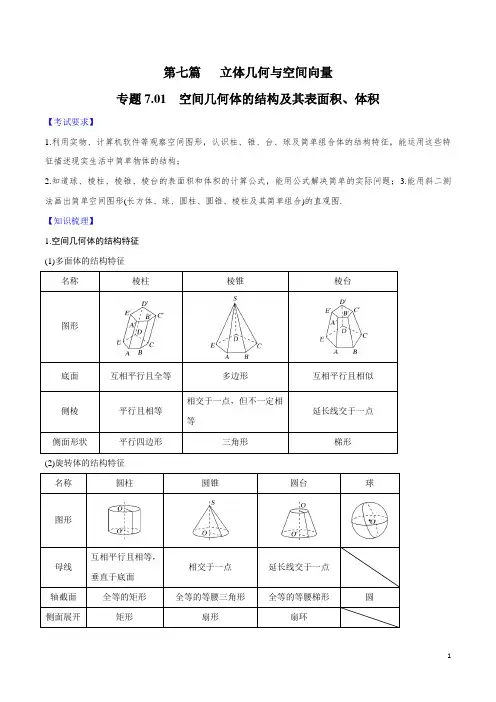
第七篇立体几何与空间向量专题7.01空间几何体的结构及其表面积、体积【考试要求】1.利用实物、计算机软件等观察空间图形，认识柱、锥、台、球及简单组合体的结构特征，能运用这些特征描述现实生活中简单物体的结构；2.知道球、棱柱、棱锥、棱台的表面积和体积的计算公式，能用公式解决简单的实际问题；3.能用斜二测法画出简单空间图形(长方体、球、圆柱、圆锥、棱柱及其简单组合)的直观图.【知识梳理】1.空间几何体的结构特征(1)多面体的结构特征名称棱柱棱锥棱台图形底面互相平行且全等多边形互相平行且相似相交于一点，但不一定相延长线交于一点侧棱平行且相等等侧面形状平行四边形三角形梯形(2)旋转体的结构特征名称圆柱圆锥圆台球图形互相平行且相等，相交于一点延长线交于一点母线垂直于底面轴截面全等的矩形全等的等腰三角形全等的等腰梯形圆侧面展开矩形扇形扇环图2.直观图空间几何体的直观图常用斜二测画法来画，其规则是：(1)原图形中x 轴、y 轴、z 轴两两垂直，直观图中，x ′轴、y ′轴的夹角为45°(或135°)，z ′轴与x ′轴、y ′轴所在平面垂直.(2)原图形中平行于坐标轴的线段，直观图中仍分别平行于坐标轴.平行于x 轴和z 轴的线段在直观图中保持原长度不变，平行于y 轴的线段长度在直观图中变为原来的一半.3.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱 圆锥 圆台侧面展开图侧面积公式 S 圆柱侧＝2πrl S 圆锥侧＝πrl S 圆台侧＝π(r 1＋r 2)l4.空间几何体的表面积与体积公式 名称几何体表面积 体积柱 体(棱柱和圆柱)S 表面积＝S 侧＋2S 底 V ＝S 底h锥 体(棱锥和圆锥) S 表面积＝S 侧＋S 底 V ＝13S 底h台 体(棱台和圆台) S 表面积＝S 侧＋S 上＋S 下 V ＝13(S 上＋S 下＋S 上S 下)h球 S ＝4πR 2 V ＝43πR 3【微点提醒】1.台体可以看成是由锥体截得的，易忽视截面与底面平行且侧棱延长后必交于一点.2.正方体的棱长为a ，球的半径为R ，则与其有关的切、接球常用结论如下 ：(1)若球为正方体的外接球，则2R ＝3a ；(2)若球为正方体的内切球，则2R ＝a ；(3)若球与正方体的各棱相切，则2R ＝2a .3.长方体的共顶点的三条棱长分别为a ，b ，c ，外接球的半径为R ，则2R ＝a 2＋b 2＋c 2.4.正四面体的外接球与内切球的半径之比为3∶1.【疑误辨析】1.判断下列结论正误(在括号内打“√”或“×”)(1)有两个面平行，其余各面都是平行四边形的几何体是棱柱.( )(2)有一个面是多边形，其余各面都是三角形的几何体是棱锥.( )(3)用斜二测画法画水平放置的∠A 时，若∠A 的两边分别平行于x 轴和y 轴，且∠A ＝90°，则在直观图中，∠A ＝45°.( )(4)锥体的体积等于底面面积与高之积.( )【教材衍化】2.(必修2P10B1改编)如图，长方体ABCD －A ′B ′C ′D ′被截去一部分，其中EH ∥A ′D ′.剩下的几何体是( )A.棱台B.四棱柱C.五棱柱D.六棱柱3.(必修2P27练习1改编)已知圆锥的表面积等于12π cm 2，其侧面展开图是一个半圆，则底面圆的半径为( )A.1 cmB.2 cmC.3 cmD.32cm【真题体验】4.(2016·全国Ⅱ卷)体积为8的正方体的顶点都在同一球面上，则该球的表面积为( )A.12πB.323πC.8πD.4π5.(2017·全国Ⅲ卷)已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( )A.πB.3π4C.π2D.π46.(2019·菏泽一中月考)用斜二测画法画水平放置的矩形的直观图，则直观图的面积与原矩形的面积之比为________.【考点聚焦】考点一 空间几何体的结构特征【例1】 (1)给出下列命题：①在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线；②直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥；③棱台的上、下底面可以不相似，但侧棱长一定相等.其中正确命题的个数是( )A.0B.1C.2D.3 (2)给出下列命题：①棱柱的侧棱都相等，侧面都是全等的平行四边形；②在四棱柱中，若两个过相对侧棱的截面都垂直于底面，则该四棱柱为直四棱柱；③存在每个面都是直角三角形的四面体；④棱台的侧棱延长后交于一点.其中正确命题的序号是________.【规律方法】 1.关于空间几何体的结构特征辨析关键是紧扣各种空间几何体的概念，要善于通过举反例对概念进行辨析，即要说明一个命题是错误的，只需举一个反例.2.圆柱、圆锥、圆台的有关元素都集中在轴截面上，解题时要注意用好轴截面中各元素的关系.3.既然棱(圆)台是由棱(圆)锥定义的，所以在解决棱(圆)台问题时，要注意“还台为锥”的解题策略.【训练1】下列命题正确的是()A.两个面平行，其余各面都是梯形的多面体是棱台B.两个面平行且相似，其余各面都是梯形的多面体是棱台C.以直角梯形的一条直角腰所在的直线为旋转轴，其余三边旋转形成的面所围成的旋转体是圆台D.用平面截圆柱得到的截面只能是圆和矩形考点二空间几何体的直观图【例2】已知正三角形ABC的边长为a，那么△ABC的平面直观图△A′B′C′的面积为()A.34a2 B.38a2 C.68a2 D.616a2【规律方法】1.画几何体的直观图一般采用斜二测画法，其规则可以用“斜”(两坐标轴成45°或135°)和“二测”(平行于y 轴的线段长度减半，平行于x 轴和z 轴的线段长度不变)来掌握.2.按照斜二测画法得到的平面图形的直观图，其面积与原图形的面积的关系S 直观图＝24S 原图形.【训练2】 如果一个水平放置的图形的斜二测直观图是一个底角为45°，腰和上底均为1的等腰梯形，那么原平面图形的面积是( ) A.2＋ 2B.1＋22C.2＋22D.1＋ 2考点三 空间几何体的表面积【例3】 (1)若正四棱锥的底面边长和高都为2，则其全面积为________.(2)圆台的上、下底面半径分别是10 cm 和20 cm ，它的侧面展开图的扇环的圆心角是180°，那么圆台的表面积为________(结果中保留π).(3)如图直平行六面体的底面为菱形，若过不相邻两条侧棱的截面的面积分别为Q 1，Q 2，则它的侧面积为______.【规律方法】 1.求解有关多面体侧面积的问题，关键是找到其特征几何图形，如棱柱中的矩形、棱台中的直角梯形、棱锥中的直角三角形，它们是联系高与斜高、边长等几何元素间的桥梁，从而架起求侧面积公式中的未知量与条件中已知几何元素间的联系.2.多面体的表面积是各个面的面积之和；组合体的表面积注意衔接部分的处理.3.旋转体的表面积问题注意其侧面展开图的应用.【训练3】(1)圆柱的侧面展开图是边长为6π和4π的矩形，则圆柱的表面积为()A.6π(4π＋3)B.8π(3π＋1)C.6π(4π＋3)或8π(3π＋1)D.6π(4π＋1)或8π(3π＋2)(2)(必修2P36A10改编)一直角三角形的三边长分别为6 cm，8 cm，10 cm，绕斜边旋转一周所得几何体的表面积为________.考点四空间几何体的体积【例4】(1)(必修2P27例4改编)圆柱的底面直径与高都等于球的直径，则球的体积与圆柱的体积比V球∶V柱为()A.1∶2B.2∶3C.3∶4D.1∶3(2)(2018·天津卷)已知正方体ABCD－A1B1C1D1的棱长为1，除面ABCD外，该正方体其余各面的中心分别为点E，F，G，H，M(如图)，则四棱锥M－EFGH的体积为________.【规律方法】 1.(直接法)规则几何体：对于规则几何体，直接利用公式计算即可.2.(割补法)不规则几何体：当一个几何体的形状不规则时，常通过分割或者补形的手段将此几何体变为一个或几个规则的、体积易求的几何体，然后再计算.经常考虑将三棱锥还原为三棱柱或长方体，将三棱柱还原为平行六面体，将台体还原为锥体.3.(等积法)三棱锥：利用三棱锥的“等积性”可以把任一个面作为三棱锥的底面.(1)求体积时，可选择“容易计算”的方式来计算；(2)利用“等积性”可求“点到面的距离”，关键是在面中选取三个点，与已知点构成三棱锥.【训练4】 (必修2P28A3改编)如图，将一个长方体用过相邻三条棱的中点的平面截出一个棱锥，则该棱锥的体积与剩下的几何体体积的比为________.考点五 多面体与球的切、接问题【例5】 (经典母题)(2016·全国Ⅲ卷)在封闭的直三棱柱ABC －A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ，AB ＝6，BC ＝8，AA 1＝3，则V 的最大值是( )A.4πB.9π2C.6πD.32π3【迁移探究1】 若本例中的条件变为“直三棱柱ABC －A 1B 1C 1的6个顶点都在球O 的球面上”，若AB ＝3，AC ＝4，AB ⊥AC ，AA 1＝12，求球O 的表面积.【迁移探究2】 若本例中的条件变为“正四棱锥的顶点都在球O 的球面上”，若该棱锥的高为4，底面边长为2，求该球的体积.【规律方法】1.与球有关的组合体问题，一种是内切，一种是外接.球与旋转体的组合通常是作它们的轴截面解题，球与多面体的组合，通过多面体的一条侧棱和球心，或“切点”、“接点”作出截面图，把空间问题化归为平面问题.2.若球面上四点P ，A ，B ，C 中PA ，PB ，PC 两两垂直或三棱锥的三条侧棱两两垂直，可构造长方体或正方体确定直径解决外接问题.【训练5】 (2019·北京海淀区调研)三棱锥P －ABC 中，平面PAC ⊥平面ABC ，AB ⊥AC ，PA ＝PC ＝AC ＝2，AB ＝4，则三棱锥P －ABC 的外接球的表面积为( )A.23πB.234πC.64πD.643π【反思与感悟】1.几何体的截面及作用(1)常见的几种截面：①过棱柱、棱锥、棱台的两条相对侧棱的截面；②平行于底面的截面；③旋转体中的轴截面；④球的截面.(2)作用：利用截面研究几何体，贯彻了空间问题平面化的思想，截面可以把几何体的性质、画法及证明、计算融为一体.2.棱台和圆台是分别用平行于棱锥和圆锥的底面的平面截棱锥和圆锥后得到的，所以在解决棱台和圆台的相关问题时，常“还台为锥”，体现了转化的数学思想.3.转化与化归思想：计算旋转体的侧面积时，一般采用转化的方法来进行，即将侧面展开化为平面图形，“化曲为直”来解决，因此要熟悉常见旋转体的侧面展开图的形状及平面图形面积的求法.【易错防范】1.求组合体的表面积时：组合体的衔接部分的面积问题易出错.2.底面是梯形的四棱柱侧放时，容易和四棱台混淆，在识别时要紧扣定义，以防出错.【核心素养提升】【直观想象与逻辑推理】——简单几何体的外接球与内切球问题1.直观想象主要表现为利用几何图形描述问题，借助几何直观理解问题，运用空间想象认识事物，解决与球有关的问题对该素养有较高的要求.2.简单几何体外接球问题是立体几何中的难点和重要的考点，此类问题实质是解决球的半径长或确定球心O的位置问题，其中球心的确定是关键.一、知识要点1.外接球的问题(1)必备知识：①简单多面体外接球的球心的结论.结论1：正方体或长方体的外接球的球心是其体对角线的中点.结论2：正棱柱的外接球的球心是上下底面中心的连线的中点.结论3：直三棱柱的外接球的球心是上下底面三角形外心的连线的中点.②构造正方体或长方体确定球心.③利用球心O与截面圆圆心O1的连线垂直于截面圆及球心O与弦中点的连线垂直于弦的性质，确定球心.(2)方法技巧：几何体补成正方体或长方体.2.内切球问题(1)必备知识：①内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等.②正多面体的内切球和外接球的球心重合.③正棱锥的内切球和外接球球心都在高线上，但不一定重合.(2)方法技巧：体积分割是求内切球半径的通用做法.二、突破策略1.利用长方体的体对角线探索外接球半径【例1】已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的表面积是()A.16πB.20πC.24πD.32π【评析】若几何体存在三条两两垂直的线段或者三条线有两个垂直，可构造墙角模型(如下图)，直接用公式(2R)2＝a2＋b2＋c2求出R.2.利用长方体的面对角线探索外接球半径【例2】三棱锥中S－ABC，SA＝BC＝13，SB＝AC＝5，SC＝AB＝10.则三棱锥的外接球的表面积为______.【评析】 三棱锥的相对棱相等，探寻球心无从着手，注意到长方体的相对面的面对角线相等，可在长方体中构造三棱锥，从而巧妙探索外接球半径.3.利用底面三角形与侧面三角形的外心探索球心【例3】 平面四边形ABCD 中，AB ＝AD ＝CD ＝1，BD ＝2，BD ⊥CD .将其沿对角线BD 折成四面体A ′BCD ，使平面A ′BD ⊥平面BCD .若四面体A ′BCD 的顶点在同一球面上，则该球的体积为( ) A.32π B.3π C.23π D.2π【评析】 三棱锥侧面与底面垂直时，可紧扣球心与底面三角形外心连线垂直于底面这一性质，利用底面与侧面的外心，巧探外接球球心，妙求半径.4.利用直棱柱上下底面外接圆圆心的连线确定球心【例4】 一个正六棱柱的底面是正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为98，底面周长为3，则这个球的体积为________.【评析】 直棱柱的外接球、圆柱的外接球模型如下图其外接球球心就是上下底面外接圆圆心连线的中点.5.锥体的内切球问题(1)题设：如图①，三棱锥P －ABC 是正三棱锥，求其内切球的半径.图①第一步：先画出内切球的截面图，E ，H 分别是两个三角形的外心；第二步：求DH ＝13CD ，PO ＝PH －r ，PD 是侧面△ABP 的高； 第三步：由△POE ∽△PDH ，建立等式：OE DH ＝PO PD，解出r . (2)题设：如图②，四棱锥P －ABC 是正四棱锥，求其内切球的半径.图②第一步：先画出内切球的截面图，P ，O ，H 三点共线；第二步：求FH ＝12BC ，PO ＝PH －r ，PF 是侧面△PCD 的高； 第三步：由△POG ∽△PFH ，建立等式：OG HF ＝PO PF，解出r . (3)题设：三棱锥P －ABC 是任意三棱锥，求其的内切球半径.方法：等体积法，三棱锥P －ABC 体积等于内切球球心与四个面构成的四个三棱锥的体积之和； 第一步：先画出四个表面的面积和整个锥体体积；第二步：设内切球的半径为r ，球心为O ，建立等式：V P －ABC ＝V O －ABC ＋V O －PAB ＋V O －PAC ＋V O －PBC ⇒V P －ABC ＝13S △ABC ·r ＋13S △PAB ·r ＋13S △PAC ·r ＋13S △PBC ·r ＝13(S △ABC ＋S △PAB ＋S △PAC ＋S △PBC )·r ； 第三步：解出r ＝3V P －ABC S O －ABC ＋S O －PAB ＋S O －PAC ＋S O －PBC6.柱体的内切球问题【例5】 体积为4π3的球与正三棱柱的所有面均相切，则该棱柱的体积为________.【分层训练】【基础巩固题组】(建议用时：40分钟)一、选择题1.下列说法中，正确的是( )A.棱柱的侧面可以是三角形B.若棱柱有两个侧面是矩形，则该棱柱的其他侧面也是矩形C.正方体的所有棱长都相等D.棱柱的所有棱长都相等2.一个球的表面积是16π，那么这个球的体积为( )A.163π B.323π C.16π D.24π3.纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北，现在沿该正方体的一些棱将正方体剪开，外面朝上展平，得到如图所示的平面图形，则标“△”的面的方位是( )A.南B.北C.西D.下4.《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺.问：积及为米几何？”其意思为：“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有( )A.14斛B.22斛C.36斛D.66斛5.如图所示，正三棱柱ABC －A 1B 1C 1的底面边长为2，侧棱长为3，D 为BC 中点，则三棱锥A －B 1DC 1的体积为( )A.3B.32C.1D.32二、填空题6.一水平放置的平面四边形OABC ，用斜二测画法画出它的直观图O ′A ′B ′C ′如图所示，此直观图恰好是一个边长为1的正方形，则原平面四边形OABC 面积为________.7.现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为________.8.(2019·济南调研)祖暅(公元前5～6世纪)，祖冲之之子，是我国齐梁时代的数学家.他提出了一条原理：“幂势既同，则积不容异.”这句话的意思是：两个等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现，比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为2b，高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面于距平面β任意高d处可横截得到S圆及S环两截面，可以证明S圆＝S环总成立.据此，短轴长为4 cm，长轴为6 cm的椭球体的体积是________ cm3.三、解答题9.如图所示，正四棱台的高是17 cm，两底面边长分别为4 cm和16 cm，求棱台的侧棱长和斜高.10.现需要设计一个仓库，它由上下两部分组成，上部的形状是正四棱锥P－A1B1C1D1，下部的形状是正四棱柱ABCD－A1B1C1D1(如图所示)，并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍，若AB＝6 m，PO1＝2 m，则仓库的容积是多少？【能力提升题组】(建议用时：20分钟)11.(2019·石家庄模拟)用长度分别为2，3，5，6，9(单位：cm)的五根木棒连接(只允许连接，不允许折断)，组成共顶点的长方体的三条棱，则能够得到的长方体的最大表面积为()A.258 cm2B.414 cm2C.416 cm2D.418 cm212.已知三棱锥S－ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC＝2，则此棱锥的体积为()A.26 B.36 C.23 D.2213.如图所示，在透明塑料制成的长方体ABCD－A1B1C1D1容器中灌进一些水，将容器底面一边BC固定于地面上，再将容器倾斜，随着倾斜程度的不同，以下命题：①水的形状成棱柱状；②水面EFGH的面积不变；③A1D1始终与水面EFGH平行.其中正确命题的序号是________.14.如图，长方体ABCD－A1B1C1D1中，AB＝16，BC＝10，AA1＝8，点E，F分别在A1B1，D1C1上，A1E＝D1F＝4.过点E，F的平面α与此长方体的面相交，交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由)；(2)求平面α把该长方体分成的两部分体积的比值.。

探究一
探究二
素养形成
当堂检测
反思感悟 棱锥、棱台结构特征问题的判断方法
(1)举反例法
结合棱锥、棱台的定义举反例直接说明关于棱锥、棱台结构特征
的某些说法不正确.
(2)直接法
棱锥
棱台
定底面
只有一个面是多边形, 两个互相平行的面,即
此面即为底面
为上、下底面
看侧棱
相交于一点
延长后相交于一点
探究一
探究二
素养形成
答案:③
探究一
探究二
素养形成
当堂检测
反思感悟 关于棱柱的辨析 (1)紧扣棱柱的结构特征进行有关概念辨析. ①两个面互相平行;②其余各面是四边形;③相邻两个四边形的公 共边互相平行. (2)多注意观察一些实物模型和图片便于反例排除. 特别提醒:求解与棱柱相关的问题时,首先看是否有两个平行的面 作为底面,再看是否满足其他特征.
探究一
探究二
素养形成
当堂检测
方法点睛(1)绘制展开图:绘制多面体的平面展开图要结合多面体 的几何特征,发挥空间想象能力或者是亲手制作多面体模型.在解 题过程中,常常给多面体的顶点标上字母,先把多面体的底面画出 来,然后依次画出各侧面,便可得到其平面展开图. (2)由展开图复原几何体:若是给出多面体的平面展开图,来判断是 由哪一个多面体展开的,则可把上述过程逆推.同一个几何体的平 面展开图可能是不一样的,也就是说,一个多面体可有多个平面展 开图.
探究一
探究二
素养形成
当堂检测
几何体的平面展开图 典例(1)请画出如图所示的正方体的平面展开图;
(2)如图是两个几何体的平面展开图,请问各是什么几何体?
探究一
探究二
素养形成

备考2020年中考一轮复习点对点必考题型题型02 简单几何体的三视图考点解析1．简单几何体的三视图（1）画物体的主视图的口诀为：主、俯：长对正；主、左：高平齐；俯、左：宽相等．（2）常见的几何体的三视图：圆柱的三视图：2．简单组合体的三视图（1）画简单组合体的三视图要循序渐进，通过仔细观察和想象，再画它的三视图．（2）视图中每一个闭合的线框都表示物体上的一个平面，而相连的两个闭合线框常不在一个平面上．（3）画物体的三视图的口诀为：主、俯：长对正；主、左：高平齐；俯、左：宽相等．3．由三视图判断几何体（1）由三视图想象几何体的形状，首先，应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状．（2）由物体的三视图想象几何体的形状是有一定难度的，可以从以下途径进行分析：①根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，以及几何体的长、宽、高；②从实线和虚线想象几何体看得见部分和看不见部分的轮廓线；③熟记一些简单的几何体的三视图对复杂几何体的想象会有帮助；④利用由三视图画几何体与有几何体画三视图的互逆过程，反复练习，不断总结方法．五年中考1．（2019•成都）如图所示的几何体是由6个大小相同的小立方块搭成，它的左视图是（ ）A．B．C．D．【点拨】找到从左面看所得到的图形即可，注意所有的看到的棱都应表现在左视图中．【解析】解：从左面看易得第一层有2个正方形，第二层左边有1个正方形，如图所示：故选：B．2．（2018•成都）如图所示的正六棱柱的主视图是（ ）A．B．C．D．【点拨】根据主视图是从正面看到的图象判定则可．【解析】解：从正面看是左右相邻的3个矩形，中间的矩形的面积较大，两边相同．故选：A．3．（2017•成都）如图所示的几何体是由4个大小相同的小立方体组成，其俯视图是（ ）A．B．C．D．【点拨】根据从上边看得到的图形是俯视图，可得答案．【解析】解：从上边看一层三个小正方形，故选：C．4．（2016•成都）如图所示的几何体是由5个大小相同的小立方块搭成，它的俯视图是（ ）A．B．C．D．【点拨】找到从上面看所得到的图形即可，注意所有的看到的棱都应表现在俯视图中．【解析】解：从上面看易得横着的“”字，故选：C．5．（2015•成都）如图所示的三视图是主视图是（ ）A．B．C．D．【点拨】根据原图形得出其主视图，解答即可．【解析】解：A、是左视图，错误；B、是主视图，正确；C、是俯视图，错误；D、不是主视图，错误；故选：B．一年模拟1．（2019·锦江一诊）有一透明实物如图，它的主视图是（ ）A．B．C．D．【点拨】细心观察图中几何体摆放的位置和形状，根据主视图是从正面看到的图象判定则可．【解析】解：正面看，它是中间小两头大的一个图形，里面有两条虚线，表示看不到的轮廓线．故选：B．2．（2019·成华一诊）如图所示的几何体，它的左视图是（ ）A ．B ．C ．D ．【点拨】根据左视图即从物体的左面观察得到的视图，进而得出答案．【解析】解：如图所示的几何体的左视图为：．故选：D ．3．（2019·武侯一诊）如图所示的支架（一种小零件）的两个台阶的高度和宽度分别相等，则它的主视图为（ ）A ．B ．C ．D ．【点拨】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．【解析】解：从正面看去，是两个有公共边的矩形，如图所示：故选：D ．4．（2019·成华二诊）如图是由6个大小相同的立方体组成的几何体，在这个几何体的三视图中，是中心对称图形的是（ ）A．主视图B．左视图C．俯视图D．主视图和左视图【点拨】根据从上边看得到的图形是俯视图，可得答案．【解析】解：从上边看是一个十字，“十”字是中心对称图形，故选：C．5．（2019·青羊一诊）观察下列几何体，主视图、左视图和俯视图都是矩形的是（ ）A．B．C．D．【点拨】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．【解析】解：A、主视图为矩形，俯视图为圆，错误；B、主视图为矩形，俯视图为矩形，正确；C、主视图为等腰梯形，俯视图为圆环，错误；D、主视图为三角形，俯视图为有对角线的矩形，错误．故选：B．6．（2019·青羊二诊）图中三视图对应的正三棱柱是（ ）A．B．C．D．【点拨】利用俯视图可淘汰C、D选项，根据主视图的侧棱为实线可淘汰B，从而判断A选项正确．【解析】解：由俯视图得到正三棱柱两个底面在竖直方向，由主视图得到有一条侧棱在正前方，于是可判定A选项正确．故选：A．7．（2019·武侯二诊）下面四个立体图形，从正面、左面、上面观察都不可能看到长方形的是（ ）A．B．C．D．【点拨】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．依此找到从正面、左面、上面观察都不可能看到长方形的图形．【解析】解：A、主视图为长方形，左视图为长方形，俯视图为长方形，故本选项错误；B、主视图为长方形，左视图为长方形，俯视图为圆，故本选项错误；C、主视图为等腰三角形，左视图为等腰三角形，俯视图为圆，从正面、左面、上面观察都不可能看到长方形，故本选项正确；D、主视图为三角形，左视图为三角形，俯视图为有对角线的矩形，故本选项错误．故选：C．8．（2019·锦江二诊）如图，该立体图形的俯视图是（ ）A．B．C．D．【点拨】根据几何体的三视图，即可解答．【解析】解：如图所示的立体图形的俯视图是C．故选：C．9．（2019·高新一诊）如图是由几个相同小正方体组成的立体图形的俯视图，图上的数字表示该位置上小正方体的个数，这个立体图形的左视图是（ ）A．B．C．D．【点拨】根据从左边看得到的图形是左视图，可得答案．【解析】解：根据该几何体中小正方体的分布知，其左视图共2列，第1列有1个正方形，第2列有3个正方形，故选：B．10．（2019·武侯二诊）如图所示的几何体的左视图是（ ）A．B．C．D．【点拨】找到从几何体的左面看所得到的图形即可，注意所有的看到的棱都应表现在左视图中．【解析】解：从左面看，得到的视图是A．故选：A．精准预测1．如图所示几何体的左视图正确的是（ ）A．B．C．D．【点拨】找到从几何体的左面看所得到的图形即可，注意所有的看到的棱都应表现在左视图中．【解析】解：从几何体的左面看所得到的图形是：故选：A．2．下列立体图形中，主视图是三角形的是（ ）A．B．C．D．【点拨】根据从正面看得到的图形是主视图，可得图形的主视图．【解析】解：A、C、D主视图是矩形，故A、C、D不符合题意；B、主视图是三角形，故B正确；故选：B．3．如图是某兴趣社制作的模型，则它的俯视图是（ ）A ．B ．C ．D ．【点拨】根据俯视图即从物体的上面观察得得到的视图，进而得出答案．【解析】解：该几何体的俯视图是：由两个长方形组成的矩形，且矩形的之间有纵向的线段隔开．故选：B ．4．如图所示几何体，从左面看是（ ）A ．B ．C ．D ．【点拨】从左面看到的是左面位置上下两个正方形，右面的下方一个正方形，由此得出答案即可．【解析】解：左面位置上下两个正方形，右面的下方一个正方形的图形是．故选：B ．5．下列几何体中，从正面看（主视图）是长方形的是（ ）A ．B ．C ．D ．【点拨】主视图是分别从物体正面看，所得到的图形．【解析】解：圆锥的主视图是等腰三角形，圆柱的主视图是长方形，圆台的主视图是梯形，球的主视图是圆形，故选：B ．6．学校超市的货架上摆放着某品牌方便面，从三个不同的方向看可以看到下图所示的形状图，则货架上的方便面至多有（ ）A．7盒B．8盒C．9盒D．10盒【点拨】由从三个不同的方向看到的形状，可以在俯视图上，标出相应的摆放的最多数量，进而求出答案，做出选择．【解析】解：由从三个不同的方向看到的形状，可以在俯视图上，标出相应的摆放的最多数量，求出至多有9盒，故选：C．7．如图是由小立方块搭成的几何体，则从左面看到的几何体的形状图是（ ）A．B．C．D．【点拨】从左面看到的图形是两列，其中第一列有两个正方形，第二列有1个正方形，做出判断即可．【解析】解：从左面正投影所得到的图形为选项B．故选：B．8．如图是由5个完全相同的小正方体搭成的几何体，如果将小正方体A放到小正方体B的正上方，则它的（ ）A．左视图会发生改变B．俯视图会发生改变C．主视图会发生改变D．三种视图都会发生改变【点拨】根据从上面看得到的图形事俯视图，从正面看得到的图形是主视图，从左边看得到的图形是左视图，可得答案．【解析】解：如果将小正方体A放到小正方体B的正上方，则它的主视图会发生改变，俯视图和左视图不变．故选：C．9．如图是由6个大小相同的立方体组成的几何体，在这个几何体的三视图中，是中心对称图形的是（ ）A．主视图B．左视图C．俯视图D．主视图和左视图【点拨】根据从上边看得到的图形是俯视图，可得答案．【解析】解：从上边看是一个田字，“田”字是中心对称图形，故选：C．10．如图，下列选项中不是正六棱柱三视图的是（ ）A．B．C．D．【点拨】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．【解析】解：正六棱柱三视图分别为：三个左右相邻的矩形，两个左右相邻的矩形，正六边形．故选：A．11．如图，是某个几何体从不同方向看到的形状图（视图），这个几何体的表面能展开成下面的哪个平面图形？（ ）A．B．C．D．【点拨】由主视图和左视图可得此几何体为柱体，根据俯视图是圆可判断出此几何体为圆柱，进一步由展开图的特征选择答案即可．【解析】解：∵主视图和左视图都是长方形，∴此几何体为柱体，∵俯视图是一个圆，∴此几何体为圆柱，因此图A是圆柱的展开图．故选：A．12．如图，下列水平放置的几何体中，左视图不是矩形的是（ ）A．B．C．D．【点拨】根据左视图是从左面看到的视图，对各选项分析判断后利用排除法求解．【解析】解：A、圆柱的左视图是矩形，故本选项错误；B、圆锥的左视图是等腰三角形，故本选项正确；C、三棱柱的左视图是矩形，故本选项错误；D、长方体的左视图是矩形，故本选项错误．故选：B．13．如图所示的支架是由两个长方体构成的组合体，则它的左视图是（ ）A．B．C．D．【点拨】根据从左边看得到的图形是左视图，可得答案．【解析】解：从左边看下边是一个中间为虚线的矩形，故选：A．14．桌上摆放着一个由相同正方体组成的组合体，其俯视图如图所示，图中数字为该位置小正方体的个数，则这个组合体的左视图为（ ）A．B．C．D．【点拨】俯视图中的每个数字是该位置小立方体的个数，分析其中的数字，得左视图有3列，从左到右分别是2，3，2个正方形．【解析】解：由俯视图中的数字可得：左视图有3列，从左到右分别是2，3，2个正方形．故选：D．15．如图所示的几何体，从上面看得到的图形是（ ）A．B．C．D．【点拨】根据从上边看得到的图形是俯视图，可得答案．【解析】解：从上边看是一个六边形，中间为圆．故选：D．。

年级：辅导科目：数学课时数：课题立体几何（一）教学目的教学内容一、知识网络二、命题分析立体几何在高考中考查的主要内容有：空间几何体的性质、线面关系的判定与证明、表面积与体积的运算、空间几何体的识图，空间中距离、角的计算等．从近几年高考来看，一般以2～3个客观题来考查线面关系的判定、表面积与体积、空间中的距离与角、空间几何体的性质与识图等，以1个解答题来考查线面关系的证明以及距离、角的计算．在高考中属于中档题目．而三视图作为新课标的新增内容，在2011年高考中，有多套试卷在此知识点命题，主要考查三视图和直观图，特别是通过三视图来确定原图形的相关量．预计今后高考中，三视图的考查不只在选择题、填空题中出现，很有可能在解答题中与其他知识点结合在一起命题.三、复习建议在2012年高考复习中注意以下几个方面：(1)从命题形式来看，涉及立体几何内容的命题形式最为多变，除保留传统的“四选一”的选择题外，还尝试开发了“多选填空”、“完型填空”、“构造填空”等题型，并且这种命题形式正在不断完善和翻新；解答题则设计成几个小问题，此类题目往往以多面体为依托，第一小问考查线线、线面、面面的位置关系，后面几问考查面积、体积等度量关系，其解题思路也都是“作——证——求”，强调作图、证明和计算相结合．在2012年高考复习中注意以下几个方面：(1)从命题形式来看，涉及立体几何内容的命题形式最为多变，除保留传统的“四选一”的选择题外，还尝试开发了“多选填空”、“完型填空”、“构造填空”等题型，并且这种命题形式正在不断完善和翻新；解答题则设计成几个小问题，此类题目往往以多面体为依托，第一小问考查线线、线面、面面的位置关系，后面几问考查面积、体积等度量关系，其解题思路也都是“作——证——求”，强调作图、证明和计算相结合．(3)从方法上来看，着重考查公理化方法，如解答题注重理论推导和计算相结合，考查转化的思想方法，如要把立体．4．空间几何体的直观图画空间几何体的直观图常用画法，基本步骤是：(1)在已知图形中取互相垂直的x轴、y轴，两轴相交于点O，画直观图时，把它们画成对应的x′轴、y′轴，两轴相交于点O′，且使∠x′O′y′＝ .(2)已知图形中平行于x轴、y轴的线段，在直观图中分别画成平行于的线段．(3)已知图形中平行于x轴的线段，在直观图中保持原长度，平行于y轴的线段，长度变为．(4)在已知图形中过O点作z轴垂直于xOy平面，在直观图中对应的z′轴也垂直于x′O′y′平面，已知图形中平行于z轴的线段，在直观图中仍平行于z′轴且长度．5．中心投影与平行投影(1)平行投影的投影线互相，而中心投影的投影线相交于一点．(2)从投影的角度看，三视图和用斜二测画法画出的直观图都是在投影下画出来的图形．（三）基础自测1．(2010·北京理)一个长方体去掉一个小长方体，所得几何体的正(主)视图与侧(左)视图分别如右图所示，则该几何体的俯视图为( )[答案] C[解析] 本题考查了三视图知识，解题的关系是掌握三视图与直观图的知识，特别是应明确三视图是从几何体的哪个方向看到的．由三视图中正(主)视图、侧(左)视图得到几何体的直观图如图所示，所以该几何体的俯视图为C.2．(2010·福建理)如图，若Ω是长方体ABCD—A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体，其中E为线段A1B1上异于B1的点，F为线段BB1上异于B1的点，且EH∥A1D1，则下列结论中不正确．．．的是( ) A．EH∥FG B．四边形EFGH是矩形 C．Ω是棱柱 D．Ω是棱台[答案] D[解析] ∵EH∥A1D1，∴EH∥B1C1∴B1C1∥面EFGH，B1C1∥FG，∴Ω是棱柱，故选D.3．右图为水平放置的正方形ABCO，它在直角坐标系xOy中点B的坐标为(2,2)，则在用斜二测画法画出的正方形的直观图中，顶点B′到x′轴的距离为( )A.12B.22C．1 D. 2[答案] B[解析] 如图，在平面直观图中，B′C′＝1，∠B′C′D′＝45°，∴B′D′＝2 2 .4．已知某物体的三视图如图所示，那么这个物体的形状是( )A．六棱柱 B．四棱柱 C．圆柱 D．五棱柱[答案] A[解析] 由俯视图可知，该物体的形状是六棱柱，故选A.5．用小正方体搭成一个几何体，如图是它的主视图和左视图，搭成这个几何体的小正方体最多为________个．[答案] 7[解析] 由主视图和左视图知，该几何体由两层组成，底层最多有3×2＝6个，上层只有1个，故最多为7个．6．(2010·新课标理)正(主)视图为一个三角形的几何体可以是________．(写出三种)[答案] 三棱锥、三棱柱、圆锥(其他正确答案同样给分)．[解析] 本题考查空间几何体的三视图．本题属于开放性题目，答案不唯一．正视图是三角形的几何体，最容易想到的是三棱锥，其次是四棱锥、圆锥；对于五棱锥、六棱锥等，正视图也可以是三角形．7．已知某几何体的俯视图是如图所示的矩形，正视图(或称主视图)是一个底边长为8、高为4的等腰三角形，侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形．(1)求该几何体的体积V ；(2)求该几何体的侧面积S .[分析] 由三视图的形状大小，还原成几何体；再利用体积公式和表面积公式求解．[解析] (1)由该几何体的俯视图、主视图、左视图可知，该几何体是四棱锥．且四棱锥的底面ABCD 是边长为6和8的矩形，高VO ＝4，O 点是AC 与BD 的交点．∴该几何体的体积V ＝13×8×6×4＝64. (2)如图所示，OE ⊥AB ，OF ⊥BC ，侧面VAB 中，VE ＝VO 2＋OE 2＝42＋32＝5，∴S △VAB ＝12×AB ×VE ＝12×8×5＝20， 侧面VBC 中，VF ＝VO 2＋OF 2＝42＋42＝42，∴S △VBC ＝12×BC ×VF ＝12×6×42＝12 2. ∴该几何体的侧面积S ＝2(S △VAB ＋S △VBC )＝40＋24 2.[点评] 由三视图还原成几何体，需要对常见的柱、锥、台、球的三视图非常熟悉，有时还可根据三视图的情况，还原成由常见几何体组合而成的组合体．（四）典型例题1.命题方向：空间几何体的结构特征[例1] 下列命题中，成立的是( )A ．各个面都是三角形的多面体一定是棱锥B ．四面体一定是三棱锥C ．棱锥的侧面是全等的等腰三角形，该棱锥一定是正棱锥D ．底面多边形既有外接圆又有内切圆，且侧棱相等的棱锥一定是正棱锥[分析] 结合棱锥、正棱锥的概念逐一进行考查．[解析] A 是错误的，只要将底面全等的两个棱锥的底面重合在一起，所得多面体的每个面都是三角形，但这个多面体不是棱锥；B 是正确的，三个面共顶点，另有三边围成三角形是四面体也必定是个三棱锥；对于C ，如图所示，棱锥的侧面是全等的等腰三角形，但该棱锥不是正棱锥；D 也是错误的，底面多边形既有内切圆又有外接圆，如果不同心，则不是正多边形，因此不是正棱锥．[答案] B[点评] 本题考查棱锥、正棱锥的概念以及四面体与三棱锥的等价性，当三棱锥的棱长都相等时，这样的三棱锥叫正四面体．判断一个命题为真命题要考虑全面，应特别注意一些特殊情况．跟踪练习1：以下命题：①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥；②以直角梯形的一腰为轴旋转一周所得的旋转体是圆台；③圆柱、圆锥、圆台的底面都是圆；④一个平面截圆锥、得到一个圆锥和一个圆台．其中正确命题的个数为( )A．0 B．1 C．2 D．3[答案] A[解析] ①应以直角三角形的一条直角边为轴旋转才可以得到圆锥；②以直角梯形垂直于底边的一腰为轴旋转可得到圆台；③它们的底面为圆面，④用平行于圆锥底面的平面截圆锥，可得到一个圆锥和圆台．应选A.2.命题方向：直观图[例2] 若已知△ABC的平面直观图△A′B′C′是边长为a的正三角形，那么原△ABC的面积为( )A.32a2 B.34a2 C.62a2 D.6a2[解析] 如图是△ABC的平面直观图△A′B′C′.作C′D′∥y′轴交x′轴于D′，则C′D′对应△ABC的高CD，∴CD＝2C′D′＝2·2·C′O′＝22·32a＝6a.而AB＝A′B′＝a，∴S△ABC＝12·a·6a＝62a2[答案] C[点评] 解决这类题的关键是根据斜二测画法求出原三角形的底和高，将水平放置的平面图形的直观图，还原成原来的图形，其作法就是逆用斜二测画法，也就是使平行于x轴的线段的长度不变，而平行于y轴的线段长度变为直观图中平行于y′轴的线段长度的2倍．跟踪练习2已知正三角形ABC 的边长为a ，那么△ABC 的平面直观图△A ′B ′C ′的面积为( )A.34a 2B.38a 2C.68a 2D.616a 2 [分析] 先根据题意画出直观图，然后根据直观图△A ′B ′C ′的边长及夹角求解．[答案] D[解析] 如图①、②所示的实际图形和直观图．由②可知，A ′B ′＝AB ＝a ，O ′C ′＝12OC ＝34a ， 在图②中作C ′D ′⊥A ′B ′于D ′，则C ′D ′＝22O ′C ′＝68a . ∴S △A ′B ′C ′＝12A ′B ′·C ′D ′＝12×a ×68a ＝616a 2. 3.命题方向：三视图[例3] 下列图形中的图(b)是根据图(a)中的实物画出的主视图和俯视图，你认为正确吗？若不正确请改正并画出左视图．[解析] 主视图和俯视图都不正确．主视图的上面的矩形中缺少中间小圆柱形成的轮廓线(用虚线表示)；左视图的轮廓是两个矩形叠放在一起，上面的矩形中有2条不可视轮廓线．下面的矩形中有一条可视轮廓线(用实线表示)，该几何体的三视图如图所示：[点评] 简单几何体的三视图的画法应从以下几个方面加以把握：(1)搞清主视、左视、俯视的方向，同一物体由放置的位置不同，所画的三视图可能不同．(2)看清简单组合体是由哪几个基本元素组成．(3)画三视图时要遵循“长对正，高平齐，宽相等”的原则，还要注意几何体中与投影垂直或平行的线段及面的位置关系．跟踪练习3(2010·浙江文)若某几何体的三视图(单位：cm)如图所示，则此几何体的体积是( )A.3523cm 3B.3203cm 3C.2243cm 3D.1603cm 3 [答案] B[解析] 本题考查了三视图及几何体体积的求解．由三视图可知，该几何体是由一个正四棱台和一个长方体构成的一个组合体，V 台＝13×2×(16＋42×82＋64)＝2243cm 3， V 长方体＝4×4×2＝32cm 3 ∴V 总＝V 台＋V 长方体＝2243＋32＝3203cm 3.（五）思想方法点拨：1．要注意牢固把握各种几何体的结构特点，利用它们彼此之间的联系来加强记忆，如棱柱、棱锥、棱台为一类；圆柱、圆锥、圆台为一类；或分成柱体、锥体、台体三类来分别认识．只有对比才能把握实质和不同，只有联系才能理解共性和个性．2．要适当与平面几何的有关概念、图形和性质进行对比，通过平面几何与立体几何相关知识的比较，丰富自己的空间想象力．对组合体可通过把它们分解为一些基本几何体来研究．3．画图时要紧紧把握住一斜——在已知图形中垂直于x 轴的线段，在直观图中均与x 轴成45°；二测——两种度量形式，即在直观图中，平行于x 轴的线段长度不变，平行于y 轴的线段变为原长度的一半．4．三视图(1)几何体的三视图的排列规则：俯视图放在主视图的下面，长度与主视图一样，左视图放在主视图右面，高度与主视图一样，宽度与俯视图一样，即“长对正，高平齐，宽相等”．注意虚、实线的区别．(2)应用：在解题的过程中，可以根据三视图的形状及图中所涉及到的线段的长度，推断出原几何图形中的点、线、面之间的关系及图中的一些线段的长度，这样我们就可以解出有关的问题．5．本节常涉及一些截面问题，它把空间图形的性质、画法及有关论证、计算融为一体，常见的、基本的截面问题，如直截面、对角截面、中截面等，要求熟知并掌握．要知道这些截面的形状、位置，并能画出其图形，这常常可以将较难的问题变得简单，如“用一个平面截一个球，截面是圆面”这一点很重要，它把有关球的一些问题转化为圆的问题来解决．(六)课后强化作业一、选择题1．(2010·陕西理)若某空间几何体的三视图如图所示，则该几何体的体积是( )A.13B.23 C ．1 D ．2[答案] C[解析] C 该几何体是如图所示的直三棱柱V ＝12×1×2×2＝1. 2．下列命题中：①与定点的距离等于定长的点的集合是球面；②球面上三个不同的点，一定都能确定一个圆；③一个平面与球相交，其截面是一个圆，其中正确命题的个数为( )A ．0B ．1C ．2D ．3[答案] C[解析] 命题①、②都对，命题③一个平面与球相交，其截面是一个圆面，故选C.[点评] 要注意球与球面的区别．3．(2009·上海文，16)如图，已知三棱锥的底面是直角三角形，直角边长分别为3和4，过直角顶点的侧棱长为4，且垂直于底面，该三棱锥的主视图是( )[答案] B[解析] 本题考查三视图的基本知识及空间想象能力．由题可知，选B.4．如果一个空间几何体的主视图与左视图均为全等的等边三角形，俯视图为一个半径为1的圆及其圆心，那么这个几何体的体积为( )A.33πB.233πC.3πD.π3- 11 - [答案] A[解析] 由三视图知，该几何体是底半径为1的圆锥，轴截面是边长为2的正三角形，∴高为3，体积V ＝33π. 5．如图，△O ′A ′B ′是△OAB 水平放置的直观图，则△OAB 的面积为( )A ．6B ．3 2C ．6 2D ．12[答案] D[解析] 若还原为原三角形，则易知OB ＝4，OA ⊥OB ，OA ＝6，∴S △AOB ＝12×4×6＝12. 6．棱长为1的正方体ABCD －A 1B 1C 1D 1的8个顶点都在球O 的表面上，E 、F 分别是棱AA 1、DD 1的中点，则直线EF 被球O 截得的线段长为( )A.22 B ．1 C ．1＋22 D. 2 [答案] D[解析] 由条件知球O 半径为32，球心O 到直线EF 的距离为12，由垂径定理可知直线EF 被球O 截得的线段长d ＝2⎝ ⎛⎭⎪⎫322－⎝ ⎛⎭⎪⎫122＝ 2. 7．(2010·广东)如图所示，△ABC 为正三角形，AA ′∥BB ′∥CC ′，CC ′⊥平面ABC 且3AA ′＝32BB ′＝CC ′＝AB ，则多面体ABC －A ′B ′C ′的正视图(也称主视图)是( )[答案] D[解析] 本小题考查线面垂直的判定方法及三视图的有关概念．由于AA ′∥BB ′∥CC ′及CC ′⊥平面ABC ，知BB ′⊥平面ABC ，又CC ′＝32BB ′，且△ABC 为正三角形，故正(主)视图为D.8．用单位正方体搭一个几何体，使它的主视图和俯视图如图所示，则它的体积的最小值与最大值分别为( )A ．9与13B ．7与10C ．10与16D ．10与15[答案] C [解析] 由俯视图知几何体有三行和三列，且第三列的第一行，第二行都没有小正方体，其余各列各行都有小正- 12 -。

§7.1基本立体图形、简单几何体的表面积与体积考试要求 1.利用实物、计算机软件等观察空间图形，认识柱、锥、台、球及简单组合体的结构特征，能运用这些特征描述现实生活中简单物体的结构.2.知道球、棱(圆)柱、棱(圆)锥、棱(圆)台的表面积和体积的计算公式，能用公式解决简单的实际问题.3.能用斜二测画法画出简单空间图形(长方体、球、圆柱、圆锥、棱柱及其简单组合体)的直观图．1．空间几何体的结构特征(1)多面体的结构特征名称棱柱棱锥棱台图形底面互相平行且全等多边形互相平行且相似侧棱平行且相等相交于一点但不一定相等延长线交于一点侧面形状平行四边形三角形梯形(2)旋转体的结构特征名称圆柱圆锥圆台球图形母线互相平行且相等，垂直于底面相交于一点延长线交于一点轴截面 矩形 等腰三角形 等腰梯形 圆面 侧面展开图 矩形扇形扇环2.直观图(1)画法：常用斜二测画法． (2)规则：①原图形中x 轴、y 轴、z 轴两两垂直，直观图中，x ′轴、y ′轴的夹角为45°或135°，z ′轴与x ′轴和y ′轴所在平面垂直．②原图形中平行于坐标轴的线段，直观图中仍分别平行于坐标轴，平行于x 轴和z 轴的线段在直观图中保持原长度不变，平行于y 轴的线段长度在直观图中变为原来的一半． 3．圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧＝2πrlS 圆锥侧＝πrlS 圆台侧＝π(r 1＋r 2)l4.柱、锥、台、球的表面积和体积名称 几何体 表面积 体积 柱体(棱柱和柱) S 表面积＝S 侧＋2S 底 V ＝Sh 锥体(棱锥和圆锥)S 表面积＝S 侧＋S 底 V ＝13Sh台体(棱台和圆台)S 表面积＝S 侧＋S 上＋S 下 V ＝13(S 上＋S 下＋S 上S 下)h球S ＝4πR 2V ＝43πR 3微思考1．斜二测画法中“三变”与“三不变”指的是什么？ 提示“三变”⎩⎪⎨⎪⎧x 轴和y 轴的夹角改变，与y 轴平行的线段的长度变为原来的一半，图形改变.。

以用“斜”(两坐标轴成45°或135°)和“二测”(平行于y
轴的线段长度减半，平行于 x 轴和 z 轴的线段长度不变)来
掌握.
(2)按照斜二测画法得到的平面图形的直观图，其面积
与原图形的面积的关系：S
＝ 直观图
2 4S
原图形.
【变式训练】
一个水平放置的图形的斜二测直观图是一个底角为
45°，腰和上底均为 22的等腰梯形，那么原平面图形的面积
由斜二测画法可知，A′B′＝AB＝a，O′C′＝21OC
＝ 43a，在图 6-1-6 中作 C′D′⊥A′B′于 D′，则 C′D′
＝ 22O′C′＝ 86a.所以 S△A′B′C′＝21A′B′·C′D′＝
12·a·86a＝ 166a2.
答案：D
【题后反思】
(1)画几何体的直观图一般采用斜二测画法，其规则可
3.(教材改编题)如图 6-1-1，长方体 ABCD-A′B′C′D′
被截去一部分，其中 EH∥A′D′.剩下的几何体是(
)
A.棱台 C.五棱柱 答案：C
图 6-1-1 B.四棱柱 D.六棱柱
题组三 真题展现
4.(2021 年新高考Ⅰ)已知圆锥的底面半径为 2，其侧 面展开图为一个半圆，则该圆锥的母线长为( )
A.2
B.2 2
C.4
D.4 2
答案：B
5.(2020 年全国Ⅰ)如图 6-1-2，在三棱锥 P-ABC 的平面 展开图中，AC＝1，AB＝AD＝ 3 ，AB⊥AC，AB⊥AD， ∠CAE＝30°，则 cos∠FCB＝________.
答案：－14
图 6-1-2
考点一 空间几何体的结构特征
[例 1] (1)给出下列命题：

栏目索引
文数
课标版
第一节 空间几何体及其三视图、直观图
教材研读
栏目索引
1.空间几何体的结构特征
多 (1)棱柱:侧棱都① 平行且相等 ,上、下底面平行且是② 全等 的多边形. 面 (2)棱锥:底面是多边形,侧面是有一个公共顶点的三角形. 体 (3)棱台:可以由平行于棱锥底面的平面截棱锥得到,其上、下底面是③ 相似 多边形
旋 (1)圆柱:可以由④ 矩形 绕其任一边所在直线旋转得到. 转 (2)圆锥:可以由直角三角形绕其⑤ 直角边 所在直线旋转得到. 体 (3)圆台:可以由直角梯形绕其⑥ 垂直于底边的腰 所在直线或等腰梯形绕其上、下
底边中点的连线所在直线旋转得到,也可由平行于圆锥底面的平面截圆锥得到. (4)球:可以由半圆或圆绕其⑦ 直径 所在直线旋转得到
栏目索引
2.三视图与直观图
三视图 画三视图的规则:长对正,高平齐,宽相等 空间几何体的直观图常用⑧ 斜二测 画法来画,规则如下: (1)原图形中x轴、y轴、z轴两两垂直(原点为O),直观图中相应x'轴,y'轴满足∠x'O'y'=
直观图 ⑨ 45°(或135°) (O'为原点),z'轴与x'轴和y'轴所在平面垂直. (2)原图形中平行于坐标轴的线段在直观图中仍 平行于相应坐标轴 ,平行于x轴 和z轴的线段长度在直观图中保持原长度 不变 ,平行于y轴的线段长度在直观 图中长度为 原来的一半
栏目索引
2-1 (2014课标Ⅰ,8,5分)如图,网格纸的各小格都是正方形,粗实线画出 的是一个几何体的三视图,则这个几何体是 ( )
A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱 答案 B 由题中三视图可知该几何体的直观图如图所示,则这个几何 体是三棱柱,故选B.

由此可见，面数最少的多面体是四面体，即三棱锥．四面体在 立体几何中的作用相当于三角形在平面几何中的作用．例如， 平面上的多边形都可以由三角形拼合而成，而空间中的多面体 都可以由四面体拼合而成．
与平面上的正多边形类似，在空间中可以考虑正多面体．如果一个 多面体的所有面都是全等的正三角形或正多边形，每个顶点聚集的 棱的条数都相等，这个多面体就叫做正多面体（ｒｅｇｕｌａｒｐ ｏｌｙｈｅｄｒｏｎ）．图１１３ １给出了五种不同的正多体．事 实上，用本节“课后阅读”中所介绍多面体的欧拉定理，可以验证 只有这五种正多面体．
旋转面是大学空间解析几何课程中的 内容之一．我们这里只关注最简单的 情况：一条直线a绕同一平面内的另
一条直线l旋转一周所形成的曲面： 圆柱面或圆锥面．当直线a与直线l平 行时，得到的是圆柱面；当直线a与 直线l相交（但不垂直）时，得到的 是圆锥面（图１１３３）．直线a称
为圆柱面或圆锥面的母线．在圆锥面
课本练习
１．我国古代数学著作《九章算术》中研究过一种叫“鳖（biē）臑 （nào）”的几何体（见《九章算术》卷第五“商功”之一六），它 指的是由四个直角三角形围成的四面体．用你学过的立体几何知识说 明这种四面体确实存在
如图，先作一个底面为直角三角形的直棱柱AEF—BDC，其中∠BCD 是直角。 用平面ACD截此直三棱柱，则几何体A-BCD就是满足要求的“鳖臑”，这是 因为AB⊥平面BCD，所以△ABD、△ABC是直角三角形；又已知∠BCD为直 角，所以△BCD是直角三角形；最后，由CD⊥平面ABCF，推出CD⊥CA，即 ∠ACD为直角，所以△ACD是直角三角形。这样几何体A—BCD的四个面都是 直角三角形，即它是一个“鳖臑”。
我们迄今所见的多面体（如棱柱、棱锥、正多面体等）都是简单多 面体．但要构造一个非简单多面体也不难．如图１１-３-４，这是 一个中间有一个长方体空洞的十六面体，往这样的橡胶多面体充气， 得到的是一个游泳圈，而不是球．算一算，对于图１１- ３- ４的 多面体，V＋F－E等于多少．

绝密★启用前2020年普通高等学校招生全国统一考试课标1理科数学2020年全国1高考数学与2020全国1高考数学难度方面相对持平，在选择题和填空题方面难度有所提升，解答题方面难度有所减缓.在保持稳定的基础上，进行适度创新，尤其是选择填空压轴题.试卷内容上体现新课程理念，贴近中学数学教学，坚持对基础性的考查，同时加大了综合性、应用性和创新性的考查，如理科第2、3、10、11、12、16、19题，文科第2、4、9、12、19题.1.体现新课标理念，重视对传统核心考点考查的同时，增加了对数学文化的考查，如理科第2题，文科第4题以中国古代的太极图为背景，考查几何概型.2.关注通性通法.试卷淡化了特殊的技巧，全面考查通性通法，体现了以知识为载体，以方法为依托，以能力考查为目的的命题要求.3.考查了数学思想、数学能力、数学的科学与人文价值，体现了知识与能力并重、科学与人文兼顾的精神.如理科第6、10、13、15题，文科第5、12、13、16题对数形结合思想的考查；理科第11，文科第9题对函数与方程思想的考查；理科第12、16题对数学的科学与人文价值的考查.4.体现了创新性，如理科第19题，文科第19题立意新、情景新、设问新，增强了学生数学应用意识和创新能力.命题趋势：（1）函数与导数知识：以函数性质为基础，考查函数与不等式综合知识，如理科第5题，；以基本初等函数为背景考查构造新函数解决比较大小问题，如理科第11题；对含参单调性以及零点问题的考查，如理科21题，比较常规.（2）三角函数与解三角形知识：对三角函数图像与性质的考查，如理科第9题；；对解三角形问题的考查，如理科第17题.重视对基础知识与运算能力的考查.（3）数列知识：对数列性质的考查，如理科第4题；突出了数列与现实生活的联系，考查学生分析问题的能力，如理科第12题，难点较大.整体考查比较平稳，没有出现偏、怪的数列相关考点.（4）立体几何知识：对立体几何图形的认识与考查，如理科第7题，试题难度不大，比较常规；对简单几何体的体积知识的考查，如理科第16题，用到函数知识进行解决，体现了综合性，难度较大，立体几何解答题的考查较常规，如理科对二面角的考查.（5）解析几何知识：对圆锥曲线综合知识的考查，如理科第15题，难度偏大；解答题考查较为常规，考查直线与圆锥曲线的位置关系，难度中等，重视对学生运算能力的考查.【试卷解析】一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合A ={x |x <1}，B ={x |31x <}，则 A ．{|0}A B x x =<I B ．A B =R U C ．{|1}A B x x =>UD ．A B =∅I【答案】A2．如图，正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是A ．14 B ．π8 C ．12D ．π4【答案】B 【解析】试题分析：设正方形边长为a ，则圆的半径为2a ，则正方形的面积为2a ，圆的面积为24a π.由图形的对称性可知，太极图中黑白部分面积相等，即各占圆面积的一半.由几何概型概率的计算公式得，此点取自黑色部分的概率是221248a a ππ⋅=，选B. 秒杀解析：由题意可知，此点取自黑色部分的概率即为黑色部分面积占整个面积的比例，由图可知其概率1142p <<，故选B.【考点】几何概型【名师点睛】对于几何概型的计算，首先确定事件类型为几何概型并确定其几何区域（长度、面积、体积或时间），其次计算基本事件区域的几何度量和事件A 区域的几何度量，最后计算()P A . 3．设有下面四个命题1p ：若复数z 满足1z ∈R ，则z ∈R ；2p ：若复数z 满足2z ∈R ，则z ∈R ；3p ：若复数12,z z 满足12z z ∈R ，则12z z =；4p ：若复数z ∈R ，则z ∈R .其中的真命题为 A.13,p pB ．14,p pC ．23,p pD ．24,p p【答案】B4．记n S 为等差数列{}n a 的前n 项和．若4524a a +=，648S =，则{}n a 的公差为A ．1B ．2C ．4D ．8【答案】C 【解析】试题分析：设公差为d ，45111342724a a a d a d a d +=+++=+=，611656615482S a d a d ⨯=+=+=，联立112724,61548a d a d +=⎧⎨+=⎩解得4d =，故选C.秒杀解析：因为166346()3()482a a S a a +==+=，即3416a a +=，则4534()()24168a a a a +-+=-=，即5328a a d -==，解得4d =，故选C. 【考点】等差数列的基本量求解【名师点睛】求解等差数列基本量问题时，要多多使用等差数列的性质，如{}n a 为等差数列，若m n p q +=+，则m n p q a a a a +=+.5．函数()f x 在(,)-∞+∞单调递减，且为奇函数．若(11)f =-，则满足21()1x f --≤≤的x 的取值范围是 A ．[2,2]-B ．[1,1]-C ．[0,4]D ．[1,3]【答案】D6．621(1)(1)x x++展开式中2x 的系数为 A ．15B ．20C ．30D ．35【答案】C 【解析】试题分析：因为6662211(1)(1)1(1)(1)x x x x x++=⋅++⋅+，则6(1)x +展开式中含2x 的项为2226115C x x ⋅=，621(1)x x⋅+展开式中含2x 的项为44262115C x x x ⋅=，故2x 前系数为151530+=，选C. 【考点】二项式定理【名师点睛】对于两个二项式乘积的问题，第一个二项式中的每项乘以第二个二项式的每项，分析好2x 的项共有几项，进行加和.这类问题的易错点主要是未能分析清楚构成这一项的具体情况，尤其是两个二项式展开式中的r 不同.7．某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为A．10 B．12 C．14 D．16【答案】B8．右面程序框图是为了求出满足3n−2n>1000的最小偶数n，那么在和两个空白框中，可以分别填入A．A>1 000和n=n+1B．A>1 000和n=n+2C．A≤1 000和n=n+1D．A≤1 000和n=n+2【答案】D9．已知曲线C1：y=cos x，C2：y=sin (2x+2π3)，则下面结论正确的是A．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C2B．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C2C．把C1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C2D．把C1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C2 【答案】D 【解析】试题分析：因为12,C C 函数名不同，所以先将2C 利用诱导公式转化成与1C 相同的函数名，则222:sin(2)cos(2)cos(2)3326C y x x x ππππ=+=+-=+，则由1C 上各点的横坐标缩短到原来的12倍变为sin 2y x =，再将曲线向左平移12π个单位得到2C ，故选D. 【考点】三角函数图像变换.【名师点睛】对于三角函数图像变换问题，首先要将不同名函数转换成同名函数，利用诱导公式，需要重点记住sin cos(),cos sin()22ππαααα=-=+；另外，在进行图像变换时，提倡先平移后伸缩，而先伸缩后平移在考试中经常出现，无论哪种变换，记住每一个变换总是对变量x 而言.10．已知F 为抛物线C ：y 2=4x 的焦点，过F 作两条互相垂直的直线l 1，l 2，直线l 1与C 交于A 、B 两点，直线l 2与C 交于D 、E 两点，则|AB |+|DE |的最小值为 A ．16B ．14C ．12D ．10【答案】A2222||sin cos()2p pDE παα==-，所以22222211||||4()cos sin cos sin p p AB DE αααα+=+=+ 2222222211sin cos 4()(cos sin )4(2)4(22)16cos sin cos sin αααααααα=++=++≥⋅+=11．设x 、y 、z 为正数，且235x y z ==，则A ．2x <3y <5zB ．5z <2x <3yC ．3y <5z <2xD ．3y <2x <5z【答案】D12．几位大学生响应国家的创业号召，开发了一款应用软件.为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案：已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…，其中第一项是20，接下来的两项是20，21，再接下来的三项是20，21，22，依此类推.求满足如下条件的最小整数N ：N >100且该数列的前N 项和为2的整数幂.那么该款软件的激活码是 A ．440B ．330C ．220D ．110【答案】A【解析】试题分析：由题意得，数列如下：11,1,2,1,2,4,1,2,4,,2k -LL L则该数列的前(1)122k k k ++++=L 项和为 1(1)1(12)(122)222k k k k S k ++⎛⎫=+++++++=-- ⎪⎝⎭L L 要使(1)1002k k +>，有14k ≥，此时122k k ++<，所以2k +是之后的等比数列11,2,,2k +L 的部分和，即1212221t t k -+=+++=-L ，所以2314tk =-≥，则5t ≥，此时52329k =-=， 对应满足的最小条件为293054402N ⨯=+=，故选A. 【考点】等差数列、等比数列的求和.【名师点睛】本题非常巧妙的将实际问题和数列融合在一起，首先需要读懂题目所表达的具体含义，以及观察所给定数列的特征，进而判断出该数列的通项和求和.另外，本题的难点在于数列里面套数列，第一个数列的和又作为下一个数列的通项，而且最后几项并不能放在一个数列中，需要进行判断. 二、填空题：本题共4小题，每小题5分，共20分.13．已知向量a ，b 的夹角为60°，|a |=2，|b |=1，则| a +2 b |= . 【答案】2314．设x，y满足约束条件2121x yx yx y+≤⎧⎪+≥-⎨⎪-≤⎩，则32z x y=-的最小值为.【答案】5-15．已知双曲线C：22221x ya b-=（a>0，b>0）的右顶点为A，以A为圆心，b为半径作圆A，圆A与双曲线C 的一条渐近线交于M、N两点.若∠MAN=60°，则C的离心率为________.23【考点】双曲线的简单性质.【名师点睛】双曲线渐近线是其独有的性质，所以有关渐近线问题受到出题者的青睐.做好这一类问题要抓住以下重点：①求解渐近线，直接把双曲线后面的1换成0即可；②双曲线的焦点到渐近线的距离是b；③双曲线的顶点到渐近线的距离是abc.16．如图，圆形纸片的圆心为O，半径为5 cm，该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形.沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D、E、F重合，得到三棱锥.当△ABC的边长变化时，所得三棱锥体积（单位：cm3）的最大值为_______.【答案】415【考点】简单几何体的体积【名师点睛】对于三棱锥最值问题，肯定需要用到函数的思想进行解决，本题解决的关键是设好未知量，利用图形特征表示出三棱锥体积.当体积中的变量最高次是2次时可以利用二次函数的性质进行解决，当变量是高次时需要用到求导得方式进行解决.三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答. （一）必考题：共60分. 17．（12分）△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知△ABC 的面积为23sin a A（1）求sin B sin C ;（2）若6cos B cos C =1，a =3，求△ABC 的周长.【考点】三角函数及其变换.【名师点睛】在处理解三角形问题时，要注意抓住题目所给的条件，当题设中给定三角形的面积，可以使用面积公式建立等式，再将所有边的关系转化为角的关系，有时需将角的关系转化为边的关系；解三角形问题常见的一种考题是“已知一条边的长度和它所对的角，求面积或周长的取值范围”或者“已知一条边的长度和它所对的角，再有另外一个条件，求面积或周长的值”，这类问题通法思路是：全部转化为角的关系，建立函数关系式，如sin()y A x b ωϕ=++，从而求出范围，或利用余弦定理以及基本不等式求范围；求具体的值直接利用余弦定理和给定条件即可. 18.（12分）如图，在四棱锥P-ABCD 中，AB//CD ，且90BAP CDP ∠=∠=o .（1）证明：平面PAB ⊥平面PAD ；（2）若PA =PD =AB =DC ，90APD ∠=o ，求二面角A -PB -C 的余弦值.则3cos ,||||3⋅==-<>n m n m n m ， 所以二面角A PB C --的余弦值为33-. 【考点】面面垂直的证明，二面角平面角的求解【名师点睛】高考对空间向量与立体几何的考查主要体现在以下几个方面：①求异面直线所成的角，关键是转化为两直线的方向向量的夹角；②求直线与平面所成的角，关键是转化直线的方向向量和平面的法向量的夹角；③求二面角，关键是转化为两平面的法向量的夹角.建立空间直角坐标系和表示出所需点的坐标是解题的关键. 19．（12分）为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸（单位：cm ）．根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布2(,)N μσ．（1）假设生产状态正常，记X 表示一天内抽取的16个零件中其尺寸在(3,3)μσμσ-+之外的零件数，求(1)P X ≥及X 的数学期望；（2）一天内抽检零件中，如果出现了尺寸在(3,3)μσμσ-+之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．（ⅰ）试说明上述监控生产过程方法的合理性； （ⅱ）下面是检验员在一天内抽取的16个零件的尺寸：9.95 10.12 9.969.96 10.01 9.92 9.98 10.04 10.269.9110.1310.029.2210.0410.059.95经计算得16119.9716i i x x ===∑，161622221111()(16)0.2121616i ii i s x x x x ===-=-≈∑∑，其中i x 为抽取的第i 个零件的尺寸，1,2,,16i =⋅⋅⋅．用样本平均数x 作为μ的估计值ˆμ，用样本标准差s 作为σ的估计值ˆσ，利用估计值判断是否需对当天的生产过程进行检查？剔除ˆˆˆˆ(3,3)μσμσ-+之外的数据，用剩下的数据估计μ和σ（精确到0.01）． 附：若随机变量Z 服从正态分布2(,)N μσ，则(33)0.997 4P Z μσμσ-<<+=，160.997 40.959 2=，0.0080.09≈．试题解析：（1）抽取的一个零件的尺寸在(3,3)μσμσ-+之内的概率为0.9974，从而零件的尺寸在(3,3)μσμσ-+之外的概率为0.0026，故~(16,0.0026)X B .因此(1)1(0)10.99740.0408P X P X ≥=-==-=.X 的数学期望为160.00260.0416EX =⨯=.20.（12分）已知椭圆C ：2222=1x y a b+（a >b >0），四点P 1（1,1），P 2（0,1），P 3（–1，32），P 4（1，32）中恰有三点在椭圆C 上. （1）求C 的方程；（2）设直线l 不经过P 2点且与C 相交于A ，B 两点.若直线P 2A 与直线P 2B 的斜率的和为–1，证明：l 过定点.（2）设直线P 2A 与直线P 2B 的斜率分别为k 1，k 2，如果l 与x 轴垂直，设l ：x =t ，由题设知0t ≠，且||2t <，可得A ，B 的坐标分别为（t ，24t -，（t ，24t -）. 则221242421t t k k ---++==-，得2t =，不符合题设. 从而可设l ：y kx m =+（1m ≠）.将y kx m =+代入2214x y +=得222(41)8440k x kmx m +++-=由题设可知22=16(41)0k m ∆-+>.设A （x 1，y 1），B （x 2，y 2），则x 1+x 2=2841kmk -+，x 1x 2=224441m k -+.而12121211y y k k x x --+=+121211kx m kx m x x +-+-=+ 1212122(1)()kx x m x x x x +-+=.由题设121k k +=-，故1212(21)(1)()0k x x m x x ++-+=.即222448(21)(1)04141m kmk m k k --+⋅+-⋅=++.解得12m k +=-. 当且仅当1m >-时，0∆>，欲使l ：12m y x m +=-+，即11(2)2m y x ++=--， 所以l 过定点（2，1-）【考点】椭圆的标准方程，直线与圆锥曲线的位置关系.【名师点睛】椭圆的对称性是椭圆的一个重要性质，判断点是否在椭圆上，可以通过这一方法进行判断；证明直线过定点的关键是设出直线方程，通过一定关系转化，找出两个参数之间的关系式，从而可以判断过定点情况.另外，在设直线方程之前，若题设中为告知，则一定要讨论直线斜率不存在和存在情况，接着通法是联立方程组，求判别式、韦达定理，根据题设关系进行化简. 21.（12分）已知函数2()(2)x xf x ae a e x =+--.（1）讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围.（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分. 22．[选修4―4：坐标系与参数方程]（10分）在直角坐标系xOy 中，曲线C 的参数方程为3cos ,sin ,x y θθ=⎧⎨=⎩（θ为参数），直线l 的参数方程为4,1,x a t t y t =+⎧⎨=-⎩（为参数）. （1）若a =−1，求C 与l 的交点坐标；（2）若C 上的点到l 17 a.【解析】试题分析：（1）先将曲线C 和直线l 化成普通方程，然后联立求出交点坐标；（2）直线l 的普通方程为440x y a +--=，设C 上的点(3cos ,sin )θθ，l 的距离为17d =.对a 进行讨23．[选修4—5：不等式选讲]（10分）已知函数f （x ）=–x 2+ax +4，g (x )=│x +1│+│x –1│.（1）当a =1时，求不等式f （x ）≥g （x ）的解集；（2）若不等式f （x ）≥g （x ）的解集包含[–1，1]，求a 的取值范围.【解析】试题分析：（1）将1a =代入，不等式()()f x g x ≥等价于2|1||1|40x x x x -+++--≤，对x 按1x <-，11x -≤≤，1x >讨论，得出最值的解集；（2）当[1,1]x ∈-时，()2g x =.若()()f x g x ≥的解集包含[1,1]-，。

的关系： r R2 d 2
5.旋转体
一条平面曲线绕着它所在的平面内的一条定直线旋转所形成的曲面叫做旋转面；该定直
线叫做旋转体的轴；封闭的旋转面围成的几何体叫做旋转体．
6.简单组合体
常见的组合体有三种：多面体与多面体的组合；
多面体与旋转体的组合；旋转体与旋转体的组合.其基
本形式实质上有两种：一种是由简单几何体拼接而成
叫底面 O 的半径，线段 SO 是圆锥的高．
S 顶点
(2)圆的简单性质
①平行于底面的截面都是圆； ②过轴的截面是全等的等腰三角形；
侧面
轴 母线
③圆锥的侧面展开图是扇形． 3.圆台 (1)圆台的定义
O B
A 底面
以直角梯形垂直于底边的腰所在的直线为旋转轴，旋转一周所形成的集合体叫做圆台．
如右图，旋转轴叫圆台的轴（即上、下底面圆心的连线）；在轴上这条边
4.球
(1)球的定义
半圆绕着它的直径所在的直线旋转一周而形成的几何体叫做球． 如右图，半圆的圆心
叫球的球心；半圆的半径叫做球的半径； 半圆的直径叫做球的直径；半圆弧旋转而成的曲面叫做球面．
(2)球的简单性质
A 直径
用一个平面去截球，截面是圆面，而且球心和截面圆心的连线
O
垂直于截面，球心到截面的距离 d 与球的半径 R 及截面圆的半径 r 有下面 球面
4．棱台和圆台的体积： (1) 如 果 台 体 的 上 、 下 底 面 面 积 分 别 为 S′ 、 S ， 高 是 h ， 则 它 的 体 积 是 V 台 体 ＝
㤶(h + h' + hh').
(2)如果圆台的上、下底面半径分别是 r′、r，高是 h，则它的体积是 V 圆台＝ 㤶( + ' +