《几种常见的几何体》随堂练习

7.1 几种常见的几何体1.半圆面绕它的直径旋转一周形成.2.一个正方体有个面.3.“枪挑一条线,棍扫一大片”这个现象说明: .4.根据几何体的特征,填写它们的名称.(1) :上下两个底面是大小相同的圆,侧面是由长方形围成的.(2) :6个面都是长方形.(3) :6个面都是正方形.(4) :上下底面是形状大小相同的多边形,侧面是长方形.(5) :下底面是圆,上方有一个顶点,侧面是由扇形围成的.(6) :下底面是多边形,上方有一个顶点.5.在小学里,我们曾学过圆柱的体积计算公式:V=πR2h(R是圆柱底面半径,h为圆柱的高).现有一个长方形,长为2cm,宽为1cm,分别以它的两边所在的直线为轴旋转一周,得到的几何体的体积分别是多少?它们之间有何关系?6.18世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察如图所示的几种简单多面体模型,解答下列问题:(1)根据上面多面体模型,完成表格中的空格:你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是. (2)一个多面体的面数与顶点数相等,有12条棱,这个多面体是面体参考答案1.【解析】半圆面绕它的直径旋转360度形成球.答案：球2.【解析】正方体有6个面.答案：63.【解析】“枪挑一条线,棍扫一大片”这个现象说明:点动成线,线动成面.答案：点动成线,线动成面4.【解析】由几何体的特征可知,几何体的名称依次为:(1)圆柱.(2)长方体.(3)正方体.(4)棱柱.(5)圆锥.(6)棱锥.5.【解析】(1)当以长方形的宽所在的直线为轴旋转时,如图①,得到的圆柱的底面半径为2cm,高为1cm.所以其体积V1=π×22×1=4π(cm3).(2)当以长方形的长所在的直线为轴旋转时,如图②,得到的圆柱的底面半径为1cm,高为2cm,所以其体积V2=π×12×2=2π(cm3).因此,得到的两个几何体的体积之间的关系为V1=2V2.6.【解析】(1)四面体的棱数为6;正八面体的顶点数为6;关系式为:V+F-E=2.(2)由题意得:V=F,所以F+F-12=2,解得F=7.7.2.1 直棱柱的侧面展开图1.下列几何体中，直棱柱的是。

北航附中高二简单几何体综合练习 2011-9-16班级________ 姓名_________1. 点1O 为圆锥的高中靠近顶点的一个三等分点，过1O 与地面平行的截面面积是底面面积的 （ ）A ．13B ．23C ．14D ．192. 圆柱的轴截面是边长为5cm 的正方形ABCD ，则圆柱侧面上从A 到C 的最短距离是 （ ）A ．10cmB cmC ．cmD ． cm3. 若圆锥的轴截面是一个面积为2的正三角形，那么其内接球的半径是（ ）A ．4π cmB ．6 cmC cmD cm4. 已知半径为5的球的两个平行截面的周长非别为6π和8π，则两个平行截面间的距离是 （ ）A ．1B ．2C ．1或7D ．2或65. 棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上，E 、F 分别是棱1AA 、1DD 的中点，则直线EF 被球O 截得的线段长为 （ ）A ．B ．1C ．1+ D6. 顶点在同一个球面上的正四棱柱1111ABCD A B C D -中，AB=1，1AA =，则A 、C 两点间的球面距离为 （ ）A ．4πB ．2π C ．4 D ．2 7. 下列命题中真命题的个数是 （ ） ① 正方形的平行投影一定是菱形 ② 平行四边形的平行投影一定是平行四边形 ③ 三角形的平行投影一定是三角形A ．0B ．1C ．2D ．48. 如果图形所在的平面不平行于投射线，那么下列说法正确的是 （ ）A ．矩形的平行投影一定是矩形 B. 梯形的平行投影一定是梯形C ．正方形的平行投影一定是矩形 D. 正方形的平行投影一定是菱形9. 利用斜二测画法得到的① 三角形的直观图是三角形； ② 平行四边形的直观图是平行四边形； ③ 正方形的直观图是正方形； ④ 菱形的直观图是菱形；以上结论正确的是 （ ）A ．①②B ．①C ．③④D ．①②③④10. 如图所示是水平放置的三角形ABC 的直观图， '''//A B y 轴，则△ABC 是 （ ） A ．等边三角形 B ．等腰三角形 C ．直角三角形 D ．等腰直角三角形 11. 将一个边长为a 的正方体，切成27个全等的小正方体，则其表面积增加了（ ）A ．26aB ．212aC ．218aD ．224a12. 圆台的上、下底面半径和高的比为1:4:4，母线长为10，则圆台的侧面积为（ ）A ．81πB ．100πC ．14πD ．169π13. 把底面半径为8cm 的圆锥，放倒在平面内，使圆锥在此平面内绕圆锥顶点S滚动，当这个圆锥在平面内转回到原位置时，圆锥本身滚动了2.5周，则圆 锥的母线长为_____________，表面积等于___________.14. 一个正方体内接于一个球，过球心作一截面，如图所示，则截面的可能图形是______________① ② ③ ④15. 已知一个圆柱的侧面展开图是一个正方形，则这个圆柱的全面积和侧面积的比是_______________ .16. 一个直角梯形的上、下底面和高的比值为1:2，求它旋转后的圆台的上底面积、下底面面积和侧面积的比为______________.17. 两个球的表面积之差为48π，它们的大圆周长之和为12π，则这两个球的半径之差为_______________ .18. 一个圆锥的主视图和左视图均为正三角形，其面积为S ，则圆锥侧面积为___________19. 棱长为a 的正四面体的外接球的半径为________，内切球的半径为_______.20. 一个正三棱锥的底面边长为6，那么这个三棱锥的体积是____21. 三棱柱111ABC A B C -中，若E 、F 分别为AB 、AC 的中点，平面11EB C F 将三棱柱分成体积为12V V 、的两部分，那么12V V :=___________22. 一个圆柱和一个圆锥的轴截面分别是边长为a 的正方形和正三角形，则圆柱和圆锥的表面积之比是__________23. 已知圆锥的底面半径为r ，高为h ，正方体1111ABCD A B C D -内接于圆锥，求这个正方体的棱长.。

11．线动成面
【分析】利用雨刷可看成线，扇面是面，即可求出答案．
【详解】汽车的雨刷在挡风玻璃上画出一个扇面，这说明线动成面的数学原理．
故答案为：线动成面．
【点睛】本题考查了点，线，面、体，此题较简单，解题时要灵活应用点、线、面、体之间的关系．
12．②
【分析】易得此几何体为两个底面相同且相连的圆锥的组合体，主视图是从几何体正面看到的图形．
8．由4个面围成；面与面相交形成6条线，直线有5条，曲线有1条．
【分析】由题意直接根据立体图形的基本知识结合图形进行分析即可得出答案．
【详解】解：由图可知，该几何体由4个面围成；
面与面相交形成6条线，直线有5条，曲线有1条．
【点睛】本题考查认识立体图形的知识，比较简单，注意基本知识的掌握．
9．见解析．
12．将图所示的Rt△ABC绕AB旋转一周所得的几何体的主视图是图中的________（只填序号）．
参考答案：
1．C
【分析】观察截面形状可发现，长方体内部的圆自上而下由大圆逐渐变成小圆、点，符合圆锥截面的性质．
【详解】解：观察截面形状可知，这个长方体的内部构造是长方体中间有一圆锥状空洞，
故选：C．
【点睛】本题考查了截一个几何体，解答的关键是熟悉常见的几何体的截面，由截面的形状想象复杂几何体的组成．
【详解】解：Rt△ABC绕斜边AB旋转一周所得的几何体是两个底面相等相连的圆锥，圆锥的主视图是等腰三角形，所以该几何体的左视图是两个底边相等的等腰三角形相连，并且上面的等腰三角形较大，故为图②．
故答案为②．
【点睛】本题考查了空间想象能力及几何体的三视图；发挥空间想象能力，确定旋转一周所得的几何体形状是关键．
【分析】根据生活中常见的几何体的特征进行求解即可得到答案．

2017-2018学年七年级数学上册综合训练几何体的展开与折叠随堂测试（新版）新人教版
编辑整理：
尊敬的读者朋友们：
这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2017-2018学年七年级数学上册综合训练几何体的展开与折叠随堂测试（新版）新人教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2017-2018学年七年级数学上册综合训练几何体的展开与折叠随堂测试（新版）新人教版的全部内容。

几何体的展开与折叠（随堂测试)
1.如图是正方体的一个表面展开图,若将它折叠成原来的正方体，则与
边c 重合的是边，与边l 重合的是边, 与边a 重合的是边．
g
f
l
a
2.小明用如图所示的硬纸片折成了一个正方体盒子,里面装了一瓶墨
水，只凭观察，选出墨水在哪个盒子中（）
A．B．C．D．
3.7 个棱长为 1 的正方体组成如图所示的几何体．
(1）画出该几何体的三视图；
（2)该几何体的体积是立方单位,表面积是平方
单位．
i
j k
e
d
c
b
m
n
【参考答案】1
．b，g，f 2．B
3. （1)略；（2）7，28。

2019-2020学年度初中九年级下册数学第7章空间图形的初步认识7.1几种常见的几何体青岛版课后练习八十一第1题【单选题】用一个平面去截一个长方体，截面不可能是( )A、梯形B、五边形C、六边形D、圆【答案】：【解析】：第2题【单选题】指出图中几何体截面的形状( )A、B、C、D、【答案】：【解析】：第3题【单选题】右图可以折叠成的几何体是( )A、三棱柱B、四棱柱C、圆柱D、圆锥【答案】：【解析】：第4题【单选题】用一个平面去截一个几何体，得到的截面是四边形，这个几何体可能是( )A、圆锥B、球体C、圆柱D、以上都有可能【答案】：【解析】：第5题【单选题】如图，用一平面竖直地去截放在桌面上的圆柱，下列结论正确的有( )个.① 截面呈正方形② AD∥BC，AB∥CD③ AB⊥BC，AD⊥AB ④ AD=BC，AB=CDA、一B、二C、三D、四【答案】：【解析】：第6题【单选题】如图，一个正方体截去一个角后，剩下的几何体面的个数和棱的条数分别为( )A、6，11B、7，11C、7，12D、6，12【答案】：【解析】：第7题【单选题】如图，图1是一个底面为正方形的直棱柱；现将图1切割成图2的几何体，则图2的俯视图是( )A、B、C、D、【答案】：【解析】：第8题【单选题】下列说法不正确的是( )A、球的截面一定是圆B、组成长方体的各个面中不可能有正方形C、从三个不同的方向看正方体，得到的都是正方形D、圆锥的截面可能是圆【答案】：【解析】：第9题【单选题】如图是一个几何体的三视图，则这个几何体的侧面积是【】A、18cm^2B、20cm^2C、（18+2）cm^2D、（18+4）cm^2【答案】：【解析】：第10题【单选题】若干个正方体形状的积木摆成如图所示的塔形，平放于桌面上，上面正方体的下底四个顶点是下面相邻正方体的上底各边中点，最下面的正方体棱长为1，如果塔形露在外面的面积超过7，则正方体的个数至少是( )A、2B、3C、4D、5【答案】：【解析】：第11题【填空题】用一个平面去截圆锥，截面______是三角形（填“可能”或“不可能”）．【答案】：【解析】：第12题【填空题】用一个平面截长方体、五棱柱、圆柱和圆锥，不能截出三角形的是______A、圆柱【答案】：【解析】：第13题【解答题】如图，截一个正方体，可以得到三角形，但要得到一个最大的等边三角形，你会切吗？你能说出你的切法吗？【答案】：【解析】：第14题【解答题】如图所示的正方体被竖直截取了一部分，求被截取的那一部分的体积．（棱柱的体积等于底面积乘高）【答案】：【解析】：第15题【解答题】如图，在平整的地面上，有若干个完全相同的棱长为10cm的小正方体堆成一个几何体．（1）这个几何体由个小正方体组成．（2）如果在这个几何体的表面喷上黄色的漆，则在所有的小正方体中，有? 个正方体只有一个面是黄色，有? 个正方体只有两个面是黄色，有? 个正方体只有三个面是黄色．（3）这个几何体喷漆的面积为? cm^2 ．? 【答案】：【解析】：。

基础巩固强化1.纸制的正方体的六个面根据其实际方位分别标记为上、下、东、南、西、北，现在沿该正方体的一些棱将正方体剪开，外面朝上展平，得到如图所示的平面图形，则标“△”的面的方位是( )A ．南B ．北C ．西D ．下[答案] A[解析] 将所给图形还原为正方体，如图所示，最上面为上，最右面为东，则前面为△，可知“△”的实际方位为南．2．一个球与一个正三棱柱的三个侧面和两个底面都相切，已知这个球的体积为32π3，那么这个三棱柱的体积是( )A ．963B ．483C ．243D ．16 3 [答案] B[解析] 已知正三棱柱的高为球的直径，底面正三角形的内切圆是球的大圆．设底面正三角形的边长为a ，球的半径为R ，则a ＝23R ，又43πR 3＝32π3，∴R ＝2，a ＝43，于是V ＝34a 2·2R ＝48 3.3．(2012·新课标全国，7)如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为( )A ．6B ．9C ．12D ．18[答案] B[解析] 由三视图知，该几何体是一个三棱锥，由俯视图知三棱锥的底面是等腰三角形，底边长为6，底边上的高为3，面积S ＝12×6×3＝9，由正视图和侧视图可知棱锥的高为3，∴体积V ＝13×9×3＝9.4．(文)若某空间几何体的三视图如图所示，则该几何体的体积是( )A ．2B ．1 C.23 D.13[答案] B[解析] 由几何体的三视图可知，该几何体是直三棱柱，其直观图如图所示，其体积为V ＝12×2×1×2＝1.(理)(2011·潍坊二检)如图是一个长方体截去一个角后所得多面体的三视图，则该多面体的体积为( )A.1423B.2843C.2803D.1403[答案] B [解析]截去一角在正视图中位于左侧上部，在侧视图中位于右侧上部，结合俯视图可知，截去的一角应位于几何体的上部左前方，可画出多面体的形状如图．这个多面体是由长方体截去一个正三棱锥而得到的，所以所求多面体的体积V ＝V 长方体－V 正三棱锥＝4×4×6－13×(12×2×2)×2＝2843.5．(文)一空间几何体的三视图如图所示，则该几何体的体积为( )A ．2π＋2 3B ．4π＋2 3C ．2π＋233 D ．4π＋233[答案] C[解析] 由几何体的三视图可知，该几何体是由一个底面直径和高都是2的圆柱和一个底面边长为2，侧棱长为2的正四棱锥叠放而成．故该几何体的体积为V ＝π×12×2＋13×(2)2×3＝2π＋233，故选C.[点评] 由三视图想象几何体的形状时，一要注意常见柱、锥、台的三视图结构特征，二要注意方位，三要注意细节．本题中正视图与侧视图都不变，若俯视图中把外部的圆改为正方形，则几何体就是上部为正四棱锥，下部为正四棱柱的组合体．(理)(2011·湖南文，4)设下图是某几何体的三视图，则该几何体的体积为( )A ．9π＋42B ．36π＋18 C.92π＋12 D.92π＋18[答案] D[解析] 由三视图可知，该几何体是一个球体和一个长方体的组合体．其中，V 球＝43π·(32)3＝9π2，V 长方体＝2×3×3＝18.所以V 总＝92π＋18.6.(2012·山西高考联合模拟)一个几何体是由若干个相同的正方体组成的，其正视图和侧视图如图所示，则这个几何体最多可由这样的正方体组成的个数为( )A ．12个B ．13个C ．14个D ．18个[答案] B[解析] 由正视图知该几何体有三列，左右两排都存在2层的情形，中间一排，只有一层，由侧视图知，该几何体有三行，前后两排都存在2层的情形，中间一排只有一层，因此此几何体最多可由13个小正方体组成，你能求出最少可由多少个小正方体构成吗？7．圆台的上、下底半径分别为2和4，母线长为4，则截得此圆台的圆锥侧面展开图的中心角为________．[答案] π[解析] 如图，设PD ＝x ，则24＝x x ＋4，∴x ＝4，∴θ＝48×2π＝π.8．一个底面半径为1，高为6的圆柱被一个平面截下一部分，如图(1)所示，截下部分的母线最大长度为2，最小长度为1，则截下部分的体积是________．[答案] 3π2[解析] 根据对称性把它补成如图(2)所示的圆柱，这个圆柱的高是3，体积是所求几何体体积的2倍，故所求的几何体的体积是12×π×12×3＝3π2.故填3π2.9．圆柱内切球的表面积为4π，则圆柱的表面积为________． [答案] 6π[解析] 设球半径为R (R >0)，则圆柱的底面半径为R ，高为2R ，由条件知，4πR 2＝4π，∴R ＝1.∴圆柱的表面积S ＝2π·R 2＋2πR ·2R ＝6πR 2＝6π.10．已知P 在矩形ABCD 的边DC 上，AB ＝2，BC ＝1，F 在AB 上且DF ⊥AP ，垂足为E ，将△ADP 沿AP 折起，使点D 位于D ′位置，连接D ′B 、D ′C 得四棱锥D ′－ABCP .(1)求证：D ′F ⊥AP ；(2)若PD ＝1，且平面D ′AP ⊥平面ABCP ，求四棱锥D ′－ABCP 的体积．[解析] (1)∵AP ⊥D ′E ，AP ⊥EF ，D ′E ∩EF ＝E ， ∴AP ⊥平面D ′EF ，∴AP ⊥D ′F .(2)∵PD ＝1，∴四边形ADPF 是边长为1的正方形， ∴D ′E ＝DE ＝EF ＝22，∵平面D ′AP ⊥平面ABCP ，D ′E ⊥AP ，∴D ′E ⊥平面ABCP ， ∵S 梯形ABCP ＝12×(1＋2)×1＝32，∴V D ′－ABCP ＝13×D ′E ×S 梯形ABCP ＝24.能力拓展提升11.如图，正方体ABCD －A 1B 1C 1D 1的棱长为2.动点E ，F 在棱A 1B 1上，点Q 是棱CD 的中点，动点P 在棱AD 上．若EF ＝1，DP ＝x ，A 1E ＝y (x ，y 大于零)，则三棱锥P －EFQ 的体积( )A ．与x ，y 都有关B ．与x ，y 都无关C ．与x 有关，与y 无关D ．与y 有关，与x 无关[答案] C[解析] 设P 到平面EFQ 的距离为h ，则V P －EFQ ＝13×S △EFQ ·h ，由于Q 为CD 的中点，∴点Q 到直线EF 的距离为定值2，又EF ＝1，∴S △EFQ 为定值，而P 点到平面EFQ 的距离，即P 点到平面A 1B 1CD 的距离，显然与x 有关与y 无关，故选C.12．(2011·陕西文，5)某几何体的三视图如图所示，则它的体积为( )A ．8－2π3B ．8－π3C ．8－2πD.2π3[答案] A[解析] 由三视图知，原几何体为如图所示一正方体挖去一个与正方体等高底面是正方形的内切圆的圆锥，则其体积为V ＝23－13π×12×2＝8－2π3.故选A. 13．(2011·东北三校)一个几何体的三视图及部分数据如图所示，侧视图为等腰三角形，俯视图为正方形，则这个几何体的体积等于( )A.13B.23C.156D.6224[答案] A[解析] 由三视图知，这是一个四棱锥，其底面为正方形，一条侧棱垂直于底面其长度为2，底面正方形对角线长为1，∴边长为22，体积V ＝13×(22)2×2＝13.14．(文)一等边圆柱(轴截面是正方形的圆柱)的表面积为24π，一圆锥与此圆柱一个底面重合，顶点在另一个底面上，则此圆锥的表面积为________．[答案] 4(5＋1)π[解析] 设圆柱底半径为R ，则2πR 2＋2πR ·2R ＝24π，∴R ＝2， ∴圆锥的底半径为R ＝2，高为4，母线长l ＝22＋42＝25，∴圆锥的表面积S ＝πR 2＋πRl ＝4π＋45π＝4(5＋1)π.(理)圆锥的高为4，侧面积为15π，其内切球的表面积为________．[答案] 9π[解析]设圆锥底面半径为r (r >0)，则母线长l ＝16＋r 2，由πrl ＝15π得r ·16＋r 2＝15，解之得r ＝3，∴l ＝5.设内切球半径为R ，作出圆锥的轴截面如图，则BD ＝BO 1＝3，PD ＝5－3＝2，PO ＝4－R ，∵OD ⊥PB ，∴R 2＋4＝(4－R )2，∴R ＝32， ∴球的表面积S ＝4πR 2＝9π.15．(文)(2011·安徽省淮南市模拟)如图是以正方形ABCD为底面的正四棱柱被一平面所截得的几何体，四边形EFGH为截面，且AB＝BC＝2，AE＝1，BF＝DH＝2，CG＝3.(1)证明：截面四边形EFGH是菱形；(2)求几何体C－EFGH的体积．[解析](1)证明：因为平面ABFE∥平面CDHG，且平面EFGH分别交平面ABFE、平面CDHG于直线EF、GH，所以EF∥GH.同理，FG∥EH.因此，四边形EFGH为平行四边形．因为BD⊥AC，而AC为EG在底面ABCD上的射影，所以EG⊥BD.因为BF綊DH，所以FH∥BD.因此，FH⊥EG.所以四边形EFGH是菱形．(2)解：连接CE、CF、CH、CA，则V C－EFGH＝V－V C－ABFE－V C－ADHE，其中V是几何体的体积，∵AE＝1，BF＝DH＝2，CG＝3且几何体是以正方形ABCD为底面的正四棱柱的一部分，所以该几何体的体积为V＝(2)2×2＝4，V C－ABFE＝13×S四边形ABFE×BC＝13×12(AE＋BF)×AB×BC＝16×(1＋2)×2×2＝1.同理，得V C－ADHE＝1，所以，V C－EFGH＝V－V C－ABFE－V C－ADHE＝4－1－1＝2，即几何体C－EFGH的体积为2.(理)(2011·江西文)如图在△ABC中，∠B＝π2，AB＝BC＝2，P为AB边上一动点，PD∥BC交AC于点D，现将△PDA沿PD翻折至△PDA ′，使平面PDA ′⊥平面PBCD .(1)当棱锥A ′－PBCD 的体积最大时，求P A 的长；(2)若点P 为AB 的中点，E 为A ′C 的中点，求证：A ′B ⊥DE .[解析] (1)令P A ＝x (0<x <2)，则A ′P ＝PD ＝x ，BP ＝2－x ，因为A ′P ⊥PD 且平面A ′PD ⊥平面PBCD ，故A ′P ⊥平面PBCD .所以V A ′－PBCD ＝13Sh ＝16(2－x )(2＋x )x ＝16(4x－x 3)．令f (x )＝16(4x －x 3)，由f ′(x )＝16(4－3x 2)＝0，得x ＝23 3.当x ∈(0，233)时，f ′(x )>0，f (x )单调递增；当x ∈(233，2)时，f ′(x )<0，f (x )单调递减．所以，当x ＝233时，f (x )取得最大值，即当V A ′－PBCD 最大时，P A ＝233.(2)设F 为A ′B 的中点，连接PF ，FE ，则有EF 綊12BC ，PD 綊12BC ，∴EF 綊PD ，∴四边形EFPD 为平行四边形，∴DE ∥PF .又A ′P ＝PB ，所以PF ⊥A ′B ，故DE ⊥A ′B .16．(2012·新课标全国文，19)如图，在三棱柱ABC －A 1B 1C 1中，侧棱垂直于底面，∠ACB ＝90°，AC ＝BC ＝12AA 1，D 是棱AA 1的中点．(1)证明：平面BDC 1⊥平面BDC ；(2)平面BDC 1分此棱柱为两部分，求这两部分体积的比．[分析] (1)证两个平面垂直，可转化为在其中一个平面内找到一条直线与另一个平面垂直；(2)平面BDC1分棱柱成两部分，下面部分B－ADC1C为四棱锥，可直接求体积，上面部分可用间接法求得体积，从而确定两部分体积之比．[解析](1)由题设知BC⊥CC1，BC⊥AC，CC1∩AC＝C，所以BC⊥平面ACC1A1.又DC1⊂平面ACC1A1，所以DC1⊥BC.由题设知∠A1DC1＝∠ADC＝45°，所以∠CDC1＝90°，即DC1⊥DC.又DC∩BC＝C，所以DC1⊥平面BDC.又DC1⊂平面BDC1，故平面BDC1⊥平面BDC.(2)设棱锥B－DACC1的体积为V1，AC＝1.由题意得，V1＝13×1＋22×1×1＝12.又三棱柱ABC－A1B1C1的体积V＝1，所以(V－V1) V1＝1 1.故平面BDC1分此棱柱所得两部分体积的比为1 1.[点评]本题考查线面的位置关系及几何体体积的求法．求解几何体的体积时，若遇不规则的几何体时，经常采用割补法和间接法求其体积．1．用单位正方体搭几何体，使它的正视图和俯视图如图所示，则符合条件的几何体体积的最小值与最大值分别是()A．9,13 B．7,16C．10,15 D．10,16[答案] D[解析]由俯视图知底层有七个小正方体，结合正视图知，最左边一列，最多都是三层，最少只有一行是三层，故左边一列最多9个、最少5个；中间一列最多都是二层有6个，最少只有一行二层，共4个；右边一列只一层一行，故最多9＋6＋1＝16个，最少5＋4＋1＝10个．2．一个几何体的三视图如图，该几何体的表面积为()A．280 B．292C．360 D．372[答案] C[解析]由三视图知该几何体是两个长方体的组合体，上面的长方体的表面积为(6×8)×2＋(8×2)×2＋6×2＝140.下面的长方体的表面积为(10×8)×2＋(10×2)×2＋(8×2)×2－6×2＝220.故表面积为140＋220＝360.选C.3．如图，已知在多面体ABC－DEFG中，AB、AC、AD两两互相垂直，平面ABC∥平面DEFG，平面BEF∥平面ADGC，AB＝AD ＝DG＝2，AC＝EF＝1，则该多面体的体积为()A．2B．4C．6D．8[答案] B[解析] 补成长方体ABMC －DEFN 并连接CF ，易知三棱锥F －BCM 与三棱锥C －FGN 的体积相等，故几何体体积等于长方体的体积4.故选B.[点评] 1.也可以用平面BCE 将此几何体分割为两部分，设平面BCE 与DG 的交点为H ，则ABC －DEH 为一个直三棱柱，由条件易证EH 綊FG 綊BC ，平面BEF ∥平面CHG ，且△BEF △CHG ，∴几何体BEF －CHG 是一个斜三棱柱，这两个三棱柱的底面都是直角边长为2和1的直角三角形，高都是2，∴体积为4.2．如图(2)，几何体ABC －DEFG 也可看作棱长为2的正方体中，取棱AN 、EK 的中点C 、F ，作平面BCGF 将正方体切割成两部分，易证这两部分形状相同，体积相等，∴V ABC －DEFG ＝12×23＝4.4．在一个倒置的正三棱锥容器内放入一个钢球，钢球恰与棱锥的四个面都接触，过棱锥的一条侧棱和高作截面，正确的截面图形是( )[答案] B[解析]球与正三棱锥底面的切点为底面正三角形的中心，故在截面图中，此切点将截面三角形的这一条边(底面正三角形的高)分为1 2两部分，截面过三棱锥的高和一条侧棱，故截面图中球大圆与侧棱外离且圆心在三角形的高(即棱锥的高)上，这条高应是顶点与底面中心的连线段，故选B.5．四棱锥P－ABCD的底面为正方形，侧面P AD为等边三角形，且侧面P AD⊥底面ABCD，点M在底面正方形ABCD内(含边界)运动，且满足MP＝MC，则点M在正方形ABCD内的轨迹一定是()[答案] B[解析]由满足条件MP＝MC，可知点M应在线段PC的所有中垂线构成的平面α内，又点M在正方形ABCD内，所以点M的轨迹平面α与平面ABCD的交线，则必为直线，故D不正确．又BP不等于BC，故A不正确．由题意知PD＝DC，所以D点在M的轨迹上．设E、F分别为AB、AD的中点，连接PF、EF，则PF⊥EF.设AB＝2，则PF＝3，EF＝2，所以PE＝ 5.在Rt△CBE中，BC＝2，BE＝1，则CE＝5＝EP，所以AB边中点E也在点M的轨迹上，则点M的轨迹为线段DE.6．(2012·吉林省实验中学模拟)一个几何体的三视图如图所示，其中俯视图与侧视图均为半径是 1 的圆，则这个几何体的体积是( )A.4π3B ．π C.2π3D.π3[答案] B[解析] 由三视图知，该几何体是半径为1的球去掉了半球的一半，故几何体是34个球，体积V ＝34×(43π·13)＝π.7．(2012·河南六市联考)如图，已知四棱锥P－ABCD中，底面ABCD是直角梯形，AB∥DC，∠ABC＝45°，DC＝1，AB＝2，P A⊥平面ABCD，P A＝1.(1)求证：AB∥平面PCD；(2)求证：BC⊥平面P AC；(3)若M是PC的中点，求三棱锥M－ACD的体积．[解析](1)由已知底面ABCD是直角梯形，AB∥DC，又AB⊄平面PCD，CD⊂平面PCD，∴AB∥平面PCD.(2)在直角梯形ABCD中，过C作CE⊥AB于点E，则四边形ADCE 为矩形，∴AE＝DC＝1又AB＝2，∴BE＝1，在Rt△BEC中，∠ABC＝45°，∴CE＝BE＝1，CB＝2，∴AD＝CE＝1，则AC＝AD2＋CD2＝2，AC2＋BC2＝AB2，∴BC⊥AC.又P A⊥平面ABCD，∴P A⊥BC，又P A∩AC＝A，∴BC⊥平面P AC.(2)∵M是PC中点，∴M到平面ADC的距离是P到平面ADC距离的一半．∴V M－ACD＝13S△ACD·(12P A)＝13×(12×1×1)×12＝112.。

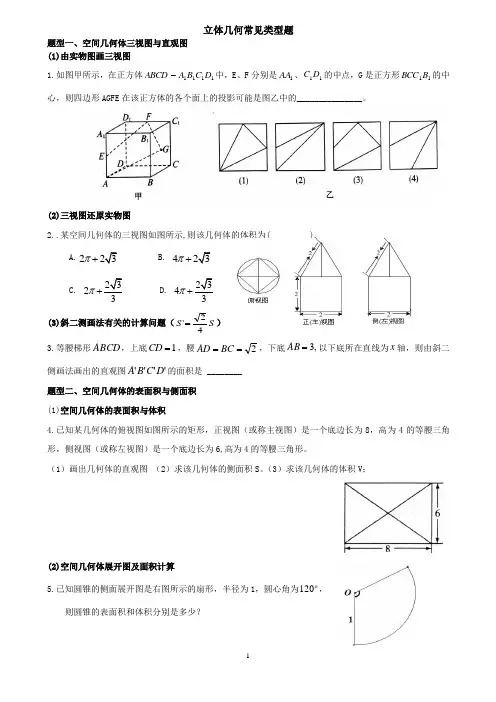
立体几何常见类型题题型一、空间几何体三视图与直观图 (1)由实物图画三视图1.如图甲所示，在正方体1111D C B A ABCD -中，E 、F 分别是1AA 、11D C 的中点，G 是正方形11B BCC 的中心，则四边形AGFE 在该正方体的各个面上的投影可能是图乙中的_______________。

(2)三视图还原实物图2..某空间几何体的三视图如图所示,则该几何体的体积为( ). A.223π+ B. 423π+ C. 2323π+D. 2343π+ (3)斜二测画法有关的计算问题（S S 42'=） 3.等腰梯形ABCD ，上底1=CD ，腰2==BC AD ，下底,3=AB 以下底所在直线为x 轴，则由斜二侧画法画出的直观图''''D C B A 的面积是 ________ 题型二、空间几何体的表面积与侧面积 (1)空间几何体的表面积与体积4.已知某几何体的俯视图如图所示的矩形，正视图（或称主视图）是一个底边长为8，高为4的等腰三角形，侧视图（或称左视图）是一个底边长为6,高为4的等腰三角形。

（1）画出几何体的直观图 （2）求该几何体的侧面积S 。

（3）求该几何体的体积V ；(2)空间几何体展开图及面积计算5.已知圆锥的侧面展开图是右图所示的扇形，半径为1，圆心角为ο120， 则圆锥的表面积和体积分别是多少？(3)割补法和等体积法求体积6.如图，正方体''''D C B A ABCD -的棱长为2，E 是AB 的中点， 求:(1)三棱锥EC A B '-的体积V . (2)求B 点到平面EC A '的距离。

类型三.证明线面平行1.在正方体1111ABCD A B C D -中，E 是1AA 的中点， 求证： 1//A C 平面BDE 。

2.正方体1111ABCD A B C D -，O 是底ABCD 对角线的交点. 求证： C1O ∥面11AB D ； 考点：法1：利用平行四边形 法2：利用面面平行的性质类型四.证明面面平行1. 正方体ABCD —A 1B 1C 1D 1中．(1)求证：平面A 1BD ∥平面B 1D 1C ； (2)若E 、F 分别是AA 1，CC 1的中点，求证：平面EB 1D 1∥平面FBD ．2.在正方体1111ABCD A B C D -中，E 、F 、G分别是AB 、AD 、11C D 的中点.求证：平面1D EF ∥平面BDG .A ED 1CB 1DCBAD 1ODBAC 1B 1A 1C A 1AB 1C 1 CD 1D G EF类型五.证明线面垂直1. 正方体''''ABCD A B C D -中，求证：（1）''AC B D DB ⊥平面；（2）''BD ACB ⊥平面. （考点：线面垂直的判定定理）2. ,在正方体1111ABCD A B C D -中，M 为1CC 的中点，AC 交BD 于点O ，求证：1AO ⊥平面MBD ． 考点：线面垂直的判定，运用勾股定理寻求线线垂直3. 已知ABC ∆中90ACB ∠=o ,SA ⊥面ABC ,AD SC ⊥, 求证：AD ⊥面SBC ．4. 四面体ABCD 中，,,AC BD E F =分别为,AD BC 的中点，且22EF AC =，90BDC ∠=o ，求证：BD ⊥平面ACD5. 如图，在四棱锥P ABCD -中，底面ABCD 是060DAB ∠= 且边长为a 的菱形，侧面PAD 是等边三角形，且平面PAD 垂 直于底面ABCD ． G 为AD 的中点，求证：BG ⊥平面PAD ； （考点：利用面面垂直性质定理）类型六.证明面面垂直1. 如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点. 求证：平面1A AC ⊥平面BDE . （考点：面面垂直的判定）ABD CA ’D ’B ’C ’SDCBA2.如图，过S 引三条长度相等但不共面的线段SA 、SB 、SC ，且∠ASB=∠ASC=60°，∠BSC=90°，求证：平面ABC ⊥平面BSC ． 考点：面面垂直的判定（证二面角是直二面角）类型七.证明线线垂直1. 在正方体ABCD-A ’B ’C ’D ’中，M 为DD ’的中点，O 为AC 的中点，AB=2 证明：B ’O ⊥AC 考点：法1：线面垂直→线线垂直 法2：勾股定理法3：等腰三角形三线合一。

7.1 几种常见的几何体
一、选择题
1、下列各组几何体中是多面体的一组是（）
A．三棱柱四棱台球圆锥
B．三棱柱四棱台正方体圆台
C．三棱柱四棱台正方体六棱锥
D．圆锥圆台球半球
2、下列说法正确的是（）
A．有一个面是多边形，其余各面是三角形的多面体是棱锥
B．有两个面互相平行，其余各面均为梯形的多面体是棱台
C．有两个面互相平行，其余各面均为平行四边形的多面体是棱柱
D．棱柱的两个底面互相平行，侧面均为平行四边形
3、下面多面体是五面体的是（）
A．三棱锥 B．三棱柱
C．四棱柱 D．五棱锥
4、下列说法错误的是（）
A．一个三棱锥可以由一个三棱锥和一个四棱锥拼合而成
B．一个圆台可以由两个圆台拼合而成
C ．一个圆锥可以由两个圆锥拼合而成
D．一个四棱台可以由两个四棱台拼合而成
5、下面多面体中有12条棱的是（）
A ．四棱柱 B．四棱锥
C．五棱锥 D．五棱柱
6、在三棱锥的四个面中，直角三角形最多可有几个（）
A．1 个 B．2 个
C．3个 D．4个
二、填空题
7、一个棱柱至少有——————个面，面数最少的棱柱有——————个顶点，有———
个棱.
————
8、一个棱柱有10个顶点，所有侧棱长的和为60，则每条侧棱长为———————。

9、把等腰三角形绕底边上的高旋转1800，所得的几何体是————。

参考答案：
一、1-6
二、7、5 6 9
8、12
9、圆锥。

第一章丰富的图形世界一、知识梳理一.几种常见的几何体1．柱体① 棱柱体：〔如图（1)(2）〕，图中上下两个面称棱柱的底面，周围的面称棱柱的侧面，面与面的交线是棱柱的棱．其中侧面与侧面的交线是侧棱，棱与棱的交点是顶点．点拨：正方体和长方体是特殊的棱柱，它们都是四棱柱．正方体是特殊的长方体．② 圆柱：图（3）中上下两个圆面是圆柱的底面，这两个底面是半径相同的圆，周围是圆柱的侧面．点拨：棱柱和圆柱统称柱体．2．锥体① 圆锥：〔如图（4）〕图中的圆面是圆锥的一个底面，中间曲面是圆锥的侧面，圆锥只有一个顶点．② 棱锥：〔如图（5）〕图中下面多边形面是棱锥的一个底面，其余各三角形面是棱锥的侧面．点拨：棱锥和圆锥统称锥体．3．台体1 圆台：〔如图（6）〕图中上下两个大小不同的圆面是圆台的底面，中间曲面是圆台的侧面．2 棱台：〔如图（7）〕图中上下两个大小不同的多边形是棱台的底面，其余四边形是棱台的侧面．4．球体：〔如图（8）〕图中半圆绕其直径旋转而成的几何体，球体表面是曲面．二．几何体的展开图1. 圆柱、圆锥、正三棱锥、正四棱锥、正五棱锥、正三棱柱的展开图：2. 正方体的平面展开图(有11种):三．用平面截一个几何体出现的截面形状1.用一个平面去截正方体，可能出现下面几种情况：三角形正方形长方形梯形五边形六边形点拨：用平面去截几何体，所得的截面就是这个平面与几何体每个面相交的线所围成的图形．正方体只有六个面，所以截面最多有六条边，即截面边数最多的图形是六边形．2. 几种常见的几何体的截面:几何体截面形状正方体三角形、正方形、长方形、梯形、五边形、六边形圆柱圆、长方形、正方形、……圆锥圆、三角形、……球圆点拨：用平面去截圆柱体，可以与圆柱的三个面(两个底面，一个侧面)同时相交，由于圆柱侧面为曲面，相交得到是曲线，无法截出三角形．四．识别物体的三视图1．主视图、左视图、俯视图的定义从不同方向观察同一物体，从正面看图叫主视图，从左面看图叫左视图，从上面看图叫做俯视图．2．几种几何体的三视图(1)正方体：三视图都是正方形．(2)球体：三视图都是圆．(3)圆柱体：(4)圆锥体：点拨：圆锥的主视图、左视图都是三角形，而俯视图的图中有一个点表示圆锥的顶点，因为从上往下看圆锥时先看到圆锥的顶点，再看到底面的圆．3．用若干个小正方体搭成几何体的三视图如图：从正面看2列每列1层;从左面看2列每列1层;从上面看2列左列2层右列1层．则三视图是：点拨：①主视图与俯视图列数相同，俯视图中每列的方框内的最大数字即为主视图本列的层数．②左视图的列数与俯视图的行数相同，俯视图每一横行的方框内的最大数字即为左视图中的列的层数．二、课堂精讲例题例1常见几何体的特征(1)列说法中，正确的个数是（）.①柱体的两个底面一样大；②圆柱、圆锥的底面都是圆；③棱柱的底面是四边形；④长方体一定是柱体；⑤正棱柱的侧面一定是长方形.（A）2个（B）3个（C）4个（D）5个【难度分级】A【试题来源】经典试题【解析】n棱柱的数量特征如下：它有3n条棱，(n＋2)个面，侧面一定是长方形．对于完全相同的面则需注意．棱柱的侧棱都是相等的但底面边长不一定相等，因此以底面边长和侧棱为长和宽的侧面的大小不一定相同。

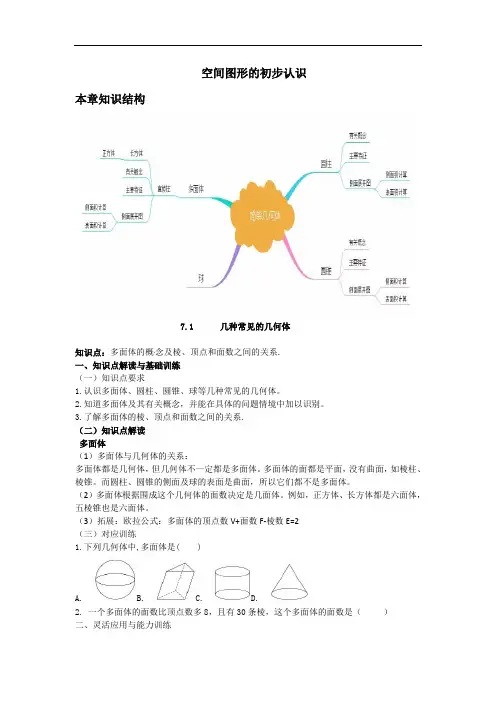
空间图形的初步认识本章知识结构7.1 几种常见的几何体知识点：多面体的概念及棱、顶点和面数之间的关系.一、知识点解读与基础训练（一）知识点要求1.认识多面体、圆柱、圆锥、球等几种常见的几何体。

2.知道多面体及其有关概念，并能在具体的问题情境中加以识别。

3.了解多面体的棱、顶点和面数之间的关系.（二）知识点解读多面体（1）多面体与几何体的关系：多面体都是几何体，但几何体不一定都是多面体。

多面体的面都是平面，没有曲面，如棱柱、棱锥。

而圆柱、圆锥的侧面及球的表面是曲面，所以它们都不是多面体。

（2）多面体根据围成这个几何体的面数决定是几面体。

例如，正方体、长方体都是六面体，五棱锥也是六面体。

（3）拓展：欧拉公式：多面体的顶点数V+面数F-棱数E=2（三）对应训练1.下列几何体中,多面体是( )A. B. C. D.2. 一个多面体的面数比顶点数多8，且有30条棱，这个多面体的面数是（）二、灵活应用与能力训练1.基础训练（1）在如图所示的几何体中，多面体是（）。

（填序号）（2）在雨地里放置一个无盖的容器，如果雨水均匀地落入容器，容器内水面高度h与时间t 的函数图象如图所示，那么这个容器的形状可能是（）2.能力提升（1）如下图,一正方体截去一角后,剩下的几何体面的个数和棱的条数分别为( ) A. 6，14 B. 7，14C. 7，15D. 6，15（2）下列四幅图像近似刻画两个变量之间的关系，请按图象顺序将下面四种情景与之对应排序①一辆汽车在公路上匀速行驶（汽车行驶的路程与时间的关系）②向锥形瓶中匀速注水（水面的高度与注水时间的关系）③将常温下的温度计插入一杯热水中（温度计的读书与时间的关系）④一杯越来越凉的水（水温与时间的关系）A．①②④③B．③④②①C．①④②③D．③②④①三、解析与答案：一、知识点解读与基础训练（三）对应训练 1.B 2. 20二、灵活应用与能力训练1.（1）①②③⑤（2）B2.（1）C （2）D。

棱柱
(1) (2) (4) (7)
思考2：这些几何体各有多少个面?每 个面都是什么图形？
棱锥
(3) (5) (6)
(8)
棱柱、棱锥、棱台都是由一些平面多边形围成的几何体. 由若干个平面多边形围成的几何体叫做多面体.
面
棱 顶点 食盐晶体 明矾晶体 石膏晶体
围成多面体的各个多边形叫做多面体的面. 相邻两个面的公共边叫做多面体的棱. 棱与棱的公共点叫做多面体的顶点.
1. 2. 3.
4.
课本P93习题7d960590c677cc.html
思考3：下面这些几何体是多面体吗?他们有 什么共同的特点？
思考3：你学习过哪些几何体的表面积公式 和体积公式？你能用字母表示他们吗？
四种常见几何体表面积与体积公式 1.长方体 表面积=2（ab+bc+ca）
体积=abc（a、b、c分别长、宽、高）
2.正方体 表面积=6 体积= （这里a为正方体的棱长）
3.圆柱体 侧面积=2πRh 全面积=2πRh+2πR2=2πR（h+R） 体积=πR2h （这里R表示圆柱体底面圆的半径，h表示圆柱的高） 4.圆锥体 侧面积=πRl 全面积=πRl+πR2 体积= πR2h（这里R、l、h表示圆锥体底面圆的 半径、母线长和高）
/view/781432.htm
棱锥的分类
思考：仿照棱柱，说出棱锥的分类
棱锥的分类： 按底面多边形的边数，可以分为三棱锥、 四棱锥、五棱锥、……
还有一类几何体也是我们常见1/xin_003080621162523414104113.jp g
墨西哥太阳金字塔
【我要了解更多
/i?ct=201326592&cl=2&nc=1&lmmp;fm=index&pv=&z=0&ie=utf-

三年级数学上册几何体的初步认识复习题题一: 描述几何体请用简短的语句描述以下几何体的形状和特征：1.立方体：近似于骰子形状的几何体，具有六个面，每个面都是正方形。

2.圆柱体：由两个平行的圆面和一侧面组成的几何体。

3.圆锥体：由一个圆锥面和一个封闭的顶点组成的几何体。

4.球体：形状类似于足球的几何体，表面是光滑的，没有面或尖角。

题二: 辨认图形请根据以下描述，选择正确的几何体：1.描述：有一个圆形的底面，一条侧边可视为一个长方形。

选项：圆锥体、立方体、圆柱体、球体正确答案：圆锥体2.描述：有一个六个面都是正方形的几何体。

选项：圆锥体、立方体、圆柱体、球体正确答案：立方体3.描述：侧面是一条曲线，底面是圆形的几何体。

选项：圆锥体、立方体、圆柱体、球体正确答案：圆锥体4.描述：外观纹理光滑，没有边或角的几何体。

选项：圆锥体、立方体、圆柱体、球体正确答案：球体题三: 补全几何体属性请根据以下描述，补全几何体的属性：1.球体表面特征: 光滑面或边的数量: 无面和边底面形状: 无底面顶点数量: 无顶点与其他几何体的共性: 具有旋转对称性2.立方体表面特征: 六个平面面或边的数量: 6个面，12条边底面形状: 正方形顶点数量: 8个顶点与其他几何体的共性: 具有六个面都是正方形的特征3.圆柱体表面特征: 两个平面和一个侧面面或边的数量: 3个面，2个圆形面和1个矩形侧面底面形状: 圆形顶点数量: 2个顶点与其他几何体的共性: 具有一个圆形底面和一个平行于底面的圆形面4.圆锥体表面特征: 一个锥形面和一个封闭的顶点面或边的数量: 2个面，1个圆锥面和1个封闭顶点底面形状: 圆形顶点数量: 1个顶点与其他几何体的共性: 具有一个圆形底面和一个封闭顶点以上是对几何体的初步认识的复习题，通过对几何体形状和属性的描述和辨认，可以帮助学生巩固对几何体的理解和记忆。

E G
C
M
F
┑
B HD
例4 如图，某地有两所大学和两条交叉的公路．图
中点M，N表示大学，OA，OB表示公路，现方案修
建一座物资仓库，希望仓库到两所大学的距离相同，
到两条公路的距离也相同，你能确定出仓库P应该建
在什么位置吗？请在图中画出你的设计．(尺规作图，
不写作法，保存作图痕迹) A
M O
N
B
解：如以以下图：
验证猜测 角的平分线上的点到角的两边的距离相等
：如图， ∠AOC= ∠BOC,点P在OC上，PD⊥OA,PE⊥OB,
垂足分别为D,E.
求证：PD=PE. 证明：∵ PD⊥OA,PE⊥OB，
∴ ∠PDO= ∠PEO=90 °. 在△PDO和△PEO中， O
A
D C
P
E
B
∠PDO= ∠PEO，
∠AOC= ∠BOC， ∴ △PDO ≌ △PEO(AAS).
• 他们的课程，无论是在内容和形式上，都是经过认真 研判，把各学科的核心素养作为教学主线。既涵盖城市 中小学、又包括乡村大局部学校的教学模式。適合全國 大局部教學大區。本課件就是從全國一等獎作品中，优 选出的具有代表性的作品。示范性强，有很大的推广价 值。
第7章 空间图形的初步认识 7.1 几种常见的几何体
1. 如图，DE⊥AB，DF⊥BG，垂足分别 是E，F， DE =DF， ∠EDB= 60°，那么 ∠EBF= 60 度，BE= BF .
B
2.△ABC中, ∠C=90°,AD平分∠CAB,且 BC=8,BD=5,那么点D到AB的距离是 3 .
A E
C D
F G
C D
A
EB
3.用三角尺可按下面方法画角平分线：在∠AOB的两边上，分 别取OM=ON,再分别过点M,N作OA,OB的垂线，交点为P，画 射线OP,那么OP平分∠AOB.为什么？

最新Word 欢送下载
常见的几种几何体的外表积的计算公式
难易度：★★★
关键词：立体图形
答案：
①圆柱体外表积：2πR2+2πRh 〔R为圆柱体上下底圆半径，h为圆柱体高〕②圆锥体外表
积：πr2+nπ〔r为圆锥体低圆半径，h为其高，n为圆锥侧面展开图中扇形的圆心角〕③长方体外表积：2〔ab+ah+bh〕〔a为长方体的长，b为长方体的宽，h为长方体的高〕④正方体外表积：6a2〔a为正方体棱长〕
【举一反三】
典例：一个长方体的长为4cm，宽为3cm，高为5cm，请求出：
〔1〕长方体所有棱长的和．
〔2〕长方体的外表积．
思路引导：此题考查长方体的棱长总和、外表积公式〔1〕长方体的棱长总和=4〔长+宽+高〕；〔2〕长方体的外表积=2〔长×宽+长×高+宽×高〕，把相关数字代入即可．长方体的长、宽、高分别为4cm，3cm，5cm，〔1〕这个长方体的棱长总和为4×〔4+3+5〕=48cm，故长方体所有棱长的和为48cm．〔2〕外表积2×〔4×3+4×5+3×5〕=2×47=94cm2．故长方体的外表积为94cm2．
标准答案：〔1〕48cm〔2〕94cm2。

生活中的 立体图形
常见几何体
常见几何体 的分类标准
圆柱、圆锥、正方体、 长方体、棱柱、球等
1.按形状分类； 2.按有无曲的面分类； 3.按有无顶点分类
棱柱、棱锥 的特征
四棱柱
新知探究 知识点2 棱柱与棱锥
棱柱有哪些特征呢？
特征 (1)棱柱的所有侧棱 长都相等； (2)棱柱的上、下底 面的形状相同、大小 相同，都是多边形， 并且互相平行； (3)棱柱的侧面的形 状都是平行四边形.
新知探究 知识点2 棱柱与棱锥
棱柱的分类
(1)人们通常根据底面图形的边数将棱柱分为三棱柱、四
第3章 图形的初步认识
3.1 生活中的立体图形
华东师大版
1.通过实物和模型抽象出几何体，发展抽象能力.
2.能描述常见几何体的形状特征，能对它们进行简 单分类.
3.掌握棱柱的特征，能找出面的个数、棱的条数、 顶点的个数.
问题 观察下面的图片，你认识这些几何体吗？
球
正方体
圆柱
长方体
圆锥
在日常生活中你见 过哪些与它们形状 相类似的物品呢？
问题 观察下面的图片，你认识这些几何体吗？
球
正方体
圆柱
长方体
圆锥
知识点1 常见的几何体及分类
小 明 的 书 房
问题 看一看哪些物体的形状与你在小学学过的几何体类似？
新知探究 知识点1 常见的几何体及分类 常见的几何体
正方体
圆柱
球
棱柱
长方体
圆锥
棱锥
新知探究 知识点1 常见的几何体及分类 想一想：你对以上的立体图形如何分类？根据什么理由.
(1)
(2)
(3)
(4)
(5) (6)

小升初数学图形与几何知识点分类复习《常见的立体图形》二一、选择题1．一块圆柱形橡皮泥，底面积是12平方厘米，高是5厘米，如果把它捏成底面同样大小的圆锥，这个圆锥的高是（）厘米。

A．10B．60C．5D．152．下边是一个无盖正方体的展开图，和字母A相对的面是（）。

A．字母B B．字母C C．字母D D．字母E3．一个正方体的棱长扩大到原来的3倍，则表面积扩大到原来的（）倍。

A．6B．9C．274．如图，若不让水溢出来，则量杯中最多可以放入（）个这样的苹果。

A．4B．3C．25．圆柱和圆锥的体积和高都相等，已知圆锥的底面积是9cm2，圆柱的底面积是（）。

A．9cm2B．3cm2C．27cm26．至少（）个相同的小正方体才能拼成一个大正方体。

A．4B．8C．107．下图是一个正方体的展开图，在这个正方体中，和“美”相对的面是（）。

A．建B．晋C．丽D．城8．把一个长10cm、宽8cm、高6cm的长方体，切成两个相等的长方体，它们的表面积之和比原来最多增加（）平方厘米。

A．480B．160C．96D．809．仔细看图，郑州二七纪念塔（如图）是为纪念京汉铁路工人大罢工修建的纪念性建筑物。

下面图（）是站在位置①拍摄的。

A．B．C．10．一个正方体的棱长总和是48分米，它的表面积是（）。

A．64平方分米B．96平方分米C．144平方分米D．72平方分米11．小猫沿着小路自东向西奔跑，它看到下面三幅图的先后顺序是（）。

A．①①①B．①①①C．①①①12．一个长方体形状的玻璃容器，从里面量长为50厘米，宽为40厘米，高为45厘米。

向容器里注水，当容器内的水体第1次出现正方形面时，容器里有水（）升。

A．90B．100C．80D．8113．一个立体图形，从上面看是，从右面看是，搭成这个立体图形最多需要（）个小正方体。

A．4B．5C．6D．714．下面的图形中，（）是正方体的表面展开图。

A．B．C．D．15．一个正方体的棱长扩大3倍，则它的表面积扩大（）。

1.如图，说出下图中的一些物体的形状所对应的立 体图形.
对应于长方体
对应于球 对应于圆柱体
2.图中的各立体图形的表面中包含哪些平 面图形？试指出这些平面图形在立体图形 中的位置.
包含圆与长方形，圆 位于圆柱体的上底和 下底，长方形位于圆 柱体的侧面.
包ቤተ መጻሕፍቲ ባይዱ圆，圆位于圆锥 的底面.
2.图中的各立体图形的表面中包含哪些平 面图形？试指出这些平面图形在立体图形 中的位置.
包含长方形、五边 形，长方形位于棱 柱的侧面，五边形 位于棱柱的上下底.
包含三角形、六 边形，三角形位 于棱锥的侧面， 六边形位于棱柱 的底面.
包含长方形、三 角形，长方形位 于侧面和地面， 三角形位于底面.