数值分析作业复化求积公式

复化求积公式复化求积公式是计算定积分的一种常用方法。

它的基本思想是将区间分成多个小区间，用每个小区间上的函数近似代替原函数，然后将这些小区间的近似结果相加得到总的近似结果。

这个方法的优点是能够适用于各种函数类型，而且在计算机上也可以很方便地实现。

具体来说，我们可以将区间[a, b]均匀地分成n个小区间，每个小区间的长度都为Δx = (b-a)/n。

然后我们在每个小区间上选择一个点xi（可以是小区间的左端点、右端点、中点等）作为代表，然后计算这些小区间上的函数值f(xi)。

这样我们就得到了n个高度为f(xi)的矩形，它们的面积就是Δx * f(xi)。

将这n个矩形的面积相加，就得到了近似的定积分的结果。

单个小区间的近似结果可以表示为Δx * f(xi)。

为了得到更精确的结果，我们可以进一步增加小区间的数量，即取n趋向于无穷大的极限。

这样，我们就可以得到复化求积公式的一般形式：∫[a, b] f(x) dx ≈ Δx/2 * [f(x0) + 2f(x1) + 2f(x2) + ... + 2f(x(n-1)) + f(xn)]其中，Δx = (b-a)/n，x0 = a，xn = b，xi 是每个小区间上的代表点。

复化求积公式的精确度与小区间的数量n有关，通常情况下，n越大，近似结果越精确。

但是同时也需要注意，小区间的数量过大会导致计算量过大，需要更多的时间和计算资源。

复化求积公式在实际应用中有很重要的作用，特别是在数值计算和科学工程领域。

通过这个方法，我们可以近似地计算各种复杂的函数的定积分，例如概率密度函数、信号处理中的卷积运算等。

同时，复化求积公式也为数值积分提供了一种计算机实现的思路，可以通过编程语言实现自动计算定积分的功能。

总之，复化求积公式是计算定积分的一种重要方法，通过将区间分成多个小区间，用每个小区间上的函数近似代替原函数，并将这些小区间结果相加，从而获得近似结果。

它在实际应用中具有广泛的适用性和指导意义，为求解各种复杂问题提供了一种有效的数值计算方法。

复化求积公式的算法及其应用复化求积公式是数值计算方法中重要的一种技术，用于近似计算函数的积分值。

该方法通过将积分区间等分为多个小区间，并在每个小区间上使用求积公式来估计函数在该区间上的积分值。

本文将介绍复化求积公式的算法及其应用。

一、复化求积公式算法1.复化梯形求积公式复化梯形求积公式是复化求积公式中最简单的一种，其基本思想是将积分区间等分为若干个小区间，然后在每个小区间上使用梯形求积公式计算积分值，最后将所有小区间的积分值相加得到最终的积分值。

算法步骤：1)将积分区间[a,b]等分为n个小区间，每个小区间的长度为h=(b-a)/n。

2) 在每个小区间上使用梯形求积公式计算积分值，即Ii=h/2*(f(xi)+f(xi+1))，其中xi=a+i*h，i=0,1,2,...,n-13)将所有小区间的积分值相加得到最终的积分值，即I≈I0+I1+I2+...+In-12. 复化Simpson求积公式复化Simpson求积公式是一种更为精确的复化求积公式，它通过在每个小区间上使用Simpson求积公式来计算积分值，从而提高了计算精度。

算法步骤：1)将积分区间[a,b]等分为n个小区间，每个小区间的长度为h=(b-a)/n。

2) 在每个小区间上使用Simpson求积公式计算积分值，即Ii=h/6*(f(xi)+4f(xi+h/2)+f(xi+h))，其中xi=a+i*h，i=0,1,2,...,n-13)将所有小区间的积分值相加得到最终的积分值，即I≈I0+I1+I2+...+In-1二、复化求积公式应用1.数学分析中的数值积分计算，用于计算函数的定积分值。

2.物理学中的积分计算，用于计算物理量的平均值或总量。

3.统计学中的积分计算，用于计算概率密度函数的面积值。

4.工程学中的积分计算，用于计算工程问题中的各种积分量。

5.金融学中的积分计算，用于计算金融衍生品的价格或价值。

总结：复化求积公式是一种重要的数值计算方法，在数学、物理、统计、工程、金融等领域中有广泛的应用。

利用数值积分公式求解积分方程分别用复化求积公式和高斯
型求积公式
数值积分方法通常用于求解无法解析求解的定积分问题，其中复化求积公式和高斯型求积公式是两种常见的数值积分方法。

1. 复化求积公式：
复化求积公式是通过将积分区间等分成多个小区间，并在每个小区间上采用简单的数值积分公式来逼近原积分问题。

常见的复化求积公式包括梯形法则和Simpson法则。

梯形法则：将积分区间[a, b]等分成n个小区间，每个小区间
用梯形面积的方法求解，然后将各个小区间的积分结果相加得到最终的积分近似值。

Simpson法则：将积分区间[a, b]等分成n个小区间，每个小区
间用Simpson公式求解，然后将各个小区间的积分结果相加得到最终的积分近似值。

2. 高斯型求积公式：
高斯型求积公式是通过将积分区间映射为[-1, 1]上的积分问题，然后通过选取合适的节点和权重，将原积分问题转化为有限个加权节点的求和问题。

常见的高斯型求积公式包括Gauss-Legendre公式和Gauss-Hermite公式。

Gauss-Legendre公式：适用于求解定义在[-1, 1]区间上的定积
分问题，根据节点个数的不同，可以得到不同阶数的Gauss-Legendre公式。

Gauss-Hermite公式：适用于求解定义在整个实数轴上的定积分问题，通过选取合适的节点和权重，将原积分问题转化为有限个加权节点的求和问题。

总结：复化求积公式适用于一般的定积分问题，可以通过合理选择划分区间和数值积分公式来提高数值积分的精度。

而高斯型求积公式通常适用于具有特殊形式或定义域的定积分问题，可以通过选取合适的节点和权重来获得较高的数值积分精度。

数值分析第六次程序作业PB09001057 孙琪【问题】利用复化梯形积分公式和复化3点Gauss 积分公式计算积分的通用程序计算下列积分；I 1(f )=∫e −x2dx 10, I 2(f )=∫11+x 2dx 4, I 3(f )=∫12+cos (x)dx 2π, 取节点x i ， i =0,…,N,N 为2k ,k =0,1,…,7，给出误差表格并简单分析你得到的数据。

【复化梯形积分公式】梯形法则：对两个节点相应的积分法则称为梯形法则：∫f (x )dx ≈b −a2ba [f (a )+f (b )] 如果划分区间[a,b]为：a =x 0<x 1<⋯<x n =b那么在每个区间上可应用梯形法则，此时节点未必是等距的，由此得到复合梯形法则：∫f (x )dx =∑∫f (x )dx x ix i−1ni=1ba ≈12∑(x i −x i−1)[f (x i−1)+f (x i )]ni=1对等间距h=(b-a)/n 及节点x i =a +ih ，复合梯形法则具有形式：∫f (x )dx ≈h2[f (a )+2∑f (a +ih )n−1i=1+f (b )]ba误差项为：−112(b −a )h 2f ′′(δ)【复化3点Gauss 积分公式】对给定的正的权函数w ，高斯求积法则的一般形式是：∫f (x )w (x )dx ba≈∑A i f(x i )ni=0对f ∈n 次多项式精确成立， A i =∫w(x)∏x−x j x i −x jnj=0j≠ibadx 。

复化3点Gauss 积分公式中：首先通过坐标变换将[x i ，x i+1]变为[-1,1]，然后通过三点高斯积分公式：∫f (x )dx 1−1≈59f (−√35)+89f (0)+59f (√35)计算即可。

最后将所有的区间加起来就得到我们要的结果。

【算法分析】复合梯形法则和复化3点Gauss 积分法则的算法上述描述中都已介绍了，在此不多做叙述。

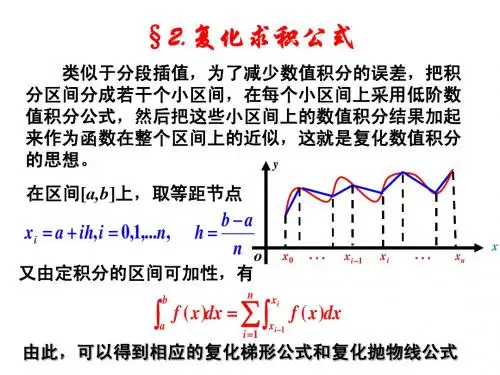
§3 复化求积公式● 复化求积法的基本思想：将积分区间],[b a n 等分，可得到1+n 个求积节点：kh a x k +=，),,1,0(n k Λ=，其中nab h -=，对积分111()()k kn n bx k axk k I f x dx f x dx I +--=====∑∑⎰⎰在每一个小区间1[,]k k x x +上利用n 阶牛顿-柯特斯公式计算，然后对每个区间的近似积分值求和，用所得的值近似代替原积分值。

如此得到的求积公式称为复化求积公式。

● 复化梯形公式：（每个小区间上利用梯形公式求积）111110()()(()())2k kn bx ax k n k kk k k I f x dx f x dxx x f x f x +-=-++===-≈+∑⎰⎰∑求和展开得：0112111(()())(()())2(()())(()2()())2n n n n k k hT f x f x f x f x f x f x hf a f x f b --==++++++=++∑L其中，na b h -=复化辛甫生公式: （每个小区间上用辛甫生公式求积） 1、公式：112101110()()(()4()())6k kn bxax k n k kk k k k I f x dx f x dxx x f x f x f x +-=-+++===-≈++∑⎰⎰∑ 12k x +表示为区间1[,]k k x x +的中点。

求和展开得：13221201121((()4()())(()4()6())(()4()())n n n n hS f x f x f x f x f x f x f x f x f x --=+++++++++L121101(()4()2()())6n n k k k k hf a f x f x f b --+===+++∑∑ 其中：na b h -=。

复化柯特斯公式：（每个小区间上用柯特斯公式求积）1141324101101()()(7()32()9012()32()7())k kn bxax k n k kk k k k k k I f x dx f x dxx x f x f x f x f x f x +-=-++=+++==-≈++++∑⎰⎰∑ 12k x +为1[,]k k x x +的中点，14k x +，34k x +为1[,]k k x x +的四分之一分点。

复化求积公式复化求积复化求积是数值计算中一种常用的数值积分方法，用于近似计算函数的定积分。

1. 方法介绍复化求积的基本思想是将要求解的定积分区间划分为若干个小区间，并对每个小区间采用数值积分方法进行近似计算，最后将各小区间的积分结果相加得到整个定积分的近似值。

2. 公式列表以下是复化求积的常用公式：矩形公式矩形公式是最简单的复化求积公式，将每个小区间近似为一个矩形，并取矩形的高度为该小区间上函数值的平均值。

矩形公式的表达式如下：∫[a, b] f(x) dx ≈ (b - a) * (f(a) + f(b)) / 2其中，a和b为积分区间的上下限。

梯形公式梯形公式是复化求积中常用的公式，将每个小区间近似为一个梯形，并取梯形的高度为该小区间上函数值的平均值。

梯形公式的表达式如下：∫[a, b] f(x) dx ≈ (b - a) * (f(a) + f(b)) / 2其中，a和b为积分区间的上下限。

辛普森公式辛普森公式是复化求积中精度更高的公式，将每个小区间近似为一个二次曲线，并取二次曲线的高度为该小区间上函数值的平均值。

辛普森公式的表达式如下：∫[a, b] f(x) dx ≈ (b - a) * (f(a) + 4 * f((a + b) / 2) + f(b)) / 6其中，a和b为积分区间的上下限。

3. 示例说明以求解函数f(x) = x^2在区间[0, 1]上的定积分为例，通过复化求积方法进行近似计算。

矩形公式计算将区间[0, 1]划分为n个小区间，每个小区间的宽度为h = (1 - 0) / n。

利用矩形公式计算每个小区间的积分值，然后将所得结果相加。

∫[0, 1] x^2 dx ≈ (1 - 0) * (f(0) + f(1)) / 2= (1 - 0) * (0^2 + 1^2) / 2= 1/2梯形公式计算同样将区间[0, 1]划分为n个小区间，每个小区间的宽度为h = (1 - 0) / n。

数值分析第六次程序作业PB09001057 孙琪【问题】利用复化梯形积分公式和复化3点Gauss 积分公式计算积分的通用程序计算下列积分；I 1(f )=∫e −x2dx 10, I 2(f )=∫11+x 2dx 4, I 3(f )=∫12+cos (x)dx 2π, 取节点x i ， i =0,…,N,N 为2k ,k =0,1,…,7，给出误差表格并简单分析你得到的数据。

【复化梯形积分公式】梯形法则：对两个节点相应的积分法则称为梯形法则：∫f (x )dx ≈b −a2ba [f (a )+f (b )] 如果划分区间[a,b]为：a =x 0<x 1<⋯<x n =b那么在每个区间上可应用梯形法则，此时节点未必是等距的，由此得到复合梯形法则：∫f (x )dx =∑∫f (x )dx x ix i−1ni=1ba ≈12∑(x i −x i−1)[f (x i−1)+f (x i )]ni=1对等间距h=(b-a)/n 及节点x i =a +ih ，复合梯形法则具有形式：∫f (x )dx ≈h2[f (a )+2∑f (a +ih )n−1i=1+f (b )]ba误差项为：−112(b −a )h 2f ′′(δ)【复化3点Gauss 积分公式】对给定的正的权函数w ，高斯求积法则的一般形式是：∫f (x )w (x )dx ba≈∑A i f(x i )ni=0对f ∈n 次多项式精确成立， A i =∫w(x)∏x−x j x i −x jnj=0j≠ibadx 。

复化3点Gauss 积分公式中：首先通过坐标变换将[x i ，x i+1]变为[-1,1]，然后通过三点高斯积分公式：∫f (x )dx 1−1≈59f (−√35)+89f (0)+59f (√35)计算即可。

最后将所有的区间加起来就得到我们要的结果。

【算法分析】复合梯形法则和复化3点Gauss 积分法则的算法上述描述中都已介绍了，在此不多做叙述。

数值分析复化梯形公式复化公式程序
分别用复化梯形公式、复化Simpson 公式计算定积分dx e x ?+201，取n=2,4,8,16分别验证结果（精确值I=）。

复化梯形公式求定积分:
function I=tquad(x,y)
%复化梯形求积公式，其中，
%x 为向量，被积函数自变量的等距结点； %y 为向量，被积函数在结点处的函数值； n=length(x);
m=length(y);
%积分自变量的结点数应与它的函数值的个数相同h=(x(n)-x(1))/(n-1);
a=[1 2*ones(1,n-2) 1];
I=h/2*sum(a.*y);
复化Simpson 公式求定积分：
function I=squad(x,y)
%复化Simpson 求积公式，其中，
%x 为向量，被积函数自变量的等距结点； %y 为向量，被积函数在结点处的函数值； n=length(x);
m=length(y);
%积分自变量的结点数应与它的函数值的个数相同if rem(n-1,2)~=0
I=tquad(x,y);
return;
end
N=(n-1)/2;
h=(x(n)-x(1))/N;
a=zeros(1,n);
for k=1:N
a(2*k-1)=a(2*k-1)+1;
a(2*k)=a(2*k)+4;
a(2*k+1)=a(2*k+1)+1; end
I=h/6*sum(a.*y);。

数值计算方法上机题目3计算定积分的近似值：221x e xe dx =⎰ 要求：（1）若用复化梯形公式和复化Simpson 公式计算，要求误差限71021-⨯=ε，分别利用他们的余项估计对每种算法做出步长的事前估计；（2）分别利用复化梯形公式和复化Simpson 公式计算定积分；（3）将计算结果与精确解比较，并比较两种算法的计算量。

解：（1) x xe x f =)(,所以x x k xe ke x f +=)()(，x x xe e x f +=2)(''，x x xe e x f +=4)()4(x x xe e x f +=6)()6(对于复化梯形公式： )(12)(''2ηf h a b f R n --=，2max ''4)(e f =η，n h 1= 代入数据可知 7221021124-⨯≤n e ，57.7018≥n 取7019=n对于复化Simpson 公式 )()2(180)()4(4ηf h a b f R n --=，2max )4(6)(e f =η，n h 1= 代入数据可知 742102128806-⨯≤n e ，56.23≥n 取24=n（2）复化梯形公式：函数function y=fun(x)y=x*exp(x);程序：clcClear% 复化梯形计算format longa=1;b=2;n=7019;% 区间划分为m等份h=(b-a)/n;% 步长，根据误差限由该算法的余项作事前估计得到ty1=fun(a)+fun(b);ty2=0;for i=1:n-1x=a+i*h1;ty2=ty2+fun(x);endT=h*(ty1+2*ty2)/2;T对于复化Simpson公式clcClear% 复化Simpon计算format longa=1;b=2;n=24;% 区间划分为n等份h=(b-a)/(2*n);% 步长，根据误差限由该算法的余项作事前估计得到sy1=fun(a)+fun(b);sy2=0;sy3=0;for j=1:2*n-1x=a+j*h2;if rem(j,2)==0sy3=sy3+fun(x);elsesy2=sy2+fun(x);endendS=h*(sy1+4*sy2+2*sy3)/3;S% 精确值Exactanswer=exp(2)运算结果：T =7.389056127230221S =7.389056126214707Exactanswer =7.389056098930650（3）比较可知复化梯形公式的计算量较大1．用共轭梯度法和G-S迭代法分别求解下面的方程组：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-14514103131021310321x x x 迭代20次或满足()(1)1110k k x x --∞-<时停止计算。