复化求积公式
- 格式:ppt
- 大小:601.50 KB
- 文档页数:12





复化求积公式的算法及其应用复化求积公式是数值计算方法中重要的一种技术,用于近似计算函数的积分值。
该方法通过将积分区间等分为多个小区间,并在每个小区间上使用求积公式来估计函数在该区间上的积分值。
本文将介绍复化求积公式的算法及其应用。
一、复化求积公式算法1.复化梯形求积公式复化梯形求积公式是复化求积公式中最简单的一种,其基本思想是将积分区间等分为若干个小区间,然后在每个小区间上使用梯形求积公式计算积分值,最后将所有小区间的积分值相加得到最终的积分值。
算法步骤:1)将积分区间[a,b]等分为n个小区间,每个小区间的长度为h=(b-a)/n。
2) 在每个小区间上使用梯形求积公式计算积分值,即Ii=h/2*(f(xi)+f(xi+1)),其中xi=a+i*h,i=0,1,2,...,n-13)将所有小区间的积分值相加得到最终的积分值,即I≈I0+I1+I2+...+In-12. 复化Simpson求积公式复化Simpson求积公式是一种更为精确的复化求积公式,它通过在每个小区间上使用Simpson求积公式来计算积分值,从而提高了计算精度。
算法步骤:1)将积分区间[a,b]等分为n个小区间,每个小区间的长度为h=(b-a)/n。
2) 在每个小区间上使用Simpson求积公式计算积分值,即Ii=h/6*(f(xi)+4f(xi+h/2)+f(xi+h)),其中xi=a+i*h,i=0,1,2,...,n-13)将所有小区间的积分值相加得到最终的积分值,即I≈I0+I1+I2+...+In-1二、复化求积公式应用1.数学分析中的数值积分计算,用于计算函数的定积分值。
2.物理学中的积分计算,用于计算物理量的平均值或总量。
3.统计学中的积分计算,用于计算概率密度函数的面积值。
4.工程学中的积分计算,用于计算工程问题中的各种积分量。
5.金融学中的积分计算,用于计算金融衍生品的价格或价值。
总结:复化求积公式是一种重要的数值计算方法,在数学、物理、统计、工程、金融等领域中有广泛的应用。




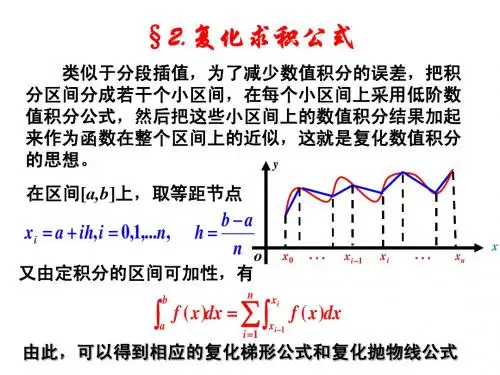
§3 复化求积公式● 复化求积法的基本思想:将积分区间],[b a n 等分,可得到1+n 个求积节点:kh a x k +=,),,1,0(n k Λ=,其中nab h -=,对积分111()()k kn n bx k axk k I f x dx f x dx I +--=====∑∑⎰⎰在每一个小区间1[,]k k x x +上利用n 阶牛顿-柯特斯公式计算,然后对每个区间的近似积分值求和,用所得的值近似代替原积分值。
如此得到的求积公式称为复化求积公式。
● 复化梯形公式:(每个小区间上利用梯形公式求积)111110()()(()())2k kn bx ax k n k kk k k I f x dx f x dxx x f x f x +-=-++===-≈+∑⎰⎰∑求和展开得:0112111(()())(()())2(()())(()2()())2n n n n k k hT f x f x f x f x f x f x hf a f x f b --==++++++=++∑L其中,na b h -=复化辛甫生公式: (每个小区间上用辛甫生公式求积) 1、公式:112101110()()(()4()())6k kn bxax k n k kk k k k I f x dx f x dxx x f x f x f x +-=-+++===-≈++∑⎰⎰∑ 12k x +表示为区间1[,]k k x x +的中点。
求和展开得:13221201121((()4()())(()4()6())(()4()())n n n n hS f x f x f x f x f x f x f x f x f x --=+++++++++L121101(()4()2()())6n n k k k k hf a f x f x f b --+===+++∑∑ 其中:na b h -=。
复化柯特斯公式:(每个小区间上用柯特斯公式求积)1141324101101()()(7()32()9012()32()7())k kn bxax k n k kk k k k k k I f x dx f x dxx x f x f x f x f x f x +-=-++=+++==-≈++++∑⎰⎰∑ 12k x +为1[,]k k x x +的中点,14k x +,34k x +为1[,]k k x x +的四分之一分点。

复化求积公式复化求积复化求积是数值计算中一种常用的数值积分方法,用于近似计算函数的定积分。
1. 方法介绍复化求积的基本思想是将要求解的定积分区间划分为若干个小区间,并对每个小区间采用数值积分方法进行近似计算,最后将各小区间的积分结果相加得到整个定积分的近似值。
2. 公式列表以下是复化求积的常用公式:矩形公式矩形公式是最简单的复化求积公式,将每个小区间近似为一个矩形,并取矩形的高度为该小区间上函数值的平均值。
矩形公式的表达式如下:∫[a, b] f(x) dx ≈ (b - a) * (f(a) + f(b)) / 2其中,a和b为积分区间的上下限。
梯形公式梯形公式是复化求积中常用的公式,将每个小区间近似为一个梯形,并取梯形的高度为该小区间上函数值的平均值。
梯形公式的表达式如下:∫[a, b] f(x) dx ≈ (b - a) * (f(a) + f(b)) / 2其中,a和b为积分区间的上下限。
辛普森公式辛普森公式是复化求积中精度更高的公式,将每个小区间近似为一个二次曲线,并取二次曲线的高度为该小区间上函数值的平均值。
辛普森公式的表达式如下:∫[a, b] f(x) dx ≈ (b - a) * (f(a) + 4 * f((a + b) / 2) + f(b)) / 6其中,a和b为积分区间的上下限。
3. 示例说明以求解函数f(x) = x^2在区间[0, 1]上的定积分为例,通过复化求积方法进行近似计算。
矩形公式计算将区间[0, 1]划分为n个小区间,每个小区间的宽度为h = (1 - 0) / n。
利用矩形公式计算每个小区间的积分值,然后将所得结果相加。
∫[0, 1] x^2 dx ≈ (1 - 0) * (f(0) + f(1)) / 2= (1 - 0) * (0^2 + 1^2) / 2= 1/2梯形公式计算同样将区间[0, 1]划分为n个小区间,每个小区间的宽度为h = (1 - 0) / n。