复化求积公式
- 格式:ppt
- 大小:2.11 MB
- 文档页数:3


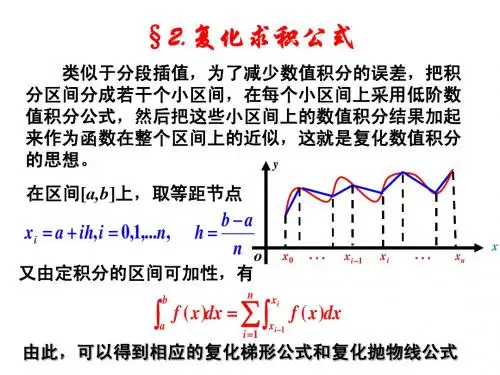







§3 复化求积公式● 复化求积法的基本思想:将积分区间],[b a n 等分,可得到1+n 个求积节点:kh a x k +=,),,1,0(n k Λ=,其中nab h -=,对积分111()()k kn n bx k axk k I f x dx f x dx I +--=====∑∑⎰⎰在每一个小区间1[,]k k x x +上利用n 阶牛顿-柯特斯公式计算,然后对每个区间的近似积分值求和,用所得的值近似代替原积分值。
如此得到的求积公式称为复化求积公式。
● 复化梯形公式:(每个小区间上利用梯形公式求积)111110()()(()())2k kn bx ax k n k kk k k I f x dx f x dxx x f x f x +-=-++===-≈+∑⎰⎰∑求和展开得:0112111(()())(()())2(()())(()2()())2n n n n k k hT f x f x f x f x f x f x hf a f x f b --==++++++=++∑L其中,na b h -=复化辛甫生公式: (每个小区间上用辛甫生公式求积) 1、公式:112101110()()(()4()())6k kn bxax k n k kk k k k I f x dx f x dxx x f x f x f x +-=-+++===-≈++∑⎰⎰∑ 12k x +表示为区间1[,]k k x x +的中点。
求和展开得:13221201121((()4()())(()4()6())(()4()())n n n n hS f x f x f x f x f x f x f x f x f x --=+++++++++L121101(()4()2()())6n n k k k k hf a f x f x f b --+===+++∑∑ 其中:na b h -=。
复化柯特斯公式:(每个小区间上用柯特斯公式求积)1141324101101()()(7()32()9012()32()7())k kn bxax k n k kk k k k k k I f x dx f x dxx x f x f x f x f x f x +-=-++=+++==-≈++++∑⎰⎰∑ 12k x +为1[,]k k x x +的中点,14k x +,34k x +为1[,]k k x x +的四分之一分点。

复化求积公式复化求积复化求积是数值计算中一种常用的数值积分方法,用于近似计算函数的定积分。
1. 方法介绍复化求积的基本思想是将要求解的定积分区间划分为若干个小区间,并对每个小区间采用数值积分方法进行近似计算,最后将各小区间的积分结果相加得到整个定积分的近似值。
2. 公式列表以下是复化求积的常用公式:矩形公式矩形公式是最简单的复化求积公式,将每个小区间近似为一个矩形,并取矩形的高度为该小区间上函数值的平均值。
矩形公式的表达式如下:∫[a, b] f(x) dx ≈ (b - a) * (f(a) + f(b)) / 2其中,a和b为积分区间的上下限。
梯形公式梯形公式是复化求积中常用的公式,将每个小区间近似为一个梯形,并取梯形的高度为该小区间上函数值的平均值。
梯形公式的表达式如下:∫[a, b] f(x) dx ≈ (b - a) * (f(a) + f(b)) / 2其中,a和b为积分区间的上下限。
辛普森公式辛普森公式是复化求积中精度更高的公式,将每个小区间近似为一个二次曲线,并取二次曲线的高度为该小区间上函数值的平均值。
辛普森公式的表达式如下:∫[a, b] f(x) dx ≈ (b - a) * (f(a) + 4 * f((a + b) / 2) + f(b)) / 6其中,a和b为积分区间的上下限。
3. 示例说明以求解函数f(x) = x^2在区间[0, 1]上的定积分为例,通过复化求积方法进行近似计算。
矩形公式计算将区间[0, 1]划分为n个小区间,每个小区间的宽度为h = (1 - 0) / n。
利用矩形公式计算每个小区间的积分值,然后将所得结果相加。
∫[0, 1] x^2 dx ≈ (1 - 0) * (f(0) + f(1)) / 2= (1 - 0) * (0^2 + 1^2) / 2= 1/2梯形公式计算同样将区间[0, 1]划分为n个小区间,每个小区间的宽度为h = (1 - 0) / n。
复化中矩形求积公式余项复化中矩形求积公式余项,这可真是个有点复杂但又超级有趣的数学概念啊!咱们先来说说啥是复化中矩形求积公式。
想象一下,你有一条弯弯曲曲的曲线,就像你在公园里走的那种没有规律的小道。
现在你想知道这条小道下面的面积大概是多少。
那咱们就把这条小道切成好多好多的小段,每一小段都近似看成一个矩形。
比如说,把区间 [a, b] 分成 n 等分,每个小区间的长度就是 h = (b - a) / n 。
然后在每个小区间的中点找一个点,以这个点的函数值乘以小区间的长度,把所有这些乘积加起来,这就是复化中矩形求积公式啦。
但是,这里面就有个小问题,咱们这样算出来的面积并不是完全准确的,总会有那么一点点误差,这就是余项啦。
我记得有一次给学生们讲这个的时候,有个小家伙特别较真儿。
他瞪着大眼睛问我:“老师,为啥就不能完全算准呢?”我笑着跟他说:“这就好比你用尺子量一个弯弯曲曲的线,尺子是直的,线是弯的,怎么可能量得一点不差呀!”这小家伙似懂非懂地点点头。
那这个余项到底咋算呢?其实它跟函数的高阶导数有关系。
简单来说,函数越弯曲,余项就可能越大。
咱们来举个例子,假如有个函数 f(x) = x²,要在区间 [0, 1] 上用复化中矩形求积公式来算面积。
分成 10 等分,算出来的结果和准确值一比较,就能看到那个小小的误差。
在实际应用中,了解这个余项很重要哦。
比如说在工程计算里,如果对精度要求很高,就得搞清楚这个余项有多大,看看咱们用的方法合不合适。
再比如说,在做科学研究的时候,一点点误差可能就会导致完全不同的结论。
所以得把这个余项控制在一个能接受的范围内。
总之,复化中矩形求积公式余项虽然有点复杂,但只要咱们认真琢磨,就能搞清楚它的门道,让数学为咱们的学习和生活服务!怎么样,这下对复化中矩形求积公式余项是不是有点感觉啦?。