结构力学虚功原理最小势能原理解题示例

9 虚功原理和结构的位移计算习题1. 引言虚功原理是结构力学中一项重要的基本原理，它可以用于解决各种结构的位移计算问题。

本文将通过一些习题来演示如何应用虚功原理进行位移计算。

2. 虚功原理简介虚功原理是指在结构力学中，结构在虚位移下所进行的虚功等于零。

虚位移是指结构在受力作用下的无限小位移，不违反实际情况下的几何和边界条件。

利用虚功原理，可以建立结构的平衡方程，并求解未知的位移。

3. 习题一考虑一个简支梁，受到一个集中力F作用在梁的中点。

已知梁的长度L和截面的惯性矩I，求梁的最大挠度。

解答：根据虚功原理，可以得到以下方程：$$\\int_{0}^{L} M \\cdot \\delta dL - F \\cdot \\delta\\cdot \\frac{L}{2} = 0$$其中M为弯矩，$\\delta$为虚位移。

由弯矩与挠度之间的关系，可以得到：$$M = -\\frac{F}{2}L + F \\cdot x$$代入上述方程，得到：$$\\int_{0}^{L} \\left(-\\frac{F}{2}L + F \\cdot x\\right) \\cdot \\delta dL - F \\cdot \\delta \\cdot \\frac{L}{2} = 0$$对上述方程两边进行积分并整理，可以得到：$$\\frac{FL^3}{6EI} = \\delta$$所以梁的最大挠度为$\\frac{FL^3}{6EI}$。

4. 习题二考虑一个简支梁，长度为L，弹性模量为E，截面惯性矩为I，受到一个均布载荷q作用在梁上。

已知梁的两端处的位移分别为0和$\\delta_1$，求梁上某一点的位移。

解答：根据虚功原理，可以得到以下方程：$$\\int_{0}^{L} \\left(-M\\right) \\cdot \\delta dL -\\int_{0}^{L} q \\cdot \\delta dL = 0$$对上述方程两边进行积分并代入弯矩与挠度之间的关系，可以得到：$$\\frac{1}{2}EI \\cdot \\delta - \\frac{qL^2}{2} \\cdot \\delta = 0$$整理上述方程，可以求解出$\\delta$的值。

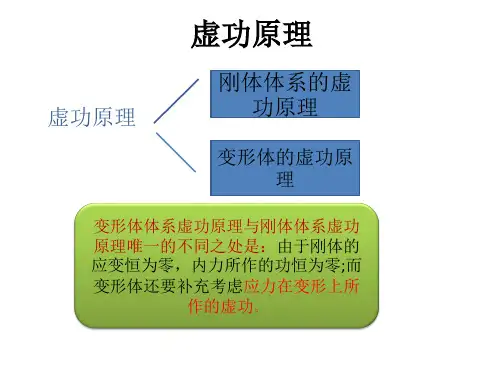
采用最小势能原理求解应力分量全文共四篇示例，供读者参考第一篇示例：最小势能原理是弹性力学中一个非常重要的原理，它可以用来求解应力分量的问题。

弹性力学是研究固体材料受到外力作用后发生变形的力学学科，而应力是描述固体材料内部受力情况的物理量。

在实际工程中，我们经常需要求解材料内部受力状态，从而设计合适的结构来满足工程需求。

而最小势能原理可以帮助我们更好地求解这些问题。

最小势能原理是从变分原理和势能公式出发推导出来的，在弹性力学中有非常广泛的应用。

它的基本思想是，当一个固体材料受到外力作用时，它的应变能和弹性势能有最小值。

在求解应力分量时，我们可以利用最小势能原理推导出应力的求解方程，并通过求解这个方程来得到材料内部的应力分布。

在应用最小势能原理求解应力分量时，首先我们需要建立适当的应力模型，通常是根据胡克定律建立弹性模型。

然后我们需要根据最小势能原理列出变分问题的表达式，再通过变分运算求取势能的最小值。

通过这样的方法，我们可以得到材料内部受力情况的详细信息。

最小势能原理在工程领域应用非常广泛，特别是在材料力学、结构力学以及土木工程等领域。

通过应用最小势能原理求解应力分量，我们可以更好地了解材料内部的受力情况，为设计和分析工程结构提供有力的支撑。

第二篇示例：最小势能原理是结构力学中一种用来求解结构各部分内应力的方法。

通过该原理，可以将结构的变形过程看作是势能最小化的过程，从而推导出结构内应力的分布。

在工程实践中，采用最小势能原理求解应力分量是一种常见的方法，具有较高的准确性和可靠性。

我们来看一下最小势能原理的基本思想。

在结构受力的过程中，结构会产生内部应力，这些内部应力是由外部荷载作用在结构上所产生的。

假设结构在荷载作用下发生微小变形，为了求解结构各部分的内应力，我们可以假定变形过程是虚功平衡的，即在变形过程中，外部力所做的虚功等于内部力所做的虚功。

根据这一假定，可以得到结构的最小势能表达式为：Π = ∫V σij εij dV其中Π表示结构的总势能，σij代表结构的应力分量，εij代表结构的应变分量，V表示结构的体积。

虚位移原理和最小势能原理嘿，朋友们！今天咱来聊聊虚位移原理和最小势能原理呀。

你说这虚位移原理啊，就好像是一个神奇的魔法规则。

想象一下，一个物体在各种力的作用下，它可能有很多种潜在的运动方向和方式，就像我们面对很多选择一样。

而虚位移原理呢，就是帮我们找出在这些可能中，哪种最有可能发生。

就好比你站在十字路口，要决定往哪边走，虚位移原理就是那个能告诉你最优路径的小指南。

再来说说最小势能原理，这可真是个有趣的家伙！它就像是物体的一种“偷懒”天性。

物体总是倾向于处在势能最小的状态，就好像我们都喜欢找最舒服的姿势待着一样。

比如说一个球，它肯定是会滚到最低的地方才安稳呢，这就是它在追求最小势能呀。

你看，在我们的日常生活中，不也常常能看到类似的情况吗？比如我们都喜欢走最省力的路，找最轻松的方式做事。

这和最小势能原理不是很像吗？而且啊，这两个原理可不仅仅是理论上的东西哦。

工程师们在设计各种结构的时候，可都得好好考虑它们呢。

要是不遵循这些原理，那设计出来的东西可能就不牢固，说不定哪天就出问题啦。

想想看，如果建一座桥，不考虑虚位移原理和最小势能原理，那桥可能摇摇晃晃的，谁敢走啊？或者制造一个机器，不按照这些原理来，那不是浪费材料又达不到效果嘛。

在大自然中也到处都是它们的身影呢！那些山川河流的形成，不也是各种力量作用的结果，遵循着这些原理吗？是不是很神奇呢？所以啊，可别小看了这虚位移原理和最小势能原理。

它们就像是隐藏在物理世界里的智慧密码，等待着我们去发现和运用。

它们让我们更好地理解这个世界，也让我们能创造出更美好的东西。

我们应该好好研究它们，利用它们，让它们为我们的生活和社会发展发挥更大的作用呀！这不就是物理学的魅力所在嘛！原创不易，请尊重原创，谢谢!。

虚功原理例题虚功原理是力学中的一个重要原理，它是用来分析静力学和动力学问题的有效方法。

虚功原理的应用范围非常广泛，可以用来求解各种复杂的结构和力学问题。

下面，我们通过一些例题来深入理解虚功原理的应用。

例题一，弹簧力的虚功。

假设有一个弹簧，其劲度系数为k，原长为l0。

现有一个质量为m的物体，静止放在弹簧的一端，另一端固定在墙上。

现在用一个外力F缓慢地将物体拉伸至位移x处，然后保持静止。

求弹簧的变形量和外力F。

解，根据虚功原理，外力F对物体所做的虚功等于弹簧对物体所做的虚功。

因为在静止状态下物体受到的合外力为零，所以外力F和弹簧的弹力大小相等，方向相反。

虚功原理可以表示为Fδx = kxδx，即Fdx = kxdx，两边积分得到∫Fdx = ∫kxdx，解得F = kx。

例题二，斜面上的物体。

有一质量为m的物体放在倾角为α的光滑斜面上，斜面的长度为L。

现在用一个外力F水平地拉动物体，使其在斜面上运动，求外力F。

解，根据虚功原理，外力F对物体所做的虚功等于重力对物体所做的虚功。

在斜面上，物体受到的重力分解为垂直于斜面方向和平行于斜面方向的两个分力，其中平行于斜面方向的分力不做虚功。

所以外力F对物体所做的虚功等于重力在斜面方向上的分力mgsinα与位移L的乘积，即Fδx = mgsinαδx，解得F = mgsin α。

例题三，摩擦力的虚功。

有一质量为m的物体放在水平面上，施加一个外力F使其运动，求外力F。

解，根据虚功原理，外力F对物体所做的虚功等于摩擦力对物体所做的虚功。

摩擦力的大小与物体所受的压力成正比，所以外力F对物体所做的虚功等于摩擦力f与位移x的乘积，即Fδx = fδx，解得F = f。

通过以上例题的分析，我们可以看到虚功原理在力学问题中的重要应用。

它可以帮助我们求解各种复杂的力学问题，是力学分析中的重要工具。

希望通过这些例题的学习，能够对虚功原理有更深入的理解，为进一步学习力学打下坚实的基础。

悬臂梁是工程中常见的结构之一，其在受力作用下会产生弯曲变形。

为了准确计算悬臂梁的弯曲情况，工程师常常利用虚功原理和最小势能原理进行分析和计算。

本文将介绍虚功原理和最小势能原理的基本概念，并结合实际案例，详细阐述利用这两种原理来计算悬臂梁弯曲的方法和步骤。

一、虚功原理的基本概念虚功原理是结构力学中的基本原理之一，它是由法国工程师达朗贝尔提出的。

虚功原理的核心思想是，当结构受力产生变形时，外力所做的虚功等于内力所做的实功。

在应用虚功原理计算悬臂梁弯曲时，首先要确定梁的受力情况，然后利用虚功原理建立相应的方程，通过对结构进行虚位移，得出悬臂梁的弯曲方程，并进行求解。

二、最小势能原理的基本概念最小势能原理是另一种常用的结构力学分析方法，它也被称为变分原理。

最小势能原理的核心思想是，在受力平衡的条件下，结构的势能达到极小值。

利用最小势能原理计算悬臂梁弯曲的过程，首先要确定梁的受力情况和边界条件，然后建立势能方程，通过对势能方程进行变分，得出悬臂梁的弯曲方程，并进行求解。

三、利用虚功原理计算悬臂梁弯曲的方法和步骤1.确定悬臂梁的受力情况，包括外力和内力；2.建立虚功方程，根据虚功原理，外力所做的虚功等于内力所做的实功；3.通过对结构进行虚位移，得出悬臂梁的弯曲方程；4.根据悬臂梁的边界条件和约束条件，进行方程求解，得出梁的弯曲情况。

四、利用最小势能原理计算悬臂梁弯曲的方法和步骤1.确定悬臂梁的受力情况和边界条件；2.建立梁的势能方程，根据最小势能原理，势能达到极小值时，梁处于受力平衡状态；3.对势能方程进行变分，得出悬臂梁的弯曲方程；4.根据悬臂梁的约束条件，进行方程求解，得出梁的弯曲情况。

五、实例分析以一根悬臂梁受均布载荷为例，利用虚功原理和最小势能原理进行弯曲计算。

首先确定悬臂梁的受力情况和边界条件，然后分别建立虚功方程和势能方程，通过对方程进行求解，得出悬臂梁的弯曲方程和受力分布情况。

六、结论通过本文的介绍和实例分析，可以看出利用虚功原理和最小势能原理计算悬臂梁弯曲的方法是科学严谨的。

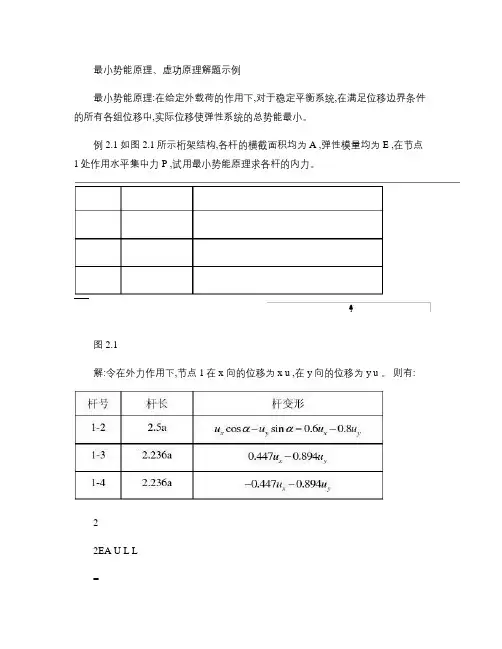
第十一章最小势能原理11.1 概述一、静力法二、能量法1、最小势能原理2、最小余能原理。

11.2 线弹性变形体系的变形势能一、弹性体的应变能的概念。

（1）拉伸应变能（11-1）式中N是轴力，EA是截面抗拉刚度，Δl为杆件的伸长量，U表示变形能。

（2）弯曲应变能（11-2）式中M是弯矩，EI是截面抗弯刚度，κ为曲率。

（3）剪切应变能梁发生横力弯曲时，除有弯曲应变能外，还有剪切应变能（11-3）式中Q是剪力，GA/k是截面抗剪刚度，γ0为平均剪应变，k 是与截面切应力分布规律有关的系数。

（4）圆轴扭转应变能11-4）式中M n是扭矩，GI p是截面抗扭刚度，φ为扭转角，I p是截面极惯性矩。

应变能有以下的性质。

（1）应变能总是正的，因为在它的计算公式中，M、N和Q都是二次方。

（2）计算应变能时不能应用叠加原理，即体系在几个力同时作用下的应变能，不能由这几个力分别作用下的应变能相叠加而得到（以单个杆同时受轴力N1和N2的作用为例），即（3）应变能是状态函数。

从式（11-6）可以看出，只要体系的最后变形状态确定，应变能即惟—地确定。

也就是说，如果有几组荷载作用于同一体系，不论其作用的先后次序如何，只要最后的变形形态相同，则在体系内储存的变形势能也都相同。

11.3 线性变形体系的最小势能原理首先给出线性变形体系总势能Π的定义，即Π＝U＋W （11-7）式中U为体系的应变能，W为体系的外力势能。

设结构上作用荷载P1、P2、P3、…、P n。

结构在某一位移状态中与荷载P i对于应的位移为Δi，则结构的外力势能为（11-8）图11-1 例11-1图11.4 里兹法一、里兹法是建立在最小势能原理基础上的一种近似分析方法。

其基本思路是在位移的级数展开式中取有限项，使无限多个未知参数变为有限个，并根据最小势能原理应用势能的驻值条件来求解。

里兹法就是将一个无限自由度体系用有限自由度体系来代替，并依据最小势能原理求得近似解。

匀质杆AB始终在平面内，A端靠在墙上，B端在一光滑曲面上，如图所示。

若无论B在何处杆均受力平衡，求曲面方程。

如图所示，四根相同的长度为l的光滑轻杆由铰链连接成菱形，一轻绳系在两对角线之间，下部挂一重量为P的重物，系统放置于两根等高相距为2a（2a<2l）的杆上，求绳中的张力？（φ角已知）如图所示，一竖立在竖直平面内的半圆空心管，管内刚好装有2n个光滑小珠子，已知每个珠子重力为W，求第i个珠子与第i+1个珠子的作用力Ni。

如图所示，一个外半径为R1，内半径为R2的圆柱形电容器，竖直地插进相对介电常数为εr 的密度为ρ的电解液中，若将电容器接上电压为U 的电源，求电解液中液面上升的高度第一题，常规做法用受力分析，建立水平竖直方向平衡方程，暴力解之。

（约束力合力沿法向）能量方法，利用随遇平衡，势能V 恒不变，解得y=f(x)。

（具体见高妙）虚功原理：因为此题为理想约束，主动力为重力，虚位移中主动力做功为0，即 P δyc=0 yc=常量由几何关系：yc=y+2221x l - 故yc=y+2221x l -=常量 因x=0时y=0，故常量=21故y=21⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--2x 11l第二题，直接虚功原理……建立如图所示坐标系，把绳子忽略，于是两个拉力变为主动力T ，另一个主动力为P ，约束为理想约束，则有：x A =lsin ϕ ϕδϕδcos x l A =………………………………………..①ϕδϕϕδϕϕδϕ2sin sin 2cot cos 2al y a l y P P +-=-=……………….②由虚功原理得：-2T P A P y x δδ+=0 将①②代入，得T=P ⎪⎪⎭⎫⎝⎛-ϕϕϕtan cos sin 22l a第三题设任意珠子的球心到管的圆心为OO ’长度为R ，前面i 个球为系统质心为C ，设CO 长度为L 。

由虚功原理：N ()θθθθαd Wd L iWd d R cos i sin cos i == 其中α=n4π即N αθcos cos i R iWL =现在的目的就是求质心的位置函数L 和θ 由对称性已知角度θ=ααi i =221求L 用旋转矢量，如图所示I 个大小为mR 、方向一次相差角度2α的矢量和的大小应该为imL 有：()()ααααsin sin sin sin 22imL i i R L i mR ==即代入N 的表达式得：()()()()W n n i i i W R i i i P iWR iWL N i ⎪⎪⎪⎪⎭⎫ ⎝⎛====2sin 2sin cos sin cos sin cos cos sin sin cos cos ππαααααααααθ第四题为了求液面上升高度，就得求液体所受电场力。

虚功原理例题虚功原理是力学中的一个重要原理，它在解决静力学和动力学问题中有着广泛的应用。

虚功原理的核心思想是系统受力平衡时，任何虚位移所做的功都为零。

通过虚功原理，我们可以简化和系统化力学问题的求解过程，使得复杂的力学问题变得更加清晰和易于理解。

下面，我们通过几个例题来深入理解虚功原理的应用。

例题一：如图所示，质量为m的物体通过绳子和光滑的滑轮与墙面连接，滑轮的质量可以忽略不计。

求当物体下降h时，绳子所做的功。

解析：根据虚功原理，我们可以假设物体下降了Δh的虚位移，此时绳子所做的虚功可以表示为W=mgΔh。

由于绳子是光滑的，所以滑轮对绳子所做的虚功为零。

根据虚功原理，物体所受的重力和绳子的拉力平衡，因此绳子所做的虚功也为零。

所以绳子所做的功为零。

例题二：一个质量为m的物体放在倾角为θ的光滑斜面上，斜面的长度为L。

求当物体下降h时，重力对斜面所做的功。

解析：当物体下降h时，我们可以假设斜面上升Δh的虚位移，此时重力对斜面所做的虚功可以表示为W=mgΔh。

根据虚功原理，斜面对物体的支持力与物体下降的高度有关，所以斜面对物体所做的虚功也不为零。

根据几何关系，斜面对物体所做的功可以表示为W=mgLsinθ。

因此，重力对斜面所做的功为W=mgLsinθ。

例题三：一个质量为m的物体通过绳子与墙面连接，绳子的另一端连接着一个质量为M的物体。

求当物体下降h时，绳子对墙面的拉力所做的功。

解析：当物体下降h时，我们可以假设绳子下降Δh的虚位移，此时绳子对墙面的拉力所做的虚功可以表示为W=TΔh。

根据虚功原理，绳子对墙面的拉力与物体下降的高度有关，所以绳子对墙面的拉力所做的虚功不为零。

因此，绳子对墙面的拉力所做的功为W=Th。

通过以上例题的分析，我们可以看到虚功原理在力学问题中的重要作用。

它不仅可以简化问题的求解过程，还可以帮助我们更加深入地理解力学问题背后的物理本质。

希望通过这些例题的讲解，能够对虚功原理有一个更加清晰的认识。