下载文档原格式
最小势能原理、虚功原理解题示例最小势能原理：在给定外载荷的作用下，对于稳定平衡系统，在满足位移边界条件的所有各组位移中，实际位移使弹性系统的总势能最小。
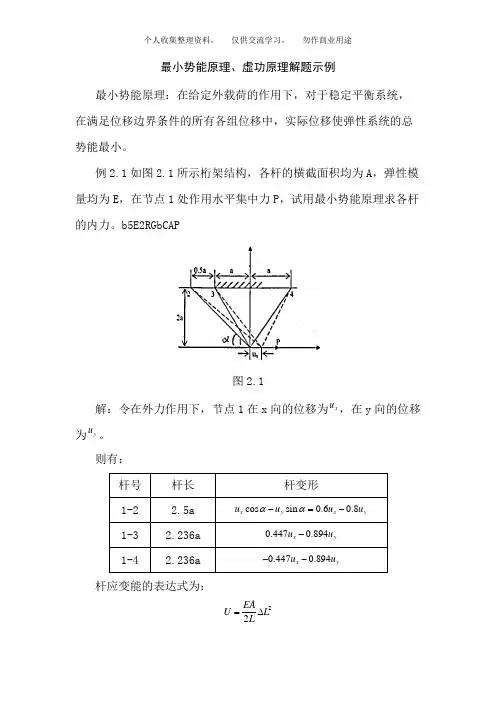
例2.1如图2.1所示桁架结构，各杆的横截面积均为A ，弹性模量均为E ，在节点1处作用水平集中力P，试用最小势能原理求各杆的内力。
图2.1解：令在外力作用下，节点1在x 向的位移为，在y 向的位移为。
x u y u 则有：杆号杆长杆变形1-22.5acos sin 0.60.8x y x y u u u u αα-=-1-32.236a0.4470.894x y u u -1-42.236a0.4470.894x y u u --杆应变能的表达式为：22EA U L L=∆则系统的总势能为：固树 （一）一次主题党词找标准、找差词，交流思想体会集中学习，每次确定习。
支部每季度召开于担当作为”、“坚1。
（三）开展“四个讲班子成到联系区县X X 局带头家学者给党员干部习教育实施方以下简称，做合“()()()()222220.60.80.4470.8942 2.52 2.2360.4470.8942 2.2360.1610.1920.486i xx y x y x y x x x y y xU Pu EA EAu u u u a aEAu u Pu a EA u u u u Pu a∏=-=-+-⨯⨯+---⨯=-+-∑由最小势能原理可知，当结构处于稳定平衡状态时，有：0;0x yu u ∂∏∂∏==∂∂即：()()0.3230.19200.1920.9720x y x y EAu u P a EAu u a--=-+=解得：3.510.694x y Pa u EA Pa u EA==杆的内力可由公式：求得，故各杆的内力为：EAN L L=∆1213140.620.4250.979N PN PN P---===-例2.2如图2.2所示的梁，其上作用有均布载荷q ，试用最小势能原理求其挠度曲线。
9 虚功原理和结构的位移计算习题1. 引言虚功原理是结构力学中一项重要的基本原理，它可以用于解决各种结构的位移计算问题。
本文将通过一些习题来演示如何应用虚功原理进行位移计算。
2. 虚功原理简介虚功原理是指在结构力学中，结构在虚位移下所进行的虚功等于零。
虚位移是指结构在受力作用下的无限小位移，不违反实际情况下的几何和边界条件。
利用虚功原理，可以建立结构的平衡方程，并求解未知的位移。
3. 习题一考虑一个简支梁，受到一个集中力F作用在梁的中点。
已知梁的长度L和截面的惯性矩I，求梁的最大挠度。
解答：根据虚功原理，可以得到以下方程：$$\\int_{0}^{L} M \\cdot \\delta dL - F \\cdot \\delta\\cdot \\frac{L}{2} = 0$$其中M为弯矩，$\\delta$为虚位移。
由弯矩与挠度之间的关系，可以得到：$$M = -\\frac{F}{2}L + F \\cdot x$$代入上述方程，得到：$$\\int_{0}^{L} \\left(-\\frac{F}{2}L + F \\cdot x\\right) \\cdot \\delta dL - F \\cdot \\delta \\cdot \\frac{L}{2} = 0$$对上述方程两边进行积分并整理，可以得到：$$\\frac{FL^3}{6EI} = \\delta$$所以梁的最大挠度为$\\frac{FL^3}{6EI}$。
4. 习题二考虑一个简支梁，长度为L，弹性模量为E，截面惯性矩为I，受到一个均布载荷q作用在梁上。
已知梁的两端处的位移分别为0和$\\delta_1$，求梁上某一点的位移。
解答：根据虚功原理，可以得到以下方程：$$\\int_{0}^{L} \\left(-M\\right) \\cdot \\delta dL -\\int_{0}^{L} q \\cdot \\delta dL = 0$$对上述方程两边进行积分并代入弯矩与挠度之间的关系，可以得到：$$\\frac{1}{2}EI \\cdot \\delta - \\frac{qL^2}{2} \\cdot \\delta = 0$$整理上述方程，可以求解出$\\delta$的值。
结构力学虚功原理结构力学虚功原理是结构力学中的一个重要概念，它是通过能量方法来分析结构的力学性能和变形规律的一种理论工具。
虚功原理的提出，为结构力学的研究和工程实践提供了一种简洁而有效的分析方法，对于工程结构的设计和优化具有重要意义。
首先，我们来看一下虚功原理的基本假设。
虚功原理假设结构在受力作用下，其位移满足虚位移的要求。
所谓虚位移，是指在结构受力作用下，结构的位移不仅满足实际受力平衡条件，还需满足虚位移的平衡条件。
这个假设为后续的分析提供了基础，也是虚功原理得以应用的前提。
虚功原理的核心思想是能量守恒。
在结构受力作用下，结构内部会产生应变能和变形能，而外部施加的力会做功。
根据能量守恒的原理，结构受力平衡时，内部的能量增加等于外部做功，这就是虚功原理的基本表达式。
通过对这个表达式的分析，可以得到结构的受力方程和变形规律，为结构设计和分析提供了重要的依据。
虚功原理的应用非常广泛，它可以用于分析各种类型的结构，包括梁、柱、桁架等。
在工程实践中，虚功原理常常被用于分析复杂结构的受力性能，比如钢结构、混凝土结构等。
通过虚功原理的分析，可以得到结构的内力分布、变形情况，为结构的设计和施工提供了重要的参考依据。
除此之外，虚功原理还可以用于结构的优化设计。
通过对结构受力性能的分析，可以找到结构的薄弱环节，进而对结构进行合理的优化设计，提高结构的受力性能和使用效率。
这对于工程结构的安全性和经济性都具有重要意义。
总的来说，结构力学虚功原理是结构力学中的重要理论工具，它通过能量方法来分析结构的受力性能和变形规律，为工程结构的设计、分析和优化提供了重要的理论依据。
在工程实践中，虚功原理的应用具有重要的意义，可以帮助工程师更好地理解和分析结构的受力性能，为工程结构的设计和施工提供重要的参考依据。
通过对虚功原理的深入研究和应用，可以推动结构力学理论的发展，为工程结构的安全性和经济性提供更好的保障。
最小势能原理、虚功原理解题示例
最小势能原理：在给定外载荷的作用下，对于稳定平衡系统，在满足位移边界条件的所有各组位移中，实际位移使弹性系统的总势能最小。
例2.1 如图2.1所示桁架结构，各杆的横截面积均为A ，弹性模量均为E ，在节点1处作用水平集中力P ，试用最小势能原理求各杆的内力。
图2.1
解：令在外力作用下，节点1在x 向的位移为x u ，在y 向的位移为y u 。
则有：
2
2EA U L L
=
∆ 则系统的总势能为：
()()()()
222220.60.80.4470.8942 2.52 2.2360.4470.8942 2.2360.1610.1920.486i x
x y x y x y x x x y y x
U Pu EA EA
u u u u a a
EA
u u Pu a EA u u u u Pu a
∏=-=
-+-⨯⨯+---⨯=-+-∑ 由最小势能原理可知，当结构处于稳定平衡状态时，有：
0;0x y
u u ∂∏∂∏
==∂∂ 即：
()()0.3230.19200.1920.9720x y x y EA
u u P a
EA
u u a
--=-+=
解得：
3.510.694x y Pa u EA Pa u EA =
=
杆的内力可由公式：EA
N L L
=
∆求得，故各杆的内力为： 1213140.620.4250.979N P N P N P
---===-
例2.2 如图2.2所示的梁，其上作用有均布载荷q ，试用最小势能原理求其挠度曲线。
图2.2
解：令梁的挠度函数为()x ω，它必须满足以下几个条件：
1、必须满足几何边界条件，但不一定满足平衡条件和力的边界条件；
2、由于有均布载荷q 的作用，故()x ω应为x 的4次多项式。
故，考虑到梁左侧为固支，可设：
()()22012x x a a x a x ω=--
梁右侧需满足：
()|0x L x ω==
且梁右侧没承受弯矩，有：
()
220x L
d x dx ω==（力的边界条件）
代入边界条件，有：
()342
120.60.4x x L a L x L L ω⎛⎫=-+ ⎪⎝
⎭
等截面梁的弯曲应变能表达式为：2
220
1
2L
z d U EJ dx dx ω⎛⎫= ⎪⎝⎭
⎰
【根据平面假设，梁在受弯曲变形后，其横截面仍保持为平面，它一方面有挠度()x ω，一方面横截面在梁变形过程中旋转了一个角度
d dx
ω
，由于该转角的存在，使得距离中性轴为y 处的x 方向的位移为d u y dx ω
=-，应变22x d y dx ωε=-，
弯曲应力为22x d yE dx ω
σ=-，因此，等截面梁的弯曲应变能为：
2
2
2
2
2222001111
2222L
L
x x x z V V A
d d U dV E dV E dx y dA EJ dx dx dx ωωσεε⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰】
则系统的总势能为：
()()()2
220
012L
L d x EJ dx q x x dx dx ωω⎧⎫⎡⎤⎪⎪∏=-⎨⎬⎢⎥⎣⎦⎪⎪⎩⎭
⎰
⎰ 由最小势能原理可知，当结构处于稳定平衡状态时，有：
0δ∏=
又：
()()()()()()()()222
20044
0034342211122009.60.60.40.60.40
L
L
L L L L d x d EJ x dx q x x dx dx dx d x EJ x dx q x x dx dx a x x x x EJ L x a dx qL x a dx L L L L L ωδδωδωωδωδωδδ⎡⎤∏=-⎢⎥⎣⎦
=-⎛⎫⎛⎫=-+--+ ⎪ ⎪⎝⎭⎝
⎭=⎰⎰⎰⎰⎰⎰ 【()231231.2 1.6x x x L x a L L δωδ⎛⎫
=-+ ⎪⎝⎭】 由于变分可取任意值，故有：
119.69.6qL
EJa qL
a EJ
=⇒
=
所以：
()2342
20.60.49.6qL x x x x EJ L L ω⎛⎫=-+ ⎪⎝⎭
虚功原理：当弹性体在外载荷作用下处于平衡状态时，对任意为约束所容许的虚位移，外力虚功等于内力虚功。
虚功原理又称为虚位移原理。
例2.3
P
图2.3
解：令在外载荷P 作用下，梁的转角为α，则各杆的变形为：
12323L L L L L L α
α
α∆=∆=∆=
给梁施加一个虚位移：δα 则外力虚功为：
7
2
W PL δδα=
虚应变能为：
()()
()123231223314EA EA EA U L L L L L L L L L
EAL EAL δδαδαδααδααδα
=
∆+∆+∆=+⨯+⨯= 由虚功原理，有：W U δδ=，即：
7
142
4P PL EAL EA
δααδαα=⇒
=
故梁的位移为：
4Px
d x EA
α==
图2.4
【虚功原理的其它例题可参见理论力学（静力学）第四章第7节】
例2.2 若用虚功原理求解，其步骤如下：
解：令梁的挠度函数为()x ω，它必须满足以下几个条件：
1、必须满足几何边界条件，但不一定满足平衡条件和力的边界条件；
2、由于有均布载荷q 的作用，故()x ω应为x 的4次多项式。
故，考虑到梁左侧为固支，可设：
()()22012x x a a x a x ω=--
梁右侧需满足：
()|0x L x ω==
且梁右侧没承受弯矩，有：
()
220x L
d x dx ω==
代入边界条件，有：
()342
120.60.4x x L a L x L L ω⎛⎫=-+ ⎪⎝
⎭
等截面梁的弯曲应变能表达式为：2
220
1
2L
z d U EJ dx dx ω⎛⎫= ⎪⎝⎭
⎰
给梁施加一个虚位移：()342
120.60.4x x x a L x L L δωδ⎛⎫=-+ ⎪⎝⎭
则其外力虚功为：
()()0
L
W q x x dx δδω=⎰
虚应变能为：
()()22
2
2
L
d x d U EJ x dx dx dx ωδδω⎡⎤=⎢⎥⎣
⎦⎰
由虚功原理，有：W U δδ=，即：
()
()()()44003434
2211122009.60.60.40.60.4L
L L L d x EJ x dx q x x dx
dx a x x x x EJ L x a dx qL x a dx L L L L L ωδωδωδδ=⎛⎫⎛⎫-+=-+ ⎪ ⎪⎝⎭⎝⎭⎰⎰⎰⎰ 由于虚位移是任意的，故：
119.69.6qL
EJa qL
a EJ
=⇒
=
所以：
()2342
20.60.49.6qL x x x x EJ L L ω⎛⎫=-+ ⎪⎝⎭
【由此可以看出，虚位移原理和最小势能原理是一致的，都是从能量的角度来阐述超静定结构在平衡状态所需满足的条件，即用能量方程来替代变形协调条件。
在做题时，个人觉得最小势能原理具有更好的操作性。
】。
