宁夏银川市第一中学2020届高三数学上学期第三次月考试题文【含答案】

高三数学（理）试卷一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知全集为R ，集合{}2xA y y ==，{}240B x x =∈-≤Z ，则下列结论正确的是（ ）． A. {}0,1,2A B =B. [)1,A B ∞=+C.()(],1RA B =-∞ D.(){}2,1,0RA B =--【答案】D 【解析】 【分析】先求解集合,A B 再判断即可. 【详解】{}{}21xA y y y y ===≥,{}{}2402,1,0,1,2B x x =∈-≤=--Z .故{}1,2AB =,A 错误.{}[)2,1,01,A B =-∞-+,B 错误.()(]{},12RA B =-∞.C 错误.(){}2,1,0RA B =--.D 正确.故选：D【点睛】本题主要考查了集合间的基本运算,属于基础题型. 2.设a ，b ∈R ，那么“＞1”是“a ＞b ＞0”的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 充要条件D. 既不充分也不必要条件 【答案】B 【解析】试题分析：a ＞b ＞0，可推出，而当，时，例如取a=﹣2，b=﹣1，显然不能推出a＞b ＞0，由充要条件的定义可得答案．解：由不等式的性质，a ＞b ＞0，可推出，而当，时，例如取a=﹣2，b=﹣1，显然不能推出a ＞b ＞0． 故是a ＞b ＞0的必要不充分条件．故选B ．考点：必要条件、充分条件与充要条件的判断．3.已知,x y ∈R ，i 为虚数单位，且()2i 15i x y +-=+，则()1i x y+-=（ ）． A. 2- B. 2i - C. 2D. 2i【答案】B 【解析】 【分析】根据复数相等的性质求解,x y 再计算()1i x y+-即可.【详解】因为()2i 15i x y +-=+,故25,1x y +=-=解得3,1x y .故()()21i 1i 2x yi +-=-=-.故选：B【点睛】本题主要考查了复数的基本运算,属于基础题型. 4..若log 2log 20a b <<，则（ ） A. 01a b <<< B. 01b a <<< C. 1a b >> D. 1b a >>【答案】B 【解析】 【分析】利用对数函数的性质求解．【详解】∵log 2lo 1g 20log a b a <<=，∴0＜a ＜1，0＜b ＜1，∵2＞1，要使log b 2＜0 ∴0＜b ＜1，∵log 2log 20a b <<，∴a ＞b ，且0＜a ＜1，∴01b a <<<． 故选B ．【点睛】本题考查两个数的大小的比较，注意对数函数的性质的合理运用，属于基础题．5.在ABC 中，3AB =，4AC =，BC =AC 边上的高为（ ）．A.2C. D. 【答案】B 【解析】 【分析】利用余弦定理求解A 的大小,再利用AC 边上的高sin h AB A =⋅即可.【详解】易得222916131cos 2242AB AC BC A AB AC +-+-===⋅,又()0,A π∈.故3A π=.故AC 边上的高sin 2h AB A =⋅=. 故选：B【点睛】本题主要考查了解三角形的运用,需要根据题意选取合适的公式求解即可.属于基础题型.6.若()()21ln 22f x x b x =-++在()0,∞+上是减函数，则b 的取值范围是（ ）．A. ()1,-+∞B. ()0,∞+C. (],1-∞-D. (],0-∞【答案】D 【解析】 【分析】根据减函数的导函数值在区间上小于等于0求解即可. 【详解】()'2bf x x x =-++,由题02b x x -+≤+在()0,∞+上恒成立.又20x +>故()2b x x ≤+在()0,∞+上恒成立.又()2y x x =+对称轴1x =-.故()2y x x =+在()0,∞+单调递增.故()20y x x =+>,故0b ≤. 故选：D【点睛】本题主要考查了利用导函数解决单调性的问题,同时也考查了恒成立问题的参变分离方法,属于基础题型.7.设a ，b 均为单位向量，且它们的夹角为2π3，当a kb -取最小值时，实数k 的值为（ ）． A. 12- B. 1- C.12D. 1【答案】A 【解析】 【分析】将a kb -平方再分析最值即可. 【详解】()222221a kb a ka b kbk k -=-⋅+=++.故当12k =-时, a kb -取最小值.故选：A【点睛】本题主要考查了平行向量的模长运用,常用平方再分析的方法,属于基础题型. 8.已知函数()2cos2f x x x =+，则下列结论正确的是（ ）． A. ()f x 的图像关于直线π12x =对称 B. ()f x 的图像向左平移π6个单位后为偶函数图像C. ()f x 的图像关于点5π,06⎛⎫⎪⎝⎭对称 D. ()f x 的最小正周期为π，且在π0,3⎡⎤⎢⎥⎣⎦上为增函数 【答案】B 【解析】 【分析】利用辅助角公式化简再分析即可.详解】()2cos 22sin(2)6f x x x x π=+=+.对A,代入π12x =有2=1263πππ⨯+,不为正弦函数对称轴.故A 错误. 对B, ()f x 的图像向左平移π6个单位后为()2sin 22sin 22cos 2662g x x x x πππ⎡⎤⎛⎫⎛⎫=++=+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦为偶函数,故B 正确.对C,代入5π6x =有52sin(2)066ππ⨯+≠,故C 错误. 对D,()f x 最小正周期为π,在π0,3⎡⎤⎢⎥⎣⎦上52,666x πππ⎡⎤+∈⎢⎥⎣⎦不为单调递增区间.故D 错误. 故选：B【点睛】本题主要考查了辅助角公式的运用以及三角函数图像的性质判定,属于基础题型. 9.函数f(x)＝log 2|x|，g(x)＝－x 2＋2，则f(x)·g(x)的图象只可能是( ) A. B. C. D.【答案】C 【解析】因为函数f(x)，g(x)都为偶函数， 所以f(x)·g(x)也为偶函数， 所以图象关于y 轴对称，排除A ，D ； f(x)·g(x)＝(－x 2＋2)log 2|x|，当0<x<1时，f(x)·g(x)<0，排除B ，故选C. 10.已知数列{}n a ，若点()(),n n a n +∈N 均在直线()83y k x =-+上，则{}na 的前15项和等于（ ）． A. 42 B. 45C. 48D. 51【答案】B 【解析】 【分析】利用等差数列性质求解即可.【详解】{}n a 的前15项和15815S a =,又()88833a k =-+=,故1581545S a ==.故选：B【点睛】本题主要考查了等差数列的的性质及求和公式,属于基础题型. 11.已知函数()2n y a xn +=∈N 的图像在1x =处的切线斜率为1n a+，且当1n =时，此切线过点()2,3，则7a 的值为（ ）． A. 8 B. 16 C. 32 D. 64【答案】D 【解析】 【分析】求导后利用导函数的几何意义求解数列的递推公式,再推导出{}n a 为等比数列,求通项公式再求7a 即可.【详解】由题'2n y a x =,故12n n a a +=.又当1n =时,此切线过点()2,3,此时斜率1'2y a =,故切线方程为()1322y a x -=-,且与21y a x =相切.联立方程得()22111113222430a x a x a x a x a +-=⇒-+-=.显然10a ≠.故判别式()()21111244301a a a a --=⇒=. 故{}n a 是以11a =为首项,公比为2的等比数列.故12n n a .故67264a ==.故选：D【点睛】本题主要考查了导数的几何意义以及数列的递推公式求解通项公式的方法.需要根据导数的几何意义求解对应的切线方程,再利用与二次函数相切则联立方程判别式为0的方法等.属于中等题型.12.已知奇函数()f x 满足()()()2f x f x x -=-∈R ，且[]0,1x ∈时，()()2log 1f x x =+，则关于x 的方程()()001f x m m -=<<在区间[]4,8-上的所有根之和是（ ）． A. 10 B. 8 C. 6 D. 4【答案】C 【解析】 【分析】根据函数的性质,且已知[]0,1x ∈时,()()2log 1f x x =+,可画出对应的函数图像,再分析()()001f x m m -=<<在区间[]4,8-上的所有根之和即可.【详解】由题,()()()2f x f x x -=-∈R ,则()()()24f x f x f x =-+=+,故()f x 周期为4.又奇函数()f x 关于()0,0对称,且()()2()f x f x f x -=-=-,故()f x 关于1x =-对称, 又[]0,1x ∈时,()()2log 1f x x =+则可画出区间[]4,8-上对应的函数图像.易得()()001f x m m -=<<即()()01f x m m =<<在区间[]4,8-上的根分别关于-3,1,5对称,故零点之和为()23156⨯-++=⎡⎤⎣⎦. 故选：C【点睛】本题主要考查了根据函数的关系推导函数性质以及函数图像的问题.需要先根据[]0,1x ∈时,()()2log 1f x x =+,画出[]0,1x ∈的图像,再根据函数性质补全图像.再利用图像求得零点之和.属于中等题型.二、填空题13.已知π3cos()6x -=，则πcos cos()3x x +-=__________． 【答案】-1 【解析】 【分析】注意观察角x 、36x x ππ--、的关系可发现x 、3x π-均能用已知角和特殊角6π表示出来，再用和差角公式展开即可求得结果． 【详解】πcos cos()3x x +-=][cos cos 6666x x ππππ⎡⎤⎛⎫⎛⎫-++-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 332cos cos 216632x ππ⎛⎫⎛⎫=-=⨯-⨯=- ⎪ ⎪ ⎪⎝⎭⎝⎭ 故答案为-1．【点睛】三角函数求值的三种类型(1)给角求值：关键是正确选用公式，以便把非特殊角的三角函数转化为特殊角的三角函数. (2)给值求值：关键是找出已知式与待求式之间的联系及函数的差异. ①一般可以适当变换已知式，求得另外函数式的值，以备应用； ②变换待求式，便于将已知式求得的函数值代入，从而达到解题的目的.(3)给值求角：实质是转化为“给值求值”，先求角的某一函数值，再求角的范围，确定角. 14.设向量1e ，2e 分别为单位向量，且夹角为π3，若122a e e =-，122b e e =+，则⋅=a b ______．【答案】32【解析】 【分析】根据平面向量的数量积运算即可.【详解】()()221212112233222322222e e e e a e e e e b -+=+⋅-=+-=⋅=⋅. 故答案为：32【点睛】本题主要考查了平面向量的基本运算,属于基础题型. 15.已知向量()2,3a =，()1,2b =-，若ma nb +与2a b -共线，则nm=______． 【答案】2- 【解析】 【分析】根据向量共线的方法分析系数关系即可.【详解】因为ma nb +与2a b -共线,故()()()220ma nb a b m a n b λλλ+=-⇒-++=, 又()2,3a =,()1,2b =-不共线,根据平面向量基本定理得0,20m n λλ-=+=. 故22n m λλ-==-. 故答案为：2-【点睛】本题主要考查了平行向量的性质与用法,直接根据平面向量基本定理判定即可.属于基础题型.16.已知数列{}n a 与{}n b 满足()1111nn n n n a b b a +++=+-，()312nnb +-=，且12a =，设数列{}n a 的前n 项和为n S ，则64S =______．【答案】560- 【解析】 【分析】分n 为奇数和偶数两种情况讨论即可.【详解】由()312nnb +-=,故当n 为偶数时,2n b =；当n 为奇数时,1n b =.又()1111nn n n n a b b a +++=+-,12a =故12121220204a b b a a a a +=⇒+=⇒=-. 故当n 为偶数时, 122n n a a ++=；当n 为奇数时, 120n n a a ++=.所以当n 为偶数时, 111122120n n n n n n a a a a a a ++--+=⎧⇒-=⎨+=⎩,即奇数项为公差为1的等差数列. 当n 为奇数时, 111120222n n n n n n a a a a a a ++--+=⎧⇒-=-⎨+=⎩即偶数项为公差为-2的等差数列. 又12a =,故641234636413632464...(...)(...)S a a a a a a a a a a a a =++++++=+++++++13632464(...)(...)(23...33)(4...66)a a a a a a =+++++++=+++-++32(233)32(466)16(35)56022⨯+⨯+=-=⨯-=-.故答案为：560-【点睛】本题主要考查了奇偶数列的求和问题,需要根据n 为奇数和偶数两种情况进行分类讨论,求和的时候再直接写出各项进行计算分析即可.属于中等题型.三、解答题17.在ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，已知()()2222sin sin 0bc A b a C -+-=．（1）求证：a ，b ，c 成等比数列； （2）若π3B =，试判断ABC 的形状． 【答案】（1）证明见解析（2）等边三角形【解析】 【分析】(1)利用正弦定理以及因式分解的方法证明20b ac -=即可. (2)利用余弦定理以及(1)中的2b ac =化简求得a c =即可. 【详解】（1）由已知应用正弦定理得()()22220b c a ba c -+-=,即()()20b aca c -+=,由于0a c +>,则20b ac -= 故a ,b ,c 成等比数列． （2）若π3B =,则222222cos b a c ac B a c ac ++-=+-, 由（1）知2b ac =,则2220+-=a c ac ,即a c =, 所以a b c ==,故ABC 为等边三角形．【点睛】本题主要考查了正余弦定理在解三角形中的运用,需要根据题目信息选择合适的定理进行化简分析,属于中等题型.18.设向量()sin 2,2a x =，()1,sin b x =，()f x a b =⋅，角A ，B ，C 分别为ABC 的三个内角，若()f x 在x A =处取得极值．（1）试求A 与()f A 的值；（2）当1AB AC ⋅=，求ABC 的最小外接圆半径． 【答案】（1）π3A =，()f A =2（2）3【解析】 【分析】(1)化简()f x a b =⋅再求导根据在x A =处取得极值可得π3A =,再算得()f A 即可.(2)化简1AB AC ⋅=,再利用余弦定理与基本不等式可得2BC ≥再利用正弦定理求外接圆的半径满足的关系式即可.【详解】（1）由()sin 2,2a x =,()1,sin b x =得()sin 22sin f x a b x x =⋅=+,则()()()22cos22cos 4cos 2cos 222cos 1cos 1f x x x x x x x '=+=+-=-+,由于()f x 在x A =处取得极值,那么()()()22cos 1cos 10f A A A '=-+=, 解得1cos 2A =或cos 1A =-． 又0πA <<,则π3A =,()2ππsin 2sin 332f A =+=． （2）若1AB AC ⋅=,即πcos 13AB AC ⋅=,则2AB AC ⋅=,所以222π2cos 23BC AB AC AB AC AB AC =+-⋅≥⋅=,即2BC ≥ 则2sin sin 3BCR A =≥=故ABC ． 【点睛】本题主要考查了解三角形与向量、导数以及基本不等式的综合运用,需要根据题意选择合适的公式进行化简,同时注意观察余弦定理中的结构找到基本不等式的用法即可.属于中等题型.19.已知数列{}n a 的前n 项和22n S n n =+．（1）求数列{}n a 的通项公式；（2）若等比数列{}n b 满足21b a =，423b a a =+，求数列{}n b 的前n 项和n T ．【答案】（1）()21n a n n +=+∈N（2）()3212n -或()1212n ⎡⎤--⎣⎦ 【解析】【分析】(1)分1,2n n =≥两种情况,利用通项公式与前n 项和的关系求解即可.(2)利用基本量法求解等比数列{}n b 的首项与公比,再利用求和公式求解即可.【详解】（1）由22n S n n =+得13a =,且2n ≥时,()()221212121n n n a S S n n n n n -=-=+----=+,显然13a =满足21n a n =+,故()21n a n n +=+∈N．（2）若等比数列{}n b 满足21b a =,423b a a =+,则由（1）得21341312b b q b b q ==⎧⎨==⎩,解得1322b q ⎧=⎪⎨⎪=⎩,或1322b q ⎧=-⎪⎨⎪=-⎩． 所以()()()1312132211122n nn n b q T q --===---或()()3121221122n n n T ⎡⎤---⎣⎦⎡⎤==--⎣⎦+ 【点睛】本题主要考查了根据前n 项和与求通项公式的方法,同时也考查了等比数列的基本量求法即求和的问题,属于中等题型.20.在数列{}n a 中，123a =，若函数()31f x x =+在点()()1,1f 处的切线过点()1,n n a a +． （1）求证：数列12n a ⎧⎫-⎨⎬⎩⎭是等比数列； （2）求数列{}n a 的通项公式与前n 项和公式n S ．【答案】（1）证明见解析（2）()113234n n ++- 【解析】【分析】 (1)求导后求导切线方程,代入()1,n n a a +求得131n n a a +=-,再构造数列证明即可.(2)根据(1)中构造的等比数列求出()1312n n a =+,再分组求和即可. 【详解】（1）由()31f x x =+得()23f x x '=,()12f =,()13f '=,则()f x 在点()()1,1f 处的切线方程为()()()111y f f x '-=-,即31y x =-．又此切线过点()1,n n a a +,则131n n a a +=-,即111322n n a a +⎛⎫-=- ⎪⎝⎭． 故12n a ⎧⎫-⎨⎬⎩⎭是公比为3的等比数列． （2）又12a =,由（1）知1111133222n n n a a -⎛⎫-=-⋅=⋅ ⎪⎝⎭,则()1312n n a =+,()()1313113232134n n n S n n +⎡⎤-⎢⎥=+=+--⎢⎥⎣⎦． 【点睛】本题主要考查了导数的几何意义以及构造数列求通项公式的方法,同时也考查了分组求和以及等比数列求和公式等.属于中等题型.21.已知()()2x f x ax e =+，()242g x x x =-++． 对于函数()f x 、()g x ，若存在常数k ，b ，使得x ∀∈R ，不等式()()f x kx b g x ≥+≥都成立，则称直线是y kx b =+函数()f x 与()g x 的分界线．（1）讨论函数()f x 的单调性；（2）当2a =时，试探究函数()f x 与()g x 是否存在“分界线”？若存在，求出分界线方程；若不存在说明理由．【答案】（1）见解析（2）2a =时，()f x 与()g x 存在“分界线42y x =+”，理由见解析【解析】【分析】(1)求导后分0a =,0a >与0a <三种情况讨论即可.(2)由题意,代入0x =时,有2b =,再根据二次函数的恒成立问题求得4k =,再证明()()()()()21220x h x f x kx b x e x =-+=+-+≥即可.【详解】（1）由()()2x f x ax e =+得()()2xf x ax a e '=++, 若0a =时,有()20xf x e '=>,则()f x 在R 上单调递增； 若0a ≠时,由()0f x '=解得21x a =--, 若0a >时,对于2,1x a ⎛⎫∈-∞-- ⎪⎝⎭,有()0f x '<；21,x a ⎛⎫∈--+∞ ⎪⎝⎭,有()0f x '>, 则()f x 在2,1a ⎛⎫-∞-- ⎪⎝⎭上单调递减,在21,a ⎛⎫--+∞ ⎪⎝⎭上单调递增； 若0a <时,对于2,1x a ⎛⎫∈-∞-- ⎪⎝⎭,有()0f x '>；21,x a ⎛⎫∈--+∞ ⎪⎝⎭,有()0f x '<,则()f x 在2,1a ⎛⎫-∞-- ⎪⎝⎭上单调递增,在21,a ⎛⎫--+∞ ⎪⎝⎭上单调递减． （2）当2a =时,()()21x f x x e =+,()242g x x x =-++,若()()f x kx b g x ≥+≥对x ∀∈R 都成立,即()22142x x e kx b x x +≥+≥-++对x ∀∈R 都成立． 则0x =时,有22b ≥≥；且242kx b x x +≥-++,对x ∀∈R 都成立,即2b =,()2420x k x b +-+-≥对x ∀∈R 都成立． 所以2b = ,4k =．此时,令()()()()()2122xh x f x kx b x e x =-+=+-+, 则()()224xh x x e '=+-, 令()()224()x h x x e t x '=+-=，在(,2]-∞-上()()224()0xh x x e t x '=+-=<恒成立， 又在()2,-+∞上()()230xt x x e '=+>， ∴()()224x h x x e '=+-在()2,-+∞单增且()()0020240h e '=+-=， 从而有0x ≥时,()0h x '≥；20x -<<时,()0h x '<,即在(),0-∞()0h x '<所以()h x 在(),0-∞上递减,在()0,∞+上递增．因此()()00h x h ≥=,即()42f x x ≥+．故2a =时,()f x 与()g x 存在“分界线42y x =+”．【点睛】本题主要考查了含参数的单调性讨论以及新定义的函数问题.主要是根据题意,代入特殊值找到对应的参数,再利用恒成立问题求解即可.属于难题.22.在平面直角坐标系xOy 中，曲线1C 的参数方程为2cos 2sin 2x y ϕϕ=⎧⎨=-⎩（ϕ为参数），在以O 为极点，x 轴的正半轴为极轴的极坐标系中，曲线2C 的极坐标方程为πcos 4ρθ⎛⎫+= ⎪⎝⎭ （1）求曲线1C 和2C 的直角坐标方程；（2）若点P 为1C 上任意一点，求点P 到2C 的距离的取值范围．【答案】（1）()2224x y ++=，20x y --=（2）[]0,2 【解析】【分析】(1)易得2cos 2sin 2x y ϕϕ=⎧⎨=-⎩表示圆,再利用极坐标中的公式化简πcos 4ρθ⎛⎫+= ⎪⎝⎭. (2)设曲线1C 上的任意一点()2cos ,2sin 2P ϕϕ-,求出P 到曲线2C 的距离公式,再利用三角函数的值域求解即可.【详解】（1）由2cos 2sin 2x y ϕϕ=⎧⎨=-⎩消去参数ϕ,得()2224x y ++=, 则曲线1C 的普通方程为()2224x y ++=．由πcos 4ρθ⎛⎫+= ⎪⎝⎭得cos sin 22ρθρθ-=即2x y -=． 则曲线2C 的直角坐标方程为20x y --=．（2）曲线1C 上的任意一点()2cos ,2sin 2P ϕϕ-到曲线2C 的距离为π2cos 4d ϕ⎛⎫===+ ⎪⎝⎭, 故点P 到曲线2C 的距离的取值范围为[]0,2．【点睛】本题主要考查了参数方程与极坐标和直角坐标的互化,同时也考查了利用参数方程求距离最值的问题,属于中等题型.。

银川第一中学理科数学试卷含答案注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．作答时，务必将答案写在答题卡上。

写在本试卷及草稿纸上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合}13|{},1|{2<=≤=xx B x x A ，则=)(B C A R Y A ．}0|{<x x B ．}10|{≤≤x xC ．}01|{<≤-x xD ．}1|{-≥x x2．若复数z 与其共轭复数z 满足i z z 312+=-，则=||z A ．2B ．3C ．2D ．53．抛物线214y x =的准线方程是 A ．2-=xB ．2-=yC ．1-=xD ．1-=y4．若向量)2,1(+=x 与)1,1(-=平行，则|2+|=a b r rA 2B ．322C ．32D ．225．已知n m ,是两条不重合的直线，βα,是两个不重合的平面，则下列命题中，错误的是 A ．若α⊥⊥m n m ,，则α//nB ．若αα⊄n m n m ,//,//，则α//nC ．若βα⊥⊥⊥n m n m ,,，则βα⊥D ．若βαα//,//m ，则β//m 或β⊂m 6．已知函数y =f (x )的部分图像如图，则f (x )的解析式可能是 A ．()tan f x x x =+ B ．()sin 2f x x x =+ C ．1()sin 22f x x x =- D ．1()cos 2f x x x =-7．为了加强“精准扶贫”，实现伟大复兴的“中国梦”，某大学派遣甲，乙，丙，丁，戊五位同学参加A,B,C 三个贫困县的调研工作，每个县至少去1人，且甲，乙两人约定去同一个贫困县，则不同的派遣方案共有 A ．24B ．36C ．48D ．648．已知函数41()2x xf x -=，0.30.30.3(2),(0.2),(log 2)a f b f c f ===，则,,a b c 的大小关系为A ．c b a <<B ． b a c <<C ．b c a <<D ．c a b <<9．天文学中，为了衡量星星的明暗程度，古希腊天文学家喜帕恰斯（Hipparchus ）在公元前二世纪首先提出了星等这个概念。

银川一中2025届高三年级第一次月考语文试卷命题教师：注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．作答时，务必将答案写在答题卡上，写在本试卷及草稿纸上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、现代文阅读（35分）（一）现代文阅读Ⅰ（本题共5小题，19分）阅读下面的文字，完成1～5题。

材料一：习近平总书记指出：在几千年历史长河中，中国人民始终团结一心、同舟共济，建立了统一的多民族国家，发展了56个民族多元一体、交织交融的融洽民族关系，形成了守望相助的中华民族大家庭。

从古至今，各民族都为祖国大家庭的形成和发展贡献了力量。

形成了多元一体的中华民族大家庭是中华文明具有突出的统一性的重要历史表现。

“多元一体”中的“多元”和“一体”深刻反映了中华民族各民族内在的多样性和统一性之间辩证和谐的共同体关系，恰如其分地反映了中华文明起源和发展的模式。

目前我国有56个民族，各民族在漫长的历史进程中形成了各自的文化传统，此为“多元”。

不过，这些民族从来不是以相互隔绝、相互排斥状态出现的，各民族大杂居小聚居，相互嵌入，具有不可分割的内在联系，形成了共同体，此即“一体”，这就是中华民族。

在中华民族共同体中各民族之间你中有我、我中有你，谁也离不开谁，形成了强烈的共同体意识、共同价值追求和文化认同，56个民族这个“多元”在中华民族这个“一体”中得到充分体现。

鸦片战争以后，中国逐步沦为半殖民地半封建社会，国家蒙辱、人民蒙难、文明蒙尘，中国人民遭受了前所未有的劫难。

一部中国近代史就是各族人民团结起来救亡图存的历史。

在外来侵略寇急祸重的严峻形势下，我国各族人民手挽着手、肩并着肩，英勇奋斗，浴血奋战，打败了穷凶极恶的侵略者，捍卫了民族独立和自由，共同书写了中华民族保卫祖国、抵御外侮的壮丽史诗。

在中华民族和中华文明的危急时刻，各民族总是能够同仇敌忾、保家卫国，生动体现了中华文明突出的统一性。

（摘编自邢广程《深刻理解中华文明突出的统一性》）材料二:中华文明突出的统一性，决定了中华民族各民族文化会从多元走向一体。

银川一中2018届高三年级第三次月考数 学 试 卷（理）命题人：第Ⅰ卷 (选择题 共60分)一、选择题：本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1．函数412-=x y 的定义域为(){}11log |,2<-=x x N M ，全集R U =，则图形中阴影部分表示的集合是A.{}12|<≤-x x B . {}22|≤≤-x x C. {}21|≤<x x D. {}2|<x x2．已知i 为虚数单位，复数z 满足z （1﹣i ）=1+i ，则z 的共轭复数是 A ．1B ．﹣1C ．iD ．﹣i3．下列函数在其定义域上既是奇函数又是减函数的是 A ．x x f 2)(=B ．x x x f sin )(=C ．xx f 1)(=D ．||)(x x x f -= 4．在等差数列{}n a 中，5225,3S a ==，则=7aA ．13B ．12C ．15D ．145．已知R y x ∈、，且0>>y x ，则 A. 011>-yxB. 02121<⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛yxC. 0log log 22>+y xD.0sin sin >-y x6．下列四个结论：①若0>x ，则x x sin >恒成立；②命题“若0sin =-x x ，则0=x ”的逆否命题为“若0≠x ，则0sin ≠-x x ”； ③在△ABC 中，“A >B ”是“sinA >sinB ”的充要条件.；④命题“R x ∈∀，0ln >-x x ”的否定是“0ln ,000<-∈∃x x R x ”． 其中正确结论的个数是 A ．1个 B ．2个C ．3个D ．4个7．设曲线11-+=x x y 在点)3,2(处的切线与直线01=++y ax 平行，则=aA ．2B ．12-C ．2-D ．128．已知函数()()1221,1log 3,1x x f x x x -⎧-≥⎪=⎨--<⎪⎩，若()()11f a f a =-=，则A. 2B. 2-C. 1D. 1- 9．函数ax xy +=2的图象不可能是10．设方程1|ln |2=x x 有两个不等的实根1x 和2x ，则 A ．021<x xB ．121=x xC ．121>x xD ．1021<<x x11．将函数)0)(3sin(2)(>-=ωπωx x f 的图象向左平移ωπ3个单位，得到函数)(x g y =的图象．若)(x g y =在⎥⎦⎤⎢⎣⎡4,0π上为增函数，则ω的最大值为A ．1B ．2C ．3D ．412．函数()f x 为R 上的奇函数，且当x ≥0时，2()f x x =,对任意的x ∈[t,t 十2]，不等式()2()f x t f x +≥恒成立，则实数t 的取值范围是A ．，+∞） B ．（0,2] C ．[,-1]⋃[0] D ．[2,+∞）第Ⅱ卷（非选择题 共90分）本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22题～第23题为选考题，考生根据要求做答． 二、填空题：本大题共4小题，每小题5分．13．已知向量,夹角为 60，且72|2|,2||=-=b a a ，则=||b ．14．已知函数3)(x e x f x +=，若)23()(2-<x f x f ，则实数x 的取值范围是__________． 15．已知O 为ABC ∆内一点，且1()2AO OB OC =+，AD t AC =，若,,B O D 三点共线，则t 的值为_________．16．已知)(x f 是定义在R 上的函数，)('x f 是)(x f 的导函数，给出如下四个结论：①若0)()('>+xx f x f ，且e f =)0(，则函数)(x xf 有极小值0；②若0)(2)('>+x f x xf ，则()n n f f 2)2(41<+，*∈N n ； ③若0)()('>-x f x f ，则)2016()2017(ef f >；④若0)()('>+x f x f ，且1)0(=f ，则不等式x e x f -<)(的解集为()+∞,0. 所有正确结论的序号是 ．三、解答题：解答应写出文字说明，证明过程或演算步骤. 17.（本小题满分12分）已知向量)sin ,(),,(cos αα21=-=n m ，其中),(20πα∈，且n m ⊥．（1）求α2cos 的值； （2）若1010=-)sin(βα，且),(20πβ∈，求角β的值． 18．（本小题满分12分）已知等比数列{}n a 的公比1q >，且满足：23428a a a ++=，且32a +是24,a a 的等差中项.（1）求数列{}n a 的通项公式； （2）若1122log ,S n n n n n b a a b b b ==+++，求使6221>⋅++n n n S 成立的正整数n 的最小值？19．（本小题满分12分）在△ABC 中，角C B A 、、所对的边为c b a 、、，且满足22266cos A cos B cos(A )cos(A )ππ-=-+.（1）求角B 的值；（2）若a b ≤=3，求c a -2的取值范围.20.（本小题满分12分）已知数列{}n a 中，12a =，23a =，其前n 项和n S 满足1121n n n S S S +-+=+（2n ≥，*n ∈N ）．（1）求数列{}n a 的通项公式；（2）设14(1)2(n an n n b λλ-=+-⋅为非零整数，*n ∈N ），试确定λ的值，使得对任意*n ∈N ，都有n n b b >+1成立．21.（本小题满分12分）已知a >0，函数2(),()ln f x ax x g x x =-=.(1)若12a =，求函数()2()y f x g x =-的极值， (2)是否存在实数a ，使得()()f x g ax ≥成立？若存在，求出实数a 的取值集合；若不存在，请说明理由．请考生在第22、23两题中任选一题做答，如果多做．则按所做的第一题记分．做答时请写清题号。

宁夏银川一中2021年高三第三次月考理综化学试题1.化学与生活密切相关。

下列说法错误的是．．Ａ．用灼烧的方法可以区分蚕丝和人造纤维Ｂ．食用油反复加热会产生稠环芳香烃等有害物质Ｃ．福尔马林可用来浸制标本，因其可使蛋白质变性Ｄ．医用消毒酒精中乙醇的浓度为95%【答案】D【解析】【详解】Ａ．蚕丝的主要成分为蛋白质，在灼烧时有烧焦羽毛的气味，其他有机物没有此气味，所以可以用灼烧的方法可以区分蚕丝和人造纤维，故正确；Ｂ．食用油属于油脂，反复加热发生化学变化，会产生稠环芳香烃等有害物质，故正确；Ｃ．福尔马林是甲醛的水溶液，可使蛋白质变性，所以可用来浸制标本，故正确；Ｄ．医用消毒酒精中乙醇的浓度为75%，故错误。

故选D。

的是2.N A表示阿伏加德罗常数的值，下列说法不正确．．．Ａ． 28g 乙烯和丙烯混合物中的极性键数目为4N AＢ． 32g Cu和32g S 充分反应，转移电子数为N AＣ．精炼铜时，若阳极失去0.1 N A个电子，则阴极增重3.2gＤ．等物质的量的钠分别在足量的氧气和氯气中燃烧，转移电子数相等【答案】B【解析】【详解】Ａ．乙烯和丙烯的最简式为CH2，含有2个极性键，28g 乙烯和丙烯混合物认为含有最简式CH2的物质的量为2mol，则含有极性键数目为4N A，故正确；Ｂ．32gCu和32g S 充分反应是生成0.25mol硫化亚铜，转移电子为0.5mol，故错误；Ｃ．精炼铜时，阳极是粗铜，粗铜中的活泼金属先溶解生成离子形式，然后是铜溶解，阴极是铜离子得到电子生成铜单质，所以若阳极失去0.1 N A个电子，则阴极得到0.1 N A个电子，则阴极增重3.2g，故正确；Ｄ．钠和氧气或氯气反应时都是生成钠离子，所以等物质的量的钠分别在足量的氧气和氯气中燃烧，转移电子数相等，故正确。

故选B。

3.下列实验操作不能达到实验目的的是．．【答案】D【解析】【详解】Ａ．硫酸铵能通过半透膜，但蛋白质分子不能通过半透膜，所以能进行分离，故正确；Ｂ．铝和氢氧化钠反应但镁不反应，故能分离，故正确；Ｃ．四氯化碳的密度比水大，在下层，碘易溶于四氯化碳，从分液漏斗下口放出碘的四氯化碳溶液，从上口倒出水，故正确；Ｄ．要检验硫酸根离子，先加入盐酸，不产生沉淀，后加入氯化钡溶液，产生白色沉淀，说明溶液含有硫酸根离子，若盐酸和氯化钡同时加入，则银离子可以干扰，故错误。

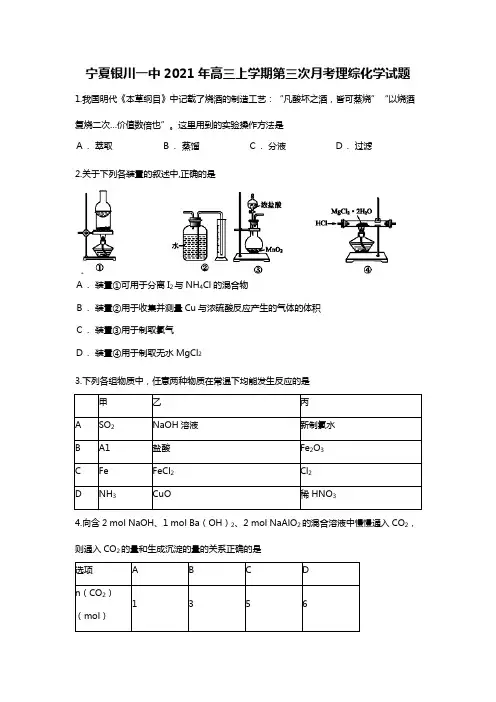
宁夏银川一中2021年高三上学期第三次月考理综化学试题1.我国明代《本草纲目》中记载了烧酒的制造工艺：“凡酸坏之酒，皆可蒸烧”“以烧酒复烧二次…价值数倍也”。

这里用到的实验操作方法是Ａ．萃取Ｂ．蒸馏Ｃ．分液Ｄ．过滤2.关于下列各装置的叙述中,正确的是Ａ．装置①可用于分离I2与NH4Cl的混合物Ｂ．装置②用于收集并测量Cu与浓硫酸反应产生的气体的体积Ｃ．装置③用于制取氯气Ｄ．装置④用于制取无水MgCl23.下列各组物质中，任意两种物质在常温下均能发生反应的是甲乙丙A SO2NaOH溶液新制氯水B A1盐酸Fe2O3C Fe FeCl2Cl2D NH3CuO稀 HNO34.向含2 mol NaOH、1 mol Ba（OH）2、2 mol NaAlO2的混合溶液中慢慢通入CO2，则通入CO2的量和生成沉淀的量的关系正确的是选项A B C Dn（CO2）1356（mol）n（沉淀）（mol）02225.根据下列实验操作和现象所得到的结论正确的是选项实验操作现象结论A 将KI和FeCl3溶液在试管中混合后，加入CCl4，振荡，静置下层溶液显紫红色氧化性：Fe3+>I2B向AgNO3溶液中滴加过量氨水溶液澄清Ag+与NH3∙H2O能大量共存C将可调高度的铜丝伸入到稀HNO3中溶液变蓝Cu与稀HNO3发生置换反应D 向稀HNO3中加入过量铁粉，再滴入少量KSCN溶液溶液变红稀HNO3将Fe氧化为Fe3+6.FeCl3易潮解、易升华，实验室制备FeCl3的装置如图所示（加热和夹持装置略去）。

下列说法正确的是Ａ．导管g的作用是增强装置的气密性Ｂ．试剂X和试剂Y分别为浓硫酸、饱和食盐水Ｃ．直接用E接收产物比用导管连接的优点是可防止堵塞Ｄ． F中浓硫酸的作用是防止G中氢氧化钠进入E7.某强酸性溶液中可能存在Al3+、Fe2+、NH4+、Ba2+、Cl-、CO32-、SO42-、NO3-中的若干种，现取适量溶液进行如下实验：下列有关判断不正确的是Ａ．原溶液中一定有Fe2+、SO42-、H+、NH4+、Al3+Ｂ．原溶液中一定没有Ba2+、CO32-、NO3-Ｃ．步骤③中反应的离子方程式为2AlO2-+CO2+3H2O2Al（OH）3↓+ CO32-Ｄ．气体A、B之间能发生反应8.氮的氧化物（NO x）是大气污染物之一，工业上在一定温度和催化剂条件下用NH3将NO x还原生成N2，某同学在实验室中对NH3与NO x反应进行了探究。

银川一中2025届高三年级第一次月考语文试卷命题教师：注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．作答时，务必将答案写在答题卡上，写在本试卷及草稿纸上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、现代文阅读（35分）（一）现代文阅读Ⅰ（本题共5小题，19分）阅读下面的文字，完成1～5题。

材料一：习近平总书记指出：在几千年历史长河中，中国人民始终团结一心、同舟共济，建立了统一的多民族国家，发展了56个民族多元一体、交织交融的融洽民族关系，形成了守望相助的中华民族大家庭。

从古至今，各民族都为祖国大家庭的形成和发展贡献了力量。

形成了多元一体的中华民族大家庭是中华文明具有突出的统一性的重要历史表现。

“多元一体”中的“多元”和“一体”深刻反映了中华民族各民族内在的多样性和统一性之间辩证和谐的共同体关系，恰如其分地反映了中华文明起源和发展的模式。

目前我国有56个民族，各民族在漫长的历史进程中形成了各自的文化传统，此为“多元”。

不过，这些民族从来不是以相互隔绝、相互排斥状态出现的，各民族大杂居小聚居，相互嵌入，具有不可分割的内在联系，形成了共同体，此即“一体”，这就是中华民族。

在中华民族共同体中各民族之间你中有我、我中有你，谁也离不开谁，形成了强烈的共同体意识、共同价值追求和文化认同，56个民族这个“多元”在中华民族这个“一体”中得到充分体现。

鸦片战争以后，中国逐步沦为半殖民地半封建社会，国家蒙辱、人民蒙难、文明蒙尘，中国人民遭受了前所未有的劫难。

一部中国近代史就是各族人民团结起来救亡图存的历史。

在外来侵略寇急祸重的严峻形势下，我国各族人民手挽着手、肩并着肩，英勇奋斗，浴血奋战，打败了穷凶极恶的侵略者，捍卫了民族独立和自由，共同书写了中华民族保卫祖国、抵御外侮的壮丽史诗。

在中华民族和中华文明的危急时刻，各民族总是能够同仇敌忾、保家卫国，生动体现了中华文明突出的统一性。

（摘编自邢广程《深刻理解中华文明突出的统一性》）材料二:中华文明突出的统一性，决定了中华民族各民族文化会从多元走向一体。

宁夏银川市第一中学2020届高三上学期第五次月考数学（文）试卷学校：___________一、选择题1.已知集合{}0,1,2,3,4,5,6,7,8U =,{}1,3,4,6A =,{}0,1,2,5,7,8B =，则()U A C B I =（ ） A ．{}3,4,6 B ．{}1,3,6C ．{}3,4,5D ．{}1,4,61.答案：A 解析：2.已知(,)a bi a b +∈R 是1ii +的共轭复数，则a bi +=（ ）A ．1B ．12CD 2.答案：D 解析：3.下列说法中，正确的是（ ）A ．命题“若22am bm <，则a b <”的逆命题是真命题B ．命题“0x R ∃∈，2000x x ->”的否定是“x R ∀∈，20x x -≤”C ．命题“p 且q ”为假命题，则命题“p ”和命题“q ”均为假命题D ．已知x R ∈，则“2x > 是4x >”的充分不必要条件 3.答案：B 解析：4.已知双曲线()2222100x y a b a b-=>>的一个焦点与圆()22525x y -+=的圆心重合，且双曲线）A ．221520x y -= B ．2212520x y -= C ．221205x y -= D ．2212025x y -= 4.答案：A 解析：5.若πsin 23α⎛⎫+= ⎪⎝⎭，则cos2α=（ ）A ．13B ．23C ．13-D ．23-5.答案：C解析：∵πsin 2a ⎛⎫+=⎪⎝⎭∴cos 3α=∴2211cos 22cos 12133αα⎛⎫=-=⨯-=- ⎪⎝⎭6.设{}n a 是公差不为0的等差数列，12a =且136,,a a a 成等比数列，则{}n a 的前n 项和n S =（ ）A ．2744n n+ B ．2533n n+ C ．2324n n+D ．2n n +6.答案：A解析：设数列{}n a 的公差为d ， 则根据题意得()()222225d d +=⋅+， 解得12d =或0d = (舍去)， 所以数列{}n a 的前n 项和()211722244n n n n nS n -=+⨯=+7.已知椭圆2222:1(0)y x C a b a b+=>>双曲线222x y -=的渐近线与椭圆C 有四个交点，以这四个交点为顶点的四边形的面积为16，则椭圆C 的方程为（ ）A ．221128y x +=B ．221126y x +=C ．221164y x += D ．221205y x +=7.答案：D 解析：8.执行如图所示的程序框图，若输入10n =，则输出的S 的值是（ ）A ．910B ．1011C. 1112D ．9228.答案：B 解析：9.已知向量)a =r在向量(),1b n =r方向上的投影为3，则a r 与b r 的夹角为（ ）A ．30︒B ．60︒C ．30︒或150︒D ．60︒或120︒9.答案：A 解析：10.ABC ∆的内角,,A B C 的对边分别为,,a b c ,若cos cos cos 23C b A a B =+=,则ABC ∆的外接圆的面积为（ ） A. 3π B. 6πC. 9πD. 12π10.答案：C解析：∵cos cos 2b A a B +=,∴222222222b c a a c b b a bc ac+-+-⋅+⋅=, ∴2c =,由cos 3C =,得1sin 3C =,∴226,31sin 3c R R C ====, 239S ππ=⨯=,故选C11.已知直线()200kx y k k -+=>与抛物线2:8C y x =相交于A 、B 两点，F 为C 的焦点，若2FA FB =,则k =（ ）A ．13BC ．23D11.答案：D解析：由题意，联立()282y xy k x ⎧=⎪⎨=+⎪⎩，得()22224840k x k x k +-+=设()()11221212,,,,0,0,0,0A x y B x y x x y y >>>> ∴124x x = ○1 由抛物线的定义，122,2FA x FB x =+=+ ∵2FA FB = ∴1222x x =+ ○2 由○1○2解得21x =∴(1,B ，代入()2y k x =+，得k =12.已知对任意的[1,e]x ∈，总存在唯一的[1,1]y ∈-，使得2ln e 0yx y a +-=成立，其中e 为自然对数的底数，则实数a 的取值范围为（ ） A ．[1,e] B ．1(1,e 1)e++ C ．1(,1e]e+D ．1(1,e]e+12.答案：D解析：由2ln 0yx y e a +-=成立，解得2ln yy e a x =-，∴对任意的1[]x e ∈，，总存在唯一的1[]1y ∈-，，使得2ln 0yx y e a +-=成立，∴2111a e --≥-（），且2101a e -≤⨯，解得11a e e +≤≤，其中11a e=+时，y 存在两个不同的实数，因此舍去，a 的取值范围是11,e e ⎛⎫+⎪⎝⎭. 二、填空题13.已知()f x 是定义在R 上的周期为2的偶函数，当[2,0]x ∈-时，()2xf x =-，则(5)f =__________.13.答案：21-解析：∵()f x 是定义在R 上的周期为4的偶函数， 当[]2,0x ∈-时，()2xf x =-，∴()()()1151122f f f -==-=-=-。

银川高级中学2019-2020学年高三上学期第三次月考试卷数学含答案 班级__________ 座号_____ 姓名__________ 分数__________ 一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1． 已知定义在R 上的奇函数f （x ）满足f （x ）=2x ﹣4（x ＞0），则{x|f （x ﹣1）＞0}等于（ ）A ．{x|x ＞3}B ．{x|﹣1＜x ＜1}C ．{x|﹣1＜x ＜1或x ＞3}D ．{x|x ＜﹣1}2． 若动点),(),(2211y x B y x A 、分别在直线： 011=-+y x 和2l ：01=-+y x 上移动，则AB 中点M 所在直线方程为（ ）A ．06=--y xB ．06=++y xC ．06=+-y xD ．06=-+y x 3． 单位正方体（棱长为1）被切去一部分，剩下部分几何体的三视图如图所示，则（ ）A ．该几何体体积为B ．该几何体体积可能为C ．该几何体表面积应为+D ．该几何体唯一4． 底面为矩形的四棱锥P -ABCD 的顶点都在球O 的表面上，且O 在底面ABCD 内，PO ⊥平面ABCD ，当四棱锥P -ABCD 的体积的最大值为18时，球O 的表面积为（ ） A ．36π B ．48π C ．60πD ．72π5． 已知向量=（﹣1，3），=（x ，2），且，则x=（ ）A ．B ．C ．D ．6． 自圆C ：22(3)(4)4x y -++=外一点(,)P x y 引该圆的一条切线，切点为Q ，切线的长度等于点P 到原点O 的长，则点P 轨迹方程为（ ） A ．86210x y --=B ．86210x y +-=C ．68210x y +-=D ．68210x y --=【命题意图】本题考查直线与圆的位置关系、点到直线的距离，意在考查逻辑思维能力、转化能力、运算求解能力．7． 下列函数中，与函数()3x xe ef x --=的奇偶性、单调性相同的是（ ）A．(ln y x = B ．2y x = C ．tan y x = D ．xy e =8． 集合{}|42,M x x k k Z ==+∈，{}|2,N x x k k Z ==∈，{}|42,P x x k k Z ==-∈，则M ，N ，P 的关系（ ）A ．M P N =⊆B ．N P M =⊆C ．M N P =⊆D ．M P N ==9． 已知实数[1,1]x ∈-，[0,2]y ∈，则点(,)P x y 落在区域20210220x y x y x y +-⎧⎪-+⎨⎪-+⎩……… 内的概率为（ ） A.34B.38C.14D.18【命题意图】本题考查线性规划、几何概型等基础知识，意在考查数形结合思想及基本运算能力.10．一个空间几何体的三视图如图所示，其中正视图为等腰直角三角形，侧视图与俯视图为正方形，则该几何体的体积为（ ）A ．64B ．32C ．643D ．32311．与向量=（1，﹣3，2）平行的一个向量的坐标是（ ） A．（，1，1） B ．（﹣1，﹣3，2） C．（﹣，，﹣1） D ．（，﹣3，﹣2）12．将函数f （x ）=3sin （2x+θ）（﹣＜θ＜）的图象向右平移φ（φ＞0）个单位长度后得到函数g （x ）的图象，若f （x ），g （x ）的图象都经过点P （0，），则φ的值不可能是（ ） A．B ．πC．D．二、填空题（本大题共4小题，每小题5分，共20分.把答案填写在横线上）13．如图，在三棱锥P ABC -中，PA PB PC ==，PA PB ⊥，PA PC ⊥，PBC △为等边三角形，则PC与平面ABC 所成角的正弦值为______________.【命题意图】本题考查空间直线与平面所成角的概念与计算方法，意在考查学生空间想象能力和计算能力．14．设某总体是由编号为01,02,…,19,20的20个个体组成，利用下面的随机数表选取6个个体，选取方法是从随机数表第1行的第3列数字开始从左到右依次选取两个数字，则选出来的第6个个体编号为________．【命题意图】本题考查抽样方法等基础知识，意在考查统计的思想． 15．若执行如图3所示的框图，输入，则输出的数等于 。

21-银川一中2020届高三第一次月考（理科）参考答案一．选择题：DADAB,BDBCC,AC二、填空题：13.（2,5）14.π-15.32π-16.232ln+17．解：（1）212cos 212sin 231cos sin 322cos 1)(-ω-ω=-ωω+ω-=x x x x x x f =.21)62sin(-π-ωx ∵函数)(x f 的最小正周期为,0,>ωπ且21)62sin()(,1,22+-=∴==∴πωπωπx x f 解得…………6分（2）65,3[622,12[πππππ-∈-∴-∈x x ，根据正弦函数的图象可得：当)62sin()(,3,262ππππ-===-x x g x x 时即取最大值1．当)62sin()(,12,362ππππ-=-=-=-x x g x x 时即最小值.23-212162sin(2321≤-π-≤--∴x ,即)(x f 的值域为]21,231[+-…………12分18.(1)有三角函数的定义，得3cos(,cos 21παα+==x x 因,62ππ∈(α，41cos =α,则.415)41(1cos 1sin 2=-=-=αα……3分∴.8531415234121sin 23cos 21)3cos(2-=⋅-⋅=-=+=ααπαx ……6分(2)有已知，得),3sin(,sin 21παα+==y y ∴.2sin 41sin cos 2121111ααα=⋅=⋅=y x s ……7分322sin(41)]3sin()3cos([21||||21222παπαπα+-=+⋅+-=⋅=y x s ……9分122S S =,得.02cos )322sin(22sin =⇒+-=απαα……11分又,62ππ∈(α,),3(2ππα∈,∴.422παπα=⇒=……12分19．解：（Ⅰ）当m=0时，f(x)=-x 2+3.此时3()()3h x xf x x x ==-+，则2()33h x x '=-+.由()0h x '=，解得1x =±.………………3分由⇒〉'0)(x h 11〈〈-x ;1,10)(〉〈-⇒〈'x x x h 或;∴()h x 在(,1)-∞-，(1,)+∞上单调递减，在(1,1)-上单调递增.………5分所以()h x 有极小值(1)2h -=-，()h x 有极大值(1)2h =.…………6分（Ⅱ）由2()e 30xf x m x =-+=，得23ex x m -=.所以“()f x 在区间[2,4]-上有两个零点”等价于“直线y m =与曲线23()ex x g x -=，[2,4]x ∈-有且只有两个公共点”.……………8分对函数()g x 求导，得223()e xx x g x -++'=.由()0g x '=，解得11x =-，23x =.………………9分由⇒〉'0)(x g 31〈〈-x ;由⇒〈'0)(x g 3,1〉〈-x x 或.∴()g x 在(2,1)--，(3,4)上单调递减，在(1,3)-上单调递增.……10分又因为2(2)e g -=，(1)2e g -=-，36(3)(2)e g g =<-，413(4)(1)eg g =>-，所以当4132e e m -<<或36e m =时，直线y m =与曲线23()e x x g x -=，[2,4]x ∈-有且只有两个公共点.∴当4132e e m -<<或36e m =时，函数()f x 在区间[2,4]-上有两个零点.……12分20．（1）由于21()ax f x x +'=．当0a ≥时，对于(0,)x ∈+∞，有()0f x '>在定义域上恒成立，即()f x 在(0,)+∞上是增函数．当0a <时，由()0f x '=，得1(0,)x a =-∈+∞．当1(0,)x a∈-时，()0f x '>，()f x 单调递增；当1(,)x a∈-+∞时，()0f x '<，()f x 单调递减．………………………6分（3）当1a =时，1(1)ln(1)1f x x x -=---，[)2,x ∈+∞．令1()ln(1)251g x x x x =---+-．2211(21)(2)()21(1)(1)x x g x x x x --'=+-=----．当2x >时，()0g x '<，()g x 在(2,)+∞单调递减．又(2)0g =，所以()g x 在(2,)+∞恒为负．………………………10分所以当[2,)x ∈+∞时，()0g x ≤．即1ln(1)2501x x x ---+-≤．故当1a =，且2x ≥时，(1)25f x x --≤成立．………………………12分.21.（Ⅰ）由已知可得'()0f x ≥在[1,]+∞上恒成立。

银川市一中2020届高三上学期第四次月考数学（文）试卷一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知i z i -=+⋅)1(，那么复数z 对应的点位于复平面内的A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．已知集合{}2|1M x Z x =∈≤，{}R |12N x x =∈-<<，则M N =IA ．{1,0,1}-B ．{0,1}C ．{1,0}-D ．{1}3．已知数列{}n a 为等差数列，且π=++1371a a a ,则=+)sin(86a aA ．21 B ．21-C ．23 D ．23-4．设向量(2,1),(,1)x x =+=a b , 则"1"x =是“//a b ”的A ．充分但不必要条件B ．必要但不充分条件C ．充要条件D ．既不充分也不必要条件5．直线3430x y -+=与圆221x y +=相交所截的弦长为A ．45B ．85C ．2D ．36．如图，一个简单空间几何体的三视图其主视图与侧视图都是边长为2的正三角形，俯视图轮廓为正方形，则此几何体的表面积是 A ．443+B ．12C ．43D ．87．已知函数x x f x 3log )51()(-=，实数x 0是方程0)(=x f 的解，若01x x 0<<，则)(1x f 的值俯视图主视图侧视图A ．恒为负数B ．等于零C ．恒为正数D ．可正可负8．将函数x y 2cos =的图象向左平移4π个单位长度，所得函数的解析式是 A ．)42cos(π+=x yB ．)42cos(π-=x yC ． x y 2sin -=D ．x y 2sin =9．已知点F 1、F 2分别是椭圆x 2a 2＋y 2b2＝1(a ＞b ＞0)的左、右焦点，过F 1且垂直于x 轴的直线与椭圆交于A 、B 两点，若△ABF 2为正三角形，则椭圆的离心率是A ．2B ． 2C ．3D ．3310．已知双曲线),2(*1221N n n a a x a y a n n n n ∈≥=---的焦点在y 轴上，一条渐近线方程是x y 2=，其中数列}{n a 是以4为首项的正项数列，则数列}{n a 通项公式是A ．nn a -=32 B ．nn a 22=C ．132-=n n aD ．12+=n n a11．在三棱柱ABC －A 1B 1C 1中，已知BC=AB=1,0190=∠BCC ，AB 丄侧面BB 1C 1C ，且直线C 1B 与底面ABC 所成角的正弦值为552,则此三棱柱的外接球的表面积为 A ．π3B ．π4C ．π5D ．π612．已知函数32()f x x x ax b =-++，12,(0,1)x x ∀∈且 12x x ≠，都有1212|()()|||f x f x x x -<-成立，则实数a 的取值范围是 A ．2(1,]3--B ．2(,0]3-C ．2[,0]3-D ．[1,0]-二、填空题（本大题共4个小题，每小题5分，共20分．把答案填在题中横线上．）13．设双曲线x 2a 2－y 29＝1(a >0)的渐近线方程为3x ±2y ＝0，则a 的值为________.14．某银行开发出一套网银验证程序，验证规则如下：（1）有两组数字，这两组数字存在一种对应关系；第一组数字,,a b c 对应 于第二组数字2,2,3a b c b a c +++；（2）进行验证时程序在 电脑屏幕上依次显示产生第二组数字，用户要计算出第一组数 字后依次输入电脑，只有准确输入方能进入，其流程图如图， 试问用户应输入a,b,c 的值是__________.15．已知圆4)2()(:221=++-y a x C 与圆1)2()(:222=+++y b x C相外切，则ab 的最大值为_________.16．在双曲线2222:1(00)x y C a b a b-=>>，的右支上存在点A ，使得点A 与双曲线的左、右焦点1F ，2F 形成的三角形的内切圆P 的半径为a ，若12AF F △的重心G 满足12PG F F ∥，则双曲线C 的离心率为__________.三、解答题：解答应写出文字说明、证明过程或演算步骤。

银川一中2020届高三年级第二次月考文 科 数 学注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．作答时，务必将答案写在答题卡上。

写在本试卷及草稿纸上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知{}21|<<-=x x A ，{}02|2<-=x x x B ，则=B A A ．(－1，0) B ．(0，2) C ．(－2，0) D ．(－2，2)2．在复平面内，复数)2(i i -所对应的点位于 A ．第一象限B ．第二象限C ．第三象限D ．第四象限 3．设函数()()1232e ,2log 1,2x x f x x x -⎧<⎪=⎨-≥⎪⎩，则=)]2([f f A ．2 B ．3 C ．4 D ．54．中国古代数学著作《算法统宗》中有这样一个问题：“三百七十八里关，初行健步不为难，次日脚痛减一半，六朝才得到其关，要见次日行里数，请公仔细算相还．”其意思为：有一个人走378里路，第一天健步行走，从第二天起脚痛每天走的路程为前一天的一半，走了6天后到达目的地，请问第三天走了A ．192里B ．96里C ．48里D ．24里5．已知向量＝(1，2)，＝(2，－2)，＝(m ，1）．若∥(2＋)，则m= A ．0 B ．1C ．2D ．36．设3log π=a ，3.0π=b ，π3.0log =c ，则A. a b c >>B. a c b >>C. b c a >>D. b a c >> 7．曲线2ln y x x =-在1x =处的切线的倾斜角为α，则)22cos(πα+的值为 A ．54B ．54-C ．53D ．53-8．等差数列{a n }的首项为1，公差不为0.若a 2，a 3，a 6成等比数列，则{a n }的前8项和为 A ．－48 B ．－96 C ．36 D ．729．记不超过实数x 的最大整数为[]x ，则函数()[]f x x =称作取整函数，取整函数在科学和工程上有广泛应用．下面 的程序框图是与取整函数有关的求和问题，若输出的S 的值为5，则判断框内填入的条件可以是 A ． ?6≤k B ．?4≤kC ．?5≤kD ．?3≤k10．已知数列{}n a 满足n a a n n 21+=+，11=a ，则=15a A ．111B ．211C ．311D ．41111．已知正方形ABCD 的边长为2，M 为平面ABCD 内一点(包含边界)，则AC MB MA ⋅+)( 的最小值为 A ．11-B ．12-C ．13-D ．14-12．已知()f x ，()g x 都是定义在R 上的函数，()0g x ≠，()()()()f x g x f x g x ''<，且()()()01x f x a g x a a =>≠且，()()()()115112f f g g -+=-，若数列()()f n g n ⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭的前n 项和大于20202019，则n 的最小值为 A ．8B ．9C ．10D ．11二、填空题：本题共4小题，每小题5分，共20分.13．设函数ax x a x x f 3)1()(23--+=．若()f x 为奇函数，则函数)(x f 的单调递减区间为____________.14．已知向量a 与b 的夹角为120°，2||=a ，1||=b ，则=-2|b ________. 15．函数x x x f sin 3cos )(2+= ])2,0[(π∈x 的最大值是 ．16．已知数列{}n a 满足11=a ，12+=+n n n a a a (*∈N n )，数列{}n b 是单调递增数列， 且k b -=1，nn n a a k n b )1)(2(1+-=+(*∈N n ),则实数k 的取值范围为____________.三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22、23为选考题，考生根据要求作答.（一）必考题：共60分. 17．(12分)已知等差数列{}n a 的前n 项和为n S ，52-=a ，126-=S ． （1）求{}n a 的通项公式；（2）求n s ，并求当n 取何值时n S 有最小值.18．(12分)已知)cos 3,sin 2(x x a =→，)cos 2,(cos x x b -=→，函数3)(+⋅=→→b a x f ， (1)求函数y ＝f (x )的单调增区间和对称轴方程； (2)若1)(≥x f ，求x 的取值范围.19.（12分）已知等比数列{a n }的前n 项和为S n ，且满足22ks n n += (k ∈R)． (1)求k 和数列{a n }的通项公式；(2)若数列{b n }满足b n ＝1（2n ＋1）log 2（a n ·a n ＋1），求数列{b n }的前n 项和T n .20．（12分）在平面四边形ABCD 中，π=∠+∠C A ,1=AB ,3=BC ,2==DA CD . (1)求C ∠和四边形ABCD 的面积； (2)若E 是BD 的中点，求CE .21．(12分)已知R a ax x x x f ∈+-=,2ln )(2. (1)若0=a ，求)(x f 在],1[e 上的最小值； (2)求)(x f 的极值点；(3)若)(x f 在],1[e e内有两个零点，求a 的取值范围.(二)选考题：共10分.请考生在第22、23两题中任选一题做答，如果多做．则按所做的第一题记分. 22．[选修4－4：坐标系与参数方程]已知圆⎪⎩⎪⎨⎧θ+=θ+=sin 22cos 22:y x C （θ为参数），以坐标原点O 为极点，以x 轴正半轴为极轴建立极坐标系，点,A B 的极坐标分别为()()1,,1,0π. （1）求圆C 的极坐标方程；（2）若P 为圆C 上的一动点，求22||PA PB +的取值范围.23．[选修4－5：不等式选讲]已知,,a b c 为正数，且满足1abc =，证明： （1）222111a b c a b c++≤++； （2）333()()()24a b b c c a +++++≥．银川一中2020届高三年级第二次月考（文科）参考答案一．选择题 B AACC DDACB BD二．填空题 13.)1,1(- 14.32 15.47 16.32<k 三. 解答题17.解析：（1）设{a n }的公差为d ，由题意得⎩⎨⎧-=+-=+452511d a d a ．..............2分得a 1=–7，d =2．...........................................................................4分所以{a n }的通项公式为a n =2n –9．..................................................6分 （2）由（1）得S n =n 2–8n =（n –4）2–16...........................................10分所以当n =4时，S n 取得最小值，最小值为–16．..............................12分18. 解析：（1）3cos 32cos sin 2)(2+-=x x x x fx x 2cos 32sin -==)32sin(2π-x .............................................2分单调增区间为)](125,12[z k k k ∈++-ππππ.........................................4分 对称轴方程为z k k x ∈+=,2125ππ.................................................6分 （2）由1)(≥x f 得21)32sin(≥-πx 得z k k x k ∈+≤-≤+,2653226πππππ........10分 所以x 的取值范围为)](127,4[z k k k ∈++ππππ...............................12分 19解析：(1)当n ≥2时，由2S n ＝2n ＋1＋k (k ∈R )得2S n －1＝2n＋k (k ∈R )，......2分所以2a n ＝2S n －2S n －1＝2n，即a n ＝2n －1(n ≥2)，........................4分又a 1＝S 1＝2＋2k，当k ＝－2时，a 1＝1符合数列{a n }为等比数列， 所以{a n }的通项公式为a n ＝2n －1................................................6分(2)由(1)可得log 2(a n ·a n ＋1)＝log 2(2n －1·2n)＝2n －1，.........................8分所以b n ＝1（2n ＋1）（2n －1）＝12⎝ ⎛⎭⎪⎫12n －1－12n ＋1，.........................10分所以T n ＝b 1＋b 2＋…＋b n ＝12(1－13＋13－15＋…＋12n －1－12n ＋1)＝n2n ＋1...........12分20. 解析(1)由题设及余弦定理得 BD 2=BC 2+CD 2-2BC·CDcos C =13-12cos C,①BD 2=AB 2+DA 2-2AB·DAcos A=5+4cos C.②.......................................2分由①②得cos C=,故C=60°,BD=..........................................4分四边形ABCD 的面积S=AB·DAsin A+BC·CDsin C=×1×2+×3×2sin 60° =2. .........................................................6分....(2) 由)(21+=得 .......................8分 )2(41222CB CD CB CD CE ∙++=...............10分=)2132294(41⨯⨯⨯++ =419 所以219=CE .....................................................12分 21. 解析：（1）xx x f 2'21)(-=，................................2分因为],1[e x ∈，所以0)('<x f所以)(x f 在],1[e 上是减函数，所以最小值为21)(e e f -=.........................................4分（2）定义域为),0(+∞，x ax x x f 122)(2'++-=令0)('=x f 得22,222221++=+-=a a x a a x ................................6分因为0,021><x x ，所以当),0(2x x ∈时，0)('>x f ，当),(2+∞∈x x 时0)('<x f所以)(x f 在),0(2x 单调递增，在),(2+∞x 单调递减，所以2x 为极大值点，无极小值点................................................8分(3).由02ln 2=+-ax x x ，得x x x a ln 2-=，令x x x x g ln )(-=22'ln 1)(x xx x g +-=x x x h ln 1)(2+-=当)1,0(∈x 时，0)1()(=<h x h ，当),1(+∞∈x 时0)1()(=>h x h所以g(x)在]1,1[e 上是减函数，在],1[e 上是增函数，...............................10分e e e g e e g g 1)(,2)1(,1)1(2-===所以e e a 1212-≤<得e e a 21212-≤<.............................................12分 22.解：解析：（1）把圆C 的参数方程化为普通方程为()()22222x y -+-=，即224460x y x y +--+=，..................2分由222,c o s,s i n x y x y ρρθρθ+===， 得圆C 的极坐标方程为24c o s4s i n 60ρρθρθ--+=.................5分（2）设()2c o s ,2s i n ,,P A B θθ的直角坐标分别为()()1,0,1,0-，.....7分则()()()()222222||3212PA PB θθθθ+=+++++++[]2216sin 6,384πθ⎛⎫=++∈ ⎪⎝⎭所以22||PA PB +的取值范围为[]6,38.....10分 23.解析：（1）1abc =，111bc ac ab a b c∴++=++．由基本不等式可得222222,,222b c a c a b bc ac ab +++≤≤≤，.........2分 于是得到222222222111222b c a c a b a b c a b c +++++≤++=++．........5分 （2）由基本不等式得到332()8()a b a b ab +≥⇒+≥，332()8()b c b c bc +≥+≥，332()8()c a c a ac +≥⇒+≥．...7分于是得到333333222()()()8()()()a b b c c a ab bc ac ⎡⎤+++++≥++⎢⎥⎣⎦824≥⨯=．...10分。

银川一中2020届高三年级第三次月考（文科）参考答案一、选择题：13. 2x-y-2=0 14. 7 15. 4(1)21(2)n n a n n =⎧=⎨+≥⎩ 16. 4-三、简答题：17、解： (1)证明 连接OE ，如图所示． ∵O 、E 分别为AC 、PC 的中点，∴OE ∥PA.∵OE 面BDE ，PA 面BDE ， ∴PA ∥面BDE............................................6分 (2)证明 ∵PO ⊥面ABCD ，∴PO ⊥BD.在正方形ABCD 中，BD ⊥AC ，又∵PO∩AC＝O ，∴BD ⊥面PAC. 又∵BD 面BDE ，∴面PAC ⊥面BDE......................12分 18.试题解析：（1）411=+n n a a ,∴数列}{n a 是首项为41，公比为41的等比数列，∴*)()41(N n a n n ∈=. 因为2log 341-=n n a b ，所以232)41(log 341-=-=n b nn .（2）由（1）知，23,)41(-==n b a n n n , 所以,)41()23(n n n c +-=所以,)41()23()41)53()41(7)41(4411132n n n n n S +-+(+-+++++++=-Λ])41()41)41()41(41[)]23()53(741[132n n n n +(++++++-+-++++=-ΛΛn n n n n n )41(313123411])41(1[412)231(2⋅-+-=--+-+=.19．() ()()2222211,sin sin,sin1sin,0,,2362,366521,652cos61332AD BDABD BDB BADBD BBAD BAD BADADADB ABDADC ACDAD CD AD CDCD CDCDππππππππ∆==∠⨯∠==<∠<∴∠=∴∠=--=∴∆∠=∆=+-⎛⎫=+-⨯- ⎪⎪⎝⎭+Qg g证明:在中由正弦定理是等腰三角形由知,AB=BD=1,在中,AC3100,5(1.311sin1322ABCCD CDS AB BC Bλ∆-==-∴∴=⨯⨯=⨯⨯=解得舍去), CD=2BC=BD+CD=3, =20.解析：（Ⅰ）因为1AA ABC⊥平面，所以⊥1CC平面ABC.而⊂1CC平面11BBCC,所以平面⊥ABC平面11BBCC. ………2分因为线段BC的中点为，且.ABC AD BC∆⊥是等腰三角形，所以而BCCCBBABCABCAD=⋂⊂11,平面平面平面,11AD CBB C⊥所以平面.111C E CBB C⊂又因为面，1.AD C E⊥所以（Ⅱ）1AA ABC⊥平面，1AA AC⊥则.90BAC∠=o，即AC AB⊥.又AB AC A⋂=，所以11AC ABB A⊥平面，故1111AC ABB A⊥平面，所以11A EC∆是直角三角形.在三棱柱111ABC A B C-中，11//AC A C，直线1AC C E、所成角的余弦为12，则在11ECARt∆中，111cos2AC E∠=，112AC AC==，所以1A E=………7分在EBARt11∆中，112A B=，所以1B E=.因为1AA=1BB的靠近点的三等分点.因为,324222221313111111=⨯⨯⨯⨯=⋅=∆-CASVEBAEBAC所以11B A DEV-=11D A B EV-=1112C A B EV-.322=21.（1）由题意，函数()()211ln 1(0)22f x x x m x m x =+-+++>， 则()11f x x m x'=+--， 因为2x =是函数()f x 的极值点，所以()122102f m +'=--=，故32m =， 即()152f x x x =+-'，令()215252022x x f x x x x-+'=+-=>，解得102x <<或2x >.令()225202x x f x x'-+=<，解得122x <<,所以()f x 在10,2⎛⎫ ⎪⎝⎭和()2,+∞上单调递增，在1,22⎛⎫⎪⎝⎭上单调递减. （2）由()11f x x m x'=+--， 当1m ≤时，()0f x '>，则()f x 在()1,+∞上单调递增， 又()10f =，所以()211ln 1022x x m x m +-+++>恒成立； 当1m >时，易知()11f x x m x'=+--在()1,+∞上单调递增， 故存在()01,x ∈+∞，使得()00f x '=，所以()f x 在()01,x 上单调递减，在()0,x +∞上单调递增， 又()10f =，则()00f x <，这与()0f x >恒成立矛盾. 综上，1m ≤.22.(1)曲线C 的普通方程为22(1)1x y -+= ，极坐标方程为2cos ρθ= ------4分(2)设11(,)P ρθ，则有2cos 3ρθπθ=⎧⎪⎨=⎪⎩解得111,3πρθ== --6分 设22(,)Q ρθ，则有2sin()33πρθπθ⎧+=⎪⎪⎨⎪=⎪⎩解得223,3πρθ==--8分所以2PQ = . --10分23.解：（1）f(x)＋f(x ＋4)＝|x －1|＋|x ＋3|＝⎩⎪⎨⎪⎧－2x －2，x ＜－3，4，－3≤x≤1，2x ＋2，x ＞1．当x ＜－3时，由－2x －2≥8，解得x≤－5； 当－3≤x≤1时，f(x)≤8不成立；当x ＞1时，由2x ＋2≥8，解得x≥3．……………………………………………4分 所以，不等式f(x)≤4的解集为{x|x≤－5，或x≥3}．……………………………5分 （2）f(ab)＞|a|f( ba )，即|ab －1|＞|a －b|． …………………………………………6分∵因为|a|＜1，|b|＜1，∴|ab －1|2－|a －b|2＝(a 2b 2－2ab ＋1)－(a 2－2ab ＋b 2)＝(a 2－1)(b 2－1)＞0，所以，|ab －1|＞|a －b|．故所证不等式成立．…………………………………10分。

高三数学（文）试卷一、单选题1.设全集U= {}0,1,2,3,4,5，集合{1,3},{3,5}A B ==，则U ()C A B =A. ｛0，4｝B. ｛1，5｝C. ｛2，0，4｝D.｛2，0，5｝ 【答案】C 【解析】{}{}{}1,33,51,3,5A B ⋃=⋃= ，因为全集U = {}0,1,2,3,4,5，所以()U C A B ⋃= {}024，，，选C. 2.设i 是虚数单位，复数21iz i=+，则z =（ ）A. 1B. 2C.D.【答案】D 【解析】 【分析】先化简运算复数z ，然后求出模长即可. 【详解】解：因为复数()()()2122211112i i i i z i i i i -+====+++-所以z ==故选D【点睛】本题考查了复数的运算与模长，属于基础题. 【此处有视频，请去附件查看】3.已知3sin 35πα⎛⎫+= ⎪⎝⎭，则()cos 6πα-=（ ） A. 35 B.35 C. 45D. 45-【答案】A【解析】 【分析】利用诱导公式可求出cos 6πα⎛⎫-⎪⎝⎭的值. 【详解】由诱导公式可得3cos cos sin 63235ππππααα⎡⎤⎛⎫⎛⎫⎛⎫-=+-=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦. 故选：A.【点睛】本题考查利用诱导公式求值，解题的关键就是要明确两角之间的关系，考查计算能力，属于基础题.4.下列函数中，是偶函数的是（ ） A. ()22f x x x =+B. ()cos 3f x x π⎛⎫=+ ⎪⎝⎭C. ()2log f x x =D. ()2log f x x =【答案】D 【解析】 【分析】分析各选项中函数的奇偶性，可得出合适的选项. 【详解】对于A 选项，函数()22f x x x=+的对称轴为直线1x =-，该函数不是偶函数；对于B 选项，函数()cos 3f x x π⎛⎫=+⎪⎝⎭为非奇非偶函数； 对于C 选项，函数()2log f x x =的定义域为()0,∞+，不关于原点对称，该函数为非奇非偶函数；对于D 选项，函数()2log f x x =的定义域为{}0x x ≠，关于原点对称，且()()22log log f x x x f x -=-==，该函数为偶函数.故选：D.【点睛】本题考查函数奇偶性的判断，熟悉基本初等函数的奇偶性以及函数奇偶性的定义是判断的关键，考查推理能力，属于基础题.5.在ABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，若222a b c bc =++，则A =（ ）A. 30°B. 60°C. 120°D. 150°【答案】C 【解析】 【分析】根据余弦定理化简已知条件，求得1cos 2A =-，由此求得A 角的大小.【详解】由已知222a b c bc =++及余弦定理，得2221cos 222b c a bc A bc bc +--===-，所以120A =︒．故选C ．【点睛】本小题主要考查利用余弦定理解三角形，属于基础题. 6.设平面向量()a=1,2，()b=2,y -，若a b ，则2a b -等于（ ）A. 4B. 5C.D. 【答案】D 【解析】 【分析】利用向量共线定理即可得出y ，从而计算出2a b -的坐标，利用向量模的公式即可得结果. 【详解】//,220a b y ∴-⨯-=，解得4y =-，()()()221,22,44,8a b ∴-=---=，222484a b ∴-=+= D.【点睛】本题主要考查平面向量平行的性质以及向量模的坐标表示，属于中档题. 利用向量的位置关系求参数是出题的热点，主要命题方式有两个：（1）两向量平行，利用12210x y x y -=解答；（2）两向量垂直，利用12120x x y y +=解答.7.等差数列{}n a 中，若159371139,27a a a a a a ++=++=，则数列{}n a 前11项的和为 A. 121 B. 120C. 110D. 132【答案】A 【解析】设等差数列{}n a 的公差为d ，∵159371139,27a a a a a a ++=++=， ∴()()3711159612a a a a a a d ++-++==-, ∴2d =-,∴159131239a a a a d ++=+=, 解得121a =. ∴1111102111(2)1212S ⨯=⨯+⨯-=．选A ． 8.函数ln y x x =的单调递减区间是 （ ） A. 1(,)e -+∞ B. 1(,)e --∞ C. 1(0,)e - D. (,)e +∞【答案】C 【解析】 【分析】由题意，可得()f x '和定义域，由()0f x '<，即可求解函数的递减区间. 【详解】由题意，可得()ln 1,(0)f x x x =+>'，令()0f x '<，即ln 10x +<，解得10x e -<<，即函数的递减区间为1(0,)e -.【点睛】本题主要考查了利用导数求解函数的单调区间，其中根据函数的解析式求得函数的导数，利用()0f x '<求解，同时注意函数的定义域是解答的关键，着重考查了推理与运算能力.9.函数sin y x x =-在[],ππ-上的图象是( )A. B.C. D.【答案】B【详解】试题分析：以x -代x 得，()sin()sin x x x x ---=-,所以函数sin y x x =-为偶函数，图象关于y 轴对称，排除D;令2x π=，得函数值2y π=-，排除A 、C ，选B.考点：1.函数的奇偶性；2.函数的图象.10.若等比数列{}n a 的各项均为正数，且68139122a a a a +=，则2122220log log log a a a +++=（ ）．A. 50B. 60C. 100D. 120【答案】A 【解析】分析：由题意结合等比数列的性质和对数的运算法则整理计算即可求得最终结果.详解：因为等比数列{}n a 的各项均为正数，且68139122a a a a +=， 所以6101122a a =， 所以510112a a =，所以2122220log a log a log a +++()21220log a a a =()1021011log a a =()2101110log a a =52102log =10550=⨯=．本题选择A 选项.点睛：本题主要考查等比数列的性质，对数的运算法则等知识，意在考查学生的转化能力和计算求解能力.11.在等腰三角形ABC 中，4AB AC ==，6BC =，点P ，Q 是边BC 上的两个三等分点，则AP AQ ⋅=（ ） A. 0B. 3C. -6D. 6【解析】 【分析】先取BC 中点D 为坐标原点，以BC 所在直线为x 轴，以DA 所在直线为y 轴建立平面直角坐标系，再求出P Q A 、、坐标，得到AP 与AQ 坐标，进而可求出其数量积.【详解】如图，取BC 中点D 为坐标原点，以BC 所在直线为x 轴，以DA 所在直线为y 轴建立平面直角坐标系，因为4AB AC ==，6BC =，则A 点坐标为()0,7，P 点坐标为()1,0-，Q 点坐标为()1,0，所以()1,7AP =--，()1,7AQ =-，所以6AP AQ ⋅=.故选D【点睛】本题主要考查向量的数量积运算，可采用建系的方法求出向量的坐标，进而可求出结果，属于基础题型.12.已知()f x 为定义在R 上的奇函数，当0x <时，()()21xf x x e =+，以下列命题：①当0x >时，()()21xf x x e =- ②()0f x <的解集为11,0,22⎛⎫⎛⎫-∞- ⎪ ⎪⎝⎭⎝⎭③函数()f x 共有2个零点 ④12,x x R ∀∈，都有()()122f x f x -< 其中正确命题个数是（ ） A. 1 B. 2C. 3D. 4【答案】B 【解析】 【分析】首先根据奇函数，求0x >时，函数的解析式，然后再判断②③④，再判断④时， 转化为()()12max 2f x f x -<成立.【详解】①设0x >，0x -<()f x 是奇函数，()()()()2121x x f x f x x e x e --∴=--=--+=-，∴①不成立；②当0x <时，()210xx e +< ，解得：21x <-； 当0x >时，()210xx e --< ，解得：102x <<，综上：不等式的解集是11,0,22⎛⎫⎛⎫-∞-⎪ ⎪⎝⎭⎝⎭，故②正确； ③由②可知()f x 有两个零点，分别是12x =-和12x =，()f x 是R 上的奇函数，()00f ∴= ，()f x ∴有3个零点，分别是11,0,22x =-.故③不正确； ④当0x >时，()21xx f x e -=， ()32xx f x e -'=，当32x =时，()0f x '=， 当30,2x ⎛⎫∈ ⎪⎝⎭时，()0f x '>，()f x 单调递增， 当3,2x ⎛⎫∈+∞ ⎪⎝⎭时，()0f x '<，()f x 单调递减，∴当32x =时，()f x 取得最大值，32322f e -⎛⎫= ⎪⎝⎭， ()f x 是奇函数，()f x ∴的最小值是32322f e -⎛⎫-=- ⎪⎝⎭，()()()33322212max 2242f x f x eee----=--=< ，∴12,x x R ∀∈，都有()()122f x f x -<，故④正确.故正确的有②④. 故选：B【点睛】本题考查根据函数的奇偶性，求函数的解析式，并判断分段函数的性质，本题的关键是①式的正确判断，根据函数的奇偶性求函数的解析式时，求0x >的解析式，那就需设0x >，再根据函数的奇偶性，求()f x 的解析式，本题的易错点是③，函数的零点个数，不要忘记0x =.二、填空题13.若3sin 5α=，则cos2=α______. 【答案】725【解析】 【分析】利用二倍角余弦公式可求出cos2α的值.【详解】由二倍角余弦公式可得2237cos 212sin 12525αα⎛⎫=-=-⨯=⎪⎝⎭. 故答案为：725. 【点睛】本题考查二倍角余弦值的计算，熟练利用二倍角余弦公式计算是解题的关键，考查计算能力，属于基础题.14.在等差数列{}n a 中，已知16112a a a π++=，则6sin a 的值为______.【解析】 【分析】利用等差中项的性质计算出6a ，即可计算出6sin a 的值.【详解】由等差中项的性质可得1611632a a a a π++==，623a π∴=，因此，62sin sinsin sin 333a ππππ⎛⎫==-==⎪⎝⎭故答案为：2. 【点睛】本题考查等差中项性质的应用，同时也考查了利用诱导公式求值，考查计算能力，属于基础题.15.ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ，若3A π=，ABC S ∆=，则AB AC ⋅=______.【答案】2 【解析】 【分析】利用三角形的面积公式可求出bc 的值，然后利用平面向量数量积的定义可计算出AB AC ⋅的值.【详解】由三角形的面积公式可得11sin sin 223ABC S cb A cb π∆====，解得4cb =.由平面向量数量积的定义可得1cos 422AB AC cb A ⋅==⨯=. 故答案为：2.【点睛】本题考查利用三角形面积求其它量，同时也考查了平面向量数量积的计算，涉及平面向量数量积的定义，考查计算能力，属于中等题. 16.已知数列{}n a 中，11a =，11n n a a n +=++，则数列n a n ⎧⎫⎨⎬⎩⎭的前n 项和为______. 【答案】()43n n + 【解析】 【分析】利用累加法求出n a ，可得出数列n a n ⎧⎫⎨⎬⎩⎭的通项公式，然后利用等差数列的求和公式可求出数列n a n ⎧⎫⎨⎬⎩⎭的前n 项和. 【详解】11n n a a n +=++，1n n a a n -∴-=，()()()()12132111232n n n n n a a a a a a a a n -+∴=+-+-++-=++++=，12n a n n +∴=， ()111111222n n n a a n n n ++++-=-=+，则数列n a n ⎧⎫⎨⎬⎩⎭为等差数列.因此，数列n a n ⎧⎫⎨⎬⎩⎭的前n 项和为()113224n n n n +⎛⎫+ ⎪+⎝⎭=.故答案为：()43n n +.【点睛】本题考查累加法求数列通项，同时也考查了等差数列求和公式的应用，考查计算能力，属于中等题.三、解答题17.已知数列{}n a 是等差数列，12a =，12312a a a ++=． （1）求数列{}n a 的通项公式； （2）令3nn a b =，求数列{}n b 的前n 项和n S ．【答案】（1）2n a n =；（2）9(19)9(91)198n nn S -==--【解析】 试题分析：(1)利用题意首先求得公式为2，然后利用等差数列通项公式可得2n a n =.(2) 利用题意可得数列{}n b 是首项为9，公比9q =的等比数列，结合等比数列求和公式可得()9918nn S =-. 试题解析：（1）∵数列{}n a 是等差数列，由12312a a a ++=，得2312a =，∴24a =， 由12a =，所以公差21422d a a =-=-=， ∴数列{}n a 的通项公式2n a n =.（2）239nnn b ==，11999n n n n b b ++==， ∴数列{}n b 是首项为9，公比9q =的等比数列， 数列{}n b 的前n 项和()()919991198n nnS -==--18.ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ，已知()cos 2cos b C a c B =-. （1）求B ； （2）若2c =，b =ABC ∆的面积.【答案】（1）3π；（2【解析】 【分析】（1）利用正弦定理边角互化思想求出cos B 的值，结合角B 的范围可得出角B 的值； （2）利用余弦定理求出a 的值，利用三角形的面积公式可求出ABC ∆的面积.【详解】（1）()cos 2cos b C a c B =-，由正弦定理得()sin cos 2sin sin cos B C A C B =-， 则()()2sin cos sin cos cos sin sin sin sin A B B C B C B C A A π=+=+=-=，sin 0A >，1cos 2B ∴=，0B π<<，因此，3B π=； （2）由余弦定理得2222cos b a c ac B =+-，即2427a a +-=，整理得2230a a --=.0a >，解得3a =，因此，ABC ∆的面积为11sin 3222ABC S ac B ∆==⨯⨯=. 【点睛】本题考查利用正弦定理和余弦定理解三角形，同时也考查了三角形面积的计算，解题时要结合三角形已知元素的类型选择正弦定理或余弦定理解三角形，考查计算能力，属于中等题.19.已知数列{a n }的首项a 1＝1，a n ＋1＝42nn a a + (n ∈N *)．(1)证明：数列11{}2n a -是等比数列；(2)设b n ＝nna ，求数列{b n }的前n 项和S n .【答案】（1）见解析（2）2(1)224n n n n ++-+ 【解析】试题分析:（1）根据等比数列定义，代入条件化简即得111211122n n a a +-=- （2）先求出1n a ，再利用分组求和以及错位相减法得数列{b n }的前n 项和S n .试题解析：解：(1)证明：∵a n ＋1＝，∴＝＝＋.∴－＝.又∵a 1＝1，∴－＝，∴数列是以为首项，为公比的等比数列．(2)解：由(1)知－＝·n －1＝，即＝＋，∴b n ＝＝＋. 设T n ＝＋＋＋…＋，① 则T n ＝＋＋…＋＋，②①－②，得T n ＝＋＋…＋－＝1－－，∴T n ＝2－－.又∵ (1＋2＋3＋…＋n )＝，∴数列{b n }的前n 项和S n ＝2－＋.点睛：用错位相减法求和应注意的问题(1)要善于识别题目类型，特别是等比数列公比为负数的情形；(2)在写出“n S ”与“n qS ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“n n S qS -”的表达式；(3)在应用错位相减法求和时，若等比数列的公比为参数，应分公比等于1和不等于1两种情况求解.20.已知()2cos ,1m x x =+，()cos ,n x y =-，满足m n ⊥． （1）将y 表示为x 的函数()f x ，并求()f x 的最小正周期；（2）已知a 、b 、c 分别为锐角ABC ∆的三个内角A 、B 、C 对应的边长，()()f x x R ∈的最大值是2f A ⎛⎫⎪⎝⎭，且a =ABC ∆周长L 的取值范围． 【答案】（1）()2sin 216f x x π⎛⎫=++ ⎪⎝⎭，最小正周期为π；（2）(3+. 【解析】 【分析】（1）由m n ⊥，可得出()2cos cos y x x x =+，利用二倍角降幂公式以及辅助角公式可将函数()y f x =的解析式化简，然后利用周期公式可计算出函数()y f x =的最小正周期；（2）由题意可得02A π<<，可得出6A π+的取值范围，结合题中条件求出A 的值，然后利用正弦定理将L 表示为角B 的三角函数，并求出角B 的取值范围，利用正弦函数的基本性质可求出L 的取值范围. 【详解】（1）()2cos ,1m x x =+，()cos ,n x y =-，满足m n ⊥，()2cos cos 0m n x x x y ∴⋅=+-=，()22cos cos cos 2cos 2cos 21y x x x x x x x x ∴=+=+=++2sin 216x π⎛⎫=++ ⎪⎝⎭，因此，函数()y f x =的最小正周期为22T ππ==； （2）由题意可知，函数()y f x =的最大值为2sin 126A f A π⎛⎫⎛⎫=++⎪ ⎪⎝⎭⎝⎭. A 为锐角，则02A π<<，2663A πππ∴<+<，则62A ππ+=，解得3A π=.由正弦定理2sin sin sin sin3b c a B C A ====，2sin b B ∴=，2sin c C =，()2sin2sin2sin2sinL a b c B C B A B∴=++=+=++12sin2sin2sin2sin32B B B B Bπ⎛⎫⎛⎫=++=++⎪⎪ ⎪⎝⎭⎝⎭3sin6B B Bπ⎛⎫=+=+⎪⎝⎭ABC∆为锐角三角形，且3Aπ=，则22BCππ⎧<<⎪⎪⎨⎪<<⎪⎩，即2232BBπππ⎧<<⎪⎪⎨⎪<-<⎪⎩，解得62Bππ<<，2363Bπππ<+<，sin126Bπ⎛⎫<+≤⎪⎝⎭，则36Bπ⎛⎫<++⎪⎝⎭因此，ABC∆的周长L的取值范围是(3+.【点睛】本题考查三角函数解析式化简以及正弦型函数周期的计算，同时也考查了三角形周长取值范围的计算，一般转化为以某角为自变量的三角函数值域问题求解，考查计算能力，属于中等题.21.已知函数2()(1)lnf x a x x=--.（1）若()y f x=在2x=处取得极小值，求a的值；（2）若()0f x≥在[1,)+∞上恒成立，求a的取值范围；【答案】（1）18a=；（2）12a≥.【解析】试题分析：（1）求函数2()(1)lnf x a x x=--的导数1()2f x axx='-，由(2)0f'=求之即可；（2）分0a≤、12a<<、12a≥分别讨论函数的单调性，由单调性求出函数在区间[1,)+∞上的最小值，由min()0f x≥求之即可.试题解析：（1）∵()f x定义域为(0,)+∞，1'()2f x axx=-，∵()f x在2x=处取得极小值，∴'(2)0f=，即18a=.此时，经验证2x=是()f x的极小值点，故18a=（2）∵1'()2f x ax x=-， ①当0a ≤时，'()0f x <，∴()f x 在[1,)+∞上单调递减， ∴当1x >时，()(1)0f x f <=矛盾②当0a >时，221'()ax f x x-=，令'()0f x >，得x >；'()0f x <，得0x <<. （ⅰ1>，即102a <<时，x ∈时，'()0f x <，即()f x 递减，∴()(1)0f x f <=矛盾. （ⅱ1≤，即12a ≥时， [1,)x ∈+∞时，'()0f x >，即()f x 递增，∴()(1)0f x f ≥=满足题意.综上，12a ≥考点：1.导数与函数的单调性、极值；2.函数与不等式.22.已知圆的极坐标方程为：2cos 604πρθ⎛⎫--+= ⎪⎝⎭. （1）将极坐标方程化为普通方程；（2）若点(,)P x y 在该圆上，求x y +的最大值和最小值. 【答案】（1）224460x y x y +--+= （2）最大值为6，最小值为2 【解析】 【分析】（1）将2cos 604πρθ⎛⎫--+= ⎪⎝⎭先由两角差的余弦公式展开，再化为普通方程．（2）由题可知圆的参数方程为22x y θθ⎧=+⎪⎨=+⎪⎩ （θ为参数），因为点(,)P x y 在该圆上，所以()2,2P θθ+，所以可得42sin 4x y πθ⎛⎫++⎪⎝+⎭=，从而得出答案． 【详解】（1）由圆的极坐标方程为：2cos 604πρθ⎛⎫--+= ⎪⎝⎭可得2cos 6022ρθθ⎛⎫-++= ⎪⎪⎝⎭，即24cos 4sin 60ρρθρθ--+= 所以直角坐标方程224460x y x y +--+=（2）由（1）可知圆的方程为()()22222x y -+-=所以圆的参数方程为22x y θθ⎧=+⎪⎨=+⎪⎩ ，（θ为参数）因为点(,)P x y在该圆上，所以()2,2P θθ所以2242sin 4x y πθθθ+=⎛⎫+++=++ ⎪⎝⎭因为sin 4πθ⎛⎫+⎪⎝⎭的最大值为1，最小值为1- 所以x y +的最大值为6，最小值为2【点睛】极坐标与参数方程是高考的重要选修考点，学生应准确掌握极坐标方程与普通方程的互化，与圆锥曲线有关的最值问题可转化为三角函数求最值．。

宁夏银川市第一中学2020届高三数学上学期第三次月考试题 理注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．作答时，务必将答案写在答题卡上。

写在本试卷及草稿纸上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．已知集合{}05|2>-=x x x A ，则C R A = A ．{}50|≤≤x xB ．{}0|<x xC ．{}5|>x xD ．{}05|≤≤-x x2．设i 是虚数单位，如果复数2a ii-+的实部与虚部是互为相反数，那么实数a 的值为 A ．3B ．13C ．13-D ．3-3．若向量m =（0，-2），n =（3，1），则与n m +2共线的向量可以是 A ．（3，-1） B ．（-1，3） C ．（3-，-1） D ．（3,1--）4．设a ，b R ∈，那么“1ab>”是“0a b >>”的 A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件 5．某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为 A ．2 B ．C ．D ．6．等比数列{}n a 的首项为32，公比为12-，前n 项和为n S ，则当*n N ∈时，1n nS S -的最小值与最大值的比值为 A ．125-B ．107-C ．109D ．1257．某汽车公司的A ,B 两个装配厂可装配甲、乙两种不同型号的汽车,若A 厂每小时可装配1辆甲型车和2辆乙型车,B 厂每小时可装配3辆甲型车和1辆乙型车.现要装配40辆甲型车和40辆乙型车,若要使所费的总工作时数最少,则这两个装配厂的工作时数分别为A ．16,8B ．15,9C ．17,7D ．14,108．已知正数,x y 满足1=+y x ，则141x y++的最小值为A ．5B ．314 C ．92D ．29．已知函数()cos f x x x =+，把函数()f x 的图象向右平移3π个单位，再把图象的横坐标缩小到原来的一半，得到函数()g x 的图象，当0,2x π⎡⎤∈⎢⎥⎣⎦时，方程()0g x k -=有两个不同的实根，则实数k 的取值范围为 A．⎡⎣B．)2C ．[]1,2D ．[)1,210．执行如图所示的程序框图，输出的S 值为A ．12017-B ．12018-C ．12019-D ．12020-11．甲、乙、丙三人中,一人是教师、一人是记者、一人是医生.已知:丙的年龄比医生大;甲的年龄和记者不同;记者的年龄比乙小.根据以上情况,下列判断正确的是 A ．甲是教师,乙是医生,丙是记者 B ．甲是医生,乙是记者,丙是教师 C ．甲是医生,乙是教师,丙是记者 D ．甲是记者,乙是医生,丙是教师 12．已知定义在R 上的连续奇函数()f x 的导函数为()f x '，当0x >时，()()0f x f x x'+>，则使得()()()2213310xf x x f x +-->成立的x 的取值范围是 A ．()1,+∞B ．()11,1,5⎛⎫-+∞ ⎪⎝⎭C ．1,15⎛⎫⎪⎝⎭D ．(),1-∞二、填空题：本大题共4小题，每小题5分，共20分.13．已知函数b x ab ax x f --+=)1()(2，如果不等式()0f x >的解集为()1,3-，那么不等式开始n =1,s =011+++=n n s sn =n +1n <2019? 否是输出S 结束()20f x -<的解集为________________.14．观察下列各式：31=1，3321+2=3，33321+2+3=6，333321+2+3+4=10，…，由此推得：33331+2+3+n = ．15．若函数()sin()(0,0)6f x A x A πωω=->>如图所示,则图中的阴影部分的面积为 . 16．底面半径为1cm 的圆柱形容器里放有四个半径为21cm 使水面恰好浸没所有铁球，则需要注水体积为 cm 3.三、解答题：共70分，解答时应写出必要的文字说明、演算步骤.第17～21题为必考题，第22、23题为选考题. （一）必考题：共60分 17．（12分）设数列{a n }的前n 项和为S n .已知S 2=4,a n+1=2S n +1,n∈N *. (1)求通项公式a n .(2)求数列{a n -n-2}的前n 项和.18．（12分）某工厂利用辐射对食品进行灭菌消毒，现准备在该厂附近建一职工宿舍，并对宿舍进行防辐射处理，建房防辐射材料的选用与宿舍到工厂距离有关.若建造宿舍的所有费用p (万元)和宿舍与工厂的距离x (km )的关系为)80(53≤≤+=x x kp ,若距离为1km 时，测算宿舍建造费用为100万元.为了交通方便，工厂与宿舍之间还要修一条道路，已知购置修路设备需5万元，铺设路面每公里成本为6万元，设f (x )为建造宿舍与修路费用之和.(1)求f (x )的表达式(2)宿舍应建在离工厂多远处，可使总费用f (x )最小并求最小值.19．（12分）如图，在四边形ABCD 中，,2,AC CD AD ==2.3ADC π∠=（1）求CAD ∠的正弦值；（2）若2BAC CAD ∠=∠，且△ABC 的面积是△ACD 面积的4倍，求AB 的长.20．（12分）各项均为正数的等比数列{}n a 中，已知152,512,n a a T ==是数列{}2log n a 的前n 项和.（1）求数列{}n a 的通项公式； （2）求n T ； （3）求满足20131011)11()11)(11(32>---n T T T 的最大正整数n 的值. 21．（12分）已知函数()ln 3f x a x ax =-- (0)a ≠． (1)讨论()f x 的单调性；(2)若()(1)40f x a x e +++-≤对任意2[,]x e e ∈恒成立，求实数a 的取值范围（e 为自然常数）；(3)求证：22221111ln(1)ln(1)ln(1)...ln(1)1234n++++++++<*(2,)n n N ≥∈． (二)选考题：共10分。

理科数学试卷注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．作答时，务必将答案写在答题卡上。

写在本试卷及草稿纸上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合}13|{},1|{2<=≤=xx B x x A ，则=)(B C A R Y A ．}0|{<x x B ．}10|{≤≤x xC ．}01|{<≤-x xD ．}1|{-≥x x2．若复数z 与其共轭复数z 满足i z z 312+=-，则=||z A ．2B ．3C ．2D ．53．抛物线214y x =的准线方程是 A ．2-=xB ．2-=yC ．1-=xD ．1-=y4．若向量)2,1(+=x 与)1,1(-=平行，则|2+|=a b r rA 2B ．322C ．32D ．225．已知n m ,是两条不重合的直线，βα,是两个不重合的平面，则下列命题中，错误的是 A ．若α⊥⊥m n m ,，则α//nB ．若αα⊄n m n m ,//,//，则α//nC ．若βα⊥⊥⊥n m n m ,,，则βα⊥D ．若βαα//,//m ，则β//m 或β⊂m 6．已知函数y =f (x )的部分图像如图，则f (x )的解析式可能是 A ．()tan f x x x =+ B ．()sin 2f x x x =+ C ．1()sin 22f x x x =- D ．1()cos 2f x x x =-7．为了加强“精准扶贫”，实现伟大复兴的“中国梦”，某大学派遣甲，乙，丙，丁，戊五位同学参加A,B,C 三个贫困县的调研工作，每个县至少去1人，且甲，乙两人约定去同一个贫困县，则不同的派遣方案共有 A ．24B ．36C ．48D ．648．已知函数41()2x xf x -=，0.30.30.3(2),(0.2),(log 2)a f b f c f ===，则,,a b c 的大小关系为A ．c b a <<B ． b a c <<C ．b c a <<D ．c a b <<9．天文学中，为了衡量星星的明暗程度，古希腊天文学家喜帕恰斯（Hipparchus ）在公元前二世纪首先提出了星等这个概念。