中考数学创新题目

初中数学竞赛创新试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是最小的正整数？A. -2B. 0C. 1D. 22. 如果一个圆的半径是5厘米，那么它的周长是多少厘米？A. 10πB. 15πC. 20πD. 25π3. 一个数的平方是16，这个数可能是：A. 2B. 4C. -2D. C和-24. 一个直角三角形的两条直角边分别为3和4，那么它的斜边长度是：A. 5B. 6C. 7D. 85. 如果一个数的绝对值是5，那么这个数可能是：A. 5C. A和BD. 06. 一个数的立方是-27，这个数是：A. -3B. 3C. -27D. 277. 一个数的倒数是1/4，那么这个数是：A. 4B. 1/4C. 1/2D. 18. 一个数的平方根是4，那么这个数是：A. 16B. -16C. 4D. -49. 如果一个数的平方是25，那么这个数的立方是：A. 125B. 250C. 375D. 62510. 一个数的立方根是-2，那么这个数是：A. -8B. 8D. 2二、填空题（每题3分，共15分）11. 一个数的平方是9，这个数是_________。

12. 如果一个数的平方根是2，那么这个数是_________。

13. 一个数的立方是64，这个数是_________。

14. 一个数的倒数是2/3，那么这个数是_________。

15. 如果一个数的立方根是3，那么这个数是_________。

三、解答题（每题5分，共55分）16. 一个直角三角形的斜边长度是13厘米，其中一个直角边是5厘米，求另一个直角边的长度。

17. 一个数列的前三项是1, 1, 2，每一项都是前两项的和，求这个数列的第10项。

18. 一个圆的直径是14厘米，求这个圆的面积。

19. 一个数的平方是25，求这个数的平方根。

20. 一个数的立方是-125，求这个数。

四、证明题（每题10分，共20分）21. 证明：对于任意一个正整数n，n的平方总是大于或等于n。

一、选择题（每题5分，共25分）1. 下列选项中，不属于实数的是（）A. 2.5B. -3C. √4D. π答案：D解析：实数包括有理数和无理数，π是无理数，不属于实数。

2. 已知一元二次方程 x^2 - 5x + 6 = 0，其两个根分别为 a 和 b，则 a + b 的值为（）A. 5B. 6C. -5D. -6答案：A解析：根据一元二次方程的求根公式，可得 a + b = -(-5) = 5。

3. 在直角坐标系中，点 A(2,3) 关于 y 轴的对称点坐标为（）A. (-2,3)B. (2,-3)C. (-2,-3)D. (2,3)答案：A解析：点 A(2,3) 关于 y 轴的对称点坐标为 (-2,3)。

4. 下列函数中，y 是 x 的反比例函数的是（）A. y = 2x + 3B. y = x^2 - 1C. y = 1/xD. y = 3x答案：C解析：反比例函数的形式为 y = k/x（k ≠ 0），故选 C。

5. 已知等差数列 {an} 的首项 a1 = 3，公差 d = 2，则第 10 项 an 的值为（）A. 21B. 23C. 25D. 27答案：C解析：等差数列的通项公式为 an = a1 + (n - 1)d，代入数据得 an = 3 + (10 - 1)×2 = 25。

二、填空题（每题5分，共25分）6. 若 a > b，则 |a| - |b| 的值为 _______。

答案：a - b解析：因为 a > b，所以 |a| = a，|b| = b，所以 |a| - |b| = a - b。

7. 若二次函数 y = ax^2 + bx + c（a ≠ 0）的图像开口向上，则 a 的取值范围是 _______。

答案：a > 0解析：二次函数的图像开口向上，说明 a 的值必须大于 0。

8. 在直角三角形 ABC 中，∠A = 90°，∠B = 30°，则 AC 的长度是 AB 的_______ 倍。

一、选择题（每题3分，共30分）1. 下列哪个函数是奇函数？A. y = x^2B. y = |x|C. y = x^3D. y = x^4答案：C解析：奇函数的定义是f(-x) = -f(x)，只有C选项满足此条件。

2. 在直角坐标系中，点A(2,3)，点B(5,1)，则线段AB的中点坐标为：A. (3,2)B. (4,2)C. (3,1)D. (4,1)答案：B解析：中点坐标公式为((x1+x2)/2, (y1+y2)/2)，代入得(4,2)。

3. 若等差数列{an}的公差d=2，且a1+a5=18，则a3的值为：A. 8B. 10C. 12D. 14答案：B解析：由等差数列性质，a1+a5 = 2a3，代入得2a3=18，解得a3=9。

4. 若sinA=1/2，cosB=3/5，且A、B均为锐角，则tan(A+B)的值为：A. 1B. 2C. 3D. 4答案：B解析：利用正切和公式tan(A+B) = (tanA+tanB)/(1-tanAtanB)，代入得tan(A+B) = (1/2+3/5)/(1-1/23/5) = 2。

5. 若等比数列{an}的公比q=2，且a1+a3=24，则a5的值为：A. 64B. 32C. 16D. 8答案：A解析：由等比数列性质，a1a3 = a2^2，代入得a1a3 = 2^22^2 = 16，又因为a1+a3=24，解得a1=4，a3=20，所以a5=a3q^2=202^2=64。

二、填空题（每题4分，共20分）6. 已知函数f(x)=2x-1，则f(-3)的值为______。

答案：-7解析：将x=-3代入函数f(x)中，得f(-3)=2(-3)-1=-7。

7. 在△ABC中，若a=3，b=4，c=5，则△ABC是______三角形。

答案：直角解析：根据勾股定理，a^2+b^2=c^2，代入得3^2+4^2=5^2，满足条件，所以△ABC 是直角三角形。

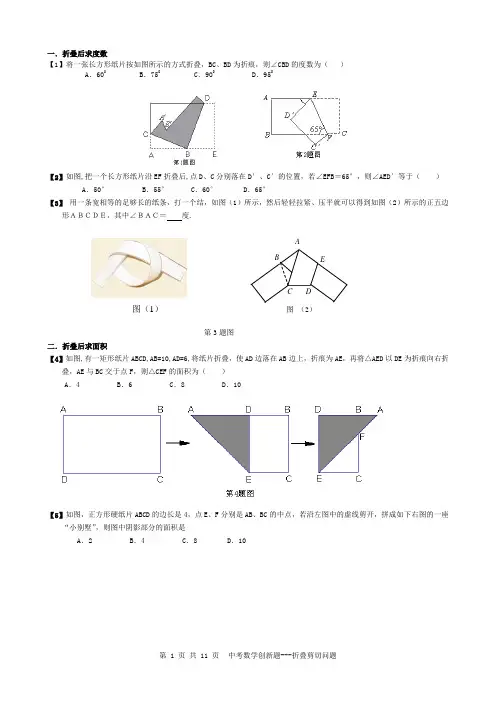
一．折叠后求度数【1】将一张长方形纸片按如图所示的方式折叠，BC、BD为折痕，则∠CBD的度数为（）A．600 B．750 C．900 D．950【2】如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置，若∠EFB＝65°，则∠AED′等于（）A．50° B．55°C．60° D．65°【3】用一条宽相等的足够长的纸条，打一个结，如图（1）所示，然后轻轻拉紧、压平就可以得到如图（2）所示的正五边形ＡＢＣＤＥ，其中∠ＢＡＣ＝度.二．折叠后求面积【4】如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F，则△CEF的面积为（）A．4 B．6 C．8 D．10【5】如图，正方形硬纸片ABCD的边长是4，点E、F分别是AB、BC的中点，若沿左图中的虚线剪开，拼成如下右图的一座“小别墅”，则图中阴影部分的面积是A．2 B．4 C．8 D．10图（1）第3题图A图（2）【6】如图a ，ABCD 是一矩形纸片，AB ＝6cm ，AD ＝8cm ，E 是AD 上一点，且AE ＝6cm 。

操作：（1）将AB 向AE 折过去，使AB 与AE 重合，得折痕AF ，如图b ；（2）将△AFB 以BF 为折痕向右折过去，得图c 。

则△GFC 的面积是（ ）A.1cm 2B.2 cm 2C.3 c m 2D.4 cm 2三．折叠后求长度【7】如图，已知边长为5的等边三角形ABC 纸片，点E 在AC 边上，点F 在AB 边上，沿着EF 折叠，使点A 落在BC 边上的点D 的位置，且ED BC ⊥，则CE 的长是（ ）（A）15 （B）10-（C）5 （D）20-四．折叠后得图形 【8】将一张矩形纸对折再对折（如图），然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形是（ ）A ．矩形 B．菱形【9】在下列图形中，（ ）A. B. C. D.【10】小强拿了张正方形的纸如图（1），沿虚线对折一次如图（2），再对折一次得图（3），然后用剪刀沿图（3）中的虚线（虚线与底边平行）剪去一个角，再打开后的形状应是( )E A A ABB B CC C GD D D FF F图a图b图c第6题图第7题图第8题图第9题图【11】如图，把矩形ABCD 对折，折痕为MN （图甲），再把B 点叠在折痕MN 上的B '处。

一、选择题（每题5分，共25分）1. 下列各数中，是实数的是（）A. √-1B. √4C. √0D. √-92. 若a=2，b=-3，则下列代数式中值为正的是（）A. a+bB. a-bC. a×bD. a÷b3. 下列函数中，表示一次函数的是（）A. y=3x+5B. y=x^2-2x+1C. y=2x+√xD. y=|x|+14. 在直角坐标系中，点A（-2，3）关于原点对称的点的坐标是（）A. （-2，3）B. （2，-3）C. （-2，-3）D. （2，3）5. 下列图形中，面积最大的图形是（）A. 正方形B. 长方形C. 等腰三角形D. 等边三角形二、填空题（每题5分，共25分）6. 若x^2-5x+6=0，则x的值为______。

7. 已知一元二次方程x^2+px+q=0的判别式△=25，则p的值为______。

8. 在直角三角形ABC中，∠C=90°，AB=10cm，AC=6cm，则BC的长度为______cm。

9. 若a，b，c是等差数列的前三项，且a+b+c=12，a+c=8，则b的值为______。

10. 已知函数y=2x+1，若x的取值范围是[1,3]，则y的取值范围是______。

三、解答题（每题10分，共40分）11. （10分）已知一元二次方程x^2-4x+3=0，求：（1）方程的两个实数根；（2）若x是方程的根，求x+1的值。

12. （10分）在直角坐标系中，点P（2，-3）到直线y=-x+4的距离为______。

13. （10分）已知数列{an}的通项公式为an=3n-2，求：（1）数列的前5项；（2）数列的前n项和S_n。

14. （10分）已知函数y=2x-3，若x的取值范围是[2,4]，求y的取值范围。

四、附加题（20分）15. （10分）在平面直角坐标系中，已知点A（3，2），点B（-1，5），求：（1）直线AB的斜率；（2）直线AB的截距；（3）直线AB的方程。

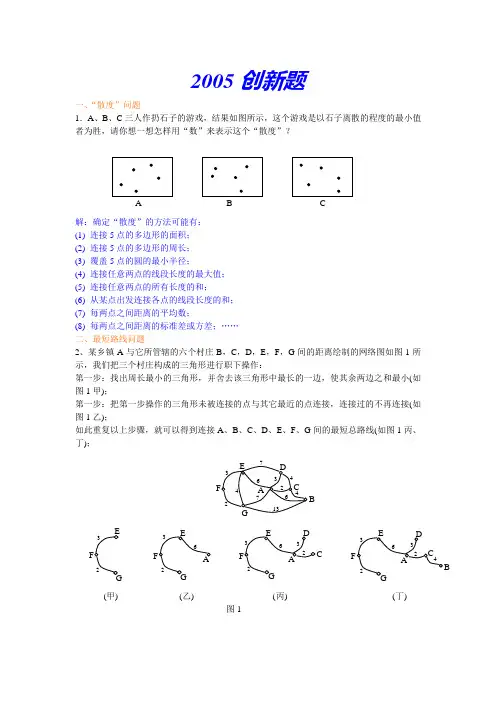
2005创新题一、“散度”问题1．A 、B 、C 三人作扔石子的游戏，结果如图所示，这个游戏是以石子离散的程度的最小值者为胜，请你想一想怎样用“数”来表示这个“散度”？解：确定“散度”的方法可能有： (1) 连接5点的多边形的面积； (2) 连接5点的多边形的周长； (3) 覆盖5点的圆的最小半径；(4) 连接任意两点的线段长度的最大值； (5) 连接任意两点的所有长度的和；(6) 从某点出发连接各点的线段长度的和； (7) 每两点之间距离的平均数；(8) 每两点之间距离的标准差或方差；…… 二、最短路线问题2、某乡镇A 与它所管辖的六个村庄B ，C ，D ，E ，F ，G 间的距离绘制的网络图如图1所示，我们把三个村庄构成的三角形进行职下操作：第一步：找出周长最小的三角形，并舍去该三角形中最长的一边，使其余两边之和最小(如图1甲)；第一步：把第一步操作的三角形未被连接的点与其它最近的点连接，连接过的不再连接(如图1乙)；如此重复以上步骤，就可以得到连接A 、B 、C 、D 、E 、F 、G 间的最短总路线(如图1丙、丁)；A BCB(甲) (乙) (丙) (丁) 图1现有一张某城市七个居民区的距离绘制图(如图2)单位：千米。

请完成： (1) 画出连接这开七个小区的最短路线；(2) 如果要在这七个小区间的铺设煤气管道，而且每生米管道费用为a 元，每个小区有一个调度室，造价为b 元，那么连接这七个小区的管道最低费用是多少？解：如下图，要标明数字，最短距离为1.5+1.4+1.8+2.1+1.4=9.7千米(图正确每一步1分，答案2分)；(2)(9.7a+7b)元。

三、直角三角形面积与周长关系问题3、已知：Rt △ABC 中，∠C=900，∠A ，∠B ，∠C 的对边分别为a ，b ，c ，设△ABC 的面积为S ，周长为L 。

探索SL的值与a+b-c 的值之间的关系。

(1)填表：(2)观察后猜测：如果a ，b ，c 为已知数，且a+b-c=m ，则L=___________(用含m 的式子表示)；(3) 证明(2)中的结论。

一、选择题（每题3分，共30分）1. 下列各组数中，成等差数列的是（）A. 2, 5, 8, 11, 14B. 3, 6, 9, 12, 15C. 4, 8, 12, 16, 20D. 5, 10, 15, 20, 25答案：A解析：等差数列的定义是相邻两项之差为常数，观察选项A，相邻两项之差均为3，故选A。

2. 已知函数f(x) = 2x + 1，若f(x) + f(-x) = 9，则x的值为（）A. 2B. 3C. 4D. 5答案：C解析：将x和-x分别代入函数f(x)中，得到f(x) + f(-x) = 2x + 1 + 2(-x) +1 = 2，由题意知f(x) + f(-x) = 9，所以2 = 9，解得x = 4。

3. 在直角坐标系中，点A(2, 3)，点B(-3, -4)，则线段AB的中点坐标为（）A. (2, 3)B. (-1, -1)C. (1, 2)D. (-1, 2)答案：B解析：线段AB的中点坐标为两个端点坐标的平均值，即中点坐标为((2 + (-3))/2, (3 + (-4))/2) = (-1, -1)。

4. 已知等腰三角形的底边长为6，腰长为8，则该三角形的周长为（）A. 22B. 24C. 26D. 28答案：D解析：等腰三角形的两腰长度相等，周长为底边长加上两腰长，即周长为6 + 8 + 8 = 22。

5. 下列函数中，在定义域内单调递增的是（）A. y = x^2B. y = -x^2C. y = x^3D. y = -x^3答案：C解析：函数y = x^3在定义域内单调递增，因为其导数y' = 3x^2恒大于0。

二、填空题（每题5分，共25分）6. 已知数列{an}的通项公式为an = 3n - 2，则第10项an = __________。

答案：28解析：将n = 10代入通项公式，得到a10 = 3 10 - 2 = 28。

7. 若sinα = 0.6，cosα = 0.8，则tanα = __________。

数学中考创新题型选择题汇总1. 已知函数f(x) = x^2 - 2x + 1，求f(x)的零点个数。

2. 已知a、b、c为三角形的三边，且满足a^2 + b^2 = c^2，求证三角形ABC是直角三角形。

3. 已知等差数列{an}的首项a1=1，公差d=2，求第10项a10的值。

4. 已知函数g(x) = x^3 - 3x^2 + 3x - 1，求g(x)的导数。

5. 已知等比数列{bn}的首项b1=2，公比q=2，求第6项b6的值。

6. 已知函数h(x) = log2(x+1)，求h(x)的反函数。

7. 已知函数f(x) = ax^2 + bx + c，其中a、b、c为常数，且a≠0，求f(x)的顶点坐标。

8. 已知等差数列{cn}的首项c1=1，公差d=2，求第10项c10的值。

9. 已知函数g(x) = x^3 - 3x^2 + 3x - 1，求g(x)的极值点。

10. 已知函数h(x) = log2(x+1)，求h(x)的定义域。

11. 已知函数f(x) = ax^2 + bx + c，其中a、b、c为常数，且a≠0，求f(x)的单调区间。

12. 已知等比数列{dn}的首项d1=2，公比q=2，求第6项d6的值。

13. 已知函数g(x) = x^3 - 3x^2 + 3x - 1，求g(x)的拐点坐标。

14. 已知函数h(x) = log2(x+1)，求h(x)的值域。

15. 已知函数f(x) = ax^2 + bx + c，其中a、b、c为常数，且a≠0，求f(x)的奇偶性。

16. 已知等差数列{en}的首项e1=1，公差d=2，求第10项e10的值。

17. 已知函数g(x) = x^3 - 3x^2 + 3x - 1，求g(x)的单调递增区间。

18. 已知函数h(x) = log2(x+1)，求h(x)的单调递减区间。

19. 已知函数f(x) = ax^2 + bx + c，其中a、b、c为常数，且a≠0，求f(x)的周期。

数学中考创新题型选择题汇总1. 某学校计划为教职工提供两种不同的健康保险方案。

方案A的年保费为1200元，方案B的年保费为800元。

若学校有教职工500人，教职工们平均选择方案A和方案B的人数之比为2:3，那么选择方案A的人数是____人。

2. 一个等差数列的第一个数是5，公差是3，那么这个等差数列的第10个数是多少？3. 一次函数的图像是一条直线，已知这条直线的斜率为2，并且它与x轴的交点是(1, 0)，那么这条直线的方程是什么？4. 一个圆的半径增加了10%，原来的面积是π，那么新的面积是多少？5. 一个长方体的长、宽、高分别是8cm、5cm和3cm，那么这个长方体的对角线长度是多少？6. 三个连续的整数，中间的整数是5，那么这三个整数是什么？7. 一个班级有40名学生，其中有20名女生和20名男生。

如果从班级中随机选择2名学生，那么选出的两名学生中至少有一名女生的概率是多少？8. 一个正方体的边长是4cm，那么它的对角线长度是多少？9. 一个数列的前三项分别是1、2和3，每一项都比前一项多2，那么这个数列的第10项是多少？10. 一个三角形的两边分别是6cm和8cm，第三边的长度是多少？11. 一个圆锥的底面半径是3cm，高是5cm，那么这个圆锥的体积是多少？12. 一个等差数列的前两项分别是1和3，公差是2，那么这个等差数列的第10项是多少？13. 一个正方体的对角线长度是12cm，那么这个正方体的边长是多少？14. 一个班级有30名学生，其中有15名女生和15名男生。

如果从班级中随机选择2名学生，那么选出的两名学生中至少有一名女生的概率是多少？15. 一个圆的半径增加了20%，原来的面积是π，那么新的面积是多少？16. 一个等差数列的前两项分别是2和4，公差是2，那么这个等差数列的第10项是多少？17. 一个长方体的长、宽、高分别是4cm、3cm和2cm，那么这个长方体的对角线长度是多少？18. 三个连续的整数，中间的整数是7，那么这三个整数是什么？19. 一个班级有50名学生，其中有25名女生和25名男生。

初三数学创新试题及答案一、选择题（每题3分，共30分）1. 若一个数的平方等于4，则这个数是（）。

A. 2B. -2C. 2或-2D. 以上都不是答案：C2. 下列哪个选项是一元二次方程的一般形式？（）A. ax^2 + bx + c = 0B. ax^2 + bx - c = 0C. ax^2 - bx + c = 0D. ax^2 + bx + c答案：A3. 已知函数y = 2x + 3，当x = 1时，y的值是（）。

A. 5B. 4C. 3D. 2答案：A4. 一个等腰三角形的两边长分别为3和5，那么这个三角形的周长是（）。

A. 11B. 13C. 16D. 无法确定答案：B5. 下列哪个选项是不等式的基本性质？（）A. 如果a > b，那么a + c > b + cB. 如果a > b，那么ac > bcC. 如果a > b，那么a/c > b/cD. 如果a > b，那么a^2 > b^2答案：A6. 一个圆的半径为5，那么这个圆的面积是（）。

A. 25πB. 50πC. 75πD. 100π答案：C7. 已知一个直角三角形的两条直角边长分别为3和4，那么这个三角形的斜边长是（）。

A. 5B. 6C. 7D. 8答案：A8. 一个数的立方等于-27，那么这个数是（）。

A. 3B. -3C. 9D. -9答案：B9. 一个正比例函数的图象经过点（2，6），那么这个函数的解析式是（）。

A. y = 3xB. y = 2xC. y = 4xD. y = 6x答案：A10. 一个反比例函数的图象经过点（3，4），那么这个函数的解析式是（）。

A. y = 12/xB. y = 9/xC. y = 6/xD. y = 4/x答案：C二、填空题（每题4分，共20分）11. 一个数的绝对值等于5，那么这个数是_________。

答案：±512. 一个二次函数的顶点坐标为（1，-2），那么这个函数的解析式可以是_________。

一、选择题（每题5分，共25分）1. 已知二次函数y=ax^2+bx+c（a≠0）的图像开口向上，且顶点坐标为（1，-2），则下列哪个选项是正确的？A. a=1，b=2，c=-1B. a=1，b=-2，c=1C. a=-1，b=2，c=-1D. a=-1，b=-2，c=12. 在等腰三角形ABC中，AB=AC，点D为BC的中点，AD=5cm，BC=10cm，则三角形ABC的周长为：A. 15cmB. 20cmC. 25cmD. 30cm3. 下列哪个选项是关于x的一次函数？A. y=2x^2-3x+1B. y=x^3-2x^2+1C. y=-3x+4D. y=2x^2+3x+14. 在平面直角坐标系中，点A（2，3）关于y轴的对称点为B，则点B的坐标为：A.（-2，3）B.（2，-3）C.（-2，-3）D.（2，3）5. 已知正方体ABCD-A1B1C1D1的棱长为2cm，则它的体积为：A. 8cm^3B. 16cm^3C. 24cm^3D. 32cm^3二、填空题（每题5分，共25分）6. 若方程x^2-4x+3=0的两个根分别为x1和x2，则x1+x2=______。

7. 在△ABC中，∠A=60°，∠B=45°，则∠C=______。

8. 若a、b、c是等差数列，且a+b+c=12，则a+c=______。

9. 若x、y满足方程组\[\begin{cases}2x+y=7 \\x-3y=-1\end{cases}\]则x=______。

10. 若点P（2，3）在直线y=2x+1上，则点P到直线y=2x+1的距离为______。

三、解答题（每题10分，共30分）11. （1）若等腰三角形ABC的底边BC=8cm，腰AB=AC=10cm，求三角形ABC的周长。

（2）已知等腰三角形ABC的底边BC=6cm，顶角∠A=60°，求三角形ABC的面积。

12. （1）若一元二次方程x^2-4x+3=0的两个根分别为x1和x2，求x1^2+x2^2的值。

一、选择题（每题5分，共25分）1. 下列哪项不属于数学中的创新概念？A. 分数运算B. 几何图形的面积计算C. 质数分解D. 概率论2. 在解决数学问题时，以下哪种方法最符合创新思维？A. 死记硬背B. 类比法C. 逆向思维D. 直接计算3. 下列哪个数是黄金分割比例？A. 0.618B. 0.601C. 0.619D. 0.6174. 在以下数学定理中，哪个定理不属于创新成果？A. 欧几里得定理B. 欧拉公式C. 约翰逊-纳什均衡D. 费马大定理5. 以下哪个数学问题在历史上被证明是具有创新意义的？A. 求解勾股定理B. 计算圆周率πC. 发现斐波那契数列D. 解析几何的创立二、填空题（每题5分，共25分）6. 创新思维在数学中的应用，可以体现在对_______的探索上。

7. 黄金分割比例在自然界和艺术中广泛存在，其近似值为_______。

8. 欧拉公式在复数领域具有重大意义，公式为：_______。

9. 在解决数学问题时，可以运用_______、_______等方法来提高解题效率。

10. 费马大定理经过数百年研究，最终在_______年被证明。

三、解答题（每题15分，共45分）11. 阅读以下材料，结合所学知识，完成下列问题。

材料：近年来，我国在数学领域取得了一系列创新成果，如陈景润证明的哥德巴赫猜想、王元发现的王元-贝尔不等式等。

这些成果不仅提升了我国数学在国际上的地位，也为数学研究提供了新的思路和方法。

（1）请列举一个我国在数学领域取得的创新成果，并简要说明其意义。

（5分）（2）结合所学知识，谈谈创新思维在数学研究中的作用。

（5分）（3）作为一名中学生，你认为应该如何培养自己的创新思维？（5分）12. 阅读以下材料，完成下列问题。

材料：在解决数学问题时，逆向思维可以帮助我们从不同角度思考问题，从而找到解决问题的方法。

（1）请举例说明逆向思维在解决数学问题中的应用。

（5分）（2）结合所学知识，谈谈逆向思维在数学学习中的重要性。

初中数学创新试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是所有偶数的公因数？A. 1B. 2C. 3D. 4答案：B2. 如果一个数的平方是36，那么这个数是多少？A. 6B. -6C. 6或-6D. 以上都不是答案：C3. 下列哪个选项表示的是一个二次函数？A. y = 2x + 3B. y = x^2 - 4x + 4C. y = 3x^3 - 2xD. y = 5答案：B4. 一个长方形的长是宽的两倍，如果宽是4厘米，那么长方形的周长是多少？A. 24厘米B. 28厘米C. 32厘米D. 36厘米答案：A5. 一个数加上它的相反数等于？A. 0B. 1C. -1D. 2答案：A6. 一个圆的半径是5厘米，那么它的面积是多少？A. 78.5平方厘米B. 25平方厘米C. 50平方厘米D. 100平方厘米答案：A7. 一个等腰三角形的两个底角相等，如果一个底角是45度，那么顶角是多少度？A. 45度B. 60度C. 90度D. 180度答案：C8. 一个数的立方根是2，那么这个数是多少？A. 8B. 6C. 4D. 2答案：A9. 如果一个数除以3余1，除以4余2，那么这个数最小是多少？A. 7B. 10C. 13D. 14答案：C10. 下列哪个选项是所有奇数的公倍数？A. 1B. 3C. 5D. 以上都不是答案：D二、填空题（每题3分，共30分）1. 一个数的绝对值是5，这个数可能是______。

答案：±52. 一个等差数列的首项是2，公差是3，那么第5项是______。

答案：173. 如果一个三角形的两边长分别是3厘米和4厘米，那么第三边的长x必须满足______。

答案：1 < x < 74. 一个数的平方是25，那么这个数的立方是______。

答案：125或-1255. 一个圆的直径是10厘米，那么它的周长是______。

答案：31.4厘米6. 如果一个数的倒数是2，那么这个数是______。

初三数学创新试题及答案一、选择题（每题3分，共15分）1. 下列哪个数是无理数？A. 3.14159B. 0.33333…C. πD. √22. 如果一个二次方程的判别式Δ < 0，那么这个方程：A. 有一个实数解B. 有两个实数解C. 没有实数解D. 有无穷多个解3. 一个圆的半径是5，那么它的面积是：A. 25πB. 50πC. 100πD. 200π4. 一个正方体的棱长为a，它的表面积是：A. 6aB. 6a²C. 12aD. 12a²5. 一个数的平方根是它本身，这个数是：A. 0B. 1C. -1D. 以上都不是二、填空题（每题3分，共15分）6. 一个数的相反数是它自己，这个数是______。

7. 如果一个角的度数是45°，那么它的余角是______。

8. 一个直角三角形的两条直角边分别是3和4，那么它的斜边长是______。

9. 一个数的绝对值是10，这个数可以是______或______。

10. 如果一个分数的分子和分母都乘以同一个数，那么它的值______。

三、解答题（每题10分，共20分）11. 已知一个等腰三角形的底边长为6，两腰相等，且周长为18，求两腰的长度。

12. 某工厂生产一批零件，每件零件的成本为5元，售价为10元。

如果工厂希望获得的利润为总成本的60%，求每件零件的售价。

四、证明题（每题10分，共10分）13. 证明：在直角三角形中，斜边的中线等于斜边的一半。

五、综合题（每题10分，共10分）14. 某班级有40名学生，其中30名学生参加了数学竞赛，20名学生参加了物理竞赛，5名学生同时参加了数学和物理竞赛。

求只参加数学竞赛的学生人数。

答案：一、选择题1. C2. C3. B4. B5. A二、填空题6. 07. 45°8. 59. 10，-10 10. 不变三、解答题11. 设两腰的长度为x，则底边长为6，周长为18，所以2x + 6 = 18，解得x = 6。

初三数学创新试题及答案在数学的海洋里，创新试题总能激发学生的思维火花。

下面是一道初三数学的创新试题，旨在考察学生对函数、几何和代数的综合运用能力。

试题：小明在一次数学竞赛中遇到了一个有趣的问题。

题目是这样的：给定一个二次函数 \( y = ax^2 + bx + c \)，其中 \( a \)、\( b \)和 \( c \) 是常数，且 \( a \neq 0 \)。

这个二次函数的图像与\( x \) 轴交于点 \( A \) 和 \( B \)，且 \( A \) 和 \( B \) 的横坐标分别为 \( x_1 \) 和 \( x_2 \)。

现在，小明需要找到一个新的二次函数 \( y = Ax^2 + Bx + C \)，使得它的图像与原函数的图像关于 \( x \) 轴对称，并且与 \( y \) 轴交于点 \( D \)，其纵坐标为 \( C \)。

小明首先需要确定原函数与 \( x \) 轴的交点坐标，然后根据对称性找到新函数的表达式，最后计算出点 \( D \) 的坐标。

解答：首先，我们知道二次函数 \( y = ax^2 + bx + c \) 与 \( x \) 轴的交点可以通过解方程 \( ax^2 + bx + c = 0 \) 得到。

根据韦达定理，\( x_1 \) 和 \( x_2 \) 是这个方程的两个根，因此有 \( x_1+ x_2 = -\frac{b}{a} \) 和 \( x_1 \cdot x_2 = \frac{c}{a} \)。

由于新函数的图像与原函数关于 \( x \) 轴对称，我们可以推断新函数的形式为 \( y = -ax^2 - bx - c \)。

这是因为关于 \( x \) 轴的对称意味着 \( y \) 值取反，而 \( x^2 \) 和 \( x \) 的系数保持不变。

接下来，我们需要找到新函数与 \( y \) 轴的交点 \( D \)。

一、选择题（每题5分，共50分）1. 已知函数f（x）=x^2-2ax+1，其中a为常数，若f（x）的图象开口向上，且顶点坐标为（1，-1），则a的值为（）A. 0B. 1C. 2D. -12. 在直角坐标系中，点A（-1，2），B（3，-4），C（x，y）在直线y=kx+b上，若AC的斜率与BC的斜率互为相反数，则k的值为（）A. 1B. -1C. 2D. -23. 已知等差数列{an}的前n项和为Sn，若S10=55，S20=110，则数列的公差d为（）A. 1B. 2C. 3D. 44. 已知圆O的半径为r，点P在圆上，且∠POA=30°，若OP=2r，则∠AOB的度数为（）A. 60°B. 90°C. 120°D. 150°5. 已知正方体ABCD-A1B1C1D1，若AB=3，则正方体的体积V为（）A. 27B. 36C. 54D. 726. 已知等比数列{an}的公比为q，若a1=1，a3+a5=24，则q的值为（）A. 2B. 3C. 4D. 67. 已知函数f（x）=2x-3，若函数g（x）=f（2x+1）+f（x-1），则g（x）的解析式为（）A. g（x）=3x-6B. g（x）=5x-6C. g（x）=7x-6D. g（x）=9x-68. 已知等差数列{an}的前n项和为Sn，若S10=55，S20=110，则数列的首项a1为（）A. 1B. 2C. 3D. 49. 已知圆O的半径为r，点P在圆上，且∠POA=45°，若OP=2r，则∠AOB的度数为（）A. 90°B. 120°C. 135°D. 150°10. 已知正方体ABCD-A1B1C1D1，若AB=4，则正方体的表面积S为（）A. 64B. 96C. 128D. 144二、填空题（每题5分，共50分）11. 若函数f（x）=x^2+bx+c的图象开口向上，且顶点坐标为（-1，-2），则b=____，c=____。

中考创新试题赏析系列四（杂题篇）一、与数有关的问题例1、（浙江台州）火车票上的车次号有两个意义，一是数字越小表示车速越快，1～98次为特快列车，101～198次为直快列车，301～398次为普快列车，401～498次为普客列车；二是单数与双数表示不同的行驶方向，其中单数表示从北京开出，双数表示开往北京。

根据以上规定,杭州开往北京的某一直快列车的车次号可能是（）。

（A）20 （B）119 （C）120 （D）319答案：选（C）。

例2、（浙江嘉兴）有一种数字游戏，可以产生“黑洞数”，操作步骤如下：第一步，任意写出一个自然数（以下称为原数）；第二步，再写一个新的三位数，它的百位数字是原数中偶数数字的个数，十位数字是原数中奇数数字的个数，个位数字是原数的位数；以下每一步，都对上一步得到的数，按照第二步的规则继续操作，直至这个数不再变化为止。

不管你开始写的是一个什么数，几步之后变成的自然数总是相同的。

最后这个相同的数就叫它为“黑洞数”。

请你以2004为例尝试一下（可自选另一个自然数作检验，不必写出检验过程）：2004，一步之后变为，再变为，再变为，…，“黑洞数”是。

解：2004→404→303→123。

因此“黑洞数”为123。

例3、（湖北荆门）计算机利用的是二进制数，它共有两个数码0、1，将一个十进制数转化为二进制数，只需把该数写成若干个2n数的和，依次写出1或0即可，如：19(十)=16+2+1=1×24+0×23+0×22+1×21+1×20=10011（二）为二进制下的5位数，则十进制数2004是二进制下的（）（A）10位数（B）11位数（C）12位数（D）13位数=++++++解：2004102451225612864164109876543210 1212121212021202120202 =⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=11111010100答案（B）。

数学中考创新题型选择题汇总1. 已知等差数列{a_n}的首项为a_1，公差为d，那么第n项可以表示为：A. a_n = a_1 + (n-1)dB. a_n = a_1 - (n-1)dC. a_n = a_1 * (n-1)dD. a_n = a_1 / (n-1)d2. 下列函数中，属于指数函数的是：A. f(x) = x^2B. f(x) = x^3C. f(x) = 2^xD. f(x) = x^(-1)3. 已知直角三角形的一个锐角为30度，那么这个直角三角形的两个直角边长度的比是：A. 1:1B. 1:2C. 2:1D. 2:24. 若a^2 + b^2 = c^2，那么根据勾股定理，a、b、c满足的关系是：A. a = b + cB. b = a + cC. c = a + bD. a = b - c5. 已知函数f(x) = x^2 - 4x + 3，那么这个函数的顶点坐标是：A. (1, 2)B. (-2, 3)C. (2, -1)D. (-1, 0)6. 已知a^2 + b^2 = c^2，那么根据勾股定理，a、b、c满足的关系是：A. a = b + cB. b = a + cC. c = a + bD. a = b - c7. 若函数f(x) = x^2 - 4x + 3，那么这个函数的顶点坐标是：B. (-2, 3)C. (2, -1)D. (-1, 0)8. 已知等差数列{a_n}的首项为a_1，公差为d，那么第n项可以表示为：A. a_n = a_1 + (n-1)dB. a_n = a_1 - (n-1)dC. a_n = a_1 * (n-1)dD. a_n = a_1 / (n-1)d9. 下列函数中，属于指数函数的是：A. f(x) = x^2B. f(x) = x^3C. f(x) = 2^xD. f(x) = x^(-1)10. 已知直角三角形的一个锐角为30度，那么这个直角三角形的两个直角边长度的比是：A. 1:1B. 1:2D. 2:211. 若a^2 + b^2 = c^2，那么根据勾股定理，a、b、c满足的关系是：A. a = b + cB. b = a + cC. c = a + bD. a = b - c12. 已知函数f(x) = x^2 - 4x + 3，那么这个函数的顶点坐标是：A. (1, 2)B. (-2, 3)C. (2, -1)D. (-1, 0)13. 已知等差数列{a_n}的首项为a_1，公差为d，那么第n项可以表示为：A. a_n = a_1 + (n-1)dB. a_n = a_1 - (n-1)dC. a_n = a_1 * (n-1)dD. a_n = a_1 / (n-1)d14. 下列函数中，属于指数函数的是：A. f(x) = x^2B. f(x) = x^3C. f(x) = 2^xD. f(x) = x^(-1)15. 已知直角三角形的一个锐角为30度，那么这个直角三角形的两个直角边长度的比是：A. 1:1B. 1:2C. 2:1D. 2:216. 若a^2 + b^2 = c^2，那么根据勾股定理，a、b、c满足的关系是：A. a = b + cB. b = a + cC. c = a + bD. a = b - c17. 已知函数f(x) = x^2 - 4x + 3，那么这个函数的顶点坐标是：A. (1, 2)B. (-2, 3)C. (2, -1)D. (-1, 0)18. 已知等差数列{a_n}的首项为a_1，公差为d，那么第n项可以表示为：A. a_n = a_1 + (n-1)dB. a_n = a_1 - (n-1)dC. a_n = a_1 * (n-1)dD. a_n = a_1 / (n-1)d19. 下列函数中，属于指数函数的是：A. f(x) = x^2B. f(x) = x^3C. f(x) = 2^xD. f(x) = x^(-1)20. 已知直角三角形的一个锐角为30度，那么这个直角三角形的两个直角边长度的比是：A. 1:1B. 1:2C. 2:1D. 2:221. 若a^2 + b^2 = c^2，那么根据勾股定理，a、b、c满足的关系是：A. a = b + cB. b = a + cC. c = a + bD. a = b - c22. 已知函数f(x) = x^2 - 4x + 3，那么这个函数的顶点坐标是：A. (1, 2)B. (-2, 3)C. (2, -1)D. (-1, 0)23. 已知等差数列{a_n}的首项为a_1，公差为d，那么第n项可以表示为：A. a_n = a_1 + (n-1)dB. a_n = a_1 - (n-1)dC. a_n = a_1 * (n-1)dD. a_n = a_1 / (n-1)d24. 下列函数中，属于指数函数的是：A. f(x) = x^2B. f(x) = x^3C. f(x) = 2^xD. f(x) = x^(-1)25. 已知直角三角形的一个锐角为30度，那么这个直角三角形的两个直角边长度的比是：A. 1:1B. 1:2C. 2:1D. 2:226. 若a^2 + b^2 = c^2，那么根据勾股定理，a、b、c满足的关系是：A. a = b + cB. b = a + cC. c = a + bD. a = b - c27. 已知函数f(x) = x^2 - 4x + 3，那么这个函数的顶点坐标是：A. (1, 2)B. (-2, 3)C. (2, -1)D. (-1, 0)28. 已知等差数列{a_n}的首项为a_1，公差为d，那么第n项可以表示为：A. a_n = a_1 + (n-1)dB. a_n = a_1 - (n-1)dC. a_n = a_1 * (n-1)dD. a_n = a_1 / (n-1)d29. 下列函数中，属于指数函数的是：A. f(x) = x^2B. f(x) = x^3C. f(x) = 2^xD. f(x) = x^(-1)30. 已知直角三角形的一个锐角为30度，那么这个直角三角形的两个直角边长度的比是：A. 1:1B. 1:2C. 2:1D. 2:231. 若a^2 + b^2 = c^2，那么根据勾股定理，a、b、c满足的关系是：A. a = b + cB. b = a + cC. c = a + bD. a = b - c32. 已知函数f(x) = x^2 - 4x + 3，那么这个函数的顶点坐标是：A. (1, 2)B. (-2, 3)C. (2, -1)D. (-1, 0)33. 已知等差数列{a_n}的首项为a_1，公差为d，那么第n项可以表示为：A. a_n = a_1 + (n-1)dB. a_n = a_1 - (n-1)dC. a_n = a_1 * (n-1)dD. a_n = a_1 / (n-1)d34. 下列函数中，属于指数函数的是：A. f(x) = x^2B. f(x) = x^3C. f(x) = 2^xD. f(x) = x^(-1)35. 已知直角三角形的一个锐角为30度，那么这个直角三角形的两个直角边长度的比是：A. 1:1B. 1:2C. 2:1D. 2:236. 若a^2 + b^2 = c^2，那么根据勾股定理，a、b、c满足的关系是：A. a = b + cB. b = a + cC. c = a + bD. a = b - c37. 已知函数f(x) = x^2 - 4x + 3，那么这个函数的顶点坐标是：A. (1, 2)B. (-2, 3)C. (2, -1)D. (-1, 0)38. 已知等差数列{a_n}的首项为a_1，公差为d，那么第n项可以表示为：A. a_n = a_1 + (n-1)dB. a_n = a_1 - (n-1)dC. a_n = a_1 * (n-1)dD. a_n = a_1 / (n-1)d39. 下列函数中，属于指数函数的是：A. f(x) = x^2B. f(x) = x^3C. f(x) = 2^xD. f(x) = x^(-1)40. 已知直角三角形的一个锐角为30度，那么这个直角三角形的两个直角边长度的比是：A. 1:1B. 1:2C. 2:1D. 2:241. 若a^2 + b^2 = c^2，那么根据勾股定理，a、b、c满足的关系是：A. a = b + cB. b = a + cC. c = a + bD. a = b - c42. 已知函数f(x) = x^2 - 4x + 3，那么这个函数的顶点坐标是：A. (1, 2)B. (-2, 3)C. (2, -1)D. (-1, 0)43. 已知等差数列{a_n}的首项为a_1，公差为d，那么第n项可以表示为：A. a_n = a_1 + (n-1)dB. a_n = a_1 - (n-1)dC. a_n = a_1 * (n-1)dD. a_n = a_1 / (n-1)d44. 下列函数中，属于指数函数的是：A. f(x) = x^2B. f(x) = x^3C. f(x) = 2^xD. f(x) = x^(-1)45. 已知直角三角形的一个锐角为30度，那么这个直角三角形的两个直角边长度的比是：A. 1:1B. 1:2C. 2:1D. 2:246. 若a^2 + b^2 = c^2，那么根据勾股定理，a、b、c满足的关系是：A. a = b + cB. b = a + cC. c = a + bD. a = b - c47. 已知函数f(x) = x^2 - 4x + 3，那么这个函数的顶点坐标是：A. (1, 2)B. (-2, 3)C. (2, -1)D. (-1, 0)48. 已知等差数列{a_n}的首项为a_1，公差为d，那么第n项可以表示为：A. a_n = a_1 + (n-1)dB. a_n = a_1 - (n-1)dC. a_n = a_1 * (n-1)dD. a_n = a_1 / (n-1)d49. 下列函数中，属于指数函数的是：A. f(x) = x^2B. f(x) = x^3C. f(x) = 2^xD. f(x) = x^(-1)50. 已知直角三角形的一个锐角为30度，那么这个直角三角形的两个直角边长度的比是：A. 1:1B. 1:2C. 2:1D. 2:2。