当前位置：文档之家 › 平面简单力系

平面简单力系

  • 格式：doc
  • 大小：1.37 MB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

平面力系的简化

平面力系的简化

分布力系合力的大小等 于力系分布图形的面积
解 ： 先求合力的大小。在梁上距左端为x处取一微段dx， 其上作用力大小为qxdx。将分布力系向合力作用点简化，分布 载荷的合力为
x 1 FR = ∫ q x d x = ∫ q d x = ql 0 0 l 2
l l
目录
再求合力作用线位置。设合力FR的作用线距左端的距离为h， 微段dx上的作用力对点A的矩为–(qxdx) x。由合力矩定理，
目录
五、合力矩定理 平面任意力系的合力对作用面内任一点之矩，等于 力系中各力对同一点之矩的代数和。即： O ( FR ) = ∑ M O ( Fi ) M 证明：
平面汇交力系是平面一般力系的特例，对平面汇交力系， 合力矩定理成立。
目录
例2-2
三角形分布载荷作用在水平梁AB上，最大载荷
集度为q，梁长l。试求该力系的合力。
tan α =
′ FR y ′ FR x
α = 70 . 84 °
M O = ∑ M O ( F ) = −3F1 − 1.5W1 − 3.9W2 = −2355 kN⋅ m
目录
′ FR x = 232.9 kN
′ FR y = −670.1kN
M O = −2355 kN⋅ m
（2）求合力： FR= FR’ = 709.4 kN
点的矩为： 力F对B点的矩为： 对 点的矩为
M B ( F ) = M B ( Fx ) + M B ( Fy ) = − Fx b = − Fb cos α = − 3Fb 2
目录
实例
二、力偶 1、力偶的定义
大小相等、方向相反但不共线的两个平行力组成的力系， 大小相等、方向相反但不共线的两个平行力组成的力系，称为 力偶。 力偶。记作(F，F ′)

平面任意力系的简化

平面任意力系的简化

附加力偶系可以合成为一个力偶，其力偶矩为
MO M1 M 2
M n MO (F1 ) MO (F2 )
MO (Fn ) MO (Fi )
称为原力系对简化中心O的主矩，主矩与简化中心的选择有关。
结论：
平面任意力系向作用面内任一点O简化，可得一个力和一个力偶，这 个力等于该力系的主矢，作用线通过简化中心O ；这力偶的矩等于该力系 对简化中心O的主矩。主矢与简化中心位置无关，而主矩一般与简化中心 位置有关。 主矢的解析表达式为
3.力的平移定理是平面任意力系简化为平面汇交力系和平面力偶系
的依据。
B
d
F
＝
F″ A
B
d
F′
F′
M
F
A
＝
A
B
2. 平面任意力系向作用面内一点简化·主矢与主矩
F1
F2
y ′ FR j O y MO i x
O
简化 中心 Fn
F1 F1
F2 F2
Fn Fn
F1′
M1
M2 O Mn
′ F2 x
F1 C O
3m
F4
30° x
( F'Rx )2 ( F'Ry )2 4.662kN FR
y
主矢方向
F'Rx cos( F'R , i ) 0.986 FR F'Ry cos( F'R , j ) 0.165 FR
2、求主矩MO
( F'R , i ) 9.5 ( F'R , i ) 80.5
M1 M O (F1 )
M 2 M O (F2 ) M n M O (Fn )

平面力系简化的四种结果

平面力系简化的四种结果

平面力系简化的四种结果
1. 平面力系简化为一个力
当一个平面力系的合力和力矩等于零时，可以简化为一个力。

这个力的大小和方向由合力的大小和方向决定，作用点则由力矩为零的条件决定。

简化为一个力后，可以用这个力来计算物体的平衡条件，减少计算的复杂性。

2. 平面力系简化为两个力
当平面力系中的合力不为零，但力矩等于零时，可以简化为两个力。

这两个力的大小和方向由合力的大小和方向决定，作用点则由力矩为零的条件决定。

简化为两个力后，可以将平面力系分解为两个简单的力，便于计算物体的平衡条件。

3. 平面力系简化为一个力和一个力矩
当平面力系中的合力和力矩均不为零时，可以简化为一个力和一个力矩。

这个力的大小和方向由合力的大小和方向决定，作用点则由力矩不为零的条件决定。

简化为一个力和一个力矩后，可以通过力的作用点和力矩的大小和方向来计算物体的平衡条件。

4. 平面力系无法简化
当平面力系中的合力和力矩均不为零，且无法简化为一个力和一个力矩时，需要保持平面力系的复杂性进行计算。

在这种情况下，需要考虑力的合成、力矩的叠加等复杂计算方法，以求得物体的平衡
条件。

总结起来，平面力系简化的四种结果为：简化为一个力、简化为两个力、简化为一个力和一个力矩，以及无法简化。

这些简化结果的应用可以大大简化平面力系的计算过程，提高计算的效率和准确性。

在实际应用中，根据平面力系的特点和计算需求，选择合适的简化方法可以更好地解决力学问题。

平面任意力系的简化

平面任意力系的简化
F' F" F
作用在刚体上的力是滑移矢量。
定理：作用在刚体上的力，沿其作用线移动后， 不改变其作用效应。
刚 体
变 形 体
作用于刚体上力的三要素:大小、方向、作用线.
2、力的平移
F
F
A
B
A
B
F
A
B
MB
A rBA
B
力的平移定理:作用在刚体上某一点的 力F可以平移到刚体内任一点，但必须 同时附加一个力偶，这个附加力偶的矩 等于原来的力F对新作用点的矩。
❖ 平移定理分析：平面内的一个力和一个力偶也可以合成一个 力。
2、平面任意力系向一点简化
Fn
o
据力的平移定理
An
A2
O
O
A1
F2
F1 O为简化中心
FR 为一个作用在O点上的力。 MO 为一个作用在刚体上的力偶。
•主矢
•主矩
（与简化中心O无关）
（与简化中心O有关）
结论：平面任意力系向作用面内任一点简化， 可得到一个力和一个力偶，该力的作用线通过 简化中心，其大小原力系的主矢，该力偶的力 偶矩等于原力系对简化中心的主矩。
机械设计基础
平面任意力系的简化
❖ 1、力的平移定理
加减平衡力系原理：
在刚体上增加或减去一组平衡力系，不会改变 原力系对刚体的作用效应。
加减平衡力系原理
F
A
F
B
若 {P1, P2,, Pm} {0} 则 {F1, F2,, Fn}
{F1, F2,, Fn , P1, P2,, Pm}
力沿作用线移动 力的可传性： F
(F2
F3 )
j
n
MO ri Fi

理论力学平面力系的简化和平衡

理论力学平面力系的简化和平衡

原力偶系的合力偶矩
n
M Mi i 1
只受平面力偶系作用的刚体平衡充要条件：
n
M Mi 0 i 1
对BC物块对B点取矩，以逆时针为正列方程应为：
M 2 M B (FC ) M FCY a FCx b M FC (b a) cos45 0
[例] 在一钻床上水平放置工件,在工件上同时钻四个等直径 的孔,每个钻头的力偶矩为 m1m2 m3 m4 15Nm 求工件的总切削力偶矩和A 、B端水平反力?
两轴不平行即 条件：x 轴不 AB
可，矩心任意
连线
mA (Fi ) 0 mB (Fi ) 0 mC (Fi ) 0
③三矩式 条件：A,B,C不在
同一直线上
上式有三个独立方程，只能求出三个未知数。
4. 平面一般力系的简化结果分析
简化结果： 主矢R ，主矩 MO ，下面分别讨论。 ① R =0， MO =0，则力系平衡,下节专门讨论。 ② R =0,MO≠0 即简化结果为一合力偶, MO=M 此时刚
解除约束，可把支反
力直接画在整体结构
的原图上）
解除约束
由
mA (Fi
)
0
P2a N B
3a0,
N B
2P 3
X 0 XA 0
Y 0 YB NB P0,
YA
P 3
2.5物体系统的平衡、静定与超静定问题
1、物体系统的平衡问题 物体系统（物系）：由若干个物体通过约束所组成的系统叫∼。 [例]
外力：外界物体作用于系统上的力叫外力。 内力：系统内部各物体之间的相互作用力叫内力。
N2个物体受平面汇交力系（或平面平行力系）
X 0 Y 0
2*n2个独立平衡方程
N3个物体受平 X 0 面任意力系 Y 0

第2章平面简单力系习题

第2章平面简单力系习题

第2章 平面简单力系习题1.是非题（对画√，错画×）2-1.汇交力系平衡的几何条件是力的多边形自行封闭。

（ ）2-2.两个力F 1、F 2在同一轴上的投影相等，则这两个力大小一定相等。

（ ） 2-3.力F 在某一轴上的投影等于零，则该力一定为零。

（ ） 2-4.合力总是大于分力。

（ ）2-5.平面汇交力系求合力时，作图的力序可以不同，其合力不变。

（ ） 2-6.力偶使刚体只能转动，而不能移动。

（ ） 2-7.任意两个力都可以合成为一个合力。

（ ）2-8.力偶中的两个力在其作用面内任意直线段上的投影的代数和恒为零。

（ ）:2-9.平面力偶矩的大小与矩心点的位置有关。

（ ） 2-10.力沿其作用线任意滑动不改变它对同一点的矩。

（ ） 2.填空题（把正确的答案写在横线上）2-11.作用在刚体上的三个力使刚体处于平衡状态，其中两个力汇交于一点，则第三个力的作用线 。

2-12.力的多边形自行封闭是平面汇交力系平衡的 。

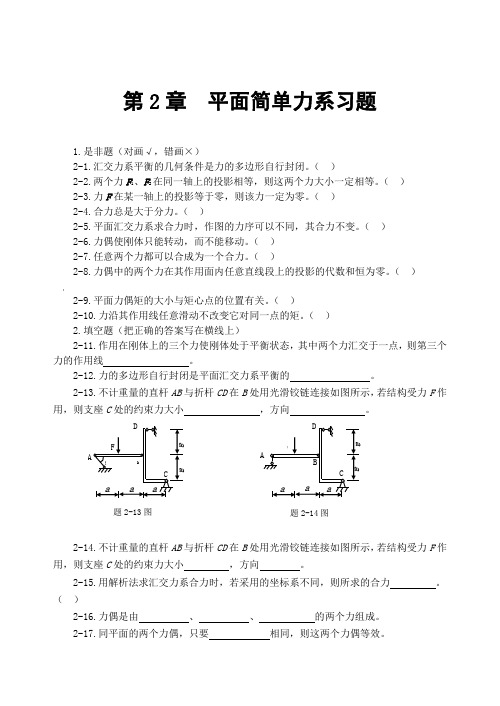
2-13.不计重量的直杆AB 与折杆CD 在B 处用光滑铰链连接如图所示，若结构受力F 作用，则支座C 处的约束力大小 ，方向 。

2-14.不计重量的直杆AB 与折杆CD 在B 处用光滑铰链连接如图所示，若结构受力F 作用，则支座C 处的约束力大小 ，方向 。

2-15.用解析法求汇交力系合力时，若采用的坐标系不同，则所求的合力 。

（ ）2-16.力偶是由 、 、 的两个力组成。

2-17.同平面的两个力偶，只要 相同，则这两个力偶等效。

题2-13图题2-14图?2-18.平面系统受力偶矩M =的作用，如图所示，杆AC 、B C 自重不计，A 支座约束力大小 ，支座约束力大小 。

2-19.如图所示，梁A 支座约束力大小 ，B 支座约束力的大小 。

"2-20.平面力偶系的平衡条件 。

3.简答题2-21用解析法求平面汇交力系的平衡问题时，x 和y 轴是否一定相互垂直当x 和y 轴不垂直时，对平衡方程0011=F=F ni yini xi ∑∑==有何限制条件为什么2-22.在刚体的A 、B 、C 、D 四点作用有四个大小相等、两两平行的力，如图所示，这四个力组成封闭的力的多边形，试问此刚体平衡吗若使刚体平衡，应如何改变力系中力的方向2-23.力偶不能单独与一个力相平衡，为什么如图所示的轮子又能平衡呢2-24.在保持力偶矩大小、转向不变的情况下，如图所示，可否将力偶矩M 移动到AC 上移动后A 、B 支座的约束力又如何！题2-19图F 1F 2 F 3、A题2-22图 B C D 题2-23F 题2-18图x 图 2-6&2-25.如何正确理解投影和分力、力对点的矩和力偶矩的概念 4.计算题2-26.如图所示，固定在墙壁上的圆环受三个绳子的拉力作用，力F 1沿水平方向，F 3沿铅直方向，F 2与水平成40°角，三个力的大小分别F 1=2kN ，F 2=，F 3=，求力系的合力。

平面一般力系的简化

O m2
F1
m1
x
F2
(a)
(b)
1.简化方法
向一点简化
一般力系（任意力系）
（未知力系）
FR（已知力系）
汇交力系合力
4
附加力偶的合力偶矩
2.主矢与主矩
①. 主矢：指原平面一般力系各力的矢量和
。
主矢 的 解析求法
大小： 方向： 注意：因以主它矢与等简于化原中力心系的各位力置的无矢关量。和,所
4、固定端（插入端）约束 在工程中常见的有：
A 雨搭
车刀
固定端（插入端）约束的构造
Fi A
约束反力
①认为Fi这群力在同一 平面内;
7
MA
FA
A
MA A
FA y FA x
② 将Fi向A点简化得一 力和一力偶;
③FA方向不定可用正交 分力FAx, FAy表示;
④ FAx, FAy ,MA为固定端 约束反力; ⑤ FAx, FAy限制物体平动, MA为限制转动。
A (a)
B F
F A (b)
m B A
(c)
2
讨论
①力线平移定理揭示了力与力偶的关系：力 力+力偶
②力线平移定理可考察力对物体的作用效应。
P
e
O
A
P
m
O
A
（刚体、变形体两 种情况）
③力线平移定理是力系简化的理论基础。 3
二、 平面一般力系向一点简化
Fn
An O
A2
F1
A1 F2
y Fn mn
5
②主矩：指原平面一般力系对简化中心之矩的代数和 。
大小：
主矩 MO 正、负规定 ： 转向 +

平面力系的简化

平面 力系 的简
化
设合力在两个坐标轴上的投影分别为Rx，Ry，根据合 力投影定理，它们与各分力在两个坐标轴上的投影满足
下式要求。
Rx=F1x+F2x+…+Fnx=∑Fix Ry=F1y+F2y+…+Fny=∑Fiy
（2-12）
由合力的投影可以求出合力的大小和方向。
大小：
（2-13）
方向：
（2-14）
平面 力系 的简
化
力系的主矢是由原力系中的各分力的大小 和方向决定的，与简化中心的位置无关；而主 矩等于原力系中的各力对简化中心力矩的代数 和，当简化中心的位置不同时，得到的主矩的 大小和转向一般是不同的，即主矩与简化中心 的位置有关。
平面 力系 的简
化
2.平面任意力系简化结果的分析
平面任意力系向其作用面内的任意一点简化，得到 一个主矢R和一个主矩MO，但实际力系的作用情况不同 时，简化的结果也不一样，具体情况包括下面几种。
平面 力系 的简
化
1.几何法
如图2-4（a）所示，在刚体上作用一汇交力系，汇交点 为刚体上的O点。根据力的可传性原理，将各力沿作用线移 至汇交点，成为共点力系，然后根据平行四边形法则，依次 将各力两两合成，求出作用在O点的合力R。也可以连续应用 力的三角形法则，逐步合成求出合力R，如图2-4（b）所示。
平面汇交力系的简化的合力的大小和方向等于各分
力的矢量和，即R=F1+F2+…+Fn=∑Fi
（2-15）
平面 力系 的简
化
1.平面任意力系向一点的简化
平面任意力系向其作用面内任意一 点简化，可得到一个力和一个力偶。该 力作用于简化中心，其大小和方向等于 原力系的各力的矢量和；该力偶的力偶 矩等于原力系中各力对简化中心力矩的 代数和。

平面力系向一点简化的结果

平面力系向一点简化的结果1. 介绍平面力系好，咱们今天聊聊一个在工程和物理中常见的概念——平面力系的简化。

这听起来可能有点复杂，但其实挺有趣的，像在解谜一样。

简单来说，平面力系就是一个平面上的所有力的集合。

比如，你拿一个木板，板子上可能有好几个力在作用，比如重力、支持力，甚至你往上推，它也会有个力的作用。

2. 力的合成与分解2.1 力的合成首先，我们得知道怎么把这些力搞定。

咱们可以把它们合成一个简单的力。

这就像你把几根不同的棍子绑在一起，变成一根强壮的大棍子。

这样一来，处理起来就简单多了。

比如说，如果你有三个力，分别作用在不同的点上，你可以把它们合成一个力，这样你就只需要考虑一个力的影响，不用一一分析每个力。

2.2 力的分解力的分解呢，就像你把一根大棍子拆成几根小棍子。

这样你可以把一个复杂的力，分解成几个简单的分力。

举个例子，你推一个物体，它的力可以分解成水平和垂直两个方向的力，这样你就可以分别处理它们对物体的影响了。

3. 向一点简化3.1 为什么要简化到一点？现在咱们说说“向一点简化”这回事。

这个操作其实是为了让问题更简单，更容易解决。

想象一下，如果你要分析一个庞大的力系统，直接上手可能会觉得头大。

不过，如果你把所有的力合并成一个作用在某个点上的力，那问题就简化了。

这样，你就能把这个力看作是集中在一个点上的，就像把整个庞然大物缩成一个小点，这样处理起来方便多了。

3.2 实际操作实际操作中，你要找一个“合成点”——也就是那个所有力合成后的点。

这个点的位置，通常可以通过把所有作用力的效果合并来确定。

比如说，你有几个力作用在不同的点上，你可以把它们的合成结果放到一个特定的点上，这个点就是你简化后的“作用点”。

这个点上作用的力和原来的力系统产生的效果是一样的。

4. 应用实例说到这里，咱们来看看实际中的应用。

比如，在建筑设计中，工程师们常常用到这种简化的方法。

他们需要确定建筑上各个地方的力如何作用，如果每个力都单独计算，那工作量大得不可思议。

第三章平面力系


(3)若FR‘≠0，MO‘≠0，这时根据力的平移定理的 逆过程，可以进一步简化成一个作用于另一点 的合力。
(4) FR‘=0，MO‘=0，则力系是平衡力系 。 综上所述，平面一般力系简化的最后结果 (即合成结果)可能是一个力偶，或者是一个合 力，或者是平衡。 3-1-3合力矩定理 当FR‘=0，MO‘≠0 时，还可进一步简化为一 M o ( FR ) FR d 合力，合力对点的矩是 / / 而 Mo mo ( F ) FR d M o 所以 Mo (FR ) mO (F )
3-1-2简化结果的分析 平面一般力系向一点简化，一般可得到一 个力和一个力偶，但这并不是最后简化结果。 根据主矢与主矩是否存在，可能出现下列几种 情况： (1)若FR‘=0，MO‘≠0，说明原力系与一个力偶等 效，而这个力偶的力偶矩就是主矩。 (2)若FR‘≠0，MO‘=0 ，则作用于简化中心的主 矢FR'就是原力系FR的合力，作用线通过简化中 心。
228 .9kN m
计算结果为正值表示是逆时针转向。
因为主矢
≠0，主矩 FR
/ Mo ，如图 0 (b)所示，
所以还可进一步合成为一个合力FR。 FR的大小、 方向与FR‘相同，它的作用线与点的距离为
M O 228.9 d 0.375m FR 612.9
因为MO正，故m0(FR)也应为正，即合力FR 应在点O左侧，
X
F F
0
二力矩形式的平衡方程 (简称二矩式)
在力系作用面内任取两点A、B及X轴，平 面一般力系的平衡方程可改写成两个力矩方程 和一个投影方程的形式，即
F m m
X
0 0 0
A
B
式中轴不与A、B两点的连线垂直。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

习 题
基本题
3.1、已知F 1=150N ，F 2=200N ，F 3=250N 及F 4=100N 。

试用图解法求合力。

答：R=352N ；3316'o α=
习题３－１图
3.4、图示结构由杆借助钢板连接而成，试求其中两杆所受的力F 1和F 2。

图中已知力的单位为kN 。

答: F 1=1.389kN ； F 2=-0.354kN
习题３－4图
3.5、图示起重机支架的AB 、AC 杆用铰链支承在可旋转的立柱上，并在A 点用铰链互相连接。

由绞车D 水平引出钢索绕过滑轮A 起吊重物，如重物重P =20kN ，滑轮的尺寸和各杆的自重忽略不计。

试求杆AB 和AC 所受的力。

答：F AC =-27.3kN ； F AB =-7.32kN
习题３－5图
3.8、图示支架由AB 、AC 杆组成，A 、B 、C 三处都为铰接，在A 点悬挂重量为Q 的重物。

试求在图示四种情况下，AB 、AC 杆受力的大小和拉压情况。

杆的自重忽略不计。

答：(a)S AC =-1.155Q, S AB =0.577Q
(b)S AC =-0.3674Q, S AB =1.064Q
(c)S AC =-0.866Q, S AB =0.5Q
(d)S AB =S AC =0.577Q
习题３－8图
3.9. 一450N 的力作用在A 点，方向如图。

求：（a ）此力对D 点的矩；（b ）要得到与（a ）相同的力矩，在Ｃ点所加水平力的大小和指向；（c ）要得到与（a ）相同的力矩，在C 点应加的最小的力。

答：（a ）88.8N m -⋅；（b ）395N ←；（c ）280,45N ∠
习题３－9图
3.10、在AB 梁的中央作用一力偶矩m=100kN·m ，转向如图所示。

梁的跨度l =5m ，不计自重。

试求A 、B 支座的约束力。

答：R A =R B =20kN
习题３－10图
提高题
3.16如图所示，两杆件AB 、BC 由光滑的套筒B 连接。

已知力偶矩A m 为100N·m ，求在图示两种连接方式中使物体系平衡的力偶矩C m 和C 点的约束力。

答：(a) 252,1087,435C Cx Cy m N m R N R N =⋅=←=↑
(b) 184,600,800C Cx Cy m N m R N R N =⋅=←=↑
习题３－１6图。