当前位置：文档之家 › 第四章平面一般力系

第四章平面一般力系

  • 格式：doc
  • 大小：350.00 KB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

平面一般力系

平面一般力系

A(x,y) Fx y
odx
X
=xFy-yFx
mo(F) =±Fd
例题 求图示力系合成的结果。
已知：F1 100N，F2 100 2N，F3 50N，M 500N.m
y
F2 450 (-3,2)
(2,1)
F1 5 β 12
O
x
cosβ=12/13 sinβ=5/13
M (0,-4)
YA MA
XA
示例：求力系的合力大小和作用点。
2kN/m 5kN 3kNm
A
xC
B R
2m 1m 1m
R 2 2 5 1kN RxC 2 21 5 2 3 3kNm xC 3m
M (0,-4)
F3
MO = mO(Fi)= - F1 cosβ × 1 + F1 sinβ ×2 + F2 cos 450 × 2- F2 sin 450 ×3+M+F3 ×4=580N.m
因为主矢、主矩均不为0，所以简化的最终结果 为一个合力，此合力的大小和方向与主矢相同。
4、求合力的作用线位置：
固定端（插入端）约束 雨搭
车刀
§4-3平面一般力系的简化结果分析
简化结果： 主矢 R ，主矩 MO 。 ① R =0， MO =0 原力系为平衡力系 力②偶R系=等0,效MO≠0 主矩与简化中心O无关。原力系与一平面 ③ R ≠0,MO =0, 简化结果就是合力 与简化中心有关，
（换个简化中心，主矩不为零） 原力系与一平面汇交力系等效
F3
解:1、取0点为简化中心，建立图示坐标系：
主矢： FR/= Fi 主矩： M0 = m0(Fi)
2、求力系的主矢

平面一般力系

平面一般力系

A
l 2
求解结果相同：
a
y
FAx
FAy
A
P
B
Q
l
FT
l FT P Qa l sin 13.2kN 2

x
B
FAx T cos 11.43kN
FAy 2.1kN
P
Q
§4-4 平面一般力系的平衡条件与平衡方程
F 0 F 0 M F 0
l 2
F
y
0
M
A
l F 0 FT sin l P Qa 0 （3）
a
l
FAx
P
B
Q
2
3）解平衡方程 由（3）式
l FT P Qa l sin 13.2kN 2
y Ay F
A
FT
由（1）和（2）式得 FAx T cos 11.43kN
主矢
主矢与简化中心无关，而主矩一般与简化中心有关。
§4-2 平面一般力系向作用面内一点简化 主矢与主矩
三、主矢的计算
主矢的计算方法与汇交力系的计算方法相同。 主矢的计算：几何法，解析法。 解析法：
FRx Fix Fix FRy Fiy Fiy
x B P Q
FAy 2.1kN
M
B
4）其他形式平衡方程的求解 FAx FT cos 0 Fx 0 l M A F 0 FT sin l P 2 Qa 0
C

l Q l a P FAy l 0 F 0 2

第四章平面一般力系

第四章平面一般力系

解：研究AB梁，受力如图所示
由 X 0 ,X A 0
mA(F)0;
解得：
RBaqaa2mP2a0
Y0 YAR Bq a P 0
R B q 2 m a a 2 P 2 2 0 0 .8 0 1 .8 2 6 2 1 0 ( k 2 )N Y A P q R B a 2 2 0 0 . 8 0 1 2 2 ( k 4 )N 18
约束反力;
⑤ YA, XA限制物体平动,
MA为限制转动。
11
§4-6 平面平行力系的平衡方程
平面平行力系:各力的作用线在同一平面内且相互平行的力系。
设有F1, F2 … Fn 各平行力系， 向O点简化得：
主R 矢 R' F O
主 M O 矩 m O (F i) F ix i
合力作用线的位置为：
24
再研究AB杆，受力如图
由 m C 0 , S B siC n Y A B A 0 C
解 得 :SBB C YA siA nC 0 4.8 9 1 4 .6106.7N
5
与假设方向相反。
25
[例5] 起重机位于连续梁上，已知： P=10kN, Q=50kN, CE 铅垂, 不 计梁重。 求：支座A ,B和D点的反力。
m＝？
o
m E
解：①以AB杆为研究对象，其受力图为：
YA
m A 0 ,p A H S 1 A B 0
A pH B
30o
D
A
pH B
S1
XA
22
S1
3
p (kN) 3
C
② 再以销钉C为研究对象，其受力图为：
X 0 , S 1 c o s 3 0 o S 3 s i n S 2 c o s 3 0 o 0

工程力学—第四章平面一般力系

工程力学—第四章平面一般力系
面一般力系来处理。
有什么特点？
各力的作用线
不汇交于一点
平面一般力系——各力的作用线都在同一平面内，但既不汇交
于一点，也不平行。
······
｛F1，F2 ，···Fn｝
平面汇交力系和平面力偶系是平面一
般力系的特例。平面一般力系是工程中最
常见的力系。
§4-1 力线平移定理
作用在刚体上的力F，可以平移到同一刚体上的任一点O，但必须同
例如，道路给轮子的力等。
FN
几种分布荷载：
体分布荷载：荷载（力）分布在整个构件内部各
点上。例如，构件的自重等。
面分布荷载：分布在构件表面上。例如，风
压力、雪压力等。
线分布荷载：荷载分布在狭长范围内，如沿构件
的轴线分布。
1、荷载的单位
(1) 集中荷载的单位，即力的单位 (N，kN)。
分布荷载的大小用集度表示，指密集程度。
合力偶，其力偶矩MO ，作用于刚体平面。
所得平面汇交力系（F1’ , F2’ , ··· Fn’ ）可以合成为一个作用于O点的合矢量F’：
F’=∑Fi’ =∑Fi
合矢量F’称为原平面一般力系对简化中心O的主矢（如图c）。
所得的平面附加力偶系（M1 , M2 , ·
·
·Mn）可以合成为一个的力偶,其力偶矩MO
a
例4-1 题图
m
(
a

b
)
50
(
3

1
.
5
)
1
例题 4-1 m



37
.
5
t
3
c
6
(2) 满载时, m2=25 t , x < a, 由(a) 式得

第4章 平面一般力系

第4章 平面一般力系
B d F A F″ B d F′ F
§4-1 力线平移定理
A
F′ B M=Fd d A
(a)
(b)
(c)
M B (F ) Fd M M B (F )
可见，一个力可以分解为一个与其等值平行的
力和一个位于平移平面内的力偶。反之，一个力
偶和一个位于该力偶作用面内的力，也可以用一
个位于力偶作用面内的力来等效替换。
线分布荷载：荷载分布在狭长范围内，如沿构 件的轴线分布。 1. 荷载的单位 (1) 集中荷载的单位，即力的单位 (N，kN)。 分布荷载的大小用集度表示，指密集程度。
(2) 体分布荷载的单位： N/m3 ，
(3) 面分布荷载的单位： N/m2 ，
(4) 线分布荷载的单位： N/m 。 2. 分布荷载的计算方法 (1) 均布荷载：集度为常数的分布荷载。 例如图中的均布荷载的合力为：
FR
y xc x A l
由此可见，分布荷载合力
q0
的大小等于荷载集度图的面积。
x
x
C
B
合力作用线的位置为：
MA 2 xc l FR y q 0 l / 2 3 q 0 l 2 / 3
例题 4-2
已知水坝的坝前水深 h=10 m , 求1 m长的坝面 上水压力的合力之大小和作用线的位置。
FR′
O
MO
合力矩定理 平面一般力系如果有合力，则合力对该力系 作用面内任一点之矩等于力系中各分力对该点之 矩的代数和。
证明： 如下图所示，显然有
M O ( FR ) FR d M O , M O M O ( F ), M O ( FR ) M O ( F )
FR′ FR′ O MO O′ FR

第四章平面一般(任意)力系

第四章平面一般(任意)力系
解决物系的平衡问题的基本方法是将物系拆开成若干个单个物体,对 每个物体列平衡方程,联立求解.
例1:图示连续梁,求A、B、C三处的约束反力。 q M 再研究AB：（或整体ABC） B l l C M
A
A
B
XA-XB=0 YA-YB=0
解：先以BC为研究对象，做受力图 q B C 列平衡方程
y x q2 B
q1 解：研究AB，受力如图：X 建坐标如图
A
A
YA
NB X 0 XA=0 q1l q2l =0 Y 0 YA+ NB 2 1 2 l m 0 o N B 2l q1l l q2l (l ) 0 A
2
3
2
下面讨论分布载荷合力Q的大小： c
Q
qx q1
O
x
x l dx
Q q x dx
q1 qx x l
l
q1l = 分布载荷的面积 2
0
q1 xdx l
分布载荷合力Q的作用位置：
Qc q x dx x
q1l 而Q 2
l
0
1 q1 2 2 q l x dx 1 3 l
mA 0 或 mB 0
o AB ∥ Fi
x
注意：不论采用哪种形式的平衡方程，其独立的 平衡方程的个数只有两个，对一个物体来讲,只能 解两个未知量,不得多列！
§6.静定与超静定问题, 物系的平衡 静定问题: 未知数全部能够由平衡方程来求得的问题 静不定问题: 未知数的个数多于(独立的)平衡方程的个数, 不能够由 平衡方程来求得全部的未知数的问题,也称之为超静定 问题. 超静定次数 = 未知量的总数－平衡方程的个数 例:

第4章 平面一般力系

第4章 平面一般力系

第四章 平面一般力系学习目标：1.理解力的平移定理和平面一般力学向一点简化。

2.能用力的平移定理和平面一般力学向一点简化解决实际问题。

在前面两章中已经研究了平面汇交力系和平面力偶系的合成与平衡，本章将在此基础上讨论平面一般力系的简化与平衡问题。

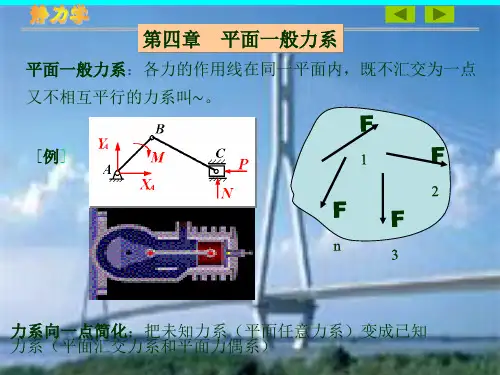
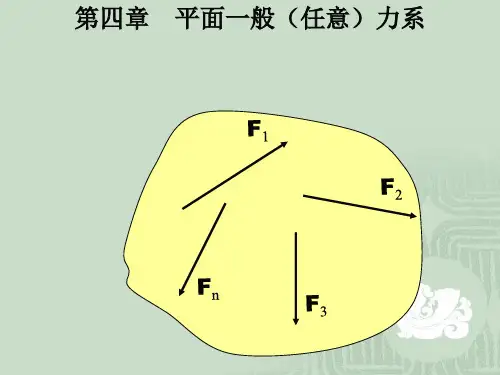
所谓平面一般力系，是指位于同一平面内的诸力，其力的作用线既不汇交于一点，也不互相平行的情况。

工程计算中的很多实际问题都可简化为平面一般力系问题来处理。

图4-1a 所示的房架，它所承受的恒载、风载以及支座约束力可简化为如图4-1b 所示的平面一般力系。

图4-2a 所示的吊车，横梁AB 的自重P 、荷载F 、拉杆BC 的拉力N F 以及支座约束力Ax F 、Ay F ，也可视为一个平面一般力系，如图4-2b 所示。

第一节 力的平移定理图4-1图4-2平移定理 作用在刚体上某点的力F ，可以平行移动到该刚体上任一点，但必须同时附加一个力偶，其力偶矩等于原来的力F 对平移点之矩。

如图4-3所示，设力F 作用于刚体上的A 点。

如在刚体上任取一点B ，在该点加上等值、反向且与力F 平行的力F '和F '',并使F F F =''='，如图4-3b 。

显然，力系（F ，F '，F ''）与力F 是等效的。

但力系（F ，F '，F ''）可看作是一个作用在B 点的力F '和一个力偶（F , F ''）。

于是原来作用在A 点的力F ，现在被一个作用在B 点的力F '和一个力偶（F , F ''）等效替换，如图4-3c 。

这就是说，可以把作用于A 点的力F 平移到另一点B ，但必须同时附加一个力偶，其矩为Fd M =。

其中，d 为附加力偶的力偶臂。

由图易见，d 就是点B 到力F 作用线的垂直距离，所以乘积Fd 也就是原力F 对于点B 之矩，即B M (F ) Fd =因此得=M B M (F ) （4-1） 即力线向一点平移时所得附加力偶矩等于原力对平移点之矩。

静力学第4章平面一般力系

静力学第4章平面一般力系

第四章 平面一般力系
【本章重点内容】
力线平移定理; 平面一般力系向作用面内一点简化; 平面一般力系简化结果分析; 平面一般力系的平衡条件与平衡方程.
第四章 平面一般力系
§4-1 工程中的平面一般力系问题
§4-1 工程中的平面一般力系问题
平面一般力系 作用在物体上诸力的作用线都分布在同一平面内，既
力线向一点平移时所得 附加力偶等于原力对平 移点之矩.
力偶M′与M 平衡.
第四章 平面一般力系
§4-3 平面一般力系向一点简化 主矢与主矩
§4-3 平面一般力系向一点简化 主矢与主矩
一、平面一般力系向作用面内一点简化
rr
F1′ = F1
rr
F2′ r
...=
F2 r
Fn′ = Fn
r M1 = MO (F1)
主矩MO
∑ MO =
MO
r (F
)
=
−1m
⋅
F1
−
3m
⋅
F2
+
2m
⋅
sin
30o
⋅
F3
+
M
= −1m ×1kN - 3m ×1kN + 2m × 1 × 2kN + 4kN ⋅ m 2
= 2kN ⋅ m
§4-4 简化结果的分析 合力矩定理
合力 方向 主矩
FR′ = 3.39kN α = −36.2°
§4-3 平面一般力系向一点简化 主矢与主矩
主矩的计算
主矩的计算方法与力矩和平面力偶系的计算方法相同. 主矩的计算
平面一般力系向一点简化，得到力对简化点的力矩和.
主矩大小
∑r
MO = MO(Fi )

第四章 平面一般力系

第四章 平面一般力系

点O的力
， ，
（平面汇交力系）
附加力偶
（平面力偶系）
分别合成 这两个力系
（原来各力的矢量和）
（原来各力对点一 个力和一个力偶。
这个力等于该力系的主矢，即平面一般力系中所有各力的矢量 和
作用线通过简化中心O； 这个力偶的矩等了该力系对于点O的主矩，即这些力对于任选简 化中心O的矩的代数和
方程只是前三个方程的线性组合，因而不是独立的。我们 可以利用这个方程来校核计算的结果。
§4-6 平面平行力系的平衡方程
平面平行力系:各力的作用线在同一平面内且相互平行的力系。 如图所示，设物体受平面平行力系 的作用。
平行力系的独立平衡方程的数目 只有两个，即：
或
注：其中A、B两点的连线不得与各力平行。
平面一般力系平衡的必要和充分条件
平面一般力系平衡的充要条件是：所有各力在两个任选的坐 标轴上的投影的代数和分别等于零．以及各力对于任意点的 矩的代数和也等于零。
平面一般力系 的平衡方程 (一矩式)
（三个方程， 求解三个未知数）
支架的横梁AB与斜杆DC彼此以铰链C相联接，并各 以铰链A、D连接于铅直墙上。如图所示。已知AC＝CB；杆 DC与水平线成 角；载荷P＝10kN，作用于B处。设梁和杆 的重量忽略不计，求铰链A的约束反力和杆DC所受的力。 解：(1)取AB梁为研究对象。 (2)画受力图。 (3)列平衡方程。 (a) (b)
解: (1)当满载时，为使起重机不 绕点B翻倒。在临界情况下 。
当空载时，为使起重机不绕点 A翻倒。在临界情况下 。
(2)当平衡荷重 的反力？
时，求满载时轨道A、B给起重机轮子
解:(2)根据平面平行力系的平衡方程，有：
解得
利用多余的不独立方程 来校验以上计算结果是否正确。

第4章：平面一般力系

第4章：平面一般力系
一个作用在简化中心的主矢；和一个对简化中心 的主矩。
§4–1 平面一般力系的简化•主矢与主矩
§4–1 平面一般力系的简化•主矢与主矩
三、主矢、主矩的求法：
1、主矢可接力多边形规则作图求得，或用解析
法计算。
R Rx2 Ry2
Fx 2
Fy 2
方向余弦：
cosR, x Fx R
cosR, y Fy R
② 求主矩：
L O
m o
F
2F cos60 2F 3F sin30 0.5
2
3
4
（2）、求合成结果：合成为
一个合力R，R的大小、方向与 R’相同。其作用线与O点的垂
2m
y
F2
60°
A
F1
O
3m
y A
B
F3
F4 C 30° x
B
直距离为： d Lo 0.51m R
Lo
R/ R
O d
C
x
§4–3 平面一般力系的平衡条件和平衡方程
4、联立求解：
MA=-38.6 kN•m (顺时针） NAy
NAx= 0
A
NAx
C
T
B
NAy=-19.2 kN （向下）
MA Q
§4–4 平面平行力系的平衡
平面平行力系平衡的充要条件：
力系中各力的代数和等于零 ，以这些力对 任一点的矩的代数和也等于零。
平面平行力系的平衡方程：
一矩式： Fy 0 , mOF 0
Fx 0 :
N Ax 0
Fy 0 :
N Ay Q ND 0
mAF 0 :
3 2 Q 2ND M 0
4、联立求解：
y

工程力学第四章平面一般力系

工程力学第四章平面一般力系
详细描述
平面一般力系简化的目的是将复杂的力系简化为更简单的形式，以便分析刚体的平衡状 态。通过力的平移定理，我们可以将平面一般力系简化为一个合力和一个力矩，或者一 组力和力矩的代数和。这个合力或力和力矩的代数和代表了原力系对刚体的作用效果。
简化后的力系更易于理解和分析，有助于解决工程实际问题。
Part
平衡条件的推导
根据力的平移定理，将平面力系中的所有力平移到同一点， 然后根据合力矩为零和合力为零的条件，推导出平面力系的 平衡条件。
Part
04
平面力系的平衡方程
平衡方程的推导
01
02
03
力的合成与分解
根据力的平行四边形法则， 将力进行合成或分解为多 个分力。
力的投影
将力投影到坐标轴上，得 到力在x轴和y轴上的分量。
STEP 01
分析受力情况
解决静力学问题
利用平衡方程，求解平面 内物体的受力情况，解决 静力学问题。
STEP 03
验证结构稳定性
利用平衡方程，验证结构 的稳定性，确保结构在各 种工况下的安全可靠。
通过平衡方程，分析物体 在平面内的受力情况，判 断物体的运动状态。
Part
03
平面力系的平衡条件
平衡条件的概念
平衡条件是一个物理概念，描述的是物 体在力系作用下保持静止的状态，而平 衡方程是一个数学表达式，用于描述这
一状态。
平衡条件是定性描述，而平衡方程则是 定量描述。平衡方程通过数学符号和运 算，将平衡条件的定性描述转化为可求
解的定量关系。
平衡条件是解决平衡问题的前提，而平 衡方程则是解决问题的工具。通过建立 平衡方程，可以求解未知量，得出物体
平衡条件与平衡方程的联系

第04章 平面一般力系汇总

第04章 平面一般力系汇总
F 1 qh 1 (9.8110) 10 491kN 22
d 2 h 2 10 6.67m 33
4.2 平面一般力系的平衡条件
一、平衡的必要与充分条件 所以平面任意力系平衡的充要条件为：
力系的主矢 FR' 和主矩 MO 都等于零，即：
FR' ( Fx )2 ( Fy )2 0
第四章 平面一般力系
主讲人：李锦学
如打乒乓球，若球拍对球作用的力其作用线通过球心 （球的质心），则球将平动而不旋转；但若力的作用线与 球相切——“削球”，则球将产生平动和转动。
c
F
c
(a)
F
c F
m
(b)
4.1 平面一般力的简化
4.1.1 平面一般力系向一点简化
平移 定理
基本力 系简化
一、简化方法
Fx FR'
,
cos(FR'
,
j)
Fy FR'
注意：因以主它矢与等简于化原中力心系的各位力置的无矢关量。和,所
主矩 MO
大小： MO MOi MO (Fi )
正、负规定 ： 转向 +
–
注意：因主矩等于各力对简化中心之矩的代数和， 所以它的大小和转向一般与简化中心有关。
三、结论
平面一般力系向作用面内任一点简化 ，一般可以得到一力和一力偶 ； 该力作用于简化中心 ，其大小及方向等于该力系的主矢 ，该力偶之
分布荷载的计算方法
（1）均布荷载：集度为常数的分布荷载。 如图所示的均布荷载，其合力为：
F q l 10.9116 174.6kN,
作用线则通过梁的中点。 F
q=10.91kN/m
16 m
F A
F B

第四章平面一般力系的平衡方程及其应用简化及平衡方程分解

第四章平面一般力系的平衡方程及其应用简化及平衡方程分解

2）列平衡方程，求解未知量
m 0
FRA 4 cos 450 m 0
解得：
FRA
FRB
m 4 cos450
3.5kN
Fx 0 FP FRBx 0
Fy 0
FRA FRBy q 3 0
mB (F) 0
FP
3
FRA
3
q
3
3 2
0
解得：
FRBx 5kN
FRA 28kN
FRBy 38kN
2.平衡方程的二矩式
Fx 0 mA(F)
0
（A与B两点的连线不垂直于x轴）
mB
(F
)
0
3.平衡方程的三矩式
第四章 平面一般力系的简化及平衡方程
§4.1 平面一般力系的简化 §4.2 平面一般力系的平衡方程及其应用 §4.3 物体系的平衡问题
§ 4-2 平面一般力系的平衡方程及其应用
平面一般力系平衡的必要和充分条件：力系的主矢和力
系对于任一点的矩都等于零，即： FR' 0, M0 0
由此平衡条件可导出不同形式的平衡方程。
1.平面汇交力系的平衡方程
1）平面汇交力系平衡的必要与充分 的解析条件是：各力在两个坐标轴 上投影的代数和分别等于零
Fx 0
Fy
0
2）平面汇交力系平衡的必要与充分 的几何条件是：力多边形自行封闭
利用几何法求解平面汇交力系的平衡 问题时，画出自行封闭的力多边形 ， 然后按比例尺从力多边形中直接量出 未知力的大小即可。
16 0.8
2
20
12(kN)
FRAy P qa FRB 20 20 0.8 12 24(kN)
[例]如图所示一钢筋混凝土刚架的计算简图，其左侧面受到一水平

平面一般力系概论

平面一般力系概论

平面任意力系 的平衡方程
力系的主矢 FR 和主矩 MO 都等于零
FR' ( Fx )2 ( Fy )2 0
MO MO (Fi ) 0
Fx 0
Fy 0
MO(Fi ) 0
21
平面任意力系的平衡方程另两种形式
F x
0
M A 0
M B 0
二矩式 两个取矩点连线，不得与投影轴垂直
Fx FR
, cos(FR' ,
j)
Fy FR
简化中心 (与简化中心位置无关) [因主矢等于各力的矢量和]
12
主矩MO （转动效应）
大小：MO MO (Fi )
方向： 方向规定 + —
简化中心： (与简化中心有关) （因主矩等于各力对简化中心取矩的代数和）
固定端（插入端）约束
雨搭
车刀
13
固定端（插入端）约束的约束反力：
第四章 平面一般（任意）力系
平面一般力系：各力的作用线在同一平面内，既不汇交为一点 又不完全相互平行的力系叫平面一般力系。
F1 Fn
F2 F3
F4
FAy FAx
F FN
1
2
研究方法：
力线平移定理 平面任意力系
平面汇交力系 平面力偶系
合成 FR=Fi
平衡
Fx=0 Fy =0
合成 M=Mi 平衡 Mi =0
合力: FR ' F1 F2 F3 Fi 主矢
合力偶矩： MO M1 M2 M3
MO (F1) MO (F2) MO (Fi ) 对O点主矩
大小：FR ' F 'Rx 2 F 'Ry 2 ( Fx )2 ( Fy )2

建筑力学 第四章 平面一般力系

建筑力学 第四章 平面一般力系
分析方法：
整体 求解刚体系统的平衡问题，主要依据前 面给出的平衡理论。 局部
先以系统整体为研究对象，列出平衡方程，这样的方 程中不包含内力，未知量较少，解出部分未知量后，再选 择合适的单个物体为研究对象，列出平衡方程，直到求出 所有的未知量为止。 以系统的每一个物体为研究对象，列出全部的平衡方程， 然后求解。
b
qm
A x C dx B
1 qm l 2
2l / 3
l
l
合力作用点C的位置
l
qm 1 2 2 x dx R AC qxdx q l m l 0 3 0
2 AC l 3
例题4-1 在水平梁AB上作用一力偶矩为m 的力偶,在 梁的中点C处作用一集中力P它与水平的夹角为, 如 图所示。梁长为 l 且自重不计。求支座A和 B的反力
F/R
MA A

X 1m
25kN
20kN
60o
C
1m
B
30o
1m
x
18kN
FR
4、求合力的作用线位置
M A 32.64 x 0.98m = AC FRy 33.32
所以简化的最终结果为一个合力FR 。
§ 4-4 平面一般力系的平衡条件与平衡方程
一、平面一般力系的平衡条件 平面一般力系平衡的必要和充分条件是: 力系的主矢和力系对任一点的主矩都等于零。
• 平面平行力系有2个独立的平衡方程，可以 求解2个未知数。
Y 0 M A ( F ) 0 AB连线不能平行 或 于各力作用线。 M ( F ) 0 o M B ( F ) 0
•
平面汇交力系的平衡方程
各力汇交于一点 A ， M A (Fi ) 0 自然 满足。则平面汇交力系平衡方程为

工程力学静力学 第四章 平面一般力系

工程力学静力学 第四章 平面一般力系
由于简化中心O是任选的，因此上述定理适用于任一力矩中 心。利用这一定理可以求出合力作用线的位置，以及用分力矩 来计算合力矩等。
工程力学课件
例4-l 水平梁AB受三角形分布载荷的作用如图，分布载荷的最大值为 q(N/m)，梁长l。试求合力的大小及其作用线位置。
解：本题属于平面内同向平行力的合成
问题，其合力F的方向与诸分力相同。 取梁的A端为原点，在x处取微分小段dx，
工程力学课件
§4-4 简化结果的分析 合力矩定理
根据以上所述，平面力系向一点简化，可得一个主矢F’R和一个主矩Mo ①若F’R=0，Mo≠0，则原力系简化为一个力偶，力偶矩等于原力系对于 简化中心的主矩。在这种情况下，简化结果与简化中心的选择无关。这就是 说，不论向哪一点简化都是这个力偶，而且力偶矩保持不变。
应该注意，力系的主矢F’R只是原力系中各力的矢量和，所 以它与简化中心的选择无关。而力系对于简化中心的主矩MO显 然与简化中心的选择有关，选择不同的点为简化中心时，各力 的力臂一般将要改变，因而各力对简化中心之矩也将随之改变。
工程力学课件
现 在 讨 论 主 矢 F’R 的 解 析 求 法 。 通 过 O 点 作 直 角 坐 标 系 oxy(图c)。根据合力投影定理，得到:
x
l q x xdx 0l
l q x2dx 0l
q l
作用在此段的分布力为以qx，根据几何关系 有
qx
x l
q
在dx长度上的合力的大小为qxdx。故此分布力合力F的大小，可 用以下积分求出：
F
l
0 qxdx
l 0
q l
xdx
q l
[
x2 2
]l0
ql 2
工程力学课件

第四章平面一般力系

第四章平面一般力系

雨棚
RA MA
雨棚
XA A
MA YA
§4-2 平面一般力系向作用面内任一点的简化
简化结果分析
1. R 0 , MO 0
即原力系与一合力偶等效,其
MO
矩为 M=MO。故只有在此时主矩与
O
“O”的位置 无关。
2. R 0 , MO 0
即原力系与R′等效，所以称R′为原 力系的合力，且过点“O ” 。
平面 汇交 力系
R´( 过“O” 但与“O” 无关）
体转动效果的 物理量
主矢 + 主矩
意 向“O” 简化 力 系
平面 力偶 系
MO (与“O” 有关）
描述力系 对物体移 动效果的
物理量
§4-2 平面一般力系向作用面内任一点的简化
固定端约束力 固定端约束 —— 物体受约束的一端既不能沿 任何方向移动，也不能转动。如深埋在地底下 的电线杆、牢固浇筑在基础上的水泥柱及车站 的雨棚等。
MO (Fi )
即：平面任意力系的主矩MO 为力系中各个力对 点“O”力矩的代数和。
很明显，一旦“O ”的位置改变，各力偶矩的 大小和转向也随之而变，因此，MO 与“O ”有关。
§4-2 平面一般力系向作用面内任一点的简化
二、 主矢和主矩
r
大小：MO mO(Fi )
主矩 MO 方向：方向规定 +
合力矩定理
R 0 , MO 0
R´
MO
O
R´
= Od R
R" O'
=
R Od
O'
R R R d MO
R
合力矩定理 Rd MO (R) MO (F )
§4-2 平面一般力系向作用面内任一点的简化

第四章 平面一般力系

第四章 平面一般力系

刚体上的全部力在y轴上的投影代数和等于0
刚体上的全部力对任意点的力矩代数和等于0
X 0, Y 0, mo ( F ) 0.
3、左边平衡方程是从平衡条件直接推 出的，是平衡方程的基本形式。 称为“一矩式”
4、二力矩方程
X 0 （或 Y 0） , m A ( F ) 0, mB ( F ) 0.
主矩：
M0
M 0 ( Fi )
F1 1 F3 3 M F3 sin 30 2 2kNm
3.4 d 2
M 0 2kNm d 0.59m FR 3.4kN
例、 三角形分布载荷.计算其合力作用线的位置 关于载荷（主动力）分类
集中力：当载荷分布面积较小， 近似认为载荷作用与一个“点”， 这种力称为“集中力” 单位是：N， kN 分布力：当载荷分布面积较大，而不能 简化为集中力，就称分布力 分布力又分为“面分布力”和“线分布 力” 面分布力：分布在一定面积上， 又有均匀和不均匀分布 单位：
M (F ) 0 F y 0,
A
Q(6 2) P 2 W (12 2) FB 4 0
Q P W FA FB 0
解得：
FA 210 kN, FB 870 kN
FA FB
33
(2)当P1=0.5P1时，求轨道A、B给起重机轮子的反力？
所以：
M M O ( F1 ) M O ( F2 ) M O ( Fi )
与简化中心的选择有关
固定端（插入端）约束
雨搭
车刀
固定端约束限制了物体的移动和转动。因而完全被固定
12
固定端（插入端）约束的约束反力：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第4章平面一般力系1、图示平面机构，正方形平板与直角弯杆ABC 在C 处铰接。

平板在板面内受矩为M=8N ·m 的力偶作用，若不计平板与弯杆的重量，则当系统平衡时，直角弯杆对板的约束反力大小为( C )。

2 22、悬臂梁承受均匀分布载荷，支座A 处的反力有四种结果，正确的是( B )。

=ql, M A =0=ql, M A =21q l 2=ql, M A =q l 2=ql, M A =31q l 23、图示平面结构，由两根自重不计的直角弯杆组成，C 为铰链。

不计各接触处摩擦，若在D 处作用有水平向左的主动力F ，则支座A对系统的约束反力为（ C ）。

，方向水平向右B.2F ，方向铅垂向上22，方向由A 点指向C 点22，方向由A 点背离C 点4、图示平面直角弯杆ABC ，AB=3m ，BC=4m ，受两个力偶作用，其力偶矩分别为M 1=300N ·m 、M 2=600N ·m ，转向如图所示。

若不计杆重及各接触处摩擦，则A 、C 支座的约束反力的大小为（ D ）。

=300N ，F C =100N=300N ，F C =300N=100N ，F C =300N=100N ，F C =100N5、力系向某点平移的结果，可以得到( D )。

A.一个主矢量B.一个主矩C.一个合力D.一个主矢量和一个主矩6、平面一般力系向一点O 简化结果，得到一个主矢量R ′和一个主矩m0，下列四种情况，属于平衡的应是( B )。

′≠0 m0=0 ′=0 m0=0′≠0 m0≠0 ′=0 m0≠07、以下有关刚体的四种说法，正确的是( D )。

A.处于平衡的物体都可视为刚体B.变形小的物体都可视为刚体C.自由飞行的物体都可视为刚体D.在外力作用下，大小和形状看作不变的物体是刚体8、力的作用线都相互平行的平面力系称（D ）力系。

A.空间平行B：空间一般C：平面一般D：平面平行9、力的作用线既不汇交于一点，又不相互平行的力系称（B ）力系。

A：空间汇交B：空间一般C：平面汇交D：平面一般10、平面力偶系合成的结果是一个（B ）。

A：合力B：合力偶C：主矩D：主矢和主矩11、平面汇交力系合成的结果是一个（A ）。

A：合力B：合力偶C：主矩D：主矢和主矩12、平面平行力系合成的结果是（D ）。

A：合力B：合力偶C：主矩D：主矢和主矩13、图示力F=2KN对Ａ点之矩为（A ）kN·m。

A：2 B：4 C：－2 D：－414、只限物体任何方向移动，不限制物体转动的支座称（ B ）支座。

Ａ：固定铰Ｂ：可动铰Ｃ：固定端Ｄ：光滑面15、力的作用线都相互平行的力系称（ C ）力系。

Ａ：空间平行Ｂ：空间一般Ｃ：平行力系Ｄ：平面平行16、作用与反作用是作用在( B )个物体上的一对等值、反向、共线的力。

Ａ：一Ｂ：二Ｃ：三Ｄ：四、17、平面一般力系的二力矩式平衡方程的附加使用条件是( B )。

Ａ：二个矩心连线与投影轴垂直Ｂ：二个矩心连线与投影轴不垂直Ｃ：投影轴通边一个矩心Ｄ：二个矩心连线与投影轴无关18、平面一般力系的三力矩式平衡方程的附加使用条件是( D )。

Ａ：二个矩心连线与投影轴垂直Ｂ：二个矩心连线与投影轴不垂直Ｃ：投影轴通边一个矩心Ｄ：三个矩心不共线19、合力与分力之间的关系，不正确的说法为( A )。

Ａ：合力一定比分力大Ｂ：两个分力夹角越小合力越大Ｃ：合力不一定比分力大Ｄ：两个分力夹角(锐角范围内)越大合力越小20、一个静定的平面物体系它由三个单个物体组合而成，则该物体系能列出( A )个独立平衡方程。

Ａ：3 Ｂ：6 Ｃ：9 Ｄ：1221、一个静定的平面物体系它由四个单个物体组合而成，则该物体系能列出( A )个独立平衡方程。

Ａ：3 Ｂ：6 Ｃ：9 Ｄ：1222、一个静定的平面物体系它由五个单个物体组合而成，则该物体系能列出( A )个独立平衡方程。

Ａ：3 Ｂ：6 Ｃ：9 Ｄ：1223、一个静定的平面物体系它由六个单个物体组合而成，则该物体系能列出( A )个独立平衡方程。

Ａ：3 Ｂ：6 Ｃ：9 Ｄ：1224、平面汇交力系平衡的几何条件是（ D ）A 、 0,0y xB 、0)(,0,00 F m y xC 、 0,0m yD 、力多边形自行闭合25、平面汇交力系平衡的解析条件是（ A ）A 、 0,0y xB 、0)(,0,00 F m y xC 、 0,0m yD 、力多边形自行闭合26．平面一般力系的平衡方程数为（ C ）A ．1个； 个； 个；27．图示ABC 杆，固定端A 的反力是(D )=P , YA=0=P ， mA=Pa=P , YA=0=P , YA=0,mA=Pa28．图示三铰拱架中，若将作用于构件AC 上的力偶M 平移至构件BC 上，则A 、B 、C 三处的约束反力( D )A.只有C处的不改变B.只有C处的改变C.都不变D.都改变29．某简支梁AB受载荷如图所示，现分别用RA、RB表示支座A、B处的约束反力，则它们的关系为(C )。

<RB >RB=RB D.无法比较30、如右图A支座处弯矩值为（D ）A、－4KN·mC、－10KN·mD、－12KN·m31、求静力平衡问题时最首先的关键一步是（A ）A、正确画出支座反力B、选好坐标系C、正确画出受力图D、列出平衡方程式32、平衡状态是指物体相对于地球保持静止或（B ）A、转动B、匀速直线运动C、匀变速直线运动D、匀加速直线运动33、在同一坐标轴上投影相等的两个力（C ）A、一定相等B、一定不相等C、可能相等可能不相等D、无法判断34、两物体间的作用和反作用力总是（C ）A、大小相等，方向相反B、大小相等，方向相反，作用在同一物体上C、大小相等，方向相反，沿同一直线分别作用在两个物体上D、大小相等，方向相同，沿同一直线分别作用在两个物体上35、构件与支撑物固定在一起，构件在固定端既不能沿任何方向移动，也不能转动，这种支座称为 （B ）A ．固定铰支座B ．固定端支座C ．可动铰支座D ．二力杆36、平面一般力系向作用面内任一点简化的结果是 （ A ）A ．一个力和力偶B ．一个合力C ．力偶D ．力矩37、“力系中所有各力在两个坐标轴上的投影的代数和分别为零”是平面汇交力系平衡的 （D ）A ．充分条件B ．必要条件C ．充分必要条件D ．无关系38、平面一般力系的三力矩式平衡方程的附加使用条件是( D )。

Ａ：二个矩心连线与投影轴垂直 Ｂ：二个矩心连线与投影轴不垂直 Ｃ：投影轴通边一个矩心 Ｄ：三个矩心不共线39、合力与分力之间的关系，不正确的说法为( A )。

Ａ：合力一定比分力大 Ｂ：两个分力夹角越小合力越大 Ｃ：合力不一定比分力大 Ｄ：两个分力夹角(锐角范围内)越大合力越小40、平面汇交力系平衡的解析条件是（ A ）A 、 0,0y xB 、0)(,0,00 F m y xC 、 0,0m yD 、力多边形自行闭合41．平面一般力系的平衡方程数为（C ）A ．1个； 个； 个； 个。

42、平面一般力系合成的结果是（C ）。

A ：合力B ：合力偶C ：主矩D ：主矢和主矩 二、填空题1、平面一般力系向平面内任意点简化结果有四种情况，分别是________________________ 、____________________________ 、____________________________、____________________________。

【答案】主矢和主矩都不为零、主矢为零主矩不为零、主矢不为零主矩为零、主矢和主矩都为零2、平面一般力系的三力矩式平衡方程的附加条件是________________________。

【答案】A 、B 、C 三点不共线3、物体受到的力一般可分为 和 两类。

【答案】外力和内力4、图示梁固定端A 的支座反力为________、________、________。

【答案】、力的平移定理和力的可传性原理只适用于。

【答案】刚体6、力的平移定理只适用于。

【答案】刚体7、力的可传性原理只适用于。

【答案】刚体8、力是物体间的一种相互作用，这种相互作用的效果使物体的发生变化，或使物体产生___________。

【答案】机械、运动状态、形变9、加上或去掉任何一个平衡力系，并不改变原力系对刚体的作用效果，这个公理叫做___________。

【答案】加减平衡力系公理10、作用于刚体上的力可沿其作用线移动到刚体内任意一点，而不会改变___________的作用，这个原理称为___________。

【答案】该力对刚体的作用效应、力的可传递性原理11、在三力矩式方程中，要求三矩心___________。

【答案】不共线12、平面一般力系向平面内任一点简化的结果是：、平面一般力系平衡的解析条件是：。

【答案】一个力和一个力偶、主失与主矩都等于零13、合力在坐标轴上的投影，等于各分力在同一坐标轴上投影的代数和。

这就是。

【答案】合力投影定理14、如图所示外伸梁，求B点的约束反力R B =kN 。

15、悬臂梁承受均匀分布载荷，支座A 处的反力为【答案】R A =ql, M A =21q l 2三、计算题1、支座受力Ｆ，已知Ｆ＝１０ｋＮ，方向如图所示，求力Ｆ沿ｘ、ｙ轴及沿ｘ′、ｙ′轴分解的结果，并求力Ｆ在各轴上的投影。

解：（1）求力Ｆ沿ｘ、ｙ轴分解的结果力三角形为直角三角形。

)(66.8866.01030cos kN F F x)(55.01060cos kN F F y（2）求力Ｆ沿ｘ′、ｙ′轴分解的结果 力三角形为等腰三角形。

kNF F F x 1075sin 75sin)(18.5966.05.01075sin 30sin kN F F y（3）力Ｆ在各轴上的投影)(66.8866.01030cos kN F F x )(55.01060cos kN F F y)(66.8866.01030cos kN F F x )(59.2)259.0(10105cos kN F F y2、 已知F 1＝１００Ｎ， F 2 ＝５０Ｎ， F 3 ＝６０Ｎ，F 4＝８０Ｎ，各力方向如图所示，试分别求各力在ｘ轴和ｙ轴上的投影。

解：)(6.86866.010030cos 11N F F x)(55.01060cos 11N F F y)(3053504332222N F F x)(405450)434(2222N F F y090cos 33 F F x )(600cos 33N F F y)(6.56)707.0(80135cos 44N F F x )(6.56707.08045cos 44N F F y3、一钢结构节点，在沿OA 、OB 、OC 的方向受到三个力的作用，已知F 1＝1KN ，F 2＝，F 3＝2KN ，试求这三个力的合力。