最新3塑性变形的基本定律汇总
- 格式:doc
- 大小:121.50 KB
- 文档页数:7

3 塑性变形的基本定律3.1 体积不变定律及应用一、 体积不变定律内容在压力加工过程中,只要金属的密度不发生变化,变形前后金属的体积就不会产生变化。
若设变形前金属的体积为0V ,变形后的体积为1V ,则有:0V =1V =常数实际上,金属在塑性变形过程中,其体积总有一些变化,这是由于:(1)在轧制过程中,金属内部的缩孔、气泡和疏松被焊合,密度提高,因而改变了金属体积。
这就是说除内部有大量存在气泡的沸腾钢锭(或有缩孔及疏松的镇静钢锭、连铸坯)的加工前期外,热加工时,金属的体积是不变的。
(2)在热轧过程中金属因温度变化而发生相变以及冷轧过程中金属组织结构被破坏,也会引起金属体积的变化,不过这种变化都极为微小。
例如,冷加工时金属的比重约减少0.1~0.2%。
不过这些在体积上引起的变化是微不足道的,况且经过再结晶退火后其比重仍然恢复到原有的数值。
二、 体积不变定律的应用1、确定轧制后轧件的尺寸设矩形坯料的高、宽、长分别为L B H 、、,轧制以后的轧件的高、宽、长分别为l b h 、、(如图3-1所示),根据体积不变条件,则HBL V =1hbl V =2即 hbl HBL =在生产中,—般坯料的尺寸均是已知的,如果轧制以后轧件的高度和宽度也已知时,则轧件轧制后的长度是可求的,即图3-1 矩形断面工件加工前后的尺寸hbHBL l = 例题1:轧50×5角钢,原料为连铸方坯,其尺寸为120×120×3000mm ,已知50×5角钢每米理论重3.77kg ,密度为7.85t/m 3,计算轧后长度l 为多少?解:坯料体积 V 0=120×120×3000=4.32×107mm 350×5角钢每米体积为 3.77/(7.85×103÷109)=480×103mm 3由体积不变定律可得4.32×107=480×103×l轧后长度 l ≈90m2、根据产品的断面面积和定尺长度,选择合理的坯料尺寸。


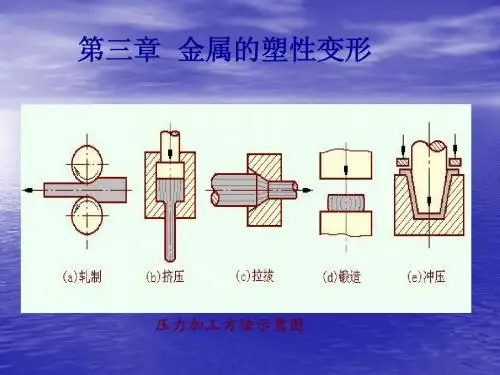
二、金属压力加工金属压力加工利用金属在外力作用并不破坏自身完整状态的条件下,稳定改变其形状与尺寸,而且也改善其组织和性能的加工方法,称为金属压力加工。
这种加工过程也是使金属产生塑性变形的过程,因此也叫做金属塑性加工。
1、锻造:主要包括两种基本方式,用于制造各种零件或型材毛坯。
(1)自由锻造(简称自由锻)-使已加热的金属坯料在上下砧之间承受冲击力(自由锻锤)或压力(压力机)而变形的过程,用于制造各种形状比较简单的零件毛坯。
(2)模型锻造(简称模锻)-使已加热的金属坯料在已经预先制好型腔的锻模间承受冲击力(自由锻锤)或压力(压力机)而变形,成为与型腔形状一致的零件毛坯,用于制造各种形状比较复杂的零件。
2、轧制:金属坯在两个旋转的轧辊之间受到压缩而产生塑性变形,使横断面缩小、形状改变、长度增加,达到用户要求的加工方法。
按轧制温度分为冷轧(金属坯料不加热)和热轧(850℃-1250℃);按加工方法分为纵轧、横轧、斜轧;按产品分为板材、棒材、型材、管材等。
3、挤压:把放置在模具容腔内的金属坯料从模孔中挤出来成形为零件的过程,包括冷挤压和热挤压,多用于壁厚较薄的零件以及制造无缝管材等。
4、冲压:使金属板坯在冲模内受到冲击力或压力而成形的过程,也分冷冲压与热冲压。
5、拉拔:将金属坯料拉过模孔以缩小其横截面的过程,用于制造如丝材、小直径薄壁管材等,也分为冷拉拔和热拉拔。
2.1、塑性变形的基本定律材料力学的解释是:在某物质的弹性限度之内,在外力作用下,应力与应变成正比,且在撤销外力之后,物体能恢复原状;超过这个限度,就不成正比了,即应力不增加、或增加很少;而应变增加的很大。
并且在撤销外力之后,物体不能恢复原状。
简单地说:物体在一定的条件下,在外力的作用下产生形变,当施加的外力撤除或消失后该物体不能恢复原状的变形叫做塑性变形。
金属在发生塑性变形时,作用在物体上的力有两种:作用力和约束反力。
2.1.1体积不变定律在压力加工过程中,只要金属的密度不发生变化,塑性变形前后的体积就不会产生变化,这一规律称为体积不变定律。


第2章 金属塑性变形的物性方程物性方程又称本构方程,是εσ-关系的数学表达形式。
弹性变形阶段有广义Hooke 定律,而塑性变形则较为复杂。
在单向受力状态下,可由实验测定εσ-曲线来确定塑性本构关系。
但在复杂受力情况下实验测定困难,因此只能在一定的实验结果基础上,通过假设、推理,建立塑性本构方程。
为了建立塑性本构方程,首先需弄清楚塑性变形的开始条件——屈服,以及进入塑性变形后的加载路径等问题。
§2.1 金属塑性变形过程和力学特点2.1.1 变形过程与特点以单向拉伸为例说明塑性变形过程与特点,如图2-1所示。
金属变形分为弹性、均匀塑性变形、破裂三个阶段。
塑性力学视s σ为弹塑性变形的分界点。
当s σσ<时,σ与ε存在统一的关系,即εσE =。
当s σσ≥以后,变形视作塑性阶段。
εσ-是非线性关系。
当应力达到b σ之后,变形转为不均匀塑性变形,呈不稳定状态。
bσ点的力学条件为0d =σ或d P =0。
经短暂的不稳定变形,试样以断裂告终。
若在均匀塑性变形阶段出现卸载现象,一部分变形得以恢复,另一部分则成为永久变形。
卸载阶段εσ-呈线性关系。
这说明了塑性变形时,弹性变形依然存在。
弹塑性共存与加载卸载过程不同的εσ-关系是塑性变形的两个基本特征。
由于加载、卸载规律不同,导致εσ-关系不唯一。
只有知道变形历史,才能得到一一对应的εσ-关系,即塑性变形与变形历史或路径有关。
这是第3个重要特征。
事实上,s σσ>以后的点都可以看成是重新加载时的屈服点。
以g 点为例,若卸载则εσ-关系为弹性。
卸载后再加载,只要g σσ<点,εσ-关系仍为弹性。
一旦超过g 点,εσ-呈非线性关系,即g 点也是弹塑性变形的交界点,视作继续屈服点。
一般有s g σσ>,这一现象为硬化或强化,是塑性变形的第4个显著特点。
在简单压缩下,忽略摩擦影响,得到的压缩s σ与拉伸s σ基本相同。
但是若将拉伸屈服后的试样经卸载并反向加载至屈服,反向屈服一般低于初始屈服。


第三章塑性变形的基本规律1、体积不变定律的概念在金属压力加工的理论研究和实际计算中,通常认为变形前后金属的体积保持不变,它是变形计算的基本依据之一。
若设变形前金属的体积为V0,变形后的体积为V1,则有:V0 = V1 =常数2、最小阻力定律的内容实践证明:物体在变形过程中,其质点有向各个方向移动的可能时,则物体内的各质点将是沿着阻力最小的方向移动,这就是通常所讲的最小阻力定律的定义。
3、弹塑性共存定律的概念和实际意义A 概念我们把金属塑性变形在加工中一定会有弹性变形存在的情况,称之为弹塑性共存定律。
B 实际意义弹塑性共存定律在轧钢中具有很重要的实际意义,可用以指导我们生产的实践。
(1)用以选择工具(2)由于弹塑性共存,轧件的轧后高度总比预先设计的尺寸要大4、极限状态理论A 极限状态的类型第一种极限状态是屈服,第二种极限状态是破坏。
屈服是金属由弹性变形转变为塑性变形的转折点,是塑性变形的开端。
破坏则是金属塑性变形过程的终结。
B 金属屈服极限σs与金属屈服的概念(1)金属屈服极限σs的概念:它是在特定条件下测得的,即是在室温下,慢速单向拉伸或单向压缩(线应力状态)时测定的金属发生屈服时的单向拉伸或单向压缩的应力值。
(2)金属的屈服:金属发生塑性变形时所需的外力大,则我们说金属难屈服,它的变形抗力就大,即不容易变形;金属发生塑性变形时所需的外力小,则我们说金属容易屈服,它的变形抗力就小,即容易变形。
C 在线应力状态下由拉伸实验建立的屈服条件拉伸一试样,当主应力σ1的数值达到该材料的屈服极限(σ1=σs )时,试样开始发生塑性变形。
D 极限状态理论它是研究弹性变形终了、塑性变形即将开始时主应力与屈服极限间关系的理论。
E 主应力差理论(Tresca 屈服条件)Tresca 屈服条件为: (3-6) F 能量理论(Mises 屈服条件)其屈服条件表达式为:(3-7)Mises 屈服条件的简化形式:(3-8)式中的m=1~1.155。


应力应变关系弹性模量 ||广义虎克定律1。
弹性模量对于应力分量与应变分量成线性关系的各向同性弹性体,常用的弹性常数包括:a 弹性模量单向拉伸或压缩时正应力与线应变之比,即b 切变模量切应力与相应的切应变之比,即c 体积弹性模量三向平均应力与体积应变θ(=εx+εy+εz)之比,即d 泊松比单向正应力引起的横向线应变ε1的绝对值与轴向线应变ε的绝对值之比,即此外还有拉梅常数λ。
对于各向同性材料,这五个常数中只有两个是独立的。
常用弹性常数之间的关系见表3-1 弹性常数间的关系。
室温下弹性常数的典型值见表3—2 弹性常数的典型值。
2。
广义虎克定律线弹性材料在复杂应力状态下的应力应变关系称为广义虎克定律。
它是由实验确定,通常称为物性方程,反映弹性体变形的物理本质.A 各向同性材料的广义虎克定律表达式(见表3—3 广义胡克定律表达式)对于圆柱坐标和球坐标,表中三向应力公式中的x 、y、z分别用r、θ、z和r、θ、φ代替。
对于平面极坐标,表中平面应力和平面应变公式中的x、y、z用r、θ、z代替。
B 用偏量形式和体积弹性定律表示的广义虎克定律应力和应变张量分解为球张量和偏张量两部分时,虎克定律可写成更简单的形式,即体积弹性定律应力偏量与应变偏量关系式在直角坐标中,i,j=x,y,z;在圆柱坐标中,i,j=r,θ,z,在球坐标中i,j=r,θ,φ。
弹性力学基本方程及其解法弹性力学基本方程|| 边界条件||按位移求解的弹性力学基本方法||按应力求解的弹性力学基本方程|| 平面问题的基本方程 || 基本方程的解法 || 二维和三维问题常用的应力、位移公式1.弹性力学基本方程在弹性力学一般问题中,需要确定15个未知量,即6个应力分量,6个应变分量和3个位移分量。
这15个未知量可由15个线性方程确定,即(1)3个平衡方程[式(2-1—22)],或用脚标形式简写为(2)6个变形几何方程[式(2—1—29)],或简写为(3)6个物性方程[式(3-5)或式(3—6)],简写为或2.边界条件弹性力学一般问题的解,在物体内部满足上述线性方程组,在边界上必须满足给定的边界条件。
3 塑性变形的基本定律3.1 体积不变定律及应用一、 体积不变定律内容在压力加工过程中,只要金属的密度不发生变化,变形前后金属的体积就不会产生变化。
若设变形前金属的体积为0V ,变形后的体积为1V ,则有:0V =1V =常数实际上,金属在塑性变形过程中,其体积总有一些变化,这是由于:(1)在轧制过程中,金属内部的缩孔、气泡和疏松被焊合,密度提高,因而改变了金属体积。
这就是说除内部有大量存在气泡的沸腾钢锭(或有缩孔及疏松的镇静钢锭、连铸坯)的加工前期外,热加工时,金属的体积是不变的。
(2)在热轧过程中金属因温度变化而发生相变以及冷轧过程中金属组织结构被破坏,也会引起金属体积的变化,不过这种变化都极为微小。
例如,冷加工时金属的比重约减少0.1~0.2%。
不过这些在体积上引起的变化是微不足道的,况且经过再结晶退火后其比重仍然恢复到原有的数值。
二、 体积不变定律的应用1、确定轧制后轧件的尺寸设矩形坯料的高、宽、长分别为L B H 、、,轧制以后的轧件的高、宽、长分别为l b h 、、(如图3-1所示),根据体积不变条件,则HBL V =1hbl V =2即 hbl HBL =在生产中,—般坯料的尺寸均是已知的,如果轧制以后轧件的高度和宽度也已知时,则轧件轧制后的长度是可求的,即图3-1 矩形断面工件加工前后的尺寸hbHBL l = 例题1:轧50×5角钢,原料为连铸方坯,其尺寸为120×120×3000mm ,已知50×5角钢每米理论重3.77kg ,密度为7.85t/m 3,计算轧后长度l 为多少?解:坯料体积 V 0=120×120×3000=4.32×107mm 350×5角钢每米体积为 3.77/(7.85×103÷109)=480×103mm 3由体积不变定律可得4.32×107=480×103×l轧后长度 l ≈90m2、根据产品的断面面积和定尺长度,选择合理的坯料尺寸。
3塑性变形的基本定
律
3 塑性变形的基本定律
3.1 体积不变定律及应用
一、体积不变定律内容
在压力加工过程中,只要金属的密度不发生变化,变形前后金属的体积就不会产生变化。
若设变形前金属的体积为
V,变形后的体积为
1
V,则有:
V=
1
V=常数
实际上,金属在塑性变形过程中,其体积总有一些变化,这是由于:
(1)在轧制过程中,金属内部的缩孔、气泡和疏松被焊合,密度提高,因而改变了金属体积。
这就是说除内部有大量存在气泡的沸腾钢锭(或有缩孔及疏松的镇静钢锭、连铸坯)的加工前期外,热加工时,金属的体积是不变的。
(2)在热轧过程中金属因温度变化而发生相变以及冷轧过程中金属组织结构被破坏,也会引起金属体积的变化,不过这种变化都极为微小。
例如,冷加工时金属的比重约减少
0.1~0.2%。
不过这些在体积上引起的变化是微不足道的,况且经过再结晶退火后其比重仍然恢复到原有的数值。
二、体积不变定律的应用
1、确定轧制后轧件的尺寸
设矩形坯料的高、宽、长分别为L
B
H、
、,轧制以后的轧件的高、宽、长分别为l
b
h、
、(如图3-1所示),根据体积不变条件,则
HBL
V=
1
hbl
V=
2
即hbl
HBL=
在生产中,—般坯料的尺寸均是已知的,如果轧制以后轧件的高度和宽度也已知时,则轧件轧制后的长度是可求的,即
图3-1 矩形断面工件加工前后的尺寸
hb
HBL l = 例题1:轧50×5角钢,原料为连铸方坯,其尺寸为120×120×3000mm ,已知50×5角钢每米理论重3.77kg ,密度为7.85t/m 3,计算轧后长度l 为多少?
解:
坯料体积 V 0=120×120×3000=4.32×107mm 3
50×5角钢每米体积为 3.77/(7.85×103÷109)=480×103mm 3
由体积不变定律可得
4.32×107=480×103×l
轧后长度 l ≈90m
2、根据产品的断面面积和定尺长度,选择合理的坯料尺寸。
例题2:某轨梁轧机上轧制50Kg/m 重轨,其理论横截面积为6580mm 2,孔型设计时选定的钢坯断面尺寸为325×280mm 2,要求一根钢坯轧成三根定尺为25m 长的重轨,计算合理的钢坯长度应为多少?
根据生产实践经验,选择加热时的烧损率为2%,轧制后切头、切尾及重轨加工余量共长1.9m ,根据标准选定由于钢坯断面的圆角损失的体积为2%。
由此可得轧后轧件长度应为
=l (3×25+1.9)×103=76900mm
由体积不变定律可得
325×280L (1-2%)(1-2%)=76900×6580
由此可得钢坯长度
L =
mm 567398
.02803256580769002=⨯⨯⨯ 故选择钢坯长度为5.7m 。
3、在连轧生产中,为了保证每架轧机之间不产生堆钢和拉钢,则必须使单位时间内金属从每架轧机间流过的体积保持相等,即
n n v F v F v F === 2211
式中 n F F F 21、为每架轧机上轧件出口的断面积,
n v v v 21、为各架轧机上轧件的出口速度,它比轧辊的线速度稍大,但可看作近似相等。
如果轧制时n F F F 21、为已知,只要知道其中某一架轧辊的速度(连轧时,成品机架的轧辊线速度是已知的),则其余的转数均可一一求出。
3.2 最小阻力定律及其应用
一、最小阻力定律内容
叙述1:物体在变形过程中,其质点有向各个方向移动的可能时,则物体内的各质点将沿着阻力最小的方向移动。
叙述2:金属塑性变形时,若接触摩擦较大,其质点近似沿最法线方向流动,也叫最短法线定律。
叙述3:金属塑性变形时,各部分质点均向耗功最小的方向流动,也叫最小功原理。
二、最小阻力定律的应用1、判断金属变形后的横断面形状。
例1:矩形六面体的镦粗
图3-2为塑压矩形断面的变化情况。
由图可清楚地看出:随着压缩量的增加,矩形断面的变化逐渐变成多面体、椭圆和圆形断面。
对于这个现象的分析:
用角平分线的方法把矩形断面划分为四个流动区域——两个梯形和两个三角形。
为什么用角平分线划分呢?因为角平分线上的质点到两个周边的最短法线长度是相等的。
因此,在该线上的金属质点向两个周边流动的趋势也是相等的。
由图可见,每个区域内的金属质点,将向着垂直矩形各边的方向移动,由于向长边方向移动的金属质点较向短边移动的多,故当压缩量增大到一定程度时,将使变形的最终断面变形为圆形。
结论:任何断面形状的柱体,当塑压量很大时,最后都将变成圆形断面。
图3-2 塑压矩形断面柱体变化规律
2.确定金属流动的方向。
例2:轧制生产中的情况
(1)利用最小阻力定律分析小辊径轧制的特点。
如图2-3
在压下量相同的条件下,对于不同辊径的轧制,其变形区接触弧长度是不相同的,小辊径的接触弧较大辊径小,因此,在延伸方向上产生的摩擦阻力较小,根据最小阻力定律可知,金属质点向延伸方向流动的多,向宽度方向流动的少,故用小辊径轧出的轧件长度较长,而宽度较小。
(2)为什么在轧制生产中,延伸总是大于宽展?首先,在轧制时,变形区长度一般总是小于轧件的宽度,根据最小阻力定律得,金属质点沿纵向流动的比沿横向流动的多,使延伸量大于宽展量;其次,由于轧辊为圆柱体,沿轧制方向是圆弧的,而横向为直线型的平面,必然产生有利于延伸变形的水平分力,它使纵向摩擦阻力减少,即增大延伸,所以,即使变形区长度与轧件宽度相等时,延伸与宽展的量也并不相等,延伸总是大于宽展
3.3 弹塑性共存定律
一、弹塑性共存定律内容
物体在产生塑性变形之前必须先产生弹性变形,在塑性变形阶段也伴随着弹性变形的产生,总变形量为弹性变形和塑性变形之和。
为了说明在塑性变形过程中,有弹性变形存在,我们通过拉伸实验为例来说明这个问题。
图2-4为拉伸实验的变化曲线(OABC),当应力小于屈服极限时,为弹性变形的范
图3-3 轧辊直径对宽展的影响
围,在曲线上表现为OA段,随着应力的增加,即应力超过屈服极限时,则发生塑性变形,在曲线上表现为ABC段,在曲线的C点,表明塑性变形的终结,即发生断裂。
从图中可以看出,
(1)变形的范围内(OA),应力与变形的关系成正比,可用虎克定律近似表示。
(2)在塑性变形的范围内(ABC),随着拉应力的增加(大于屈服极限),当加载到B点时,则变形在图中为OE段,即为塑性变形δ与弹性变形ε之和,如果加载到B点后,立即停止并开始卸载,则保留下来的变形为OF(δ),而不是有载时的OE段,它充分说明卸载后,其弹性变形部分EF(ε)随载荷的消失而消失,这种消失使变形物体的几何尺寸多少得到了一些恢复,由于这种恢复,往往在生产实践中不能很好控制产品尺寸。
(3)弹性变形与塑性变形的关系,要使物体产生塑性变形,必须先有弹性变形或者说在弹性变形的基础上,才能开始产生塑性变形,只有塑性变形而无弹性变形(或痕迹)的现象在金属塑性变形加工中,是不可能见到的。
因此,我们把金属塑性变形在加工中一定会有弹性变形存在的情况,称之为弹塑共存定律。
二、弹塑性共存定律在压力加工中的实际意义
弹塑性共存定律在轧钢中具有很重要的实际意义,可用以指导我们生产的实践。
1、用以选择工具
在轧制过程中工具和轧件是两个相互作用的受力体,而所有轧制过程的目的是使轧件具有最大程度的塑性变形,而轧辊则不允许有任何塑性变形,并使弹性变形愈小愈好。
因此,在设计轧辊时应选择弹性极限高,弹性模数大的材料;同时应尽量使轧辊在低温下工作。
相反的,对钢轧件来讲,其变形抗力愈小,塑性愈高愈好。
图3-4 拉伸时应力与变形的关系
2 由于弹塑性共存,轧件的轧后高度总比预先设计的尺寸要大
例:如图(3-5)所示,轧件轧制后的真正高度h 应等于轧制前事先调整好的辊缝高度
0h ,轧制时轧辊的弹性变形n h ∆,(轧机所有部件的弹性变形在辊缝上所增加的数值)和轧制后轧件的弹性变形M h ∆之和,即:
M n h h h h ∆+∆+=0
因此,轧件轧制以后,由于工具和轧件的弹性变形,使得轧件的压下量比我们所期望的值小。
小结:本章应重点掌握三大定律的内容,熟悉三大定律的实际应用。
图3-5 轧辊及轧件的弹性变形图。