自由度分析计算题

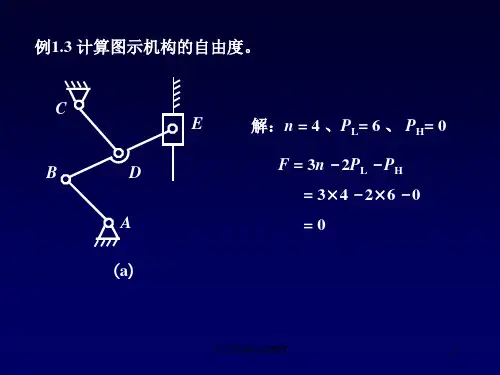
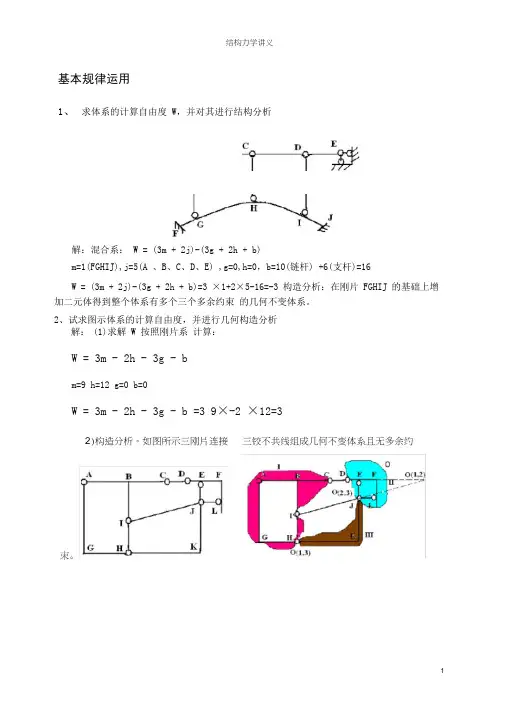
基本规律运用1、求体系的计算自由度W，并对其进行结构分析。

解：混合系：W = (3m + 2j)-(3g + 2h + b)m=1(FGHIJ),j=5(A、B、C、D、E) ,g=0,h=0，b=10（链杆）+6(支杆)=16W = (3m + 2j)-(3g + 2h + b)=3×1+2×5-16=-3构造分析：在刚片FGHIJ的基础上增加二元体得到整个体系有多个三个多余约束的几何不变体系。

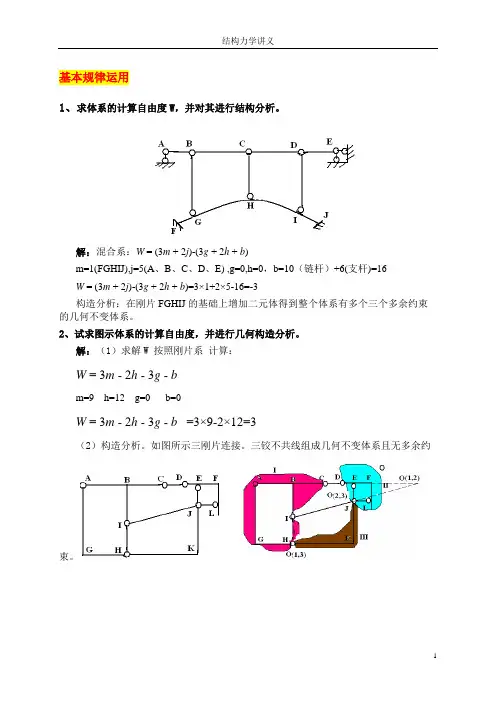
2、试求图示体系的计算自由度，并进行几何构造分析。

解：（1）求解W 按照刚片系计算：W = 3m - 2h - 3g - bm=9 h=12 g=0 b=0W = 3m - 2h - 3g - b =3×9-2×12=3（2）构造分析。

如图所示三刚片连接。

三铰不共线组成几何不变体系且无多余约束。

3、试求图示体系的计算自由度，并进行几何构造分析。

解：(1)计算W:W = (3m + 2j)-(3g + 2h + b)m=1(FGHIJ),j=5(A、B、C、D、E) ,g=0,h=0，b=10（链杆）+6(支杆)=16W = (3m + 2j)-(3g + 2h + b)=3×1+2×5-16=-3(2)结构构造分析如图示体系内部（先撤除支座及地基）由三个刚片Ⅰ、Ⅱ、Ⅲ 用三个瞬铰两两相连，且三个瞬铰在一直线上，为几何瞬变体系。

4、如图所示为三角形ABC及其他链杆所组成体系，试考察BC边上G铰不同位置与体系整体几何特性的关系，给出简要分析过程。

(a) (b)(c) (d)解：（1）观察图（a）所示体系，△BEG直接与大地固定铰支，可以将B点看做铰结点，则BE，BG为链杆，因此，与大地直接相连的约束多余三根支杆，所以将大地必须看做是一个刚片。

BG和CD与GC相连，BE和A支座与△AEF相连，通过“找对家”的思路可以找到如图所示三刚片。

G铰位于BC中间时，三虚铰共线，组成瞬变体系。

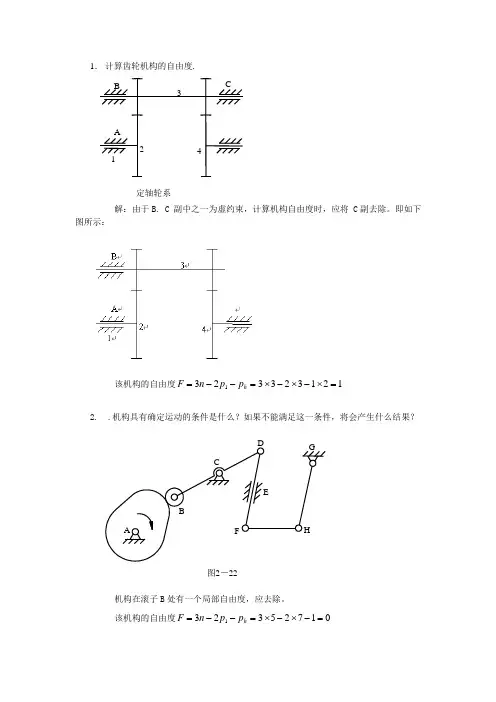
1． 计算齿轮机构的自由度.
解：由于B. C 副中之一为虚约束，计算机构自由度时，应将 C 副去除。

即如下
图所示：
该机构的自由度1213233231=⨯-⨯-⨯=--=h p p n F
2. .机构具有确定运动的条件是什么？如果不能满足这一条件，将会产生什么结果？
机构在滚子B 处有一个局部自由度，应去除。

该机构的自由度0
17253231=-⨯-⨯=--=h p p n F 定轴轮系
A
B C
1 2
3 4 图2－22
A B
C
D
G
E
H F
当自由度F=1时,该机构才能运动, 如果不能满足这一条件,该机构无法运动。

该机构当修改为下图机构，则机构可动：
N=4, PL=5, Ph=1;
F=⨯-⨯-=
自由度342511
3. 计算机构的自由度.
1)由于机构具有虚约束, 机构可转化为下图机构。

F=⨯-⨯-=
自由度342511
2)由于机构具有虚约束, 机构可转化为下图机构。

F=⨯-⨯=
自由度31211
3)由于机构具有虚约束, 机构可转化为下图机构。

F=⨯-⨯=
自由度33241
（注：专业文档是经验性极强的领域，无法思考和涵盖全面，素材和资料部分来自网络，供参考。

可复制、编制，期待你的好评与关注）。

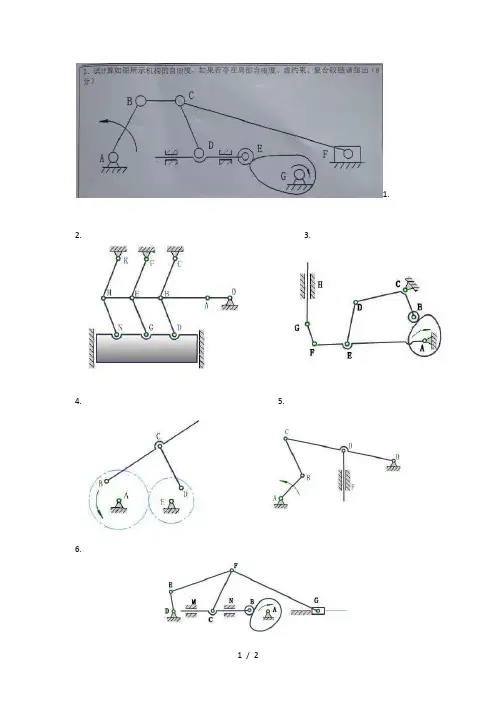
1.2. 3.4. 5.6.1.构件数n为7,低副p为9,高副pn为1,局部自由度为1,虚约束为0.E处为局部自由度,C处为复合铰链.F=3n-2p-pn=3*7-2*9-1=2（与原动件数目一致,运动确定）2. B处有复合铰链，有2个转动副。

无局部自由度。

B点左侧所有构件和运动副带入的约束为虚约束，属于与运动无关的对称部分。

n=5, PL=7, PH=0, F= 3n-2PL -PH=3×5-2×7-1×0=1。

运动链有确定运动，因为原动件数= 自由度数。

3.A处为复合铰链，因为有3个构件在此处组成成转动副，所以应算2个转动副。

B处为局部自由度，假设将滚子同构件CB固结。

无虚约束。

n=6, PL=8, PH=1, F= 3n-2PL -PH=3×6-2×8-1=1。

运动链有确定运动，因为原动件数= 自由度数。

4. 没有复合铰链、局部自由度、虚约束。

n=4, PL=5, PH=1, F= 3n-2PL -PH=3×4-2×5-1=1。

运动链有确定运动，因为原动件数= 自由度数。

5. 计算自由度：n=4, P L=6, P H=0, F= 3n-2P L -P H=3×4-2×6-1×0=0，运动链不能动。

修改参考方案如图所示。

6. F处为复合铰链，因为有3个构件在此处组成成转动副，所以应算2个转动副。

B处为局部自由度，假设将滚子同构件CB固结。

移动副M、N中有一个为虚约束，属于两构件在多处组成运动副。

n=7, PL=9, PH=1, F= 3n-2PL -PH=3×7-2×9-1=2。

运动链没有确定运动，因为原动件数< 自由度数。

1. 对于一个简单的平面桁架结构，若共有6个节点和10根构件，那么其自由度为多少？- A. 6- B. 8- C. 10- D. 122. 在一个平面梁结构中，每个支座具有多少个约束？- A. 1- B. 2- C. 3- D. 43. 计算一个刚性连接的平面框架结构的自由度时，若结构有8个节点和12根构件，自由度公式为：自由度 = 3n - 2j，其中n是节点数，j是构件数。

该结构的自由度是多少？- A. 4- B. 6- C. 8- D. 104. 一个平面结构中，假设有4个节点，6根构件，所有构件都在一个平面上，计算其自由度时需考虑：- A. 3自由度每节点，减去2自由度每构件- B. 2自由度每节点，减去1自由度每构件- C. 2自由度每节点，减去2自由度每构件- D. 3自由度每节点，减去1自由度每构件5. 对于一个三维空间的桁架结构，若有10个节点和20根构件，其自由度计算应使用的公式是：- A. 自由度 = 6n - 3j- B. 自由度 = 3n - 2j- C. 自由度 = 3n - 3j- D. 自由度 = 6n - 6j6. 在平面框架结构中，如果节点数为5，构件数为8，计算其自由度时，正确的自由度为： - A. 6- B. 8- C. 10- D. 127. 对于一个有10个节点和15根构件的平面结构，其自由度为：- A. 15- B. 18- D. 248. 一个简单的平面框架结构中有6个节点，8根构件，计算自由度时，如果框架是完全支撑的，结果是：- A. 3- B. 6- C. 9- D. 129. 对于一个空间框架结构，其中有5个节点和12根构件，计算自由度时所用的公式为： - A. 自由度 = 6n - 3j- B. 自由度 = 3n - 2j- C. 自由度 = 6n - 2j- D. 自由度 = 3n - 3j10. 若一个平面结构中节点数为7，构件数为10，且结构为刚性框架，计算其自由度时，结果为：- A. 5- B. 7- C. 9- D. 11。

自由度的计算例题及解析在统计学的世界里，自由度这个概念就像是那位在聚会中总能找到话题的朋友，既重要又让人有些摸不着头脑。

大家知道，计算自由度其实是为了解决各种统计问题，就像是给我们的数据加了一把钥匙，让我们能更好地了解背后的故事。

说到自由度，首先得了解它的含义，简单来说，就是在某些条件下，我们可以自由选择的变量数量。

就好比你在做菜的时候，有些配料可以随意放，而有些则是固定的，这个选择的自由度就体现在这里。

举个简单的例子吧，想象一下你在参加一场篮球比赛。

比赛中有五个人在场上，但如果我们说，某一个球员的得分是依赖于其他四个人的得分，那你就得考虑自由度了。

假设总得分是固定的，只有四个球员的得分是自由选择的，那么这个场上实际上就只有四个自由度。

明白了吗？就像你有四种方式来打出精彩的三分球，而不管你怎么投，最后的结果得分都是一样的。

再比如说，我们做一个简单的问卷调查，假设问卷里有五个问题。

参与者可以自由选择回答这五个问题，但如果你知道某一个问题的答案了，其他问题的选择就可能受到影响。

假设调查结果的总和是一个固定的数值，那么自由度就会减少。

想象一下，就像在一场足球赛中，某一方得分后，另一方的反击策略可能受到限制。

这样自由度就被“封锁”了，哈哈。

自由度的计算也会让人觉得头疼。

比如，做一个t检验，计算自由度时总得记住“样本数量减去1”这个规则。

哎，真是的，这就像记得别人的生日一样，得多花点心思。

以两组数据为例，如果我们有10个样本，计算自由度就得是10减去1，这样就得到了9。

其实也挺简单，只是要记住这个小规则而已。

说到这里，你可能会想，自由度到底有什么用呢？哦，亲爱的，这可是大有用处！在统计学中，自由度帮助我们确定数据的分布特征。

想象一下，如果我们想要知道一个新产品的受欢迎程度，自由度可以帮助我们分析样本数据，从而预测市场反应。

就像是一位预言家，帮你指引方向，避免在市场的迷雾中迷失自我。

自从我开始深入了解自由度后，发现它真的是一门艺术！从不同的角度来看，每一个数据背后都有故事，每一个自由度的变化也反映了数据的灵活性。

一、填空题1.机构中各个构件相对于机架能够产生独立运动的数目称为（自由度）。

2.平面机构的自由度计算公式为：（F=3n-2P L-P H）。

3.从机构结构观点来看，任何机构是由_原动件_、__机架_、_从动件三部分组成。

4.构件的自由度是指构件所具有的独立运动的数目5.两构件之间以线接触所组成的平面运动副，称为高副，它产生1个约束，而保留 2 个自由度。

6.机构中的运动副是指使两构件直接接触并产生一定相对运动的连接7.机构具有确定的相对运动条件是原动件数等于机构的自由度。

8.在平面机构中若引入一个高副将引入_1_个约束，而引入一个低副将引入_2_个约束，构件数、约束数与机构自由度的关系是F=3n-2PL -PH。

9.当两构件构成运动副后，仍需保证能产生一定的相对运动，故在平面机构中，每个运动副引入的约束至多为 2 ，至少为 1 。

10.在平面机构中，具有两个约束的运动副是低副，具有一个约束的运动副是高副。

11.计算平面机构自由度的公式为Ｆ= F=3n-2PL -PH，应用此公式时应注意判断：A. 复合铰链，B.局部自由度，C.虚约束。

12.机构中的复合铰链是指；局部自由度是指；虚约束是指。

13.机构运动简图是的简单图形。

14.机构中，若两构件之间既相互直接接触，又具有一定的相对运动，形成一种可动连接称为运动副，通过面接触而形成的联接称为低副，通过点或线接触而形成的联接称为高副。

15.构成机构的要素是零件和构件；构件是机构中的运动单元体。

16.运动副是指能使两构件之间既能保持_直接_接触，而又能产生一定的形式相对运动的_联接__。

17.图示机构要有确定运动需要有__1_个原动件。

18.平面运动副可分为低副和高副，低副又可分为转动副和移动副。

19.运动副是使两构件接触，同时又具有确定相对运动的一种联接。

平面运动副可分为低副和高副。

20.平面运动副的最大约束数为2 。

21、机构具有确定相对运动的条件是机构的自由度数目等于主动件数目。

基本规律运用1、求体系的计算自由度 W，并对其进行结构分析解：混合系： W = (3m + 2j)-(3g + 2h + b)m=1(FGHIJ),j=5(A 、B、C、D、E) ,g=0,h=0，b=10(链杆) +6(支杆)=16W = (3m + 2j)-(3g + 2h + b)=3 ×1+2×5-16=-3 构造分析：在刚片 FGHIJ 的基础上增加二元体得到整个体系有多个三个多余约束的几何不变体系。

2、试求图示体系的计算自由度，并进行几何构造分析解：(1)求解 W 按照刚片系计算：W = 3m - 2h - 3g - bm=9 h=12 g=0 b=0W = 3m - 2h - 3g - b =3 9×-2 ×12=32)构造分析。

如图所示三刚片连接三铰不共线组成几何不变体系且无多余约3、试求图示体系的计算自由度，并进行几何构造分析解：(1) 计算 W:W = (3m + 2j)-(3g + 2h + b)m=1(FGHIJ),j=5(A 、B、C、D、E) ,g=0,h=0，b=10(链杆) +6(支杆)=16W = (3m + 2j)-(3g + 2h + b)=3 ×1+2×5-16=-3(2) 结构构造分析如图示体系内部(先撤除支座及地基)由三个刚片Ⅰ、Ⅱ、Ⅲ 用三个瞬铰两两相连，且三个瞬铰在一直线上，为几何瞬变体系。

4、如图所示为三角形 ABC及其他链杆所组成体系，试考察 BC边上 G铰不同位置与体系整体几何特性的关系，给出简要分析过程。

(a) (b)(c) (d)解：（1）观察图（ a）所示体系，△ BEG直接与大地固定铰支，可以将 B点看做铰结点，则 BE，BG为链杆，因此，与大地直接相连的约束多余三根支杆，所以将大地必须看做是一个刚片。

BG和 CD与 GC相连， BE和 A支座与△ AEF相连，通过“找对家”的思路可以找到如图所示三刚片。

平面机构自由度计算例题及答案自由度是指机构中独立运动的最小单位数量，它反映了机构的灵活性和可变性。

在平面机构中，自由度的计算是非常重要的，它可以帮助我们分析和设计机构的性能。

本文将提供一个平面机构自由度计算的例题及答案，以帮助你更好地理解和应用这一概念。

例题：在下图所示的平面四杆机构中，AB为平面机构的固定基准杆，BC、CD、DA均为连杆。

BC杆可绕B点转动，CD杆可绕C点转动，DA杆可绕D点转动。

A/ \/ \/ \B--------C\ /\ /\ /\ /D问题：请计算该平面机构的自由度。

答案：1. 首先，我们需要确定机构中的连接杆关系。

根据题目给出的机构结构，我们可以看到BC杆仅与AB杆相连，CD杆仅与BC杆相连，DA杆仅与CD杆相连，因此它们之间存在着逐级连接的关系。

2. 接下来，我们需要明确机构中的独立运动。

根据题目给出的机构结构，我们可以观察到以下几种独立运动方式：a) BC杆绕点B的转动；b) CD杆绕点C的转动；c) DA杆绕点D的转动。

3. 根据独立运动的数量，我们可以得出该平面机构的自由度。

在本例中，存在3种独立运动方式，因此，该平面四杆机构的自由度为3。

以上是关于平面机构自由度计算的例题及答案。

通过对机构结构的分析，我们可以确定连接杆关系和独立运动的方式，进而计算出机构的自由度。

这对于分析和设计机构的性能具有重要意义。

总结：自由度计算是平面机构设计和分析中常用的方法之一。

它可以帮助我们了解机构的灵活性和可变性，并为机构的运动学和动力学分析提供基础。

通过了解和应用自由度计算的方法，我们可以更好地理解和解决与平面机构相关的问题。

一、机构的组成及其自由度的分析计算（共170题）1.组成机构的要素是和；构件是机构中的单元体。

2.具有、、等三个特征的构件组合体称为机器。

3.机器是由、、所组成的。

4.机器和机构的主要区别在于。

5.从机构结构观点来看，任何机构是由三部分组成。

6.运动副元素是指。

7.构件的自由度是指。

机构的自由度是指。

8.两构件之间以线接触所组成的平面运动副，称为副，它产生个约束，而保留个自由度。

9.机构中的运动副是指。

10.机构具有确定的相对运动条件是原动件数机构的自由度。

11.在平面机构中若引入一个高副将引入___个约束，而引入一个低副将引入____个约束，构件数、约束数与机构自由度的关系是12.平面运动副的最大约束数为，最小约束数为。

13.当两构件构成运动副后，仍需保证能产生一定的相对运动，故在平面机构中，每个运动副引入的约束至多为，至少为。

15.计算机机构自由度的目的是______________________________。

16.在平面机构中，具有两个约束的运动副是副，具有一个约束的运动副是副。

17.计算平面机构自由度的公式为Ｆ= ，应用此公式时应注意判断：(A) 铰链，(B) 自由度，(C) 约束。

18.机构中的复合铰链是指；局部自由度是指；虚约束是指。

19.划分机构的杆组时应先按的杆组级别考虑，机构的级别按杆组中的级别确定。

20.机构运动简图是的简单图形。

31.任何具有确定运动的机构都是由机架加原动件再加自由度为零的杆组组成的。

--------------()32.一种相同的机构组成不同的机器。

(A) 可以；(B) 不能33.机构中的构件是由一个或多个零件所组成，这些零件间产生任何相对运动。

(A) 可以；(B)不能34.有两个平面机构的自由度都等于1，现用一个带有两铰链的运动构件将它们串成一个平面机构，则其自由等于。

(A) 0；(B) 1；(C) 235.原动件的自由度应为。

(A) 1；(B) +1；(C) 036.基本杆组的自由度应为。

1． 计算齿轮机构的自由度.
解：由于B. C 副中之一为虚约束，计算机构自由度时，应将 C 副去除。

即如下图所示： 该机构的自由度1213233231=⨯-⨯-⨯=--=h p p n F
2. .机构具有确定运动的条件是什么？如果不能满足这一条件，将会产生什么结果？
机构在滚子B 处有一个局部自由度，应去除。

该机构的自由度017253231=-⨯-⨯=--=h p p n F
当自由度F=1时,该机构才能运动, 如果不能满足这一条件,该机构无法运动。

该机构当修改为下图机构，则机构可动：
N=4, PL=5, Ph=1;
自由度342511F =⨯-⨯-=
3. 计算机构的自由度.
1) 由于机构具有虚约束, 机构可转化为下图机构。

自由度342511F
=⨯-⨯-= 2) 由于机构具有虚约束, 机构可转化为下图机构。

自由度31211F =⨯-⨯= 3) 由于机构具有虚约束, 机构可转化为下图机构。

图2－
22
定轴轮系 A
B C
1 2
3 4
F=⨯-⨯=自由度33241。