弹性力学圆孔的孔口应力集中
- 格式:pdf
- 大小:1.57 MB
- 文档页数:55



采用极坐标求解弹性力学平面问题基本问题一、内容介绍在弹性力学问题的处理时,坐标系的选择从本质上讲并不影响问题的求解,但是坐标的选取直接影响边界条件的描述形式,从而关系到问题求解的难易程度。
对于圆形,楔形,扇形等工程构件,采用极坐标系统求解将比直角坐标系统要方便的多。
本章的任务就是推导极坐标表示的弹性力学平面问题基本方程,并且求解一些典型问题。
二、重点1、基本未知量和基本方程的极坐标形式;2、双调和方程的极坐标形式;3、轴对称应力与厚壁圆筒应力;4、曲梁纯弯曲、楔形体和圆孔等典型问题1 平面问题极坐标解的基本方程学习思路:选取极坐标系处理弹性力学平面问题,首先必须将弹性力学的基本方程以及边界条件通过极坐标形式描述和表达。
本节的主要工作是介绍基本物理量,包括位移、应力和应变的极坐标形式;并且将基本方程,包括平衡微分方程、几何方程和本构关系转化为极坐标形式。
由于仍然采用应力解法,因此应力函数的极坐标表达是必要的。
应该注意的是坐标系的选取与问题求解性质无关,因此弹性力学直角坐标解的基本概念仍然适用于极坐标。
学习要点:1、极坐标下的应力分量;2、极坐标平衡微分方程;3、极坐标下的应变分量;4、几何方程的极坐标表达;5、本构方程的极坐标表达;6、极坐标系的Laplace算符;7、应力函数。
1、极坐标下的应力分量为了表明极坐标系统中的应力分量,从考察的平面物体中分割出微分单元体ABCD,其由两个相距dρ的圆柱面和互成dϕ的两个径向面构成,如图所示在极坐标系中,用σρ 表示径向正应力,用σϕ 表示环向正应力,τϕρ 和τρϕ 分别表示圆柱面和径向面的切应力,根据切应力互等定理,τϕρ =τρϕ 。
首先推导平衡微分方程的极坐标形式。
考虑到应力分量是随位置的变化,如果假设AB面上的应力分量为σρ 和τϕρ,则CD面上的应力分量为如果AD面上的应力分量为σϕ 和τρϕ ,则BC面上的应力分量为。
同时,体力分量在极坐标径向ρ 和环向 ϕ方向的分量分别为F bρϕ 和F bϕ 。
4.8 半无限平面边界上受法向集中力作用的问题一弗拉芒一布辛涅斯克问题没有边界的无限大物体称为无限体。
将它用平面分成两半,每一半就称半无限体。
本节分析的是半无限的弹性平面体在边界上受一法向集中力作用的问题(图4-8)。
这一问题在实际工程问题中会经常遇到,如建筑物地基的应力和沉陷问题等。
最近发展起来的边界元数值计算法也利用这问题的解答。
假定在边界面上沿半无限平面厚度上分布有均匀压力P。
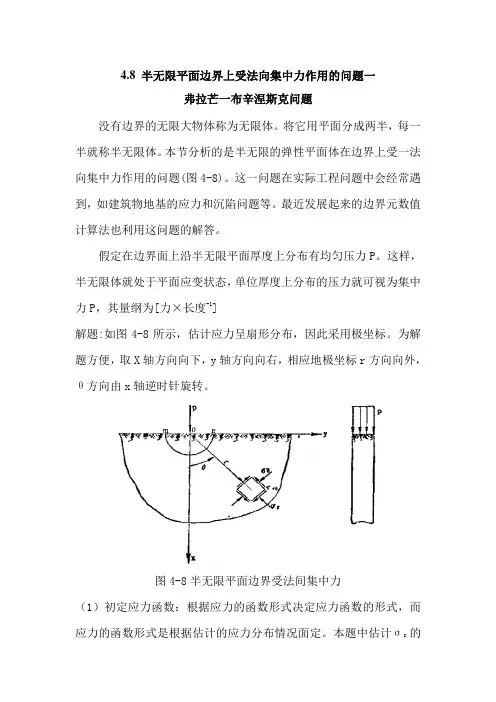
这样,半无限体就处于平面应变状态,单位厚度上分布的压力就可视为集中力P,其量纲为[力×长度-1]解题:如图4-8所示,估计应力呈扇形分布,因此采用极坐标。
为解题方便,取X轴方向向下,y轴方向向右,相应地极坐标r方向向外,θ方向由x轴逆时针旋转。
图4-8半无限平面边界受法间集中力(1)初定应力函数:根据应力的函数形式决定应力函数的形式,而应力的函数形式是根据估计的应力分布情况面定。
本题中估计σr的分布与P ,r ,θ都有关系,与P 成正比,与r 成反比。
故σr 的函数形式估计为)(θσF rPr =(a ) 式中σr 与P ,r 都是一次幂关系,这是因为只有这样,等式两边的量纲才能相等(皆为[力×长度-2])。
列出应力函数与应力分量的关系式,即(4.18)式的第一式22211θϕϕσ∂∂+∂∂=r r r r由此式可见,为使等式两边r 的幂次相等,应力函数中的r 的幂次应当比应力分量中r 的幂次高两次,所以初选应力函数的形式为)(θϕrf = (b )式中f (θ)可通过双调和方程得到。
将(b )式代入双调和方程(4.17)式得)(1)(1112222222=⎥⎦⎤⎢⎣⎡∂∂+∂∂+∂∂+∂∂θθθθf r f r r r r r )(即0)]()(2)([122443=++θθθθθf d f d d f d r (c )删去因子31r,(c )式为常系数线性微分方程,其通解为)sin cos (sin cos )(θθθθθθD C B A f +++= (d )代入(b )得)]sin cos (sin cos [θθθθθϕD C B A r +++= (e )式中A ,B ,C ,D ——待定系数,由边界条件决定。

鑫霎Ⅵ渊剥黼圆形孔洞下应力集中的实验研究肖珊1王丽华2(1.江西医学院上饶分院江西上饶3340002.江西科技师范学院江西南昌330013)[摘要]运用材料力学、弹性力学的基本原理和电测法,通过测量有圆形孔洞板圆孔周围的应力,分析圆孔周围应力集中规律;通过单纯受拉或纯弯时的情况分析、讨论叠加原理在处理应力集中问题时的具体应用方法。
[关键词]应力集中应力分布中图分类号:031文献标识码:A文章编号:1671--7597(2008)1010002--02一、前言在整个力学结构中,圆孔、凹口、圆角等是整个系统的应力集中因素,在孔、圆孔、凹口、圆角等附近存在应力集中,应力集中是引起构件破坏的主要因素,系统在这些因素和材料疲劳的共同作用下,造成断裂和破坏的机会很大,在设计的过程中把这些因素考虑进去是十分必要的。
构件中产生应力集中的原因主要有:(1)截面的急剧变化。
如:构件中的油孔、键槽、缺口、台阶等:(2)受集中力作用。
如:齿轮轮齿之间的接触点,火车军轮与钢轨的接触点等;(3)材料本身的不连续性。
如材料中的夹杂、气孔等:(4)构件中由于装配、焊接、冷加工、磨削等而产生的裂纹;(5)构件在制造或装配过程中,由于强拉伸、冷D H I、热处理、焊接等而引起的残余应力。
这些残余应力叠加上工作应力后,有可能出现较大的应力集中;(6)构件在加工或运输中的意外碰伤和刮痕。
应力集中系数可以方便地描述构件的应力集中状态。
应力集中系数可采用数学方法或实验方法求得。
实验方法有:弹性法,精密应变仪测量法,扭转薄膜比拟法,扭转电比拟法。
当实验具有足够的精度时,所得结果与理论应力集中系数非常符合。
本实验研究采用电测法,主要研究有圆形孔洞板的应力集中分布趋势。
二、研究模型和理论分析(一)圆孔边缘附近的应力以有圆形孔洞拉伸和弯曲板为研究模型,根据弹性力学理论,可以求得圆孔近的应力分布情况,圆孔附近A点(图I)的应力为:盱i O-‘|广a2渤+[z等一s爿cos41盯,=罢l z+s詈;cos28-(z詈;一s罟]c。

不同板宽的孔边的应力集中问题1 选题目的:对于如图所示的平面圆孔的孔边问题,通过数值实验的方法研究不同板宽的孔边应力集中问题,与弹性力学的解析解进行比较。
给出应力集中系数与相对孔径尺度的关系。
图一 不同板宽的孔边的应力集中问题2 背景:就无限大板宽的孔边应力集中问题,有以下弹性力学的解析解:004020002020040020020200200390)2321(90y )31)(1(2sin 2)31(2cos 2)1(2)31)(1(2cos 2)1(2422242222q R r rR rR q rR rR q rR q rR q rR rR q rR q r r r ===++==+--==+-+=--+-=),()(分布:轴上有在孔边的θσθσσθττθσθσθθθθθθ3 数值分析我们定义板宽和孔径的相对尺度的特征参数: 0R B=ξ进行研究,具体取值如表:结果如图:图2 30=ξ时的应力分布R B =ξ30 24 20 10 6图3 24=ξ时的应力分布图4 20=ξ时的应力分布图5 10=ξ时的应力分布图6 6=ξ时的应力分布4 应力集中系数如表:5 在matlab 中划出曲线:0R B =ξ30 24 20 10 6 0maxq k σ=3.0143.0323.0783.2134.0806 结论 随着0R B =ξ增大,k 值减小。

圆孔孔边的应力集中分析及优化一、引言A. 研究背景B. 研究意义C. 研究目的二、圆孔孔边应力集中分析A. 圆孔孔边的问题描述B. 应力场分析C. 应力集中因子计算D. 应力分布图分析E. 结果讨论三、圆孔孔边应力集中优化方案A. 传统优化方法B. 拓扑优化方法C. 优化结果分析比较D. 结论四、拓扑优化求解流程A. 模型准备B. 拓扑优化流程C. 拓扑优化结果分析D. 求解流程总结五、应用案例分析A. 案例背景描述B. 拓扑优化方案设计C. 优化效果分析D. 案例结果总结六、结论A. 研究回顾B. 拓扑优化的优势C. 展望未来研究方向D. 实用意义第一章:引言A. 研究背景圆孔孔边的应力集中问题一直是工程界关注的热点问题之一。
在实际工程中,许多机械零件或结构都包含圆孔,它们的设计和材料选择对工程的可靠性和安全性产生了直接影响。
因此,深入研究圆孔孔边的应力集中分析是十分必要的。
B. 研究意义圆孔孔边的应力集中分析在理论和实际工程中都有重要的应用。
从理论上来看,它可以对结构的强度和稳定性进行分析和评价,为工程设计提供参考。
从实际工程上来看,解决圆孔孔边的应力集中问题可以提高结构的可靠性,避免因应力集中导致的零件断裂、材料疲劳等问题,从而提高工程的安全性和稳定性。
C. 研究目的本文旨在深入探究圆孔孔边的应力集中分析,分析孔边应力集中的原因和特点,提出圆孔孔边应力集中的优化方案,并且通过实际案例分析验证了提出的优化方案的有效性和实用性。
第二章:圆孔孔边应力集中分析A. 圆孔孔边的问题描述圆孔孔边应力集中的问题,在工程实践中是很常见的。
当受力于孔周时,应力将会集中于孔周附近,这会导致零件或结构的强度和稳定性受到影响。
因此,了解圆孔孔边应力集中的原因和特点,对于实际工程还是非常有意义的。
B. 应力场分析对于圆孔孔边应力集中,可以采用弹性力学理论来描述应力场的分布。
在已知外载荷情况和材料的力学参数的情况下,可以利用拉普拉斯方程和应力边界条件来求解圆孔孔边的应力场分布。

不同板宽的孔边应力集中问题摘要:应用ANSYS数值模拟的方法(二维和三维)研究了含圆孔有限宽度薄板孔边应力集中问题,分析表明:平板圆孔应力集中系数的收敛性与网格划分的密度有关;应力集中系数与宽径比及长宽比有关;三维状态的内部的应力集中比二维强烈。
关键词:平面圆孔;应力集中;ANSYS;三维有限元1.引言设受力弹性体具有小孔,则孔边应力将远大于无孔时的应力,也远大于距孔稍远处的应力。
这种现象称为孔边应力集中。
孔边应力集中是局部现象,不是由于截面减小了一些而应力有所增大,而是由于开孔后发生的应力扰动所引起的。
圆孔孔边的应力可以用较简单的数学工具进行分析。
图1 平板圆[]孔如图1所示的具有小圆孔的平板,对于无限大板宽的孔边应力集中问题,有以下弹性力学解析解:在孔边的y轴上有分布:然而,实际工程上所涉及的主要是有限板宽的孔边应力集中问题,以上解析解能否适用及适用条件还值得研究。
本文就图1所示有限板宽的孔边应力集中问题,通过ANSYS软件计算其应力分布情况,采用二维模型,讨论在选取合适的网格情况下,不同的长宽比的应力集中系数变化规律及其与宽径比的关系;然后采用三维模型计算分析,与二维模型计算结果进行比较。
2.计算模型由于图1所示矩形薄板几何荷载的对称性,可选用1/4薄板作为有限元模型,坐标原点位于圆孔中心,圆孔半径R=5cm为定值,取不同的宽度和长度进行比较。
分析中采用八节点实体单元PLANE82,单元属性设置为Plane stress w/thk,弹性模量和泊松比分别为200GPa和0.3,边界条件为x=0,UX=0;y=0,UY=0。
在板远端作用有沿x轴方向的q0=1MPa的均匀分布拉力。
为了便于分析比较,定义宽径比,应力集中系数,长宽比,网格划分密度( =1时为初始网格密度,如图2所示;当 =2时,表示网格密度为初始的网格密度的2倍)。
划分的模型如图2所示。
图2 平板圆孔网格模型(网格密度 =1,长宽比 =5,宽径比 =6)3.数值模拟在同样的材料以及同样的荷载作用下,应力集中系数不仅与宽径比有关,还与网格密度以及长宽比有关。
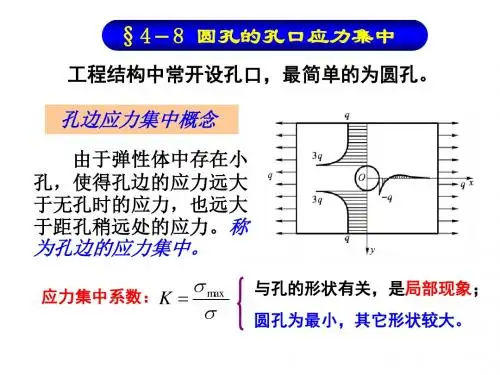
第四章平面问题的极坐标解答第8讲圆孔的孔口应力集中1在许多工程结构中,常常根据需要设置一些孔口,譬如桥梁、水坝等的泄水孔。
由于开孔,孔口附近的应力将远大于无孔时的应力,也远大于距孔口较远处的应力。
这种现象称为孔口应力集中。
本讲我们来研究“小圆孔”的孔口应力集中问题,所谓“小”,即圆孔的直径远小于弹性体的尺寸,并且孔边距弹性体的边界比较远。
2设有矩形薄板,在离开边界较远处有半径为r 的小圆孔。
坐标原点取在圆孔的中心,直角坐标轴平行于板边。
我们首先来求解两种基本荷载形式下薄板内的应力分布。
3O xyr第一种基本荷载形式:矩形薄板四边受集度为q 的均布拉力。
就薄板的边界条件而论,宜用直角坐标;就圆孔的边界条件而论,宜用极坐标。
因为我们主要考察圆孔附近的应力,所以用极坐标求解,从而需要首先将薄板的直边界“改造”为圆边界。
4O x yrq qqq5为此,我们以坐标原点为圆心,以远大于r 的某一长度R 为半径,做一个大圆。
那么在大圆周上,其应力情况当与无孔时相同,即, 0, x y xy q q 代入第3 讲得到的应力分量由直角坐标向极坐标的变换式2222cos sin sin ()sin (co 2cos cos sin )s x yxy y x xyOx yrRq qqqq6, 0q 得大圆周上的极坐标应力分量为从而原来的问题成为这样一个新问题:内半径为r 而外半径为R 的圆环,内边界自由,而外边界上受均布拉力q 。
为得到该问题的解,只需在第6 讲圆环受均布压力的拉梅解答中令120, q q qOx yrRq qqq8第二种基本荷载形式。
矩形薄板在左右两边受均布拉力q ,在上下两边受均布压力q 。
经过与前述相同的处理和分析,可知在大圆周处,应力情况当与无孔时相同,也就是,, 0.x yxy q q Ox yrRq qqq同样,代入第3 讲得到的应力分量由直角坐标向极坐标的变换式2222cos sin sin ()sin (co 2cos cos sin )s x yxy y x xy922co sin co s s 2Rq q qcos sin 2in 2s R q q可知此时大圆周上的极坐标应力分量为Ox yrR于是,原问题成为一个具有如下边界条件的圆环问题:0,0;r rcos 2,sin 2.RR q q 由于圆环外边界的应力边界条件与极角 有关,所以这不再是轴对称应力问题,无法引用第5 讲轴对称应力的一般性解答。
应力集中的实例1. 引言应力集中是指材料中的应力在某个局部区域内增加的现象。
在工程实践中,应力集中可能导致材料的破坏或失效,因此对应力集中的研究具有重要意义。
本文将介绍几个应力集中的实例,并分析其原因和对材料性能的影响。
2. 实例一:圆孔板的应力集中圆孔板是一种常见的结构,在受力时容易出现应力集中现象。
当在圆孔板上施加均匀的拉力时,应力集中会出现在孔边缘,导致孔边缘处的应力大于其他区域。
应力集中的原因主要是由于孔的存在导致了应力场的变化。
在没有孔的情况下,应力是均匀分布的,而在孔边缘附近,应力会急剧增加,形成应力集中现象。
应力集中会导致材料的破坏。
在拉伸过程中,孔边缘的应力会超过材料的屈服强度,从而导致材料的局部破坏。
因此,在设计圆孔板时,需要考虑应力集中现象,并采取相应的措施减轻应力集中。
3. 实例二:切口的应力集中切口是一种常见的材料缺陷,会导致应力集中现象。
当材料中存在切口时,切口附近的应力会明显增加,从而导致应力集中。
切口的存在会改变应力场的分布。
在切口附近,应力会急剧增加,形成应力集中。
切口的形状和尺寸对应力集中的程度有重要影响。
较小的切口可能只引起局部的应力集中,而较大的切口可能导致材料的破坏。
应力集中会对材料的性能产生重要影响。
在受力过程中,切口附近的应力会超过材料的屈服强度,从而导致材料的破坏。
因此,在设计和制造过程中,需要注意避免切口的存在,或者采取相应的措施减轻应力集中。
4. 实例三:焊接接头的应力集中焊接接头是一种常见的结构,在受力时容易出现应力集中现象。
焊接接头的应力集中主要是由于焊缝的存在导致的。
焊缝会改变材料的应力场分布。
在焊缝附近,应力会明显增加,形成应力集中。
焊接接头的几何形状和焊接工艺对应力集中的程度有重要影响。
焊缝的几何形状和尺寸,以及焊接的温度和应力都会对应力集中产生影响。
应力集中对焊接接头的性能有重要影响。
在受力过程中,焊接接头附近的应力会超过材料的屈服强度,从而导致焊接接头的破坏。
圆形孔洞下应力集中的实验研究作者:肖珊王丽华来源:《硅谷》2008年第19期[摘要]运用材料力学、弹性力学的基本原理和电测法,通过测量有圆形孔洞板圆孔周围的应力,分析圆孔周围应力集中规律;通过单纯受拉或纯弯时的情况分析、讨论叠加原理在处理应力集中问题时的具体应用方法。
[关键词]应力集中应力分布中图分类号:O31 文献标识码:A 文章编号:1671-7597(2008)1010002-02一、前言在整个力学结构中,圆孔、凹口、圆角等是整个系统的应力集中因素,在孔、圆孔、凹口、圆角等附近存在应力集中,应力集中是引起构件破坏的主要因素,系统在这些因素和材料疲劳的共同作用下,造成断裂和破坏的机会很大,在设计的过程中把这些因素考虑进去是十分必要的。
构件中产生应力集中的原因主要有:(1)截面的急剧变化。
如:构件中的油孔、键槽、缺口、台阶等;(2)受集中力作用。
如:齿轮轮齿之间的接触点,火车车轮与钢轨的接触点等;(3)材料本身的不连续性。
如材料中的夹杂、气孔等;(4)构件中由于装配、焊接、冷加工、磨削等而产生的裂纹;(5)构件在制造或装配过程中,由于强拉伸、冷加工、热处理、焊接等而引起的残余应力。
这些残余应力叠加上工作应力后,有可能出现较大的应力集中;(6)构件在加工或运输中的意外碰伤和刮痕。
应力集中系数可以方便地描述构件的应力集中状态。
应力集中系数可采用数学方法或实验方法求得。
实验方法有:弹性法,精密应变仪测量法,扭转薄膜比拟法,扭转电比拟法。
当实验具有足够的精度时,所得结果与理论应力集中系数非常符合。
本实验研究采用电测法,主要研究有圆形孔洞板的应力集中分布趋势。
二、研究模型和理论分析(一)圆孔边缘附近的应力以有圆形孔洞拉伸和弯曲板为研究模型,根据弹性力学理论,可以求得圆孔近的应力分布情况,圆孔附近A点(图1)的应力为:式中为圆孔的半径。
由(1)式可见,在孔边处,(二)应力集中系数工程上用应力集中系数来表示应力集中的程度。
圆孔孔边的应力集中分析及优化闫思江;曾显波;李凡国;陈春光【摘要】基于HyperWorks平台,在理论分析的基础上,对试样进行了有限元应力分析,分析结果与理论值吻合的很好,并对孔边进行了自由形状优化,获得了精确的孔边几何形状,降低了应力集中,为进一步疲劳分析提供了可靠的几何形状依据,大大提高疲劳试验的效率和可靠性.【期刊名称】《锻压装备与制造技术》【年(卷),期】2014(049)006【总页数】3页(P68-70)【关键词】应力集中;优化设计;HyperWorks【作者】闫思江;曾显波;李凡国;陈春光【作者单位】青岛港湾职业技术学院机械系,山东青岛266404;青岛港湾职业技术学院机械系,山东青岛266404;青岛港湾职业技术学院机械系,山东青岛266404;青岛港湾职业技术学院机械系,山东青岛266404【正文语种】中文【中图分类】TH113.10 引言在圆孔附近的局部区域内,应力急剧增大,而在离开这一区域稍远处,应力迅速减小而趋于均匀,这种由于几何形状改变而引起的应力局部增大的现象称为应力集中。
应力集中与孔径大小无关,而与孔的几何形状有关[1]。
应力集中现象将一直保持到最大局部应力到达强度极限之前。
因此,在设计构件时,应考虑应力集中的影响。
为避免应力集中造成构件的疲劳破坏,改进措施主要是改善构件外形以降低应力值[2]。
本文通过优化方法,对于不同的应力约束要求,给出合理的几何形状。
1 理论分析如图1 所示,一弹性矩形薄板受集度为q 均匀拉伸作用,板中心有一孔径为2a的圆孔,板厚为1,坐标原点取在圆孔中心,坐标平行于边界。
由于讨论圆孔孔边的应力集中问题,宜采用极坐标。
首先将外部直边界变换为圆边界,为此作如下等代变换:以圆点O 为圆心,以远大于a 的长度b 为半径作一大圆。
根据应力集中的局部性,在大圆的周边上任一点A 处的应力与无孔时相同,即σx=q,σy=τxy=0。
应用坐标变换公式,可得A 点的极坐标分量:图1 孔边应力集中于是矩形板转换成了内半径为a、外半径为b的厚壁圆筒的一个截面,根据参考文献[1]可以得到圆孔孔边的应力计算公式:根据上述公式可以得到如下结论:(1)沿孔边(r=a)的环向应力和径向应力:(2)沿y 轴(θ=±π/2)的横截面面上的环向应力:(3)沿y 轴(θ=0,π)的的横截面面上的环向应力:(4)孔边最大应力出现在θ=±π/2 处,最小应力出现在θ=0,π 处,即2 有限元分析试样为200×120mm2,厚度1mm 板,中心孔直径12mm,划分为76840 个四边形网格,施加集度q=1的载荷,参见图1。