下载文档原格式
开孔处应力集中系数的简化计算开孔处应力集中系数的简化计算1. 引言在工程设计和分析中，开孔处应力集中是一个常见的问题。
当在材料中添加孔洞或凹槽时，会导致应力场的非均匀分布，从而对材料的力学性能产生负面影响。
准确计算开孔处的应力集中系数对于工程设计和材料选择至关重要。
在本文中，我们将重点讨论开孔处应力集中系数的简化计算方法，以便工程师和研究人员能够更好地理解和应用这一概念。
2. 开孔处应力集中系数的定义开孔处应力集中系数（Stress Concentration Factor，简称SCF）是指材料在受力情况下，开孔处局部应力与远离开孔处应力的比值。
通常用K表示，其计算公式为K=σ_max/σ_nominal，其中σ_max为开孔处的最大应力，σ_nominal为远离开孔处的应力。
在工程设计中，SCF的值可以用来衡量材料在开孔处的应力集中程度，以及对其疲劳寿命和强度的影响。
3. 开孔处应力集中系数的简化计算方法在实际工程中，精确计算开孔处的应力集中系数可能非常复杂，因为需要考虑材料的几何形状、加载方式、以及材料的本构关系等多个因素。
然而，对于一些简单的几何形状和加载情况，我们可以采用一些简化的方法来估算开孔处应力集中系数。
3.1. Neuber's RuleNeuber's Rule是一种常用的简化计算方法，适用于圆形孔洞的应力集中系数估算。
根据Neuber's Rule，对于轴向受拉的材料，开孔处应力集中系数与远离开孔处应力之比可以近似为2。
这种简化计算方法在工程实践中得到了广泛的应用，尤其适用于轴向拉伸载荷作用下的材料。
3.2. Peterson's MethodPeterson's Method是另一种常用的简化计算方法，适用于不同几何形状和加载情况下的应力集中系数估算。
根据Peterson's Method，可以通过查表或计算公式来估算特定几何形状的开孔处应力集中系数。
开孔处应力集中系数的简化计算张丽;孙铁【摘要】由于各种工业和结构的要求，不可避免地要在压力容器上开孔并安装接管，开孔必然会造成器壁强度的削弱，其削弱程度的大小可通过应力集中系数的大小来体现。
通过对平板上开小圆孔边缘处的应力计算分析，得出开孔处应力集中系数的简便计算方法。
运用该方法可以准确的计算出球壳以及圆柱壳等壳体上开圆孔的应力集中系数，确定危险位置及应力的大小，为确保压力容器的安全提供必要的条件。
%Because of the requirement of various kinds of structures and industries, it’s inevitably to make holes in the pressure vessel to install nozzles, the opening will weaken the strength of vessel, and the weakened degree can be reflected by the stress concentration coefficient. Through computing and anal yzing stress of small round openings’ edge in flat, a simple computing method about the stress concentration factor was derived. Using this method can accurately calculate the stress concentration factor about lots of shells (spherical shell, cylindrical shell, etc.) to determine the dangerous position and the magnitude of stress, which may provide necessary conditions to ensure the safety of pressure vessels.【期刊名称】《当代化工》【年(卷),期】2014(000)001【总页数】2页(P142-143)【关键词】压力容器;圆孔;应力集中系数;壳体【作者】张丽;孙铁【作者单位】辽宁石油化工大学机械工程学院，辽宁抚顺 113001;辽宁石油化工大学机械工程学院，辽宁抚顺 113001【正文语种】中文【中图分类】TQ018为了使设备能够进行正常的操作、测试和检修，在壳体和端盖上往往需要有各种开孔并连接接管。
开孔板的问题（应力集中的问题）一. 引言应力集中即Stress concentration，是指受力构件由于外界因素或自身因素几何形状、外形尺寸发生突变而引起局部范围内应力显著增大的现象。
在弹性力学中，这是一类问题，应力在固体局部区域内显著增高的现象。
多出现于尖角、孔洞、缺口、沟槽以及有刚性约束处及其邻域。
应力集中会引起脆性材料断裂；使物体产生疲劳裂纹。
在应力集中区域，应力的最大值（峰值应力）与物体的几何形状和加载方式等因素有关。
局部增高的应力值随与峰值应力点的间距的增加而迅速衰减。
由于峰值应力往往超过屈服极限而造成应力的重新分配，所以，实际的峰值应力常低于按弹性力学计算出的理论峰值应力。
反映局部应力增高程度的参数称为应力集中系数k，它是峰值应力与不考虑应力集中时的应力的比值，恒大于1且与载荷大小无关。
二．产生应力集中的原因构件中产生应力集中的原因主要有：(1) 截面的急剧变化。
如：构件中的油孔、键槽、缺口、台阶等。
(2) 受集中力作用。
如：齿轮轮齿之间的接触点，火车车轮与钢轨的接触点等。
(3) 材料本身的不连续性。
如材料中的夹杂、气孔等。
(4) 构件中由于装配、焊接、冷加工、磨削等而产生的裂纹。
(5) 构件在制造或装配过程中，由于强拉伸、冷加工、热处理、焊接等而引起的残余应力。
这些残余应力叠加上工作应力后，有可能出现较大的应力集中。
(6) 构件在加工或运输中的意外碰伤和刮痕。
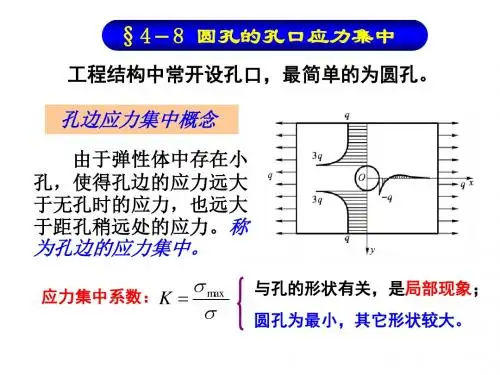
三．弹性力学中的应力集中1.工程结构中常开设孔口最简单的为圆孔。
弹性力学研究‘小孔口问题’，应符合(1)孔口尺寸＜＜弹性体尺寸，孔口引起的应力扰动局限于小范围内。
(2)孔边距边界较远（＞1.5倍孔口尺寸）孔口与边界不相互干扰。
当弹性体开孔时,在小孔口附近,将发生应力集中现象。
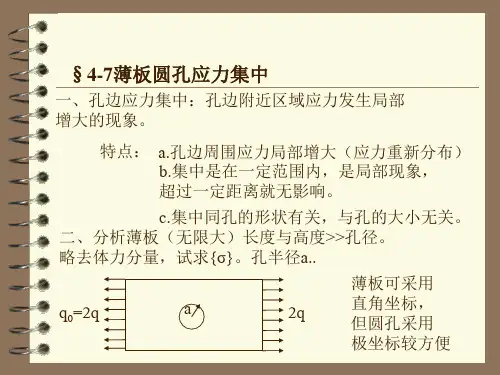
2. 孔边应力集中：孔边附近区域应力发生局部增大的现象。
特点：.（1）.孔边周围应力局部增大（应力重新分布）（2）.集中是在一定范围内，是局部现象，超过一定距离就无影响。
应力集中产生的原因及后果《应力集中产生的原因》你知道吗？在我们的生活中，很多东西都会出现应力集中的现象。
那到底为啥会这样呢？比如说一根细细的铁丝，要是上面有个小缺口，那这个缺口的地方就容易出现应力集中。
这是因为缺口改变了铁丝原本均匀的受力状态。
就好像一群小朋友整齐地排队往前走，突然有个小朋友跑开了，队伍就乱了，受力也就不均匀啦。
再比如一块木板，要是有个钉眼儿，那钉眼儿周围就可能应力集中。
这就好比一个完整的大家庭，突然少了一个人，整个家庭的结构和平衡就被打破了。
还有啊，零件的形状突变也会导致应力集中。
像那种有尖角或者突然变细的地方，力就容易在这儿扎堆。
就像我们走在路上，遇到一个急转弯，大家都容易往那个弯挤过去。
材料内部的缺陷也是原因之一。
如果材料里面有小气泡或者小裂缝，那在受力的时候，这些地方就会特别脆弱，应力也就集中在这儿了。
这就好像一个班级里，如果有几个同学总是捣乱，那老师的注意力就会集中在他们身上。
应力集中的产生往往是因为物体的结构、形状或者内部的不完美，导致了力的分布不均匀。
《应力集中产生的原因》咱们今天来聊聊应力集中是咋产生的。
再比如说，一张纸，你把一个角折起来，然后去拉这张纸，是不是折角的地方就很容易破？这也是应力集中。
那个折角就相当于受力的薄弱点。
还有那种有很多孔的铁板，孔的边缘就是应力容易集中的地方。
就好像一群人在排队，中间空了几个位置，这几个空位置周围的人就会感觉比较挤，力也就集中在这儿了。
另外，如果材料本身质量不好，有杂质或者不均匀，也会导致应力集中。
好比一群小伙伴一起跑步，有的人身体强壮，有的人身体虚弱，那虚弱的人就容易跟不上队伍，成为问题所在。
所以啊，应力集中的产生，要么是结构上有缺陷，要么是材料本身有问题。
《应力集中产生的原因》朋友，你知道应力集中是怎么来的不？还有啊，一块钢板，如果上面有个凹槽，当受到外力时，凹槽处就会承受更多的力，就像一个班级在拔河，突然有几个同学松手了，剩下的同学就会感到压力更大。
应力集中与失效分析一、引言由于构造和使用等方面的需要，往往需要在构件上开孔、沟槽、缺口、台阶等，然而，在这些部位附近，因截面尺寸的急剧变化，将产生局部的高应力，其应力峰值远大于由基本公式算得的应力值。
这种受力构件由于外界因素或自身因素几何形状、外形尺寸发生突变而引起局部范围内应力显著增大的现象称为应力集中，引起应力集中的孔、沟槽、缺口、台阶等几何体称为应力集中因素。
应力集中削弱了构件的强度，降低了构件的承载能力。
从而，应力集中处往往是构件破坏的起始点，是引起构件破坏的主要因素。
该现象普遍存在于各种构件中，大部分构件的破坏事故都是由应力集中引起的。
因此，为了确保构件的安全使用，提高产品的质量和经济效益，必须科学地处理构件的应力集中问题。
二、产生应力集中的原因构件中产生应力集中的原因主要有：(1) 截面尺寸的急剧变化。
如：构件中的油孔、键槽、缺口、台阶等。
(2) 构件受到集中力作用。
如：齿轮轮齿之间的接触点，火车车轮与钢轨的接触点等。
(3) 材料本身的不连续性。
如材料中的夹杂、气孔等。
(4) 构件中由于装配、焊接、冷加工、磨削等而产生的裂纹。
(5) 构件在制造或装配过程中，由于强拉伸、冷加工、热处理、焊接等而引起的残余应力。
这些残余应力叠加上工作应力后，有可能出现较大的应力集中。
(6) 构件在加工或运输中的意外碰伤和刮痕。
三、应力集中的物理解释如图，在构件的中间开孔拉杆，故在外力作用下，部件中尺寸发生突然变化的截面上的应力并不是均匀分布的，在圆孔边缘的应力明显大于截面上的平均应力。
应力集中的程度可以用理论应力集中系数表示：式中，为截面上的最大局部应力；为名义应力，即认为应力在截面上均匀分布而求得的力。
设图中的板宽为b，圆孔直径为d，厚度为，则可以由弹性理论或试验等方法确定。
试验结果表明，截面尺寸改变的越急剧，角越尖，孔越小，应力集中的程度越严重。
四、应力集中对构件强度的影响在静荷载作用下，各种材料对应力集中的敏感程度是不同的。
锅炉压力容器的开孔应符合哪些规定？
为了便于对锅炉、压力容器定期进行内部检验和清理，在锅炉、压力容器上应开设必要的人孔、手孔和检查孔。
开孔后，不仅降低了部件的承载能力，而且还因为开孔造成结构不连续，在开孔边会产生应力集中。
因此，在进行部件结构设计时，对锅炉、压力容器开孔的数量和尺寸作了严格的规定。
对锅炉、压力容器上开设人孔、手孔的数量规定如下：
（1）锅筒内径大于或等于800mm的水管锅炉和锅筒内径大于1000mm的锅壳式锅炉，都应在筒体或封头（管板）上开设人孔；锅筒内径为800～1000mm的锅壳式锅炉，至少应在锅筒或封头（管板）上开设一个头孔。
（2）压力容器内径≥1000mm的，应至少开设一个人孔；内径＜1000mm～≥500mm的，应开设一个人孔或两个手孔。
内径＜500～≥300mm的，至少应开设两个手孔。
锅炉受压元件上开孔的尺寸应符合下列规定：
（1）锅炉受压元件上，椭圆人孔不得小于280×380mm。
人孔圈最小的密封面宽度为18mm。
人孔门凸肩与人孔圈之间总间隙不应超过3mm（沿圆周各点上不超过1.5mm），并且凹槽的深度应达到能完整地容纳密封垫片。
（2）锅炉受压元件上，椭圆头孔不得小于220 X 320mm,颈部或孔圈高度不应超过100mm。
第 1 页
本文部分内容来自互联网，不为其真实性及所产生的后果负责，如有异议请联系我们及时删除。
孔边应力集中由于开孔，孔口附近的应力将远大于无孔时的应力，也远大于距孔口较远处的应力圣维南如果把物体的一小部分便捷上的面力变换成分布不同，但静力等效，那么近处的应力分布将有显著变化，但远处所受影响可以忽略不计。
可以简化局部边界上的应力边界条件小挠度薄板弯曲问题的三个基本假设1垂直于中面方向的线应变，即可以不计2应力分量和z相关的3个、、，远小于其余三个应力分量，因而是次要的，他们所引起的形变可以不计3薄板中面内的各店都没有平行于中面的位移弹性常数无关？具有相同的应理解常体力/在单连体的应力边界问题中，两个弹性体具有相同的边界条件，受同样分布的外力。
极小势能原理在给定的外力作用下，在满足位移边界条件的所有各组位移状态中，实际存在的一组位移应使总势能成为极值，如果考虑二阶变分总是大于或等于0.即（）就可以证明：对于稳定平衡状态，这个极值是极小值平面应变物体截面形状、面力、体力、约束、沿z 方向均不变，只有平面应变分量（）仅为xy函数的弹性力学问题对称如果弹性体的几何形状、约束情况、以及所受的力都是对称于某一轴，则所有应力、应变、位移、也都对称于这一轴。
平面应力只有平面应力分量（）存在，仅为xy函数的弹性力学问题、深梁平板坝的平板支墩逆解法先设定各种形式、满足相容方程的应力函数、并求得应力分量，然后再根据应力边界条件和弹性体边界形状看这些应力分量对应边界上什么样的面力，从而得知所选取的应力函数可以解决问题。
半逆解法针对所要求解的问题，根据弹性体的边界形状和受力情况，假设部分或全部应力分量的函数形式，得出应力函数形式。
带入相容方程求解应力函数，求解应力分量，看是否满足应力边界条件，是即可，不是另作假设。
孔边应力集中由于开孔，孔口附近的应力将远大于无孔时的应力，也远大于距孔口较远处的应力圣维南如果把物体的一小部分便捷上的面力变换成分布不同，但静力等效，那么近处的应力分布将有显著变化，但远处所受影响可以忽略不计。
可以简化局部边界上的应力边界条件小挠度薄板弯曲问题的三个基本假设1垂直于中面方向的线应变，即可以不计2应力分量和z相关的3个、、，远小于其余三个应力分量，因而是次要的，他们所引起的形变可以不计3薄板中面内的各店都没有平行于中面的位移弹性常数无关？具有相同的应理解常体力/在单连体的应力边界问题中，两个弹性体具有相同的边界条件，受同样分布的外力。
极小势能原理在给定的外力作用下，在满足位移边界条件的所有各组位移状态中，实际存在的一组位移应使总势能成为极值，如果考虑二阶变分总是大于或等于0.即（）就可以证明：对于稳定平衡状态，这个极值是极小值平面应变物体截面形状、面力、体力、约束、沿z 方向均不变，只有平面应变分量（）仅为xy函数的弹性力学问题对称如果弹性体的几何形状、约束情况、以及所受的力都是对称于某一轴，则所有应力、应变、位移、也都对称于这一轴。
平面应力只有平面应力分量（）存在，仅为xy函数的弹性力学问题、深梁平板坝的平板支墩逆解法先设定各种形式、满足相容方程的应力函数、并求得应力分量，然后再根据应力边界条件和弹性体边界形状看这些应力分量对应边界上什么样的面力，从而得知所选取的应力函数可以解决问题。
半逆解法针对所要求解的问题，根据弹性体的边界形状和受力情况，假设部分或全部应力分量的函数形式，得出应力函数形式。
带入相容方程求解应力函数，求解应力分量，看是否满足应力边界条件，是即可，不是另作假设。
孔边应力集中由于开孔，孔口附近的应力将远大于无孔时的应力，也远大于距孔口较远处的应力圣维南如果把物体的一小部分便捷上的面力变换成分布不同，但静力等效，那么近处的应力分布将有显著变化，但远处所受影响可以忽略不计。
可以简化局部边界上的应力边界条件小挠度薄板弯曲问题的三个基本假设1垂直于中面方向的线应变，即可以不计2应力分量和z相关的3个、、，远小于其余三个应力分量，因而是次要的，他们所引起的形变可以不计3薄板中面内的各店都没有平行于中面的位移弹性常数无关？具有相同的应理解常体力/在单连体的应力边界问题中，两个弹性体具有相同的边界条件，受同样分布的外力。
极小势能原理在给定的外力作用下，在满足位移边界条件的所有各组位移状态中，实际存在的一组位移应使总势能成为极值，如果考虑二阶变分总是大于或等于0.即（）就可以证明：对于稳定平衡状态，这个极值是极小值平面应变物体截面形状、面力、体力、约束、沿z 方向均不变，只有平面应变分量（）仅为xy函数的弹性力学问题对称如果弹性体的几何形状、约束情况、以及所受的力都是对称于某一轴，则所有应力、应变、位移、也都对称于这一轴。
平面应力只有平面应力分量（）存在，仅为xy函数的弹性力学问题、深梁平板坝的平板支墩逆解法先设定各种形式、满足相容方程的应力函数、并求得应力分量，然后再根据应力边界条件和弹性体边界形状看这些应力分量对应边界上什么样的面力，从而得知所选取的应力函数可以解决问题。
半逆解法针对所要求解的问题，根据弹性体的边界形状和受力情况，假设部分或全部应力分量的函数形式，得出应力函数形式。
带入相容方程求解应力函数，求解应力分量，看是否满足应力边界条件，是即可，不是另作假设。
孔边应力集中由于开孔，孔口附近的应力将远大于无孔时的应力，也远大于距孔口较远处的应力圣维南如果把物体的一小部分便捷上的面力变换成分布不同，但静力等效，那么近处的应力分布将有显著变化，但远处所受影响可以忽略不计。
可以简化局部边界上的应力边界条件小挠度薄板弯曲问题的三个基本假设1垂直于中面方向的线应变，即可以不计2应力分量和z相关的3个、、，远小于其余三个应力分量，因而是次要的，他们所引起的形变可以不计3薄板中面内的各店都没有平行于中面的位移弹性常数无关？具有相同的应理解常体力/在单连体的应力边界问题中，两个弹性体具有相同的边界条件，受同样分布的外力。
极小势能原理在给定的外力作用下，在满足位移边界条件的所有各组位移状态中，实际存在的一组位移应使总势能成为极值，如果考虑二阶变分总是大于或等于0.即（）就可以证明：对于稳定平衡状态，这个极值是极小值平面应变物体截面形状、面力、体力、约束、沿z方向均不变，只有平面应变分量（）仅为xy函数的弹性力学问题对称如果弹性体的几何形状、约束情况、以及所受的力都是对称于某一轴，则所有应力、应变、位移、也都对称于这一轴。
平面应力只有平面应力分量（）存在，仅为xy函数的弹性力学问题、深梁平板坝的平板支墩逆解法先设定各种形式、满足相容方程的应力函数、并求得应力分量，然后再根据应力边界条件和弹性体边界形状看这些应力分量对应边界上什么样的面力，从而得知所选取的应力函数可以解决问题。
半逆解法针对所要求解的问题，根据弹性体的边界形状和受力情况，假设部分或全部应力分量的函数形式，得出应力函数形式。
带入相容方程求解应力函数，求解应力分量，看是否满足应力边界条件，是即可，不是另作假设。
孔边应力集中由于开孔，孔口附近的应力将远大于无孔时的应力，也远大于距孔口较远处的应力圣维南如果把物体的一小部分便捷上的面力变换成分布不同，但静力等效，那么近处的应力分布将有显著变化，但远处所受影响可以忽略不计。
可以简化局部边界上的应力边界条件小挠度薄板弯曲问题的三个基本假设1垂直于中面方向的线应变，即可以不计2应力分量和z相关的3个、、，远小于其余三个应力分量，因而是次要的，他们所引起的形变可以不计3薄板中面内的各店都没有平行于中面的位移弹性常数无关？具有相同的应理解常体力/在单连体的应力边界问题中，两个弹性体具有相同的边界条件，受同样分布的外力。
极小势能原理在给定的外力作用下，在满足位移边界条件的所有各组位移状态中，实际存在的一组位移应使总势能成为极值，如果考虑二阶变分总是大于或等于0.即（）就可以证明：对于稳定平衡状态，这个极值是极小值平面应变物体截面形状、面力、体力、约束、沿z方向均不变，只有平面应变分量（）仅为xy函数的弹性力学问题对称如果弹性体的几何形状、约束情况、以及所受的力都是对称于某一轴，则所有应力、应变、位移、也都对称于这一轴。
平面应力只有平面应力分量（）存在，仅为xy函数的弹性力学问题、深梁平板坝的平板支墩逆解法先设定各种形式、满足相容方程的应力函数、并求得应力分量，然后再根据应力边界条件和弹性体边界形状看这些应力分量对应边界上什么样的面力，从而得知所选取的应力函数可以解决问题。
半逆解法针对所要求解的问题，根据弹性体的边界形状和受力情况，假设部分或全部应力分量的函数形式，得出应力函数形式。
带入相容方程求解应力函数，求解应力分量，看是否满足应力边界条件，是即可，不是另作假设。
孔边应力集中由于开孔，孔口附近的应力将远大于无孔时的应力，也远大于距孔口较远处的应力圣维南如果把物体的一小部分便捷上的面力变换成分布不同，但静力等效，那么近处的应力分布将有显著变化，但远处所受影响可以忽略不计。
可以简化局部边界上的应力边界条件小挠度薄板弯曲问题的三个基本假设1垂直于中面方向的线应变，即可以不计2应力分量和z相关的3个、、，远小于其余三个应力分量，因而是次要的，他们所引起的形变可以不计3薄板中面内的各店都没有平行于中面的位移弹性常数无关？具有相同的应理解常体力/在单连体的应力边界问题中，两个弹性体具有相同的边界条件，受同样分布的外力。
极小势能原理在给定的外力作用下，在满足位移边界条件的所有各组位移状态中，实际存在的一组位移应使总势能成为极值，如果考虑二阶变分总是大于或等于0.即（）就可以证明：对于稳定平衡状态，这个极值是极小值平面应变物体截面形状、面力、体力、约束、沿z方向均不变，只有平面应变分量（）仅为xy函数的弹性力学问题对称如果弹性体的几何形状、约束情况、以及所受的力都是对称于某一轴，则所有应力、应变、位移、也都对称于这一轴。
平面应力只有平面应力分量（）存在，仅为xy函数的弹性力学问题、深梁平板坝的平板支墩逆解法先设定各种形式、满足相容方程的应力函数、并求得应力分量，然后再根据应力边界条件和弹性体边界形状看这些应力分量对应边界上什么样的面力，从而得知所选取的应力函数可以解决问题。
半逆解法针对所要求解的问题，根据弹性体的边界形状和受力情况，假设部分或全部应力分量的函数形式，得出应力函数形式。
带入相容方程求解应力函数，求解应力分量，看是否满足应力边界条件，是即可，不是另作假设。
孔边应力集中由于开孔，孔口附近的应力将远大于无孔时的应力，也远大于距孔口较远处的应力圣维南如果把物体的一小部分便捷上的面力变换成分布不同，但静力等效，那么近处的应力分布将有显著变化，但远处所受影响可以忽略不计。
可以简化局部边界上的应力边界条件小挠度薄板弯曲问题的三个基本假设1垂直于中面方向的线应变，即可以不计2应力分量和z相关的3个、、，远小于其余三个应力分量，因而是次要的，他们所引起的形变可以不计3薄板中面内的各店都没有平行于中面的位移弹性常数无关？具有相同的应理解常体力/在单连体的应力边界问题中，两个弹性体具有相同的边界条件，受同样分布的外力。
