运筹学第2讲 线性规划1
- 格式:ppt
- 大小:619.50 KB
- 文档页数:55
第二章线性规划教学目的和要求:目的:使学生具备线性规划的基本知识以及应用线性规划的基本能力。
要求:理解线性规划概念,标准型,解的概念,基本定理;掌握单纯形法,人工变量法,了解图解法。
重点:线性规划标准型,解的概念,单纯形法,人工变量法。
难点:线性规划基本定理,单纯形法。
教学方法:讲授法,习题法。
学时分配:12学时 作业安排:见教材P 38.线性规划是运筹学的一个重要分支。
1939年苏联科学家康托罗维奇提出了生产组织和计划中的线性规划模型。
1947年美国学者丹捷格(George B.Dantzig)提出了求解一般线性规划问题的方法。
此后,线性规划理论日趋成熟,应用也日益广泛和深入。
第一节线性规划问题一、问题的提出在企业的生产经营活动中经常会面临这样两类问题:一是如何合理地利用有限的人力、物力、财力等资源,取得最佳的经济效果;二是在取得一定的经济效果的前提下,如何合理安排使用人力、物力、财力等资源,使花费的成本最低。
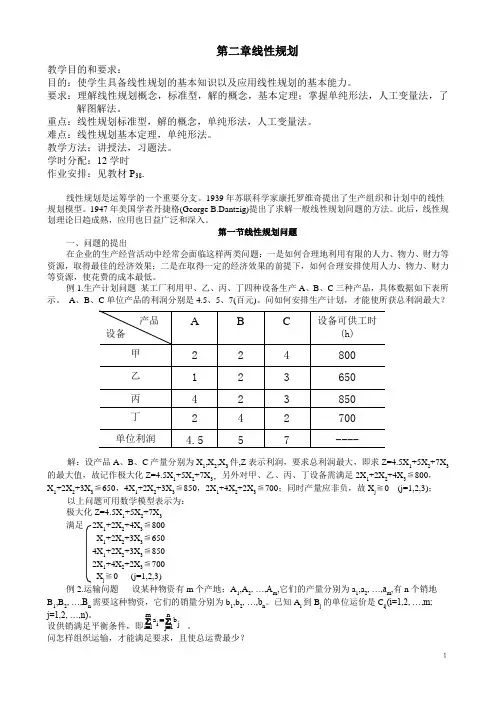
例1.生产计划问题 某工厂利用甲、乙、丙、丁四种设备生产A 、B 、C 三种产品,具体数据如下表所示。
A 、B 、C 单位产品的利润分别是4.5、5、7(百元)。
问如何安排生产计划,才能使所获总利润最大?解:设产品A 、B 、C 产量分别为X 1,X 2,X 3件,Z 表示利润,要求总利润最大,即求Z=4.5X 1+5X 2+7X 3的最大值,故记作极大化Z=4.5X 1+5X 2+7X 3,另外对甲、乙、丙、丁设备需满足2X 1+2X 2+4X 3≦800,X 1+2X 2+3X 3≦650,4X 1+2X 2+3X 3≦850,2X 1+4X 2+2X 3≦700;同时产量应非负,故X j ≧0 (j=1,2,3);以上问题可用数学模型表示为: 极大化Z=4.5X 1+5X 2+7X 3 满足 2X 1+2X 2+4X 3≦800 X 1+2X 2+3X 3≦6504X 1+2X 2+3X 3≦850 2X 1+4X 2+2X 3≦700X j ≧0 (j=1,2,3)例2.运输问题 设某种物资有m 个产地;A 1,A 2, …,A m ,它们的产量分别为a 1,a 2, …,a m ,有n 个销地B 1,B 2, …,B n 需要这种物资,它们的销量分别为b 1,b 2, …,b n 。



第二章 线性规划教学重点:线性规划可行区域的几何结构,基本可行解及可行区域的基本定理,单纯形方法,两阶段法,对偶和对偶理论,灵敏度分析。
教学难点:线性规划可行区域的几何结构,基本可行解及可行区域的基本定理,单纯形方法,两阶段法,对偶性,灵敏度分析。
教学课时:24学时主要教学环节的组织:首先通过各种形式的例子归纳出线性数学规划的一般形式,然后在详细讲解主要内容的基础上,尽可能以图形和例题的形式给以形象的说明,使学生对知识点有更直观、具体的认识。
再通过大量习题巩固知识,也可以应用软件包解决一些实际问题。
第一节 线性规划问题教学重点:线性规划问题的实例,线性规划的一般形式、规范形式和标准形式教学难点:线性规划一般形式转换成标准形式。
教学课时:2学时主要教学环节的组织:首先通过几个实例总结出线性规划问题的一般形式,再介绍如何将一般形式转换成标准形式。
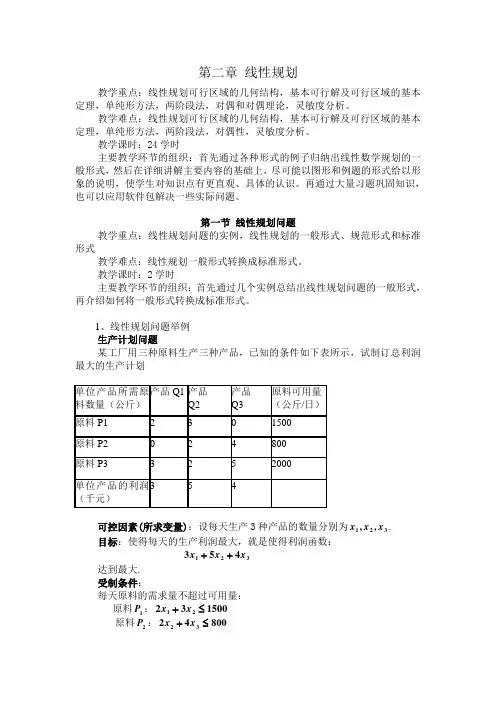
1、线性规划问题举例 生产计划问题某工厂用三种原料生产三种产品,已知的条件如下表所示,试制订总利润最大的生产计划可控因素(所求变量):设每天生产3种产品的数量分别为321,,x x x . 目标:使得每天的生产利润最大,就是使得利润函数:321453x x x ++ 达到最大. 受制条件:每天原料的需求量不超过可用量:原料1P :15003221≤+x x原料2P :8004232≤+x x原料3P :2000523321≤++x x x蕴含约束:产量为非负数0,,321≥x x x模型321453max x x x ++15003221≤+x xs.t. 8004232≤+x x2000523321≤++x x x0,,321≥x x x运输问题一个制造厂要把若干单位的产品从两个仓库2,1;=i A i 发送到零售点4,3,2,1;=j B j ,仓库 i A 能供应的产品数量为2,1;=i a i ,零售点 j B 所需的产品的数量为4,3,2,1;=j b j 。