当前位置：文档之家 › 《运筹学》第一章 线性规划

《运筹学》第一章 线性规划

  • 格式：ppt
  • 大小：1.49 MB
  • 文档页数：82

下载文档原格式

  / 82

合集下载

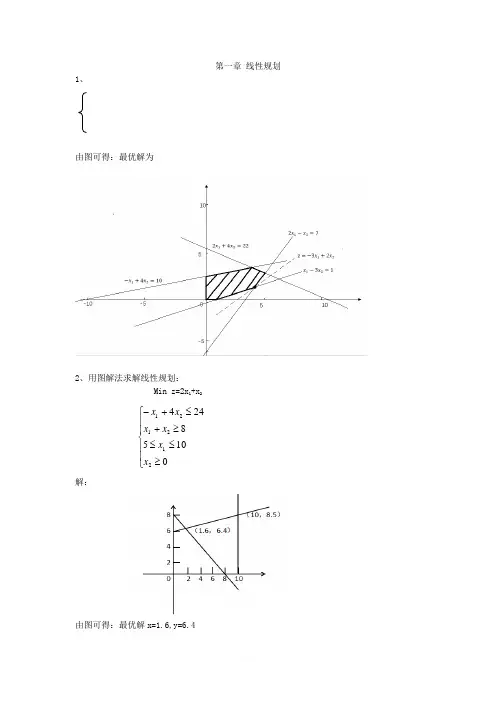
运筹学课后习题答案

运筹学课后习题答案

第一章 线性规划1、由图可得：最优解为2、用图解法求解线性规划： Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解：由图可得：最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解：由图可得：最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得：最大值⎪⎩⎪⎨⎧==+35121x x x ， 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示，在（4，2）这一点达到最大值为26将线性规划模型化成标准形式：Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解：令Z ’=-Z,引进松弛变量x 4≥0，引入剩余变量x 5≥0，并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束，321321321321,00632442392-x x x x x x x x x x x x解：令Z ’ = -z ，引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。

第一章 线性规划

第一章 线性规划
(1-8)
例 1.5 （汽油混合问题） 一种汽油的特性可用两个指标描述：其点火性用“辛烷数” 描述，其挥发性用“蒸汽压力”描述，某炼油厂有四种标准汽油，设其标号分别为 1，2， 3，4，其特性及库存量见表 1.5，将上述标准汽油适量混合，可得到两种飞机汽油，其标 号分别为 1，2，这两种飞机汽油的性能指标及产量需求见表 1.6，问应如何根据库存情况 适量混合各种标准汽油，使既满足飞机汽油的性能指标，而产量又为最高。
注：前苏联的尼古拉也夫斯克城住宅兴建计划采用了上述模型，共用了 12 个变量，10 个约束条件。
表 1.2 资源 住宅体系 砖混住宅 壁板住宅 大模住宅 资源限量 造价 (元/m2) 105 135 120 110000 (千元 钢材 (公斤/m2) 12 30 25 20000 (吨) 例 1.2 的数据表 水泥 (公斤/m2) 110 190 180 150000 (吨) 砖 (块/m2) 210 —— —— 147000 (千块) 人工 (工日/m2) 4.5 3.0 3.5 4000 (千工日)
3．线性规划模型的一般形式 以 MAX 型、≤约束为例 决策变量： x1 ,
(1-4)
, xn
目标函数： Maxz = c1 x1 +
+ cn x n
⎧a11 x1 + + a1n x n ≤ b1 ⎪ ⎪ 约束条件： s.t.⎨ ⎪a m1 x1 + + a mn x n ≤ bm ⎪ ⎩ x1 , , x n ≥ 0
2
Maxz = x1 + x 2 + x3 ⎧0.105 x1 + 0.135 x 2 + 0.120 x3 ≤ 110000 ⎪0.012 x1 + 0.030 x 2 + 0.025 x3 ≤ 20000 数学模型为: ⎪0.110 x1 + 0.190 x 2 + 0.180 x 3 ≤ 150000 (1-3) s.t ⎨ 0.210 x ≤ 147000 ⎪0.00451 x + 0.003x 2 + 0.0035 x 3 ≤ 4000 ⎪x , x , x 1 ≥ 0 ⎩ 1 2 3

《运筹学》课件 第一章 线性规划

《运筹学》课件 第一章 线性规划

10
解：令
xi=
1， Si被选中
min z= ci xi i 1 10
0， Si没被选中
xi 5
i 1
x1 x8 1 x7 x8 1
称为技术系数
b= (b1,b2, …, bm) 称为资源系数
2、非标准型
标准型
（1）Min Z = CX
Max Z' = -CX
（2）约束条件
• “≤”型约束，加松弛变量；
松弛变量
例如： 9 x1 +4x2≤360
9 x1 +4x2+ x3=360
• “≥”型约束，减松弛变量；
例、将如下问题化为标准型
数据模型与决策 (运筹学）
课程教材：
吴育华,杜纲. 《管理科学基础》，天津大学出版社。
绪论
一、运筹学的产生与发展
运筹学（Operational Research) 直译为“运作研究”。
• 产生于二战时期 • 60年代，在工业、农业、社会等各领域得到广泛应用 • 在我国，50年代中期由钱学森等引入
Min z x1 2x2 3x3
x1 x2 x3 7
s.t
.
x1 x2 x3 3x1 x2 2
x3
2
5
x1, x2 , x3 0
解：令 Min z Max z' (z' z) ，第一个约束加松弛变量x5，
第二个约束减松弛变量x6，得标准型：
Max z' x1 2x2 +3x3
x1 x2 x3 x4 7
s.t .
x1 x2 3x1
x3 x2
x5 2 2x3 5
x1 , , x5 0

第一章 线性规划

第一章 线性规划

第1章线性规划Chapter 1 Linear Programming本章内容提要线性规划是运筹学的重要内容。

本章介绍线性规划数学模型、线性规划的基本概念以及求解线性规划数学模型的基本算法——单纯形法。

学习本章要求掌握以下内容：⏹线性规划模型的结构⏹线性规划的标准形式，非标准形式转化为标准形式⏹线性规划的图解以及相应的概念。

包括：约束直线，可行半空间，可行解，可行域，凸集，极点，目标函数等值线，最优解⏹线性规划的基本概念。

包括：基，基础解，基础可行解，基变量，非基变量，进基变量，离基变量，基变换⏹单纯形法原理。

包括：基变量和目标函数用非基变量表出，检验数，选择进基变量的原则，确定离基变量的方法，主元，旋转运算⏹单纯形表。

包括初始单纯形表的构成，单纯形表运算方法⏹初始基础可行解，两阶段法⏹退化的基础可行解§1.1 运筹学和线性规划1.1.1 运筹学运筹学（Operations Research）是二十世纪三十年代二次大战期间由于战争的需要发展起来的一门学科。

当时，英国组织了一批自然科学和工程科学的学者，和军队指挥员一起，研究大规模战争提出的一些问题。

如轰炸战术的评价和改进、反潜艇作战研究等，研究结果在战争实践中取得了明显得效果。

这些研究当时在英国称为Operational Research，直译为作战研究。

战争结束以后，这些研究方法不断发展完善，并逐步形成学科理论体系，其中一些主要的理论和方法包括：线性规划，网络流，整数规划，动态规划，非线性规划，排队论，决策分析，对策论，计算机模拟等。

这些理论和方法在经济管理领域也得到了广泛应用，Operations Research也转义成为“作业研究”。

我国将Operations Research译成“运筹学”，非常贴切地将Operations Research这一英文术语所包含的作战研究和作业研究两方面的涵义都体现了出来。

现在，运筹学已经成为管理科学重要的基础理论和应用方法，是管理科学专业基本的必修课程之一。

运筹学线性规划

运筹学线性规划
主要解决以下两类问题： 1、任务确定后，如何统筹安排，做到应用尽量少的人 力和物力资源来完成任务； 2、在一定量的人力、物力资源的条件下，如何安排、 使用他们，使完成的任务最多。
4
例1.1：（计划安排问题） I 设备A(h) 0 设备B(h) 4 原材料(公斤) 2 利润(万元） 2 II 资源总量 3x2 15 3 15 0 12 s.t. 4x1 12 2 14 2x1+2x2 14 3 x1，x2 0 I,II生产多少, 可获最大利润?
s.t. x1 -x2 +x4 -x5 -x7 =2
x1 , x2 , x4 ,
…
, x7 0
12
第二节 线性规划问题的图解法及几何意义
一、线性规划问题的解的概念
0 3 1 0 0 15 4 0 0 1 0 X= 12 2 2 0 0 1 14
5
max Z= 2x1 +3x2
解:设 计划期内生产产品I、II的数量x1、x2 则该问题的数学模型为：
例1.2 成本问题
某炼油厂根据每季度需供应给合同单位汽油15万吨、煤油 12万吨、重油12万吨。该厂计划从A，B两处运回原油 提炼，已知两处的原油成分含量见表1－2；又已知从A 处采购的原油价格为每吨（包括运费）200元，B处采购 的原油价格为每吨（包括运费）290元, 问：该炼油厂该 如何从A，B两处采购原油，在满足供应合同的条件下， 使购买成本最小。 油品来源 A B min S 200x1 290x 2
解：(1) 确定可行域 x1 0 x1 =0 (横)
30
x2 0 x2=0 (纵) x1+2x2 30 x1+2x2 =30

运筹学第1章-线性规划

运筹学第1章-线性规划
凸集的数学定义:设K为n维欧氏空间的一个点集，若K中任意两个 点X1和X2连线上的所有点都属于K，即“X =αX1+(1-α) X2 ∈ K(0≤a ≤ 1)”，则称K为凸集。设X(x1，x2，…，xn)，X1(u1， u2，...，un)，X2(v1，v2，…，vn)，如图1一5所示，“X =αX1+(1α) X2 ∈ K(0≤a ≤ 1)”的证明思路如下:
下一页 返回
图解法步骤：
（1）建立坐标系； （2）将约束条件在图上表示； （3）确立满足约束条件的解的范围； （4）绘制出目标函数的图形 （5）确定最优解
用图解法求解下列线性规划问题
max z 2x1 3x2
4x1 0x2 16
s.t
10xx11
4x2 2x2
12 8
x1, x2 0
1. 1.1问题举例
(1)生产计划问题。 生产计划问题是典型的已知资源求利润最大化的问题，对于此类
问题通常有三个假设:①在某一计划期内对生产做出的安排;②生产 过程的损失忽略不计;③市场需求无限制，即假设生产的产品全部 卖出。
下一页 返回
1.一般线性规划问题的数学模型
例1 用一块连长为a的正方形铁皮做一个容 器，应如何裁剪，使做成的窗口的容积为最 大？
解：设 x1, x2分别表示从A,B两处采购的原油量（单
位：吨），则所有的采购方案的最优方案为：
min z 200x1 290x2
0.15x1 0.50x2 150000
s.t
0.20x1 0.50x1
0.30x2 0.15x2
120000 120000
x1 0, x2 0
1. 1线性规划问题与模型
也可以写成模型(1-6)和模型(1-7)的形式，其中模型(1-7)较为常用。

运筹学 线性规划习题解析

管理运筹学
第一章 线性规划
第一章 线性规划
1、某化工厂生产某项化学产品，每单位标准重 量为1000克，由A、B、C三种化学物混合而成 。产品组成成分是每单位产品中A不超过300克 ，B不少于150克，C不少于200克。A、B、C每 克成本分别为5元、6元、7元。问如何配置此化 学产品，才能使成本最低？
解：由题意设生产高级、中级、低级玩具各为 x1，x2，x3台，总利润为S元，则由题意可得本 题的线性规划模型为：
由题意可得下表条件约束：
max S=max(30x1+5x2+x3)
17x1 + 2x2+1/2x3 ≤ 500 8x1+1/2x2+1/6x3 ≤ 100 x1 ≤ 10 x2 ≤ 30 x3 ≤ 100 x1,x2,x3≥0
K1=-4
k2=-1/2
X1+2x2=28
4x1+x2=42 X1+2x2=28
解得：x1=8,x2如果原料甲增加到42吨，原最优解是否改变？
图解： x2
42
21
4x1+x2=42
4x1+x2=42 X1+2x2=42
解得：x1=6,x2=18
k=-7/5
X1+2x2=42
（2）X0一定不是可行解； （3）X0一定不是基可行解；
对
（4）X0一定不是最优解；
（5）X0一定不是基最优解。
第一章 线性规划
评讲完啦~ 谢谢大家~
10.5
42
x1
(3)如果每吨B产品的利润增加到15万元，原最优解 是否改变？
图解： x2
42
4x1+x2=42
最优解是x1+2x2=28 与x2轴的交点（0,14）

运筹学


11
目录
（三）LP问题的标准型
1.为了讨论LP问题解的概念和解的性质以及对LP问题求 解方便，必须把LP问题的一般形式化为统一的标准型：
minz=c1x1+c2x2+…+cnxn
j =1 a11 x2 + a12 x2 + + a1n xn = b1 a x + a x + + a x = b n 2n n 2 21 2 22 2 简 aij x j = bi (i = 1,2, L , m) s.t 化 j =1 x j ≥ 0( j = 1,2,L , n) am1 x2 + am 2 x2 + + amn xn = bm x1 , x2 , , xn ≥ 0
A ( 0 ,3 ) 10 15 , ) B( 7 7 5 C ( ,0 ) 2
max
Z = 5 x1 + 4 x 2
3 x 1 + 5 x 2 ≤ 15 2 x1 + x 2 ≤ 5 2 x 1 + 2 x 2 ≤ 11 x1 , x 2 ≥ 0
Z=
110 7
2x1+2x2=11
C 2.5
5x1+4x2=0 红线为目标函数的等值线 等值线. 红线为目标函数的等值线
j i= 1
j
(1.4) (1.5) (1.6)
ì n a ij x j = s .t . j = 1 í 1.从代数的角度看： x j 0 1.
b
i
可行解（Feasible Solution)： 满足约束条件(1.5)和(1.6)的 解X=(x1,x2,…,xn)T称为可行解。所有可行解构成可行解集， 即可行域。 最优解(Optimal Solution): 而使目标函数达到最大值的可 行解称为最优解，对应的目标函数值称为最优值。 求解LP问题就是求其最优解和最优值，但从代数的角 17 度去求是困难的。 目录

运筹学第1章：线性规划问题及单纯型解法


原料甲 原料乙 最低含量 VA 0.5 0.5 2 VB1 1.0 0.3 3 VB2 0.2 0.6 1.2 VD 0.5 0.2 2 0.3 0.5 单价
分别代表每粒胶丸中甲, 设 x1, x2分别代表每粒胶丸中甲, 乙两种原料的用量
5
例3,合理下料问题 , 分别代表采用切割方案1~8的套数, 的套数, 设 xj 分别代表采用切割方案 的套数
19
( f(x
)= 3
6
1.2.2 单纯型法的基本思路
确定初试基础可行解
检查是否为 最优解? 最优解?
是
求最优解的目标函数值
否 确定改善方向
求新的基础可行解
20
1.2.3 单纯型表及其格式
IV CB III XB II x1 b c1 a11 a21 c1′′= cn+1 xn+1 b1 c2′′= cn+2 xn+2 b2 x2 … xn c2 … cn a12 … a1n a22 … a2n I xn+1 cn+1 1 0 0 zn+1 xn+2 cn+2 0 1 0 zn+2 … … … … … … xn+m cn+m 0 0 1 zn+m
OBJ : max f ( x) = 6x1 + 4x2 2x1 + x2 ≤ 10 铜资源约束 x1 + x2 ≤ 8 铅资源约束 s.t. x2 ≤ 7 产量约束 x1, x2 ≥ 0 产量不允许为负值 最优解: x1 = 2, x2 = 6, max f ( x) = 36.
4
例2,配料问题(min, ≥) ,配料问题(
2 max 1 O 1 2 3 4 D 5 6 7 H 8

运筹学课件1-1线性规划问题及其数学模型

上页 下页 返回
• 第三步：确定目标函数 第三步： 以 Z 表示生产甲和乙两种产品各为x1 表示生产甲和乙两种产品各为x 时产生的经济价值， 和x2（吨）时产生的经济价值，总经济价值 最高的目标可表示为： 最高的目标可表示为：
max z＝7 x1十5 x2 z＝
这就是该问题的目标函数 这就是该问题的目标函数。 目标函数。
上页
下页
返回
• 第1步 -确定决策变量
•设 ——I x1——I的产量 ——II x2 ——II的产量
是问题中要确定的未知量， 是问题中要确定的未知量， 表明规划中的用数量表示的 方案、措施，可由决策者决 方案、措施， 定和控制。 定和控制。
x1
x2
上页
下页
返回
第2步 --定义目标函数
利润
Max Z =
x1 +
x2
上页
下页
返回
第2步 --定义目标函数
Max Z = 2 x1 + 3 x2
上页
下页
返回
对我们有 何限制?
上页
下页
返回
第3步 --表示约束条件
x1 + 2 x2 ≤ 8 4 x1 ≤ 16 4 x2 ≤ 12 x1、 x2 ≥ 0
设备 原材料A 原材料 原材料B 原材料 利润 I 1 4 0 2 II 2 0 4 3 资源限量 8 台时 16kg 12kg
上页 下页 返回
– 用向量表示
m Z = CX ax n ∑Pj xj = b i=1 x ≥ 0 j =1 2,...n , j 其 ： 中 x1 x 2 X= ... xn C = (c1, c2 , ) a1 j a2 j Pj = ... amj b 1 b 2 b= ... bm
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

③
约束方程②的系数矩阵
2 2 1 0 0 0
A 1 4
2 0
0 0
1 0
0 1
0 0
p1
p2
p3
p4
p5
p6
0 4 0 0 0 1
确定初始基B
1 0 0 0
产量分别为 x1、x2
项目
Ⅰ
设备 A（h） 0
设备 B（h） 6 调试工序（h） 1 利润（元） 2
Ⅱ 每天可用能力
5
15
2
24
1
5
1
问：应如何安排生产计划，才 能使总利润最大？
2.目标函数：设总利润为z，则
max z = 2 x1 + x2 3.约束条件：
5x2 ≤ 15
s.t.
6x1+ 2x2 ≤ 24 x1+ x2 ≤ 5
凸集
顶点
凸集
不是凸集
顶点：如果凸集C中不存在任何两个不同的点X1， X2，使X成为这两个点连线上的一个点。
（三）基本定理
定理1 若线性规划问题存在可行解，则问题的 可行域是一个凸集。
定理2 线性规划的基可行解对应线性规划问题 可行域（凸集）的顶点。
定理3 若线性规划问题有最优解，一定存在一个 基可行解是最优解。
(2)常数项bi＜0的转换：约束方程两边乘以（－1）。 (3) 约束方程的转换：由不等式转换为等式 。
aij xj bi aij xj bi
aij x j xni bi
xni 0 称为松弛变量
aij x j xni bi
xni 0 称为剩余变量
(4) 变量的变换
若存在取值无约束的变量 x，j可令
2x1
+ 2x3
≤ 34
s.t.
4x2 + 4x3 + 4x4 ≤ 52
25x1+20x2
＝200
40x3+20x4＝400
xj ≥ 0 （ j = 1,2,3,4）
2、线性规划数学模型的一般形式
目标函数： max (min)Z c1x1 c2 x2 cn xn ①
a11x1 a12 x2 a1n xn ( ) b1
——满足以上三个条件的数学模型称为线性规划
也可以记为如下形式：
目标函数： 约束条件：
n
max (min) Z c j x j j1
n
aij x j ( ) bi (i 1 2m)
j1
xj 0
(j 1 2n)
如将上例用表格表示如下：
设变量
x j ( j 1 2n)
产品 j
设 备1i
（二）数学模型
例4 某工厂生产A、B两种产品， 解：
有关资料如下表所示：
设：总成本为Z，A、B产品
工序 产品
A
C
工时
B 销售 报废 限制
工序 1 2 3 — — 12
工序 2 3 4 — — 24
单位利润 （百元）
4
10
3
－2
注：每生产单位产品 B 可得到 4 单位
副产品 C，据预测，市场上产品 C 的
（四）单纯形法迭代原理
基本思路：将模型的一般形式变成标准形式，再根 据标准型模型，从可行域中找一个基可行解，并判 断是否是最优。如果是，获得最优解；如果不是， 转换到另一个基可行解，当目标函数达到最大时， 得到最优解。
例:
m ax Z 2 x1 3 x2
2 x1 2 x2 12
x1 4 x1
2 x2
8 16
4 x2 12
x1 , x2 0
变成标准型
max Z 2x1 3x2 0x3 0x4 0x5 0x6 ①
2x1 2x2 x3
12
4xx11 2x2
x4 x5
8 16
②
4 x2
x6 12
x1 , x2 , x3 , x4 , x5 , x6 0
（二）数学模型
例5 某航运局现有船只种类、数量以及计划期内各条航线的货 运量、货运成本如下表所示：
航线号
船队 类型
1 1
2
3 2
4
拖轮
1 1 2 1
编队形式 A型 驳船 2
—
2 —
B型 驳船
—
4
4 4
货运成本 （千元／队）
36 36 72 27
货运量 （千吨）
25 20 40 20
船只种类
船只数
航线号
例：
max Z 2 x1 3 x2
2 x1 2 x2 12
⑴
x1 4 x1
2 x2
8 16
⑵ ⑶
4 x2 12
⑷
x1 0, x2 0
max Z 2 x1 3 x2
作图
x2
2 x1 2 x2 12
⑴
x1 4 x1
2 x2
8 16
⑵ ⑶
4 x2 12
⑷
x1 0, x2 0
最大销量为 5 单位，若产品 C 销售不
出去，则报废。
销量为x1、x2，产品C的销售
量为x3，报废量为x4，则：
max z = 4 x1 + 10 x2 + 3 x3
－ 2 x4
2x1 + 3x2
≤ 12
3x1 + 4x2
≤ 24
s.t.
- 4x2 +x3 + x4 = 0
x3 ≤ 5
x1、x2 、x3 、x4≥0
X 0
矩阵和向量形式：
a11 a1n
A
am1 amn
max (min) Z CX
AX ( ) b
X
0
（三）线性规划模型的标准形式1、标准形式源自max Z c j x j
x
j
aij x j 0
bi
(i 1 2m) (j1 2n )
将模型的一般形式变成标准形式，再根据标准型 模型，从可行域中找一个基本可行解，并判断是否是 最优。如果是，获得最优解；如果不是，转换到另一 个基本可行解，当目标函数达到最大时，得到最优解。
② 约束条件： am1x1 am2 x2 amn xn ( ) bm
x1 0 xn 0
③
模型特点
1 都用一组决策变量X = (x1,x2,…,xn)T表示某一方案，且 决策变量取值非负； 2 都有一个要达到的目标，并且目标要求可以表示成 决策变量的线性函数；
3 都有一组约束条件，这些约束条件可以用决策变量 的线性等式或线性不等式来表示。
解: 用 x4 替x换5 ，且x3 x，4 , x5 0
引入变量 x6 , x7
将第3个约束方程两边乘以（－1） 将极小值问题反号，变为求极大值
标准形式如下：
max Z 2 x1 x2 3( x4 x5 ) 0 x6 0 x7
5 x1 x2 ( x4 x5 ) x6 7
（一）解题步骤
1 在直角平面坐标系中画出所有的约束等式，并找出所 有约束条件的公共部分，称为可行域，可行域中的点称 为可行解。
2 标出目标函数值增加的方向。
3 若求最大（小）值，则令目标函数等值线沿（逆）目 标函数值增加的方向平行移动，找与可行域最后相交的 点，该点就是最优解。
4 将最优解代入目标函数，求出最优值。
合同货运量
拖轮
30
A型驳船
34
B型驳船
52
1
200
2
400
问：应如何编队，才能既完成合同任务，又使总货运成本为 最小？
解：
设：xj为第j号类型船队的队数（j = 1，2，3，4）， z 为总货运成本
则： min z = 36x1 + 36x2 + 72x3 + 27x4
x1 + x2 + 2x3 + x4 ≤ 30
2、特征：
⑴ 目标函数为求极大值，也可以用求极小值； ⑵ 所有约束条件（非负条件除外）都是等式，右 端常数项为非负； ⑶ 变量为非负。
3、转换方式： ⑴ 目标函数的转换
如果是求极小值即 min Z ，则c可j x j将目标函数乘以
（－1），可化为求极大值问题。
也就是：令Z Z ，可得到下式
∑ 即 maxZ′= － cj xj
(1)线性规划问题解的情况：惟一最优解；无穷 多最优解；无界解；无可行解
(2)线性规划问题的可行域是凸集（凸多边形）
(3)最优解一定是在凸集的某个顶点
(4)解题思路是，先找出凸集的任一顶点，计算 其目标函数值，再与周围顶点的目标函数值比 较，如不是最大，继续比较，直到找出最大为 止。
三、线性规划的单纯形法
∴ Xj 为基变量，否则为非基变量。
⑷基解：满足条件②，但不满足条件③的
所有解，最多为
个。C
m n
⑸基可行解：满足非负约束条件的基解，
简称基可行解。
⑹可行基：对应于基可行解的基称为可行基。
可 行 解
非可行解
基解
基可行解
（二）凸集及其顶点
凸集：如果集合C中任意两个点X1，X2,其连线上 的所有点也都是集合C中的点，称C为凸集。
⑶
⑷
(4 2)
1 234 56
0 1 234 5678
x1
⑵
⑴
∴ 最 优 解：x1 = 4 x2 = 2 最 优 值：Z = 14
有惟一最优解
（二）线性规划问题解的情况
惟一解 无穷解 无界解 无可行解
例：
max Z x1 2 x2
x1 2 x2 6 ⑴
3
x1
2 x2 x2
12 2
⑵ ⑶
x1 x2 ( 5 x1 x2