西工大,西电 孙肖子版 模电 第五章 连续系统复频域分析--答案

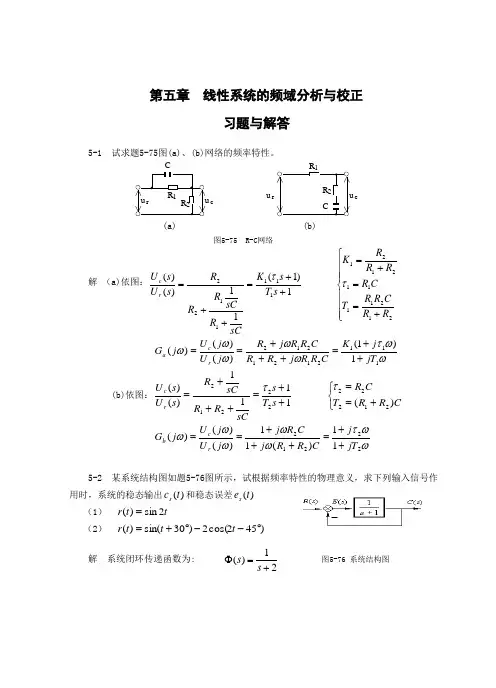
第五章 线性系统的频域分析与校正习题与解答5-1 试求题5-75图(a)、(b)网络的频率特性。

u rR 1u cR 2CCR 2R 1u ru c(a) (b)图5-75 R-C 网络解 （a)依图：⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(R R C R R T C R RR R K s T s K sCR sC R R R s U s U r c ττ ωωτωωωωω11121212121)1()()()(jT j K C R R j R R C R R j R j U j U j G r c a ++=+++==(b)依图：⎩⎨⎧+==++=+++=C R R T CR s T s sCR R sCR s U s U r c)(1111)()(2122222212ττ ωωτωωωωω2221211)(11)()()(jT j C R R j C R j j U j U j G r c b ++=+++==5-2 某系统结构图如题5-76图所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出)(t c s 和稳态误差)(t e s （1） t t r 2sin )(=（2） )452cos(2)30sin()(︒--︒+=t t t r 解 系统闭环传递函数为: 21)(+=Φs s 图5-76 系统结构图频率特性: 2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=系统误差传递函数: ,21)(11)(++=+=Φs s s G s e 则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e（1）当t t r 2sin )(=时, 2=ω，r m =1则 ,35.081)(2==Φ=ωωj ο45)22arctan()2(-=-=j ϕο4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω )452sin(35.0)2sin()2(οο-=-Φ=t t j r c m ss ϕ)4.182sin(79.0)2sin()2(ο+=-Φ=t t j r e e e m ss ϕ （2） 当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωωο5.26)21arctan()1(45.055)1(-=-===Φj j ϕ ο4.18)31arctan()1(63.0510)1(====Φj j e e ϕ )]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m s ϕϕ+-⋅Φ-++⋅Φ=οο)902cos(7.0)4.3sin(4.0οο--+=t t)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m s ϕϕ+-⋅Φ-++⋅Φ=οο )6.262cos(58.1)4.48sin(63.0οο--+=t t5-3 若系统单位阶跃响应 )0(8.08.11)(94≥+-=--t e e t h tt试求系统频率特性。

模拟电路第五章课后习题答案案场各岗位服务流程销售大厅服务岗：1、销售大厅服务岗岗位职责：1)为来访客户提供全程的休息区域及饮品;2)保持销售区域台面整洁;3)及时补足销售大厅物资,如糖果或杂志等;4)收集客户意见、建议及现场问题点；2、销售大厅服务岗工作及服务流程阶段工作及服务流程班前阶段1）自检仪容仪表以饱满的精神面貌进入工作区域2）检查使用工具及销售大厅物资情况，异常情况及时登记并报告上级。

班中工作程序服务流程行为规范迎接指引递阅资料上饮品（糕点）添加茶水工作要求1）眼神关注客人，当客人距3米距离时，应主动跨出自己的位置迎宾，然后侯客迎询问客户送客户注意事项15度鞠躬微笑问候：“您好！欢迎光临！”2）在客人前方1-2米距离领位，指引请客人向休息区，在客人入座后问客人对座位是否满意：“您好！请问坐这儿可以吗？”得到同意后为客人拉椅入座“好的，请入座！”3）若客人无置业顾问陪同，可询问：请问您有专属的置业顾问吗？，为客人取阅项目资料，并礼貌的告知请客人稍等，置业顾问会很快过来介绍，同时请置业顾问关注该客人；4）问候的起始语应为“先生-小姐-女士早上好，这里是XX销售中心，这边请”5）问候时间段为8:30-11:30 早上好11:30-14:30 中午好 14:30-18:00下午好6）关注客人物品，如物品较多，则主动询问是否需要帮助（如拾到物品须两名人员在场方能打开，提示客人注意贵重物品）；7）在满座位的情况下，须先向客人致歉，在请其到沙盘区进行观摩稍作等待；阶段工作及服务流程班中工作程序工作要求注意事项饮料（糕点服务）1）在所有饮料（糕点）服务中必须使用托盘；2）所有饮料服务均已“对不起，打扰一下，请问您需要什么饮品”为起始；3）服务方向：从客人的右面服务；4）当客人的饮料杯中只剩三分之一时，必须询问客人是否需要再添一杯，在二次服务中特别注意瓶口绝对不可以与客人使用的杯子接触；5）在客人再次需要饮料时必须更换杯子；下班程序1）检查使用的工具及销售案场物资情况，异常情况及时记录并报告上级领导；2）填写物资领用申请表并整理客户意见；3）参加班后总结会；4）积极配合销售人员的接待工作，如果下班时间已经到，必须待客人离开后下班；1.3.3.3吧台服务岗1.3.3.3.1吧台服务岗岗位职责1）为来访的客人提供全程的休息及饮品服务；2）保持吧台区域的整洁；3)饮品使用的器皿必须消毒；4）及时补充吧台物资；5）收集客户意见、建议及问题点；1.3.3.3.2吧台服务岗工作及流程阶段工作及服务流程班前阶段1）自检仪容仪表以饱满的精神面貌进入工作区域2）检查使用工具及销售大厅物资情况，异常情况及时登记并报告上级。

第五章 连续系统的s 域分析一、单项选择题X5.1（浙江大学2002年考研题）)()cos(0t t εω的拉氏变换为 。

（A ）[])()(200ωωδωωδπ-++ （B ）[])()(00ωωδωωδπ-++（C ）202ω+s s （D ）220ωω+s X5.2（北京邮电大学2004年考研题）信号⎰-=td t h t f 0)()(τττ的拉氏变换为 。

（A ）)(1s H s （B ）)(12s H s （C ）)(13s H s （D ）)(14s H sX5.3（北京邮电大学2003年考研题）信号)()(2t e t f tε=的拉氏变换及收敛域为 。

（A ）2]Re[,21)(->+=s s s F （B ）2]Re[,21)(-<-=s s s F （C ）2]Re[,21)(>-=s s s F （D ）2]Re[,21)(<+=s s s FX5.4（北京邮电大学2003年考研题）已知某信号的拉氏变换αα+=+-s e s F Ts )()(，则该信号的时间函数为（A ）)()(T t e T t ---εα （B ）)(T t e t --εα（C ）)(αεα--t et（D ）)()(T t e t ---εααX5.5（西安电子科技大学2005年考研题）单边拉普拉斯变换4)(2+=-s se s F s的原函数是 。

（A ）)1()2sin(-t t ε （B ）)1()1(2sin --t t ε （C ）)1()1(2cos --t t ε （D ）)1()2cos(-t t εX5.6（西安电子科技大学2001年考研题）单边拉普拉斯变换se ss s F 2212)(-+=的原函数是 。

（A ）)(t t ε （B ）)2(-t t ε （C ）)()2(t t ε- （D ）)2()2(--t t ε X5.7（东南大学2000年考研题）若线性时不变因果系统的H (j ω)，可由其系统函数H (s )将其中的s 换成j ω来求取，则要求该系统函数H (s )的收敛域应为 。

五章 习 题5.1 求下列各时间函数()t f 的像函数()s F 。

(1) ()()()t U e t f at--=1 (2) ()()()t U t t f φω+=sin(3) ()()()t U at e t f at-=-1 (4)()()()t U e a t f at --=11(5)()()t U t t f 2= (6) ()()()()t t U t t f δ32++= (7) ()()t tU t t f ωcos = (8)()()()t U at e t f at 1-+=-答案5.2 求下列各像函数()s F 的原函数()t f 。

(1) ()()()()()4231++++=s s s s s s F (2) ()()()126516222++++=s s s s s F(3) ()2399222++++=s s s s s F (4) ()()ss s s s F 2323++=答案(1)42)(321++++=s K s K s K s F83)4)(2()3)(1(01=⨯++++==s s s s s s s K41)2()4)(2()3)(1(22=+++++=-=s s s s s s s K83)4()4)(2()3)(1(43=+++++=-=s s s s s s s K48324183)(++++=s s s s F )()834183()(42*t U e e t f t t -++=(2)1245152393425121232)(321+++-++=+++++=s s s s K s K s K s F )()45152934512()(1232t U e e e t f tt t ---+-=(3)21122)2)(1(532)(++++=++++=s s s s s s F)()2()(2)(2t U e e t t f tt --++=δ (4)24111)2)(1(23123)(22+-++=+++-=++=s s s s s s s s s F )()4()()(2t U e e t t f tt ---+=δ5.3 求下列各像函数()s F 的原函数()t f 。

第五章 放大电路的频率响应自 测 题一、选择正确答案填入空内。

（1）测试放大电路输出电压幅值与相位的变化，可以得到它的频率响应，条件是 。

A.输入电压幅值不变，改变频率B.输入电压频率不变，改变幅值C.输入电压的幅值与频率同时变化（2）放大电路在高频信号作用时放大倍数数值下降的原因是 ，而低频信号作用时放大倍数数值下降的原因是 。

A.耦合电容和旁路电容的存在B.半导体管极间电容和分布电容的存在。

C.半导体管的非线性特性D.放大电路的静态工作点不合适（3）当信号频率等于放大电路的f L 或f H 时，放大倍数的值约下降到中频时的 。

A.0.5倍B.0.7倍C.0.9倍 即增益下降 。

A.3dBB.4dBC.5dB （4）对于单管共射放大电路，当f ＝ f L 时，与相位关系是 o U &iU &。

A.＋45˚B.－90˚C.－135˚当f ＝ f H 时，与的相位关系是 oU &i U &。

A.－45˚ B.－135˚ C.－225˚ 解：（1）A （2）B ，A （3）B A （4）C C二、电路如图T5.2所示。

已知：V C C ＝12V ；晶体管的C μ＝4pF ，f T = 50MHz ，＝100Ω, β'bb r 0＝80。

试求解： （1）中频电压放大倍数； smu A & （2）；'πC （3）f H 和f L ；（4）画出波特图。

图T5.2解：（1）静态及动态的分析估算： ∥178)(mA/V2.69k 27.1k 27.1k 17.1mV26)1(V 3mA 8.1)1(Aμ 6.22c m bee b'i s ismTEQ m b be i e b'bb'be EQe b'c CQ CC CEQ BQ EQ bBEQCC BQ −≈−⋅+=≈=Ω≈=Ω≈+=Ω≈+=≈−=≈+=≈−=R g r r R R R A U I g R r R r r r I r R I V U I I R U V I u &ββ（2）估算：'πCpF1602)1(pF214π2)(π2μc m 'μTe b'0μπe b'0T ≈++=≈−≈+≈C R g C C C f r C C C r f πππββ（3）求解上限、下限截止频率：Hz14)π(21kHz 175π21567)()(i s L 'πH s b b'e b'b s b b'e b'≈+=≈=Ω≈+≈+=CR R f RC f R r r R R r r R ∥∥∥（4）在中频段的增益为dB 45lg 20sm≈u A & 频率特性曲线如解图T5.2所示。

信号与系统分析（吴冰著）课后答案下载吴冰的《信号与系统分析》主要内容包括信号与系统的基本概念，信号与系统的时域分析，连续时间信号与系统的频域分析，连续时间系统的复频域分析，离散信号与系统的变换域分析。

以下是要与大家分享的信号与系统分析（吴冰著），供大家参考!点击此处下载???信号与系统分析（吴冰著）课后答案???丛书名 21世纪高等院校信息与通信工程规划教材——精品系列标准书号 ISBN978-7-115-26076-5编目分类 TN911.6作者解培中周波编著出版社人民邮电出版社蒋亮开本 16开印张 12.75字数 312千字页数 198页装帧平装版次第1版第1次初版时间 xx年9月本印次 xx年9月首印数 --册定价 27.00元本书系统介绍了信号与系统的基本概念、基本理论和基本分析方法，可作为普通高等院校信号与系统相关课程的教材使用，也可供工程技术人员参考。

第1章信号与系统的基本概念 11.1 信号的描述与分类 11.1.1 信号的定义与描述 11.1.2 信号的分类 21.2 系统的描述与分类 61.2.1 系统的概念 61.2.2 系统的数学模型 61.2.3 系统的分类 71.3 信号与系统分析概述 121.3.1 信号与系统分析的基本内容与方法 121.3.2 信号与系统理论的应用 13练习题 14第2章信号与系统的时域分析 172.1 典型连续时间信号 172.1.1 复指数信号 172.1.2 单位阶跃信号 182.1.3 单位冲激信号 192.1.4 冲激偶信号 232.1.5 斜坡信号 242.2 典型离散时间信号 242.2.1 复指数序列 252.2.2 单位脉冲序列 272.2.3 单位阶跃序列 282.3 连续时间信号的基本运算 29 2.3.1 替换自变量的运算 292.3.2 信号的导数与积分 312.3.3 信号的相加与相乘 322.4 离散时间信号的基本运算 33 2.4.1 替换自变量的运算 332.4.2 相加与相乘 342.4.3 差分与累加 352.5 信号的时域分解 362.5.1 交、直流分解 362.5.2 奇、偶分解 362.5.3 实部、虚部分解 372.5.4 脉冲分解 372.6 连续系统的冲激响应 392.6.1 冲激响应的定义 392.6.2 冲激响应的物理解释 39 2.6.3 冲激响应的求取 402.7 离散系统的单位脉冲响应 442.8 连续系统的零状态响应 462.8.1 卷积分析法的引出 472.8.2 确定卷积积分限的公式 472.8.3 卷积的图解 482.8.4 卷积积分的性质 512.9 离散系统的零状态响应 562.9.1 离散卷积的引出 562.9.2 离散卷积的性质 572.9.3 确定离散卷积求和限的公式 582.9.4 离散卷积的图解 592.9.5 离散卷积的列表计算 602.10 系统的全响应 60练习题 63第3章连续时间信号与系统的频域分析 74 3.1 周期信号分解为傅里叶级数 743.1.1 三角形式傅里叶级数 743.1.2 指数形式傅里叶级数 773.2 周期信号的频谱 793.2.1 周期信号的频谱 793.2.2 周期信号的频谱特点 823.2.3 周期信号的频带宽度 823.2.4 周期信号的功率谱 843.3 非周期信号的频谱密度函数——傅里叶变换 85 3.3.1 非周期信号的频谱密度函数 853.3.2 傅里叶变换 863.3.3 常用信号的傅里叶变换 873.4 傅里叶变换的性质及其应用 913.4.1 傅里叶变换的性质和应用 913.4.2 频谱资源的有限性与认知无线电 1003.5 希尔伯特变换及小波变换简介 1013.5.1 希尔伯特变换 1013.5.2 小波变换简介 1033.6 取样信号的频谱 1043.6.1 时域取样 1043.6.2 时域取样定理 1073.6.3 压缩感知简介 1083.7 连续时间系统的频域分析 1083.7.1 虚指数信号的响应 1083.7.2 正弦信号的响应 1093.7.3 直流信号的响应 1093.7.4 非正弦周期信号 1093.7.5 非周期信号的响应 1103.7.6 频域系统函数 1103.8 信号的无失真传输和理想滤波器 1123.8.1 信号的无失真传输 1123.8.2 理想滤波器 113练习题 114第4章连续时间系统的复频域分析 1204.1 拉普拉氏变换 1204.1.1 拉普拉氏变换的定义 1204.1.2 拉氏变换的收敛域 1214.1.3 常用信号的拉氏变换 1224.2 拉氏变换的性质 1234.3 拉氏反变换 1304.4 连续系统的复频域分析 1334.4.1 求解系统微分方程 1334.4.2 分析电路 1344.5 系统函数 1384.5.1 系统函数 1384.5.2 系统函数的零、极点图 1394.5.3 系统函数的零、极点分布与系统冲激响应的关系 140 4.5.4 系统的稳定性 1424.6 连续系统的模拟 1434.6.1 基本运算器 1434.6.2 连续系统的模拟 144练习题 149第5章离散信号与系统的变换域分析 153 5.1 Z变换 1535.1.1 从拉氏变换到Z变换 1535.1.2 Z变换的定义 1545.1.3 Z变换的收敛域 1555.1.4 常见信号的Z变换 1565.2 Z变换的性质 1575.3 Z反变换 1665.3.1 幂级数展开法 1665.3.2 部分分式展开法 1675.4 离散系统的Z变换分析 1695.5 离散系统函数与系统特性 1745.6 离散系统的模拟 1765.6.1 基本运算器 1765.6.2 离散系统的模拟 176练习题 178附录1 常用信号的傅里叶变换 182附录2 傅里叶变换的基本性质 183附录3 常用信号的拉氏变换 184附录4 拉氏变换的基本性质 185附录5 常用序列的Z变换 186附录6 Z变换的性质 188附录7 信号与系统常用数学公式 189部分练习题参考答案 1901.信号与系统考试题及答案2.信号与系统答案-阳光大学生网3.信号与系统第三版段哲民课后答案西北工业大学出版社4.电力系统分析第二版(孟祥萍著)课后答案下载。

第四章 习题4-1 求图题4-1所示电路的频域系统函数)()()(12ωωωj U j U j H =。

答案解：频域电路如图题4-1（b)所示。

R L j LC j U j U j H ωωωωω+-==21211)()()(4-1 求图题4-2所示电路的频域系统函数)()()(1ωωωj F j U j H c =,)()()(2ωωωj F j I j H =及相应的单位冲激响应)(1t h 与)(2t h 。

答案解： 频域电路如图题4-2(b)所示。

RC j RCj F j U j H c 111)()()(1+⨯==ωωωω)111(1)()()(2RC j RCRj F j I j H +-⨯==ωωωω)(1)]([)(1111t U e RC j H F t h tRC --==ω)(1)(1)]([)(12212t U e C R t R j H F t h t RC ---==δω4-3 图题4-3所示电路，V t U t U e t f t )](2)(10[)(+=-。

求关于)(t i 的单位冲激响应)(t h 和零状态响应)(t i 。

答案解： 频域电路如图题4-3(b)所示。

2121)()()(+⨯==ωωωωj j F j I j H所以A t U e t h t)(21)(2-=]1)([211525.5)()()(ωωπδωωωωωj j j j F j H j I +++++-==所以 At U t U e e t i t t )(21)()55.5()(2++-=--4-4 已知频域系统函数235)(22++-++-=ωωωωωj j j H ，激励)()(3t U e t f t-=。

求零状态响应)(t y 。

答案解：31)(+=ωωj j F)2)(1(31)(++++=ωωωωj j j j H211131)()()(+-+++==ωωωωωωj j j j F j H j Y所以 )()()(23t U e e e t y t t t----+=4-5 已知频域系统函数65)(2++-=ωωωωj j j H ，系统的初始状态,2)0(=y 1)0(='y ，激励)()(t U e t f t -=。

第5章习题答案1. 概念题：（1）反馈有时将输出的全部都馈送到输入端，其典型的例子是射极跟随器放大器和源极跟随器放大器。

（2）电压反馈时，反馈网路输出一定是电压吗？（不一定）并联反馈时，反馈网路的输出一定是电流吗？（是）（3）“负反馈有用，正反馈没用”这种说法对吗？（不对）按照输入端的信号耦合方式和输出端的信号取样方式负反馈共有 4 种组合形式。

（4）当希望稳定输出电压并且希望提高输入阻抗时，应引入电压串联负反馈；当负载需要恒定电流并且信号源也为电流型时，应引入电流并联负反馈；当希望稳定输出电压并且信号源为电流型时，应引入电压并联负反馈；当输入为电压信号并且输出为电流信号时，应引入电流串联负反馈。

（5）为了稳定电路的静态工作点，应引入直流负反馈；为了改善电路的动态特性，应引入交流负反馈。

（6）方框图法是分析负反馈放大器的最基本的方法，在求解A 和F 时保持F 网路的空载效应是非常重要的。

（7）有人说：“不使用反馈技术，要设计具有精密增益、高稳定度的放大器简直难于上青天”，你觉得对吗？（对）（8）设计电压电流转换电路可直接选用电流串联负反馈电路；设计电流电压转换电路可直接选用电压并联负反馈电路。

（9）如果开环放大器由3级以上的单管放大器组成，则组成的负反馈电路有可能出现自激的现象，这是因晶体管结电容形成的移相造成的。

（10）共基放大器比共射放大器频率响应好，这是因为在共基接法下，集基电容不产生加倍的米勒效应。

（11）分析放大器时，按低频段、中频段及高频段分开讨论，不但计算简单，而且意义明确。

（12）当信号频率较高时，有些负反馈放大器是不稳定的，此时可采用滞后补偿法、超前补偿法等方法进行补偿。

（13）开环放大器A 和反馈网路F 可能有量纲，例如欧姆或西门子，但环路增益是没有量纲的。

2. 电路图如图5-58所示。

（1）判断各电路中是否引入了反馈，对于引入反馈者试判断电路引入了什么性质的反馈，这些性质包括直流反馈、交流反馈、交直流反馈、局部反馈、全局反馈、电压反馈、电流反馈、串联反馈、并联反馈、正反馈、负反馈，设图中所有电容对交流信号均可视为短路；（2）就整体反馈而言，你认为哪些电路引入了深度负反馈，请写出其反馈系数表达式和闭环增益表达式。

习题5.1 填空题1.振荡器，是指通过 振荡 的方式产生周期性信号的电路。

2. 振荡器种类很多，按振荡波形分，可以分为正弦波和非正弦振荡器。

3. 自激振荡，是指 指不需要外界刺激就能产生输出信号的 的振荡现象。

4.振荡条件包括 平衡条件 和 起振条件 。

5. 正弦波振荡电路主要由四部分组成： 选频网络 、放大环节、 正反馈网络 和稳幅环节。

6. 正弦波振荡电路按照选频网络来分类，可以分为：RC 振荡电路、LC 振荡电路和石英晶体振荡电路。

7. 常见的非正弦波有 矩形波 、三角波、 锯齿波、梯形波等。

8.函数发生器，是指 能够自动产生多种波形（一般包括正弦波、方波、三角波等波形） 的电路或者仪器。

5.2 选择题1.振荡器的起振条件是（B ）。

A B2.振荡器的平衡条件是（B ）。

A B 3.RC 振荡电路适用于（B ）范围。

A 高频B 低频4.LC 振荡电路适用于（ A ）范围。

A 高频B 低频5.石英晶体振荡器适用于（B ）范围。

A 高频B 低频6.方波经过（B ）可以转换成三角波。

1=F A 1>F A 1=F A1>F AA 微分电路B 积分电路5.3 判断题1.采用微分电路可以将三角波转换成锯齿波。

（×）2.采用滞回电压比较器可以产生方波。

（√）3.改变RC充放电时间，可以改变锯齿波的锯齿方向。

（√）5.4 分析计算题1.若反馈振荡器满足起振和平衡条件，则必然满足稳定条件，这种说法是否正确？为什么？解：不正确。

因为满足起振条件和平衡条件后，振荡由小到大并达到平衡。

但当外界因素（温度、电源电压等）变化时，平衡条件受到破坏。

若不满足稳定条件，振荡起就不会回到平衡状态，最终导致停振。

2.有一桥式RC振荡器，已知RC串并联电路中的电阻R=120kΩ，C=0.001μF，求振荡。

频率f解：略。

3. 试判断图5-36所示交流通路中，哪些可能产生振荡，哪些不能产生振荡。

若能产生振荡，则说明属于哪种振荡电路。

⾃动控制原理课后习题答案第五章第五章5-2 若系统单位阶跃响应为49()1 1.80.8t t h t e e --=-+试确定系统的频率特性。

分析先求出系统传递函数，⽤j ω替换s 即可得到频率特性。

解：从()h t 中可求得：(0)0,(0)0h h '==在零初始条件下，系统输出的拉普拉斯变换()H s 与系统输出的拉普拉斯变换()R s 之间的关系为()()()H s s R s =Φ?即()()()H s s R s Φ= 其中()s Φ为系统的传递函数，⼜1 1.80.836()[()]49(4)(9)H s L h t s s s s s s ==-+=++++1()[()]R s L r t s == 则()36()()(4)(9)H s s R s s s Φ==++ 令s j ω=，则系统的频率特性为()36()()(4)(9)H j j R j j j ωωωωωΦ==++5-7 已知系统开环传递函数为)1s T (s )1s T (K )s (G 12++-=;（Ｋ、Ｔ1、Ｔ2＞０）当取ω＝１时， o 180)j (G -=ω∠,|Ｇ(ｊω)|＝０.５。

当输⼊为单位速度信号时，系统的稳态误差为0.1，试写出系统开环频率特性表达式G(ｊω)。

分析：根据系统幅频和相频特性的表达式，代⼊已知条件，即可确定相应参数。

解：由题意知：()G j ω= 021()90arctan arctan G j T T ωωω∠=---因为该系统为Ⅰ型系统，且输⼊为单位速度信号时，系统的稳态误差为0.1，即 01()lim ()0.1ss s e E s K →∞===所以：10K = 当1ω=时，(1)0.5G j ==0021(1)90arctan arctan 180G j T T ∠=---=-由上两式可求得1220,0.05T T ==，因此10(0.051)()(201)j G j j j ωωωω-+=+5-14 已知下列系统开环传递函数(参数K 、T 、T2，…，６) (1) )1s T )(1s T )(1s T (K )s (G 321+++=(2))1s T )(1s T (s K )s (G 21++=(3))1Ts (s K )s (G 2+=(4))1s T (s )1s T (K )s (G 221++=(5)3s K)s (G = (6)321s )1s T )(1s T (K )s (G ++=(7))1s T )(1s T )(1s T )(1s T (s )1s T )(1s T (K )s (G 432165++++++= (8)1Ts K)s (G -=(9)1Ts K )s (G +--= (10))1Ts (s K )s (G -= 其系统开环幅相曲线分别如图5-6(1)～(10)所⽰，试根据奈⽒判据判定各系统的闭环稳定性，若系统闭环不稳定，确定其s 右半平⾯的闭环极点数。

西北工业大学《827信号与系统》重难点解析第1讲第一章信号与系统的基本概念一、信号的主要分类(1)连续时间信号：自变量的取值是连续的离散时间信号：自变量的取值是离散的(2)周期信号：具有周期性，且是无始无终信号非周期信号：不具有周期性(3)因果信号：t＜0时，f( t) ＝0；t＞0时，f( t) ≠0的信号非因果信号：t＞0时，f( t) ＝0的信号(4)功率信号：平均功率为有限值，能量趋近于无穷；能量信号：平均功率为0，能量为有限值的信号注意：(1)两个连续周期信号的和不一定是周期信号，只有当这两个信号的周期比为有理数时，该信号才是周期信号，且周期为原信号周期的最小公倍数；(2)直流信号和有界的周期信号均为功率信号；阶跃信号和有始周期信号也是功率信号；有界的非周期信号均为能量信号；无界的周期信号和无界的非周期信号均为非功率非能量信号。

一个信号只能是功率信号和能量信号两者之一，不会两者都是，但可以两者都不是，也就是非周期非能量信号。

【例1】判断下列各信号是否为周期信号后，若为周期信号，求出其周期。

(1)f( t) ＝cos8t－sin12t(2)f(k) ＝cos k＋2sin2πk解：(1) T1＝＝T2＝＝由于＝，故f( t)为周期信号，其周期为T1和T2的最小公倍数，即T＝(2) cos k为周期信号，N1＝＝842π2π故f(k)为周期信号，为N1和N2的最小公倍数，即N＝8个间隔2cos2πk为周期信号，N2＝＝1三、δ(t )和 δ′( t ) 函数的性质【例 2】 (3t －2)[ δ(t ) ＋ δ(t －2) ]dtt 2 －2t ＋ 3) δ＇( t －2)dt(3t －2) δ(t －2)dt＝ －2 ＋ (3 ×2 －2) ＝ 2(2) 原式 ＝ － ( t 2 ＋ 3 －2t ) ＇ t ＝2 ＝ － (2t －2) t ＝2 ＝ －2四、系统的分类(1)线性系统：同时满足齐次性和叠加性的系统 非线性系统：不能同时满足以上两个条件的系统 (2)时不变系统：满足时不变的系统 时变系统：不满足时不变的系统(3)因果系统：响应不产生激励之前的系统 非因果系统：响应产生于激励之前的系统(4)稳定系统：系统的激励有界，响应也有界的系统 非稳定系统：系统的激励有界，响应无界的系统【例 3】 已知系统：a ：y ( t ) ＝2f ( t ) ＋3 b ：y ( t ) ＝f (2t ) c ：y ( t ) ＝f ( －t ) d ：y ( t ) ＝tf ( t ) 试判断上述哪些系统满足下列条件： (1)不是线性系统的是： (2)不是稳定系统的是： (3)不是时不变系统的是： (4)不是因果系统的是：解：(1) a (2)d (3)b ，c ，d (4)b ，c五、线性时不变系统的性质f ( t ) →y ( t )，f 1 ( t ) →y 1 ( t )，f 2 ( t ) →y 2 ( t )， A 1，A 2，A 为任意常数，常见性质如下： 1．齐次性：Af ( t ) →Ay ( t )2．叠加性：f 1 ( t ) ＋f 2 ( t ) →y 1 ( t ) ＋y 2 ( t )5 555西北工业大学《827 信号与系统》重难点解析3．线性：A 1f 1 ( t ) ＋A 2f 2 ( t ) →A 1 y 1 ( t ) ＋A 2 y 2 ( t ) 4．时不变性：f ( t －τ) →y ( t －τ) 5．微分性：→6．积分性：)d τ→)d τ【例 4】 一阶系统的初始状态为 y (0 － )，激励与响应分别为f ( t )，y ( t ) 。

微波电子线路习题(3-2)(1)分析：电路a 、b 线路相同，信号、本振等分加于二管，混频电流叠加输出，1D 、2D 两路长度差4λ，是典型的双管平衡混频器电路。

但a 、b 两路本振、信号输入位置互换。

在a 电路中，本振反相加于两管，信号同相加于两管，为本振反相型平衡混频器。

B 电路则为信号反相型平衡混频器。

（2）电流成分①a 电路输出电流成分：*中频分量 1,0=-=n t s ωωω *和频分量 1,=+=+n t s ωωω*本振噪声 ()πωω-==t v u t v u nl nl n nl nl n cos ,cos 21 *外来镜频干扰s l s ωωω-=2/t v g i i i i s i i i 0/1/2/1/cos 2ω=-= 不能抵消，二倍输出。

*镜频分量 2,2=-=n s l i ωωω0=io i 镜频输出抵消，但流过输入回路，在源电阻上损耗能量。

*高次分量n 奇数 两路相差πn 反相 输出叠加 n 偶数 两路相差πn 2 同相 输出抵消 ②b 电路输出电流成分：()111s u t g i =，()222s u t g i =*中频分量 1,0=-=n t s ωωω *和频分量 1,=+=+n t s ωωω*本振噪声 ()πωω-==t v u t v u nl nl n nl nl n cos ,cos 21 *外来镜频干扰s l s ωωω-=2/t v g i i i i s i i i 0/1/2/1/cos 2ω=-= 不能抵消，二倍输出。

()t v g t v g i io s l s s i ωωωcos cos /1//1/1=-=()t v g t v g i io s l s s i ωωωcos cos /1//1/1=-=*镜频分量 2,2=-=n s l i ωωω12i io i i = 镜频输出不能抵消，也会流过输入回路，在源电阻上损耗能量。