当前位置：文档之家 › 北航研究生数理统计第二次大作业-聚类分析

北航研究生数理统计第二次大作业-聚类分析

  • 格式：pdf
  • 大小：730.13 KB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

聚类分析 -发给研究生学习用

聚类分析 -发给研究生学习用

聚类分析基本原理及其案例一、相似度的测量聚类分析是分析如何对样品（或变量）进行量化分类的问题。

通常聚类分析分为Q 型聚类和R 型聚类。

Q 型聚类是对样品进行分类处理，R 型聚类是对变量进行分类处理。

1.1 样品相似性的度量在聚类分析之前，首先要分析样品间的相似性。

Q 型聚类分析，常用距离来测度样品之间的相似程度。

每个样品有p 个指标（变量）从不同方面描述其性质，形成一个p 维的向量。

如果把这n 个样品看成p 维空间中的n 个点，则两个样品间的相似程度就可用p 维空间中的亮点距离公式来度量。

两点距离公式可以从不同角度进行定义，令ij d 表示样品i X 与j X 的距离，存在以下的距离公式。

1.1.1 闵科夫斯基距离1/1()(||)pq q ij ik jk k d q X X ==-∑闵科夫斯基距离又称闵氏距离，按q 值的不同又可分成 1）绝对距离（1q =）1(1)||pij ik jk k d X X ==-∑2）欧几里得距离（2q =）21/21(2)(||)pij ik jk k d X X ==-∑3）切比雪夫距离（q =∞）1()max ||ij ik jk k pd X X ≤≤∞=-欧几里得距离较为常用，但在解决多元数据的分析问题时，他就显得不足。

一是他没有考虑到总体变异对“距离”远近的影响，显然一个变异程度大的总体可能与更多样品近些，即使他们的欧几里得距离不一定最近；另外，欧几里得距离收到变量的量纲影响，这对多元数据的处理时不利的。

为了克服这方面的不足，可用“马氏距离“的概念。

1.1.2 马氏距离设i X 与j X 是来自均值向量为μ，协方差为Σ（>0）的总体G 中的p 维样品，则两个样品间的马氏距离为21()()'()ij i j i j d M -=--X X ΣX X马氏距离又称为广义欧几里得距离。

显然，马氏距离与上述各种距离的主要不同时它考虑了观测变量之间的关联性。

北航数值分析大作业二(纯原创,高分版)

北航数值分析大作业二(纯原创,高分版)
(R_4 ,I_4 )=( 1.590313458807e+000, 0.000000000000e+000)
(R_5 ,I_5 )=(-1.493147080915e+000, 0.000000000000e+000)
(R_6 ,I_6 )=(-9.891143464723e-001, 1.084758631502e-001)
-0.8945216982
-0.0993313649
-1.0998317589
0.9132565113
-0.6407977009
0.1946733679
-2.3478783624
2.3720579216
1.8279985523
-1.2630152661
0.6790694668
-0.4672150886
6.220134985374e-001
-1.119962139645e-001
-2.521344456568e+000
-1.306189420531e+000
-3.809101150714e+000
8.132800093357e+000
-1.230295627285e+000
-6.753086301215e-001
而其本质就是
1.令 以及最大迭代步数L；
2.若m≤0，则结束计算，已求出A的全部特征值，判断 或 或m≤2是否成立，成立则转3，否则转4；
3.若 ，则得一个特征值 ，m=m-1，降阶；若 ，则计算矩阵：
的特征值得矩阵A的两个特征值，m=m-2，降阶，转2.；
4.若k≤L，成立则令
k=k+1，转2，否则结束计算，为计算出矩阵A的全部特征值；

聚类分析

聚类分析

K作为聚类个数。
7
层次类算法
1. 2. 3. 4.
早期聚合或分裂一旦形成，后期无法优化。 输入顺序敏感，不利于增量挖掘。 计算复杂度高。 簇间层次关系清晰，不须预先确定簇个数。
8
密度类算法: DBSCAN
算法参数: 最小密集区点数, 半径
1. 噪音鲁棒，擅于剔出噪音。 2. 簇形状各异，不受球形限制。 3. 时间复杂度较低，适用于对象数量多的数据。 4. 参数不易确定，且直接影响聚类结果。.
5
划分类算法：K-Means
1. 2. 3. 4.
必须预先确定聚类个数K 对噪音点敏感 只能挖掘球形簇 计算复杂度高
6
基于K-means算法的改进

噪音敏感：K-Medoids用真实对象代替簇均值作
为中心点。

数据量大：CLARANS只对采样数据聚类。
K值难确定：X-Means 选用指定数值区间的最优
17
QHB: 挖掘实例
18
知识小结

数据预处理的必要性：缺失值、噪音、值域差。 根据实际应用需求，杂交设计聚类算法。 属性的Байду номын сангаас择对聚类效果有重要影响，过多冗余 无关属性会扰乱聚类结果，可考虑属性筛选或 采用子空间多向聚类。
19
Noise Incremental clustering and insensitive to input order High dimensionality Constraint-based clustering Interpretability and usability
4
全空间聚类: 基于全局属性
3
Challenge

北航数理统计大作业2-聚类与判别分析

北航数理统计大作业2-聚类与判别分析

应用数理统计作业二学号：姓名：电话：二〇一四年十二月对NBA球队的聚类分析和判别分析摘要：NBA联盟作为篮球的最高殿堂深受广大球迷的喜爱，联盟的30支球队大家也耳熟能详，本文选取NBA联盟30支球队2013-2014常规赛赛季场均数据。

利用spss软件通过聚类分析对27个地区进行实力类型分类，并利用判断分析对其余3支球队对分类结果进行验证。

可以看出各球队实力类型与赛季实际结果相吻合。

关键词：聚类分析，判别分析，NBA目录1. 引言 (4)2、相关统计基础理论 (5)2.1、聚类分析 (5)2.2，判别分析 (6)3.聚类分析 (7)3.1数据文件 (7)3.2聚类分析过程 (9)3.3 聚类结果分析 (11)4、判别分析 (12)4.1 判别分析过程 (12)4.2判别检验 (17)5、结论 (20)参考文献 (21)致谢 (22)1. 引言1896年，美国第一个篮球组织"全国篮球联盟（简称NBL）"成立，但当时篮球规则还不完善，组织机构也不健全，经过几个赛季后，该组织就名存实亡了。

1946年4月6日，由美国波士顿花园老板沃尔特.阿.布朗发起成立了“美国篮球协会”（简称BAA）。

1949年在布朗的努力下，美国两大篮球组织BAA和NBL合并为“全国篮球协会”（简称NBA）。

NBA季前赛是 NBA各支队伍的热身赛，因为在每个赛季结束后，每支球队在阵容上都有相当大的变化，为了让各队磨合阵容，熟悉各自球队的打法，确定各队新赛季的比赛阵容、同时也能增进队员、教练员之间的沟通，所以在每个赛季开始之前，NBA就举办若干场季前赛，使他们能以比较好的状态投入到漫长的常规赛的比赛当中。

为了扩大NBA在全球的影响，季前赛有约三分之一的球队在美国以外的国家举办。

从总体上看，NBA的赛程安排分为常规赛、季后赛和总决赛。

常规赛采用主客场制，季后赛和总决赛采用七场四胜制的淘汰制。

[31]NBA常规赛从每年的11月的第一个星期二开罗，到次年的4月20日左右结束。

实验二聚类分析

实验二聚类分析

实验二聚类分析
聚类分析原理简介：聚类分析又称群分析，是一种数学分类的方法。

其基本思想如下首先认为所研究的对象存在不同的相似性，根据各种观测指标，找出一些能够度量样品之间相识程度的统计量，以此为依据，把一些相识程度大的聚为一类，关系疏远的聚合到更大的一个分类单位，直到所有的样品聚合完毕。

形成一个有小到大的分类系统，最后把分类系统用图形表示出来即是谱系图。

根据分类对象的不同又可以分为两类R型聚类和Q型聚类。

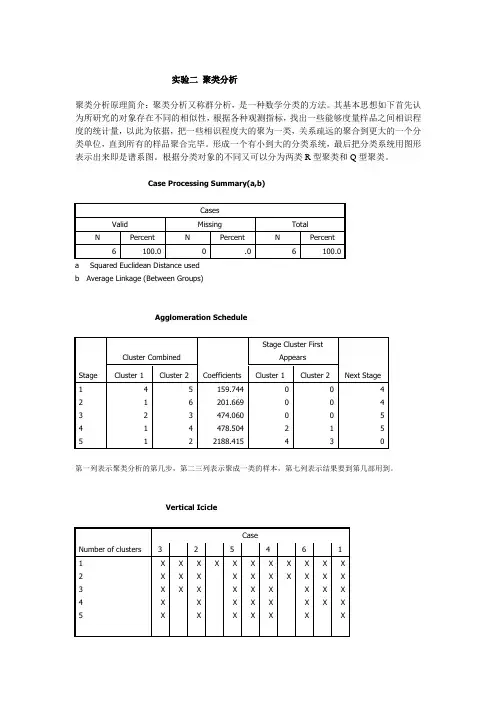
Case Processing Summary(a,b)
a Squared Euclidean Distance used
b Average Linkage (Between Groups)
Agglomeration Schedule
第一列表示聚类分析的第几步，第二三列表示聚成一类的样本，第七列表示结果要到第几部用到。

Vertical Icicle
样品分类冰柱图
Dendrogram
样品分类谱系图
可知样品分为三类，3、4为第一类，1、2为第二大类，5为孤立元素。

北航数理统计大作业 聚类分析

北航数理统计大作业 聚类分析

应用数理统计聚类分析与判别分析（第二次作业）学院：姓名：学号：2015年12月目录我国部分城市经济发展水平的聚类分析和判别分析................................. - 1 - 摘要：................................................................... - 1 -1. 引言 ................................................................ - 1 -2. 相关统计基础理论 .................................................... - 1 -2.1 聚类分析......................................................... - 1 -2.2 判别分析......................................................... - 2 -3. 模型建立 ............................................................ - 3 -3.1 设置变量......................................................... - 3 -3.2 数据收集和整理................................................... - 3 -4. 数据结果及分析 ...................................................... - 5 -4.1 聚类分析......................................................... - 5 -4.2 判别分析......................................................... - 7 -5. 结论 ............................................................... - 11 -参考文献................................................................ - 12 -我国部分城市经济发展水平的聚类分析和判别分析摘要：本文基于《中国统计年鉴》（2014年版）统计数据，统计全国各省市居民消费情况，包括各地区农村居民人均纯收入、农村居民人均现金消费、城镇居民人均可支配收入、城镇居民人均现金消费情况共4个指标，利用统计软件SPSS综合考虑各指标，对所选地区进行K-Means 聚类分析，利用Fisher 线性判别待判地区类型，进一步验证所建模型的有效性。

数理统计大作业聚类分析和判别分析

数理统计大作业（2）全国各省、市及自治区产业类型聚类分析和判别分析院（系）名称航空科学与工程学院专业名称飞行器设计与工程学生姓名熊蕾学号ZY15054022015年12月全国各省、市及自治区产业类型聚类分析和判别分析ZY1505402 熊蕾摘要本文从中国统计年鉴（2014）中获得了2013年按三次产业分地区生产总值的数据，按各省的第一产业、第二产业和第三产业产值所占地区生产总值的比值不同，对全国23个省、4个直辖市和5个少数民族自治区进行聚类分析和判别分析。

关键词经济类型聚类分析判别分析一、引言产业是指具有某种同类属性的经济活动的集合或系统，是经济社会的物质生产部门。

世界各国把各种产业划分为三大类：第一产业、第二产业和第三产业。

第一产业是指提供生产资料的产业，包括种植业、林业、畜牧业、水产养殖业等直接以自然物为对象的生产部门。

第二产业是指加工产业，利用基本的生产资料进行加工并出售，包括采矿业、制造业、电力、燃气和水的生产和供应业和建筑业。

第三产业又称服务业，它是指第一、第二产业以外的其他行业。

第三产业行业广泛。

包括交通运输业、通讯业、商业、餐饮业、金融保险业、行政、家庭服务等非物质生产部门。

我国区域经济发展不平衡，各地区的产业类型和产业结构不尽相同，因此可以以各省的第一产业、第二产业和第三产业产值所占地区生产总值的比值对全国的23个省、4个直辖市和5个少数民族自治区进行分类。

二、聚类分析2.1数据输入从中国统计年鉴中得到了2013年按三次产业分地区生产总值的数据，如下表所示，产值单位均为亿元，由于各省经济发展程度不同，地区生产总值有较大的差别，因此要算出各地区三大产业所占的比值来进行聚类和判别分析。

表 1 原始数据2.2聚类分析从表1中选出湖南、安徽和西藏三个地区的数据以待判别，对其余地区的数据进行聚类分析。

表 2 聚类分析数据将表2数据导入SPSS，进行系统聚类分析，得到以下结果：表 3 聚类表阶群集组合系数首次出现阶群集下一阶群集 1 群集 2 群集 1 群集 21 7 13 .052 0 0 92 6 12 .109 0 0 133 14 20 .174 0 0 54 3 21 .244 0 0 95 14 27 .336 3 0 166 5 24 .465 0 0 127 8 23 .602 0 0 198 11 17 .742 0 0 109 3 7 .952 4 1 1510 10 11 1.163 0 8 1711 18 28 1.381 0 0 1812 5 26 1.641 6 0 2013 4 6 1.977 0 2 1614 16 25 2.315 0 0 1815 3 15 2.673 9 0 2016 4 14 3.149 13 5 2317 2 10 3.678 0 10 2318 16 18 4.238 14 11 2119 8 22 4.814 7 0 2120 3 5 5.523 15 12 2521 8 16 6.429 19 18 2422 1 9 7.640 0 0 2623 2 4 9.318 17 16 2524 8 19 11.431 21 0 2625 2 3 14.946 23 20 2726 1 8 20.495 22 24 2727 1 2 26.551 26 25 0表4 群集成员案例8 群集7 群集 6 群集 5 群集 4 群集 3 群集1:北京 1 1 1 1 1 1 2:天津 2 2 2 2 2 2 3:河北 3 3 3 3 3 2 4:山西 4 4 4 2 2 2 5:内蒙古 3 3 3 3 3 2 6:辽宁 4 4 4 2 2 2 7:吉林 3 3 3 3 3 2 8:黑龙江 5 5 5 4 4 3 9:上海 6 6 1 1 1 1 10:江苏 2 2 2 2 2 2 11:浙江 2 2 2 2 2 2 12:福建 4 4 4 2 2 2 13:江西 3 3 3 3 3 2 14:山东 4 4 4 2 2 2 15:河南 3 3 3 3 3 2 16:湖北7 5 5 4 4 3 17:广东 2 2 2 2 2 2 18:广西7 5 5 4 4 3 19:海南8 7 6 5 4 3 20:重庆 4 4 4 2 2 2 21:四川 3 3 3 3 3 2 22:贵州 5 5 5 4 4 3 23:云南 5 5 5 4 4 3 24:陕西 3 3 3 3 3 2 25:甘肃7 5 5 4 4 3 26:青海 3 3 3 3 3 2 27:宁夏 4 4 4 2 2 2 28:新疆7 5 5 4 4 3图1聚类分析树状图从树状图中，我们定下聚类分析最终得到四个组别：1为北京和上海，可以看出这两个直辖市的总产值中，第三产业也就是服务业占有绝对优势，因此可将第一组作为第三产业为主的地区；2为天津、山西、江苏、广东等10个省份，这些省份的第二产业占有较多的比重，而第一产业仅占极少的比重，说明第2组以第二、三产业为主；第三组包括河北、河南、吉林、江西等省份，这些省份虽然也是第二产业占有的比重最大，但它们的第一产业的比重与第1、2组相比更多；第四组的各个地区是传统的鱼米之乡，可以看到它们的第一产业的比重大于其他各组。

北航研究生数理统计第二次大作业-聚类分析


Z 场均 角球数 0.11373 2.18400 -0.22977 0.02089 0.21585 0.09516 0.32725 -0.90749 -1.22314 0.51293 -0.44330 1.62698 -1.68732 0.32725 -0.83322 1.09780 1.37632 -1.83586 0.79144 1.09780 0.16943 0.94926 -1.68732 -0.13694 -0.75895 -0.50829 -0.13694 -0.44330 -1.37168
北京航空航天大学 数理统计第二次大作业
欧洲足球俱乐部竞技水平的聚类分析和判别分析
2015 年 12 月
欧洲足球俱乐部竞技水平的聚类分析和判别分析
摘要：近年来，人们对足球的关注越来越多。欧洲作为足球的发源地，其五大联 赛自然吸引着大批人的目光。尤其是欧洲冠军杯联赛更是代表着欧洲足球的最高 水平，吸引着各国最好的球队参加。本文从参加 2014-2015 赛季欧洲冠军杯联赛 的球队中选取 29 支球队，根据这些球队的一些技术统计资料，用 SPSS 软件对 其进行聚类分析，将这些球队按水平层次分为了 5 类。并选取 3 支球队，利用聚 类分析的结果对这 3 支球队进行判别分析。结果表明，聚类分类结果与判别分析 结果基本符合实际情况。
由于不同的变量之间存在着较大的数量级的差别，因此要对数据变量进行标
准化处理。本文采用 Z 得分值法标准化的方法进行标准化，用 x 的值减去 x 的
均值再除以样本的方差。也就是把个案转换为样本均值为 0、标准差为 1 的样本。
如果不同变量的变量值数值相差太大，会导致计算个案间距离时，由于绝对值较
小的数值权数较小，个案距离的大小几乎由大数值决定，标准化过程可以解决此

聚类分析实用


或变量时，两类间的相似系数即是两样品或
变量间的相d似ij 系ri数j 或
，按第一节的定
义计算。
第13页/共46页
当类内含有两个或两个以上样品或变量时，计算类 间相似系数有多种方法可供选择，下面列出5种计算 方法。用 G p，Gq 分别表示两类，各自含有np， nq个样品或变量。
37
13
第14页/共46页
第16页/共46页
3176
5．离差平方和法 又称Ward法，仅用于样 品聚类。 此法效仿方差分析的基本思想， 即合理的分类使得类内离差平方和较小，而 类间离差平方和较大。
第17页/共46页
317
例19-1 测量了3454名成年女子身高（X1）、下肢长 （X2）、腰围（X3）和胸围（X4），计算得相关矩阵：
绝对值越大表明两变量间相似程度越高。
(19-1)
同样也可考虑用Spearman秩相关系数定义非正
态变量之间的相似系数。当变量均为定性变量时，最好
用列联系数定义类间的相似系数。
第7页/共46页
样品聚类（Q型聚类）的聚类统计量（相似 系数）：2个样品间距离，越短越接近， 短则同类，长则异类。 样品聚类的基本原则：把距离短的样品归在 相同类，距离长的样品归在不同类。
以上定义的4种距离适用于定量变量，对于定性变量和 有序变量必须在数量化后方能应用。
第10页/共46页
说明：当样品各指标的单位不同时，或各指标单 位
虽相同（包括各指标都无单位），但数量级相差
大
时
，
应
先
将
各
指
xi'
标
xi xi
标准si化
，
在
计
算
距

北航数理统计第二次数理统计大作业 判别分析

数理统计大作业（二）全国各省发展程度的聚类分析及判别分析指导教师院系名称材料科学与工程院学号学生姓名2015 年 12 月21 日目录全国各省发展程度的聚类分析及判别分析 (1)摘要： (1)引言 (1)1实验方案 (2)1.1数据统计 (2)1.2聚类分析 (3)1.3判别分析 (4)2结果分析与讨论 (5)2.1聚类分析结果 (5)2.2聚类分析结果分析： (8)2.3判别分析结果 (9)2.4 Fisher判别结果分析： (11)参考文献： (16)全国各省发展程度的聚类分析及判别分析摘要：利用SPSS软件对全国31个省、直辖市、自治区(浙江、安徽、甘肃除外)的主要经济指标进行多种聚类分析，分析选择最佳聚类类数，并对浙江、湖南、甘肃进行类型判别分析。

通过这两个方法对全国各省进行发展分类。

本文选取了7项社会发展指标作为决定发展程度的影响因素，其中经济因素为主要因素，同时评估城镇化率和人口素质因素。

各项数据均来自2014年国家统计年鉴。

分析结果表明：北京市和上海市和天津市为同一类；江苏省和山东省和广东省为同一类型；河北、湖北、河南、湖南、四川、辽宁为同一类；其余的为另一类。

关键词：聚类分析、判别分析、发展引言聚类分析是根据研究对象的特征对研究对象进行分类的多元统计分析技术的总称。

它直接比较各事物之间的性质，将性质相近的归为一类，将性质差别较大的归入不同的类。

系统聚类分析又称集群分析，是聚类分析中应用最广的一种方法，它根据样本的多指标（变量）、多个观察数据，定量地确定样品、指标之间存在的相似性或亲疏关系，并据此连结这些样品或指标，归成大小类群，构成分类树状图或冰柱图。

判别分析是根据多种因素(指标)对事物的影响来实现对事物的分类，从而对事物进行判别分类的统计方法。

判别分析适用于已经掌握了历史上分类的每一个类别的若干样品，希望根据这些历史的经验（样品），总结出分类的规律性（判别函数）来指导未来的分类。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 数据采集与标准化处理
本文选取的数据来自新浪体育 2014-2015 赛季欧冠冠军杯联赛数据库。选取 2014-2015 赛季欧洲冠军杯联赛参赛球队中的 29 支球队的 7 项技术指标作为分类 的自变量，分别为场均进球数，场均失球数，场均射门数，场均角球数，场均传 球数，场均抢断数和场均控球率（单位：%）。其中，从新浪欧洲联赛数据库[1] 中可以找出这 29 支球队在 2014-2015 赛季欧洲冠军杯中的进球数、失球数、射 门数、角球数、传球数和抢断数，再除以各个球队的比赛场次即可得到所需数据。 数据整理结果如表 2.1 所示：
类问题，使不同变量的数表 2.2 经标准化后的 29 支球队的 7 项技术指标
巴塞罗那 皇家马德里
波尔图 安德莱赫特
阿森纳 沙尔克 04 尤文图斯 莫斯科中央陆军
罗马 巴黎圣日耳曼 毕尔巴鄂竞技 马德里竞技
马里博尔 顿涅茨克矿工
巴塞尔 卢多戈雷茨
1
表 2.1 29 支球队的 7 项技术指标
巴塞罗那 皇家马德里
波尔图 安德莱赫特
阿森纳 沙尔克 04 尤文图斯 莫斯科中央陆军
罗马 巴黎圣日耳曼 毕尔巴鄂竞技
马德里竞技 马里博尔 顿涅茨克矿工 巴塞尔 卢多戈雷茨 切尔西 马尔默
曼城 本菲卡 里斯本竞技 加拉塔萨雷 阿贾克斯 鲍里索夫 利物浦 摩纳哥 泽尼特 奥林匹亚科斯 希腊人竞技
Z 场均 射门数 0.81280 2.35532 0.15770 -0.31077 0.05487 0.67188 0.05106 -0.18508 -0.75638 -0.22317 0.38622 0.04344 -0.56595 -1.37339 -0.23078 -0.05939 0.95753 -0.50120 -0.18508 -.31077 1.78401 1.02228 -0.50120 -1.13725 0.19579 -1.06108 -0.94682 -0.44026 -2.78641
北京航空航天大学 数理统计第二次大作业
欧洲足球俱乐部竞技水平的聚类分析和判别分析
2015 年 12 月
欧洲足球俱乐部竞技水平的聚类分析和判别分析
摘要：近年来，人们对足球的关注越来越多。欧洲作为足球的发源地，其五大联 赛自然吸引着大批人的目光。尤其是欧洲冠军杯联赛更是代表着欧洲足球的最高 水平，吸引着各国最好的球队参加。本文从参加 2014-2015 赛季欧洲冠军杯联赛 的球队中选取 29 支球队，根据这些球队的一些技术统计资料，用 SPSS 软件对 其进行聚类分析，将这些球队按水平层次分为了 5 类。并选取 3 支球队，利用聚 类分析的结果对这 3 支球队进行判别分析。结果表明，聚类分类结果与判别分析 结果基本符合实际情况。
场均抢 断数 20.31 19.83 22.30 23.33 21.13 18.38 17.08 20.83 17.33 21.20 24.17 22.10 16.17 19.38 20.75 18.33 22.75 15.33 18.25 20.50 19.17 21.33 19.50 18.00 21.50 26.10 19.83 16.83 24.00
场均射 门数 14.62 18.67 12.90 11.67 12.63 14.25 12.62 12.00 10.50 11.90 13.50 12.60 11.00 8.88 11.88 12.33 15.00 11.17 12.00 11.67 17.17 15.17 11.17 9.50 13.00 9.70 10.00 11.33 5.17
场均失 球数 0.85 0.75 1.20 1.67 1.38 2.38 0.77 2.17 2.33 1.50 1.00 0.50 2.17 1.38 1.63 2.33 0.75 2.50 1.38 1.00 2.00 3.17 1.67 4.00 1.50 0.50 1.00 2.17 2.00
Z 场均 角球数 0.11373 2.18400 -0.22977 0.02089 0.21585 0.09516 0.32725 -0.90749 -1.22314 0.51293 -0.44330 1.62698 -1.68732 0.32725 -0.83322 1.09780 1.37632 -1.83586 0.79144 1.09780 0.16943 0.94926 -1.68732 -0.13694 -0.75895 -0.50829 -0.13694 -0.44330 -1.37168
II
1 引言
近些年，随着中国经济水平的不断繁荣进步，人民群众的生活水平也得到了 进一步的提升，随之而然的是人们生活方式以及兴趣爱好的不断变化。从以前为 了解决温饱问题而努力工作，变为现在为提高生活质量而工作。足球，作为全球 体育界最具有影响力的单项体育运动，享有“世界第一运动”的美誉，自然渐渐 进入了人们的日常生活中。
切尔西 马尔默 曼城 本菲卡 里斯本竞技 加拉塔萨雷 阿贾克斯 鲍里索夫 利物浦 摩纳哥 泽尼特 奥林匹亚科斯 希腊人竞技
Z 场均 进球数 1.38632 0.86067 1.55232 -0.06614 1.20650 0.34885 -0.09380 1.55232 -0.06614 0.03069 -0.75779 0.16902 -0.97912 0.69468 -0.52263 -0.75779 1.55232 -0.97912 -0.17680 -1.44944 0.86067 -0.97912 -0.06614 -1.44944 -0.75779 -0.93762 -0.97912 0.40418 -1.67077
由于不同的变量之间存在着较大的数量级的差别，因此要对数据变量进行标
准化处理。本文采用 Z 得分值法标准化的方法进行标准化，用 x 的值减去 x 的
均值再除以样本的方差。也就是把个案转换为样本均值为 0、标准差为 1 的样本。
如果不同变量的变量值数值相差太大，会导致计算个案间距离时，由于绝对值较
小的数值权数较小，个案距离的大小几乎由大数值决定，标准化过程可以解决此
I
目录
1 引言.......................................................................................... 1 2 数据采集与标准化处理 ......................................................... 1 3 聚类分析.................................................................................. 3
Z 场均 传球数 2.22733 1.11925 0.66563 -1.14118 0.98926 0.36825 0.48045 -0.78635 0.39833 0.89430 -0.25692 -0.92040 -0.93842 -0.54552 -0.41598 -0.37712 1.00469 -1.41908 0.63725 -0.77881 -0.50846 0.14860 0.99151 -1.58804 0.40959 -0.94856 0.05285 -0.74129 -1.56551
欧洲是现代足球的发源地，也是世界足球的中心，欧洲五大联赛也享誉世界， 每年一次的欧洲冠军联赛作为欧洲足坛最高水平的赛事，自然是人们关注的焦点。 能够打进欧洲冠军杯联赛的足球俱乐部都是欧洲各国中最顶尖的俱乐部。对于一 些老球迷来说，他们对这些球队都有着足够的了解；而对一些刚开始看球的球迷 朋友们，很多人并不了解这些世界顶级足球俱乐部之间的水平层次情况。所以， 本文利用 SPSS 软件，从参加 2014-2015 赛季欧洲冠军杯联赛的 32 支球队中，选 取 29 支球队的参赛数据，用聚类分析的方法将其按实力水平分为几类，并选则 另外 3 支球队，根据已有的类别划分情况，进行判别分析，确定其所属的水平层 次。
Z 场均 失球数 -0.90720 -1.03184 -0.47093 0.11491 -0.24657 0.99990 -1.00691 0.73814 0.93758 -0.09699 -0.72023 -1.34346 0.73814 -0.24657 0.06505 0.93758 -1.03184 1.14948 -0.24657 -0.72023 0.52624 1.98461 0.11491 3.01918 -0.09699 -1.34346 -0.72023 0.73814 0.52624
场均传 球数 667.54 569.17 528.90 368.50 557.63 502.50 512.46 400.00 505.17 549.20 447.00 388.10 386.50 421.38 432.88 436.33 559.00 343.83 526.38 400.67 424.67 483.00 557.83 328.83 506.17 385.60 474.50 404.00 330.83
场均控 球率（%）
60.92 57.11 56.33 40.92 57.18 51.28 55.09 34.90 47.30 48.65 51.17 44.26 41.75 46.28 44.74 47.17 54.15 41.52 48.49 50.42 48.57 51.50 52.75 35.55 50.05 42.95 54.78 46.62 30.45
3.1 聚类分析概述 ................................................................. 3 3.2 输出结果及分类 ............................................................. 4 4 判别分析.................................................................................. 8 4.1 判别分析概述 ................................................................. 8 4.2 输出结果 ......................................................................... 8 4.3 判别分析 ....................................................................... 12 5 结论........................................................................................ 13 参考文献.................................................................................... 13