认识三角形二

认识三角形(二) 同步练习题A组一、填空题1．已知三角形的三边分别为2，a，4，那么a的取值范围是______．2．(1)已知a，b，c是△ABC的三边长，a，b满足|a－7|＋(b－1)2＝0，c为奇数，则c＝______．(2)已知a，b，c为△ABC的三条边，化简|a＋b－c|－|b－a－c|＝______．3．(1)一个三角形的两边长为3 cm和2 cm，第三边长为奇数，则第三边的长为______cm.(2)已知三角形的三边长分别是3，x，9，则化简|x－5|＋|x－13|＝______．4．(1)若等腰三角形中有两边长分别为2和5，则这个三角形的周长为______．(2)若等腰三角形两边长分别为3和5，则它的周长为______．二、选择题5．下列长度的三条线段，能组成三角形的是( )A．4 cm，5 cm，9 cm B．8 cm，8 cm，15 cmC．5 cm，5 cm，10 cm D．6 cm，7 cm，14 cm6．若要植一块三角形草坪，两边长分别是20米和50米，则这块草坪第三边长不能为( )A．60米B．50米C．40米D．30米7．长度分别为2，3，3，4的四根细木棒首尾相连，围成一个三角形(木棒允许连接，但不允许折断)，得到的三角形的最长边长为( )A．4 B．5 C．6 D．7三、解答题9．由下列长度的三条线段能组成三角形吗？请说明理由(1)10 cm，12 cm，21 cm；(2)5 cm，5 cm，10 cm；(3)5.4 cm，7.2 cm，11 cm；(4)(k＋1) cm，(k＋2) cm，(2k＋2) cm(k>0)．10．(1)如图，已知△ABC.①若AB＝4，AC＝5，则BC边的取值范围是______；②D为BC延长线上一点，过点D作DE∥AC，交BA的延长线于点E，若∠E＝55°，∠ACD＝125°，求∠B的度数．(2)已知△ABC中，三边长分别为a，b，c，且满足a＝b＋2，b＝c＋1.①试说明b一定大于3；②若这个三角形周长为22，求a，b，c.B组一、填空题11．(1)有长度分别为10 cm，7 cm，5 cm和3 cm的四根铁丝，选其中三根组成三角形，则有______种选法．(2)等腰三角形的周长是27 cm，一腰上的中线将周长分为5∶4两部分，则这个等腰三角形的底边长为______．13．已知四边形ABCD的四边分别为a，b，c，d，若a＝3，b＝4，d＝10，则c的取值范围是______．15．△ABC中，三边之比为3：4：5，且最长边为10m，则△ABC周长为_____cm．18．有两根小棒分别长2厘米和4厘米．要围成一个等腰三角形，第三根小棒的长度应该是____厘米．二、解答题30．如图所示，D是△ABC的边AC上任意一点（不含端点），连结BD，请判断AB+BC+AC与2BD的大小关系，并说明理由．。

认识三角形（二）教学内容知识与技能：知道三角形任意两条边的和大于第三边；并会判断指定长度的三条线段能否围成三角形。

过程与方法：探究三角形三边的关系，根据三角形三边的关系解释生活中的现象；提高运用数学知识解决实际问题的能力；提高观察、思考、抽象概况能力和动手操作能力。

情感与态度：积极参与探究活动，在活动中获得成功的体验，培养学习的兴趣。

重点、难点重点在观察、操作、比较和分析中发现三角形三条边的关系。

难点应用三角形三边的关系解决实际生活中的问题。

情境导入找出图示中的三角形。

由三条线段围成的图形叫做三角形。

三角形的三边长度存在怎样的数量关系?两点之间线段最短探究新知（图示）把一根吸管任意剪成3段，能围成一个三角形吗？先做一做，在合同伴交流。

动手做一做：将多根吸管剪成不同的3段。

测出长度。

围成一圈。

通过图示，我们可以得出什么结论：当两根吸管的长度和等于第三根吸管时，不能围成三角形。

当两根吸管的长度和小于第三根吸管时，不能围成三角形。

当两根吸管的长度和大于第三根吸管时，能围成三角形。

剪一剪，围一围，填写下表。

当三条线段中的任意两条之和大于第3条边时，这三条线段才能围成三角形。

也可以说三角形任意两边之和大于第3边。

一个三角形的3个内角和是多少度？所有三角形的内角和都是180°吗？怎样去验证一下呢？拿起你的量角器，量一量每个三角形三个内角的度数吧！将三角形的三个角撕下来，拼到一起，你能发现什么？这三个内角拼在一起正好是一个平角，说明三角形的内角和是180°。

课堂练习三角形的一个内角为80°，另外两个角可能是多少度？三角形内角和是180°，除了这个80°的角，剩下两个角的度数和为：180°－80°＝100°。

课堂小结1.三角形任意两边的内角和不能小于第三边。

2.三角形的内角和为180°。

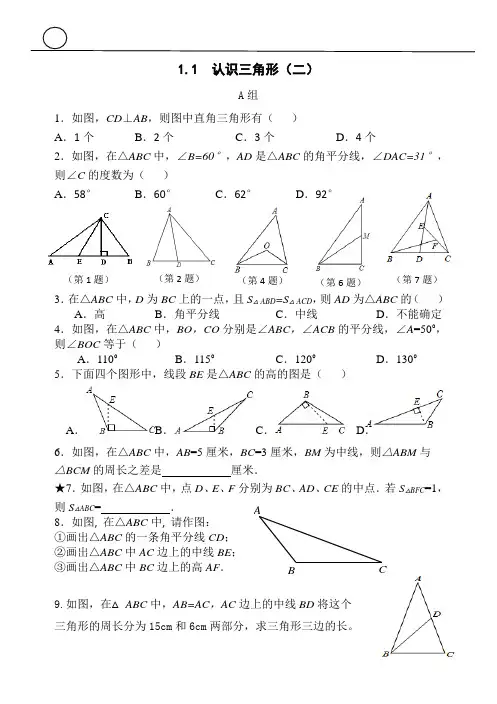
C B A （第6题） 1.1 认识三角形（二）A 组1．如图，CD ⊥AB ，则图中直角三角形有（ ）A ．1个B ．2个C ．3个D ．4个2．如图，在△ABC 中，∠B=60°，AD 是△ABC 的角平分线，∠DAC=31°，则∠C 的度数为（ ）A ．58°B ．60°C ．62°D ．92°3．在△ABC 中，D 为BC 上的一点，且S △ABD =S △ACD ，则AD 为△ABC 的（ ）A ．高B ．角平分线C ．中线D ．不能确定4．如图，在△ABC 中，BO ，CO 分别是∠ABC ，∠ACB 的平分线，∠A =50°，则∠BOC 等于（ ）A ．110°B ．115°C ．120°D ．130°5．下面四个图形中，线段BE 是△ABC 的高的图是（ ）A ．B ．C ．D ．6．如图，在△ABC 中，AB =5厘米，BC =3厘米，BM 为中线，则△ABM 与 △BCM 的周长之差是 厘米．★7．如图，在△ABC 中，点D 、E 、F 分别为BC 、AD 、CE 的中点．若S △BFC =1，则S △ABC = ． 8．如图, 在△ABC 中, 请作图：①画出△ABC 的一条角平分线CD ；②画出△ABC 中AC 边上的中线BE ；③画出△ABC 中BC 边上的高AF ．9.如图，在△ABC 中，AB=AC ，AC 边上的中线BD 将这个三角形的周长分为15cm 和6cm 两部分，求三角形三边的长。

（第1题） （第2题） （第4题） （第7题）B 组★10.如图，在△ABC 中，AB ＝AC ，P 是BC 边上任意一点，PF ⊥AB 于 点F ，PE ⊥AC 于点E ，BD 为△ABC 的高线，BD ＝8，求PF ＋PE 的值．11．如图，在△ABC 中，BO 、CO 分别是∠ABC 、∠ACB 的平分线．（1）若∠ABC=60°，∠ACB=50°，求∠BOC 的度数．（2）若∠A=60°，求∠BOC 的度数．（3）若∠A =α，求∠BOC 的度数（用α的代数式表示）．★12.如图，在△ABC 中，E 为BC 上一点，EC =2BE ，D 为AC 的中点． 设△ABC ，△ADF ，△BEF 的面积分别为,,,BEF ADF ABC S S S △△△若12=ABC S △，则BEF ADF S S △△-=_______．★13．如图，在△ABC 中，AD 是BC 边上的高线，AE 是△ABC 的角平分线．若α=∠B ，)(βαβ<=∠C ，用含βα，的代数式表示∠EAD ．2。

七年级的学生思维活跃，模仿能力强。

对新知事物满怀探求的欲望，同时他们也具备了一定的学习能力，在老师的指导下，能针对某一问题展开讨论并归纳总结，但受年龄特征的影响，他们知识迁移能力不强推理能力还需进一步培养。

通过做三角形我发现并不是任意三条木条就一定能钉成一个三角形，三角形的构成是有条件的。

”这对整节课起到了画龙点晴的作用。

整节教学活动通过讨论、精讲、合理利用模型，让学生动手操作、自主探究、合作交流达到了预期目的。

本节课实在小学初步认识三角形的基础上，又具体介绍了三角形的有关概念和三角形三边的关系。

它既是上学期所学线段和角的延续，又是后继学习全等三角形和四边形的基础。

在知识体系中具有承上启下的作用。

认识三角形（2）评测练习独立尝试1、有两边相等的三角形叫做等腰三角形。

2、三边都相等的三角形是等边三角形，也叫正三角形。

3、三角形的三边关系：（1）三角形任意两边之和第三边；（2）三角形任意两边之差第三边。

4、下面各组数分别表示三条线段的长度，试判断以它们为边是否能组成三角形。

（1）1:4:5 （2）3:3:5（3）3x、5x、7x（x为正数）（4）三条线段长度之比为4:7:6仔细阅读课本第85、86页①记住等边三角形的概念。

②记住等腰三角形的概念。

③记住等边三角形三边关系定理。

三角形是学生们平日里接触较多的一种图形，在低年级就已经直观认识过，因而本课的重点就放在三角形的稳定性、定义和分类上。

所学重难点都是由学生在操作中获得的，不是由老师讲出来，硬塞给学生。

这样做，学生就会主动参与学习，落到实处，效果也好。

在整个课堂里，老师只是充当一个参与者、引导者。

课堂总结也是通过老师的引导，由学生做出归纳，这样效果要比由老师包办好。

从这节课可以看出：一、有效地激发了学生的兴趣，促进学生主动参与。

从学生的生活入手，让学生感受三角形与生活的密切联系，从而激发学生学习三角形的热情，变“要我学”为“我要学”。

二、改变数学学习方式，引导学生经历过程。

《认识三角形》第2课时教学设计4、总结归纳，定义：（1）三条边各不相等的三角形叫作不等边三角形（2）有两条边相等的三角形叫作等腰三角形（3）三条边都相等的三角形叫作等边三角形等边三角形和等腰三角形之间有什么关系？（等边三角形是特殊的等腰三角形）5、我们可以把三角形按照三边情况进行分类（不等边三角形三角形按边分类］笠殛—缶等腰三角形I等腰二角形I等边三角形（二）三角形的三边关系。

1、探究活动1：如下图，点A为小明家，点B为学校，点C为邮局，小明想：我要到学校怎么走呀？哪一条路最近呀？为什么？学生讨论后个别回答，然后师生共同小结。

路线1：从A到C再到B的路线走；路线2：沿线段AB走请问：路线1、路线2哪条路程较短，你能说出根据吗？解：路线2较短；两点之间线段最短。

≡由此可以得到：4- BOAB ÷BO AC ÷ AR > RO2、议一议：（1）在同一个三角形中,任意两边之和与第三边有什么大小关系？（2）在同一个三角形中,任意两边之差与第三边有什么大小关系？（3）三角形三边有怎样的不等关系？通过动手实验（数学课本第85页“做一做”）同学们可以得到哪些结论? 理由是什么？3、探究活动2：做一做分别量出下面三个三角形的三边长度,并填入空格内。

Z∖ N 2(1) (2) (3)⑴a=,b=, C=。

(2) a=,b=,C=O⑶a=,b=,C=O根据你的测量结果,计算三角形的任意两边之差,并与第三边比较,完成填空：(1) a- b c,c- b a,c- a b⑵b—a c, c-a b,b—c a。

⑶a- c b,a— b c,b—c a。

你能得到什么结论?再画一些三角形试一试。

得出结论:三角形任意两边之差小于第三边。

4、归纳总结三角形任意两边之和大于第三边。

三角形任意两边之差小于第三边。

（三）典例分析1、例I有两根长度分别为5cm和8cm的木棒，用长度为2cm的木棒与它们能摆成三角形吗？为什么？长度为13Cm的木棒呢？解：取长度为2cm的木棒时，由于2+5=7<8,出现了两边之和小于第三边的情况，所以它们不能摆成三角形.取长度为13cm的木棒时，由于5+8=13, 出现了两边之和等于第三边的情况，所以它们也不能摆成三角形。