1.1认识三角形(2)

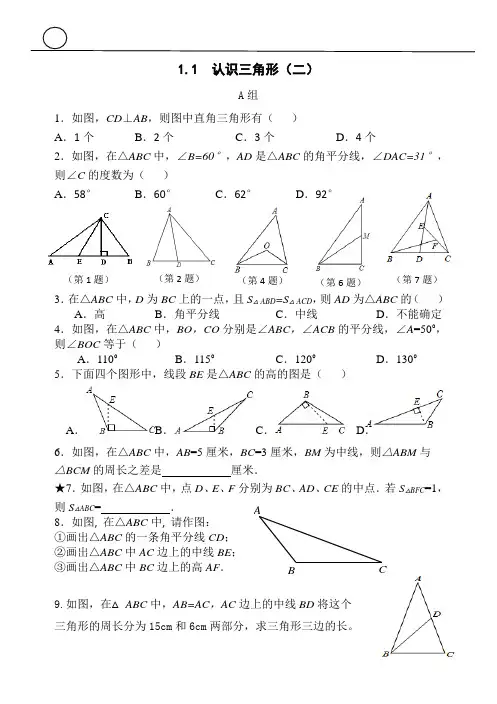
C B A （第6题） 1.1 认识三角形（二）A 组1．如图，CD ⊥AB ，则图中直角三角形有（ ）A ．1个B ．2个C ．3个D ．4个2．如图，在△ABC 中，∠B=60°，AD 是△ABC 的角平分线，∠DAC=31°，则∠C 的度数为（ ）A ．58°B ．60°C ．62°D ．92°3．在△ABC 中，D 为BC 上的一点，且S △ABD =S △ACD ，则AD 为△ABC 的（ ）A ．高B ．角平分线C ．中线D ．不能确定4．如图，在△ABC 中，BO ，CO 分别是∠ABC ，∠ACB 的平分线，∠A =50°，则∠BOC 等于（ ）A ．110°B ．115°C ．120°D ．130°5．下面四个图形中，线段BE 是△ABC 的高的图是（ ）A ．B ．C ．D ．6．如图，在△ABC 中，AB =5厘米，BC =3厘米，BM 为中线，则△ABM 与 △BCM 的周长之差是 厘米．★7．如图，在△ABC 中，点D 、E 、F 分别为BC 、AD 、CE 的中点．若S △BFC =1，则S △ABC = ． 8．如图, 在△ABC 中, 请作图：①画出△ABC 的一条角平分线CD ；②画出△ABC 中AC 边上的中线BE ；③画出△ABC 中BC 边上的高AF ．9.如图，在△ABC 中，AB=AC ，AC 边上的中线BD 将这个三角形的周长分为15cm 和6cm 两部分，求三角形三边的长。

（第1题） （第2题） （第4题） （第7题）B 组★10.如图，在△ABC 中，AB ＝AC ，P 是BC 边上任意一点，PF ⊥AB 于 点F ，PE ⊥AC 于点E ，BD 为△ABC 的高线，BD ＝8，求PF ＋PE 的值．11．如图，在△ABC 中，BO 、CO 分别是∠ABC 、∠ACB 的平分线．（1）若∠ABC=60°，∠ACB=50°，求∠BOC 的度数．（2）若∠A=60°，求∠BOC 的度数．（3）若∠A =α，求∠BOC 的度数（用α的代数式表示）．★12.如图，在△ABC 中，E 为BC 上一点，EC =2BE ，D 为AC 的中点． 设△ABC ，△ADF ，△BEF 的面积分别为,,,BEF ADF ABC S S S △△△若12=ABC S △，则BEF ADF S S △△-=_______．★13．如图，在△ABC 中，AD 是BC 边上的高线，AE 是△ABC 的角平分线．若α=∠B ，)(βαβ<=∠C ，用含βα，的代数式表示∠EAD ．2。

1.1 认识三角形（1）【教学目标】1、通过实践活动，理解三角形三个内角的和等于180o2、理解三角形的一个外角等于和它不相邻的两个内角的和3、合适用三角形的内角和外角的性质简单的几何问题4、了解三角形的分类【教学重点、难点】1．本节教学的重点是三角形三个内角和等于180o的性质是本节重点。

2．例3是立体图形，涉及的角之间的关系不易辨认，是本节难点。

【教学过程】1，合作学习：①请每个学生利用手中的三角形（已备），把三角形的三个角撕（或剪）下来，然后把这三个角拼起来，然后观察这三个角拼成了一个什么角？②请学生归纳这一结论，教师板书：三角形的三个内角的和等于180O2、三角形内角和性质的应用①口答：△ABC中，∠A=45O，∠B=60O，求∠C②△ABC中，∠A=57O18，，∠B=46O49，。

求∠C③△ABC中，∠A=∠B，∠C=110O，求∠A，∠B④△ABC中，∠A：∠B：∠C=1：2：3，求这个三角形的三个内角。

3、由上题得出图中三角形的形状①②得出的三角形的三个角都是锐角，这样的三角形称之为锐角三角形③得出的三角形有一个角是钝角，这样的三角形称之为钝角三角形④得出的三角形有一个角是直角，这样的三角形称之为直角的三角形若一个三角形为Rt△，那么它的其余两个锐角互余。

4、三角形的外角：①定义：三角形的一边和另一边相邻边组成的角，叫做三角形的外角。

由图得：∠BCE+∠ACB=180O而∠A+∠B+∠ACB=180O∴∠BCE=∠A+∠B从而得到定理：三角形的一个外角等于和它不相邻的两个内角的和②外角也并不一定绝对，要会看一个角之是内角还是外角。

5、练习：1）△ABC中，∠ACD=120O∠A=50O ，求∠B、∠ACD2）如书本例题3），已知，在△ABC 中， ∠C=Rt ∠,D 是BC 上一点，已知∠1=∠2，∠B=25O ，求∠BAD 数。

6：小结：角形的内角和性质②认识三角形的外角的概念，并能准确寻找外角和内角 7，布置作业1.1 认识三角形(2)【教学目标】1、使学生知道三角形的角平分线和中线的定义，并能熟练地画出这两种线段 2、能应用三角形的角平分线和中线的性质解决简单的数学问题 【教学重点、难点】教学重点、难点：三角形的角平分线、中线的定义及画图是本节课的重点，利用三角形的角平分线和中线的性质解决有关的计算问题是本节难点。

认识三角形学习目标1.了解三角形高、角平分线和中线的概念.2.会画三角形各条边上的高、中线，和角的平分线.3.会利用三角形的高、角平分线、中线，解决有关问题.学习重点：本节教学的重点是三角形高、角平分线和中线学习难点：利用三角形的高、角平分线、中线，解决有关问题.一、学前准备：1.已知：如图（甲）（乙）过点P 作直线L 的垂线。

2.如图：射线BD 在∠ABC 的内部，（1）若∠ABD=∠DBC 时，则射线BD 叫做∠ABC 的 ； （2）若BD 平分∠ABC ，则∠ =∠ =21∠ ； 3.如图：点M 在线段AB 上，（1）若AM=BM 时，点M 叫做线段AB 的 ；（2）若点M 是线段AB 的中点，则 = =21 ； 4.已知三角形一边为a ，这边上的高为h ，则它的面积为 .二、预习、探究，独立思考·解决问题（一）三角形的角平分线、中线、高概念1：三角形的角平分线：在三角形中， ，这个角的顶点与交点之间的线段叫做三角形的角平分线。

几何语言表达方式：（1）如图 在∆ABC 中，∠BAD=∠CAD,AD 是∆ABC 的 ；（2）若AD 是∆ABC 的角平分线，则∠ =∠ ,概念2：三角形的中线：在三角形中， ，叫做这个三角形的中线。

D B C AE 几何语言表达方式： （1）在∆ABC 中，E 是BC 的中点（ED=EC ），则 是∆ABC 中BC 边上的中线。

（2）若AE 是∆ABC 的中线，则 = , 试一试：分别画出下面每个三角形的所有的高。

概念3：三角形高的定义 ：从三角形的一个顶点线， 的线段叫做三角形的高。

符号语言：如图，AH 是△ABC 的边BC 上的高，则ＡＨ BC ，∠AHB=∠AHC= 02.由画图得：① 锐角三角形的三条高线都在三角形 部，且相交于 ；② 直角三角形斜边上的高在三角形的 部，两直角边上的高 。

三条高相交于 。

③ 钝角三角形钝角对边上的高 ，夹钝角的两条边上的高在 。

1．1 认识三角形（二）【知识提要】1．三角形三内角和为180°．2．三角形的外角性质：（1）三角形的一个外角等于和它不相邻的两个内角和；（2）三角形的三外角和为360°．3．三角形按角分类：三角形⎧⎪⎧⎨⎨⎪⎩⎩直角三角形锐角三角形斜三角形钝角三角形【学法指导】1．通过折叠，动手操作理解三角形三内角和为180°．2．运用三角形外角性质可以沟通三角形内、外角之间的关系．范例积累【例1】在△ABC中，∠A是∠B的2倍，∠C比∠A与∠B的和大12°，•求这个三角形的三个内角的度数．．【例2】如图，求∠A+∠B+∠C+∠D+∠E的度数．【例3】如图，试说明∠A+∠ABC+∠C=∠ADC．基础训练1．如图1，在△ABC中，与△ACB相邻的一个外角等于110°，∠A=40°，•则∠B的度数是（）A．30° B．50° C．60° D．70°（1） (2) (3) (4)2．在△ABC中，∠A：∠B：∠C=1：2：3，则△ABC是（）A．钝角三角形 B．锐角三角形 C．直角三角形 D．不能确定形状3．如图2，∠1、∠2、∠3是△ABC的外角，若∠1：∠2：∠3=4：3：2，则∠ABC等于（）（注意：三角形三内角和为180°，三外角和为360°）A．60° B．80° C．90° D．100°4．已知如图3，∠A、∠B、∠C、∠D、∠E五个角的和的度数是（）（注意：五角星之和为180°）A．100° B．180° C．360° D．540°5．已知在△ABC中，∠A+∠B=107°，则∠C的外角度数为___．6．如图4，用“＜”连结∠A、∠1、∠2：_ _．7．已知在△ABC中，若∠A比∠B大20°，外角∠ACD=96°，则∠A=•_ _，•∠B=__．8．如图，在四边形ABCD中，∠B=70°，∠C=50•°，•在顶点D•的一个外角为100°，则在顶点A的一个外角∠x=__ ．（注意：四边形角度之和为360°）9．如图，试求∠A+∠B+∠C+∠D+∠E+∠F的度数．10．如图，已知∠B=∠ACB=75°，∠BDE=3∠E，试求∠ADE的值．提高训练11．如图，△ABC中，D为△ABC内一点，已知∠BDC=100°，∠1=30•°，•∠2=20°，求∠A的度数．12．如图:（1）图甲是一个五角星，求∠A+∠B+∠C+∠D+∠E 的度数；（2）图甲中的点A 向下移到BE 上（如图乙），五个角的和有无变化？说说你的理由；（3）图乙中的点C 向上移到BD 上（如图丙），五个角的和有无变化？说说你的理由．应用拓展13．如图，△ABC 内有三个点D 、E 、F ，分别以A 、B 、C、D 、E 、F 这六个点为顶点画三角形．如果每个三角形的顶点都不在另一个三角形内部，那么这些三角形的所有的内角之和为（ ）A ．360°B ．900°C ．1260°D ．1440°14．设A 、B 、C 、D 为平面上的任意四点，如果其中任何三点不在一条直线上，•则△ABC 、△ABD 、△ACD 、△BCD 中至少有一个三角形的某个内角满足（ ）A ．不超过15°B ．不超过30°C ．不超过45°D ．都不对。

浙教版数学八年级上册1.1《认识三角形》说课稿2一. 教材分析《认识三角形》是浙教版数学八年级上册第一章第一节的内容。

本节课的主要任务是让学生了解三角形的定义、特性以及三角形的基本分类。

通过本节课的学习，学生能够掌握三角形的基本概念，理解三角形的性质，为后续学习三角形的相关知识打下基础。

二. 学情分析学生在七年级已经学习了平面图形的初步知识，对图形的性质和概念有一定的了解。

但是，对于三角形这一图形，他们可能只停留在表面的认识，没有深入理解其内在的性质和特点。

因此，在教学过程中，需要引导学生从实际问题出发，探究三角形的本质特征。

三. 说教学目标1.知识与技能目标：让学生掌握三角形的定义、特性以及分类，能够识别各种类型的三角形。

2.过程与方法目标：通过观察、操作、探究等方法，培养学生的空间想象能力和逻辑思维能力。

3.情感态度与价值观目标：激发学生对数学的兴趣，培养他们勇于探索、积极思考的精神。

四. 说教学重难点1.教学重点：三角形的定义、特性以及分类。

2.教学难点：三角形内在性质的理解和运用。

五. 说教学方法与手段1.教学方法：采用问题驱动法、合作学习法、探究学习法等，引导学生主动参与、积极思考。

2.教学手段：利用多媒体课件、实物模型、几何画板等辅助教学，提高学生的学习兴趣和效果。

六. 说教学过程1.导入新课：通过展示生活中常见的三角形实例，引导学生关注三角形的存在，激发学习兴趣。

2.探究三角形的定义和特性：让学生通过观察、操作、讨论等方式，自主探究三角形的定义和特性，教师适时给予引导和点拨。

3.三角形分类：引导学生根据三角形的特性，对给定的三角形进行分类，巩固所学知识。

4.实践应用：设计一些具有挑战性的问题，让学生运用所学的三角形知识解决实际问题，提高学生的应用能力。

5.总结与反思：让学生回顾本节课所学内容，总结三角形的性质和分类，反思自己的学习过程，提高自我认知。

七. 说板书设计板书设计要清晰、简洁，能够突出三角形的主要性质和分类。