品质七大手法之散布图

格式：doc
大小：106.00 KB
文档页数：6

下载文档原格式

品质七大手法(C5)-散布图

Xmax=90 Ymax=75 Xmin=10 Ymin=23
3）画出x-y轴坐标，取适当刻度

100 80 60 40

20

0
20
40
60
80
100
4）将数据点绘于x-y轴中

100 80 o 60 o 40 o o o o o o o

20

0
20
1、散布图的概念

1.2散布图的基本概念将因果关系所对应变化的数据分别描绘再x-y轴坐标系上，以掌握两个变量之间是否相关及相关的程度如何，这种图形叫“散布图”，也称作“相关图”。，
1、散布图的概念

1.3散布图的分类 1）正相关：当变量x增大时，另一变量y也增大。相关性强：如马力与载重的关系；相关性中：如收入与消费的关系；相关性弱：如体重与身高的关系。 2）负相关：当变量x增大时，另一变量y却减少。相关性强：如投资率与失业率的关系；相关性中：如举重力与年龄的关系；相关性弱：如举重力与身高的关系。

2.1散布图的制作步骤 1）确定要调查的两个变量，收集成对的数据（x1,y1),(x2,y2)….，整理成数据表；至少30足以上。
No 1 x x1 y y1
2
3 4
x2
x3 x4
y2
y3 y4
….
….
….
2、散布图的制作

2.1散布图的制作步骤 2）找出两个变量x，y的最大值及最小值； 3）以x，y的最大值及最小值建立x-y坐标，并决定适当的刻度便于描点； 4）将相对应的两个变量x，y以点的形式描在x-y坐标中； 5）记入图名、制作者、制作时间等项目； 6）判读散布图的相关性与相关程度。

品管新七大手法概述

•如何开设一家受欢迎的快餐店
•人员素质要高 •食物口味要独特
•旅游服务专业 •材料要优质
•大专文凭 •南北口味 •产•品英代语4号/6级明确 •适合各年龄层
•工艺制造独特
•配方设计
•制造加工精细 •搭配药材
•如何开设一家受欢迎的快餐店
•服务态度和蔼亲切
•着装得体 •微笑服务
•主动帮助客户
•订餐时间短
•参考
第三章亲和图
• 品质不合 • 包装错误 • 色泽太深 • 重量不合
• 交期不准 • 缺能源 • 锅炉故障 • 停电 • 停水
• 机器故障 • 设备老旧 • 保养不周 • 操作不当
• 工作效率低 • 人员疲劳 • 人员不足 • 工作环境差
• 原料管理差 • 物料延误 • 原料贮存变质
• 生产计划不周 • 订单日期太近 • 订单临时增加 • 通知生产太迟
•固定梢设置不当
•其他
•设备不当
•冲压作业效率低
第一章品管七大手法简介
五、分层法按照一定的类别，把收集到的资料加以分类整理的一种方法。注意几点: §确定分层的类别和调查的物件； §设计收集数据的表格； §收集和记录数据； §整理数据并绘制相应图表； §比较分析和最终的推论；
第一章品管七大手法简介
•散布图示例
第一章
•Y
品管七大手法简介
•Y
•强正相关
•0
•X
•0
•Y
•Y
•强负相关
•X
•弱正相关
•0
•X
•0
•弱负相关
•X
第一章品管七大手法简介
四、因果图用于寻找造成问题产生的原因，即分析原因与结果之间关系的一种方法。注意几点: §充分组织人员全面观察，从人、机、料、法、环、测方面寻找； §针对初步原因，展开深层的挖掘； §记下制图部门和人员、制图日期、参加人员；

qc七大手法之散布图

第九章散布图(Scatter Diagram)一、前言散布图有以下的作用：⒈能大概掌握缘故与结果之间是否有关联及关联的程度如何。

图2-1。

⒉能检查离岛现象是否存在。

图2-2。

⒊缘故与结果关联性高时，二者可互为替代变数。

关于过程参数或产品特性的掌握，可从缘故或结果中选择一较经济性的变数予以监测。

同时可通过观看一变数的变化来明白另一变数的变化。

二、散布图的定义特性要因图（鱼骨图）大概能够了解工程上那些缘故会阻碍第九章散布图 145XX产品的质量特性，散布图也是以这种因果关系的方式来表示其关连性。

并将因果关系所对应变化的数据分不点绘在x—y轴坐标的象限上，以观看其中的关联性是否存在。

三、散布图的制作方法以横轴（X轴）表示缘故，纵轴（Y轴）表示结果，作法如下：⒈收集成对的数据(x1,y1)，(x2,y2)，…整理成数据表。

146 品管七大手法⒉找出x,y的最大值及最小值。

⒊以x,y的最大值及最小值建立x—y坐标，并决定适当刻度便于绘点。

⒋将数据依次点于x—y坐标中，两组数据重复时以☉表示，三组数据重复时以表示。

⒌必要时，可将相关资料注记在散布图上。

⒍散布图的注意事项： ⑴是否有异常点：有异常点时，不可任意删除该异常点，除非异常的缘故已确实掌握。

⑵是否需分层：数据的获得常常因为操作人员、方法、材料、设备或时刻等的不同，而使数据的关联性受到扭曲。

a. 全体时低度关联，分层后高度关联。

b. 全体时高度关联，分层后低度关联。

第九章散布图 147YX Y XY Y Y⑶散布图是否与原有技术、经验相符：散布图若与原有技术、经验不相符时，应追查缘故与结果是否受到其他因素干涉。

四、散布图的判读依散布图的方向、形状，有以下几种关联情形：⒈完全正（负）关联：点散布在一直线上。

X X关X X⒉高度正(负)关联：缘故(X)与结果(Y)的变化近于等比例。

3.(X)4.(X)148 品管七大手法X XX X5.(Y)的变化完全不成比例。

QC七大手法教材(散布图)4

Y ● ●● ● ● ● ●●
● ● ● ●
● ● ● ● ● ● ● ●●● ● ● X
12
X
QC 七大手法教材--散布图散
5.散布图的注意事项散布图的注意事项的注意事
5-1 相关系数不等于因果关系。关系数不等因果关系不等于关系。 5-2 绘制散布图后进行判定結果为「无关」 ,系指在該数绘制散布图后进行判定結果判定結果为无关」系指在該系指在該数据区间內而言无关一步推断区间外的結果外的結果。据区间內而言无关，无法进一步推断到区间外的結果。內而言无关， 5-3 要善用层別法工具分析。善用层別法工具分析工具分析。 5-4 离群值的影响，是否会为异常值的检讨。的影响是否会为异常值检讨。会为异常值的 5-5 曲线相关无法用符号判定来检讨。关无法用符判定来检讨法用符号来检讨。 5-6 检讨因果关系时，通常以代表因，Y代表果。检讨因果关系时，通常以X代表因果关系时代表因代表果代表
Y ● ● ● ● ● ● ● ● ● ●● ● ● ● ● ●● ● ● ●● ● ● ● ● ●
X
3
QC 七大手法教材--散布图散
2.散布图的构成，特色及用途散布图的
2-2散布图的特色：散布图的特色 (1)从散布图可简单容易判断X与Y两个变量间从散布图可简单容易判断与两个变量间两个变量间: 从散布图容易判 ○是否有相关关系。是否有相关关系。关关系 ○相关关系的強弱。关关系的強弱。的強弱 ○是正相关或者負相关。是正相关或者負相关 ○是直线相关或是曲线相关。是直线或是曲线 (2)从散布图上可简单容易判断数据是否有异常趋势或从散布图上可简单容易判断数据是否有异趋势或从散布图上可简单容易判断数据是否有是有沒有必要作层別分析。是有沒有必要作层別分析。

旧QC七大手法之一散布图的一生

散布图简称：散点图对象：查找原因，用于多个变量相关性分析（有无相关、什么类型相关性、未来变量变化规律）、原因分析、要素确认。

当怀疑两个变量可能有关系，但不能确定这种关系的时候定义：是表示两个变量之间变化关系的图。

用来绘制散布图的数据必须是成对的(X,Y). 通常用垂直轴表示现象测量值Y , 用水平轴表示可能有关系的原因因素X.变体：散点图、相关图、气泡图、3D散点图、scatter、动态散点图发明人：主要发明人介绍：早期01：早期02：早期03：早期04：早期05：早期06：早期07：发展01：典型相关性判断，强正相关、强负相关、弱正相关、弱负相关、不相关、非线性相关发展02：象限相关性判断/中值相关性判断，ⅠⅡⅢⅣ发展03：发展04：发展05：发展06：发展07：发展08：概念01：两个变量之间存在的确定关系（函数关系）和非确定关系概念02：收集的成对数据（x,y）不少于30对。

太少数据相关不明显，判断变量间关系不准确。

概念03：r为相关系数1.强正相关(如容量和附料重量)r=+12.强负相关(油的粘度与温度) r=-13.弱正相关(身高和体重) 0<><>4.弱负相关(温度与步伐) -1<><>5.不相关(气压与气温) r=06.非线性相关r=0应用工具：优点：1、作用一：可以展示数据的分布和聚合情况2、作用二：可以添加趋势线，得到趋势线公式。

3、示趋势线可靠程度的R平方值4、利用散点图进行四象限分析5、作用三：辅助制图用散点图的误差线辅助制图缺点：这种关系虽然存在，但又难以用精确的公式或函示典型应用案例。

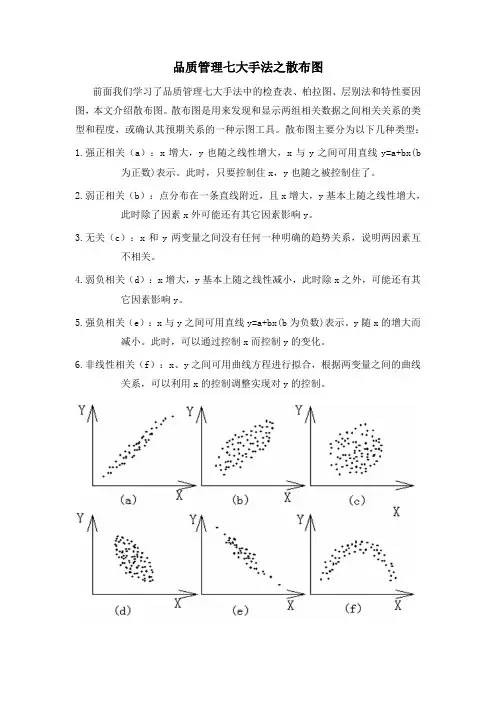
品质管理七大手法之散布图

品质管理七大手法之散布图前面我们学习了品质管理七大手法中的检查表、柏拉图、层别法和特性要因图，本文介绍散布图。

散布图是用来发现和显示两组相关数据之间相关关系的类型和程度，或确认其预期关系的一种示图工具。

散布图主要分为以下几种类型：1.强正相关（a）：x增大，y也随之线性增大，x与y之间可用直线y=a+bx(b为正数)表示。

此时，只要控制住x，y也随之被控制住了。

2.弱正相关（b）：点分布在一条直线附近，且x增大，y基本上随之线性增大，此时除了因素x外可能还有其它因素影响y。

3.无关（c）：x和y两变量之间没有任何一种明确的趋势关系，说明两因素互不相关。

4.弱负相关（d）：x增大，y基本上随之线性减小，此时除x之外，可能还有其它因素影响y。

5.强负相关（e）：x与y之间可用直线y=a+bx(b为负数)表示。

y随x的增大而减小。

此时，可以通过控制x而控制y的变化。

6.非线性相关（f）：x、y之间可用曲线方程进行拟合，根据两变量之间的曲线关系，可以利用x的控制调整实现对y的控制。

散布图的制作方法：1.一般收集至少20组以上资料；2.找出数据中的最大值与最小值；3.准备座标纸，划出纵轴、横轴的刻度，计算组距，通常纵轴代表结果，横轴代表原因，组距的计算应以数据中的最大值减小值除以所需设定的组数求得；4.将各组对应数标示在座标上；5.须填上资料的收集地点、时间、测定方法、制作者等项目。

下面用散布图展示电动自行车的工艺设计与人工时效之间的关系，由潍坊品质管理部工艺组提供的丽颖生产工艺的有关数据如下：总工时：1880秒，工位最短工时：28秒，工位最大工时：57秒工位布置：50人则人均工时：37.6秒（即理论上每37.6秒下1台车）理论人工时效=3600秒/[37.6秒（每台）*50人]=1.91台/人实际上我们计算人工时效是按最大工时（瓶颈工位工时）计算，即：实际人工时效=3600秒/[57秒（每台）*50人]=1.26台/人那么实际工时效率=1.26台（每人）/1.91台（每人）=66%，也就是说，因瓶颈工位导致的人工时效损失为34%。

QC7大手法(完整版)

2
200.00% 200.00%
554 263 387
品质部 2011-11-08
200.00%
根据不良项目分层，结果如下：
现象描述保护胶不良信息面黑点裂片信息面划伤
暗纹/水纹/云纹
边缘碰伤粘片,粘胶拉丝合计
数量 7193 878 713 240 236 182 159 31 9632
数量 2485 2257 2240 1648 1062 9632
品质部 2011-11-08
2.柏拉图
品质部 2011-11-08
定义
根据所搜集之数据，按不良原因、不良状况、不良发生位置等不同区分标准，以寻求占最大比率之原因，状况或位置的一种图形。 1897年，意大利学者柏拉图分析社会经济结构，发现绝大多数财富掌握在极少数人手里，称为“柏拉法则”。美国质量专家朱兰博士将其应用到品管上，创出了 “Vital Few, Trivial Many”(重要的少数，琐细的多数)的名词，称为“柏拉图原理”。
品质部 2011-11-08
品管七大手法所体现的精神
◆用事实与数据说话。 ◆全面预防。 ◆全因素、全过程的控制。 ◆依据PDCA循环突破状予以改善。 ◆层层分解、重点管理。
品质部 2011-11-08
1.层别法
品质部 2011-11-08
定义
针对部门别，人别，工作方法别，设备，地点等所收集的数据，按照它们共同的特征加以分类统计的一种分析方法，即为了区别各种不同的原因对结果的影响，而以个别原因为主，分别统计分析的一种方法。
素的主要类别：数据和信息系统、人员、机器设备、材料、方法、度量和环境等；
3)
4)
开始画图，把“结果”画在右边的矩形框中，然后把各类主要原

品质管制(QC)七大手法-特性要因分析图、

重点把握
柏拉图
100%
1.决定改善目标(80/20) 能够以前几项为改善的要点，可忽略最后 2.明了改善的效果几项，卲常说的“前 3.掌握重点分析三项”原则
简易有效
查检表
1.日常管理用 2.收集数据用 3.改善管理用
帮助每个人在最短时间内完成必要之数据收集
21
QC 旧 7 大手法简介
13
CATCHER
QCC小组活动流程:
1 选择课题 2 现状调查 3 设定目标 P 4 分析原因 5 确定主因 6 制定对策 D C 7 实施对策 8 检查效果目标达到 A 目标未达到
QCC小组活劢流程的管理技术主要有三个方面 1、遵循PDCA循环 2、以事实为依据，用资料说话 3、应用统计方法 Goal
层别法比较作用 1.应用层别区分法，找出借用其他图形，本身数据差异的因素而对症无固定图形下药. 2.以4M之每1M进行层别 1.了觋两种因数戒数据之间的关系。 2.发现原因不结果的关系应用范围较受限制相关易懂散布图赺势明朗
管制图
1.掌握制程现况的品质 2.发现异常及时采取行动
文件编号: 209030001A 生效日期：2010年1月18日修改日期:
品质管制(QC)七大手法
--- 特性要因分析图、柏拉图
1
请关闭手机戒调成震动
请把心帶来请充分讨论不分享请带空杯来，装点水回去
2
课程安排表
课程讲师考试
√ √ √ √
实作
√ √ √ √
助教1 助教2
汤智根吴海燕杨春会邰雪妮张志华王德闯曹刚戴石为
表面处理部
組立部

品管七大手法讲解QA必会技能

工程人员未切实验证
定位方式不合理
模修人员ቤተ መጻሕፍቲ ባይዱ修方式不当
多次折弯累积偏差
折弯间隙变化影响大品管人员未作CSI验证
锁扣不回弹
实配间隙小
对变异要求苛刻
3-3.两类特性要因图:
模具、设备
人员
模具定位不稳定模具改善不及时
品管人员检查不落实责任心不强
模具设计不合理设备维修不力
产线未做好自主检查模修人员技能不够
台湾
95% 96% 93%
大陆
94% 93% 92%
结果显示,周师傅的方法配美国材料良品率最高,为98%.
3-2.实例二: 冲压成型质量状况日报表
日期:
班别: □ 白班 □ 夜班
模号: 第一套 □ 第二套 □ 第三套 □
制程不良项目
序厂生良制制来总拉裂
其它
程程料不
小
号
商
产
品
不良数
………… ………… …… ………… ……………… … … … … … … … … … …. … … … … … … … … … … … … … … … … ... … … … … … … … … … … … … … … … … … … … … … … … … … … … … …. … … … … ………… ………… …… ………… ……………… … … … … … … … … … … … … … … … … 170 … … … 最大值 … 124 … … … … … … … … … … … … … … … … … … 最小值
3-6.直方图:
D.决定组距: 组距=全距/组数 E.决定各组之上下组界. 1.最小一组的下组界=最小值-测定值之最小位数/2 2.最小一组的上组界=下组界+组距=123.5+4=127.5 依此类推. F.作次数分配表.(如附表)

05 QC七大手法-散布图

① 能大概掌握原因与结果之间是否有关联及关联的程度如何； ② 能检查离岛现象是否存在 ③ 原因与结果关联性高时，二者可互为替代变数。
（对于过程参数或产品特性的掌握，可从原因或结果中选择一较经济性的变数予以监测。并且可通过观察一变数的变化来知道另一变数的变化。）
三、散布图适用的情况
① 散布图主要使用于解决问题之原因调查阶段。 ② 使用在开发阶段与生产准备阶段。
40.0
实例：散布图
温度与产量相關性分析
R=0.638
y = 0.2319x + 11.02 R2 = 0.4073
45.0
50.0
55.0
(℃)
判定相关方式
图解法：
正相关強：表 X 增加时， Y 也會隨之增加
负相关強：表 X 增加时则 Y減少
无相关：不論 X 的增加或減少时对 Y 的结果都沒有什麼影响
收集以下数据请以散布图解析之。
实例：散布图
NO 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
溫度 44.6 50.3 46.2 46.9 48.9 43.7 48.8 46.6 47.3 51.7 45.6 44.6 45.4 46.4 47.9 49.2 49.2 47.5 43.5 50.0 44.7 49.1 45.9 49.9 43.5
（就是当两组数据具有关联性，因此想藉由一方的控制，让另一方数据自然产生时所用的工具。）
四、散布图图应用范围
① 相对的两种变数（结果与原因） ② 变数的性质 ③ 在原因中取可以管理的特性
五、散布图作法
步骤1：明确目的决定调查的对象；步骤2：收集两种相对应数据(最少30组)并且整理写到数据表上；步骤3：分別找出两种数据之最大值及最小值；步骤4：绘纵轴、棋轴並作适当刻度(刻度大小应考虑最大值与最小值之差)

七大手法之散布图与直方图

L X’ Y’
L Y’ Y’
X’
6. 查出临界相关数据（γα ）。
249.6
＝ 0.814
176.3 533.2
根据N－2和显著性水平α查表求得γα＝0.361（α ＝ 0.05）
7. 判断。判断规则：
γ＝ 0.814 > γα＝ 0.361 ，所以钢的硬度与淬火温度呈强正相关。
后附相关系数检查表
以上三种判断方法对同一实例进行分析判断的结论是一致的。
第16页
质量管理七大手法培训教材
相关系数检查表
α
N－2
21 22 23 24 25 26 27 28 29 30
0.05
0.413 0.404 0.396 0.388 0.381 0.374 0.367 0.361 0.355 0.349
0.01
0.526 0.515 0.505 0.496 0. 487 0.478 0.470 0.463 0.456 0.449
若n I＋ n III ＞ n II＋ n IV，则判为正相关若n I＋ n III ＜ n II＋ n IV，则判为负相关
第8页
质量管理七大手法培训教材
2. 象限判断法
第9页
质量管理七大手法培训教材
3. 相关系数判断法
相关系数判断法的应用步骤：
1. 简化X、Y数据。
2. 计算X’2， Y’2，X’ Y’、（ X’ ＋ Y’ ）和（ X’ ＋ Y’ ）2。
第17页
质量管理七大手法培训教材
6.直方图
第18页
质量管理七大手法培训教材
定义
直方图是频数直方图的简称。它是用一系列宽度相等、高度不等的长方形表示数据的图。长方形的宽度表示数据范围的间隔，长方形的高度表示在给定间隔内的数据数。

QC七大手法之散布图演示文稿

3）在QC小组活动中主要用于课题选择、现状调查，也可用于原因分析、要因确认等。
二、散布图的应用步骤
1. 收集成对数据（X，Y）（至少不得少于30对）。 2. 标明 X 轴和 Y 轴。 3. 找出X和Y的最大值和最小值，并用这两个值标定横轴X和纵轴
Y。 4. 描点（当两组数据值相等，即数据点重合时，可围绕数据点画
1. 在散布图上画一条与Y 轴平行的中值线 f，使 f 线的左、右两边的点子数大致相等；
2. 在散布图上画一条与X 轴平行的中值线 g，使 g线的上、下两边的点子数大致相等；
3. f 、 g 两条线把散布图分成4个象限区域I、II、III、IV。分别统计落入各象限区域内的点子数；
4. 分别计算对角象限区内的点子数； 5. 判断规则；若n I＋ n III ＞ n II＋ n IV，则判为正相关若n I＋ n III ＜ n II＋ n IV，则判为负相关
1）对照典型图判断散布图的相关性
Y
X
D、弱负相关
除X外还有其他因素对Y有影响
1）对照典型图判断散布图的相关性
Y
X
E、不相关1）对照典型Fra bibliotek判断散布图的相关性
Y
Y
X
X
F、非线性相关
（曲线相关）
上述判断方法较简单、直观，
但较粗糙，是简易近似判断法。
象限判断法
－－象限判断法又叫中值判断法、符号检定判断法。使用此法的步骤如下：
查出临界相关数据（γα ）。 γα 可根据N－2和显著性水平α查表求得。判断。判断规则
若∣ γ ∣ ＞ γα ，则X与Y相关
若∣ γ ∣ ＜ γα ，则X与Y不相关
QC七大手法之散布图演示文稿

品管(QC)七大手法之散布图

↑Y
→X (5)無相關
→X (6)無相關
(7）負相關（強）
(7）負相關（中度）
(7）負相關（弱）
散布图制作注意事项
❖ 注意事項: 1.注意是否有異常點存在. 2.是否有假相關.
3.是否有必要層別.
•層別後的散佈圖-範例：菜包的柔軟度
y
柔
純糯米
軟
度
↑
糯米、在來米
各半
0
x
→水份
純在來米純在來米
散布图电脑案例制作
目录 1.散布图定义 2.散布图功用与用途 3.散布图的制作 4.散布图案例
散布图定义
定义：把互相有關連的對應數據，在方格紙上
以縱軸表示結果，以橫軸表示原因；然後用點表示出分布形態，根據分布的形態來判斷對應數據之間的相互關係。
散布图功用与用途
❖ 散布图的功用与用途：
1.檢定兩變數間的相關性。 2.從特性要求尋找最適要因。 3.從要因預估特性水準。
1.开启Execl档，将两个因素之数据进行整理； 2.在工具栏中直接点击图表或是插入工具，点击图表； 3.在图表导向中标准类型中选中XY散点图； 4.点击数据区域，选择EXECL档中整理的两个因素数据； 5.完成，生成图表，并右键点图表选项，将标题，XY填
入； 6.图表着色，完成。
人數：30人製作：江老師
35 21
製作日：4/3
33
(kg) 體重 31
120 122 124 126 128 130 132 134 136 138 140
身高(cm)
散布图的判读
↑Y
↑ Y
↑Y
→X （ 1）正相關（強）
→X （2）正相關（中度）

QC七大手法经典解析

对此，应如何作分层法分析？并说明分层类别。分析应如何后尾灯不亮？
月份 7月 8月 9月 10月 11月 12月
三）特性要因图绘图时应注意事项
1）集合有关全员知识与经验。 2）利用脑力激荡法。 3）寻找要因时依5W1H(what/why/where/when/who/how) 方法自问自答及依6M1E探索。 4）以事实为依据, 多利用过去资料及Know How。 5）对要因彻底深入分析追根究底。 6）把要因层别。 7）要标明品名、工程别、作成日期、操作者等。
QC七大手法经典解析
QC 七大手法第一招: 查检表集数据第二招: 柏拉图抓重点第三招: 散布图看相关第四招: 因果图追原因
QC七大手法简介
一、检查表（数据采集表）
典型检查表
一）定义
检查表示使用简单易于了解的标准化表格或图形，作业时仅需填入规定检查记号，再加以统计汇整其数据，即可提供量化分析或对比检查用。系统地收集资料和累积资料，确认事实并对资料进行粗略的整理和简单分析的统计图表。
六）检查表的应用（1）
检查表制作完成后，要让使用者了解，并且作在职训练，使用检查表时应注意下列事项并适时反映。 1)搜集数据要细心、客观，数据是否代表事实？ 2)数据是否集中在某些项目，而各项目间差异为何？ 3)某些事项是否因时间的变化而有所变化？ 4)如有异常，应马上追究原因，并采取必要措施。 5)检查的项目应随着作业的改善而改变。 6)由使用的记录即能迅速判断、采取行动。
分类的项目必须合乎问题的症结，一般的分类先从结果分类上着手，以便洞悉问题之所在；然后再进行原因分类，分析出问题产生之原因，以便采取有效的对策。将此分析的结果，依其结果与原因分别绘制柏拉图。
步骤2: 决定收集数据的期间；并按分类项目，在期间内收集数据。

QC七大手法

QC七大手法QC七大手法：层别法（流程图）、散布图、直方图、控制图、检查表、排列图、鱼骨图（因果图)新QC七大手法：亲和图（也称KJ法）、关联图、系统图、过程决定计划图（PDPC 法）、矩阵图、矩阵数据解析法、箭线图七种。

一检查表(Data collection form)层别法(Stratification)散布图(Scatter)排列图(Pareto)直方图(Histogram)因果图(Cause-Effect diagram)控制图(Control Chart)1. 检查表（Check List）以简单的数据或容易了解的方式，作成图形或表格，只要记上检查记号，并加以统计整理，作为进一步分析或核对检查用，其目的在於『现状调查』。

2. 柏拉图（Pareto Diagram）根据所搜集之数据，以不良原因、不良状况、不良发生或客户抱怨的种类、安全事故等，项目别加以分类，找出比率最大的项目或原因并按照大小顺序排列，再加上累积值的图形。

用以判断问题症结之所。

ν柏拉图应用范围:1.时间管理.，2.安全.3.士气.4.不良率.5.成本.6.营业额.7.医疗ABC法应用:A.时间管理.νB.仓务管理.νC.其它.ν柏拉图实例:3. 特性要因（因果图）图（Characteristic Diagram）一个问题的特性（结果）受一些要因（原因）的影响时，将这些要因加以整理，而成为有相互关系而且有条且有系统的图形。

其主要目的在阐明因果关系，亦称『因果图』，因其形状与鱼骨图相似故又常被称作『鱼骨图』。

图形称为特性要因图,工程鱼骨图或因果图.它为1952年日本品管权威学者石川馨博士所发明,又称“石川图”.作法:•4M1E法:(人、机、料、法、环境)•5W1H法:(What、Where、When、Who、Why、How)•创造性思考法:希望点例举法、缺点列举法、特性列案法.•脑力激荡法:“Brain Storming”严禁批评、自由奔放.•系统图法:依因果关系组合排列,作成问题点系统图.追求原因型追求对策型4.散布图（Scatter Diagram）把互相有关连的对应数据，在方格上以纵轴表示结果，以横轴表示原因，然后用点表示分布形态，根据分析的形态未研判对应数据之间的相互关系。

QC七大手法--(散布图)讲义

4
依據製作散佈圖的步驟: (1)步驟1已完成 (2) 找出數據中的最大值與最小值 ,並求出R
最大值-最小值=R
硬度熔燒溫度
59-42=17 890℃-810℃=80℃
(3)參考R,設定刻度組數,在座標軸上標上刻度。從數據表可看出硬度隨著熔燒溫度變化而變化,則我們可以設X代表熔燒溫度,Y代表硬度。
圖D
步伐
‧‧
‧‧‧‧‧‧‧‧ ‧
‧
‧ ‧ ‧
‧ ‧
‧‧ ‧‧ ‧‧
‧
‧‧
3.不相關(無關)
溫度
濕度
Y的變化與X毫無關係的情形,X與Y之間無關係,必須再調查除了X以外的原因。如氣壓與溫度,見圖E。
圖E
‧‧
溫度
‧
‧ ‧ ‧‧ ‧‧ ‧ ‧‧
‧ ‧ ‧ ‧
‧ ‧
‧
‧ ‧
‧ ‧
‧
‧
‧ ‧
氣壓
圖F
記憶
‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧
‧‧ ‧
‧ ‧‧ ‧‧‧‧‧‧‧‧‧
‧‧
‧
年齡
4.曲線相關
作記號的點會呈現某種特定形狀。X與Y並沒有呈直線定比例的變化,但是點的並列方法卻有一定的傾向。
如20年19齡/7與/3記憶,見圖F。
3
5.
零相關,如圖G 圖G
...................................
五.實例製作散佈圖
820
4
55
860
14
54
880
24
51
860
5
48
820
15
43
840
25

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第九章散布图(Scatter Diagram)
一、前言
散布图有以下的作用：
⒈能大概掌握原因与结果之间是否有关联及关联的程度如何。

图2-1。

⒉能检查离岛现象是否存在。

图2-2。

⒊原因与结果关联性高时，二者可互为替代变数。

对于过程参数或
产品特性的掌握，可从原因或结果中选择一较经济性的变数予以监测。

并且可通过观察一变数的变化来知道另一变数的变化。

二、散布图的定义
特性要因图（鱼骨图）大概可以了解工程上那些原因会影响产品的质量特性，散布图也是以这种因果关系的方式来表示其关连性。

并将因果关系所对应变化的数据分别点绘在x —y 轴坐标的象限上，以观察其中的关联性是否存在。

三、散布图的制作方法
以横轴（X 轴）表示原因，纵轴（Y 轴）表示结果，作法如下： ⒈收集成对的数据(x 1,y 1)，(x 2,y 2)，…整理成数据表。

第九章散布图 145
146 品管七大手法
Y X Y X
⒉找出x,y ⒊以x,y 的最大值及最小值建立x —y 坐标，并决定适当刻度便于绘
点。

⒋将数据依次点于x
—y 坐标中，两组数据重复时以☉表示，三组数
据重复时以表示。

⒌必要时，可将相关资料注记在散布图上。

⒍散布图的注意事项：
⑴是否有异常点：
有异常点时，不可任意删除该异常点，除非异常的原因已确实掌握。

⑵是否需分层：
数据的获得常常因为操作人员、方法、材料、设备或时间等的不同，而使数据的关联性受到扭曲。

a. 全体时低度关联，分层后高度关联。

b. 全体时高度关联，分层后低度关联。

⑶散布图是否与原有技术、经验相符：
第九章散布图 147 Y X Y X Y X Y X
散布图若与原有技术、经验不相符时，应追查原因与结果是否受到其他因素干涉。

四、散布图的判读
依散布图的方向、形状，有以下几种关联情形：
⒈完全正（负）关联：点散布在一直线上。

⒉高度正(
负)关联：原因(X)与结果(Y)的变化近于等比例。

3.中度正(负)关联：原因(X)与结果
(Y)的变化近于等比例。

4.低度正(
负)关联：原因(X)与结果(Y)的变化近于等比例。

148
X X X X X X
5.无关联：原因(X)与结果(Y)的变化完全不成比例。

6.曲线关联：原因(X)与结果(Y)的变化呈曲线变化。

五、示例 ⒈空气污染程度，与肺疾病的病例数目间的关系。

⒉天气温度(0C)与空调销售量间的关系。

六、实例演练
真空电镀的作业过程中，电子束的强度(power)影响电镀产品的X
肺疾病病例
空气污染程度销售量冷气机
温度(0C)
镀膜厚(thickness)度，希望找出二者间的相互关系。

⒈收集数据。

⒉找出x ，y 的最大值及最小值。

Xmax=100 Ymax=5.4
Xmin=50 Ymin=3.2
⒊划出X-Y 轴的坐标并取适当刻度。

⒋将数据点绘x-y 坐标中。

150 品管七大手法
X=强度(KV) Y=膜厚(μm) X
X
X=强度(KV) Y=膜厚(μm)。