下载文档原格式
有理数大小的比较说课稿一、教材分析（一）地位与作用有理数大小的比较是紧接在有理数、数轴、相反数和绝对值之后学习的。
并且数轴和绝对值又是有理数大小比较这一新知识的根基和生长点。
两者分别从形的角度和数的角度研究问题，得到了有理数大小的比较方法，并且“数”的抽象又是借助于“形”的直观，因此数轴是“有理数大小比较”中贯穿始终的主线。
（二）教学目标根据新课标的要求以及七年级学生的认知水平，我制定本节课的目标如下：1.知识与能力目标：掌握利用数轴和绝对值来比较有理数的大小的方法，初步学会数形结合的思想方法。
2.过程与方法目标：经历从现实问题中来探索有理数的大小比较，从数形两个侧面理解与解决问题，使学生体会到数形结合数学思想方法的美。
3.情感目标：从学生熟悉的现实环境中学习有理数的大小比较，体会数学知识与现实世界的联系；通过自主探索、归纳来发现知识，使学生体验成功的乐趣。
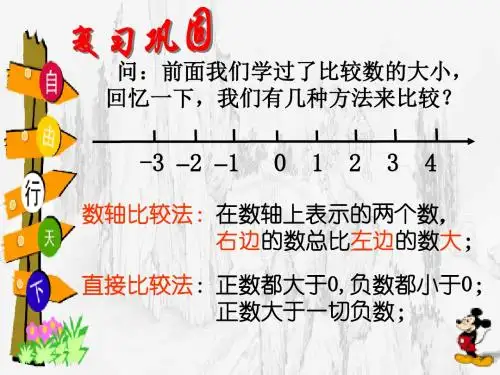
（三）教学重点与难点重点：利用数轴和绝对值来比较有理数的大小。
难点：比较两个负有理数的大小。
二、教法分析初一学生已经接触关于数轴的知识，因此，本节课采用指导探究法进行教学，通过两个师生双边活动，一是师生互动，共同探索；二是合理引导，激发学生的求知欲。
引导他们解决问题并掌握解决问题的规律和方法，增强学生的探索的能力和创造能力。
三、学法分析根据新课程理念，学生是学习的主体，教师是学习的帮助者、引导者。
考虑到这节课主要是通过老师的引导让学生自己发现知识、提高能力。
我主要引导学生亲自经历知识的产生和归纳总结过程，突出学生的主体地位，让学生经历问题的发生、发展和解决过程。
在解决问题的过程中完成教学目标。
四、教学过程：（一）情境引入生活中，我们每天都会谈及温度，比如某城市一天中4个不同时刻的气温分别是-3℃，-5℃，4℃，0℃，哪个时刻气温最高，哪个时刻气温最低？其实这个问题就可以归结为比较有理数-3，-5,4,0的大小，我们已经能够比较两个正数的大小及正数与0的大小，引入负数以后，在有理数范围内，怎样比较数的大小呢？这节课我们就来学习有理数的大小比较。
有理数的加减运算技巧在进行有理数的加减运算的时候，适当地运用一些运算技巧，可以简化运算过程，使我们的运算速度及运算正确性都有很大的提高.现举例说明一些常用的运算技巧，供同学们学习时参考.一、同号相加例1.计算：(14)(4)(2)(26)(3)++-+-+++-.解：原式 = [〔+14〕+〔+26〕]+[〔-4〕+〔-2〕+〔-3〕]=〔+40〕+〔-9〕= 31.说明：把符号相同的数结合相加，一是减少运算量，二也可以防止错误的发生.二、异号相抵例2.计算：117-48+54-116.解：原式 =〔117-116〕+〔-48+54〕= 1+6 = 7.三、相反数抵消例3.计算：77()( 2.3)(0.1)( 2.2)()( 3.5) 1010-+++-+-++++.解：原式=77[()()][( 2.3)(0.1)( 2.2)]( 3.5) 1010-+++++-+-++= 0+0+〔+3.5〕= 3.5.四、同分母相加例4.计算：11113(2)()0.25() 2436--+--++.解：原式 =11111 (2)(3) 44236-+-+=321 2(3)666 +-+= 2+133=153.五、倒序叠加例5.计算：1233989 1995199519951995 ++++.解：设12339891995199519951995S=++++，将S中各加数倒序排列，得39893988211995199519951995S=++++，∵1398923988398912()()() 199519951995199519951995 S=++++++3989399039903990199519951995=+++39903989239891995=⨯=⨯.∴3989S=.六、裂项相消例6.计算：1111178 315356399143 +++++.解：原式117813351113=+++⨯⨯⨯1111111111(1)()()39() 2323529111113 =-+-++-+-11111139(1)3 233591111=-+-++-+-1139(1)321111=-+-1=.七、分组结合例7.计算：1+2-3+4-5+6-7+…+98-99+100.解：原式1(234)(567)(9899100) =+-++-+++-+= 1+3+6+…+99= 1+3〔1+2+ (33)= 1+3×561 = 1684.八、分解约分例8.计算：1919191919 ()() 9191919191---.解：原式19100001910019119100191 91100009110091191100191⨯+⨯+⨯⨯+⨯=-+⨯+⨯+⨯⨯+⨯191010119101911010191101⨯⨯=-+⨯⨯19199191=-+=.九、拆数凑整例9.计算：7+97+997+9997+99997.解：原式＝〔10-3〕+〔100-3〕+〔1000-3〕+〔10000-3〕+〔100000-3〕＝111110-3×5＝111095.十、添项配对例10.11111 1245121024 2048102451242 +++++.分析：经过观察可以发现，每一个数与其自身相加都会得到下一个数，因此，在首项前添上一个112048后，就会产生连锁反响从第一个数一直加到最后一个数.解：原式1111111 1(11)245121024 204820482048102451242 =-+++++++ 111111(22)410242048102410245122=-+++++＝……1120492048=-+2047 20472048 =.。
