下载文档原格式
钢结构轴心受力构件计算3.1 轴心受力构件概述在钢结构中，轴心受力构件的应用十分广泛，如桁架、塔架和网架、网壳等杆件体系。
这类结构的节点通常假设为铰接，当无节间荷载作用时，杆件只受轴向力（轴向拉力或轴向压力）的作用，称为轴心受力构件（轴心受拉构件或轴心受压构件）。
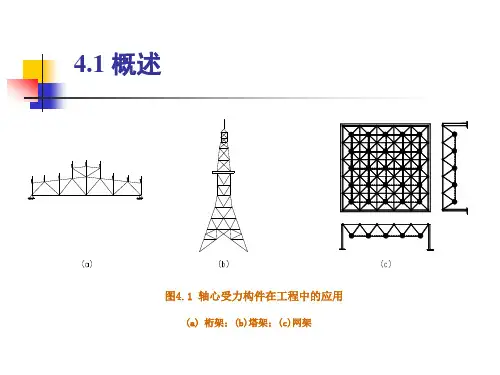
图3-1所示为轴心受力构件在工程上应用的一些实例。
图3-1 轴心受力构件在工程中的应用（a）桁架；（b）塔架；（c）网架轴心受力构件常用的截面形式可分为实腹式和格构式两大类。
（1）实腹式构件制作简单，与其他构件的连接也比较方便，常用的截面形式很多，可直接选用轧制型钢截面，如圆钢、钢管、角钢、工字钢、H 型钢、T 型钢等[图3-2（a）]；也可选用由型钢或钢板组成的组合截面[图3-2（b）]；在轻型结构中则可采用冷弯薄壁型钢截面[图3-2（c）]。
以上这些截面中，截面紧凑（如圆钢）或对两主轴刚度相差悬殊者（如单槽钢、工字钢），一般适用于轴心受拉构件，而受压构件通常采用较为开展、组成板件宽而薄的截面。
（2）格构式构件[图3-2（d）]容易使压杆实现两主轴方向的稳定性。
这种构件的刚度大、抗扭性好，用料较省。
格构式截面一般由两个或多个型钢肢件组成，肢件之间采用缀条或缀板连成整体，缀条和缀板统称为缀材。
图3-2 轴心受力杆件的截面形式（a）轧制型钢截面；（b）焊接实腹式组合截面；（c）冷弯薄壁型钢截面；（d）格构式截面3.2 轴心受力构件的强度及刚度轴心受拉构件的设计除根据结构用途、构件受力大小和材料供应情况选用合理的截面形式外，还要对所选截面进行强度和刚度验算。
强度要求就是使构件截面上的最大正应力不超过钢材的强度设计值，刚度要求就是使构件的长细比不超过容许长细比。
轴心受压构件在设计时，除使所选截面满足强度和刚度要求外，还应使其满足构件整体稳定性和局部稳定性的要求。
整体稳定性要求是使构件在设计荷载作用下不致发生屈曲而丧失承载能力；局部稳定性要求一般是使组成构件的板件宽厚比不超过规定限值，以保证板件不会屈曲，或者使格构式构件的分肢不发生屈曲。
轴心受力构件设计轴心受拉构件时需进行强度和刚度的验算，设计轴心受压构件时需进行强度、整体稳定、局部稳定和刚度的验算。
一、轴心受力构件的强度和刚度1．轴心受力构件的强度计算轴心受力构件的强度是以截面的平均应力达到钢材的屈服点为承载力极限状态f A N n ≤=σ (1) 式中 N ——构件的轴心拉力或压力设计值；n A ——构件的净截面面积；f ——钢材的抗拉强度设计值。
采用高强度螺栓摩擦型连接的构件，验算最外列螺栓处危险截面的强度时，按下式计算：f A N n≤='σ (2) 'N =)5.01(1n n N - (3)式中 n ——连接一侧的高强度螺栓总数；1n ——计算截面(最外列螺栓处)上的高强度螺栓数；0.5——孔前传力系数。
采用高强度螺栓摩擦型连接的拉杆，除按式(2)验算净截面强度外，还应按下式验算毛截面强度f A N ≤=σ (4)2．轴心受力构件的刚度计算轴心受力构件的刚度是以限制其长细比保证][λλ≤ (5) 式中 λ——构件的最大长细比；[λ]——构件的容许长细比。
二、 轴心受压构件的整体稳定1．理想轴心受压构件的屈曲形式理想轴心受压构件可能以三种屈曲形式丧失稳定：①弯曲屈曲 双轴对称截面构件最常见的屈曲形式。
②扭转屈曲 长度较小的十字形截面构件可能发生的扭转屈曲。
③弯扭屈曲 单轴对称截面杆件绕对称轴屈曲时发生弯扭屈曲。
2．理想轴心受压构件的弯曲屈曲临界力若只考虑弯曲变形，临界力公式即为著名的欧拉临界力公式，表达式为N E =22l EI π=22λπEA (6) 3．初始缺陷对轴心受压构件承载力的影响实际工程中的构件不可避免地存在初弯曲、荷载初偏心和残余应力等初始缺陷，这些缺陷会降低轴心受压构件的稳定承载力。
1）残余应力的影响当轴心受压构件截面的平均应力p f >σ时，杆件截面内将出现部分塑性区和部分弹性区。
由于截面塑性区应力不可能再增加，能够产生抵抗力矩的只是截面的弹性区，此时的临界力和临界应力应为：N cr =22l EI e π=22lEI π·I I e (7) cr σ=22λπE ·I I e (8) 式中 I e ——弹性区的截面惯性矩(或有效惯性矩)；I ——全截面的惯性矩。
钢结构设计轴心受力构件截面强度计算7.1.1 轴心受拉构件，当端部连接及中部拼接处组成截面的各板件都由连接件直接传力时，其截面强度计算应符合下列规定：1 除采用高强度螺栓摩擦型连接者外，其截面强度应采用下列公式计算：2 采用高强度螺栓摩擦型连接的构件，其毛截面强度计算应采用式（7.1.1-1），净截面断裂应按下式计算：3 当构件为沿全长都有排列较密螺栓的组合构件时，其截面强度应按下式计算：式中：N——所计算截面处的拉力设计值(N)；f——钢材的抗拉强度设计值(N／mm2)；A——构件的毛截面面积(mm2；A n——构件的净截面面积，当构件多个截面有孔时，取最不利的截面(mm2)；f u——钢材的抗拉强度最小值(N／mm2)；n——在节点或拼接处，构件一端连接的高强度螺栓数目；n1——所计算截面(最外列螺栓处)高强度螺栓数目。
7.1.2 轴心受压构件，当端部连接及中部拼接处组成截面的各板件都由连接件直接传力时，截面强度应按本标准式(7.1.1-1)计算。
但含有虚孔的构件尚需在孔心所在截面按本标准式(7.1.1-2)计算。
7.1.3 轴心受拉构件和轴心受压构件，当其组成板件在节点或拼接处并非全部直接传力时，应将危险截面的面积乘以有效截面系数η，不同构件截面形式和连接方式的η值应符合表7.1.3的规定。
表7.1.3 轴心受力构件节点或拼接处危险截面有效截面系数条文说明7.1.1 原规范在条文说明中给出了式(7.1.1-1)和式(7.1.1-2)，并指出“如果今后采用屈强比更大的钢材，宜用这两个公式来计算，以确保安全”。
当前，屈强比高于0.8的Q460钢已开始采用，为此，用这两个公式取代了净截面屈服的计算公式。
对于Q235和Q345钢，用这两个公式可以节约钢材。
当沿构件长度有排列较密的螺栓孔时，应由净截面屈服控制，以免变形过大。
7.1.2 轴压构件孔洞有螺栓填充者，不必验算净截面强度。
7.1.3 有效截面系数是考虑了杆端非全部直接传力造成的剪切滞后和截面上正应力分布不均匀的影响。
轴心受力构件的强度和刚度计算
1．轴心受力构件的强度计算
轴心受力构件的强度是以截面的平均应力达到钢材的屈服应力为承载力极限状态。
轴心受力构件的强度计算公式为
f A N
n
≤=
σ （4-1） 式中： N ——构件的轴心拉力或压力设计值；
n A ——构件的净截面面积；
f ——钢材的抗拉强度设计值。
对于采用高强度螺栓摩擦型连接的构件，验算净截面强度时一部分剪力已由孔前接触面传递。
因此，验算最外列螺栓处危险截面的强度时，应按下式计算：
f A N n
≤=
'
σ （4-2）
'N =)5.01(1
n
n N - （4-3）
式中： n ——连接一侧的高强度螺栓总数；
1n ——计算截面（最外列螺栓处）上的高强度螺栓数； 0.5——孔前传力系数。
采用高强度螺栓摩擦型连接的拉杆，除按式（4-2）验算净截面强度外，还应按下式验算毛截面强度
f A
N
≤=
σ （4-4）
式中： A ——构件的毛截面面积。
2．轴心受力构件的刚度计算
为满足结构的正常使用要求，轴心受力构件应具有一定的刚度，以保证构件不会在运输和安装过程中产生弯曲或过大的变形，以及使用期间因自重产生明显下挠，还有在动力荷载作用下发生较大的振动。
轴心受力构件的刚度是以限制其长细比来保证的，即
][λλ≤ （4-5）
式中： λ——构件的最大长细比；
[λ]——构件的容许长细比。
3. 轴心受压构件的整体稳定计算
《规范》对轴心受压构件的整体稳定计算采用下列形式：
f A
N
≤ϕ （4-25）
式中：ϕ——轴心受压构件的整体稳定系数，y
cr
f σϕ=。
整体稳定系数ϕ值应根据构件的截面分类和构件的长细比查表得到。
构件长细比λ应按照下列规定确定： （1）截面为双轴对称或极对称的构件
⎭
⎬⎫
==y y y x x x i l i l //00λλ
（4-26）
式中：x l 0，y l 0——构件对主轴x 和y 的计算长度；
x i ，y i ——构件截面对主轴x 和y 的回转半径。
双轴对称十字形截面构件，x λ或y λ取值不得小于5.07b/t （其中b/t 为悬伸板件宽厚比）。
（2）截面为单轴对称的构件
以上讨论柱的整定稳定临界力时，假定构件失稳时只发生弯曲而没有扭转，即所谓弯曲屈曲。
对于单轴对称截面，绕对称轴失稳时，在弯曲的同时总伴随着扭转，即形成弯扭屈曲。
在相同情况下，弯扭失稳比弯曲失稳的临界应力要低。
因此，对双板T 形和槽形等单轴对称截面进行弯扭分析后，认为绕对称轴（设为y 轴）的稳定应取计及扭转效应的下列换算长细比代替y λ
[]
2
/122202022222)/1(4)()(2
1
z
y z y z y
yz i e λ
λλλλλ
λ--+++=
)/7.25//(2
202ωωλl I I A i t z +=
单角钢截面和双角钢组合T 形截面绕对称轴的换算长细比可采用简化方法确定。
无任何对称轴且又非极对称的截面（单面连接的不等边单角钢除外）不宜用作轴心受压构件。
对单面连接的单角钢轴心受压构件，考虑折减系数后，可不考虑弯扭效应。
当槽形截面用于格构式构件的分肢，计算分肢绕对称轴（y 轴）的稳定性时，不必考虑扭转效应，直接y λ用查出y ϕ值。
4．工字形和H 形截面轴心受压构件的局部稳定
在单向压应力作用下，当板件进入弹塑性状态后，临界应力可用下式表达
2
2
2)()1(12b
t E k cr νπχησ-= （4-36） 式中： χ——板边缘的弹性约束系数；
η——弹性模量折减系数，根据轴心受压构件局部稳定的试验资料，可
取为
E f E f y y /)/0248.01(1013.02
2λλη-=
（4-37）
局部稳定验算考虑等稳定性，保证板件的局部失稳临界应力不小于构件整体稳定的临界应力（y f ϕ），即
y f b
t
v E ϕχβπη≥-22
2)()1(12 （4-38）
由式（4-38）即可确定板件宽厚比的限值。
（1）工字形和H 形截面的受压翼缘
工字形截面的腹板一般较薄，对翼缘板几乎没有嵌固作用，翼缘可视为三边简支一边自由的均匀受压板，取屈曲系数k ＝0.425，弹性约束系数χ＝1.0。
由式（4-38）可以得到翼缘板外伸部分的宽厚比b /t 与长细比λ的关系
y
f t b 235
)1.010(λ+≤ （4-39）
式中：λ——构件两方向长细比的较大值。
当λ＜30时，取λ=30；当λ＞100
时，取λ＝l00。
（2）工字形和H 形截面的腹板
腹板可视为四边支承板，屈曲系数k ＝4。
当腹板发生屈曲时，翼缘板对腹板将起一定的弹性嵌固作用，取约束系数χ＝1.3。
由式（4-38）经简化后得到腹板高厚比w t h /0的表达式
y
w f t h 235)5.025(0λ+≤ （4-40） 同理，可得其他截面构件的板件宽厚比限值。
轴心受力构件的强度和刚度验算
1．图1（a ）所示为一支架，其支柱的压力设计值为N ，柱两端铰接，截面无孔眼削弱。
已知：钢材等级（f ），容许长细比[]λ。
支柱选用材料的规格（y x i i A ,,），整体稳定系数ϕ值表。
验算此支柱的承载力。
图1
解：
（1）强度验算：强度因截面无孔眼削弱，可不验算强度。
（2）局部稳定验算：轧制工字形钢的翼缘和腹板均较厚，可不验算局部稳定。
（3）刚度验算。
长细比
[]λλ<=
x
x
x i l 0 []λλ<=
y
y y i l 0
（4）整体稳定验算：
y λ远大于x λ，故由y λ计算得592.0=ϕ，于是根据构件的截面分类和构件的长细比查表
得整体稳定系数ϕ值。
2
22
3205)(2.20010
135592.0101600mm N f mm N A N =<=⨯⨯⨯=ϕ
2．图2所示一上端铰接，下端固定的轴心受压柱，承受的压力设计值为N 。
已知：柱的长度，计算长度系数μ，钢材等级（f ）以及A ，x i ，y i 。
容许长细比[]λ。
柱截面的尺寸如图所示。
截面绕x 轴和y 轴分别属于b 类和c 类截面。
已知b 类截面的整体稳定系数表与c 类截面的整体稳定系数表，局部稳定验算公式：y w f t h /235)5.025(0λ+=，
y f b /235)1.010(λ+=。
验算此柱的整体稳定，刚度和局部稳定。
图2
解：
（1）计算长细比
y y y x x x i l i l /,
/00==λλ
（2）计算整体稳定系数
由题目所给的表中可以计算出y x ϕϕ,；取min ϕ （3）整体稳定验算：
f A N <)ϕ
整体稳定满足要求。
（4）刚度验算：
[]λλ<y
刚度满足要求。
（5）局部稳定验算： 翼缘宽厚比：
y f t b 235)1.010(λ+≤ 腹板高厚比：
y
w f t h 235)5.025(0λ+≤ 局部稳定满足要求。
3．如图3所示支柱上下端均为铰接且设置支撑。
支柱长度为9m ，在两个三分点处均有侧向支撑，以阻止柱在弱轴方向的过早失稳。
已知：构件的设计压力为N ，容许长细比[]λ，支柱材料的规格（A ，x i ，y i ），钢材的等级（f ）。
截面绕x 轴属于a 类截面，绕y 轴属于b 类截面，且知a 类截面的整体稳定系数表与b 类截面的整体稳定系数表。
验算此支柱的整体稳定和刚度。
图1
解：
（1）验算支柱的刚度
先计算长细比y y y x x x i l i l /,
/00==λλ
][λλ<x ，][λλ<y
刚度满足要求。
（2）验算此支柱的整体稳定
由题目所给的a 类截面的整体稳定系数表与b 类截面的整体稳定系数表中可以计算出
y x ϕϕ,；取min ϕ
进行整体稳定性验算：
f A N <)ϕ
整体稳定性满足要求。
