论述一元线性回归的基本步骤

origin线性拟合的斜率和截距
求origin线性拟合的斜率和截距，是求解一元线性回归问题的
基本步骤。

一元线性回归问题的模型可以表示为：y=ax+b，
其中a为斜率，b为截距。

要求求解origin线性拟合的斜率和截距，首先需要准备足够的
数据，即x和y的值，并将其分别放入x和y的数组中。

然后，根据x和y的值，计算出x的平均值和y的平均值，分别记为
x_mean和y_mean。

接下来，根据x和y的值，计算出x和y的方差，分别记为
x_var和y_var，以及x和y的协方差，分别记为x_cov和
y_cov。

最后，根据以上计算出的x_mean、y_mean、x_var、y_var、
x_cov和y_cov，可以计算出origin线性拟合的斜率a和截距b，其计算公式分别为：
a=x_cov/x_var
b=y_mean-a*x_mean
因此，求origin线性拟合的斜率和截距，需要准备足够的数据，并计算出x的平均值、y的平均值、x的方差、y的方差、x的
协方差和y的协方差，最后根据以上计算出的值，可以计算出origin线性拟合的斜率和截距。

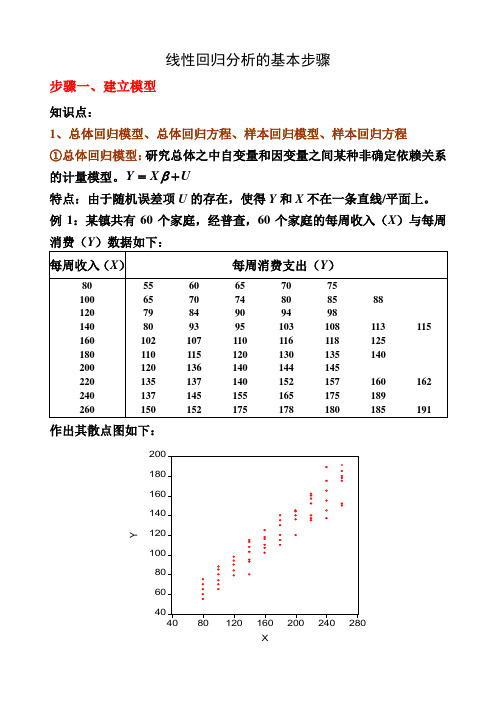
线性回归分析的基本步骤步骤一、建立模型知识点：1、总体回归模型、总体回归方程、样本回归模型、样本回归方程 ①总体回归模型：研究总体之中自变量和因变量之间某种非确定依赖关系的计量模型。

Y X U β=+特点：由于随机误差项U 的存在，使得Y 和X 不在一条直线/平面上。

例1：某镇共有60个家庭，经普查，60个家庭的每周收入（X ）与每周消费（Y ）数据如下：作出其散点图如下：②总体回归方程（线）：由于假定0EU =，因此因变量的均值与自变量总处于一条直线上，这条直线()|E Y X X β=就称为总体回归线（方程）。

总体回归方程的求法：以例1的数据为例，求出E (Y |X 由于01|i i i E Y X X ββ=+，因此任意带入两个X i 和其对应的E (Y |X i )值，即可求出01ββ和，并进而得到总体回归方程。

如将()()222777100,|77200,|137X E Y X X E Y X ====和代入()01|i i i E Y X X ββ=+可得：01001177100171372000.6ββββββ=+=⎧⎧⇒⎨⎨=+=⎩⎩以上求出01ββ和反映了E (Y |X i )和X i 之间的真实关系，即所求的总体回归方程为：()|170.6i i i E Y X X =+，其图形为：③样本回归模型：总体通常难以得到，因此只能通过抽样得到样本数据。

如在例1中，通过抽样考察，我们得到了20个家庭的样本数据：那么描述样本数据中因变量Y 和自变量X 之间非确定依赖关系的模型ˆY X e β=+就称为样本回归模型。

④样本回归方程（线）：通过样本数据估计出ˆβ，得到样本观测值的拟合值与解释变量之间的关系方程ˆˆY X β=称为样本回归方程。

如下图所示：⑤四者之间的关系：ⅰ：总体回归模型建立在总体数据之上，它描述的是因变量Y 和自变量X 之间的真实的非确定型依赖关系；样本回归模型建立在抽样数据基础之上，它描述的是因变量Y 和自变量X 之间的近似于真实的非确定型依赖关系。

线性回归分析的基本步骤步骤一、建立模型知识点：1、总体回归模型、总体回归方程、样本回归模型、样本回归方程 ①总体回归模型：研究总体之中自变量和因变量之间某种非确定依赖关系的计量模型。

Y X U β=+特点：由于随机误差项U 的存在，使得Y 和X 不在一条直线/平面上。

例1：某镇共有60个家庭，经普查，60个家庭的每周收入（X ）与每周消费（Y ）数据如下：作出其散点图如下：②总体回归方程（线）：由于假定0EU =，因此因变量的均值与自变量总处于一条直线上，这条直线()|E Y X X β=就称为总体回归线（方程）。

总体回归方程的求法：以例1的数据为例 由于01|i i i E Y X X ββ=+，因此任意带入两个X i 和其对应的E (Y |X i )值，即可求出01ββ和，并进而得到总体回归方程。

如将()()222777100,|77200,|137X E Y X X E Y X ====和代入()01|i i i E Y X X ββ=+可得：01001177100171372000.6ββββββ=+=⎧⎧⇒⎨⎨=+=⎩⎩以上求出01ββ和反映了E (Y |X i )和X i 之间的真实关系，即所求的总体回归方程为：()|170.6i i i E Y X X =+，其图形为：③样本回归模型：总体通常难以得到，因此只能通过抽样得到样本数据。

如在例1中，通过抽样考察，我们得到了20个家庭的样本数据：那么描述样本数据中因变量Y 和自变量X 之间非确定依赖关系的模型ˆY X e β=+就称为样本回归模型。

④样本回归方程（线）：通过样本数据估计出ˆβ，得到样本观测值的拟合值与解释变量之间的关系方程ˆˆY X β=称为样本回归方程。

如下图所示：⑤四者之间的关系：ⅰ：总体回归模型建立在总体数据之上，它描述的是因变量Y 和自变量X 之间的真实的非确定型依赖关系；样本回归模型建立在抽样数据基础之上，它描述的是因变量Y 和自变量X 之间的近似于真实的非确定型依赖关系。

第二章 一元线性回归模型2.1 一元线性回归模型的基本假定有一元线性回归模型（统计模型）如下， y t = β0 + β1 x t + u t上式表示变量y t 和x t 之间的真实关系。

其中y t 称被解释变量（因变量），x t 称解释变量（自变量），u t 称随机误差项，β0称常数项，β1称回归系数（通常未知）。

上模型可以分为两部分。

（1）回归函数部分，E(y t ) = β0 + β1 x t ,（2）随机部分，u t 。

图2.1 真实的回归直线这种模型可以赋予各种实际意义，居民收入与支出的关系；商品价格与供给量的关系；企业产量与库存的关系；身高与体重的关系等。

以收入与支出的关系为例。

假设固定对一个家庭进行观察，随着收入水平的不同，与支出呈线性函数关系。

但实际上数据来自各个家庭，来自同一收入水平的家庭，受其他条件的影响，如家庭子女的多少、消费习惯等等，其出也不尽相同。

所以由数据得到的散点图不在一条直线上（不呈函数关系），而是散在直线周围，服从统计关系。

“线性”一词在这里有两重含义。

它一方面指被解释变量Y 与解释变量X 之间为线性关系，即另一方面也指被解释变量与参数0β、1β之间的线性关系，即。

1ty x β∂=∂，221ty β∂=∂0 ，1ty β∂=∂，2200ty β∂=∂2.1.2 随机误差项的性质随机误差项u t 中可能包括家庭人口数不同，消费习惯不同，不同地域的消费指数不同，不同家庭的外来收入不同等因素。

所以在经济问题上“控制其他因素不变”是不可能的。

随机误差项u t 正是计量模型与其它模型的区别所在，也是其优势所在，今后咱们的很多内容，都是围绕随机误差项u t 进行了。

回归模型的随机误差项中一般包括如下几项内容： （1）非重要解释变量的省略，（2）数学模型形式欠妥， （3）测量误差等，（4）随机误差（自然灾害、经济危机、人的偶然行为等）。

2.1.3 一元线性回归模型的基本假定通常线性回归函数E(y t ) = β0 + β1 x t 是观察不到的，利用样本得到的只是对E(y t ) =β0 + β1 x t 的估计，即对β0和β1的估计。

建立一元线性回归模型
建立一元线性回归模型的步骤如下：
1.选择自变量和因变量：确定自变量和因变量之间的关系，并准备
好数据。

2.计算自变量的平均值和标准差，因变量的平均值和标准差：使用
公式计算自变量和因变量的平均值和标准差。

3.计算自变量和因变量的相关系数：使用公式计算自变量和因变量
的相关系数。

4.计算回归系数：使用公式计算回归系数。

5.建立回归方程：使用计算得到的回归系数和自变量的平均值，建
立回归方程。

6.对回归方程进行检验：使用残差平方和、残差平均值、残差标准
差和相关系数等指标对回归方程进行检验。

7.进行预测：使用建立的回归方程进行预测，得出因变量的预测值。

8.对预测结果进行评估：使用预测误差、预测精度、预测准确率等
指标对预测结果进行评估。

总的来说，建立一元线性回归模型的过程包括选择自变量和因变量、计算自变量和因变量的平均值和标准差、计算自变量和因变量的相关系数、计算回归系数、建立回归方程、对回归方程进行检验、进行预测和对预测结果进行评估。

一元线性回归分析的作用方法步骤一元线性回归分析是一种用来探究两个变量之间关系的统计方法。

它基于一个假设，即两个变量之间存在线性关系。

以下是一元线性回归分析的一般步骤：1. 数据收集：首先，需要收集所需的数据。

需要考虑收集的数据是否与研究目的相关，并确保数据的准确性和完整性。

2. 变量定义：定义自变量和因变量。

自变量是用来预测因变量的变量，而因变量是我们想要预测或解释的变量。

3. 数据探索：进行数据探索，包括数据的描述性统计和绘图。

这一步可以帮助我们了解数据的分布、异常值和离群点。

4. 模型选择：选择适当的线性模型。

这可以通过查看散点图、相关性分析和领域知识来完成。

通常，一个线性模型可以用以下方程表示：Y = β0 + β1X + ε，其中Y是因变量，X是自变量，β0和β1是回归系数，ε是误差项。

5. 模型估计：使用最小二乘法来估计回归系数。

最小二乘法的目标是找到最佳拟合直线，使得预测值与实际值之间的残差平方和最小化。

6. 模型评估：评估模型的拟合优度。

常用的指标包括R平方值和调整R平方值。

R平方值介于0和1之间，表示因变量变异性的百分比可以由自变量解释。

调整R平方值是对R平方值的修正，考虑了自变量的数量和样本量。

7. 模型解释：根据回归系数的估计值，解释自变量对因变量的影响。

根据回归系数的正负和大小，可以确定变量之间的关系是正向还是负向，并量化这种关系的强度。

8. 结果验证：验证模型的有效性和稳健性。

这可以通过对新数据集的预测进行测试，或使用交叉验证的方法来完成。

9. 结果解释：对模型结果进行解释，提供有关回归系数的结论，并解释模型对现实世界问题的意义。

总结来说，一元线性回归分析的方法步骤包括数据收集、变量定义、数据探索、模型选择、模型估计、模型评估、模型解释、结果验证和结果解释。

它们相互关联，构成了一元线性回归分析的完整过程。

第一节 两变量线性回归模型一．模型的建立1．数理模型的基本形式y x αβ=+ （2.1）这里y 称为被解释变量(dependent variable)，x 称为解释变量(independent variable)注意：（1）x 、y 选择的方法：主要是从所研究的问题的经济关系出发，根据已有的经济理论进行合理选择。

（2）变量之间是否是线性关系可先通过散点图来观察。

2．例如果在研究上海消费规律时，已经得到上海城市居民1981-1998年期间的人均可支配收入和人均消费性支出数据（见表1），能否用两变量线性函数进行分析？表1.上海居民收入消费情况年份 可支配收入 消费性支出 年份 可支配收入 消费性支出 1981 636.82 585 1990 2181.65 1936 1982 659.25 576 1991 2485.46 2167 1983 685.92 615 1992 3008.97 2509 1984 834.15 726 1993 4277.38 3530 1985 1075.26 992 1994 5868.48 4669 19861293.24117019957171.91586819871437.09128219968158.746763 19881723.44164819978438.896820 19891975.64181219988773.168662．一些非线性模型向线性模型的转化一些双变量之间虽然不存在线性关系，但通过变量代换可化为线性形式，这些双变量关系包括对数关系、双曲线关系等。

例3-2 如果认为一个国家或地区总产出具有规模报酬不变的特征，那么采用人均产出y与人均资本k的形式，该国家或者说地区的总产出规律可以表示为下列C-D生产函数形式y Akα=（2.2）也就是人均产出是人均资本的函数。

能不能用两变量线性回归模型分析这种总量生产规律？3．计量模型的设定 （1）基本形式：y x αβε=++ （2.3） 这里ε是一个随机变量，它的数学期望为0，即（2.3）中的变量y 、x 之间的关系已经是不确定的了。

第三章 一元线性回归第一部分 学习指导一、本章学习目的与要求1、掌握一元线性回归的经典假设；2、掌握一元线性回归的最小二乘法参数估计的计算公式、性质和应用；3、理解拟合优度指标：决定系数R 2的含义和作用；4、掌握解释变量X 和被解释变量Y 之间线性关系检验，回归参数0β和1β的显著性检验5、了解利用回归方程进行预测的方法。

二、本章内容提要（一）一元线性回归模型的假设条件 （1）E （i ε）=0 （i =1，2，……，n ），即随机误差项分布的均值为零。

（2）Var （i ε）=2σ （i =1,2, ……，n ），即随机误差项方差恒定，称为同方差。

（3）C o v （i ε，j ε）=0，（任意i ≠j ，i ，j =1,2, ……，n ），即随机误差项之间互不 相关。

（4）解释变量X 是非随机的，换句话说，在重复抽样下，X 的取值是确定不变的。

（5）i ε～N （0，2σ），即随机误差项服从均值为0,方差为2σ的正态分布。

前四个假定就是著名的高斯—马尔科夫假定或者称为回归分析的经典假定。

（二）一元线性回归最小二乘法估计参数的计算公式及性质 1、一元线性回归最小二乘法估计参数的计算公式为：()()()112101ˆˆˆni i xy i nxx ii x x y y S S x x y xβββ==⎧--⎪⎪==⎪⎨-⎪⎪=-⎪⎩∑∑ 2、一元线性回归最小二乘法估计参数的性质与估计量的性质 （1）残差的总和等于0，即∑=ni i1ˆε=0。

（2）残差的平方和最小，即∑=n i i12ˆε最小。

（3）被解释变量Y 的实际观测值i y 之和等于其拟合值ˆi y之和，从而i y 的均值y 与i y ˆ的均值y ˆ也相等。

（4）残差ˆi ε与ˆi y 互不相关，即1ˆˆ0ni i i y ε==∑。

（5）回归直线通过解释变量X 和被解释变量Y 的均值点(,)x y 。

3、OLS 法得到的估计量的性质（1） 线性性，即参数估计量是关于被解释变量Y 取值的线性函数。

一、一元线性回归(一)基本公式如果预测对象与主要影响因素之间存在线性关系，将预测对象作为因变量y，将主要影响因素作为自变量x，即引起因变量y变化的变量，则它们之间的关系可以用一元回归模型表示为如下形式：y=a+bx+e其中：a和b是揭示x和y之间关系的系数，a为回归常数，b为回归系数e是误差项或称回归余项。

对于每组可以观察到的变量x，y的数值xi，yi，满足下面的关系：yi =a+bxi+ei其中ei是误差项，是用a+bxi去估计因变量yi的值而产生的误差。

在实际预测中，ei是无法预测的，回归预测是借助a+bxi得到预测对象的估计值yi。

为了确定a和b，从而揭示变量y与x之间的关系，公式可以表示为：y=a+bx公式y=a+bx是式y=a+bx+e的拟合曲线。

可以利用普通最小二乘法原理(ols)求出回归系数。

最小二乘法基本原则是对于确定的方程，使观察值对估算值偏差的平方和最小。

由此求得的回归系数为：b=[∑xiyi—x∑yi]/∑xi2—x∑xia=-b式中：xi、yi分别是自变量x和因变量y的观察值，、分别为x和y的平均值.=∑xi/ n ; = ∑yi/ n对于每一个自变量的数值，都有拟合值：yi’=a+bxiyi’与实际观察值的差，便是残差项ei=yi一yi’(二)一元回归流程三)回归检验在利用回归模型进行预测时，需要对回归系数、回归方程进行检验，以判定预测模型的合理性和适用性。

检验方法有方差分析、相关检验、t检验、f检验。

对于一元回归，相关检验与t检验、f检验的效果是等同的，因此，在一般情况下，通过其中一项检验就可以了。

对于多元回归分析，t检验与f检验的作用却有很大的差异。

1．方差分析通过推导，可以得出：∑(yi—y-)2= ∑(yi—yi’)2+∑(yi—y-)2其中：∑(yi—y-)2=tss，称为偏差平方和，反映了n个y值的分散程度，又称总变差。

∑(yi—yi’)2=rss,称为回归平方和，反映了x对y线性影响的大小，又称可解释变差。

一元线性回归的基本步骤一元线性回归分析的基本步骤如下：•1、散点图判断变量关系（简单线性）；2、求相关系数及线性验证；3、求回归系数，建立回归方程；4、回归方程检验；5、参数的区间估计；6、预测；•••请点击输入图片描述•一、什么是回归分析法“回归分析”是解析“注目变量”和“因于变量”并明确两者关系的统计方法。

此时，我们把因子变量称为“说明变量”，把注目变量称为“目标变量址(被说明变量)”。

清楚了回归分析的目的后，下面我们以回归分析预测法的步骤来说明什么是回归分析法：回归分析是对具有因果关系的影响因素（自变量）和预测对象（因变量）所进行的数理统计分析处理。

只有当变量与因变量确实存在某种关系时，建立的回归方程才有意义。

因此，作为自变量的因素与作为因变量的预测对象是否有关，相关程度如何，以及判断这种相关程度的把握性多大，就成为进行回归分析必须要解决的问题。

进行相关分析，一般要求出相关关系，以相关系数的大小来判断自变量和因变量的相关的程度。

二、回归分析的目的回归分析的目的大致可分为两种：第一，“预测”。

预测目标变量，求解目标变量y和说明变量(x1，x2，…)的方程。

y=a0+b1x1+b2x2+…+bkxk+误差（方程A）把方程A叫做(多元)回归方程或者(多元)回归模型。

a0是y截距，b1，b2，…，bk是回归系数。

当k=l时，只有1个说明变量，叫做一元回归方程。

根据最小平方法求解最小误差平方和，非求出y截距和回归系数。

若求解回归方程．分别代入x1，x2，…xk的数值，预测y的值。

第二，“因子分析”。

因子分析是根据回归分析结果，得出各个自变量对目标变量产生的影响，因此，需要求出各个自变量的影响程度。

希望初学者在阅读接下来的文章之前，首先学习一元回归分析、相关分析、多元回归分析、数量化理论I等知识。

根据最小平方法，使用Excel求解y=a+bx中的a和b。

第二节一元线性回归分析本节主要内容：回归是分析变量之间关系类型的方法，按照变量之间的关系，回归分析分为：线性回归分析和非线性回归分析。

本节研究的是线性回归，即如何通过统计模型反映两个变量之间的线性依存关系.回归分析的主要内容:1.从样本数据出发，确定变量之间的数学关系式；2.估计回归模型参数；3.对确定的关系式进行各种统计检验,并从影响某一特定变量的诸多变量中找出影响显著的变量。

一、一元线性回归模型:一元线性模型是指两个变量x、y之间的直线因果关系。

理论回归模型:理论回归模型中的参数是未知的,但是在观察中我们通常用样本观察值估计参数值，通常用分别表示的估计值，即称回归估计模型：回归估计模型：二、模型参数估计：用最小二乘法估计：【例3】实测某地四周岁至十一岁女孩的七个年龄组的平均身高（单位：厘米）如下表所示某地女孩身高的实测数据建立身高与年龄的线性回归方程。

根据上面公式求出b0=80。

84，b1=4。

68。

三．回归系数的含义（2）回归方程中的两个回归系数，其中b0为回归直线的启动值，在相关图上变现为x=0时，纵轴上的一个点,称为y截距；b1是回归直线的斜率，它是自变量(x）每变动一个单位量时，因变量（y）的平均变化量。

（3）回归系数b1的取值有正负号。

如果b1为正值，则表示两个变量为正相关关系,如果b1为负值，则表示两个变量为负相关关系。

[例题·判断题］回归系数b的符号与相关系数r的符号，可以相同也可以不同.（ )答案：错误解析：回归系数b的符号与相关系数r的符号是相同的=a+bx，b<0，则x与y之间的相关系数（ )［例题·判断题]在回归直线yca。

r=0 b.r=1 c。

0<r〈1 d.—1<r〈0答案:d解析：b〈0,则x与y之间的相关系数为负即—1〈r〈0［例题·单选题］回归系数和相关系数的符号是一致的，其符号均可用来判断现象( ）a。

线性相关还是非线性相关 b.正相关还是负相关c。

第二节一元线性回‎归方程的建立一‎元线性回归分析是处理‎两个变量之间关系的最‎简单模型，它所研究的‎对象是两个变量之间的‎线性相关关系。

通过对‎这个模型的讨论，我们‎不仅可以掌握有关一元‎线性回归的知识，而且‎可以从中了解回归分析‎方法的基本思想、方法‎和应用。

一、问题‎的提出例2-1‎-1 为了研究氮含‎量对铁合金溶液初生奥‎氏体析出温度的影响，‎测定了不同氮含量时铁‎合金溶液初生奥氏体析‎出温度，得到表2-1‎-1给出的5组数据。

‎表2-1-1 ‎氮含量与灰铸铁初生‎奥氏体析出温度测试数‎据如果‎把氮含量作为横坐标，‎把初生奥氏体析出温度‎作为纵坐标，将这些数‎据标在平面直角坐标上‎，则得图2-1-1，‎这个图称为散点图。

‎从图2-1-1可以‎看出，数据点基本落在‎一条直线附近。

这告诉‎我们，变量X与Y的关‎系大致可看作是线性关‎系，即它们之间的相互‎关系可以用线性关系来‎描述。

但是由于并非所‎有的数据点完全落在一‎条直线上，因此X与Y‎的关系并没有确切到可‎以唯一地由一个X值确‎定一个Y值的程度。

其‎它因素，诸如其它微量‎元素的含量以及测试误‎差等都会影响Y 的测试‎结果。

如果我们要研究‎X与Y的关系，可以作‎线性拟合‎（2-‎1-1）二、最小二乘法‎原理如果把用回‎归方程计算得到的‎i值(i=1,2‎,…n)称为回归值，‎那么实际测量值y i与‎回归值i之间存在‎着偏差，我们把这(i=1,2,3,…‎,n)。

这样，我们就‎可以用残差平种偏‎差称为残差，记为e i‎方和来度‎量测量值与回归直线的‎接近或偏差程度。

残差‎平方和定义为:‎ (2-1-‎2) 所谓最小二乘‎法，就是选择a和b使‎Q(a,b)最小，即‎用最小二乘法得到的回‎归直线是在所有直‎线中与测量值残差平方‎和Q最小的一条。

由(‎2-1-2)式可知Q‎是关于a,b的二次函‎数，所以它的最小值总‎是存在的。

下面讨论的‎a和b的求法。