- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
探索&新知
☞ 方法3:利用镜子的反射
B
在观测者与旗杆之间的地面上平放一面 镜子,固定镜子的位置,观测者看着镜子来回 B ∵ △ADE∽△ABC 调整自己的位置,使自己能够通过镜子看到 AE DE 旗杆顶端, 测出此时观测者的脚与镜子的距 AC BC D 离、眼与脚的距离以及旗杆底部与镜子的 DE 距离就能求出旗杆的高度. AC · BC
A E
因为同学的身高AB和她的影长 人高 人影 = BE及同一时刻旗杆的影长BD 物高 物影 均可测量得出,所以代入测量 数据即可求出旗杆DC的高度.
D
B
探索&新知
☞ 方法1:利用阳光下的影子
C
A B
E
D
学以&致用 ☞ 小敏测得2m高的标杆在太阳
光下的影长为1.2m,同时又测得一颗树的影长为 12m,请你计算出这棵树的高度。 D 解:如图所示:AC表示标杆,BC表 示标杆的影长,DF表示树高,由题 意知: △ ABC∽ △ DEF
探索&新知
☞
怎样测量旗杆的高度呢?
分组讨论,合作交流
探索&新知
☞ 方法1:利用阳光下的影子
C
A
E
B
D
C A
E
B
D
C
∵太阳的光线是平行的, ∴AE∥CB, ∴∠AEB=∠CBD, ∵人与旗杆是垂直于地面的 ∴∠ABE=∠CDB ∴△AB E∽△ C D B
∴ A B=E B CD BD
注意:同一时刻
∵太阳的光线是平行的,旗杆和墙也是平行的 ∴四边形ACDB为平行四边形 ∴AC=BD=2m 地上的影子ED是旗杆的一部分CE在地上的影子 ∵ △ A'B' C' ∽△CDE A ∴ AC CB C CE ED A' 1 1.5 B 即
CE
9
1
∴ CE=6m ∴旗杆的高度AE=CE+AC=6+2=8(m)
夯实&基础 ☞
1.在相同时刻的物高与影长成比例,小明的身高 为1.5米,在地面上的影长为2米,同时一古塔在 地面上的影长为40米,则古塔高为( C ) A. 60米 B. 40米 C. 30米 D. 25米 2.如图,阳光从教室的窗户摄入室内窗户框AB在地 面上,DE=1.8m,窗户下檐到地面的距离 BC=1m,EC=1.2m,则窗户的高AB为( A ) A.1.5m B.1.6m C.1.86m D.2.16m
一时刻测得1m长的竹竿竖直时的影长为1.5m,同一 时刻测量旗杆影长时,因旗杆靠近一幢楼房,影子 不全落在地面上,有一部分落在墙上,他测得落在 地面上的影长为9m,留在墙上的影长为2m,求旗杆 的高度. A A
A'
C'
B'
A' C B
C
? 9EBຫໍສະໝຸດ 1E D C'
2
D
1.5
B'
解:过点D作DC∥BA交AE于C
A B C E F
BC AC . ∴ EF DF
12 2 DF 20( m) 1.2
所以这棵树的高度为20m。
1 .2 2 ∴ 12 DF
探索&新知
☞
方法2:利用标杆
B ∵ △AEF∽△ABC
B
∴
E A F A F
A F =E F AC BC
C E
旗杆长 B H =BC + CH = BC+AD
C
D
G
H
探索&新知
☞
方法2:利用标杆
在观测者和旗杆之间的地面上直立一根高度已知的 标杆,观测者前后调整自己的位置,当旗杆顶部、标杆 分别测出 顶部与眼睛恰好在同一直线上时, C 观测者的脚与旗杆底端的距离,以及 观测者的脚到标杆底部的距离, 观测者的眼睛与脚的距离 然后再测出标杆的高 E 即可求出旗杆的高度
测量得出,于是可求出CN的长 ∴旗杆的高CD=DN+CN=EF+CN
方法2:利用标杆
B
H
E
A F
B
C G D E C A
学以&致用 ☞ 小明为测量一棵树CD的高度,他在距
树24m处立了一根高为2m的标杆EF,然后小明前后调整自 己的位置,当他与树相距27m时,他的眼睛、标杆的顶端和 树顶端在同一直线上,已知小明的眼与脚的距离是1.6m。 C 解:过点A作AN⊥cD于点N,交EF于点M 求树的高度.
B'
C'
2 1.5
E
9
D
E A C D
AE
E
.
A
C
学以&致用 ☞
如图,在距离树高AB 18米的地面上平放着一 面镜子E,人退后到距镜 子2.1米的D处,在镜子 里恰看见树顶。若人眼 距地面1.4米,求树高。
C
解:由题意知:BE=18 米,DE=2.1米,CD=1.4米, △ ABE∽ △CDE
AB BE ∴ CD DE
∵人、标杆、树都垂直于地面 ∴∠ABF=∠EFD =∠CDF=90º ∴ AB ∥EF ∥CD∴∠EMA=∠CNA ∵∠EAM=∠CAN∴△AEM∽△CAN ∴ EM AM
M
N
E
A
CN
AN
∵AB=1.6m,EF=2m,BD=27m,FD=24m 2 1.6 3 ∴ B F D CN 27 ∴ CN=3.6m, ∴ CD=3.6+1.6=5.2 (m) 所以树的高度为5.2m
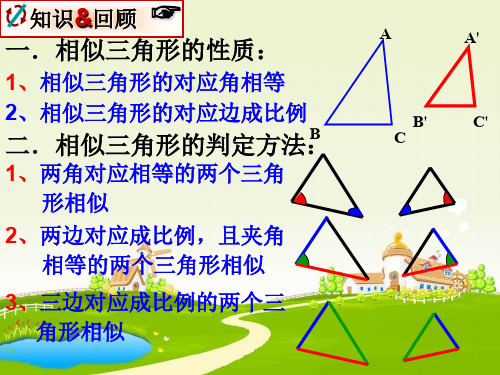
知识&回顾
☞
一.相似三角形的性质:
1、相似三角形的对应角相等 2、相似三角形的对应边成比例
A
A'
二.相似三角形的判定方法:
1、两角对应相等的两个三角 形相似 2、两边对应成比例,且夹角 相等的两个三角形相似
3、三边对应成比例的两个三 角形相似
B
B' C
C'
数学和生活有着紧密的联系 让数学走进我们的生活
能力&提升 ☞
如图,A、B两点分别位于一个池塘的两端,小芳想 用绳子测量A、B两点之间的距离,但绳子的长度 不够,一位同学帮她想了一个主意,先在地上取一 个可以直接到达A、B点的点C,找到AC、BC的中 点D、E,并且DE的长为5m,则A、B两点的距离是 多少? 5m
?
能力&提升 ☞ 某同学想测旗杆的高度,他在某
A
3 1
2
M F
N D H
B
C
E A
3 1
2
M
过A作AN⊥CD于点N,交EF于M ∵EF ⊥BD,CN⊥BD ∴ EF∥CN ∴ ∠1= ∠2 又∠3= ∠3 N ∴△AME∽△ANC
D
B
F
∴ AM EM
AN CN
∴ CN AN EM ∵四边形ABDN为矩形 ∴DN=AB
AM
∴旗杆的高CD=CN+DN=CN+AB
C
过A、E分别作EF 、CD的垂线交EF于
M,交CD于N
∴∠1=∠2 ∵标杆与旗杆平行,∴EF∥CD
E
A
1
∴∠AEM=∠ECN
2
N
∴△AME∽△ENC
AM EM ∴ EN CN
M
B
F
D
EM EN AM ∵人与标杆的距离AM、标杆与旗杆的距
∴ CN
离EN、标杆与人眼到地面距离的差EM都可
A
AB 18 ∴ 1 .4 2 .1
18 1.4 ∴AB= 2.1
=12(米)
D
E
B
所以树高为12米
积累就是知识
测量旗杆高度的方法
(1)利用阳光下的影子; (2)利用标杆; (3)利用镜子的反射.
注1.利用阳光下的影子测量旗杆高度,⑴一般 认为光线是平行的;⑵必须是同一时刻. 意2.利用镜子的反射,入射角等于反射角.
夯实&基础 ☞
3.眼距地面2m的小敏利用3m高的标杆测旗杆高 度.已知她到标杆3m,标杆与旗杆距离18m.则旗 杆的高度是 9m . 4.已知木棒长为1米,其影长为2米,同一时刻 金字塔的影长为274米,则金字塔的高度为 137米 。 5.一油桶高0.8m, A 桶内有油,一根木棒长1米, D E 从桶盖小口斜插入桶内一端 到桶底,另一端到小口,抽出 木棒,量得棒上浸油部分长为 B 0.8m.则桶内油面的高度为 C 0.64 米.