高二数学同角三角函数的基本关系1

同角三角函数的基本关系与诱导公式1．同角三角函数的基本关系(1)平方关系：sin 2α＋cos 2α＝1；(2)商数关系：sin αcos α＝tan α.2．诱导公式公式一：sin(α＋2k π)＝sin α，cos(α＋2k π)＝cos α，其中k ∈Z.公式二：sin(π＋α)＝－sin α，cos(π＋α)＝－cos α，tan(π＋α)＝tan α. 公式三：sin(－α)＝－sin α，cos(－α)＝cos α.公式四：sin(π－α)＝sin α，cos(π－α)＝－cos α.公式五：sin ）（απ-2＝cos α，cos ）（απ-2＝sin α. 公式六：sin ）（απ+2cos α，cos ）（απ+2＝－sin α. 一个口诀：诱导公式的记忆口诀为：（απ±2k ）奇变偶不变，符号看象限． 三种方法在求值与化简时，常用方法有：(1)弦切互化法：主要利用公式tan α＝sin αcos α化成正、余弦．(2)和积转换法：利用(sin θ±cos θ)2＝1±2sin θcos θ的关系进行变形、转化．(3)巧用“1”的变换：1＝sin 2θ＋cos 2θ＝cos 2θ(1＋tan 2θ)＝tan π4＝….一、已知某角的一个三角函数值，求其它三角函数值 例1：① 已知sinA=23, A 为第二象限的角，求cosA ，tanA 的值；②已知cosA=23, A 为第四象限的角，求sinA ，tanA 的值；③已知α∈⎝⎛⎭⎫π，3π2，tan α＝2，则cos α＝________；二、由某角的正切值求该角关于正弦余弦的三角函数式的值例 2：已知tan α=2,求:(1)4sin 2cos 5sin 3cos αααα-+;(2)2222sin 2sin cos cos 4cos 3sin 1αααααα---+;(3)25sin 3sin cos 2ααα+-变式(1)已知tan α＝13，求12sin αcos α＋cos 2α的值；三、关于某角的正弦与余弦之和，正弦与余弦之差，正弦与余弦之积，知一求二例3： 已知－π2<x <0，sin x ＋cos x ＝15①求sinxcosx 的值， ②求sinx+cosx 的值③求sin 2x －cos 2x 的【试一试】 (1)若α为三角形的一个内角，且sin α＋cos α＝23，则这个三角形是( )A ．正三角形B ．直角三角形C ．锐角三角形D ．钝角三角形（2）已知sin θ＋cos θ＝713，θ∈(0，π)，则tan θ＝________.四、利用诱导公式求值，化简例4： 已知sin）（2πα+＝－55，α∈(0，π)． (1)求)3cos()sin()23cos()2sin(απαπαππα++-+--的值； (2)求cos ）（απ-65的值．(2)已知sin α是方程5x 2－7x －6＝0的根，α是第三象限角， 则sin (－α－32π)cos (32π－α)cos (π2－α)sin (π2＋α)·tan 2(π－α)＝________.专项基础训练一、选择题1．已知α和β的终边关于直线y ＝x 对称，且β＝－π3，则sin α等于( )A ．－32B.32C ．－12 D.12 2． cos(－2 013π)的值为( ) A.12B ．－1C ．－32D ．03．已知f (α)＝sin (π－α)·cos (2π－α)cos (－π－α)·tan (π－α)，则f ⎝ ⎛⎭⎪⎫－25π3的值为( )A.12B ．－12C.32 D ．－324．当0<x <π4时，函数f (x )＝cos 2xcos x sin x －sin 2x的最小值是( )A.14B.12 C ．2 D ．4 二、填空题5．如果sin α＝15，且α为第二象限角，则sin ⎝ ⎛⎭⎪⎫3π2＋α＝________.6．已知sin ⎝ ⎛⎭⎪⎫α＋π12＝13，则cos ⎝ ⎛⎭⎪⎫α＋7π12的值为________．7. sin ⎝ ⎛⎭⎪⎫α＋3π2·tan (α＋π)sin (π－α)＝________.三、解答题(共22分)8． (10分)已知sin θ＋cos θ＝23(0<θ<π)，求tan θ的值．9． (12分)已知sin(3π＋θ)＝13，求cos (π＋θ)cos θ[cos (π－θ)－1]＋cos (θ－2π)sin ⎝ ⎛⎭⎪⎫θ－3π2cos (θ－π)－sin ⎝ ⎛⎭⎪⎫3π2＋θ的值．。

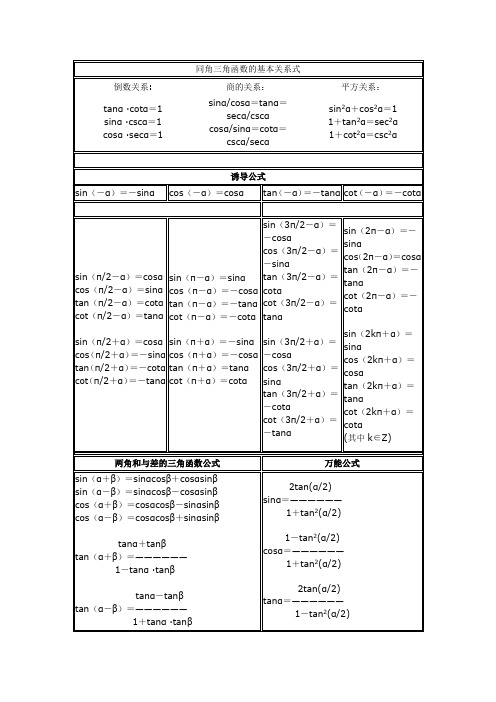
直角三角定义它有六种基本函数(初等基本表示)：三角函数数值表（斜边为r，对边为y，邻边为x。

）在平面直角坐标系xOy中，从点O引出一条射线OP，设旋转角为θ，设OP=r，P点的坐标为（x，y）有正弦函数 sinθ=y/r 正弦（sin）:角α的对边比斜边余弦函数 cosθ=x/r 余弦（cos）:角α的邻边比斜边正切函数 tanθ=y/x 正切（tan）:角α的对边比邻边余切函数 cotθ=x/y 余切（cot）:角α的邻边比对边正割函数 secθ=r/x 正割（sec）:角α的斜边比邻边余割函数 cscθ=r/y 余割（csc）:角α的斜边比对边以及两个不常用，已趋于被淘汰的函数：正矢函数 versinθ =1-cosθ余矢函数 coversθ =1-sinθsinα、cosα、tanα的定义域：sinα定义域无穷，值域【-1，+1】cosα定义域无穷，值域【-1，+1】tanα的定义域（-π/2+kπ，π/2+kπ），k属于整数，值域无穷单位圆定义六个三角函数也可以依据半径为1中心为原点的单位圆来定义。

单位圆定义在实际计算上没有大的价值；实际上对多数角它都依赖于直角三角形。

但是单位圆定义的确允许三角函数对所有正数和负数辐角都有定义，而不只是对于在0 和π/2 弧度之间的角。

它也提供了一个图像，把所有重要的三角函数都包含了。

根据勾股定理，单位圆的等式是：x^2+y^2 = 1图像中给出了用弧度度量的一些常见的角。

逆时针方向的度量是正角，而顺时针的度量是负角。

设一个过原点的线，同x轴正半部分得到一个角θ，并与单位圆相交。

这个交点的x和y坐标分别等于cos θ和sin θ。

图像中的三角形确保了这个公式；半径等于斜边且长度为1，所以有sin θ = y/1 和cos θ =x/1。

单位圆可以被视为是通过改变邻边和对边的长度，但保持斜边等于1的一种查看无限个三角形的方式。

对于大于2π 或小于−2π 的角度，可直接继续绕单位圆旋转。

同角三角函数的基本关系与诱导公式知识点[归纳·知识整合]1．同角三角函数的基本关系 (1)平方关系：sin 2α＋cos 2α＝1； (2)商数关系：tan α＝sin αcos α.[探究] 1.如何理解基本关系中“同角”的含义？提示：只要是同一个角，基本关系就成立，不拘泥于角的形式，如sin 2α3＋cos 2α3＝1，tan4α＝sin 4αcos 4α等都是成立的，而sin 2θ＋cos 2φ＝1就不成立．2．诱导公式即α＋k ·2π(k ∈Z )，－α，π±α的三角函数值，等于α的同名函数值，前面加上一个把α看成锐角时原函数值的符号；π2±α的正弦(余弦)函数值，分别等于α的余弦(正弦)函数值，前面加上一个把α看成锐角时原函数值的符号．[探究] 2.有人说sin(k π－α)＝sin(π－α)＝sin α(k ∈Z )，你认为正确吗？提示：不正确．当k ＝2n (n ∈Z )时，sin(k π－α)＝sin(2n π－α)＝sin(－α)＝－sin α； 当k ＝2n ＋1(n ∈Z )时，sin(k π－α)＝sin[(2n ＋1)·π－α]＝sin(2n π＋π－α)＝sin(π－α)＝sin α. 3．诱导公式的口诀“奇变偶不变，符号看象限”中的“符号”是否与α的大小有关？ 提示：无关，只是把α从形式上看作锐角，从而2k π＋α(k ∈Z )，π＋α，－α，π－α，π2－α，π2＋α分别是第一，三，四，二，一，二象限角． [自测·牛刀小试]1．(教材习题改编)已知cos(π＋α)＝12，则sin α的值为( )A ．±12B.12C.32D ．±32解析：选D cos(π＋α)＝－cos α＝12，∴cos α＝－12，∴sin α＝±1－cos α2＝±32.2．tan 690°的值为( ) A ．－33B.33C. 3 D ．－ 3解析：选A tan 690°＝tan(－30°＋2×360°) ＝tan(－30°)＝－tan 30°＝－33. 3．(教材习题改编)若tan α＝2，则sin α－cos αsin α＋cos α的值为( )A ．－13B ．－53C.13D.53解析：选Csin α－cos αsin α＋cos α＝tan α－1tan α＋1＝2－12＋1＝13.4．(教材习题改编)已知tan α＝3，π＜α＜32π，则cos α－sin α＝________.解析：∵tan α＝3，π＜α＜32π，∴α＝43π，∴cos α－sin α＝cos 43π－sin 43π＝－cos π3＋sin π3＝－12＋32＝3－12.答案：3－125．计算sin 10π3－2cos ⎝⎛⎭⎫－19π4＋tan ⎝⎛⎭⎫－13π3＝________. 解析：原式＝sin ⎝⎛⎭⎫2π＋4π3－2cos ⎝⎛⎭⎫4π＋3π4－tan ⎝⎛⎭⎫4π＋π3＝sin ⎝⎛⎭⎫π＋π3－2cos ⎝⎛⎭⎫π－π4－tan π3 ＝－sin π3＋2cos π4－3＝－332＋1.答案：－332＋1[例1] 已知α是三角形的内角，且sin α＋cos α＝15.(1)求tan α的值； (2)把1cos 2α－sin 2α用tan α表示出来，并求其值．[自主解答] (1)法一：联立方程⎩⎪⎨⎪⎧sin α＋cos α＝15， ①sin 2α＋cos 2α＝1， ②由①得cos α＝15－sin α，将其代入②，整理得 25sin 2α－5sin α－12＝0. ∵α是三角形内角，∴⎩⎨⎧sin α＝45，cos α＝－35，∴tan α＝－43.法二：∵sin α＋cos α＝15，∴(sin α＋cos α)2＝⎝⎛⎭⎫152，即1＋2sin αcos α＝125， ∴2sin αcos α＝－2425，∴(sin α－cos α)2＝1－2sin αcos α＝1＋2425＝4925.∵sin αcos α＝－1225<0且0<α<π，∴sin α>0，cos α<0，∴sin α－cos α>0. ∴sin α－cos α＝75.由⎩⎨⎧sin α＋cos α＝15，sin α－cos α＝75，得⎩⎨⎧sin α＝45，cos α＝－35，∴tan α＝－43.(2)1cos 2α－sin 2α＝sin 2α＋cos 2αcos 2α－sin 2α＝sin 2α＋cos 2αcos 2αcos 2α－sin 2αcos 2α＝tan 2α＋11－tan 2α. ∵tan α＝－43，∴1cos 2α－sin 2α＝tan 2α＋11－tan 2α＝⎝⎛⎭⎫－432＋11－⎝⎛⎭⎫－432＝－257.保持本例条件不变，求：(1)sin α－4cos α5sin α＋2cos α；(2)sin 2α＋2sin αcos α的值． 解：由例题可知 tan α＝－43.(1)sin α－4cos α5sin α＋2cos α＝tan α－45tan α＋2＝－43－45×⎝⎛⎭⎫－43＋2＝87. (2)sin 2α＋2sin αcos α＝sin 2α＋2sin αcos αsin 2α＋cos 2α＝tan 2α＋2tan α1＋tan 2α＝169－831＋169＝－825.———————————————————同角三角函数关系式及变形公式的应用(1)利用sin 2α＋cos 2α＝1可以实现角α的正弦、余弦的互化，利用sin αcos α＝tan α可以实现角α的弦切互化．(2)应用公式时注意方程思想的应用：对于sin α＋cos α，sin αcos α，sin α－cos α这三个式子，利用(sin α±cos α)2＝1±2sin αcos α，可以知一求二．(3)注意公式逆用及变形应用：1＝sin 2α＋cos 2α，sin 2α＝1－cos 2α，cos 2α＝1－sin 2α.1．已知sin α＝2sin β，tan α＝3tan β，求cos α. 解：∵sin α＝2sin β，tan α＝3tan β， ∴sin 2α＝4sin 2β，① tan 2α＝9tan 2β.②由①÷②得：9cos 2α＝4cos 2β.③ 由①＋③得sin 2α＋9cos 2α＝4. 又sin 2α＋cos 2α＝1， ∴cos 2α＝38，∴cos α＝±64.[例2] (1)已知cos ⎝⎛⎭⎫π6＋α＝33，求cos ⎝⎛⎭⎫5π6－α的值； (2)已知π＜α＜2π，cos(α－7π)＝－35，求sin(3π＋α)·tan ⎝⎛⎭⎫α－72π的值． [自主解答] (1)∵⎝⎛⎭⎫π6＋α＋⎝⎛⎭⎫5π6－α＝π， ∴5π6－α＝π－⎝⎛⎭⎫π6＋α. ∴cos ⎝⎛⎭⎫5π6－α＝cos ⎣⎡⎦⎤π－⎝⎛⎭⎫π6＋α ＝－cos ⎝⎛⎭⎫π6＋α＝－33， 即cos ⎝⎛⎭⎫5π6－α＝－33.(2)∵cos(α－7π)＝cos(7π－α)＝co s(π－α)＝－cos α＝－35，∴cos α＝35.∴sin(3π＋α)·tan ⎝⎛⎭⎫α－72π ＝sin(π＋α)·⎣⎡⎦⎤－tan ⎝⎛⎭⎫72π－α ＝sin α·tan ⎝⎛⎭⎫π2－α＝sin α·sin ⎝⎛⎭⎫π2－αcos ⎝⎛⎭⎫π2－α ＝sin α·cos αsin α＝cos α＝35.——————————————————— 利用诱导公式化简三角函数的思路和要求(1)思路方法：①分析结构特点，选择恰当公式；②利用公式化成单角三角函数；③整理得最简形式．(2)化简要求：①化简过程是恒等变形；②结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值.2．(1)已知sin α是方程5x 2－7x －6＝0的根，且α是第三象限角，则sin ⎝⎛⎭⎫－α－3π2cos ⎝⎛⎭⎫3π2－αtan 2(π－α)cos ⎝⎛⎭⎫π2－αsin ⎝⎛⎭⎫π2＋α＝( )A.916 B ．－916C ．－34D.34(2)设f (α)＝2sin (π＋α)cos (π－α)－cos (π＋α)1＋sin 2α＋cos ⎝⎛⎭⎫3π2＋α－sin 2⎝⎛⎭⎫π2＋α⎝⎛⎭⎫sin α≠－12，则f ⎝⎛⎭⎫－23π6＝________. 解析：(1)选B ∵方程5x 2－7x －6＝0的根为x 1＝2，x 2＝－35，由题知sin α＝－35，∴cos α＝－45，tan α＝34.∴原式＝cos α(－sin α)tan 2αsin αcos α＝－tan 2α＝－916.(2)∵f (α)＝(－2sin α)(－cos α)＋cos α1＋sin 2α＋sin α－cos 2α＝2sin αcos α＋cos α2sin 2α＋sin α＝cos α(1＋2sin α)sin α(1＋2sin α)＝1tan α， ∴f ⎝⎛⎭⎫－23π6＝1tan ⎝⎛⎭⎫－23π6＝1tan ⎝⎛⎭⎫－4π＋π6＝1tan π6＝ 3. 答案： 3[例3] 在△ABC 中，若sin(2π－A )＝－2sin(π－B )，3cos A ＝－2cos(π－B )，求△ABC 的三个内角．[自主解答] 由已知得⎩⎪⎨⎪⎧sin A ＝2sin B ①3cos A ＝2cos B ②①2＋②2得2cos 2A ＝1 即cos A ＝22或cos A ＝－22. (1)∵当cos A ＝22时，cos B ＝32， 又A 、B 是三角形的内角，∴A ＝π4，B ＝π6，∴C ＝π－(A ＋B )＝7π12.(2)∵当cos A ＝－22时，cos B ＝－32. 又A 、B 是三角形的内角， ∴A ＝3π4，B ＝5π6，不合题意．综上知，A ＝π4，B ＝π6，C ＝7π12.———————————————————1．三角形中的诱导公式在三角形ABC 中常用到以下结论： sin(A ＋B )＝sin(π－C )＝sin C ， cos(A ＋B )＝cos(π－C )＝－cos C ，tan(A ＋B )＝tan(π－C )＝－tan C ， sin ⎝⎛⎭⎫A 2＋B 2＝sin ⎝⎛⎭⎫π2－C 2＝cos C 2， cos ⎝⎛⎭⎫A 2＋B 2＝cos ⎝⎛⎭⎫π2－C 2＝sin C 2. 2．求角的一般步骤求角时，一般先求出该角的某一三角函数值，再确定该角的范围，最后求角．3．在△ABC 中，sin A ＋cos A ＝2，3cos A ＝－2cos(π－B )，求△ABC 的三个内角． 解：∵sin A ＋cos A ＝2， ∴1＋2sin A cos A ＝2，∴sin2A ＝1. ∵A 为△ABC 的内角， ∴2A ＝π2，∴A ＝π4.∵3cos A ＝－2cos(π－B )， ∴3cos π4＝2cos B ，∴cos B ＝32. ∵0＜B ＜π，∴B ＝π6.∵A ＋B ＋C ＝π，∴C ＝7π12.∴A ＝π4，B ＝π6，C ＝7π12.1个口诀——诱导公式的记忆口诀 奇变偶不变，符号看象限． 1个原则——诱导公式的应用原则 负化正、大化小、化到锐角为终了．3种方法——三角函数求值与化简的常用方法(1)弦切互化法：主要利用公式tan α＝sin αcos α化成正、余弦．(2)和积转换法：利用(sin θ±cos θ)2＝1±2sin θcos θ的关系进行变形、转化．(3)巧用“1”的变换：1＝sin 2θ＋cos 2θ＝cos 2θ(1＋tan 2θ)＝tan π4＝….3个防范——应用同角三角函数关系式与诱导公式应注意的问题(1)利用诱导公式进行化简求值时，先利用公式化任意角的三角函数为锐角三角函数，其步骤：去负—脱周—化锐．特别注意函数名称和符号的确定．(2)在利用同角三角函数的平方关系时，若开方，要特别注意判断符号． (3)注意求值与化简后的结果一般要尽可能有理化、整式化.易误警示——应用同角三角函数平方关系的误区[典例] (2011·重庆高考)若cos α＝－35，且α∈⎝⎛⎭⎫π，3π2，则tan α＝________. [解析] 依题意得sin α＝－1－cos 2α＝－45，tan α＝sin αcos α＝43.[答案] 43[易误辨析]1．解答本题时，常会出现以下两种失误(1)忽视题目中已知条件α的范围，求得sin α的两个值而致误； (2)只注意到α的范围，但判断错sin α的符号而导致tan α的值错误． 2．由同角三角函数的平方关系求sin α或cos α时，要注意以下两点(1)题目中若没有限定角α的范围，则sin α或cos α的符号应有两种情况，不可漏掉． (2)若已给出α的范围，则要准确判断在给定范围内sin α或cos α的符号，不合题意的一定要舍去．[变式训练]1．(2013·福州模拟)已知α∈⎝⎛⎭⎫π，3π2，tan α＝2，则cos α＝________. 解析：依题意得⎩⎪⎨⎪⎧tan α＝sin αcos α＝2，sin 2α＋cos 2α＝1，由此解得cos 2α＝15，又α∈⎝⎛⎭⎫π，3π2，因此cos α＝－55. 答案：－552．(2013·泰州模拟)若θ∈⎝⎛⎭⎫π4，π2，sin 2θ＝116，则cos θ－sin θ的值是________． 解析：(cos θ－sin θ)2＝1－sin 2θ＝1516.∵π4＜θ＜π2，∴cos θ＜sin θ.∴cos θ－sin θ＝－154. 答案：－154一、选择题(本大题共6小题，每小题5分，共30分) 1．α是第一象限角，tan α＝34，则sin α＝( )A.45 B.35 C ．－45D ．－35解析：选B tan α＝sin αcos α＝34，sin 2 α＋cos 2α＝1，且α是第一象限角，所以sin α＝35.2．若sin ⎝⎛⎭⎫π6＋α＝35，则cos ⎝⎛⎭⎫π3－α＝( ) A ．－35B.35C.45D ．－45解析：选B cos ⎝⎛⎭⎫π3－α＝cos ⎣⎡⎦⎤π2－⎝⎛⎭⎫π6＋α＝sin ⎝⎛⎭⎫π6＋α＝35. 3．(2013·安徽名校模拟)已知tan x ＝2，则sin 2x ＋1＝( ) A ．0 B.95 C.43D.53解析：选B sin 2x ＋1＝2sin 2x ＋cos 2x sin 2x ＋cos 2x ＝2tan 2x ＋1tan 2x ＋1＝95.4．已知f (α)＝sin (π－α)cos (2π－α)cos (－π－α)tan α，则f ⎝⎛⎭⎫－313π的值为( ) A.12 B ．－13C ．－12D.13解析：选C ∵f (α)＝sin αcos α－cos αtan α＝－cos α，∴f ⎝⎛⎭⎫－313π＝－cos ⎝⎛⎭⎫－313π＝－cos ⎝⎛⎭⎫10π＋π3 ＝－cos π3＝－12.5．(2013·西安模拟)已知2tan α·sin α＝3，－π2＜α＜0，则sin α＝( )A.32B ．－32C.12 D ．－12解析：选B 由2tan α·sin α＝3得，2sin 2αcos α＝3，即2cos 2α＋3cos α－2＝0，又－π2＜α＜0，解得cos α＝12(cos α＝－2舍去)，故sin α＝－32. 6．若sin θ，cos θ是方程4x 2＋2mx ＋m ＝0的两根，则m 的值为( ) A ．1＋ 5 B ．1－ 5 C ．1±5D ．－1－ 5解析：选B 由题意知：sin θ＋cos θ＝－m2，sin θcos θ＝m4.∵(sin θ＋cos θ)2＝1＋2sin θcos θ，∴m 24＝1＋m2，解得m ＝1±5，又Δ＝4m 2－16m ≥0， ∴m ≤0或m ≥4，∴m ＝1－ 5.二、填空题(本大题共3小题，每小题5分，共15分) 7．化简sin ⎝⎛⎭⎫π2＋α·cos ⎝⎛⎭⎫π2－αcos (π＋α)＋sin (π－α)·cos ⎝⎛⎭⎫π2＋αsin (π＋α)＝________.解析：原式＝cos α·sin α－cos α＋sin α(－sin α)－sin α＝－sin α＋sin α＝0. 答案：08．若cos(2π－α)＝53，且α∈⎣⎡⎦⎤－π2，0，则sin(π－α)＝________.解析：由诱导公式可知cos(2π－α)＝cos α，sin(π－α)＝sin α，由sin 2α＋cos 2α＝1可得，sin α＝±23，∵α∈⎣⎡⎦⎤－π2，0，∴sin α＝－23. 答案：－239．已知sin(π－α)－cos(π＋α)＝23⎝⎛⎭⎫π2＜α＜π.则sin α－cos α＝________.解析：由sin(π－α)－cos(π＋α)＝23， 得sin α＋cos α＝23，① 将①两边平方得1＋2sin α·cos α＝29，故2sin αcos α＝－79.∴(sin α－cos α)2＝1－2sin αcos α＝1－⎝⎛⎭⎫－79＝169. 又∵π2＜α＜π，∴sin α＞0，cos α＜0.∴sin α－cos α＝43.答案：43三、解答题(本大题共3小题，每小题12分，共36分) 10．已知sin(3π＋θ)＝13，求cos (π＋θ)cos θ[cos (π－θ)－1]＋cos (θ－2π)sin ⎝⎛⎭⎫θ－3π2cos (θ－π)－sin ⎝⎛⎭⎫3π2＋θ的值．解：∵sin(3π＋θ)＝－sin θ＝13，∴sin θ＝－13.∴原式＝－cos θcos θ(－cos θ－1)＋cos θcos θ·(－cos θ)＋cos θ＝11＋cos θ＋cos θ－cos 2θ＋cos θ＝11＋cos θ＋11－cos θ＝21－cos 2θ＝2sin 2θ＝2⎝⎛⎭⎫－132＝18. 11．已知关于x 的方程2x 2－(3＋1)x ＋m ＝0的两根sin θ和cos θ，θ∈(0,2π)，求： (1)sin 2θsin θ－cos θ＋cos θ1－tan θ的值； (2)m 的值；(3)方程的两根及此时θ的值． 解：(1)原式＝sin 2θsin θ－cos θ＋cos θ1－sin θcos θ＝sin 2θsin θ－cos θ＋cos 2θcos θ－sin θ ＝sin 2θ－cos 2θsin θ－cos θ＝sin θ＋cos θ. 由条件知sin θ＋cos θ＝3＋12，故sin 2θsin θ－cos θ＋cos θ1－tan θ＝3＋12.(2)由sin 2θ＋2sin θcos θ＋cos 2θ＝1＋2sin θcos θ ＝(sin θ＋cos θ)2，得m ＝32. (3)由⎩⎪⎨⎪⎧sin θ＋cos θ＝3＋12，sin θ·cos θ＝34知⎩⎨⎧sin θ＝32，cos θ＝12，或⎩⎨⎧sin θ＝12，cos θ＝32.又θ∈(0,2π)，故θ＝π6或θ＝π3.12．是否存在α∈⎝⎛⎭⎫－π2，π2，β∈(0，π)，使等式sin(3π－α)＝2cos ⎝⎛⎭⎫π2－β，3cos(－α)＝－2cos(π＋β)同时成立？若存在，求出α，β的值，若不存在，请说明理由．解：假设存在α、β使得等式成立，即有⎩⎪⎨⎪⎧sin (3π－α)＝2cos ⎝⎛⎭⎫π2－β， ①3cos (－α)＝－2cos (π＋β)， ②由诱导公式可得⎩⎪⎨⎪⎧sin α＝2sin β， ③3cos α＝2cos β， ④ ③2＋④2得sin 2α＋3cos 2α＝2，解得cos 2α＝12.又∵α∈⎝⎛⎭⎫－π2，π2，∴α＝π4或α＝－π4. 将α＝π4代入④得cos β＝32.又β∈(0，π)，∴β＝π6，代入③可知符合．将α＝－π4代入④得cos β＝32.又β∈(0，π)．∴β＝π6，代入③可知不符合．综上可知，存在α＝π4，β＝π6满足条件．1．记cos(－80°)＝k ，那么tan 100°＝( ) A.1－k 2kB ．－1－k 2kC.k1－k 2D ．－k1－k 2解析：选B ∵cos(－80°)＝cos 80°＝k ， sin 80°＝1－k 2，∴tan 80°＝1－k 2k，tan 100°＝－tan 80°＝－1－k 2k. 2．sin 585°的值为( ) A ．－22B.22C ．－32D.32解析：选A 注意到585°＝360°＋180°＋45°，因此sin 585°＝sin(360°＋180°＋45°)＝－sin 45°＝－22. 3．若cos α＋2sin α＝－5，则tan α＝( ) A.12 B ．2 C ．－12D ．－2解析：选B ∵cos α＋2sin α＝－5，结合sin 2α＋cos 2α＝1得(5sin α＋2)2＝0，∴sin α＝－255，cos α＝－55，∴tan α＝2.4．求值：sin(－1 200°)·cos 1 290°＋cos(－1 020°)·sin(－1 050)°＋tan 945°. 解：原式＝－sin 1 200°·cos 1 290°＋cos 1 020°· (－sin 1 050°)＋tan 945°＝－sin 120°·cos 210°＋cos 300°·(－sin 330°)＋tan 225° ＝(－sin 60°)·(－cos 30°)＋cos 60°·sin 30°＋tan 45° ＝32×32＋12×12＋1＝2. 5．若sin θ，cos θ是关于x 的方程5x 2－x ＋a ＝0(a 是常数)的两根，θ∈(0，π)，求cos 2θ的值．解：∵由题意知：sin θ＋cos θ＝15，∴(sin θ＋cos θ)2＝125.∴sin 2θ＝－2425，即2sin θcos θ＝－2425＜0，则sin θ与cos θ异号．又sin θ＋cos θ＝15＞0，∴π2＜θ＜3π4，∴π＜2θ＜3π2.故cos 2θ＝－1－sin22θ＝－725.。

专题17同角三角函数的基本关系和诱导公式5题型分类一、同角三角函数基本关系1、同角三角函数的基本关系（1）平方关系：22sin cos 1αα+=．（2）商数关系：sin tan ()cos 2k απααπα=≠+；【记忆口诀】奇变偶不变，符号看象限，说明：（1）先将诱导三角函数式中的角统一写作2n πα⋅±；（2）无论有多大，一律视为锐角，判断2n πα⋅±所处的象限，并判断题设三角函数在该象限的正负；（3）当n 为奇数是，“奇变”，正变余，余变正；当n 为偶数时，“偶不变”函数名保持不变即可．注：1、利用22sin cos 1αα+=可以实现角α的正弦、余弦的互化，利用sin tan cos =aa a可以实现角α的弦切互化．2、“sin cos sin cos sin cos αααααα+-，，”方程思想知一求二．222(sin cos )sin cos 2sin cos 1sin 2ααααααα+=++=+222(sin cos )sin cos 2sin cos 1sin 2ααααααα-=+-=-22(sin cos )(sin cos )2αααα++-=（一）同角求值（1）若已知角的象限条件，先确定所求三角函数的符号，再利用三角形三角函数定义求未知三角函数值．（2）若无象限条件，一般“弦化切”．（二）诱导求值与变形（1）诱导公式用于角的变换，凡遇到与2π整数倍角的和差问题可用诱导公式，用诱导公式可以把任意角的三角函数化成锐角三角函数．（2）通过2,,2πππ±±±等诱导变形把所给三角函数化成所需三角函数．（3）2,,2παβππ±=±±±等可利用诱导公式把,αβ的三角函数化（三）同角三角函数基本关系式和诱导公式的综合应用）利用同角三角函数关系式和诱导公式求值或化简时，关键是寻求条件、结论间的联系，灵活使用公式(π（四）三角恒等式的证明三角恒等式的证明中涉及到同角三角函数基本关系，和角公式，差角公式，二角公式，辅助角公式等基本知识点，理解和掌握这些基本知识点是解答该类问题的基础和关键原式得证【点睛】本题考查了利用同角三角函数关系证明三角函数恒等式,属于基础题.5-4．（2024高三·全国·专题练习）（1）求证：tan 2αsin 2α=tan 2α-sin 2α；（2）已知tan 2α=2tan 2β+1，求证：2sin 2α=sin 2β+1.【答案】（1）证明见解析；（2）证明见解析.【分析】（1）将22sin 1cos αα=-代入左式，化简即可得到右式.（2）将sin tan cos ααα=，sin tan cos βββ=代入条件，通分化简得到2212cos cos αβ=，即2cos 2α=cos 2β，然后由22sin cos 1αα+=，将余弦化成正弦即可证得结论.【详解】解析：（1）tan 2αsin 2α=tan 2α（1-cos 2α）=tan 2α-tan 2αcos 2α=tan 2α-sin 2α，则原等式得证.（2）因为tan 2α=2tan 2β+1，所以22sin cos αα+1=222sin 1cos ββ⎛⎫+ ⎪⎝⎭，即2212cos cos αβ=，从而2cos 2α=cos 2β，于是2-2sin 2α=1-sin 2β，也即2sin 2α=sin 2β+1，则原等式得证.一、单选题1．（2024·全国·模拟预测）已知2cos tan sin 5xx x =+，则cos2x =（）A ．13B ．79C ．23D ．59【答案】B【分析】利用三角函数的基本关系式得到关于sin x 的方程，再利用倍角公式即可得解.【详解】因为2cos tan sin 5x x x =+，又sin tan cos xx x=，所以sin 2cos cos sin 5x xx x =+，则222cos sin 5sin x x x =+，即2222sin sin 5sin x x x -=+，则23sin 5sin 20x x +-=，即()()3sin 1sin 20x x -+=，所以1sin 3x =或sin 2x =-（舍去），所以217cos212sin 1299x x =-=-⨯=.故选：B.2．（2024·四川巴中·模拟预测）勾股定理，在我国又称为“商高定理”，最早的证明是由东汉末期数学家赵爽在为《周髀算经》作注时给出的，他利用了勾股圆方图，此图被称为“赵爽弦图”.“赵爽弦图”是由四个全等的直角三角形和中间的一个小正方形组成的大正方形图案（如图所示），若在大正方形内随机取一点，该点落在小正方形内的概率为917，则“赵爽弦图”里的直角三角形中最小角的正弦值为（）A ．217B C ．217D 【答案】D【分析】设正方形的边长1，较小的角为θ，则中间小正方形的边长为cos sin θθ-，由题意可得29(cos sin )17θθ-=，显然可得π04θ<<，即可得到cos sin 0θθ>>，从而求出sin θ.【详解】设正方形的边长1，较小的角为θ，则中间小正方形的边长为cos sin θθ-，由题意可得29(cos sin )17θθ-=，显然π04θ<<，所以cos sin 0θθ>>，所以cos sin 17θθ-=，又229cos sin 2cos sin 17θθθθ+-=，所以2cos si 8n 17θθ=，所以22225(cos sin )cos sin 2cos sin 17θθθθθθ+==++，所以cos sin 17θθ+=，所以sin 17θ=.故选：D3．（2024·全国·模拟预测）已知2π2cos 53θ⎛⎫-= ⎪⎝⎭，则19π13π2sin cos 105θθ⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭（）A ．2-B ．2C ．23-D ．23【答案】A【分析】利用已知的三角函数值，利用换元法，结合三角函数的诱导公式，可得答案.【详解】令25m πθ=-，则22,cos 53m m πθ=+=，从而19π13π19π2π2π13π2sin cos 2sin cos 10510555m m θθ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-++=-++++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦3π2sin cos(3π)3cos 22m m m ⎛⎫=-++=-=- ⎪⎝⎭.故选：A.4．（2024·山西·模拟预测）已知α为锐角，且cos 6πα⎛⎫+= ⎪⎝⎭，则tan 3πα⎛⎫-= ⎪⎝⎭（）A．2B．CD．2【答案】D【分析】注意到πππ632αα⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭，利用同角三角函数的关系求角π6α+的正弦，再利用诱导公式求角π3α-的正弦、余弦，从而得到π3α-的正切.【详解】因为α为锐角，所以ππ2π,663α⎛⎫+∈ ⎪⎝⎭且πcos 6α⎛⎫+= ⎪⎝⎭，所以22πsin 06ππsin cos 166ααα⎧⎛⎫+> ⎪⎪⎪⎝⎭⎨⎛⎫⎛⎫⎪+++= ⎪ ⎪⎪⎝⎭⎝⎭⎩得πsin 6α⎛⎫+= ⎪⎝⎭由诱导公式得ππππsin sin cos 3266ααα⎡⎤⎛⎫⎛⎫⎛⎫-=-+=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦ππcos sin 363αα⎛⎫⎛⎫-=+=⎪ ⎪⎝⎭⎝⎭.所以πsin π33tan π32cos 3ααα⎛⎫- ⎪⎛⎫⎝⎭-== ⎪⎛⎫⎝⎭- ⎪⎝⎭.故选:D5．（2024高三上·安徽合肥·阶段练习）已知角α为钝角，且角(02π)θθ<<终边上有一点()sin ,cos P αα-，则角θ=（）A ．πα+B ．π2α+C ．2πα-D ．3π2α-【答案】B【分析】利用三角函数的诱导公式及三角函数的定义即可求解.【详解】点()sin ,cos P αα-，由诱导公式可化为ππcos ,sin 22P αα⎛⎫⎛⎫⎛⎫++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，由三角函数的定义知，π2π2k θα=++，又因为α为钝角，02πθ<<，所以π2θα=+.故选:B.6．（2024高三上·宁夏银川·阶段练习）在平面直角坐标系中，在()1,3P 在角α终边上，则()()()3333sin πcos ππsin cos 2αααα++-⎛⎫--- ⎪⎝⎭的值为（）A ．1327B ．1427C ．1427-D ．1413【答案】B【分析】根据三角函数的定义求角α的三角函数值，再利用诱导公式化简求值.【详解】因为点()1,3P 在角α终边上，则1x =，3y =，所以tan 3yxα==,()()()333333333sin πcos πsin cos 1114π227sin sin 2tan sin cos 2ααααααααα++---==+⎛⎫----- ⎪⎝⎭.故选：B7．（2024高三上·四川成都·期中）已知角α的顶点与坐标原点重合，始边与x 轴的正半轴重合，若角α的终边与23π角的终边相同，则sin()cos(2)3sin()2παπαπα+--=+()A1B1C．1D．1-【答案】C【分析】利用三角函数定义求得tan α=，再利用诱导公式化简即可.【详解】由题意得2tan tanπ3α==sin(π)cos(2π)sin cos sin cos sin cos tan 113ππcos cos sin()sin 22ααααααααααααα+------+====+=+-⎛⎫+-+ ⎪⎝⎭，故选：C.8．（2024·全国·模拟预测）已知直线:2310l x y +-=的倾斜角为θ，则()πsin πsin 2θθ⎛⎫-⋅-= ⎪⎝⎭（）A ．613B ．613-C ．25D ．25-【答案】A【分析】根据直线一般方程可求得2tan 3θ=-，再利用诱导公式及同角三角函数之间的基本关系可得其结果.【详解】由直线l 的方程为2310x y +-=，得斜率2tan 3k θ==-，则()πsin cos sin πsin sin cos 21θθθθθθ-⋅⎛⎫-⋅-=-⋅= ⎪⎝⎭22222sin cos tan 63sin cos tan 113213θθθθθθ-⋅-====++⎛⎫-+ ⎪⎝⎭；故选：A ．9．（2024·陕西宝鸡·一模）已知4ππsin 2sin 36αα⎛⎫⎛⎫-=+⎪ ⎪⎝⎭⎝⎭，则πsin 23α⎛⎫+= ⎪⎝⎭（）A ．34-B ．34C ．45-D ．45【答案】C【分析】先利用诱导公式对已知条件化简得ππcos 2sin 66αα⎛⎫⎛⎫-+=+ ⎪ ⎪⎝⎭⎝⎭；再利用同角三角函数基本关系求出2π1sin 65α⎛⎫+= ⎪⎝⎭；最后利用二倍角公式即可求解.【详解】4π3πππsin sin cos 3266ααα⎡⎤⎛⎫⎛⎫⎛⎫-=-+=-+⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.由4ππsin 2sin 36αα⎛⎫⎛⎫-=+⎪ ⎪⎝⎭⎝⎭可得：ππcos 2sin 66αα⎛⎫⎛⎫-+=+ ⎪ ⎪⎝⎭⎝⎭.因为22ππsin cos 166αα⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭，所以2π1sin 65α⎛⎫+= ⎪⎝⎭.所以2ππππ4sin 22sin cos 4sin 36665αααα⎛⎫⎛⎫⎛⎫⎛⎫+=++=-+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.故选：C.10．（2024·全国·模拟预测）已知(ππtan cos 3cos 44ααα⎛⎫⎛⎫+=-- ⎪ ⎪⎝⎭⎝⎭，则cos2α=（）AB．2C ．12-D ．1-【答案】B 【分析】由诱导公式和同角三角函数关系得到(πtan 3tan 4αα⎛⎫=-+ ⎪⎝⎭，再利用正切和角公式得到方程，求出tan 1α=，利用余弦二倍角，齐次化求出答案.【详解】因为ππππcos sin sin 4244ααα⎛⎫⎛⎫⎛⎫-=-+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以(ππtan cos 3sin 44ααα⎛⎫⎛⎫+=-+ ⎪ ⎪⎝⎭⎝⎭，故(πtan 3tan 4αα⎛⎫=-+ ⎪⎝⎭，因为πtan tanπtan 14tan π41tan 1tan tan 4ααααα++⎛⎫+== ⎪-⎝⎭-，所以(tan 1tan 31tan ααα+=--，故)(2tan 21tan 30αα-+-=，解得tan 1α=，所以)()2222222211cos sin 1tan cos2cos sin 1tan 11ααααααα---=====+++-故选：B ．11．（2024·全国·模拟预测）已知圆22:(1)(1)1C x y -+-=，过点()3,2P ，作圆C 的两条切线，切点分别为,A B ，则tan ACB ∠=（）A ．43-B ．43C ．12-D ．34【答案】A【分析】设切线的方程为2(3)y k x -=-，求得圆心C到切线的距离1d ==，求得k 的值，得到4tan 3APB ∠=，结合180APB ACB ∠+∠=︒，即可求解.【详解】由题意知，圆22:(1)(1)1C x y -+-=的圆心为(1,1)C ，半径1r =，且切线PA ，PB 的斜率都存在，设切线的方程为2(3)y k x -=-，即320kx y k --+=，因为直线与圆相切，所以圆心C到切线的距离1d =，解得10k =或2k =43，所以4tan 3APB ∠=，在四边形APBC 中，因为90APC ABC ∠=∠= ，可得180APB ACB ∠+∠=︒，所以4tan tan(180)tan 3ACB APB APB ∠=-∠=-∠=-.故选：A ．12．（2024·河南郑州·模拟预测）已知tan 2θ=，则3πsin sin 2θθ⎛⎫+= ⎪⎝⎭（）A ．35B ．12C ．12-D ．25-【答案】D【分析】利用诱导公式，平方关系和商关系即可求解.【详解】3πsin sin sin cos 2θθθθ⎛⎫+=- ⎪⎝⎭222sin cos tan 2sin cos tan 15θθθθθθ=-=-=-++.故选：D13．（2024·陕西西安·二模）已知π5cos 513α⎛⎫-= ⎪⎝⎭，则7πsin 10α⎛⎫-= ⎪⎝⎭（）A ．513-B ．513C ．-1213D ．1213【答案】A 【分析】因为7πππ1052αα⎛⎫-=-- ⎪⎝⎭，由诱导公式可得选项.【详解】7ππππ5sin sin cos 1052513ααα⎛⎫⎛⎫⎛⎫-=--=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选：A.14．（2024·广东深圳·模拟预测）已知π4sin 35α⎛⎫+= ⎪⎝⎭，则5πcos 6α⎛⎫+ ⎪⎝⎭的值为（）A ．35-B ．35C ．45-D ．45【答案】C 【分析】根据5πππ623αα⎛⎫+=++ ⎪⎝⎭，借助于诱导公式，即可求得结果．【详解】5πππcos cos 623αα⎡⎤⎛⎫⎛⎫+=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ sin 3πα⎛⎫=-+ ⎪⎝⎭45=-，5πcos 6α⎛⎫∴+ ⎪⎝⎭的值为45-，故选：C15．（2024高三上·陕西西安·阶段练习）若1sin 3A =，则()sin 6A π-的值为（）A ．13B ．13-C．3-D．3【答案】B【分析】本题考查诱导公式的基础运用，套用公式即可.【详解】利用诱导公式可得()()1sin 6sin sin 3A A A π-=-=-=-，故选：B.16．（2024高三上·陕西西安·阶段练习）若()1sin 2πα+=-，则cos α的值为（）A ．12±B ．12CD．【答案】D【分析】先化简已知得1sin =2α，再求cos α的值.【详解】由()1sin 2πα+=-得1sin =2α，所以α在第一、二象限，所以cos =2α=±.故选：D.17．（2024·贵州贵阳·模拟预测）已知πsin sin 2θθ⎛⎫-+= ⎪⎝⎭，则tan θ=（）A．B ．1-C ．1D【答案】B【分析】利用诱导公式以及同角三角函数的平方关系可得出关于sin θ、cos θ的方程组，求出这两个量的值，即可求得tan θ的值.【详解】因为πsin sin sin cos 2θθθθ⎛⎫-+=-= ⎪⎝⎭，由题意可得22sin cos sin cos 1θθθθ⎧-=⎪⎨+=⎪⎩sin 2cos 2θθ⎧=⎪⎪⎨⎪=-⎪⎩，因此，sin tan 1cos θθθ==-.故选：B.18．（2024高一下·湖南长沙·阶段练习）已知1sin cos 5αα+=，且()0,πα∈，sin cos αα-=（）A ．75±B ．75-C ．75D ．4925【答案】C【分析】将已知等式两边平方，利用三角函数的基本关系求得2sin cos αα的值，结合α的范围确定sin α与cos α的正负，再利用完全平方公式及三角函数的基本关系可求得sin cos αα-的值.【详解】因为1sin cos 5αα+=，两边平方得()21sin cos 12sin cos 25αααα+=+=，故242sin cos 025αα=-<，所以sin α与cos α导号，又因为0πα<<，所以sin 0α>，cos 0α<，所以7sin cos 5αα-====.故选：C.19．（2024高三下·重庆渝中·阶段练习）已知θ是三角形的一个内角，且满足sin cos 5θθ-=，则tan θ=（）A ．2B ．1C ．3D ．12【答案】A【分析】利用平方关系可求得42sin cos 5θθ=，可解得29(sin cos )5θθ+=，再结合θ是三角形的一个内角即可得sin ,cos θθ==tan 2θ=.【详解】将sin cos θθ-=两边同时平方可得112sin cos 5θθ-=，即42sin cos 5θθ=；所以29(sin cos )12sin cos 5θθθθ+=+=若sin +cos θθ=，解得sin θθ==，这与θ是三角形的一个内角矛盾，所以sin +cos θθ=，解得sin θθ==，此时求得tan 2θ=.故选：A.20．（2024高三上·北京·阶段练习）在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于直线y x =对称，若4sin 5α=，则cos β=（）A ．45-B ．45C ．35-D ．35【答案】B【分析】根据题意利用任意角的三角函数的定义，结合诱导公式可求得结果.【详解】因为平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于直线y x =对称，所以ππ,Z 24k k αβ+=+∈，即π2π,Z 2k k αβ+=+∈，所以π2π,Z 2k k βα=-+∈，因为4sin 5α=，所以π4cos cos 2πsin (Z)25k k βαα⎛⎫=-+==∈ ⎪⎝⎭，故选：B21．（2024·辽宁抚顺·模拟预测）已知(),0,a βπ∈，则“tan tan 1αβ=”是“2a πβ+=”的（）A ．充要条件B ．既不充分也不必要条件C ．充分不必要条件D ．必要不充分条件【答案】D【分析】根据诱导公式的逆运用以及由三角函数的概念即可判断其充分性，由2a πβ+=代入tan α化简计算即可判断其必要性，从而得出结论.【详解】若tan tan 1αβ=，则1tan ta 2n tan παββ⎛⎫==- ⎪⎝⎭，故()2k k παπβ=+-∈Z ，即()2k k παβπ+=+∈Z ．又()0,2αβπ+∈，故0k =或1k =，充分性不成立；若2παβ+=，即2παβ=-，所以1tan tan 2tan παββ⎛⎫=-= ⎪⎝⎭，所以tan tan 1αβ=，所以必要性成立．故选：D ．22．（2024·陕西榆林·二模）已知π7π1cos cos 12125αα⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭，则2πc 23os +α⎛⎫ ⎪⎝⎭=（）A ．2325-B ．2325C ．2425-D ．2425【答案】C【分析】利用诱导公式和倍角公式化简求值.【详解】7ππππcos cos sin 1212212ααα⎛⎫⎛⎫⎛⎫+=++=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，由π7π1cos cos 12125αα⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭，有ππ1cos sin 12125αα⎛⎫⎛⎫+-+= ⎪ ⎪⎝⎭⎝⎭，两边平方得π11sin 2625α⎛⎫-+= ⎪⎝⎭，则π24sin 2625α⎛⎫+= ⎪⎝⎭，故2ππππ24cos 2+=cos 2+=sin 2=225366ααα⎛⎫⎛⎫⎛⎫+-+-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选：C.23．（2024高三上·北京海淀·阶段练习）已知α为第二象限的角，且3cos 5α=-，则()sin πα-的值为（）A ．45B ．45-C ．35-D ．35【答案】A【分析】先根据平方关系求出sin α，再利用诱导公式即可得解.【详解】因为α为第二象限的角，且3cos 5α=-，所以4sin 5α=，所以()4sin πsin 5αα-==.故选：A.24．（2024高一上·山西太原·阶段练习）已知π02α<<，且π1sin 34α⎛⎫-= ⎪⎝⎭，则5πsin 6α⎛⎫-= ⎪⎝⎭（）A ．4B ．14-C ．4D ．14【答案】C【分析】根据角的范围及正弦值求出余弦值，进而利用诱导求出答案.【详解】因为π02α<<，所以ππ36π3α-<-<，又π1sin 34α⎛⎫-= ⎪⎝⎭，所以πcos 3α⎛⎫-== ⎪⎝⎭45πππππs 62in c 3sin cos os 33αααα⎛⎫⎛⎫⎛⎫⎛⎫-=+-=-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.故选：C25．（2024·全国·模拟预测）已知π1tan 22θ⎛⎫+= ⎪⎝⎭，则()33sin 2cos sin πθθθ+=+（）A ．35B ．56C ．56-D ．35-【答案】D【分析】结合诱导公式与同角三角函数的基本关系运算即可得.【详解】由题意得πsin cos 12πsin 2cos 2θθθθ⎛⎫+ ⎪⎝⎭==-⎛⎫+ ⎪⎝⎭，则tan 2θ=-，故()()33333322sin 2cos sin 2cos sin 2cos sin πsin sin sin cos θθθθθθθθθθθ+++==-+-+333323sin 2cos tan 2823sin sin cos tan tan 825θθθθθθθθ++-+=-=-=-=-++--.故选：D.26．（2024高三上·云南昆明·阶段练习）若π2αβ+=sin αβ+=tan α=（）A．2BC ．1D【答案】B【分析】由诱导公式可得出sin cos βα=，根据已知条件可得出关于sin α、cos α的方程组，解出这两个量的值，结合同角三角函数的商数关系可求得tan α的值.【详解】因为π2αβ+=，则π2βα=-，πsin sin cos 2αβαααα⎛⎫+=+-=+= ⎪⎝⎭联立22cos sin cos 1αααα+=+=⎪⎩sin cos αα⎧=⎨⎪=⎪⎩因此，sin tan cos 3ααα==故选：B.27．（2024高三上·四川成都·阶段练习）已知角α的终边过点()1,3，则πcos(π)cos()2αα-++的值是（）A．B．C．D【答案】A【分析】利用三角函数定义，结合诱导公式计算得解.【详解】由角α的终边过点()1,3，得r =，31sin r r αα====，所以πcos(π)cos()cos sin 210105αααα-++=--=--=-.故选：A28．（2024高三上·安徽·阶段练习）在平面直角坐标系xOy 中，设角α的顶点与原点O 重合，始边与x 轴的非负半轴重合，若角α的终边过点()4,3P -，则()3πsin 2cos π22αα⎛⎫++-= ⎪⎝⎭（）A ．1425-B ．1425C ．1725-D ．1725【答案】A【分析】根据任意角的三角函数的定义可得sin α，再利用诱导公式、二倍角公式运算求解.【详解】由题意得，5OP ==，则3sin 5α=-，则()3πsin 2cos π2cos 2cos 22cos 22ααααα⎛⎫++-=--=- ⎪⎝⎭()22314212sin 212525α⎡⎤⎛⎫=--=-⨯-⨯-=-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦．故选：A ．29．（2024高三上·安徽·期中）已知()sin ,cos P θθ是角π3-的终边上一点，则tan θ=（）A ．B ．C D 【答案】B【分析】由三角函数的定义可得sin ,cos θθ，进而由商数关系可求tan θ.【详解】因为()sin ,cos P θθ是角π3-的终边上一点，所以π1πcos sin ,sin cos 3232θθ⎛⎫⎛⎫-==-==- ⎪ ⎪⎝⎭⎝⎭，则sin tan cos 3θθθ==，故选：B.30．（2024高三上·安徽·期中）已知角θ的顶点在坐标原点，始边与x 轴的非负半轴重合，终边经过点()2,4P -，则()cos 2cos 2πθπθ⎛⎫--+= ⎪⎝⎭（）A ．5-B ．5-C ．0D ．5【答案】C【分析】根据终边上的点可求得：sinθ=cos θ=，再结合三角函数诱导公式从而求解.【详解】因为：r OP ==（O 为坐标原点），所以:由三角函数的定义，得sin θ==cos θ==所以：()cos 2cos sin 2cos 02πθπθθθ⎛⎫--+=+= ⎪⎝⎭.故C 项正确.故选：C.31．（2024高一上·江苏常州·阶段练习）若π1cos()63α+=，则5π5πcos()sin()63αα--+=（）A ．0B ．23C．13+D．13-【答案】A【分析】利用整体代换法与诱导公式化简求值即可.【详解】依题，令π6t α+=，则15ππsin ,ππ366t t αα⎛⎫=-=-+=- ⎪⎝⎭，5π3ππ3π3262t αα+=++=+，所以5π5πcos()sin()63αα--+3π=cos(π)sin()2t t --+cos cos 0t t =-+=.故选：A32．（2024高三上·重庆永川·期中）已知π0,2θ⎛⎫∈ ⎪⎝⎭，π2tan tan 43θθ⎛⎫+=- ⎪⎝⎭，则πcos cos 22π4θθθ⎛⎫- ⎪⎝⎭=⎛⎫+ ⎪⎝⎭（）A ．12-B ．35-C ．3D ．53【答案】B【分析】由条件π2tan tan 43θθ⎛⎫+=- ⎪⎝⎭化简求得tan 3θ=，将所求式子利用三角恒等变换化简再根据同角三角函数关系式转化为正切求得结果.【详解】由π2tan tan 43θθ⎛⎫+=- ⎪⎝⎭，即tan 12tan 1tan 3θθθ+=--，又π0,2θ⎛⎫∈ ⎪⎝⎭，解得tan 3θ=，()()22πcos cos2sin cos sin2sin cos sinπsin cos4θθθθθθθθθθθ⎛⎫-⎪-⎝⎭∴==-+⎛⎫+⎪⎝⎭2222222sin cos sin tan tan333sin cos tan1315θθθθθθθθ---====-+++.故选：B.33．（2024高一下·山东潍坊·阶段练习）下列化简正确的是（）A．()tanπ1tan1+=-B．()()sincostan360ααα-=-C．()()sinπtancosπααα-=+D．()()()cosπtanπ1sin2πααα---=-【答案】B【分析】应用诱导公式以及同角三角函数的基本关系对四个选项验证即可.【详解】对于A，由诱导公式得，()tanπ1tan1+=，故A错误；对于B，()()sin sin sincossintantan360cos aααααααα--===-- ，故B正确；对于C，()()sinπsintancosπcosααααα-==-+-，故C错误；对于D，()()()()()sincoscosπtanπcos tan cos1sin2πsin sinαααααααααα⋅----==-=---，故D错误.故选：B.二、多选题34．（2024·辽宁·模拟预测）设α为第一象限角,π1cos83α⎛⎫-=⎪⎝⎭,则（）A．5π1sin83α⎛⎫-=-⎪⎝⎭B．7π1cos83α⎛⎫+=-⎪⎝⎭C．13πsin83α⎛⎫-=-⎪⎝⎭D．πtan8α⎛⎫-=-⎪⎝⎭【答案】BD【分析】首先由题意得π8α-是第一象限角,所以πsin 83α⎛⎫-=⎪⎝⎭,再利用诱导公式和同角三角函数关系式对选项逐个计算确定正确答案.【详解】由题意得π2π2π,Z 2k k k α<<+∈,则ππ3π2π2π,Z 888k k k α-<-<+∈,若π8α-在第四象限,则ππ1cos cos 8423α⎛⎫->=⎪⎝⎭,所以π8α-也是第一象限角,即πsin 8α⎛⎫-=⎪⎝⎭5πππππ1sin sin cos cos 828883αααα⎛⎫⎛⎫⎛⎫⎛⎫-=+-=-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,A 项错误;7πππ1cos cos πcos 8883ααα⎛⎫⎛⎫⎛⎫+=-+=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,B 项正确;13π3ππππ1sin sin cos cos 828883αααα⎛⎫⎛⎫⎛⎫⎛⎫-=+-=--=--=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,C 项错误;πsin ππ8tan tan 2π88cos 8αααα⎛⎫- ⎪⎛⎫⎛⎫⎝⎭-=--=-=- ⎪ ⎪⎛⎫⎝⎭⎝⎭- ⎪⎝⎭项正确.故选:BD.35．（江苏省宜兴中学、泰兴中学、泰州中学2023-2024学年高一上学期12月联合质量检测数学试卷）质点P 和Q 在以坐标原点O 1的圆O 上逆时针作匀速圆周运动，同时出发.P 的角速度大小为2rad /s ，起点为圆O 与x 轴正半轴的交点，Q 的角速度大小为5rad /s ，起点为角π3-的终边与圆O 的交点，则当Q 与P 重合时，Q 的坐标可以为（）A ．2π2πcos ,sin 99⎛⎫ ⎪⎝⎭B ．ππcos ,sin 99⎛⎫- ⎪⎝⎭C ．5π5πcos ,sin 99⎛⎫-- ⎪⎝⎭D ．ππcos ,sin 99⎛⎫- ⎪⎝⎭【答案】ACD【分析】由题意列出重合时刻t 的表达式，进而可得Q 点的坐标，通过赋值对比选项即可得解.【详解】点Q 的初始位置1Q ，锐角1π3Q OP ∠=，设t 时刻两点重合，则π522π(N)3t t k k -∈=+，即π2π(N)93k t k +∈=，此时点ππcos 5,sin 533Q t t ⎛⎫⎛⎫⎛⎫-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，即2π10π2π10πcos ,sin 9393k k Q ⎛⎫⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭⎝⎭，(N)k ∈，当0k =时，2π2πcos ,sin 99Q ⎛⎫ ⎪⎝⎭，故A 正确；当1k =时，32π32πcos ,sin 99Q ⎛⎫ ⎪⎝⎭，即5π5πcos ,sin 99Q ⎛⎫-- ⎪⎝⎭，故C 正确；当2k =时，9,62π62πcos sin 9Q ⎛⎫ ⎪⎝⎭，即ππcos ,sin 99Q ⎛⎫- ⎪⎝⎭，故D 正确；由三角函数的周期性可得，其余各点均与上述三点重合，故B 错误，故选：ACD.36．（2024高一下·河南焦作·阶段练习）已知角,A B ，C 是锐角三角形ABC 的三个内角，下列结论一定成立的有（）A ．()sin sinBC A +=B ．sin cos 22A B C +⎛⎫= ⎪⎝⎭C ．()cos cos A B C +<D ．sin cos A B<【答案】ABC【分析】根据三角形内角和及诱导公式，三角函数单调性一一判定选项即可.【详解】由题易知()()πsin sin πsin 2A B C A B C B C A A π⎛⎫++=<⇒+=-= ⎪⎝⎭、、，πsin sin cos 222A B C C +-⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，()()cos cos πcos 0cos A B C C C +=-=-<<，即A 、B 、C 结论成立.对于D ，由锐角三角形知，2A B π+>，得ππ022B A <-<<，因此πsin sin cos 2A B B ⎛⎫>-= ⎪⎝⎭，所以错误.故选：ABC37．（2024高一下·河北沧州·阶段练习）在△ABC 中，下列关系式恒成立的有（）A ．()sin sin ABC +=B ．cos sin 22A B C +⎛⎫= ⎪⎝⎭C ．()sin 22sin20A B C ++=D ．()cos 22cos20A B C ++=【答案】ABC【分析】结合三角形的内角和定理和诱导公式，准确运算，即可求解.【详解】对于A 中，由()()sin sin sin A B C C π+=-=，所以A 正确；对于B 中由cos cos sin 2222A B C C π+⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭，所以B 正确；对于C 中，由()()()sin 22sin2sin 2sin2sin 2sin2A B C A B C C Cπ⎡⎤⎡⎤++=++=-+⎣⎦⎣⎦()sin 22sin2sin2sin20C C C C π=-+=-+=，所以C 正确；对于D 中，()cos(22)cos2cos 2cos2cos[2()]cos2A B C A B C C Cπ⎡⎤++=++=-+⎣⎦()cos 22cos2cos2cos22cos2C C C C C π=-+=+=，所以D 错误．故选：ABC.38．（2024高一上·江苏无锡·阶段练习）下列结论正确的有（）A ．sin cos 63ππαα⎛⎫⎛⎫+=- ⎪ ⎪⎝⎭⎝⎭B ．52cos sin 063ππθθ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭C ．()()22sin 15cos 751αα-++=D ．()()22sin 15sin 751αα-++=【答案】ABD【解析】本题可通过诱导公式将sin 6απ⎛⎫+ ⎪⎝⎭转化为cos 3πα⎛⎫- ⎪⎝⎭，A 正确，然后通过诱导公式将5cos 6πθ⎛⎫+⎪⎝⎭转化为2sin 3πθ⎛⎫-- ⎪⎝⎭，B 正确，最后根据()()sin 15cos 75 αα-=+以及同角三角函数关系判断出C 错误以及D 正确.【详解】A 项：sin sin cos cos 63332πππππαααα⎛⎫⎛⎫⎛⎫⎛⎫+=+-=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，A 正确；B 项：因为522cos sin sin sin 6333ππππθθπθθ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=-+=---=-- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦，所以52cos sin 063ππθθ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭，B 正确；C 项：因为()()()sin 15sin 75cos 752πααα⎡⎤-=-+=+⎢⎥⎣⎦，所以()()()222sin 15cos 752cos 751ααα-++=+≠，C 错误；D 项：()()()()2222sin 15sin 75cos 75sin 751αααα-++=+++=，D 正确，故选：ABD.【点睛】关键点点睛：本题考查诱导公式以及同角三角函数关系的应用，考查的公式有sin cos 2παα⎛⎫+= ⎪⎝⎭、()cos cos αα=-、sin cos 2παα⎛⎫-= ⎪⎝⎭、22cos sin 1αα+=等，考查化归与转化思想，是中档题.39．（2024高一上·黑龙江齐齐哈尔·期末）已知下列等式的左右两边都有意义，则下列等式恒成立的是（）A ．cos 1sin 1sin cos x xx x-=+B ．221sin 12tan sin cos tan x x x x x++=C ．()()sin 53cos 37x x -=+D ．()()sin 60cos 480x x -=+【答案】ABC【分析】对于A 、B ，由同角三角函数的基本关系进行化简证明即可，对于C 、D ，由诱导公式进行化简证明即可.【详解】对于A ，()()()()()22cos 1sin cos 1sin cos 1sin cos 1sin 1sin 1sin 1sin 1sin cos cos x x x x x x x x x x x x x x----====++--，故A 正确；对于B ，()2222222sin cos sin 1sin cos 2sin 12tan sin cos sin cos sin cos tan x x x x x x x x x x x x x x+++++===，故B 正确；对于C ，()()()sin 53sin 9037=cos 37x x x ⎡⎤-=-++⎣⎦，故C 正确；对于D ，()()()()cos 480=cos 0=cos 18060=cos 0126x x x x -⎡⎤++---⎣⎦，故D 错误.故选：ABC.三、填空题40．（2024·全国）若π10,,tan 22⎛⎫∈= ⎪⎝⎭θθ，则sin cos θθ-=．【答案】5-【分析】根据同角三角关系求sin θ，进而可得结果.【详解】因为π0,2θ⎛⎫∈ ⎪⎝⎭，则sin 0,cos 0θθ>>，又因为sin 1tan cos 2θθθ==，则cos 2sin θθ=，且22222cos sin 4sin sin 5sin 1+=+==θθθθθ，解得sin θ=或sin θ=（舍去），所以sin cos sin 2sin sin -=-=-=-θθθθθ故答案为：5-.41．（2024高一上·福建莆田·阶段练习）已知tan α=-2απ<<π，那么sin cos 1αα=+.【分析】由同角三角函数关系及已知条件求得1sin 33αα==-，代入目标式求值即可.【详解】由tan α=-2απ<<π，则1sin 33αα==-，所以sin cos 1αα=+.42．（2024高三·全国·对口高考）若sin cos 2sin cos x xx x-=+，求sin cos x x 的值为.【答案】310-/0.3-【分析】由已知求出tan 3x =-，再将sin cos x x 化为22sin cos sin cos x xx x+，利用齐次式法求值，即得答案.【详解】由sin cos 2sin cos x xx x-=+可得sin cos 2(sin cos ),sin 3cos x x x x x x -=+∴=-，因为cos 0x =不适合sin cos 2sin cos x xx x-=+，故cos 0x ≠，所以tan 3x =-，故222sin cos tan 33sin cos sin cos tan 19110x x x x x x x x -====-+++，故答案为：310-43．（2024高三上·江西南昌·阶段练习）若4tan 3θ=，则sin cos sin cos θθθθ-=+.【答案】17【分析】分式上下同除以cos θ，化弦为切，代入4tan 3θ=求值即可.【详解】4tan 3θ= ，sin 411sin cos tan 11cos 3sin 4sin cos tan 1711cos 3θθθθθθθθθθ----∴====++++.故答案为：17.44．（2024·上海浦东新·模拟预测）已知sin cos αα､是关于x 的方程2320x x a -+=的两根，则=a .【答案】56-【分析】先通过根与系数的关系得到sin ,cos αα的关系，再通过同角三角函数的基本关系即可解得.【详解】由题意：Δ41202sin cos 3sin cos 3a a αααα⎧⎪=-≥⎪⎪+=⎨⎪⎪=⎪⎩，所以13a ≤，所以()224sin cos 12sin cos 139a αααα+=+=+=，即650a +=，解得56a =-.故答案为：56-.45．（2024高三·全国·专题练习）已知1sin cos 4αα-=，则33sin cos αα-=．【答案】47128【分析】由立方差公式，得()()3322sin cos sin cos sin cos sin cos αααααααα-=-++.将1sin cos 4αα-=两边平方，解得15sin cos 32αα=，代入即可得解.【详解】由题知()()3322sin cos sin cos sin cos sin cos αααααααα-=-++，因为1sin cos 4αα-=，两边平方有112sin cos 16αα-=，所以15sin cos 32αα=，所以()3311547sin cos 1432128αα-=⨯+=.故答案为：47128.46．（2024高三上·安徽合肥·阶段练习）已知23sin 2m m α-=+，1cos 2m m α+=-+，且α为第二象限角，则()()sin 2024πcos 2023π2021πcos 2ααα+++=⎛⎫+ ⎪⎝⎭.【答案】73-/123-【分析】由已知可求出m 的取值范围，由同角三角函数的平方关系求出m 的值，可求出tan α的值，再利用诱导公式结合弦化切可求得所求代数式的值.【详解】因为23sin 2m m α-=+，1cos 2m m α+=-+，且α为第二象限角，则2302102m m m m -⎧>⎪⎪+⎨+⎪-<⎪+⎩，解得2m <-或32m >，因为22222223151010sin cos 12244m m m m m m m m αα-+-+⎛⎫⎛⎫+=+-== ⎪ ⎪++++⎝⎭⎝⎭，整理可得22730m m -+=，即()()2130m m --=，解得12m =（舍）或3m =，所以，233sin 25m m α-==+，14cos 25m m α+=-=-+，所以，sin 353tan cos 544ααα⎛⎫==⨯-=- ⎪⎝⎭，因此，()()sin 2024πcos 2023πsin cos 147112021πsin tan 33cos 2ααααααα+++-==-+=--=--⎛⎫+ ⎪⎝⎭.故答案为：73-.47．（2024·全国·模拟预测）若()223ππ1cos cos 714f x x x ⎡⎤⎤⎛⎫⎛⎫=--++ ⎪ ⎪⎢⎥⎥⎝⎭⎝⎭⎣⎦⎦，则()f x 的最大值为，()f x 的最小值为．【答案】91【分析】借助诱导公式将函数式转化，再利用两点间的距离公式将数转化为形，利用形的直观来求最值.【详解】因为πππ3π3πcos sin sin sin 1421477x x x x ⎛⎫⎛⎫⎛⎫⎛⎫+=--=-=-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，=，此式可看作点(到点3π3πcos ,sin 77x x ⎡⎤⎛⎫⎛⎫--⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦的距离．而点3π3πcos ,sin 77x x ⎡⎤⎛⎫⎛⎫-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦的轨迹是圆221+=m n ．又点(到圆心()0,0的距离为2，所以()f x 的最大值()()2max 219f x =+=，()f x 的最小值()()2min 211f x =-=．故答案为：9；1【点睛】将所给函数式展开必将陷入命题人的圈套，此时要整体把握目标，借助诱导公式将函数式转化，再利用两点间的距离公式将数转化为形，利用形的直观来求最值，既简单又节省时间．本题不仅要求学生具备扎实的基本功，具有整体把握目标的能力，还对学生分析问题和解决问题的能力、逻辑推理能力、运算求解能力等要求较高．48．（2024·四川绵阳·三模）已知π,π2θ⎛⎫∈ ⎪⎝⎭，()sin π3θ+=-，则tan θ=.【答案】【分析】根据诱导公式以及同角关系即可求解.【详解】由()sin π3θ+=-得sin 3θ=，由π,π2θ⎛⎫∈ ⎪⎝⎭可得cos θ=-，故sin tan cos θθθ==故答案为：2-49．（2024·山西阳泉·三模）已知πsin 6α⎛⎫+= ⎪⎝⎭ππ,44α⎛⎫∈- ⎪⎝⎭，则πsin 3α⎛⎫-=⎪⎝⎭．【分析】整体法诱导公式结合同角三角函数关系求出答案.【详解】因为ππ,44α⎛⎫∈- ⎪⎝⎭，所以ππ5π,61212α⎛⎫+∈- ⎪⎝⎭，故πcos 06α⎛⎫+> ⎪⎝⎭，所以πcos 6α⎛⎫+= ⎪⎝⎭ππππsin sin cos 3266ααα⎡⎤⎛⎫⎛⎫⎛⎫-=-+=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦50．（2024·浙江温州·二模）已知tan x =，则23sin 2sin cos x x x -=.【分析】利用同角三角函数的关系化简23sin 2sin cos x x x -为齐次式，再代入tan x =.【详解】因为tan x =，所以2222223sin 2sin cos 3tan 2tan 3sin 2sin cos sin cos 1tan x x x x xx x x x x x---==++、()2231⨯-==+51．（2024·黑龙江哈尔滨·二模）已知tan 2θ=，则1sin 2cos 2θθ+的值是．【答案】5【分析】利用正弦、余弦的二倍角公式以及弦化切的公式先化简，在将tan 2θ=代入即可.【详解】因为tan 2θ=，所以2211sin 2cos 22sin cos cos sin θθθθθθ=++-2222cos sin 2sin cos cos sin θθθθθθ+=+-221tan 2tan 1tan θθθ+=+-221252212+==⨯+-，故答案为：5.52．（2024高三·全国·专题练习）已知()7sin cos 0π13ααα+=<<，则tan α=．【答案】125-【分析】由同角三角函数的平方关系和商数关系，并分析三角函数值的正负即可求解.【详解】解：已知7sin cos 13αα+=①，则()2sin cos 12sin cos 69491αααα+=+=，60sin cos 0169αα=-<，0πα<< ，sin 0α∴>，则cos 0α<，sin cos 0αα->，17sin cos13αα∴-===②，联立①②，得12sin 13α=，5cos 13α=-12tan 5α∴=-，故答案为：125-.53．（2024高三上·湖南衡阳·期中）已知sin cos 3αα-=-，则sin 2α=．【答案】79【分析】sin cos 3αα-=-平方，结合同角三角函数平方关系即正弦二倍角公式求解.【详解】sin cos αα-=两边平方得：()22sin cos 12sin cos 1sin 29ααααα-=-=-=，解得：7sin 29α=.故答案为：7954．（2024·全国·模拟预测）已知π1sin 35α⎛⎫-= ⎪⎝⎭，则cos 6α5π⎛⎫-=⎪⎝⎭.【答案】15/0.2【分析】由三角函数的诱导公式化简可得.【详解】由题可得5π5ππππ1cos cos cos sin 663235αααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-=-=--=-= ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦.故答案为：1555．（2024高三上·内蒙古包头·阶段练习）若πtan 4θ⎛⎫+= ⎪⎝⎭πtan 4θ⎛⎫-=⎪⎝⎭.【答案】【分析】以π4θ+为整体，根据诱导公式运算求解.【详解】由题意可得：πππ1tan tanπ442tan 4θθθ⎡⎤⎛⎫⎛⎫-=+-=-=- ⎪ ⎪⎢⎥⎛⎫⎝⎭⎝⎭⎣⎦+ ⎪⎝⎭故答案为：56．（2024高一下·黑龙江佳木斯·开学考试）已知()1sin 535α︒-=，且27090α-︒<<-︒，则()sin 37α︒+=．【答案】【分析】设53βα︒=-,37γα︒=+,则90βγ︒+=,90γβ︒=-，从而将所求式子转化成求cos β的值，利用α的范围确定cos β的符号.【详解】设53βα︒=-,37γα︒=+,那么90βγ︒+=,从而90γβ︒=-.于是()sin sin 90cos γββ︒=-=.因为27090α︒︒-<<-,所以143323β︒︒<<.由1sin 05β=>,得143180β︒︒<<.所以cos β===所以()sin 37sin 5αγ︒+==-.故答案为：57．（2024高一上·新疆乌鲁木齐·期末）已知角α的终边与单位圆221x y +=交于点1,2⎛⎫⎪⎝⎭y P ，则3πsin 2α⎛⎫-= ⎪⎝⎭.【答案】12-/-0.5【分析】根据任意角三角比的定义和诱导公式求解.【详解】因为角α的终边与单位圆221x y +=交于点1,2⎛⎫⎪⎝⎭y P ，所以||1r OP ==13π12sin cos 212x r αα⎛⎫-=-=-=-=- ⎪⎝⎭，故答案为：12-.58．（2024高一·全国·课后作业）若角α的终边落在直线y x =上，则co 3si 22n s παπα⎛⎫⎛⎫++= ⎪ ⎪⎝⎭⎝⎭-．【分析】化简得到3sin cos cos sin 22ππαααα⎛⎫⎫⎪⎪-++=--⎝⎭⎝⎭，考虑角α为第一或第三象限角两种情况，计算得到答案.【详解】因为角α的终边落在直线y x =上，所以角α为第一或第三象限角，3sin cos cos sin 22ππαααα⎛⎫⎛⎫⎪ ⎪-++=--⎝⎭⎝⎭，当角α为第一象限角时，cos sin αα==，cos sin αα--==当角α为第三象限角时，cos sin αα==cos sin 22αα--=+=或.四、解答题59．（2024高三·全国·专题练习）已知角α的终边落在直线2y x =上．求(1)4sin 2cos 5sin 3cos αααα-+的值；(2)25sin 3sin cos 2ααα+-的值．【答案】(1)613(2)165【分析】由角α的终边落在直线2y x =上可得tan 2α=，再根据同角函数的关系求解即可.【详解】（1）由角α的终边落在直线2y x =上可得tan 2α=则原式=4tan 28265tan 310313αα--==++；（2）原式222225sin 3sin cos 5tan 3tan 20616222sin cos tan 155αααααααα+++=-=-=-=++.60．（2024高一下·安徽·期中）已知角θ的顶点为坐标原点O ，始边为x 轴的非负半轴，终边与单位圆相交于点P (),x y ，若点P 位于x 轴上方且12x y +=.(1)求sin cos θθ-的值；(2)求44sin cos θθ+的值.【答案】(2)2332【分析】（1）根据cos sin θθ+，cos sin θθ-，cos sin θθ三个直接的关系，可得sin cos θθ-.（2）由4422sin cos 12sin cos θθθθ+=-可得.【详解】（1）由三角函数的定义，1cos sin 2θθ+=，sin 0θ>，两边平方，得221cos sin 2sin cos 4θθθθ++=则32sin cos 04θθ=-<，sin 0θ>，cos 0θ<，所以sin cos 0θθ->，sin cos2θθ-=.（2）由（1）知，3sin cos 8θθ=-，4422222923sin cos (sin cos )2sin cos 126432θθθθθθ+=+-=-⨯=.。

高三数学一轮复习——同角三角函数基本关系式及诱导公式1．同角三角函数的基本关系 (1)平方关系：sin 2α＋cos 2α＝1.(2)商数关系：sin αcos α＝tan α⎝⎛⎭⎫α≠π2＋k π，k ∈Z . 2．三角函数的诱导公式概念方法微思考1．使用平方关系求三角函数值时，怎样确定三角函数值的符号？ 提示 根据角所在象限确定三角函数值的符号．2．诱导公式记忆口诀“奇变偶不变，符号看象限”中的奇、偶是何意义？提示 所有诱导公式均可看作k ·π2±α(k ∈Z )和α的三角函数值之间的关系，口诀中的奇、偶指的是此处的k 是奇数还是偶数．题组一 思考辨析1．判断下列结论是否正确(请在括号中打“√”或“×”) (1)若α，β为锐角，则sin 2α＋cos 2β＝1.( × ) (2)若α∈R ，则tan α＝sin αcos α恒成立．( × )(3)sin(π＋α)＝－sin α成立的条件是α为锐角．( × ) (4)若sin(k π－α)＝13(k ∈Z )，则sin α＝13.( × )题组二 教材改编 2．若sin α＝55，π2<α<π，则tan α＝ . 答案 －12解析 ∵π2<α<π，∴cos α＝－1－sin 2α＝－255，∴tan α＝sin αcos α＝－12.3．已知tan α＝2，则sin α＋cos αsin α－cos α的值为 ．答案 3解析 原式＝tan α＋1tan α－1＝2＋12－1＝3.4．化简cos ⎝⎛⎭⎫α－π2sin ⎝⎛⎭⎫5π2＋α·sin(α－π)·cos(2π－α)的结果为 ． 答案 －sin 2α解析 原式＝sin αcos α·(－sin α)·cos α＝－sin 2α.题组三 易错自纠5．已知sin θ＋cos θ＝43，θ∈⎝⎛⎭⎫0，π4，则sin θ－cos θ的值为 ． 答案 －23解析 ∵sin θ＋cos θ＝43，∴sin θcos θ＝718.又∵(sin θ－cos θ)2＝1－2sin θcos θ＝29，θ∈⎝⎛⎭⎫0，π4， ∴sin θ－cos θ＝－23. 6．若sin(π＋α)＝－12，则sin(7π－α)＝ ；cos ⎝⎛⎭⎫α＋3π2＝ . 答案 12 12解析 由sin(π＋α)＝－12，得sin α＝12，则sin(7π－α)＝sin(π－α)＝sin α＝12，cos ⎝⎛⎭⎫α＋3π2＝cos ⎝⎛⎭⎫α＋3π2－2π＝cos ⎝⎛⎭⎫α－π2 ＝cos ⎝⎛⎭⎫π2－α＝sin α＝12.同角三角函数基本关系式的应用1．已知α是第四象限角，sin α＝－1213，则tan α等于( )A ．－513 B.513 C ．－125 D.125答案 C解析 因为α是第四象限角，sin α＝－1213，所以cos α＝1－sin 2α＝513，故tan α＝sin αcos α＝－125. 2．已知α是三角形的内角，且tan α＝－13，则sin α＋cos α的值为 ．答案 －105解析 由tan α＝－13，得sin α＝－13cos α，将其代入sin 2α＋cos 2α＝1， 得109cos 2α＝1， 所以cos 2α＝910，易知cos α<0，所以cos α＝－31010，sin α＝1010，故sin α＋cos α＝－105. 3．若角α的终边落在第三象限，则cos α1－sin 2α＋2sin α1－cos 2α的值为 ．答案 －3。

第十二讲同角三角函数关系及诱导公式知识要点：1.同角三角函数基本关系： 〔1〕基本关系：①平方关系:sin 2α＋cos 2α＝12211tan cos αα+=②商数关系:tan α＝sin αcos α〔α≠k π＋π2，k ∈Z 〕；cot α＝cos αsin α〔α≠k π，k ∈Z 〕．③倒数关系: 1tan cot αα=〔12k απ≠〕 〔2〕常用变换形式:〔1〕根据这三大关系，假设一个角α的位置，及其一个三角函数值，那么一定能求出其余的三角函数值． 〔2〕几个常用关系式：sinα+cosα，sinα--cosα，sinα·cosα；三式之间可以互相表示。

2.诱导公式： 〔〔①六组诱导公式统一为“()2k k Z πα±∈〞，记忆口诀：奇变偶不变，符号看象限. ②求任意角的三角函数值方法和步骤：负化正---→大化小---→小化锐，表达了化归思想。

(1)利用诱导公式〔三〕将负角的三角函数变为正角的三角函数. (2)利用诱导公式〔一〕化为0°到360°间的角的三角函数. (3)进一步转化成锐角三角函数. 二.基础练习1.化简1－sin 24 的结果为－cos42.化简sin 4θ＋cos 2θ＋sin 2θcos 2θ= 13.tan θ＝2aa 2－1 (其中0＜a ＜1，θ是三角形的一个内角)，那么cos θ的值是a 2－1a ＋14.化简：2－sin 221°－cos 221°＋sin 417°＋sin 217°·cos 217°＋cos 217°解：原式＝2－〔sin 221°＋cos 221°〕＋sin 217°〔sin 217°＋cos 217°〕＋cos 217°＝2－1＋sin 217°＋cos 217°＝1＋1＝25．sin 〔π－α〕＝log 814 ，且α∈(－π2，0)，那么tan α的值是－56．︒⋅--⋅︒690cos )619cos()313tan(330sin ππ的值是.－37.求值：23456tantantan tan tan tan tan 777777πππππππ++++++8.设002900,3cos 2sin 3≤≤=-βαβα，，求βα与。

高考数学第一轮复习：《同角三角函数的基本关系与诱导公式》最新考纲1.理解同角三角函数的基本关系式：sin 2x ＋cos 2x ＝1，sin xcos x ＝tan x .2.能利用单位圆中的三角函数线推导出π2±α，π±α的正弦、余弦、正切的诱导公式.【教材导读】1．同角三角函数的基本关系中，对任意角均成立吗？提示：在tan α＝sin αcos α的关系中，须保证tan α有意义，所以须使α≠π2＋k π，k ∈Z . 2．诱导公式的功能是什么？提示：负角化正角，大角化小角，再求值．1．同角三角函数的基本关系式 (1)平方关系 sin 2 α＋cos 2 α＝1； (2)商数关系 tan α＝sin αcos α. 2．诱导公式 组序 一 二 三 四 五 六 角 2k π＋α(k ∈Z )π＋α －α π－α π2－α π2＋α 正弦 sin α －sin α －sin α sin α cos α cos_α 余弦 cos α －cos α cos α －cos_α sin α －sin α 正切tan αtan α－tan α－tan_α诱导公式可简记为：奇变偶不变，符号看象限．“奇”与“偶”指的是诱导公式k ·π2＋α中的整数k 是奇数还是偶数．“变”与“不变”是指函数的名称的变化，若k 是奇数，则正、余弦互变；若k 为偶数，则函数名称不变．“符号看象限”指的是在k ·π2＋α中，将α看成锐角时k ·π2＋α所在的象限．1．已知α和β的终边关于直线y ＝x 对称，且β＝－π3，则sin α等于( ) (A)－32 (B)32 (C)－12(D)12D 解析：因为α和β的终边关于直线y ＝x 对称，所以α＋β＝2k π＋π2(k ∈Z )．又β＝－π3，所以α＝2k π＋5π6(k ∈Z )，即得sin α＝12.故选D.2．已知f (α)＝sin (π－α)·cos (2π－α)cos (－π－α)·tan (π－α)，则f ⎝ ⎛⎭⎪⎫－25π3的值为( )(A)12 (B)－12 (C)32(D)－32A 解析：∵f (α)＝sin αcos α(－cos α)·(－tan α)＝sin αtan α＝cos α，∴f (－25π3)＝cos(－25π3)＝cos ⎝ ⎛⎭⎪⎫－π3＝12.故选A.3．若α＝11π3，则tan α·cos α等于( ) (A)12 (B)－12 (C)－32(D)32C 解析：若α＝113π，tan α·cos α＝sin αcos α·cos α＝sin α＝sin 113π＝sin ⎝ ⎛⎭⎪⎫4π－π3＝－sin π3＝－32.故选C.4．已知a ∈⎝ ⎛⎭⎪⎫π2，π，sin α＝45，则tan α＝________.解析：因为a ∈⎝ ⎛⎭⎪⎫π2，π，所以cos α＝－1－sin 2α＝－35，所以tan α＝sin αcos α＝－43. 答案：－435．已知sin x cos x ＝38，且x ∈π4，π2，则cos x －sin x ＝________. 解析：因为x ∈π4，π2， 所以sin x >cos x ， 即cos x －sin x <0，所以(cos x －sin x )2＝1－2sin x cos x ＝14，所以cos x －sin x ＝－12. 答案：－12考点一 同角三角函数的基本关系(1)已知α∈⎝ ⎛⎭⎪⎫π，3π2，tan α＝2，则cos α＝________.(2)已知sin α＋3cos α3cos α－sin α＝5，则sin 2 α－sin αcos α的值是( )(A)25 (B)－25 (C)－2(D)2解析：(1)依题意得⎩⎨⎧tan α＝sin αcosα＝2，sin 2 α＋cos 2 α＝1，由此解得cos 2 α＝15；又α∈⎝ ⎛⎭⎪⎫π，3π2，因此cos α＝－55.(2)由sin α＋3cos α3cos α－sin α＝5得tan α＋33－tan α＝5，即tan α＝2.所以sin2α－sin αcos α＝sin2α－sin αcos αsin2α＋cos2α＝tan2α－tan αtan α＋1＝25.答案：(1)－55(2)A【反思归纳】同角三角函数关系式的应用技巧(1)利用sin2α＋cos2α＝1可实现α的正弦、余弦的互化，利用sin αcos α＝tan α可以实现角α的弦切互化．(2)关系式的逆用及变形用：1＝sin2α＋cos2α，sin2α＝1－cos2α，cos2α＝1－sin2α.(3)sin α，cos α的齐次式的应用：分式中分子与分母是关于sin α，cos α的齐次式，或含有sin2α，cos2α及sin αcos α的式子求值时，可将所求式子的分母看作“1”，利用“sin2α＋cos2α＝1”代换后转化为“切”后求解．【即时训练】已知角α的始终与x轴的非负半轴重合，顶点与坐标原点重合，终边过点P(3,4)，则sin α＋2cos αsin α－cos α＝________.答案：10考点二三角函数的诱导公式(1)化简sin(kπ－α)·cos[(k－1)π－α]sin[(k＋1)π＋α]·cos(kπ＋α)，k∈Z；(2)已知sin α＝255，求tan(α＋π)＋sin⎝⎛⎭⎪⎫5π2＋αcos⎝⎛⎭⎪⎫5π2－α；(3)化简tan(π－α)cos(2π－α)sin⎝⎛⎭⎪⎫－α＋3π2 cos(－α－π)sin(－π－α).解：(1)当k＝2n＋1(n∈Z)时，原式＝sin(2nπ＋π－α)·cos(2nπ－α)sin(2nπ＋2π＋α)·cos(2nπ＋π＋α)＝sin(π－α)·cos αsin α·cos(π＋α)＝sin α·cos αsin α·(－cos α)＝－1；当k ＝2n (n ∈Z )时，原式＝sin (2n π－α)·cos (2n π－π－α)sin (2n π＋π＋α)·cos (2n π＋α)＝－sin α·(－cos α)－sin α·cos α＝－1.所以原式＝sin (k π－α)·cos[(k －1)π－α]sin[(k ＋1)π＋α]·cos (k π＋α)＝－1.(2)∵sin α＝255＞0，∴α为第一或第二象限角．当α是第一象限角时，cos α＝1－sin 2 α＝55，tan(α＋π)＋sin ⎝ ⎛⎭⎪⎫5π2＋αcos ⎝ ⎛⎭⎪⎫5π2－α＝tan α＋cos αsin α＝sin αcos α＋cos αsin α＝1sin αcos α＝52.当α是第二象限角时，cos α＝－1－sin 2 α＝－55，原式＝1sin αcos α＝－52.(3)方法一：原式＝(－tan α)·cos[π＋(π－α)]·sin ⎝ ⎛⎭⎪⎫π＋π2－αcos (π＋α)·[－sin (π＋α)]＝(－tan α)·[－cos (π－α)]·⎣⎢⎡⎦⎥⎤－sin ⎝ ⎛⎭⎪⎫π2－α(－cos α)·sin α＝－tan α·cos α·(－cos α)－cos α·sin α＝－tan α·cos αsin α＝－sin αcos α·cos αsin α＝－1.方法二：原式＝－tan α·cos (－α)·sin ⎝ ⎛⎭⎪⎫－α－π2cos (π－α)·sin (π－α)＝tan α·cos α·sin ⎝ ⎛⎭⎪⎫α＋π2－cos α·sin α＝sin αcos α·cos α－sin α＝－1.【反思归纳】 利用诱导公式化简三角函数的思路和要求(1)思路方法：①分析结构特点，选择恰当公式；②利用公式化成单角三角函数；③整理得最简形式．(2)化简要求：①化简过程是恒等变形；②结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值．【即时训练】 已知sin(3π＋θ)＝13， 求cos (π＋θ)cos θ[cos (π－θ)－1]＋cos (θ－2π)sin ⎝ ⎛⎭⎪⎫θ－3π2cos (θ－π)－sin ⎝ ⎛⎭⎪⎫3π2＋θ的值．答案：18考点三 诱导公式与同角关系的综合应用 (高频考点)已知sin θ、cos θ是关于x 的方程x 2－ax ＋a ＝0(a ∈R )的两个根．求： (1)cos 3⎝ ⎛⎭⎪⎫π2－θ＋sin 3⎝ ⎛⎭⎪⎫π2＋θ的值；(2)tan(π－θ)－1tan θ的值． 解：由已知原方程判别式Δ≥0，即(－a )2－4a ≥0，∴a ≥4或a ≤0.又⎩⎪⎨⎪⎧sin θ＋cos θ＝a ，sin θcos θ＝a ，∴(sin θ＋cos θ)2＝1＋2sin θcos θ，即a 2－2a －1＝0， ∴a ＝1－2或a ＝1＋2(舍去)， ∴sin θ＋cos θ＝sin θcos θ＝1－ 2. (1)cos 3⎝ ⎛⎭⎪⎫π2－θ＋sin 3⎝ ⎛⎭⎪⎫π2＋θ＝sin 3 θ＋cos 3 θ＝(sin θ＋cos θ)(sin 2 θ－sin θcos θ＋cos 2 θ) ＝(1－2)[1－(1－2)]＝2－2.(2)tan(π－θ)－1tan θ＝－tan θ－1tan θ＝－⎝ ⎛⎭⎪⎫tan θ＋1tan θ＝－⎝ ⎛⎭⎪⎫sin θcos θ＋cos θsin θ＝－1sin θcos θ＝－11－2＝2＋1.答案：(1)2－2 (2)2＋1【反思归纳】 熟练运用诱导公式和同角三角函数基本关系，并确定相应三角函数值的符号是解题的关键．另外，切化弦是常用的规律技巧．【即时训练】 (1)若α为三角形的一个内角，且sin α＋cos α＝23，则这个三角形是( ) (A)正三角形 (B)直角三角形 (C)锐角三角形(D)钝角三角形(2)若sin α＋π6＝－513，且α∈π2，π，则sin α＋2π3＝________. 解析：(1)因为(sin α＋cos α)2＝1＋2sin αcos α＝49， 所以sin αcos α＝－518<0，所以α为钝角．故选D. (2)因为π2<α<π，所以2π3<α＋π6<7π6， cos α＋π6＝－1－－5132＝－1213，而sin α＋2π3＝sin π2＋α＋π6＝cos α＋π6＝－1213. 答案：(1)D (2)－1213同角关系与诱导公式结合解题教材源题：化简： (1)cos α－π2sin 52π＋α·sin(α－2π)·cos(2π－α)；(2)cos 2(－α)－tan (360°＋α)sin (－α).解：(1)原式＝cos π2－αsin π2＋α·sin α·cos α＝sin αcos α·sin α·cos α＝sin 2α.(2)原式＝cos 2α－tan α－sin α＝cos 3α＋1cos α.【规律总结】 三角函数式化简目标方向 (1)用同角关系中切弦互化，统一函数名． (2)用诱导公式统一角．(3)用因式分解将式子变形，化为最简．【源题变式】已知f (x )＝sin (2π－x )·cos 32π＋xcos (3π－x )·sin 112π－x ，则f －21π4＝________.解析：因为f (x )＝sin (－x )·sin xcos (π－x )·sin6π－π2＋x＝sin 2xcos x －sin π2＋x ＝sin 2x －cos 2x ＝－tan 2x . 所以f －214π＝－tan 2－214π＝－tan 2－5π－π4＝－tan 2－π4＝－1.答案：－1课时作业基础对点练(时间：30分钟)1．已知α∈⎝ ⎛⎭⎪⎫π，32π，tan(α＋π)＝43，则cos ⎝ ⎛⎭⎪⎫α＋π4＝( )(A)210 (B)－210 (C)7210(D)－7210A 解析：由α∈⎝ ⎛⎭⎪⎫π，32π，tan(α＋π)＝43，即tan α＝43，得sin α＝－45，cos α＝－35∴cos ⎝ ⎛⎭⎪⎫α＋π4＝22(cos α－sin α)＝22⎝ ⎛⎭⎪⎫－35＋45＝210.故选A.2．已知sin ⎝ ⎛⎭⎪⎫5π2＋α＝15，那么cos α＝( ) (A)－25(B)－15(C)15 (D)25答案：C3．已知sin ⎝ ⎛⎭⎪⎫x －π4＝35，则cos ⎝ ⎛⎭⎪⎫x ＋π4＝( )(A)45 (B)35 (C)－45(D)－35 D 解析：cos ⎝ ⎛⎭⎪⎫x ＋π4＝cos ⎝ ⎛⎭⎪⎫x －π4＋π2＝－sin ⎝ ⎛⎭⎪⎫x －π4＝－35，故选D.4．已知sin α是方程5x 2－7x －6＝0的根，且α是第三象限角，则sin ⎝ ⎛⎭⎪⎫－α－3π2cos ⎝ ⎛⎭⎪⎫3π2－αtan 2(π－α)cos ⎝ ⎛⎭⎪⎫π2－αsin ⎝ ⎛⎭⎪⎫π2＋α＝( )(A)916 (B)－916 (C)－34 (D)34答案：B5．已知α是第二象限角，则cos α1＋tan 2α＋sin α·1＋1tan 2α的值为( ) (A)－2 (B)2 (C)0(D)3C 解析：原式＝cos αsin 2α＋cos 2αcos 2α＋sin αsin 2α＋cos 2αsin 2α＝cos α|cos α|＋sin α|sin α|，∵α为第二象限角，∴sin α＞0，cos α＜0，∴cos α|cos α|＋sin α|sin α|＝－1＋1＝0.故选C.6．在△ABC 中，3sin π2－A ＝3sin(π－A )，且cos A ＝－3cos(π－B )，则C 等于( ) (A)π3 (B)π4 (C)π2(D)2π3C 解析：因为3sin π2－A ＝3sin(π－A )， 所以3cos A ＝3sin A ，所以tan A ＝33， 又0<A <π，所以A ＝π6.又因为cos A ＝－3cos(π－B )， 即cos A ＝3cos B ， 所以cos B ＝13cos π6＝12，又0<B <π， 所以B ＝π3.所以C ＝π－(A ＋B )＝π2.故选C. 7．设f (sin x )＝3－cos2x ，则f (cos x )＝________. 解析：方法一：f (cos x )＝f ⎝ ⎛⎭⎪⎫sin ⎝ ⎛⎭⎪⎫π2－x＝3－cos 2⎝ ⎛⎭⎪⎫π2－x ＝3－cos(π－2x )＝3＋cos 2x .方法二：f (sin x )＝3－(1－2sin 2 x )＝2＋2sin 2 x ， ∴f (x )＝2＋2x 2，∴f (cos x )＝2＋2cos 2x ＝3＋2cos 2x －1＝3＋cos 2x . 答案：3＋cos 2x8．化简sin ⎝ ⎛⎭⎪⎫4n －14π－α＋cos ⎝ ⎛⎭⎪⎫4n ＋14π－α(n ∈Z )的结果为________． 解析：n 为偶数时，原式＝sin ⎝ ⎛⎭⎪⎫－π4－α＋cos ⎝ ⎛⎭⎪⎫π4－α ＝－cos ⎝ ⎛⎭⎪⎫π4－α＋cos ⎝ ⎛⎭⎪⎫π4－α＝0. n 为奇数时，原式＝sin ⎝ ⎛⎭⎪⎫3π4－α＋cos ⎝ ⎛⎭⎪⎫5π4－α ＝cos ⎝ ⎛⎭⎪⎫π4－α－cos ⎝ ⎛⎭⎪⎫π4－α＝0. 答案：09．已知cos π6－α＝23，则sin α－2π3＝________.解析：sin α－2π3＝sin －π2－π6－α＝－sin π2＋π6－α＝－cos π6－α＝－23.答案：－2310．已知f (α)＝sin ⎝ ⎛⎭⎪⎫－α＋π2·cos ⎝ ⎛⎭⎪⎫3π2－α·tan (α＋5π)tan (－α－π)·sin (α－3π)(1)化简f (α)；(2)若α是第三象限角，且cos ⎝ ⎛⎭⎪⎫α－3π2＝15，求f (α)的值； (3)若α＝－31π3，求f (α)的值．解：(1)f (α)＝cos α·(－sin α)·tan α(－tan α)·(－sin α)＝－cos α；(2)∵cos ⎝ ⎛⎭⎪⎫α－3π2＝－sin α， ∴sin α＝－15，cos α＝－52－15＝－25 6.∴f (α)＝25 6.(3)∵－31π3＝－6×2π＋5π3，∴f ⎝ ⎛⎭⎪⎫－31π3＝－cos ⎝ ⎛⎭⎪⎫－31π3＝－cos ⎝ ⎛⎭⎪⎫－6×2π＋5π3 ＝－cos 5π3＝－cos π3＝－12.11．已知2sin 2α＋sin αcos α－3cos 2α＝75，求tan α的值．解：由题意得2sin 2α＋sin αcos α－3cos 2αsin 2α＋cos 2α＝75， 所以2tan 2α＋tan α－3tan 2α＋1＝75， 所以10tan 2α＋5tan α－15＝7tan 2α＋7，所以3tan 2α＋5tan α－22＝0，所以(3tan α＋11)(tan α－2)＝0，所以tan α＝－113或tan α＝2.能力提升练(时间：15分钟)12．设f (x )＝⎩⎨⎧ s in πx ， (x ＜0)，f (x －1)＋1， (x ≥0)和g (x )＝⎩⎪⎨⎪⎧ cosπx ，(x ＜12)，g (x －1)＋1，(x ≥12)，则g ⎝ ⎛⎭⎪⎫14＋f ⎝ ⎛⎭⎪⎫13＋g ⎝ ⎛⎭⎪⎫56＋f ⎝ ⎛⎭⎪⎫34的值为( ) (A)2(B)3 (C)4 (D)5 B 解析：∵g (14)＝22，g (56)＝cos(－16π)＋1＝32＋1，f (13)＝sin(－23π)＋1＝－32＋1，f (34)＝sin(－π4)＋1＝－22＋1，∴原式＝3.故选B.13．已知sin θ＝13，θ∈(－π2，π2)，则sin(π－θ)·sin(32π－θ)的值为( )(A)229(B)－229 (C)19(D)－19B 解析：∵θ∈(－π2，π2)，∴cos θ＝1－sin 2θ＝223， ∴sin(π－θ)sin(3π2－θ)＝－sin θcos θ＝－13×223 ＝－229.故选B.14．在△ABC 中，已知2cos 2A －3cos(B ＋C )＝2，则A ＝________. 解析：由2cos 2A －3cos(B ＋C )＝2，得2cos 2A －3cos(π－A )＝2，即2cos 2A ＋3cos A －2＝0， 得cos A ＝12或cos A ＝－2(舍去)，则在△ABC 中，A ＝π3.答案：π315．在三角形ABC 中，求cos 2A ＋B 2＋cos 2C 2的值． 解：在△ABC 中，A ＋B ＝π－C ，所以A ＋B 2＝π2－C 2， 所以cos A ＋B 2＝cos π2－C 2＝sin C 2，所以cos 2A ＋B 2＋cos 2C 2＝sin 2C 2＋cos 2C 2＝1. 16．已知关于x 的方程2x 2－(3＋1)x ＋m ＝0的两根为sin θ和cos θ，θ∈(0,2π)，求：(1)sin θ1－1tan θ＋cos θ1－tan θ的值； (2)m 的值；(3)方程的两根及此时θ的值． 解：(1)由根与系数的关系可知⎩⎪⎨⎪⎧ sin θ＋cos θ＝3＋12 ①sin θcos θ＝m 2 ②而sin θ1－1tan θ＋cos θ1－tan θ＝sin 2 θsin θ－cos θ＋cos 2 θcos θ－sin θ ＝sin 2 θ－cos 2 θsin θ－cos θ＝sin θ＋cos θ＝3＋12. (2)由①式平方得1＋2sin θcos θ＝2＋32.∴sin θcos θ＝34.由②得m 2＝34，∴m ＝32. (3)当m ＝32时，原方程变为2x 2－(3＋1)x ＋32＝0，解得x 1＝32，x 2＝12，∴⎩⎪⎨⎪⎧ sin θ＝32cos θ＝12或⎩⎪⎨⎪⎧ cos θ＝32sin θ＝12. 又∵θ∈(0,2π)，∴θ＝π3或θ＝π6.。