实验二 典型环节的频率特性仿真分析

实验名称：典型环节模拟实验实验日期：2023年4月10日实验地点：实验室A实验人员：张三、李四、王五一、实验目的1. 理解典型环节的概念和作用。

2. 通过模拟实验，验证典型环节在系统中的作用和效果。

3. 掌握典型环节的设计方法和应用技巧。

二、实验原理典型环节是指在系统设计和分析中，对系统中的关键部分进行简化和抽象，以便于分析和设计的一种方法。

典型环节主要包括传递函数、状态方程、框图等。

三、实验材料1. 实验设备：计算机、信号发生器、示波器、数据采集卡等。

2. 实验软件：MATLAB、Simulink等。

3. 实验数据：实验所需的各种参数和模型。

四、实验步骤1. 设计典型环节模型（1）根据实验要求，确定典型环节的类型（如传递函数、状态方程等）。

（2）利用MATLAB或Simulink软件，搭建典型环节模型。

（3）对模型进行参数设置，确保模型符合实验要求。

2. 进行模拟实验（1）输入实验数据，如输入信号、系统参数等。

（2）启动模拟实验，观察典型环节在不同输入信号下的输出响应。

（3）记录实验数据，如输出信号、系统状态等。

3. 分析实验结果（1）分析典型环节在系统中的作用和效果。

（2）比较不同典型环节在相同输入信号下的输出响应。

（3）总结实验结果，提出改进建议。

五、实验结果与分析1. 实验结果（1）在输入信号为正弦波时，典型环节的输出信号为相应的正弦波。

（2）在输入信号为方波时，典型环节的输出信号为相应的方波。

（3）在输入信号为阶跃信号时，典型环节的输出信号为相应的阶跃信号。

2. 分析（1）典型环节在系统中起到了滤波、放大、延迟等作用。

（2）不同类型的典型环节对输入信号的处理效果不同，如传递函数适用于模拟信号处理，状态方程适用于数字信号处理。

（3）实验结果表明，典型环节的设计和选择对系统性能有重要影响。

六、实验结论1. 通过模拟实验，验证了典型环节在系统中的作用和效果。

2. 掌握了典型环节的设计方法和应用技巧。

频率特性实验报告频率特性实验报告引言：频率特性是描述信号在不同频率下的响应性能的重要指标。

在电子领域中，频率特性实验是非常常见的实验之一。

本文将介绍频率特性实验的目的、实验原理、实验步骤以及实验结果的分析。

一、实验目的：频率特性实验的目的是研究电路或系统在不同频率下的响应特性，了解信号在不同频率下的传输和滤波性能。

通过实验，可以掌握频率特性的测试方法和实验技巧，提高实验操作能力和数据处理能力。

二、实验原理：频率特性实验通常涉及到信号的输入和输出，以及信号的幅度和相位响应。

在实验中，常用的测试仪器有函数发生器、示波器和频谱分析仪。

1. 函数发生器：用于产生不同频率的信号作为输入信号。

可以调节函数发生器的频率、幅度和波形等参数。

2. 示波器：用于观测电路或系统的输入和输出信号波形。

示波器可以显示信号的幅度、相位和频率等信息。

3. 频谱分析仪：用于分析信号的频谱成分。

频谱分析仪可以显示信号在不同频率下的幅度谱和相位谱。

实验步骤：1. 准备实验所需的仪器和器材，包括函数发生器、示波器和频谱分析仪。

2. 连接电路或系统，将函数发生器的输出信号连接到被测电路或系统的输入端，将示波器或频谱分析仪连接到电路或系统的输出端。

3. 设置函数发生器的频率和幅度，选择适当的波形。

4. 调节示波器或频谱分析仪的参数，观测信号的波形和频谱。

5. 重复步骤3和步骤4，改变函数发生器的频率，记录不同频率下的信号波形和频谱。

实验结果分析：根据实验记录的信号波形和频谱数据，可以进行以下分析：1. 幅度响应：通过观察信号的幅度谱，可以了解电路或系统在不同频率下信号的衰减或增益情况。

如果幅度谱在不同频率下保持不变，则说明电路或系统具有平坦的幅度响应特性。

如果幅度谱在某些频率点出现峰值或谷值，则说明电路或系统对该频率具有增益或衰减。

2. 相位响应：通过观察信号的相位谱，可以了解电路或系统在不同频率下信号的相位变化情况。

相位谱可以显示信号的相位延迟或提前。

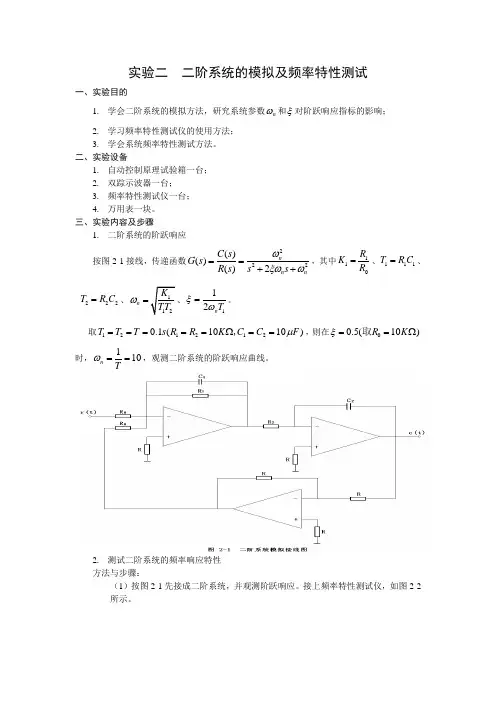
实验二 二阶系统的模拟及频率特性测试一、实验目的1. 学会二阶系统的模拟方法，研究系统参数n ω和ξ对阶跃响应指标的影响；2. 学习频率特性测试仪的使用方法；3. 学会系统频率特性测试方法。

二、实验设备1. 自动控制原理试验箱一台；2. 双踪示波器一台；3. 频率特性测试仪一台；4. 万用表一块。

三、实验内容及步骤1. 二阶系统的阶跃响应按图2-1接线，传递函数222()()()2nn nC s G s R s s s ωξωω==++，其中110R K R =、111T R C =、222T R C =、n ω=112n T ξω=。

取1212120.1(1010)T T T s R R K C C F μ=====Ω==,，则在00.5(10)R K ξ==Ω取时，110n Tω==，观测二阶系统的阶跃响应曲线。

2. 测试二阶系统的频率响应特性方法与步骤：（1）按图2-1先接成二阶系统，并观测阶跃响应。

接上频率特性测试仪，如图2-2 所示。

（2）先测试转折频率 1.592(10/)f H z rad s ω==时对应的幅值R 和相角ϕ。

设定频率 1.592FREQ clear EN TER →→→；设定前面板状态w aveform ～，d e l a y 0.1s ，inputrang AUTO ，int errator AUTO ，display mod e R 、ϕ，sw eep o ff 。

按sin gle 键，从显示窗读取对应 1.592f H z =的R 和ϕ的值。

（3）系统参数不变。

采用单次步进测量，记录f 由0.1Hz 到15Hz ，步长为0.5Hz的R 和ϕ的值。

设定最大频率 m ax 15.0f clear EN TER →→→；设定最小频率 m in 0.1f clear EN TER →→→；设定步长（0.5Hz ）/0.5Lin F step clear EN TER →∆→→→； 设定前面板状态 sw eep Lin →∆，其他与（2）同。

一、 实验名称：典型环节的时域分析和频域分析二、实验目的：(1) 理解、掌握matlab 模拟典型环节的根本方法，包括：比例环节、积分环节、一阶微分环节、惯性环节和振荡环节等。

(2) 熟悉各种典型环节的阶跃响应曲线和频域响应曲线 (3) 理解参数变化对动态特性的影响三、 实验要求：(1) 一人一机，独立完成实验内容 。

(2) 根据实验结果完成实验报告，并用A4纸打印后上交。

四、 时间：2022年11月21日 五、 地点：信自楼234实验报告：一、比例环节的时域分析和频域分析 比例环节的传递函数：()G s k(1) 当k=1:3:10时，绘制系统的阶跃响应曲线，分析ｋ值的影响情况。

程序：for k=1:3:10;num=k;den=1;G=tf(num,den);figure(1);step(G); hold on; %翻开第1个图形窗口，绘制系统的阶跃响应曲线 endfigure(1); legend('k=1','k=4','k=7','k=10'); 曲线：结果分析：时域响应的结果就是把输入信号放大k 倍。

如图，输入信号为幅值为1的阶跃信号，因此，输出是幅值为k 的阶跃信号。

程序：for k=1:3:10;num=k;den=1;G=tf(num,den);figure(1);bode(G);hold on; %翻开第1个图形窗口，绘制系统的阶跃响应曲线 endfigure(1); legend('k=1','k=4','k=7','k=10');曲线：结果分析：比例环节对幅频有影响，输出信号的幅值为输入信号的20*lgk倍。

比例环节对相位没有影响，如图显示，相位特性为一条0度的程度线。

二、积分环节的时域分析和频域分析积分环节的传递函数：1 ()G ss=(1) 当k=1:3:10时，绘制系统()kG ss=的阶跃响应曲线，分析曲线特点。

实验二典型环节的频率特性仿真分析一、实验目的和要求（1）熟悉如何通过MA TLAB语言编程来进行仿真实验。

（2）通过绘制典型环节的频率特性曲线，正确理解频率特性的概念，明确频率特性的物理意义。

二、实验主要仪器和设备装有Matlab软件的计算机三、实验内容分别改变以下几个典型环节的相关参数，观察系统（或环节）的频率特性，并分析其相关参数改变对频率特性的影响。

比例环节（K）积分环节（STi1）一阶惯性环节（STKc+1）一阶微分环节（STD+1）典型二阶环节（2222nnnSSKωξωω++）四、实验方法wn=5;k=1;g1=tf([k*wn*wn],[1 2*0.4*wn wn*wn]); g2=tf([k*wn*wn],[1 2*0.8*wn wn*wn]); g3=tf([k*wn*wn],[1 2*1.2*wn wn*wn]); figure(1);step(g1);hold onstep(g2);hold onstep(g3); figure(2) bode(g1); hold on bode(g2); hold on bode(g3); figure(3); nyquist(g1); hold on nyquist(g2);hold on nyquist(g3);五、实验数据记录(1) 比例环节G(S)= K ;参数值分别为K1= 1 ；K2= 2 ；K3= 3 ； 单位阶跃响应曲线：00.10.20.30.40.50.60.70.80.9111.21.41.61.822.22.42.62.83Step ResponseTim e (sec)A mp l i t u d eBode 图：02468M a gn it u d e (d B )10-1-0.500.51P h a s e (d e g )Bode D iagramFrequency (rad/sec)Nyquist 曲线：-0.500.51 1.52 2.5-1-0.8-0.6-0.4-0.200.20.40.60.81Nyquist DiagramReal AxisI m a g i n a r y A x i s（2）积分环节G(S)= ;参数值分别为Ti1= 1 ；Ti2= 2 ；Ti3= 3 ； 单位阶跃响应曲线：0500100015002004006008001000120014001600Step ResponseTim e (sec)A m p l i t u d eBode 图ST i 1-30-20-1010M a g n i t u d e (d B)10101-90-45P h a s e (d e g )Bode DiagramFrequency (rad/sec)Nyquist 曲线：-1-0.8-0.6-0.4-0.200.20.40.60.81-10-8-6-4-20246810Nyquist DiagramReal AxisI m a g i n a r y A x i s(3)一阶惯性环节G(S)=S T Kc 1 ;令K 不变（取K= 1 ），改变Tc 取值：Tc1= 1 ；Tc2= 2 ；Tc3= 3 ； 单位阶跃响应曲线：0246810121416180.10.20.30.40.50.60.70.80.91Step ResponseTim e (sec)A m p l i t u d eBode图：-50-40-30-20-100M a g n i t u d e (d B )10-210-110101102-90-45P h a s e (d e g )Bode DiagramFrequency (rad/sec)Nyquist 曲线-1-0.8-0.6-0.4-0.200.20.40.60.81-0.5-0.4-0.3-0.2-0.100.10.20.30.40.5Nyquist DiagramReal AxisI m a g i n a r y A x i s（4）一阶微分环节G(S)= S T D 1 ;改变TD 取值：TD1= 1 ；TD2= 2 ；TD3= 3 ； 单位阶跃响应曲线：00.20.40.60.8100.511.522.53From: In(1)00.20.40.60.81From: In(2)Step ResponseTime (sec)A m p l i t u d eBode 图：0246810From: In(1)T o : O u t (1)10101-1-0.500.51T o : O u t (1)From: In(2)10101Bode DiagramFrequency (rad/sec)M a g n i t u d e (d B ) ; P h a s e (d e g )Nyquist 曲线：（5）典型二阶环节G(S)= 2222nn nS S K ωξωω++ ；令K 不变（取K= 1 ），① 令ωn= 5 ，ξ取不同值：ξ1=0；ξ2= 0.2 ,ξ3= 0.5 ,（0<ξ<1）；ξ4=1；ξ5= 1.2 （ξ≥1）；单位阶跃响应曲线：024681012141618200.20.40.60.811.21.41.61.82Step ResponseTime (sec)A m p l i t u d eBode 图：-100-80-60-40-20020M a g n i t u d e (d B)10-110101102103-180-135-90-450P h a s e (d e g )Bode DiagramFrequency (rad/sec)Nyquist 曲线：-0.500.51 1.522.5x 1015-3-2-1123Nyquist DiagramReal AxisI m a g i n a r y A x i s② 令ξ=0，ωn 取不同值：ωn1= 1 ；ωn2= 2 ；02468101214161820-0.50.511.522.5Step ResponseTime (sec)A m p l i t u d eBode 图：-100-50050100150M a g n i t u d e (d B )10-110101102-360-315-270-225-180P h a s e (d e g )Bode DiagramFrequency (rad/sec)Nyquist 曲线：-2-1012345x 1015-1.5-1-0.50.511.5Nyquist DiagramReal AxisI m a g i n a r y A x i s③ 令ξ=0.216，ωn 取不同值：ωn1= 1 ；ωn2= 2 ；246810121400.511.5Step ResponseTime (sec)A m p l i t u d eBode 图：Nyquist 曲线-1-0.500.51 1.5-2.5-2-1.5-1-0.500.511.522.5Nyquist DiagramReal Axis I m a g i n a r y A x i s六、实验结果分析Nyquist 图（1）比例环节的幅频特性、相频特性均与频率ω无关。

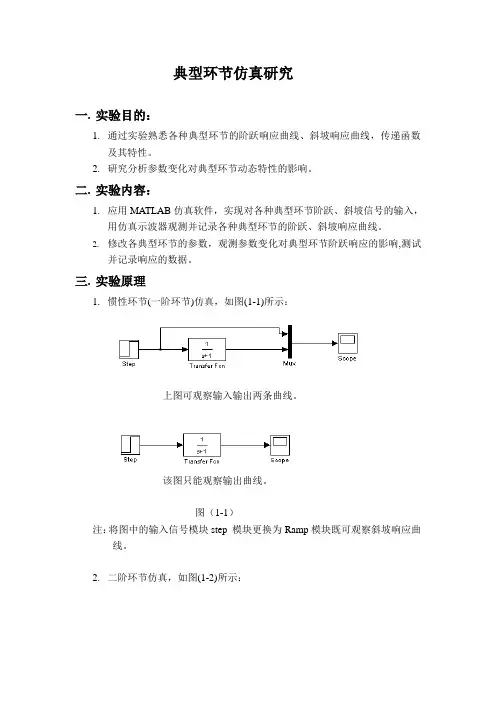
典型环节仿真研究一.实验目的：1.通过实验熟悉各种典型环节的阶跃响应曲线、斜坡响应曲线，传递函数及其特性。

2.研究分析参数变化对典型环节动态特性的影响。

二.实验内容：1.应用MATLAB仿真软件，实现对各种典型环节阶跃、斜坡信号的输入，用仿真示波器观测并记录各种典型环节的阶跃、斜坡响应曲线。

2.修改各典型环节的参数，观测参数变化对典型环节阶跃响应的影响,测试并记录响应的数据。

三.实验原理1.惯性环节(一阶环节)仿真，如图(1-1)所示：上图可观察输入输出两条曲线。

该图只能观察输出曲线。

图（1-1）注：将图中的输入信号模块step 模块更换为Ramp模块既可观察斜坡响应曲线。

2.二阶环节仿真，如图(1-2)所示：或图（1-2）3.积分环节仿真，如图(1-3)所示：图（1-3）4.比例积分环节仿真，如图(1-4)所示：图（1-4）5.比例+微分环节仿真，如图(1-5)所示：图（1-5）6.比例+积分+微分环节仿真，如图(1-6)所示：图（1-6）四.实验步骤:1.进入WINDOWS操作系统；2.进入MATLAB COMMAND WINDOW(双击桌面上的MATLAB图标进入)；3.进入SIMULINK 窗口(在MATLAB COMMAND WINDOW 窗口中,键入SIMULINK 后按回车键) 或单击工具栏中的图标；4.移动鼠标到FILE 菜单,单击鼠标左键,打开FILE 菜单的子菜单.5.点击NEW ----(MODEL)，建立一个新的系统窗口（MODEL窗口）；6.参照第三部分的原理图，用鼠标将左边Simulink Library Browser窗口中的各个模块拖动到右边的MODEL窗口；方法如下：（1）移动光标到Sources 模块，点击后出现Sources 模块的内容，将该模块中的Step Fcn(阶跃信号)选中，然后按住鼠标左键将其拖到Untitled窗口；（2）在Untitled窗口中，将光标移到Step Fcn模块双击鼠标左键产生属性对话框，在该对话框中可以选择阶跃起始时间，初始值和阶跃值；（3）SIMULINK窗口中的Continuous模块打开，将Transfer Fcn(传递函数)模块移到Untitled窗口中；（4）在Untitled窗口中,将鼠标移动到Transfer Fcn模块双击鼠标左键产生属性对话框，在该对话框中可以设置传递函数的分子、分母多项式的系数；（5）将SIMULINK窗口中的Sinks模块打开，将Scope示波器模块移到Untitled窗口；（6）将鼠标移动到Scope模块，双击鼠标左键产生属性对话框，在该对话框中可以选择Horizontal Range(水平范围)和Vertical Range(垂直范围)。

典型环节(或系统)的频率特性测量一·实验目的1 学习和掌握测量典型环节(或系统)频率特性曲线的方法和技能。

2 学习根据实验所得频率特性曲线求取传递函数的方法。

二·实验要求1 用实验方法完成一阶惯性环节的频率特性曲线测试。

2 用实验方法完成典型二阶系统开环频率特性曲线的测试。

3 根据测得的频率特性曲线求取各自的传递函数。

4 用软件仿真方法求取一阶惯性环节频率特性和典型二阶系统开环频率特性 并与实验所得结果比较。

三·实验步骤1 熟悉实验箱上的信号源,掌握改变正弦波信号幅值和频率的方法。

利用实验箱上的模拟电路单元,参考本实验附录设计并连接“一阶惯性环节”模拟电路(如用U9+U8连成)或“两个一阶惯性环节串联”的模拟电路(如用U9+U11连成)。

2 利用实验设备完成一阶惯性环节的频率特性曲线测试。

无上位机时 利用实验箱上的信号源单元U2所输出的正弦波信号作为环节输入 即连接箱上U2的“正弦波”与环节的输入端(例如对一阶惯性环节即图1.5.2的Ui)。

然后用示波器观测该环节的输入与输出(例如对一阶惯性环节即测试图1.5.2的Ui和Uo)。

注意调节U2的正弦波信号的“频率”电位器RP5与“幅值”电位器RP6 测取不同频率时环节输出的增益和相移(测相移可用“李沙育”图形),从而画出环节的频率特性。

有上位机时 必须在熟悉上位机界面操作的基础上 充分利用上位机提供的虚拟示波器与信号发生器功能。

为了利用上位机提供的虚拟示波器与信号发生器功能 接线方式将不同于上述无上位机情况。

仍以一阶惯性环节为例 此时将Ui连到实验箱U3单元的O1或O2(D/A通道的输出端,这个是通过上位机选择其中的一路输出),将Uo连到实验箱U3单元的I1(A/D通道的输入端),然后再将你选择的D/A输出通道测试信号O1(如果选择的是O1)连接到这组A/D输入的另一采集输入端I2,然后连接设备与上位机的USB通信线。

实验题目：典型环节频域特性的仿真实验一、实验目的：1、加深了解系统频率特性的概念。

2、学习使用Matlab软件绘制Nyquist图、Bode图的基本方法。

3、掌握典型环节的频率特性。

二、实验设备：Matlab三、实验内容：用Matlab绘制典型环节（比例、积分、微分、惯性、二阶）的Nyquis图、Bode图，研究频率特性。

四、实验步骤：1.绘制比例环节传递函数g(s)=K的频率特性图。

运行Matlab，进入命令窗口，键入命令：num=[1];den=[0,0,2];G1=tf(num,den)nyquist(G1) (回车)则显示传递函数g(s)=2，及对应的Nyquist图曲线，观察并分析曲线，然后记录该曲线，并要求在曲线图上注明频率ω的变化情况。

再键入命令：gridbode(G1) (回车)则显示对应的Bode图曲线，观察并分析曲线，然后记录该曲线，并要求在曲线图上注明纵、横坐标。

2.绘制积分环节传递函数g(s)=1/Ts 的频率特性图。

运行Matlab，进入命令窗口，键入命令：num=[1];den=[0,3,0];G1=tf(num,den)nyquist(G1) (回车)则显示传递函数g(s)=1/4s ，及对应的Nyquist图曲线，观察并分析曲线，然后记录该曲线，并要求在曲线图上注明频率ω的变化情况。

再键入命令：gridbode(G1) (回车)则显示对应的Bode图曲线，观察并分析曲线，然后记录该曲线，并要求在曲线图上注明纵、横坐标。

3.绘制微分环节传递函数g(s)=Ts 的频率特性图。

运行Matlab，进入命令窗口，键入命令：gridbode(G1) (回车)则显示对应的Bode图曲线，观察并分析曲线，然后记录该曲线，并要求在曲线图上注明纵、横坐标。

五、仿真和实验结果记录比例环节Nyquist图曲线（K=2）比例环节Bode图曲线积分环节Nyquist图曲线（T=3）积分环节Bode图曲线微分环节Nyquist图曲线（T=3）微分环节Bode图曲线惯性环节Nyquist图曲线（T=5) 惯性环节Bode图曲线二阶环节Nyquist图曲线（ξ=0.9）二阶环节Bode图曲线六、实验结果分析。

实验报告
实验名称：
典型环节的频率特性实验
实验目的：
加深理解系统频率特性的物理概念；掌握系统频率特性的实验方法；
掌握频率特性的Bode 图Nquist图的绘制。

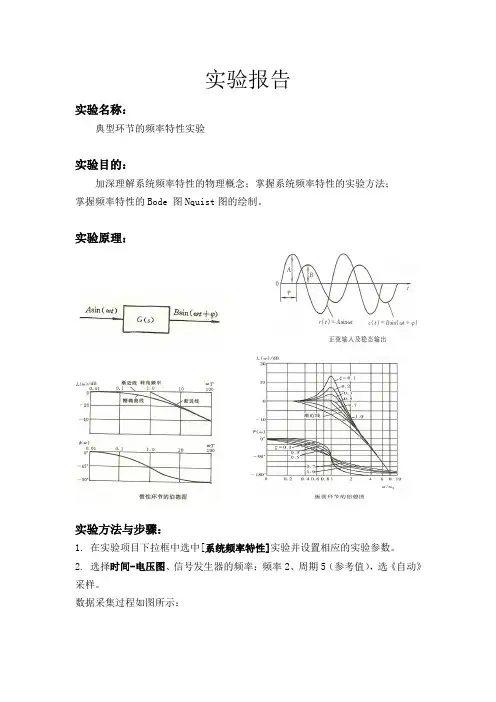
实验原理：
实验方法与步骤：
1. 在实验项目下拉框中选中[系统频率特性]实验并设置相应的实验参数。

2. 选择时间-电压图、信号发生器的频率：频率2、周期5（参考值），选《自动》采样。

数据采集过程如图所示：
3、待数据采样结束后点击按钮，即可显示出所测量的波特图。

4、在完成步骤3后，在显示区单击鼠标右键，即出现奈氏图。

实验内容：
1、做一阶系统的频率特性实验，画出该系统的Bode 图与Nquist图。

2、二阶系统的频率特性实验，画出该系统的Bode 图与Nquist图。

3、改变二阶系统的阻尼比ζ，观察欠阻尼与临界阻尼情况下的频率特性。

3、确定系统的转角频率、幅值穿越频率、截至频率的实测值。

●实验报告
1、图示一阶系统频率特性实验的Bode 图与Nquist图。

2、二阶振荡系统（欠阻尼）频率特性实验的Bode 图与Nquist图。

3、确定系统的转角频率、谐振频率、截至频率的实测值。

4、填写实验数据与响应曲线。