布儒斯特定律

布儒斯特角原理布儒斯特角原理（Brewster's Angle）是光学中的一个重要概念，它描述了入射光线与介质表面的夹角与反射光线的偏振状态之间的关系。

根据这一原理，当光线以一定角度入射到介质表面时，反射光线将完全偏振为垂直于入射面的偏振态。

本文将详细探讨布儒斯特角原理的基本原理、应用以及实验验证。

布儒斯特角原理是由苏格兰物理学家大卫·布儒斯特（David Brewster）在19世纪初提出的。

他发现，当光线从一个介质垂直入射到另一个介质表面时，存在一个特殊的入射角使得反射光线完全偏振。

这个入射角被称为布儒斯特角，用θ表示。

根据布儒斯特角原理，当入射角等于布儒斯特角时，反射光线的偏振状态为垂直于入射面的偏振态。

布儒斯特角原理的解释基于光的偏振性质和折射定律。

光是一种电磁波，具有电场和磁场振动方向垂直的特性。

当光线从一个介质进入另一个介质时，根据折射定律，入射角和折射角之间存在一定的关系。

而对于特定的入射角，折射光线的偏振态与入射光线的偏振态有关。

在布儒斯特角下，折射光线与反射光线之间的振动方向恰好垂直，因此反射光线完全偏振。

布儒斯特角原理在实际应用中具有重要意义。

例如，它可以用来设计反射镜、滤光片和偏振片等光学元件。

利用布儒斯特角原理，可以选择特定的入射角度，使得反射光线具有所需的偏振态，从而实现对光的控制。

此外，布儒斯特角原理还可以用于测量材料的折射率和表面薄膜的厚度。

为了验证布儒斯特角原理，可以进行简单实验。

首先，选取一个透明的材料作为实验样品，如玻璃或塑料片。

然后，将样品固定在一个可以旋转的支架上，并利用一个光源照射到样品上。

通过调节光源的位置和入射角度，观察反射光线的偏振态变化。

当入射角等于布儒斯特角时，可以观察到反射光线变为完全偏振的现象。

通过测量入射角和折射角，可以计算出样品的折射率，并与理论值进行比较，从而验证布儒斯特角原理的准确性。

布儒斯特角原理是光学中的重要概念，描述了入射光线与介质表面的夹角与反射光线的偏振状态之间的关系。

什么事布儒斯特角
简介
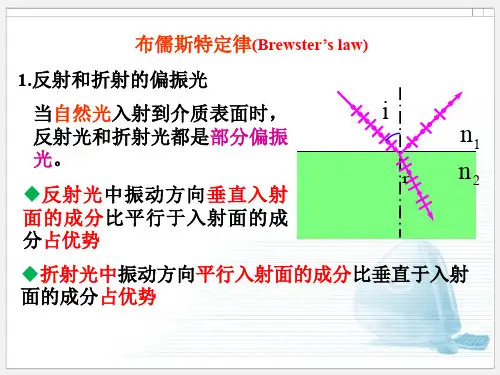
自然光经电介质界面反射后，反射光为线偏振光所应满足的条件。

首先由英国物理学家D.布儒斯特于1815 年发现。

自然光在电介质界面上反射和折射时，一般情况下反射光和折射光都是部分偏振光，只有当入射角为某特定角时反射光才是线偏振光，其振动方向与入射面垂直，此特定角称为布儒斯特角或起偏角，用θb表示。

此规律称为布儒斯特定律。

光以布儒斯特角入射时，反射光与折射光互相垂直。

玻片堆是由许多表面互相平行的玻璃片组成，自然光以布儒斯特角入射时，垂直于入射面的振动分量在每个界面上均要发生反射，而平行于入射面的振动分量则完全不能反射，故从玻片堆透出的光基本上只包含平行分量。

玻片堆可用作起偏器。

自然光在两种各向同性媒质分界面上反射、折射时，反射光和折射光都是部分偏振光。

反射光中垂直振动多于平行振动，折射光中平行振动多于垂直振动。

当入射角满足关系式tgi0=n2/n1 时，反射光为振动垂直于入射面的线偏振光，
该式称为布儒斯特定律（Brewster law) ，i0为起偏振角或布儒斯特角。

当光线以起偏振角入射时，反射光和折射光的传播方向互相垂直，即：i0+r=90
编辑本段
求法
布儒斯特角等于两种介质的折光率之比的反正切。

设θ1为入射角，θ2为折射角。

我们有
如果反射角和折射角垂直，则：
整理，得：
其中n1和n2为该两种介质的折射率。

布儒斯特定律
波特定律是19世纪德国物理学家叶布儒斯特提出的一条电气学定律，它表明一定条
件下通过电阻传递的电流与电位头之间有一个成比例的关系，即I/V值恒定，称为电阻R。

叶布儒斯特提出的这条电气学定律是十九世纪初的一个非常重要的理论成果，被许多有关
电子设备的发明利用起来，成为电子学中的基础定律之一。

波特定律的本质是描述一种电气定律，电流的大小与电压的大小成反比，即I(电流)
除以V(电压)即为等值的电阻R。

它概括了电阻传递的电流与电量头之间的基本比例关系，并成功地把复杂而变化多端的电阻联系到一个简单而稳定的数学关系上来，从而为物理学
和工程学的进一步发展奠定了理论基础。

波特定律最初的表达是：当通过电阻的电流与通
电的电压满足一定条件时，它们之间的比率保持不变，也就是关于电子学中的某种电子标
准电压的单位，就是波特定律。

从理论上看，叶布儒斯特定律说明电流流过电阻时，经放大器接收到叶布儒斯特定律
结果，那么可解释任何电子设备所运行的电子，只要给定一个结果电压和一个给定电阻，
就可以知道放大器应该输出的电流电压。

从实际应用来看，这条定律有很多好处，它是电
子的导线机械技术和系统的基础，它也是制作电子组件或构造电子系统时必不可少的内容，是电子电路上很重要的标准。

此外，波特定律的出现，为研发电子设备的设计者提供了参考依据，他们可以根据电
路的安排，按程序设计出合适的电子设备，并检验出较佳的电路方案，因此，叶布儒斯特
定律对科技创新发展有着非常重要的意义。

一、实验目的1. 理解布儒斯特角的概念及其产生的原理。

2. 通过实验验证布儒斯特定律，即反射光和折射光垂直。

3. 掌握使用偏振片和分光计测量布儒斯特角的方法。

二、实验原理布儒斯特角（Brewster's angle）是指当光线从一种介质入射到另一种介质时，反射光完全偏振的条件所对应的入射角。

根据布儒斯特定律，当光线以布儒斯特角入射时，反射光和折射光互相垂直。

布儒斯特角的计算公式为：\[ \tan(\theta_B) = \frac{n_2}{n_1} \]其中，\( \theta_B \) 是布儒斯特角，\( n_1 \) 和 \( n_2 \) 分别是入射介质和折射介质的折射率。

三、实验器材1. 分光计2. 偏振片3. 玻璃平板4. 可调光源5. 秒表6. 刻度尺四、实验步骤1. 将分光计调整至水平，确保其稳定性。

2. 将玻璃平板放置在分光计的平台上，调整光源使其垂直照射到玻璃平板上。

3. 将偏振片固定在分光计的光路上，使其与光束垂直。

4. 观察反射光，旋转偏振片，寻找反射光强度最弱的位置，此时反射光为线偏振光。

5. 记录此时偏振片的旋转角度，即为布儒斯特角。

6. 重复步骤4和5，测量多次，取平均值作为实验结果。

五、实验结果与分析通过多次测量，得到布儒斯特角的平均值为 \( \theta_B = 56.7^\circ \)。

根据布儒斯特定律，理论计算得到的布儒斯特角为：\[ \tan(\theta_B) = \frac{n_2}{n_1} = \frac{1.5}{1} = 1.5 \]\[ \theta_B = \arctan(1.5) \approx 56.3^\circ \]实验结果与理论计算值基本一致，说明实验结果可靠。

六、实验总结通过本次实验，我们成功测量了布儒斯特角，验证了布儒斯特定律。

实验过程中，我们掌握了使用偏振片和分光计测量布儒斯特角的方法。

此外，实验结果也表明，在测量过程中，需要注意光源的稳定性和偏振片的旋转角度，以保证实验结果的准确性。

选择性实验：二十六利用布儒斯特定律测量玻璃折射率一、目的要求利用光反射后的起偏振作用，应用布儒斯特定律测量平面玻璃对钠光的折射率。

实验要求达到：1.认识光的偏振特性。

2.学会分光仪的调节方法。

3.理解和正确判断布儒斯特角的反射位置。

二、仪器设备分光仪、平面反射镜（或棱镜）、检偏器、钠光灯。

三、参考书目1.程守洙、江之永：《普通物理学》第三册（第三版），p.214－218。

2.杨之昌、王潜智、邱榴贞：《物理光学实验》上册，p.198－205。

3.R·M·惠特利、J·亚伍德：《伦敦工学院200个物理实验》，p.166－168。

4.李允中、潘维济：《基础光学实验》，p.107－114。

5.A·M·波蒂斯、H·D·杨：《大学物理实验》，p.219－224。

6.D·哈里德、R·瑞斯尼克：《物理学》第二卷第二册，p.577－579。

四、实验原理光是电磁波，是横波。

凡振动仅限于光传播方向平面内的一个固定方向，这种光称为偏振光。

一个原子或分子在某一瞬间所发出的光（亦称波列）是偏振光。

然而各原子或分子各自发出的光其振动方向各不相同，因而它们的组合——自然光是非偏振的，且没有一个振动方向占有优势。

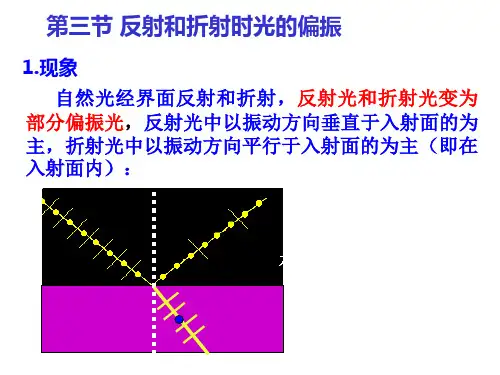
实验证明，自然光在两种媒质的界面上反射或折射时，发射光或折射光都将成为部分偏振光（即某一振动方向上占优势）。

图1就是在空气与玻璃界面上（MM’）自然光经反射和折射后光振动的变化情况。

图中黑点表示垂直纸面的振动方向，短线表示平行于入射面的振动方向，它们的多寡反映了两个方向的强弱。

从图中可以看到，自然光从空气入射到玻璃后，反射光R 中垂直纸面的振动占优势，而折射光R ’中平行入射面的振动占优势，它们都变成了部分偏振光。

这一实验事实可用菲涅耳公式加以证知。

实验还发现，反射光和折射光的偏振化程度还与入射角i 密切相关。

布儒斯特（Brewster ）从实验中确定，当入射角达到一个特定值时，反射光R 将是完全偏振光（一切光振动方向均垂直于纸面）。

布儒斯特效应布鲁斯特效应（Brewster effect），又称作布儒斯特角，是一种光学现象，是在光线射入介质表面时发生的现象。

它被命名为苏格兰物理学家大卫·布鲁斯特，他在1812年首次描述了这一现象。

布儒斯特角是指入射角等于反射角时，反射光线的振动方向与入射光线的振动方向垂直。

布儒斯特角可以通过斯奈尔定律，即折射角等于入射角来推导。

布儒斯特角的产生原理与光线的偏振性有关。

偏振光是只在一个特定方向上振动的光波。

当光线射入介质表面时，反射光与折射光两个方向上的振动可能不同步，这取决于入射角度。

当光线以特定入射角射入介质表面时，反射光的振动方向与入射光的振动方向垂直，这就是布儒斯特角。

布儒斯特效应在很多实际应用中发挥着重要作用。

例如，偏振墨镜就是基于布儒斯特效应设计的。

布儒斯特角的特殊性质使得透过偏振墨镜的光线可以消除在特定方向上振动的光波，减少反射和散射。

这样可以降低眩光，提高视觉舒适度和图像清晰度。

此外，布儒斯特角还在光学器件中发挥着重要作用。

例如，透过布儒斯特角可以设计出全反射镜，用于激光和光纤通信等技术中。

全反射镜可以反射光线而几乎不消耗能量，这使得它们成为高效的光学设备。

布儒斯特效应在天文学中也有应用。

例如，太阳光线在大气层中的散射现象中，布儒斯特角可以解释为什么天空呈现出蓝色。

大气中的气体和悬浮在空气中的粒子会使光线发生散射，但由于蓝光的波长比红光更短，所以蓝光更容易发生散射。

当太阳光线以接近布儒斯特角的入射角度射入大气层中时，蓝光的散射会超过红光，使得天空呈现出蓝色。

布儒斯特效应的研究对于理解光的行为和性质具有重要意义。

它揭示了光与物质相互作用的机制，对于光学和光电子学的发展具有重要的指导作用。

研究布儒斯特效应的过程中，科学家们还发现了更多有趣的光学现象和光学材料，为我们探索光的奥秘提供了更多可能性。

总之，布儒斯特效应是光学中重要的现象之一，它在很多应用领域发挥着关键作用，从偏振墨镜到全反射镜，再到大气散射，都离不开布儒斯特效应的解释和应用。

光波在左手材料中的菲涅尔公式和布儒斯特定律
当光波从一种介质进入另一种介质时，会发生反射、折射和透射等现象。

这些现象可以用菲涅尔公式和布儒斯特定律来描述。

但是，在一些左手材料中，由于其电磁性质的不同，菲涅尔公式和布儒斯特定律需要做出相应的修改。

首先，我们来看左手材料中的菲涅尔公式。

在右手材料中，根据菲涅尔公式，反射光和折射光的反射角和折射角都是相等的。

而在左手材料中，由于其左旋的特性，反射光和折射光的反射角和折射角是不相等的。

具体来说，当光线从右手材料入射时，反射光的反射角和折射光的折射角都是按照右手材料的菲涅尔公式计算。

但是当光线从左手材料入射时，反射光的反射角和折射光的折射角就需要按照左手材料的菲涅尔公式计算。

接下来，我们来看左手材料中的布儒斯特定律。

在右手材料中，布儒斯特定律规定了入射角、折射角和介质折射率之间的关系。

而在左手材料中，布儒斯特定律需要做出修改。

具体来说，当光线从右手材料入射时，折射角仍然可以按照右手材料的布儒斯特定律计算。

但是当光线从左手材料入射时，折射角需要按照左手材料的布儒斯特定律计算。

同时，由于左手材料的电磁性质与右手材料相反，所以左手材料的折射率是负数。

因此，当光线从左手材料中出射时，其折射角也会是负数。

总之，在左手材料中，由于其电磁性质的不同，菲涅尔公式和布儒斯特定律需要做出相应的修改。

这些修改对于理解左手材料的光学
性质具有重要意义。