下载文档原格式
探讨偏振光的反射和折射问题摘要本文介绍了几种不同种类偏振光的特征以及它们在介质界面的反射与折射现象。
利用菲涅耳公式具体分析反射光和折射光的偏振状态,得出反射光的偏振状态与介质折射率、入射光的偏振态及入射角有关,折射光的偏振态与界面折射无关的结论,这有利于我们分析电磁波在自由空间或有限区域的传播特性,从而掌握整个电磁波的传播规律。
关键词偏振光;反射;折射0 引言1809年马吕斯(E·L·Malus)发现了反射光的偏振现象。
光的电磁理论建立以后,我们才进一步认识到在自由空间传播的光波是一种纯粹的横波,其电矢量和磁矢量都垂直于光的传播方向。
纵波的振动方向与波的传播方向一致,因此纵波具有轴对称性,即从垂直波传播方向的各个方向与观察纵波情况完全相同。
而横波对于传播方向的轴来说不具备对称性。
这种不对称性叫做偏振[2]。
只有横波才具备偏振的性质。
反射光和折射光的偏振现象是光学中的重要内容。
1 偏振光及其分类光的横波性表现为振动的不对称性,称光波的偏振态。
光波的偏振态通常分为自然光、部分偏振光、线偏振光、圆偏振光和椭圆偏振光。
1.1 自然光光源发出的光波不是偏振光,因原子分子发出的光波不是无限长的连绵不断的简谐波,而是一些断断续续的波列,每一波列持续时间在10-8s以下,波列间没有固定的相位关系,而且振动方向是无规的,这种光称自然光。
对于自然光Imax=Imin,P=0。
1.2 部分偏振光介于自然光和偏振光之间,可看作两个振动方向相互垂直、振幅不等的线偏振光,没有固定的相位关系。
为了定量区分,定义光的偏振度P=(ImaxImin分别是与最大振幅和最小振幅相应的光强)。
1.3 (直线)平面偏振光如果光振动矢量保持在一个平面内,如光沿y轴方向传播,光振动矢量沿Z轴,并且发生在yoz平面内,这叫(直线)平面偏振光,简称偏振光。
1.4 圆偏振光1)固定空间一点来看,每一点光矢量随时间匀速旋转,矢量长度不变,端点描绘成一个圆,光矢量旋转的频率为v;2)固定一时刻来看,空间各点的光矢量排列在一条螺旋线上;3)随时间推移,波形(螺旋线)向前传播,在传播方向上各点相位越来越落后。
光的偏振实验方法总结光的偏振是指光波在传播过程中的振动方向。
而光的偏振实验方法是一种用来研究光的偏振性质的实验手段。
本文将对常见的光的偏振实验方法进行总结和介绍。
I. 光的偏振现象简介在探讨光的偏振实验方法之前，我们首先需要了解光的偏振现象。
光的偏振可以分为线偏振、圆偏振和非偏振光。
线偏振光是指光波振动方向只存在于一个平面内，而圆偏振光则是指振动方向按照圆周轨迹运动。
非偏振光则是指振动方向在各个方向上都有。
II. 光的偏振实验方法1. 波片法波片法是一种常见且重要的光的偏振实验方法。
其原理基于光的偏振现象，通过使用不同的波片，可以改变光波的偏振状态。
常见的波片有半波片和四分之一波片。
在实验中，我们可以通过旋转波片来改变光波的振动方向，从而实现光的偏振状态的调节和观察。
2. 偏振片法偏振片法是另一种常用的光的偏振实验方法。
它利用了具有特定光学性质的偏振片，可以选择性地透过或吸收特定方向上的光振动。
实验中，可以通过叠加两个偏振片，并调节它们之间的夹角，来观察光的偏振状态的变化。
3. 布儒斯特角测量法布儒斯特角测量法是一种利用光的偏振现象进行测量的方法。
根据布儒斯特定律，当入射光的折射角等于特定角度时，反射光变为全反射。
通过测量布儒斯特角，可以得到光的折射率以及光的偏振性质。
4. 双折射法双折射法是一种利用物质的双折射性质研究光的偏振现象的实验方法。
当光波通过具有双折射性质的物质时，会分离成两个不同方向振动的光波。
通过观察双折射晶体中不同方向光振动的现象，可以推测光的偏振状态。
5. 泽尼克斯板法泽尼克斯板是一种特殊的偏振装置，通过它可以产生特定的偏振状态。
在泽尼克斯板实验中，通过选择不同的泽尼克斯板以及旋转它们的方向，可以观察到光的偏振状态的变化。
III. 光的偏振实验的应用光的偏振实验方法在科学研究和实际应用中具有广泛的应用价值。
以下为一些常见应用领域：1. 光学仪器：光的偏振实验方法可以帮助设计和制造光学仪器，如偏振镜、偏振滤波器等。
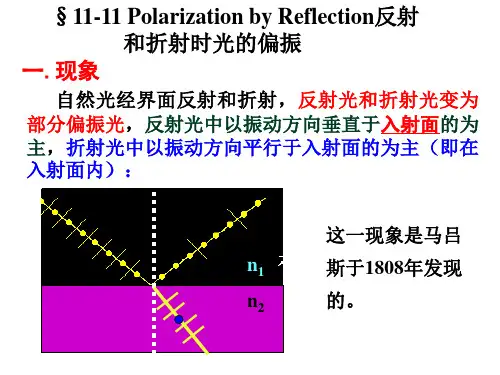
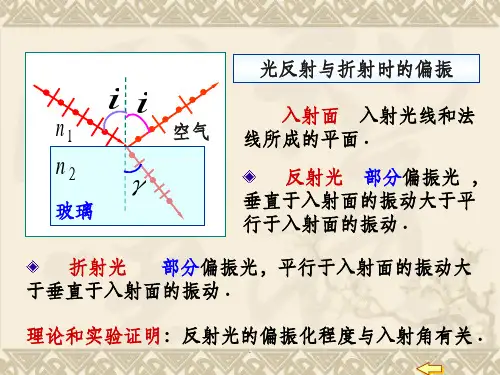
布儒斯特定律（一）、光在反射和折射中的偏振实验表明，一般情况下，自然光入射到两种介质的界面上时，产生的反射光和折射光都是部分偏振光，反射光中垂直于入射面的光振动较强，折射光中平行于入射面的光振动较强，如下图（a ）所示。
（二）、布儒斯特定律实验还指出，反射光和折射光的强度以及偏振化的程度都与入射角的大小有关。
特别是，当入射角i 等于某一特定值时，反射光是完全偏振光，振动方向垂直于入射面，见上图（b ）。
这个特定的入射角称为起偏振角，用0i 表示，它的大小取决于两种介质的相对折射率。
实验进一步告诉我们，当光以起偏振角入射到两种介质的界面上时，反射光线和折射光线相互垂直，如上图（b ）所示。
于是有根据折射定律(a)自然光经过反射和折射后，产生部分偏振光(b)入射角为布儒斯特角时，反射光为偏振光式中1n 和2n 分别为入射光和折射光所在介质的折射率。
由于00cosi sinr =，得到上述结果称为布儒斯特定律，表示起偏振角与介质折射率的关系，故0i 又称为布儒斯特角。
（三）、讨论当0i i =时，反射光为完全偏振光，而折射光一般仍然是部分偏振光，而且偏振化程度不高。
因为对于多数透明介质，折射光的强度要比反射光的强度大很多。
例如，当自然光由1n 1=的空气射向50.1n 2=的玻璃时，01203.56)n n (arctan i ==，入射光中平行于入射面的光振动全部被折射，垂直于入射面的光振动也有85%被折射，反射光只占垂直入射面光振动15%。
由于一次反射得到的偏振光的强度很小，折射光的偏振化程度又不高，为了能够增强反射光的强度和提高折射光的偏振化程度，可以把许多相互平行的玻璃片叠在一起，构成一玻璃片堆，见上图（a ）。
自然光以布儒斯特角入射时，容易证明（见图（b ）），光在各层玻璃面上的反射和折射都满足布儒斯特定律，这样就可以在多次的反射和折射中使反射光的强度增强，使折射光的偏振化程度提高。
当玻璃片足够多时，就可以在反射和透射方向分别得到光振动方向互相垂直的两束偏振光。
光的折射和反射的偏振特性一、引言光，作为现代科技发展的重要基础，其性质和行为一直是物理学研究的重要领域。
光的折射和反射是光最基本的性质之一，它们在日常生活中和科技应用中都有着广泛的应用。
而光的偏振现象，则是光的一种特殊性质，对于光的折射和反射过程有着重要的影响。
本文将详细介绍光的折射和反射的偏振特性，以帮助读者更深入地理解光的本质和行为。
二、光的折射和反射2.1 光的折射光的折射是指光从一种介质进入另一种介质时，由于介质的光速不同，光线会产生方向上的改变。
根据斯涅尔定律，入射角和折射角之间存在以下关系：[ n_1 (_1) = n_2 (_2) ]其中，( n_1 )和( n_2 )分别是光在第一种和第二种介质中的折射率，( _1 )和( _2 )分别是光在第一种和第二种介质中的入射角和折射角。
2.2 光的反射光的反射是指光从一种介质射到另一种介质的界面上时，一部分光会返回原介质中的现象。
根据反射定律，入射角和反射角之间存在以下关系：[ _1 = _2 ]其中，( _1 )是光在第一种介质中的入射角，( _2 )是光在第二种介质中的反射角。
三、光的偏振3.1 偏振的概念偏振是指光波中电场矢量在空间中的特定方向上的振动。
与非偏振光相比，偏振光具有特定的振动方向，这使得偏振光在某些方面具有独特的性质和应用。
3.2 偏振片的应用偏振片是一种可以使得光波中的电场矢量在特定方向上振动的光学元件。
通过偏振片，可以实现对光的偏振状态的控制和调节。
当偏振片的偏振方向与光波的振动方向平行时，偏振片允许光通过；当偏振片的偏振方向与光波的振动方向垂直时，偏振片则阻止光通过。
3.3 马吕斯定律马吕斯定律是描述偏振光通过偏振片时，光强与偏振片的偏振方向之间的关系。
当偏振片的偏振方向与光波的振动方向平行时，光强达到最大值；当偏振片的偏振方向与光波的振动方向垂直时，光强达到最小值。
4.1 折射的偏振特性当偏振光通过介质时，由于介质对不同振动方向的电场矢量具有不同的折射率，因此光在折射过程中会发生变化。
《大学物理AII 》作业 No.4 光的偏振班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、判断题：（用“T ”和“F ”表示）[ F ] 1．横波具有偏振性，纵波不具有偏振性。
解：由横波、纵波、偏振定义P91可得。
[ T ] 2．偏振片让平行于偏振化方向的电场分量通过，吸收垂直于这个方向的电场分量。
解：由偏振片性质P94知。
[ F ] 3．自然光入射到介质分界面时，如果入射角大于它的布儒斯特角，则反射光为线偏振光。
解：由光入射到介质分界面时形成反射、折射的起偏规律P95知。
[ T ] 4．双折射晶体中，光沿光轴方向传播，不发生双折射现象。
解：由双折射晶体中光轴定义P96知。
[ T ] 5．光是一种电磁波，我们把电场强度矢量称为光矢量。
解：由P90只有电场强度矢量引起视觉和感光作用知。
二、选择题：1．如图所示的偏振片可以得到偏振化方向平行于y 轴的偏振光。
当自然光入射时，将偏振片绕如图所示的光传播的方向顺时针转动︒40，通过偏振片的光强是： [ ] (A) 增大 (B) 减小(C) 不变 (D) 不能确定解：因自然光是非偏振光，故将偏振片绕如图所示的光传播的方向顺时针转动︒40，并没改变自然光振动方向与偏振片偏振化方向关系，故光强不变。
故选C2．当第三块偏振片以45º插入两块偏振方向正交的偏振片时，会有部分的光出射。
如果不是用单一的一块45º偏振片插入，而是中间插入N 块偏振片组，每片的偏振化方向平均转过90º/（N+1）。
[ ] (A) 没有光出射 (B) 出射的光更少(C) 出射的光一样多 (D) 出射的光更多解：设两块偏振方向正交的偏振片放置在 x 方向y ，自然光入射，则当第三块偏振片以45º插入时由偏振片起偏规律和右偏振化方向关系有 自然光通过偏振片1后光强为：21I I =强度为1I 线偏振光通过偏振片2后光强为：（马吕期定律）)45(cos 2)45(cos 20212︒=︒=I I I 强度为2I 线偏振光通过偏振片3后光强为：)45(cos )45(cos 2)45(cos 220223︒︒=︒=I I I 80I =若中间插入N 块偏振片组，每片的偏振化方向平均转过90º/（N+1），由偏振片起偏规律和y x︒45右偏振化方向关系有出射光光强为)190(cos 2)190(cos )190(cos )190(cos 2)1(202220+︒=+︒+︒+︒=+N I N N N I I N（其中：共有N +1项)190(cos 2+︒N 连乘） 例：若N=1，则有0)11(20125.0)1190(cos 2I I I =+︒=+若N=2，则有0)12(20211.0)1290(cos 2I I I =+︒=+若N=3，则有0)13(20265.0)1390(cos 2I I I =+︒=+上述例子表明N 越大，透射光强越多。
浅谈布儒斯特角及其光学应用摘要：随着科学技术的日益发展，现今除了利用布儒斯特角获得线偏振光外与布儒斯特角相关的实验概念，如其计算和测量等等在生产生活、科学研究、高校教学等方面均有十分广泛的用途和非常突出的实用价值。
因此，深入研究布儒斯特角，进一步拓展布儒斯特定律的实际应用，是现代光学的一个非常有价值的研究方向。
本文首先对布儒斯特角的来源向读者做了简单介绍，指出布儒斯特做了大量实验，终于在1815年，他发现当反射光与折射光垂直时，反射光完全偏振。
然后对布儒斯特角、布儒斯特定律、布儒斯特窗、布儒斯特条纹、布儒斯特体视镜等相关概念做了叙述。
紧接着为了读者更能清楚的理解布儒斯特定律，我简单对光的偏振现象为大家做了阐述。
最后，因为布儒斯特定律在生活中的应用有很多,并且具有很强的实用价值和可操作性,所以我们在了解研究布儒斯特角时，要对其应用进行合理的分类，本文中，我们将其应用分为四大类，即布儒斯特角在生产生活中的应用、在科学研究中的应用、在高校教学中的应用以及其他应用。
对于每类应用，我们会举出相应的实例，并为大家解释其中的原理。
关键词：布儒斯特角；布儒斯特定律；布儒斯特窗；光的偏振；光的波动性；On the Brewster angle and opticalapplicationsAbstract: With the development of science and technology, Now, In addition to using the Brewster angle to get outside of linearly polarized light, Concepts and experiments related to the Brewster angle, As its calculation and measurement in production and life, Scientific research, Teaching and other universities are very versatile and very prominent practical value. Therefore, In-depth study of the Brewster angle, Further expand the practical application of Brewster's law, Is a very valuable research direction of modern optics.Firstly, the source of the Brewster angle to the reader a brief introduction, Said: Brewster's done a lot of experiments, and finally in 1815, he found that when the reflection and refraction of light perpendicular to the light, the reflected light is completely polarized. Second, do a narrative to the Brewster angle, Brewster's law, Brewster windows, Brewster fringes Brewster stereoscope and other related concepts do a narrative. And then for the reader to understand Brewster's law more clearly, I simply described light polarization phenomena for everyone. Finally, because there are many uses of Brewster Law in life and has strong practical value and operability so when we learn the Brewster angle, we need make a reasonable classification of its uses, In this article, We make its uses into four categories, That Brewster angle in the production of life, In scientific applications, in university teaching and other applications. For each type of application, I will cite the appropriate instance and explain the principle.Keywords: Brewster angle; Brewster Law; Brewster window;Polarization of the light;Wave nature of light前言振动状态的传播就是波动，波动时物质运动的一种很普遍的形式。
反射光与折射光的偏振自然光可分解为振动方向互相垂直的两种光。
自然光射到两种透明介质的分界面上发生反射和折射时，由于反射率和折射率与光的振动方向有关，反射光和折射光都将成为部分偏振光，在特殊情况下，反射光将是线偏振光。
用E P 表示平行于入射面的电矢量振动的振幅，E P1、E ’P1、E ’P2分别代表入射光、反射光和折射光的电矢量振动的振幅；i 表示入射角，r 表示折射角，则根据菲涅耳公式（参见“菲涅耳公式”），反射比,)tan()tan(p1p1p r i r i E E r +-='=（1） 透射比).cos()sin(cos sin 2p12p p r i r i ir E E t -+==(2)用S E 表示垂直于入射面的电矢量振动的振幅,1S E 、1S E '、2S E 分别代表入射光、反射光和折射光的电矢量振动的振幅，则反射比,)sin()sin(11r i r i E E r S S S +--='=（3） 透射比).sin(cos sin 212r i ir E E t S S S +==（4）由（1）式可知，当2π=+r i时，0/11P ='E E P。
这表示反射光中没有平行于入射面的电矢量，即反射光成为垂直于入射面的线偏振光。
所以这是利用反射从自然光得到偏振光的一种方法。
这时的入射角i 叫做偏化角，通常用p i 表示。
由于rr n i n r i sin ,sin sin ,22p 1p ==+πp cos i =，所以.arctan ,tan 12p 12p n ni n n i ==（5） 这个公式所表示的规律叫做布儒斯特定律，p i 又叫布儒斯特角。
反射引起偏振的现象是法国物理学家马吕斯（Malus,Etienne Louis,1775～1812）在1808年发现的。
反射起偏的规律，即布儒斯特定律，是英国物理学家布儒斯特（Breuster,D.B.1781～1868）在1812年发现的。
反射光的偏振及布儒斯特角的测量实验说明书北京方式科技有限责任公司反射光的偏振特性—布儒斯特角的测量光是一种横波，它的振动方向是与传播方向相互垂直的。
偏振是指光波的振动方向在空间上的一种相对取向的现象。
当这个振动方向在垂直于传播方向的平面内可取所有可能的方向，并且没有一个方向占优势时，我们称之为自然光或非偏振光。
而如果有某一个方向上的振动占优势时，则称之为部分偏振光。
只有一个单一的振动方向的光叫线偏振光，而在一个振动周期内其振动矢量的端点的轨迹为一个圆或椭圆时，我们称之为圆偏振光或椭圆偏振光。
在我们日常生活和工作中，太阳光、照明用光一般多为自然光。
而自然光经过一些材料的反射和透射后可能变成部分偏振光。
自然光经过一些特殊材料，如偏振片或双折射晶体材料制作的棱镜后，就会变成线偏振光，一些激光器也可产生很好的线偏振光。
线偏振光经过波片后就可能成为椭圆偏振光。
一、实验目的1.用最小偏向角法测量棱镜材料的折射率。
2.测量通过起偏器、1/4波片后的光的偏振特性，了解线偏振光、圆偏振光和椭圆偏振光的特点。
3.通过观察从棱镜材料表面反射回来的光的偏振特性，了解反射光的偏振特性，测量出布儒斯特角。
4.用测量值验证布儒斯特角公式的正确性。
二、实验原理1.棱镜材料的折射率的测量当一束光斜入射于棱镜表面时，其光路如下图。
由(1)式可得：2sin2sinminA A n δ+=(3) 因此，只要我们测量出min δ，就可得到材料相对于该测量光的折射率n 。
2. 偏振光1) 偏振光的数学描述：对于线偏振光和椭圆偏振光，在数字上我们常用两个垂直振动的合成来描述。
在以光传播方向相垂直的平面内取一个直角坐标系，将代表振动特性的电矢量E 分解成Ex 和Ey ，它们是同频ω，假设相位相差δ，振幅分别为Ex 和Ey ，即t A E x x ωcos = (4) )cos(δω+=t Ay E y (5) 消去t ，上式可变成δδ222sin cos 2=⋅-⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛y y x x y y x x A E A E A E A E (6) 这是一个椭圆的方程，因其系数行列式大于零：222221cos sin 0cos 1x x y x y x y yA A A A A A A A δδδ⎛⎫-⎪⎪=≥ ⎪- ⎪ ⎪⎝⎭(7)当δ=0或π时， 0sin =δ 1cos ±=δ 上式为：0222=⋅±⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛y y x x y y xxA E A E A E AE (8) y yxx E A A E ±= 这是一个线性方程：斜率为 y A ，振幅为22y x A A +，它代表一束线偏振光 当δ=±π/2时，1sin 2=δ 0cos =δ；椭圆方程变为：221y x x y E E A A⎛⎫⎛⎫+= ⎪ ⎪ ⎪⎝⎭⎝⎭ (9)这是一个标准的椭圆方程，其主轴在X 、Y 方向。
