广义线性回归分析(协方差分析)

在方差分析中，我们初步介绍了线性模型的思想，实际上，线性模型只是方差分析的模型化，其统计检验仍然是依照方差分解原理进行F检验。

线性模型作为一种非常重要的数学模型，通常可以分为方差分析模型、协方差分析模型、线性回归模型、方差分量模型等，根据表现形式又可以分为一般线性模型、广义线性模型、一般线性混合模型、广义线性混合模型。

下面我们就根据分析目的来介绍线性模型一、方差分析模型：使用线性模型进行方差分析的时候涉及一些基本概念：===============================================(1)因素与水平因素也称为因子，在实际分析中，因素就是会对结果产生影响的变量，通常因素都是分类变量，如果用自变量和因变量来解释，那么因素就是自变量，结果就是因变量。

一个因素下面往往具有不同的指标，称为水平，表现在分类变量上就是不同类别或取值范围，例如性别因素有男、女两个水平，有时取值范围是人为划分的。

(2)单元因素各水平之间的组合，表现在列联表中就是某个单元格，有些实验设计如拉丁方设计，单元格为空或无。

(3)元素指用于测量因变量值的最小单位，其实也就是具体的测量值。

根据具体的实验设计，列联表的一个单元格内可以有一个或多个元素，也可能没有元素。

(4)均衡如果一个实验设计中任一因素的各水平在所有单元格中出现的次数相同，且每个单元格内的元素数也相同，那么该实验就是均衡的。

不均衡的实验设计在分析时较为复杂，需要对方差分析模型作特别的设置才行。

(5)协变量有时，我们在分析某些因素的影响时，需要排除某个因素对因变量的影响，这个被排除的因素被称为协变量，(6)交互作用如果一个因素的效应大小在另一个因素的不同水平下表现的明显不同，则说明这两个因素之间存在交互作用。

交互作用是多因素分析时必须要做的，这样分析的结果才会全面。

(7)固定因素和随机因素是因素的两个种类，固定因素是指该因素的所有水平，在本次分析中全部出现，从分析结果就可以获知全部水平的情况。

摘要广义线性模型是一类现如今十分重要的数学模型，它是经典线性模型的推广，在当今社会有着广泛的应运。

在医学、生物以及经济等数据的统计和分析上有着很深的意义。

它可适用于离散的数据和连续的数据，尤其是前者，像属性数据、计数数据等等。

广义线性模型包括了许多模型，其中有方差分析模型、线性回归、交替响应的对数和概率单位模型、计数的多项响应模型、对数线性模型以及生存数据的一些常用模型等等。

本论文前两章讨论了广义线性模型的研究现状以及广义线性模型的基本理论。

第三章通过医学、生物和经济三个方面的实例来研究广义线性模型在日常生活中的广泛应用。

医学方面讨论了新药试验过程中广义线性模型对于新药的有效性研究提供了一种最为合适且快捷的方案。

生物方面通过浙江省一个水稻区域试验来说明广义线性模型在非平衡数据的处理上较与经典线性回归模型有着很显著的优越性。

经济方面则通过车辆保险费率厘定的实例来说明广义线性模型处理数据的简便与快捷。

三个方向的研究与探讨都说明了广义线性模型在现今社会生活中有着无法替代的存在感，在各个领域都有着极其广泛的应用。

关键词：广义线性模型；数据分析；timi分级；极大似然估计AbstractThe generalized linear model is a kind of mathematical model which is very important nowadays. It is the popularization of the classical linear model. It is widely used in today's society. In the medical, biological and economic data and statistical analysis and has a deep meaning. It can be applied to discrete data and continuous data, especially the former, like attribute data, count data and so on. The generalized linear model includes a number of models, including variance analysis models, linear regression, logarithm of alternating responses and probability unit models, counting multiple response models, logarithmic linear models, and some common models of survival data. The first two chapters of this paper discuss the general situation of generalized linear model and the basic theory of generalized linear model. The third chapter studies the broad application of generalized linear model in daily life through medical, biological and economic aspects. In this paper, the generalized linear model of the new drug trial is discussed in the medical field, which provides a most suitable and quick solution for the effectiveness of the new drug. The biological aspect shows that the generalized linear model has a significant superiority with the classical linear regression model in the treatment of non - equilibrium data through a rice regional experiment in Zhejiang Province. Economic aspects of the vehicle through the insurance rate to determine the examples to illustrate the generalized linear model of data processing is simple and fast. The study and discussion of the three directions show that the generalized linear model has an irreplaceable sense of existence in today's social life and has a wide range of applications in various fields.Key words: Generalized linear model; data analysis; timi classification; maximum likelihood estimation目录摘要 (I)Abstract (II)目录.................................................................................................................... I II 第一章绪论.. (1)1.1课题研究目的与意义 (1)1.2国内外研究现状 (1)第二章广义线性模型的研究 (3)2.1两种线性模型 (3)2.2常见的广义线性模型 (3)2.3广义线性模型的优点 (4)2.4广义线性模型的两种参数估计方法 (4)2.4.1极大似然估计 (4)2.4.2两参数估计 (9)第三章广义线性模型在数据分析中的应用 (11)3.1 广义线性模型在timi分级影响因素分析中的应用 (11)3.2 广义线性模型在水稻区域试验中的应用 (13)3.2.1实例 (15)3.2.2分析与结果比较 (16)3.2.3分析与展望 (17)3.3 广义线性模型在汽车保险定价中的应用 (17)3.4 广义线性模型在保险赔款预估中的应用 (19)第四章总结 (24)参考文献 (25)致谢 (26)第一章绪论1.1课题研究目的与意义广义线性模型是从线性模型演变过来的，但是它比经典的线性模型适应性更强，在处理很多数据分析问题中表现出很多优点。

协方差分析协方差分析（ANCOVA）是一种在统计学中常用的方法，用于比较两个或更多组之间的平均值是否存在差异，并控制一个或多个可能存在的共同协变量的影响。

在本文中，将介绍协方差分析的基本概念、假设前提、模型、效应检验、应用注意事项等内容。

一、基本概念协方差分析是一种结合了方差分析（ANOVA）和回归分析的技术，旨在研究组间的差异是否受到一个或多个协变量的影响。

协变量指的是可能影响因变量的其他变量，例如年龄、性别、智力水平等。

通过控制协变量的影响，协方差分析可以更准确地评估组间的差异是否真正存在。

二、假设前提三、模型在协方差分析中，需要估计各组的平均值（μ）和回归系数（β1和β2），以及误差项的方差（σ²）。

通过比较组间方差与误差项方差的比值，可以判断在控制协变量的情况下，组间的差异是否显著。

四、效应检验另外，还可以通过比较回归系数的显著性来判断协变量对因变量的影响。

如果协变量的回归系数显著，表示协变量对因变量的影响在各组之间存在差异。

五、应用注意事项在进行协方差分析时，需要注意以下几点：1.选择合适的协变量：选择与因变量相关的协变量，以减少协变量的影响，提高结果的准确性。

2.检验协变量与因变量之间的线性关系：协变量与因变量之间的关系应该是线性的，否则可能导致结果不准确。

3.选择适当的控制组：选择适当的控制组进行比较，以保证对组间差异的探究更有说服力。

4.检验方差齐次性假设：协方差分析要求各组之间的方差应该是齐次的，如果方差齐次性假设不成立，可能导致结果失真。

5.做出合理的解释：协方差分析仅能提供组间的比较结果，不能得出因果关系的结论。

因此，在解释结果时应谨慎，并结合实际情况进行合理解释。

总结：协方差分析是一种在统计学中常用的方法，用于比较组间平均值是否存在差异，并控制可能存在的共同协变量的影响。

通过协方差分析，可以更准确地评估组间差异的显著性，并提供合理的解释。

在进行协方差分析时，需要注意选择合适的协变量、检验线性关系、选择适当的控制组、检验方差齐次性假设，并做出合理的解释。

第十章协方差分析协方差分析（Analysis of Covariance，简称ANCOVA）是一种多元统计方法，用于在考虑一个或多个共变量（covariates）的情况下，评估一个或多个自变量（independent variables）对于因变量（dependent variable）的影响。

在实际研究中，常常会遇到一些与因变量相关但未被考虑的其他变量，而这些变量可能会对因变量与自变量之间的关系产生干扰。

ANCOVA通过引入共变量来修正这种干扰，从而提高自变量对因变量的解释效果。

ANCOVA的基本思想是通过构建一个线性回归模型，将自变量、共变量以及其交互项作为预测变量，将因变量作为被预测变量，进而评估自变量对因变量的影响。

在这个过程中，共变量的作用是控制或削弱对因变量的影响，从而更准确地评估自变量的效果。

在进行ANCOVA分析之前，需要满足一些前提条件。

首先，因变量和自变量之间应该存在线性关系。

其次，各个共变量与自变量和因变量之间也应该存在线性关系。

最后，自变量与因变量之间的差异不能完全由共变量解释。

在进行ANCOVA分析时，需要进行一些统计检验来评估因变量与自变量、共变量之间的关系。

例如，可以计算自变量和因变量之间的相关系数，使用方差分析来比较组间差异，以及计算共变量与因变量的相关系数等。

ANCOVA的优势在于可以更准确地评估自变量对因变量的影响，同时控制其他可能干扰的因素。

此外，ANCOVA还可以用于提高实验的统计效力，减少研究中可能出现的偏差。

然而，ANCOVA也存在一些局限性。

首先，ANCOVA要求共变量与自变量和因变量之间存在线性关系，因此如果数据不符合线性假设，则ANCOVA可能不适用。

其次，ANCOVA要求样本量足够大，才能保证结果的可信度。

此外，ANCOVA对于共变量和自变量之间的交互作用也存在敏感性。

总结来说，协方差分析是一种有效的多元统计方法，可以用于控制共变量的干扰，评估自变量对因变量的影响。

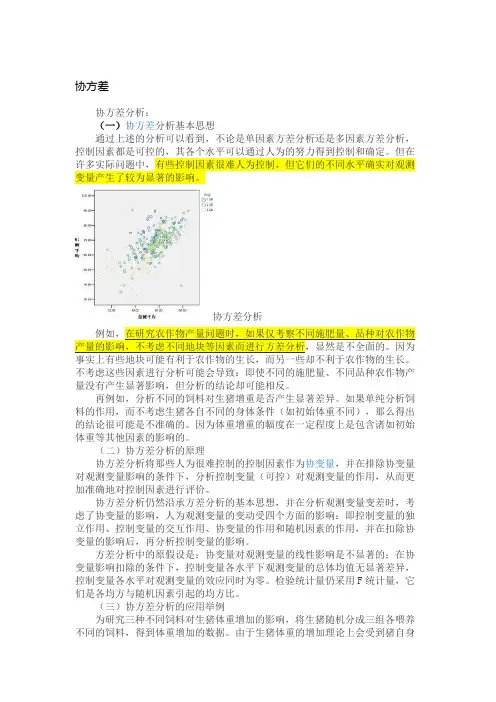
协方差协方差分析：（一）协方差分析基本思想通过上述的分析可以看到，不论是单因素方差分析还是多因素方差分析，控制因素都是可控的，其各个水平可以通过人为的努力得到控制和确定。

但在许多实际问题中，有些控制因素很难人为控制，但它们的不同水平确实对观测变量产生了较为显著的影响。

协方差分析例如，在研究农作物产量问题时，如果仅考察不同施肥量、品种对农作物产量的影响，不考虑不同地块等因素而进行方差分析，显然是不全面的。

因为事实上有些地块可能有利于农作物的生长，而另一些却不利于农作物的生长。

不考虑这些因素进行分析可能会导致：即使不同的施肥量、不同品种农作物产量没有产生显著影响，但分析的结论却可能相反。

再例如，分析不同的饲料对生猪增重是否产生显著差异。

如果单纯分析饲料的作用，而不考虑生猪各自不同的身体条件（如初始体重不同），那么得出的结论很可能是不准确的。

因为体重增重的幅度在一定程度上是包含诸如初始体重等其他因素的影响的。

（二）协方差分析的原理协方差分析将那些人为很难控制的控制因素作为协变量，并在排除协变量对观测变量影响的条件下，分析控制变量（可控）对观测变量的作用，从而更加准确地对控制因素进行评价。

协方差分析仍然沿承方差分析的基本思想，并在分析观测变量变差时，考虑了协变量的影响，人为观测变量的变动受四个方面的影响：即控制变量的独立作用、控制变量的交互作用、协变量的作用和随机因素的作用，并在扣除协变量的影响后，再分析控制变量的影响。

方差分析中的原假设是：协变量对观测变量的线性影响是不显著的；在协变量影响扣除的条件下，控制变量各水平下观测变量的总体均值无显著差异，控制变量各水平对观测变量的效应同时为零。

检验统计量仍采用F统计量，它们是各均方与随机因素引起的均方比。

（三）协方差分析的应用举例为研究三种不同饲料对生猪体重增加的影响，将生猪随机分成三组各喂养不同的饲料，得到体重增加的数据。

由于生猪体重的增加理论上会受到猪自身身体条件的影响，于是收集生猪喂养前体重的数据，作为自身身体条件的测量指标。

gls 和ols 的协方差
GLS（广义最小二乘法）和OLS（普通最小二乘法）是统计学中常用的回归分析方法。

协方差是用来衡量两个随机变量之间的关系强度和方向的统计量。

在回归分析中，协方差可以帮助我们理解自变量和因变量之间的关联程度。

首先，让我们来看GLS和OLS的定义。

OLS是一种回归分析方法，它通过最小化观测数据的残差平方和来估计模型参数。

这意味着它假设误差方差在所有自变量的取值上都是相同的，即误差项是同方差的。

而GLS则是一种更一般化的回归方法，它允许误差项的方差在不同的自变量取值下不同，因此可以更好地处理异方差性（即误差项方差不相等）的情况。

接下来，我们来看GLS和OLS的协方差。

在回归分析中，我们通常关心的是残差的协方差。

残差是因变量的观测值与回归模型预测值之间的差异，它们的协方差可以帮助我们评估模型的拟合程度和误差的相关性。

在OLS中，残差的协方差通常被假定为常数，因为OLS假设误差项是同方差的。

而在GLS中，由于允许误差项的方差在不同自变量取值下不同，因此残差的协方差也可以根据具体的模型设定而变化。

总的来说，GLS和OLS的协方差都是在回归分析中用来衡量误差项之间关联程度的重要统计量。

通过对协方差的分析，我们可以更好地理解回归模型的拟合情况和误差的特性。

在实际应用中，选择合适的回归方法和对协方差的合理处理都对建立准确的回归模型和进行有效的统计推断至关重要。

spss学习系列23.协⽅差分析（⼀）原理⼀、基本思想在实际问题中，有些随机因素是很难⼈为控制的，但它们⼜会对结果产⽣显著影响。

如果忽略这些因素的影响，则有可能得到不正确的结论。

这种影响的变量称为协变量（⼀般是连续变量）。

例如，研究3种不同的教学⽅法的教学效果的好坏。

检查教学效果是通过学⽣的考试成绩来反映的，⽽学⽣现在考试成绩是受到他们⾃⾝知识基础的影响，在考察的时候必须排除这种影响。

协⽅差分析将那些难以控制的随机变量作为协变量，在分析中将其排除，然后再分析控制变量对于观察变量的影响，从⽽实现对控制变量效果的准确评价。

协⽅差分析要求协变量应是连续数值型，多个协变量间互相独⽴，且与控制变量之间没有交互影响。

前⾯单因素⽅差分析和多因素⽅差分析中的控制变量都是⼀些定性变量，⽽协⽅差分析中既包含了定性变量（控制变量），⼜包含了定量变量（协变量）。

协⽅差分析在扣除协变量的影响后再对修正后的主效应进⾏⽅差分析，是⼀种把直线回归或多元线性回归与⽅差分析结合起来的⽅法，其中的协变量⼀般是连续性变量，并假设协变量与因变量间存在线性关系，且这种线性关系在各组⼀致，即各组协变量与因变量所建⽴的回归直线基本平⾏。

当有⼀个协变量时，称为⼀元协⽅差分析，当有两个或两个以上的协变量时，称为多元协⽅差分析。

⼆、协⽅差分析需要满⾜的条件（1）⾃变量是分类变量，协变量是定距变量，因变量是连续变量；对连续变量或定距变量的协变量的测量不能有误差；（2）协变量与因变量之间的关系是线性关系，可以⽤协变量和因变量的散点图来检验是否违背这⼀假设；协变量的回归系数（即各回归线的斜率）是相同的，且不等于0，即各组的回归线是⾮⽔平的平⾏线。

否则，就有可能犯第⼀类错误，即错误地接受虚⽆假设；（3）⾃变量与协变量相互独⽴，若协⽅差受⾃变量的影响，那么协⽅差分析在检验⾃变量的效应之前对因变量所作的控制调整将是偏倚的，⾃变量对因变量的间接效应就会被排除；（4）各样本来⾃具有相同⽅差σ2的正态分布总体，即要求各组⽅差齐性。

我们知道，混合线性模型是一般线性模型的扩展，而广义线性模型在混合线性模型的基础上又做了进一步扩展，使得线性模型的使用范围更加广阔。

每一次的扩展，实际上都是模型适用范围的扩展，一般线性模型要求观测值之间相互独立、残差(因变量)服从正态分布、残差(因变量)方差齐性，而混合线性模型取消了观测值之间相互独立和残差(因变量)方差齐性的要求，接下来广义线性模型又取消了对残差(因变量)服从正态分布的要求。

残差不一定要服从正态分布，可以服从二项、泊松、负二项、正态、伽马、逆高斯等分布，这些分布被统称为指数分布族，并且引入了连接函数，根据不同的因变量分布、连接函数等组合，可以得到各种不同的广义线性模型。

要注意，虽然广义线性模型不要求因变量服从正态分布，但是还是要求相互独立的，如果不符合相互独立，需要使用后面介绍的广义估计方程。

=================================================一、广义线性模型广义线性模型的一般形式为：有以下几个部分组成1.线性部分2.随机部分εi3.连接函数连接函数为单调可微(连续且充分光滑)的函数，连接函数起了"y的估计值μ"与"自变量的线性预测η"的作用，在一般线性模型中，二者是一回事，但是当自变量取值范围受限时，就需要通过连接函数扩大取值范围，因此在广义线性模型中，自变量的线性预测值是因变量的函数估计值。

广义线性模型设定因变量服从指数族概率分布，这样因变量就可以不局限于正态分布一种形式，并且方差可以不稳定。

指数分布族的概率密度函数为其中θ和φ为两个参数，θ为自然参数，φ为离散参数，a,b,c为函数广义线性模型的参数估计：广义线性模型的参数估计一般不能使用最小二乘法，常用加权最小二乘法或极大似然法。

回归参数需要用迭代法求解。

广义线性模型的检验和拟合优度：广义线性模型的检验一般使用似然比检验、Wald检验。

模型的比较用似然比检验，回归系数使用Wald检验。