线性回归模型的广义刀切最小二乘估计
- 格式:pdf
- 大小:140.97 KB
- 文档页数:4

最小二乘估计原理最小二乘估计是一种常用的参数估计方法,它可以用来估计线性回归模型中的参数。
在实际应用中,最小二乘估计被广泛应用于数据拟合、信号处理、统计分析等领域。
本文将介绍最小二乘估计的原理及其应用。
最小二乘估计的原理是基于最小化观测值与模型预测值之间的误差平方和来进行参数估计。
在线性回归模型中,我们通常假设因变量Y与自变量X之间存在线性关系,即Y = β0 + β1X + ε,其中β0和β1是待估参数,ε是误差项。
最小二乘估计的目标是找到最优的β0和β1,使得观测值与模型预测值之间的误差平方和最小。
为了形式化地描述最小二乘估计的原理,我们可以定义损失函数为误差的平方和,即L(β0, β1) = Σ(Yi β0 β1Xi)²。
最小二乘估计的思想就是通过最小化损失函数来求解最优的参数估计值。
为了找到最小化损失函数的参数估计值,我们可以对损失函数分别对β0和β1求偏导数,并令偏导数等于0,从而得到最优的参数估计值。
在实际应用中,最小二乘估计可以通过求解正规方程来得到参数的闭式解,也可以通过梯度下降等迭代方法来进行数值优化。
无论采用何种方法,最小二乘估计都能够有效地估计出线性回归模型的参数,并且具有较好的数学性质和统计性质。
除了在线性回归模型中的应用,最小二乘估计还可以推广到非线性回归模型、广义线性模型等更加复杂的模型中。
在这些情况下,最小二乘估计仍然是一种有效的参数估计方法,并且可以通过一些变形来适应不同的模型结构和假设条件。
总之,最小二乘估计是一种重要的参数估计方法,它具有简单直观的原理和较好的数学性质,适用于各种统计模型的参数估计。
通过最小化观测值与模型预测值之间的误差平方和,最小二乘估计能够有效地估计出模型的参数,并且在实际应用中取得了广泛的成功。
希望本文对最小二乘估计的原理有所帮助,谢谢阅读!。

广义回归模型一、概述广义回归模型是一种用于数据分析和建模的统计方法,它可以用来描述两个或多个变量之间的关系。
该模型可以通过最小化误差平方和来拟合数据,并根据数据中的变量来预测未知的结果。
广义回归模型是线性回归模型的扩展,它包含了其他类型的回归模型,如逻辑回归、泊松回归等。
二、线性回归模型1. 定义线性回归模型是一种广义回归模型,它假设因变量与自变量之间存在线性关系。
该模型可以用以下公式表示:Y = β0 + β1X1 + β2X2 + … + βpXp + ε其中,Y表示因变量,X1、X2、…、Xp表示自变量,β0、β1、β2、…、βp表示系数,ε表示误差项。
2. 最小二乘法最小二乘法是一种常用的拟合线性回归模型的方法。
该方法通过最小化残差平方和来确定最佳拟合直线。
3. 模型评估为了评估线性回归模型的拟合效果,可以使用以下指标:(1)R方值:R方值越接近1,则说明该模型对数据的拟合效果越好。
(2)均方误差(MSE):MSE越小,则说明该模型对数据的预测效果越好。
三、逻辑回归模型1. 定义逻辑回归模型是一种广义线性回归模型,它用于建立因变量与自变量之间的非线性关系。
该模型可以用以下公式表示:P(Y=1|X) = e^(β0 + β1X1 + β2X2 + … + βpXp) / (1 + e^(β0 +β1X1 + β2X2 + … + βpXp))其中,P(Y=1|X)表示给定自变量时因变量为1的概率,e表示自然对数的底数,β0、β1、β2、…、βp表示系数。
2. 模型评估为了评估逻辑回归模型的拟合效果,可以使用以下指标:(1)准确率:准确率越高,则说明该模型对数据的拟合效果越好。
(2)召回率:召回率越高,则说明该模型对正样本的识别能力越强。
四、泊松回归模型1. 定义泊松回归模型是一种广义线性回归模型,它用于建立因变量与自变量之间的非线性关系。
该模型可以用以下公式表示:ln(μ) = β0 + β1X1 + β2X2 + … + βpXp其中,μ表示因变量的均值,β0、β1、β2、…、βp表示系数。

广义最小二乘法的推导1. 引言广义最小二乘法(Generalized Least Squares, GLS)是一种用于解决线性回归问题的方法。
与最小二乘法相比,GLS可以处理数据中存在异方差(heteroscedasticity)和自相关(autocorrelation)的情况,提高了回归模型的准确性和效果。
在本文中,我们将详细推导广义最小二乘法的数学原理和推导过程。
首先,我们将介绍最小二乘法的基本概念和原理,然后讨论广义最小二乘法的推导过程,并最后给出一个示例来说明广义最小二乘法的应用。
2. 最小二乘法最小二乘法是一种常用的用于拟合线性回归模型的方法。
其基本思想是通过最小化残差平方和来选择最优的回归系数。
对于一个具有n个数据点的线性回归模型:Y=Xβ+ε其中,Y是n维的因变量向量,X是n行p列的自变量矩阵,β是p维的系数向量,ε是n维的误差向量。
最小二乘法的目标是找到最优的β,使得残差平方和最小:εTεminβ通过对目标函数求导,并令导数等于零,可以得到最优解的闭式解表达式:β̂=(X T X)−1X T Y其中,β̂表示最优的回归系数。
3. 广义最小二乘法最小二乘法假设误差项具有同方差且不相关的性质,然而在实际问题中,数据往往存在异方差和自相关的情况。
为了解决这些问题,我们引入广义最小二乘法。
3.1 异方差问题当误差项具有异方差性质时,最小二乘法的估计结果可能是偏误的。
为了解决异方差问题,我们可以对误差项进行加权处理。
假设误差项的方差为σi2,我们可以使用加权最小二乘法来估计回归系数。
目标函数可以表示为:minεT Wεβ其中,W是一个对角矩阵,对角线元素为σi−2。
通过对目标函数求导,并令导数等于零,可以得到最优解的闭式解表达式:β̂GLS=(X T WX)−1X T WYβ̂GLS表示广义最小二乘法的估计系数。
3.2 自相关问题当误差项存在自相关性质时,最小二乘法的估计结果也可能是偏误的。
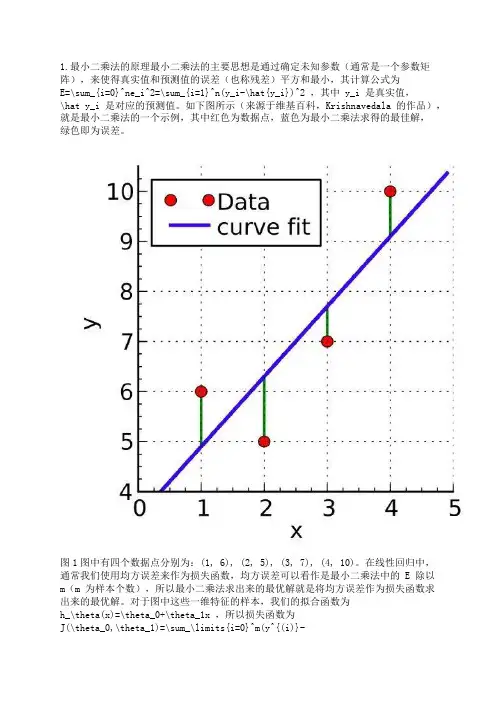
1.最小二乘法的原理最小二乘法的主要思想是通过确定未知参数(通常是一个参数矩阵),来使得真实值和预测值的误差(也称残差)平方和最小,其计算公式为E=\sum_{i=0}^ne_i^2=\sum_{i=1}^n(y_i-\hat{y_i})^2 ,其中 y_i 是真实值,\hat y_i 是对应的预测值。
如下图所示(来源于维基百科,Krishnavedala 的作品),就是最小二乘法的一个示例,其中红色为数据点,蓝色为最小二乘法求得的最佳解,绿色即为误差。
图1图中有四个数据点分别为:(1, 6), (2, 5), (3, 7), (4, 10)。
在线性回归中,通常我们使用均方误差来作为损失函数,均方误差可以看作是最小二乘法中的 E 除以m(m 为样本个数),所以最小二乘法求出来的最优解就是将均方误差作为损失函数求出来的最优解。
对于图中这些一维特征的样本,我们的拟合函数为h_\theta(x)=\theta_0+\theta_1x ,所以损失函数为J(\theta_0,\theta_1)=\sum_\limits{i=0}^m(y^{(i)}-h_\theta(x^{(i)}))^2=\sum_\limits{i=0}^m(y^{(i)}-\theta_0-\theta_1x^{(i)})^2 (这里损失函数使用最小二乘法,并非均方误差),其中上标(i)表示第 i 个样本。
2.最小二乘法求解要使损失函数最小,可以将损失函数当作多元函数来处理,采用多元函数求偏导的方法来计算函数的极小值。
例如对于一维特征的最小二乘法, J(\theta_0,\theta_1) 分别对 \theta_0 , \theta_1 求偏导,令偏导等于 0 ,得:\frac{\partial J(\theta_0,\theta_1)}{\partial\theta_0}=-2\sum_\limits{i=1}^{m}(y^{(i)}-\theta_0-\theta_1x^{(i)}) =0\tag{2.1}\frac{\partial J(\theta_0,\theta_1)}{\partial\theta_1}=-2\sum_\limits{i=1}^{m}(y^{(i)}-\theta_0-\theta_1x^{(i)})x^{(i)} = 0\tag{2.2}联立两式,求解可得:\theta_0=\frac{\sum_\limits{i=1}^m(x^{(i)})^2\sum_\limits{i=1}^my^{(i)}-\sum_\limits{i=1}^mx^{(i)}\sum_\limits{i=1}^mx^{(i)}y^{(i)}}{m\sum_\limits{i=1}^m(x^{(i)})^2-(\sum_\limits{i=1}^mx^{(i)})^2} \tag{2.3}\theta_1=\frac{m\sum_\limits{i=1}^mx^{(i)}y^{(i)}-\sum_\limits{i=1}^mx^{(i)}\sum_\limits{i=1}^my^{(i)}}{m\sum_\limits{i=1}^m(x^{(i)})^2-(\sum_\limits{i=1}^mx^{(i)})^2} \tag{2.4}对于图 1 中的例子,代入公式进行计算,得: \theta_0 = 3.5, \theta_1=1.4,J(\theta) = 4.2 。

线性回归与最小二乘法线性回归是一种常用的统计分析方法,也是机器学习领域的基础之一。
在线性回归中,我们通过寻找最佳拟合直线来对数据进行建模和预测。
最小二乘法是线性回归的主要方法之一,用于确定最佳拟合直线的参数。
1. 线性回归的基本原理线性回归的目标是找到一条最佳拟合直线,使得预测值与实际值之间的误差最小。
我们假设线性回归模型的形式为:Y = β₀ + β₁X₁ +β₂X₂ + … + βₙXₙ + ε,其中Y是因变量,X₁、X₂等是自变量,β₀、β₁、β₂等是回归系数,ε是误差项。
2. 最小二乘法最小二乘法是一种求解线性回归参数的常用方法。
它的基本思想是使所有样本点到拟合直线的距离之和最小化。
具体来说,我们需要最小化残差平方和,即将每个样本点的预测值与实际值之间的差的平方求和。
3. 最小二乘法的求解步骤(1)建立线性回归模型:确定自变量和因变量,并假设它们之间存在线性关系。
(2)计算回归系数:使用最小二乘法求解回归系数的估计值。
(3)计算预测值:利用求得的回归系数,对新的自变量进行预测,得到相应的因变量的预测值。
4. 最小二乘法的优缺点(1)优点:最小二乘法易于理解和实现,计算速度快。
(2)缺点:最小二乘法对异常点敏感,容易受到离群值的影响。
同时,最小二乘法要求自变量与因变量之间存在线性关系。
5. 线性回归与其他方法的比较线性回归是一种简单而强大的方法,但并不适用于所有问题。
在处理非线性关系或复杂问题时,其他方法如多项式回归、岭回归、lasso回归等更适用。
6. 实际应用线性回归及最小二乘法广泛应用于各个领域。
在经济学中,线性回归用于预测GDP增长、消费者支出等经济指标。
在医学领域,线性回归被用于预测疾病风险、药物剂量等。
此外,线性回归还可以应用于电力负荷预测、房价预测等实际问题。
总结:线性回归和最小二乘法是统计学和机器学习中常用的方法。
线性回归通过拟合一条最佳直线,将自变量与因变量之间的线性关系建模。

最小二乘法与线性回归模型线性回归是一种常用的统计分析方法,用于研究因变量与一个或多个自变量之间的关系。
在线性回归中,我们经常使用最小二乘法来进行参数估计。
本文将介绍最小二乘法和线性回归模型,并探讨它们之间的关系和应用。
一、什么是最小二乘法最小二乘法是一种数学优化技术,旨在寻找一条直线(或者更一般地,一个函数),使得该直线与一组数据点之间的误差平方和最小化。
简而言之,最小二乘法通过最小化误差的平方和来拟合数据。
二、线性回归模型在线性回归模型中,我们假设因变量Y与自变量X之间存在线性关系,即Y ≈ βX + ε,其中Y表示因变量,X表示自变量,β表示回归系数,ε表示误差。
线性回归模型可以用来解决预测和关联分析问题。
三、最小二乘法的原理最小二乘法的基本原理是找到一条直线,使得该直线与数据点之间的误差平方和最小。
具体而言,在线性回归中,我们通过最小化残差平方和来估计回归系数β。
残差是观测值与估计值之间的差异。
在最小二乘法中,我们使用一组观测数据(x₁, y₁), (x₂, y₂), ..., (xₙ, yₙ),其中x表示自变量,y表示因变量。
我们要找到回归系数β₀和β₁,使得残差平方和最小化。
残差平方和的表达式如下:RSS = Σ(yᵢ - (β₀ + β₁xᵢ))²最小二乘法的目标是最小化RSS,可通过求导数等方法得到最优解。
四、使用最小二乘法进行线性回归分析使用最小二乘法进行线性回归分析的一般步骤如下:1. 收集数据:获取自变量和因变量的一组数据。
2. 建立模型:确定线性回归模型的形式。
3. 参数估计:使用最小二乘法估计回归系数。
4. 模型评估:分析回归模型的拟合优度、参数的显著性等。
5. 利用模型:使用回归模型进行预测和推断。
五、最小二乘法与线性回归模型的应用最小二乘法和线性回归模型在多个领域都有广泛的应用。
1. 经济学:通过线性回归模型和最小二乘法,经济学家可以研究经济指标之间的关系,如GDP与失业率、通胀率之间的关系。

广义最小二乘估计为blue的若干条件广义最小二乘估计是一种常用的参数估计方法,它可以用来估计线性回归模型中的参数。
在广义最小二乘估计中,我们需要满足一些条件,才能得到BLUE(Best Linear Unbiased Estimator)估计量。
下面,我们将详细介绍这些条件。
1. 线性模型广义最小二乘估计要求模型是线性的,即因变量和自变量之间的关系可以用线性方程来表示。
例如,y = β0 + β1x1 + β2x2 + ε就是一个线性模型,其中y是因变量,x1和x2是自变量,β0、β1和β2是待估参数,ε是误差项。
2. 随机抽样广义最小二乘估计要求样本是随机抽样的,即每个样本都是独立地从总体中抽取的。
这个条件的目的是确保样本的代表性和可靠性。
3. 高斯-马尔科夫定理广义最小二乘估计要求误差项ε满足高斯-马尔科夫定理,即误差项的期望为0,方差为常数,且误差项之间是不相关的。
这个条件的目的是确保误差项的无偏性和方差的稳定性。
4. 多重共线性广义最小二乘估计要求自变量之间不存在多重共线性,即自变量之间不具有高度相关性。
如果存在多重共线性,会导致估计量的方差变大,从而影响估计结果的可靠性。
5. 方差齐性广义最小二乘估计要求误差项的方差在不同的自变量取值下是相等的,即方差齐性。
如果误差项的方差不齐,会导致估计量的方差不稳定,从而影响估计结果的可靠性。
广义最小二乘估计为blue的若干条件包括线性模型、随机抽样、高斯-马尔科夫定理、多重共线性和方差齐性。
只有在满足这些条件的情况下,我们才能得到BLUE估计量,从而得到可靠的估计结果。
因此,在进行参数估计时,我们需要认真考虑这些条件,并尽可能满足它们。


两则广义最小二乘法例题广义最小二乘法是一种用于估计线性回归模型参数的方法。
它适用于当回归模型存在异方差性(即误差方差不恒定)或者误差项之间存在相关性的情况。
下面是一个广义最小二乘法的例题:一、假设你正在研究某个城市的房价,你收集到了以下数据:对于n个房屋,你记录了它们的面积(X)、卧室数量(Z)以及售价(Y)。
你希望建立一个回归模型来预测房屋售价。
首先,我们可以假设回归模型的形式为:Y = β0 + β1X + β2Z + ε其中,Y是售价,X是面积,Z是卧室数量,ε是误差项。
为了使用广义最小二乘法估计模型参数,我们需要对误差项的方差进行建模。
假设误差项的方差为异方差的,即Var(ε) = σ^2 * f(Z),其中σ^2是常数,f(Z)是卧室数量的某个函数。
我们可以使用最小二乘法来估计模型参数β0、β1和β2。
首先,我们需要构造一个加权最小二乘问题,其中每个样本的残差平方会被一个权重因子所加权。
权重因子可以根据样本的特征值进行计算,以反映异方差性的影响。
在广义最小二乘法中,我们需要估计的参数为β0、β1和β2,以及函数f(Z)的形式和参数。
一种常见的方法是使用加权最小二乘法来求解该问题,其中权重因子可以通过对误差项的方差进行估计得到。
具体的计算过程可以使用迭代的方法进行。
需要注意的是,实际应用中可能存在多种处理异方差性的方法,具体的选择取决于数据的特点和研究目的。
二、假设你是一家电子产品公司的数据分析师,你希望通过回归分析来预测一种新产品的销售量。
你收集到了以下数据:对于n个销售点,你记录了它们的广告费用(X)、竞争对手的广告费用(Z)以及销售量(Y)。
你希望建立一个回归模型来预测销售量。
假设回归模型的形式为:Y = β0 + β1X + β2Z + ε其中,Y是销售量,X是该公司的广告费用,Z是竞争对手的广告费用,ε是误差项。
然而,你发现误差项的方差与广告费用的大小有关,即存在异方差性。
你决定使用广义最小二乘法来估计模型参数。

最小二乘法求解线性回归问题最小二乘法是回归分析中常用的一种模型估计方法。
它通过最小化样本数据与模型预测值之间的误差平方和来拟合出一个线性模型,解决了线性回归中的参数估计问题。
在本文中,我将详细介绍最小二乘法在线性回归问题中的应用。
一、线性回归模型在介绍最小二乘法之前,先了解一下线性回归模型的基本形式。
假设我们有一个包含$n$个观测值的数据集$(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)$,其中$x_i$表示自变量,$y_i$表示因变量。
线性回归模型的一般形式如下:$$y=\beta_0+\beta_1 x_1+\beta_2 x_2+\dots+\beta_px_p+\epsilon$$其中,$\beta_0$表示截距,$\beta_1,\beta_2,\dots,\beta_p$表示自变量$x_1,x_2,\dots,x_p$的系数,$\epsilon$表示误差项。
我们希望通过数据集中的观测值拟合出一个线性模型,即确定$\beta_0,\beta_1,\dots,\beta_p$这些未知参数的值,使得模型对未知数据的预测误差最小化。
二、最小二乘法的思想最小二乘法是一种模型拟合的优化方法,其基本思想是通过最小化优化问题的目标函数来确定模型参数的值。
在线性回归问题中,我们通常采用最小化残差平方和的方式来拟合出一个符合数据集的线性模型。
残差代表观测值与模型估计值之间的差异。
假设我们有一个数据集$(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)$,并且已经选定了线性模型$y=\beta_0+\beta_1 x_1+\beta_2 x_2+\dots+\beta_p x_p$。
我们希望选择一组系数$\beta_0,\beta_1,\dots,\beta_p$,使得模型对数据集中的观测值的预测误差最小,即最小化残差平方和(RSS):$$RSS=\sum_{i=1}^n(y_i-\hat{y}_i)^2$$其中,$y_i$表示第$i$个观测值的实际值,$\hat{y}_i$表示该观测值在当前模型下的预测值。
最小二乘法公式求线性回归方程最小二乘法是一种估计统计模型参数的常用方法,它是统计学领域中普遍使用的线性回归模型,回归模型指根据一个或多个自变量,研究它们对一个因变量的影响,从而建立变量之间的函数模型从而预测因变量的方法.最小二乘法可以用来快速求解线性回归问题.一、定义:最小二乘法(Least Squares Method, LSM)是统计学上用来估计未知参数的一种方法。
它通过最小化误差平方和来拟合模型参数,可以说是最经常用来求解回归方程的算法。
该算法由拉格朗日在18月1日提出,被广泛应用在统计学的各个领域.二、求解线性回归方程的原理:最小二乘法求解线性回归问题的思路是利用“损失函数”也就是误差平方和来求解。
《数学模型简明介绍》一书中提出了极小化损失函数这个思想。
它提出,在实际应用中,经常会把一组数学统计量来描述一组现象,并建立关系模型,用《数学模型简明介绍》中下文中所述的最小二乘法(LSM)模型来说,它的基本思想就是把待求的参数的残差(即模型和真实值之间的误差)平方和最小化,它就是最小二乘回归模型的标准假设函数了。
三、求解线性回归方程的步骤:1、通过数据样本建立数学模型,即y=ax+b;2、使得残差平方和最小,用下面的公式来求点X1到Xn这些点到线所有残差平方和,即:Σr^2=Σ(y-ax-b)^2;;3、得到残差平方和的偏导为零,求解得到结果,最小二乘法估计出的结果得到的系数a和b具有最小的残差平方和,即最小的均方根误差:a=Σ(x-x_平均数)(y-y_平均数)/Σ(x-x_平均数)^2;b=y_平均数-ax_平均数;四、求解线性回归方程的应用:1、最小二乘法可以用来拟合任意数据点及求解线性回归方程;2、可用于计算常见指标如样本均值,样本方差,协方差等统计特征以及诊断判断正确性;3、可用于数据预测;4、最小二乘法为回归分析提供了基础,研究多元回归模型,最小二乘法解析解也就能被推广到多元回归分析中;5、它可以用来估计广义线性模型(generalized linear model)的参数;6、最小二乘法能对线性不可分数据进行二分类判断;7、它可以用来提高决策树算法的准确性;8、最小二乘法可以用来求最优解,优化问题,最小投资成本,最优生产调度,最短路径。
两阶段最小二乘法和广义矩估计法标题:从最小二乘法到广义矩估计法:深度解析两阶段最小二乘法和广义矩估计法引言:在统计建模和数据分析中,两阶段最小二乘法和广义矩估计法是常用的方法,用于处理数据中的噪声和误差。
本文将重点探讨这两种方法的原理、应用场景以及它们在统计学中的作用。
第一部分:最小二乘法1.1 介绍两阶段最小二乘法1.1.1 定义和基本原理1.1.2 两阶段最小二乘法的主要步骤1.2 两阶段最小二乘法的应用举例1.2.1 线性回归分析案例1.2.2 时间序列分析案例第二部分:广义矩估计法2.1 广义矩估计法的概念和基本原理2.1.1 广义矩估计法的基本思想2.1.2 广义矩估计法与最小二乘法的区别2.2 广义矩估计法的应用举例2.2.1 概率分布拟合案例2.2.2 非线性回归分析案例第三部分:两阶段最小二乘法与广义矩估计法的比较3.1 相似之处3.1.1 基于样本的估计方法3.1.2 都可以用于参数估计和模型拟合3.2 不同之处3.2.1 理论基础和假设前提3.2.2 算法步骤和计算复杂度结论:两阶段最小二乘法和广义矩估计法都是常用的参数估计方法,但在理论假设和计算步骤上存在一些差异。
两阶段最小二乘法适用于线性模型和数据点较多的情况,广义矩估计法则更加灵活,并适用于非线性模型和无需特定分布假设的情况。
在实际应用中,根据具体问题和数据特征,我们可以选择合适的方法来进行参数估计和模型拟合。
个人观点:作为数据分析领域中不可或缺的方法之一,两阶段最小二乘法和广义矩估计法在实践中发挥了重要作用。
我认为,这两种方法的选择应该根据问题的特点和数据的性质进行。
在实际工作中,我们需要深入理解这些方法的原理和适用范围,以便能够灵活应用和合理解释结果。
参考文献:[1] Smith, M. A. et al. (1992). "Two-Stage Least Squares and Generalized Methods of Moments". Journal of Economic Perspectives, 6(2), 187-198.[2] Chamberlain, G. (1987). "Asymptotic efficiency in estimation with conditional moment restrictions". Journal of Econometrics, 34(3), 305-334.注意:以上是一个关于两阶段最小二乘法和广义矩估计法的示范文章,实际情况中可能需要更多针对指定主题的内容和细节。
估计回归系数的最小二乘法原理一、引言最小二乘法是一种常用的回归分析方法,用于估计自变量和因变量之间的关系。
在实际应用中,我们通常需要通过样本数据来估计回归系数,以便预测未知的因变量值。
本文将介绍最小二乘法原理及其应用。
二、最小二乘法原理最小二乘法是一种寻找最优解的方法,在回归分析中,它被用来寻找使预测值和实际值之间误差平方和最小的回归系数。
具体地说,我们假设有n个样本数据,每个样本数据包含一个自变量x和一个因变量y。
我们希望找到一个线性模型y = β0 + β1x + ε,其中β0和β1是待估参数,ε是误差项。
我们可以通过求解下面的最小化目标函数来得到β0和β1:min Σ(yi - β0 - β1xi)^2这个目标函数表示所有样本数据预测值与实际值之间误差平方和的总和。
我们希望找到一个β0和β1的组合,使得这个总和尽可能地小。
三、最小二乘法求解为了求解上述目标函数的最优解,我们需要对其进行微积分,并令其导数等于0。
具体地说,我们需要求解下面的两个方程组:Σyi = nβ0 + β1ΣxiΣxiyi = β0Σxi + β1Σ(xi)^2这两个方程组分别表示回归线的截距和斜率的估计值。
通过解这两个方程组,我们可以得到最小二乘法的估计结果。
四、最小二乘法的应用最小二乘法在实际应用中非常广泛,尤其是在经济学、统计学和金融学等领域。
例如,在股票市场上,我们可以使用最小二乘法来预测股票价格的变化趋势。
在医学研究中,我们可以使用最小二乘法来确定药物剂量与治疗效果之间的关系。
五、总结最小二乘法是一种常用的回归分析方法,它通过寻找使预测值和实际值之间误差平方和最小的回归系数来估计自变量和因变量之间的关系。
在实际应用中,我们可以使用最小二乘法来预测未知的因变量值,并确定自变量和因变量之间的关系。
gls广义最小二乘法模型广义最小二乘法(GLS)模型是一种基于回归分析的方法,通常用于建立变量之间的线性关系模型。
该模型假设变量之间存在线性关系,并通过最小化残差平方和来估计模型参数。
通常,GLS模型中的变量可以是定量变量,也可以是分类变量。
GLS模型的基本思想是对数据进行加权,并将加权后的数据用于回归分析。
加权的目的是根据数据的精确程度调整每个观测值的贡献,这样更准确地估计模型参数。
在GLS中,加权方法通常是通过协方差矩阵来完成的。
协方差矩阵是一个描述随机向量之间协方差关系的矩阵。
在GLS模型中,协方差矩阵使用来表示数据中每个变量之间的关系。
协方差矩阵可以考虑观测值的误差结构和误差的家族分布。
通常,GLS根据数据的特性来选择协方差矩阵。
在GLS模型中,可以使用不同的协方差矩阵来估计参数。
常见的协方差矩阵有以下几种类型:1.同方差协方差矩阵。
这种协方差矩阵假设观测值的误差具有相同的方差,通常用于数据具有相同误差结构的情况。
2.数值型协方差矩阵。
这种协方差矩阵假定观测值的误差与观测值的数值有关,通常用于数据包含噪声和测量误差的情况。
3.时间序列协方差矩阵。
这种协方差矩阵假设时间间隔对观测值的误差有影响,通常用于数据是时间序列的情况。
4.分层协方差矩阵。
这种协方差矩阵假设数据具有多个层次结构,通常用于多层次数据的情况。
GLS模型在估计参数时,考虑了数据之间的协方差结构,因此可以更准确地估计参数。
此外,GLS还可以处理不同数据类型和误差结构的数据。
例如,GLS可以适用于含有分类变量的数据,这些变量不能用于普通的最小二乘法。
总之,GLS是一种强大的回归分析方法,可以更准确地估计模型参数。
它可以适用于不同类型和误差结构的数据,并且可以通过使用不同的协方差矩阵来适应数据。
由于其广泛的应用领域,GLS已成为许多领域中主要的数据分析方法之一。