大学物理作业7参考答案
- 格式:ppt
- 大小:576.50 KB
- 文档页数:19

©物理系_2015_09《大学物理CII》作业No.7 热力学第二定律班级________ 学号________ 姓名_________ 成绩_______一、判断题:(用“T”和“F”表示)[ F ] 1.在任意的绝热过程中,只要系统与外界之间没有热量传递,系统的温度就不会发生变化。
此说法不对.在绝热过程中,系统与外界无热量交换,Q=0.但不一定系统与外界无作功,只要系统与外界之间有作功的表现,由热力学第一定律Q=E+W,可知,E=-W,即对应有内能的改变.而由E=νC,T可知,有E,一定有T,即有温度的变化.[ F ] 2.在循坏过程中系统对外做的净功在数值上等于p-V图中封闭曲线所包围的面积,因此封闭曲线包围的面积越大,循坏效率就越高。
有人说,因为在循环过程中系统对外做的净功在数值等于p-V图中封闭曲线所包围的面积,所以封闭曲线所包围的面积越大,循环效率就越高,对吗?答:不正确,因为循环效率取决于系统对外做的净功和系统由高温热源吸收的热量,只有在从高温热源吸收的热量一定的情况下,封闭曲线所包围的面积越大,即系统对外所做的净功越多,循环效率越高,如果从高温热源吸收的热量不确定,则循环效率不一定越高[ F ] 3.系统经历一正循坏后,系统与外界都没有变化。
系统经历一正循环后,系统的状态没有变化;(2)系统经历一正循环后,系统与外界都没有变化;(3)系统经历一正循环后,接着再经历一逆循环,系统与外界亦均无变化。
解说法(1)正确,系统经历一正循环后,描述系统状态的内能是单值函数,其内能不变,系统的状态没有变化。
说法(2)错误,系统经过一正循环,系统内能不变,它从外界吸收热量,对外作功,由热力学第二定律知,必定要引起外界的变化。
说法(3)错误,在正逆过程中所引起外界的变化是不能消除的。
[ F ] 4.第二类永动机不可能制成是因为违背了能量守恒定律。
解:第二类永动机并不违背能量守恒定律,但它违背了热力学第二定律。


7大学物理习题及综合练习答案详解-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN库仑定律7-1 把总电荷电量为Q 的同一种电荷分成两部分,一部分均匀分布在地球上,另一部分均匀分布在月球上,使它们之间的库仑力正好抵消万有引力,已知地球的质量M =5.98l024kg ,月球的质量m =7.34l022kg 。
(1)求 Q 的最小值;(2)如果电荷分配与质量成正比,求Q 的值。
解:(1)设Q 分成q 1、q 2两部分,根据题意有 2221rMmG r q q k=,其中041πε=k 即 2221q k q GMm q q Q +=+=。
求极值,令0'=Q ,得 0122=-kq GMmC 1069.5132⨯==∴k GMm q ,C 1069.51321⨯==k q GMm q ,C 1014.11421⨯=+=q q Q (2)21q m q M =,k GMm q q =21 kGMm m q mq Mq ==∴2122 解得C 1032.61222⨯==kGm q , C 1015.51421⨯==m Mq q ,C 1021.51421⨯=+=∴q q Q 7-2 三个电量为 –q 的点电荷各放在边长为 l 的等边三角形的三个顶点上,电荷Q (Q >0)放在三角形的重心上。
为使每个负电荷受力为零,Q 值应为多大?解:Q 到顶点的距离为 l r 33=,Q 与-q 的相互吸引力为 20141rqQ F πε=, 两个-q 间的相互排斥力为 220241l q F πε=据题意有 10230cos 2F F =,即 2022041300cos 412rqQl q πεπε=⨯,解得:q Q 33= 电场强度7-3 如图7-3所示,有一长l 的带电细杆。
(1)电荷均匀分布,线密度为+λ,则杆上距原点x 处的线元d x 对P 点的点电荷q 0 的电场力为何?q 0受的总电场力为何(2)若电荷线密度λ=kx ,k 为正常数,求P 点的电场强度。


⼤学物理学(课后答案)第7章第七章课后习题解答、选择题7-1处于平衡状态的⼀瓶氦⽓和⼀瓶氮⽓的分⼦数密度相同,分⼦的平均平动动能也相同,则它们[](A) 温度,压强均不相同(B)温度相同,但氦⽓压强⼤于氮⽓的压强(C)温度,压强都相同(D)温度相同,但氦⽓压强⼩于氮⽓的压强3分析:理想⽓体分⼦的平均平动动能τk= kT,仅与温度有关,因此当氦⽓和氮2⽓的平均平动动能相同时,温度也相同。
⼜由理想⽓体的压强公式p =nkT ,当两者分⼦数密度相同时,它们压强也相同。
故选( C)O7-2理想⽓体处于平衡状态,设温度为T,⽓体分⼦的⾃由度为i ,则每个⽓体分⼦所具有的[](A)动能为-kT (B)动能为丄RT2 2(C)平均动能为^kT (D)平均平动动能为^RT分析:由理想⽓体分⼦的的平均平动动能3 kT和理想⽓体分⼦的的平均动能2T⼆丄kT ,故选择(C)O27-3三个容器A、B、C中装有同种理想⽓体,其分⼦数密度n相同,⽽⽅均根1/2 1/2 1/2速率之⽐为V A : V B : V C 1:2:4 ,则其压强之⽐为P A : P B : P C[](A) 1:2:4 (B) 1:4:8 (C) 1 : 4 : 16 (D) 4:2:1分析:由分⼦⽅均根速率公式= J3RT,⼜由物态⽅程p = nkT ,所以当三容器中得分⼦数密度相同时,得p1: P2: P3 =T1 :T2 :T3 =1:4:16 O故选择(C)O7-4图7-4中两条曲线分别表⽰在相同温度下氧⽓和氢⽓分⼦的速率分布曲线。
如果(VP O和(V P 分别表⽰氧⽓和氢⽓的最概然速率,则[](A)图中a表⽰氧⽓分⼦的速率分布曲线且V P O z V P H= 4(B) 图中a表⽰氧⽓分⼦的速率分布曲线且V P O/ V P H? =1/4(C) 图中b表⽰氧⽓分⼦的速率分布曲线且V P O / V P H=1/4(D) 图中b表⽰氧⽓分⼦的速率分布曲线且V P O/ V P H2 =4分析:在温度相同的情况下,由最概然速率公式'..P=I j2RT及氢⽓与氧⽓的摩尔质量M H2£M o2,可知氢⽓的最概然速率⼤于氧⽓的最概然速率,故曲线a对应于氧分⼦的速率分布曲线。

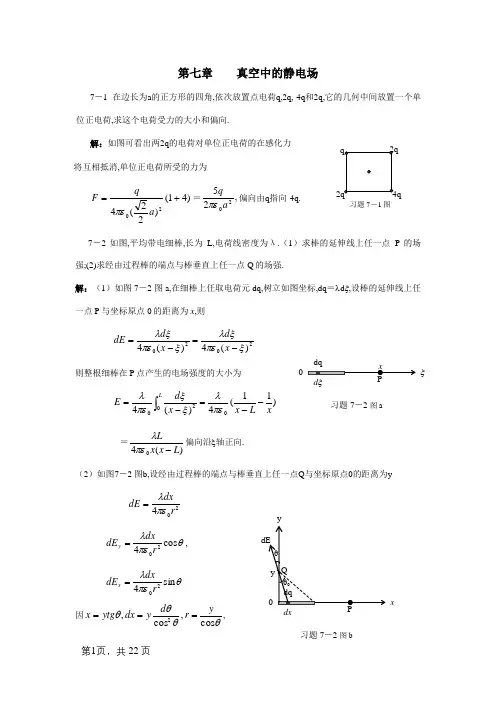
第七章 真空中的静电场7-1 在边长为a 的正方形的四角,依次放置点电荷q,2q,-4q 和2q,它的几何中间放置一个单位正电荷,求这个电荷受力的大小和偏向.解:如图可看出两2q 的电荷对单位正电荷的在感化力 将互相抵消,单位正电荷所受的力为)41()22(420+=a q F πε=,2520a qπε偏向由q 指向-4q.7-2 如图,平均带电细棒,长为L,电荷线密度为λ.(1)求棒的延伸线上任一点P 的场强;(2)求经由过程棒的端点与棒垂直上任一点Q 的场强.解:(1)如图7-2 图a,在细棒上任取电荷元dq,树立如图坐标,dq =λd ξ,设棒的延伸线上任一点P 与坐标原点0的距离为x ,则2020)(4)(4ξπεξλξπεξλ-=-=x d x d dE则整根细棒在P 点产生的电场强度的大小为 )11(4)(40020xL x x d E L--=-=⎰πελξξπελ=)(40L x x L-πελ偏向沿ξ轴正向.(2)如图7-2 图b,设经由过程棒的端点与棒垂直上任一点Q 与坐标原点0的距离为y204r dxdE πελ=θπελcos 420rdxdE y =, θπελsin 420r dxdE x =因θθθθcos ,cos ,2yr d ydx ytg x ===,习题7-1图dqξd ξ习题7-2 图axdx习题7-2 图by代入上式,则)cos 1(400θπελ--=y =)11(4220Ly y+--πελ,偏向沿x 轴负向.θθπελθd ydE E y y ⎰⎰==000cos 4 00sin 4θπελy ==2204Ly y L+πελ7-3 一细棒弯成半径为R 的半圆形,平均散布有电荷q,求半圆中间O 处的场强. 解:如图,在半环上任取d l =Rd θ的线元,其上所带的电荷为dq=λRd θ.对称剖析E y =0.θπεθλsin 420R Rd dE x =⎰⎰==πθπελ0sin 4R dE E xR02πελ= 2022R q επ=,如图,偏向沿x 轴正向.7-4 如图线电荷密度为λ1的无穷长平均带电直线与另一长度为l .线电荷密度为λ2的平均带电直线在统一平面内,二者互相垂直,求它们间的互相感化力.解:在λ2的带电线上任取一dq,λ1的带电线是无穷长,它在dq 处产生的电场强度由高斯定理轻易得到为,xE 012πελ=两线间的互相感化力为θθπελθd y dE E x x ⎰⎰-=-=0sin4x习题7-3图λ1 习题7-4图⎰⎰==x dx dF F 0212πελλ⎰=la x dx 0212πελλ,ln 2021ala +πελλ如图,偏向沿x 轴正向. 7-5 两个点电荷所带电荷之和为Q,问它们各带电荷若干时,互相感化力最大? 解:设个中一个电荷的带电量是q,另一个即为Q -q,若它们间的距离为r,它们间的互相感化力为204)(rq Q q F πε-=互相感化力最大的前提为04220=-=r qQ dq dF πε 由上式可得:Q=2q,q=Q/27-6 一半径为R 的半球壳,平均带有电荷,电荷面密度为σ,求球心处电场强度的大小. 解:将半球壳细割为诸多细环带,其上带电量为θθπσθπσd R rRd dq sin 222==dq 在o 点产生的电场据(7-10)式为304R ydqdE πε=,θcos R y =θθπεθπσπd R R dE E cos 4sin 200303⎰⎰==)(sin sin 200θθεσπd ⎰=20202sin 2πθεσ=4εσ=.如图,偏向沿y 轴负向. 7-7 设匀强电场的电场强度E 与半径为R 的半球面临称轴平行,盘算经由过程此半球面电场强度的通量.习题7-6图成为闭合曲面高斯,对此高斯曲面电通量为0, 即021=⋅+⋅=⋅⎰⎰⎰S S SS d E S d E S d E2211R E S d E S d E S S S π-=⋅-=⋅=ψ⎰⎰7-8 求半径为R,带电量为q 的空心球面的电场强度散布.解: 因为电荷散布具有球对称性,因而它所产生的电场散布也具有球对称性,与带电球面齐心的球面上各点的场强E 的大小相等,偏向沿径向.在带电球内部与外部区域分离作与带电球面齐心的高斯球面S 1与S 2.对S 1与S 2,运用高斯定理,即先盘算场强的通量,然后得出场强的散布,分离为04d 21==⋅=⎰r E S πψS E得 0=内E (r<R )24d 2επψqr E S ==⋅=⎰S Errˆ204q πε=外E (r>R) 7-9 如图所示,厚度为d 的“无穷大”平均带电平板,体电荷密度为ρ,求板表里的电场散布.解:带电平板平均带电,在厚度为d/2的等分街面上电场强度为零,取坐标原点在此街面上,树立如图坐标.对底面积为A,高度分离为x <d/2和x >d/2的高斯曲面运用高斯定理,有d ρψAxEA ==⋅=⎰S E r习题7-18图2d 2ερψd A EA S ==⋅=⎰S E)2( 202d x i d E > ερ=7-10 一半径为R 的无穷长带电圆柱,其体电荷密度为)(0R r r ≤=ρρ,ρ0为常数.求场强散布.解: 据高斯定理有⎰⎰==⋅VSdV rl E S d E ρεπ012R r ≤时:⎰'''=rr ld r r krl E 022πεπ⎰''=rr d r lk202επ=rl E π23230r lk επn e kr E 023ε=→R r >时:⎰'''=Rr ld r r krl E 022πεπ⎰''=Rr d r lk202επ=rl E π23230R lk επn e rkR E 033ε=→7-11 带电为q.半径为R 1的导体球,其外齐心肠放一金属球壳,球壳内.外半径为R 2.R 3. (1)球壳的电荷及电势散布;(2)把外球接地后再绝缘,求外球壳的电荷及球壳表里电势散布; (3)再把内球接地,求内球的电荷及外球壳的电势. 解:(1)静电均衡,球壳内概况带-q,外概况带q 电荷. 据(7-23)式的结论得:),)(111(4132101R r R R R q V ≤+-=πε );)(111(212R r R qV ≤≤+-=习题7-10图r),(432303R r R R q V ≤≤=πε).(4304R r rq V ≥=πε (2)),)(11(412101R r R R q U ≤-=πε );)(11(421202R r R R r qV ≤≤-=πε),(0323R r R V ≤≤=).(034R r V >>= (3)再把内球接地,内球的电荷及外球壳的电荷从新散布设静电均衡,内球带q /,球壳内概况带-q /,外概况带q /-q.),)((41132101R r R q q R q R q V ≤-'+'-'=πε 得:21313221R R R R R R qR R q +-='=-'=3034R qq V πε)(4)(213132021R R R R R R q R R +--πε)(32R r R ≤≤ 7-12 一平均.半径为R 的带电球体中,消失一个球形空腔,空腔的半径r(2r<R),试证实球形空腔中随意率性点的电场强度为匀强电场,其偏向沿带电球体球心O 指向球形空腔球心O /. 证实:运用补缺法,此空腔可视为同电荷密度的一个完全的半径为R 的大球和一个半径为r 与大球电荷密度异号完全的小球构成,两球在腔内随意率性点P 产生的电场分离据〔例7-7〕成果为03ερ11r E =, 03ερ22r E -= E =E 1+E 2=03ερ1r 03ερ2r - o o '=3ερ上式是恒矢量,得证.习题7-12图7-13 一平均带电的平面圆环,内.外半径分离为R 1.R 2,且电荷面密度为σ.一质子被加快器加快后,自圆环轴线上的P 点沿轴线射向圆心O.若质子到达O 点时的速度正好为零,试求质子位于P 点时的动能E K .(已知质子的带电量为e,疏忽重力的影响,OP=L )解:圆环中间的电势为⎰=210042R R r rdr V πεπσ )(2120R R -=εσ圆环轴线上p 点的电势为⎰+=2122042R R P Lr rdrV πεπσ)(22221222022021L R L R L r R R +-+=+=εσεσ质子到达O 点时的速度正好为零有k P E E E +=0p k E E E -=→0 p k eV eV E -=0=210()2e R R σε=-02e σε-210(2e R R σε=- 7-14 有一半径为R 的带电球面,带电量为Q,球面外沿直径偏向上放置一平均带电细线,线电荷密度为λ,长度为L (L>R ),细线近端离球心的距离为L.设球和细线上的电荷散布固定,试求细线在电场中的电势能.解:在带电细线中任取一长度为dr 的线元,其上所带的电荷元为dq=λdr,据(7-23)式带电球面在电荷元处产生的电势为rQ V 04πε=电荷元的电势能为: rdrQ dW 04πελ=细线在带电球面的电场中的电势能为:习题7-13图r习题7-14图===⎰⎰LLr dr Q dW W 204πελ2ln 40πελQ*7-15 半径为R 的平均带电圆盘,带电量为Q.过盘心垂直于盘面的轴线上一点P 到盘心的距离为L.试求P 点的电势并运用电场强度与电势的梯度关系求电场强度.解:P 到盘心的距离为L,p 点的电势为⎰+=RP Lr rdrV 022042πεπσ)(222220220L L R L r R -+=+=εσεσ 圆盘轴线上随意率性点的电势为⎰+=Rxr rdrx V 022042)(πεπσ)(22222200220x x R RQ x r R -+=+=πεεσ运用电场强度与电势的梯度关系得:i x R xR Q i dx dV x E)1(2)(22220+-=-=πε P 到盘心的距离为L,p 点的电场强度为:i L R LR Q L E)1(2)(22220+-=πε7-16 两个齐心球面的半径分离为R 1和R 2,各自带有电荷Q 1和Q 2.求:(1)各区城电势散布,并画出散布曲线;(2)两球面间的电势差为若干?解:(1)据(7-23)式的结论得各区城电势散布为),( )(411221101R r R Q R Q V ≤+=πε );( )1(41212102R r R R r Q V ≤≤+=πε ).( 420213R r rQ Q V ≥+=πε(2)两球面间的电势差为p习题7-15图习题7-16图==⎰dr rQ V R R 21201124πε )11(42101R R Q -πε 7-17 一半径为R 的无穷长带电圆柱,其内部的电荷平均散布,电荷体密度为ρ,若取棒概况为零电势,求空间电势散布并画出电势散布曲线. 解: 据高斯定理有R r ≤时:22ερππl r rl E S d E S==⋅⎰ n e r E 02ερ=→ R r =时,V=0,则 R r ≤时:⎰=R r rdr V 02ερ)(4220r R -=ερR r >时:022ερππlR rl E S d E S==⋅⎰ n e r R E 022ερ=→ ⎰=Rrr dr R V 022ερrR R ln 202ερ= 空间电势散布并画出电势散布曲线大致如图.7-18 两根很长的同轴圆柱面半径分离为R 1.R 2,带有等量异号的电荷,两者的电势差为U,求:(1)圆柱面单位长度带有若干电荷?(2)两圆柱面之间的电场强度.解:设圆柱面单位长度带电量为λ,则两圆柱面之间的电场强度大小为E λ=习题7-10图r由上式可得:120ln 2R R U=πελ 所以n e r E 02πελ=)( ln 2112R r R e rR R Un <<⋅= 7-19 在一次典范的闪电中,两个放电点间的电势差约为109V,被迁徙的电荷约为 30库仑,假如释放出来的能量都用来使00C 的冰熔化成00C 的水,则可熔化若干冰?(冰的熔 ×105J ﹒kg -1)解:两个放电点间的电势差约为109V,被迁徙的电荷约为30库仑,其电势能为J W p 91030⨯=上式释放出来的能量可熔化冰的质量为:=⨯⨯=∆591034.31030m ×104kg 7-20 在玻尔的氢原子模子中,电子沿半径为a 的玻尔轨道上绕原子核作圆周活动.(1)若把电子从原子中拉出来须要战胜电场力作若干功?(2)电子在玻尔轨道上活动的总能量为若干?解:电子沿半径为a 的玻尔轨道上绕原子核作圆周活动,其电势能为aeeW p 04πε-=(1)把电子从原子中拉出来须要战胜电场力作功为:ae W W p 024πε=-=外(2)电子在玻尔轨道上活动的总能量为:k p E W W +=221mv W p += →a v m a e 22024=πε 2mv ae 024πε=221mv E k =∴ae 028πε=电子的总能量为:221mv W W p +=a e 024πε-=a e 028πε+ae 028πε-=第八章 静电场中的导体与电介质8-1 点电荷+q 处在导体球壳的中间,壳的表里半径分离为R l 和R 2,试求,电场强度和电势的散布.解:静电均衡时,球壳的内球面带-q.外球壳带q 电荷 在r<R 1的区域内rr q ˆ4E 201πε=,)111(42101R R r qU +-=πε 在R 1<r<R 2的区域内,02=E .,4202R q U πε=在r>R 2的区域内:.ˆ4E 203r r πεq=.403rq U πε= 8-2 把一厚度为d 的无穷大金属板置于电场强度为E 0的匀强电场中,E 0与板面垂直,试求金属板两概况的电荷面密度.解:静电均衡时,金属板内的电场为0,金属板概况上电荷面密度与紧邻处的电场成正比 所以有,001E εσ-=.002E εσ=8-3 一无穷长圆柱形导体,半径为a ,单位长度带有电荷量λ1,其外有一共轴的无穷长导体圆简,表里半径分离为b 和c,单位长度带有电荷量λ2,求(1)圆筒表里概况上每单位长度的电荷量;(2)求电场强度的散布.解:(1)由静电均衡前提,圆筒表里概况上每单位长度的电荷量为;,21λλλ+-(2)在r<a 的区域内:E=0R 2R 1习题 8-1图q-q qE 0E 0习题 8-2图σ1 σ2在a<rb 的区域内:E r012πελ=e n在r>b 的区域内:E r0212πελλ+=e n8-4 三个平行金属板A.B 和C,面积都是200cm 2,A.B 相距,A.C 相距,B.C 两板都接地,如图所示.假如A 板带正电×10-7C,略去边沿效应(1)求B 板和C 板上感应电荷各为若干?(2)以地为电势零点,求A 板的电势.解:(1)设A 板两侧的电荷为q 1.q 2,由电荷守恒 道理和静电均衡前提,有A q q q =+21(1) 1q qB -=,2q qC -=(2)依题意V AB =V AC ,即101d S q ε=202d Sq ε112122q q d dq ==→代入(1)(2)式得 q 1=×10-7C,q 2×10-7C,q B ×10-7C,q C =-q 2×10-7C,(2)101d S q U A ε==202d S q ε==⨯⨯⨯⨯⨯⨯----312471021085810200102.×103V 8-5 半径为R 1=l.0cm 的导体球带电量为×10-10C ,球外有一个表里半径分离为R 2=和R 3=的齐心导体球壳,壳带有电量Q=11×10-10C ,如图所示,求(1)两球的电势;(2)用导线将两球衔接起来时两球的电势;(3)外球接地时,两球电势各为若干?(以地为电势零点)解:静电均衡时,球壳的内球面带-q.外球壳带q+Q 电荷 (1))(4132101R Qq R q R q U ++-=πε代入数据 )41113111(101085.814.34100.1212101++-⨯⨯⨯⨯⨯=---UA BC习题 8-4图d 1d 2q+Q=×102V2024R Qq U πε+=4)111(101085.814.34100.121210+⨯⨯⨯⨯⨯=---=×102V(2)用导线将两球衔接起来时两球的电势为2024R Q q U πε+=4)111(101085.814.34100.121210+⨯⨯⨯⨯⨯=---=×102V (3)外球接地时,两球电势各为)(412101R q R q U -=πε)3111(101085.814.34100.1212101-⨯⨯⨯⨯⨯=---U =60V 02=U8-6 证实:两平行放置的无穷大带电的平行平面金属板A 和B 相向的两面上电荷面密度大小相等,符号相反,相背的两面上电荷面密度大小等,符号雷同.假如两金属板的面积同为100cm 2,带电量分离为Q A =6×10-8 C 和Q B =4×10-8C,略去边沿效应,求两个板的四个概况上的电面密度.证:设A 板带电量为Q A .两侧的电荷为q 1.q 2, B 板板带电量为Q B.两侧的电荷为q 3.q 4.由电荷守恒有A Q q q =+21(1)B Q q q =+43(2)在A 板与B 板内部取两场点,金属板内部的电场为零有020122εεS q S q -0220403=--εεS qS q ,得04321=---q q q q (3) 020122εεS q S q +0220403=-+εεS qS q ,得04321=-++q q q q (4) 联立上面4个方程得:241B A Q Q q q +==,232BA Q Q q q -=-= 即相向的两面上电荷面密度大小相等,符号相反,相背的两面上电荷面密度大小等,符号2习题 8-6图q 1 q 4雷同,本题得证.假如两金属板的面积同为100cm 2,带电量分离为Q A =6×10-8 C 和Q B =4×10-8C,则=⨯⨯⨯+==--844110101002)46(σσ×10-6C/m 2, =⨯⨯⨯-=-=--843210101002)46(σσ×10-6C/m 2 8-7 半径为R 的金属球离地面很远,并用细导线与地相联,在与球心相距离为D=3R 处有一点电荷+q,试求金属球上的感应电荷.解:设金属球上的感应电荷为Q,金属球接地 电势为零,即04400=+DQ Rq πεπε3Rq q Q D =-=-8-8 一平行板电容器,南北极板为雷同的矩形,宽为a,长为b,间距为d,今将一厚度为t .宽度为a 的金属板平行地向电容器内拔出,略去边沿效应,求拔出金属板后的电容量与金属板拔出深度x 的关系.解:设如图左边电容为C 1,右边电容为C 2d x b a C )(01-=εtd ax C -=02ε阁下电容并联,总电容即金属板后的电容量与金属板拔出深度x 的关系,为d x b a C C C )(021-=+=εtd ax-+0ε=)(0td txb d a -+ε 8-9 收音机里的可变电容器如图(a )所示,个中共有n 块金属片,相邻两片的距离均为d,奇数片联在一路固定不动(叫定片)偶数片联在起而可一同迁移转变(叫动片)每片的外形如图(b )所示.求当动片转到使两组片重叠部分的角度为θ时,电容器的电容.解:当动片转到使两组片重叠部分的角度t习题 8-8图为θ时,电容器的电容的有用面积为1802)(2122⨯-=θπr r S 360)(2122θπr r -=此构造相当有n-1的电容并联,总电容为dS n C 0)1(ε-==d r r n 360)()1(21220--θπε8-10 半径都为a 的两根平行长直导线相距为d (d>>a ),(1)设两直导线每单位长度上分离带电十λ和一λ求两直导线的电势差;(2)求此导线组每单位长度的电容.解:(1)两直导线的电电场强度大小为rE 022πελ⨯= 两直导线之间的电势差为⎰=r dr V 0πελ⎰-=ad ar dr 0πελaa d -=ln 0πελ (2)求此导线组每单位长度的电容为VC λ==aa d -ln0πε8-11 如图,C 1=10μF,C 2=5μF,C 3=5μF,求(1)AB 间的电容;(2)在AB 间加上100V 电压时,求每个电容器上的电荷量和电压;(3)假如C 1被击穿,问C 3上的电荷量和电压各是若干?解:(1)AB 间的电容为20155)(321213⨯=+++=C C C C C C C =μF;(2)在AB 间加上100V 电压时,电路中的总电量就是C 3电容器上的电荷量,为C CV q q 4631073.31001073.3--⨯=⨯⨯===C C q 10151073.3642121⨯⨯=+=--(a)(b)习题 8-9图AC 1C 2 oV V 75251003=-=C V C q 46111105.2251010--⨯=⨯⨯== C V C q 462221025.125105--⨯=⨯⨯==(3)假如C 1被击穿,C 2短路,AB 间的100V 电压全加在C 3上,即V 3=100V , C 3上的电荷量为C V C q 46333100.5100105--⨯=⨯⨯==8-12 平行板电容器,南北极间距离为l.5cm ,外加电压39kV ,若空气的击穿场强为30kV/cm ,问此时电容器是否会被击穿?现将一厚度为的玻璃拔出电容器中与两板平行,若玻璃的相对介电常数为7,击穿场强为100kV/cm ,问此时电容器是否会被击穿?成果与玻璃片的地位有无关系?解:(1)未加玻璃前,南北极间的电场为cm kV cm kV E /30/265.139<==不会击穿(2)加玻璃后,南北极间的电压为3973.02.1=+EE cm kV cm kV E /30/31>=→ 空气部分会击穿,此后,玻璃中的电场为cm kV cm kV E /100/1303.039>==,玻璃部分也被击穿.成果与玻璃片的地位无关. 8-13 一平行板电容器极板面积为S ,两板间距离为d,其间充以相对介电常数分离为εr1.εr2,的两种平均电介质,每种介质各占一半体积,如图所示.若疏忽边沿效应,求此电容器的电容.解:设如图左边电容为C 1,右边电容为C 2d S C r 2/101εε= dS C r 2/202εε=阁下电容并联,总电容为V习题 8-12图习题 8-13图=+=21C C C +d S r 2/10εεdS r 2/20εε)2(210r r d S εεε+=8-14 平行板电容器南北极间充满某种介质,板间距d 为2mm,电压600V ,如武断开电源后抽出介质,则电压升高到1800V .求(1)电介质相对介电常数;(2)电介质上极化电荷面密度;(3)极化电荷产生的场强.解:设电介质抽出前后电容分离为C 与C /0022002253620050035550(1),1800,3600600(2)310/210(1) 5.3110/1800(3),910/210910/310/610/r r r r S SC C Q CU C U d d S S U V U U d d U V U V E V m d mD E E C m U VE E E E V m d mE E E V m V m V εεεεεεεσεεε---'''===='∴===='===⨯⨯∴=-=-=⨯''=+===⨯⨯'∴=-=⨯-⨯=⨯m0022002253620050035550(1),1800,3600600(2)310/210(1) 5.3110/1800(3),910/210910/310/610/r r r r S SC C Q CU C U d d S S U V U U d d U V U V E V m d mD E E C m U VE E E E V m d mE E E V m V m V εεεεεεεσεεε---'''===='∴===='===⨯⨯∴=-=-=⨯''=+===⨯⨯'∴=-=⨯-⨯=⨯m8-15 圆柱形电容器是由半径为R 1的导体圆柱和与它共轴的导体圆筒构成.圆筒的半径为R 2,电容器的长度为L,其间充满相对介电常数为εr 的电介质,设沿轴线偏向单位长度上圆柱的带电量为+λ,圆筒单位长度带电量为-λ,疏忽边沿效应.求(1)电介质中的电位移和电场强度;(2)电介质极化电荷面密度. 解:0110220122,22(1)(1),22rr r r r ds D rl lD E r r P D E P D E R R πλλλππεεελελσεσεεπεπ⋅=⋅=∴==--==-===-=⎰取同轴圆柱面为高斯面,由介质中的高斯定理可得D8-16 半径为R 的金属球被一层外半径为R /的平均电介质包裹着,设电介质的相对介电常数为εr ,金属球带电量为Q,求(1;(3)金属球的电势. 解:12122121222000012100220021(1)4,44411(2)()444(3)r r R R rr R R Q D ds D r Q D D r D D Q QE E r r Q QU E dl E dl r R R Q U E dl rU E dl E ππεεεπεεπεπεεπεπε'∞'∞'∞⋅=⋅=∴==∴=====⋅+⋅=-+''=⋅=⋅+⎰⎰⎰⎰⎰取同心高斯球面,由介质的高斯定理得介质层内的电势介质层外的电势=金属球的电势101011()44R R r Q Qdl R R R πεεπε'⋅=-+''⎰8-17 球形电容器由半径为R 1的导体球和与它齐心的导体球壳构成,球壳内半径为R 2,其间有两层平均电介质,分界面半径为r,电介质相对介电常数分离为εr1.εr2,如图所示.求(1)电容器的电容;(2)当内球带电量为+Q 时各介质概况上的约束电荷面密度. 解:习题 8-16图21221221212220102010221022011021211221221(1)4,4,441111()()444()(r r r r rR R rr r r r r r r Q D ds D r Q D D r D D Q QE E r r Q Q U E dl E dl r R R rR R r QC U R R r R R ππεεεεπεεπεεπεεπεεπεεεεεεε⋅=⋅=∴==∴====∴=⋅+⋅=-+-∴==-+-⎰⎰⎰取同心高斯球面,由介质的高斯定理得1110112211112342221222)11(1)(1),(1)44111(1),(1),(1)444r r r r r r Q Q D E R R Q Q Q r r R σεσεεππσσσεεεπππ=-=-∴=--=-=--=-8-18 一平行板电容器有两层介质(如图),εr1=4,εr2=2,厚度为d 1=,d 2=,极板面积S=40cm 2,南北极板间电压为200V .(1)求每层电介质中的能量密度;(2)盘算电容器的总能量;(3)盘算电容器的总电容.解:02112210122121122223110101122232202022020112210102121/221(1)/43350,15011() 1.110/,2211() 2.210/22(2)r r r r e r r e r r r r r r SU Q C d d S U Q C d d U V U VU E J m d U E J m d S SC C d d C S S C C d εεεεεεωεεεεωεεεεεεεεεεεε--⨯=====⨯∴==∴===⨯===⨯==++227002020*******0010212121122200 3.51022(3)2 1.7910r r r r W CU d S SC C d d C FS SC C d d εεεεεεεεεεε--=∴==⨯⨯=⨯====⨯++8-19 平板电容器的极板面积S=300cm 2南北极板相距d 1=3mm,在南北极板间有一个与地绝缘的平行金属板,其面积与极板的雷同,厚度d 1=1mm.当电容器被充电到600V 后,拆去电源,然后抽出金属板,问(1)电容器间电场强度是否变更;(2)抽出此板需作若干功?解:R 1 R 2r习题 8-17图习题 8-18图11531115322(1),600 3.010/(31)103,21.5600 3.010/3102,22SSQ CU Ud d d d U VE V m d d mSUSd d Qd UU U S d d d dU V E V m E d m Q QW W C C εεεεε--==--===⨯--⨯-''==='-'⨯'===⨯=⨯'=='00000未拆电源前,C=拆去电源并抽出金属板后,C ==C 所以电场强度没有发生变化。

第七章机械波一。
选择题1。
机械波的表示式为(SI),则(A)其振幅为3m(B)其波速为10m/s (C)其周期为1/3s (D)波沿x轴正向传播2。
一平面简谐波沿x轴正向传播,时波形图如图示,此时处质点的相位为(A) 0 (B) π(C)π/2 (D) - π/23. 频率为100Hz、波速为300m/s的简谐波,在传播方向上有两点同一时刻振动相位差为π/3,则这两点相距(A) 2m(B)21。
9m(C) 0.5m(D)28。
6m4。
一平面简谐波在介质中传播,某瞬时介质中某质元正处于平衡位置,此时它的能量为(A) 动能最大,势能为零 (B)动能为零,势能最大(C) 动能为零,势能为零(D)动能最大,势能最大5. 一平面简谐波在弹性介质中传播,下述各结论哪个是正确的?(A)介质质元的振动动能增大时,其弹性势能减小,总机械能守恒(B) 介质质元的振动动能和弹性势能做周期性变化,但二者的相位不相同(C) 介质质元的振动动能和弹性势的相位在任一时刻都相同,但二者的数值不相等(D)介质质元在其平衡位置处弹性势能最大6。
两相干波源S1、S2发出的两列波长为λ的同相位波列在P点相遇,S1到P点的距离是r1,S2到P点的距离是r2,则P点干涉极大的条件是(A)(B)(C)(D)7. 两相干波源S1和S2相距λ/4(λ为波长),S1的相位比S2的相位超前,在S1、S2连线上,S1外侧各点(例如P点)两波干涉叠加的结果是(A) 干涉极大(B) 干涉极小(C)有些点干涉极大,有些点干涉极小(D)无法确定8。
在波长为λ的驻波中,任意两个相邻波节之间的距离为(A) λ (B) 3λ/4 (C) λ/2(D)λ/4二。
填空题9。
一声波在空气中的波长是0.25m,传播速度时340m/s,当它进入另一种介质时,波长变成了0。
37m,则它在该介质中的传播速度为__________________。
10. 平面简谐波沿x轴正向传播,波动方程为,则处质点的振动方程为_________________,处质点与处质点振动的相位差为_______。

大学物理练习七答案参考一、 选择题:1. 在空间有一非均匀电场,其电力线分布如图所示。
在电场中作一半径为R 的闭合球面S ,已知通过球面上某一面元S ∆的电场强度通量为e ∆Φ,则通过该球面其余部分的电场强度通量为[ A ] (A)e ∆Φ- (B)e SSR ∆Φ∆∆-24π (C)e SR ∆Φ∆24π (D) 0通过该球面其余部分的电场强度通量=0e ∆Φ-2. 有两个点电荷电量都是+q ,相距为2 a 。
今以左边的点电荷所在处为球心,以a 为半径作一球形高斯面。
在球面上取两块相等的小面积S 1和S 2,其位置如图所示。
设通过S 1和S 2的电场强度通量分别为1Φ和2Φ,通过整个球面的电场强度通量为s Φ,则 [ D ](A)s ΦΦ>Φ,21=0/εq (B)021/2,εq s =ΦΦ<Φ (C)021/,εq s =ΦΦ=Φ (D)021/,εq s =ΦΦ<Φ解∶通过S 1的电场强度通量分别为1Φ,有穿进又有穿出; 但通过S 2的电场强度通量分别为2Φ,只有穿出. 故,21Φ<Φ据高斯定理通过整个球面的电场强度通量为s Φ只与面内电荷有关。
3.图示为一具有球对称性分布的静电场的E ~ r 关系曲线。
请指出该静电场是由下列哪种带电体产生的? [ D ](A) 半径为R 的均匀带电球面。
(B) 半径为R 的均匀带电球体。
(C) 半径为R 、电荷体密度Ar =ρ(A 为常数)的非均匀带电球体。
(D) 半径为R 、电荷体密度r A /=ρ (A 为常数)的非均匀带电球体。
204rqE i πε∑=4.在磁感应强度为B的均匀磁场中作一半径为r 的半球面S ,S 边线所在平面的法线方向单位矢量n与B 的夹角为α,则通过半球面S 的磁通量为 [ D ](A) .2B r π (B) 2.2B r π (C) απsin 2B r -. (D) απcos 2B r -.第6题图 . 第7题图5 .四条皆垂直于纸面的载流细长直导线,每条中的电流皆为I 。


习题77-1 一半径r =10 cm 的圆形回路放在B =0.8 T 的均匀磁场中,回路平面与B 垂直.当回路半径以恒定速率=80drdtcm/s 收缩时,求回路中感应电动势的大小. 解: 回路磁通 2πr B BS m ==Φ感应电动势大小40.0d d π2)π(d d d d 2====trr B r B t t m Φε V7-2 如题7-2图所示,载有电流I 的长直导线附近,放一导体半圆环MeN 与长直导线共面,且端点MN 的连线与长直导线垂直.半圆环的半径为b ,环心O 与导线相距a .设半圆环以速度v 平行导线平移.求半圆环内感应电动势的大小和方向及MN 两端的电压U M -U N .题7-2解: 作辅助线MN ,则在MeNM 回路中,沿v方向运动时0d =m Φ ∴ 0=MeNM ε 即 MN MeN εε= 又∵ ⎰+-<+-==ba ba MN ba ba Iv l vB 0ln 2d cos 0πμπε 所以MeN ε沿NeM 方向,大小为ba b a Iv -+ln20πμ M 点电势高于N 点电势,即ba ba Iv U U N M -+=-ln 20πμ题7-37-3 如题7-3图所示,在两平行载流的无限长直导线的平面内有一矩形线圈.两导线中的电流方向相反、大小相等,且电流以d Id t的变化率增大,求:(1)任一时刻线圈内所通过的磁通量; (2)线圈中的感应电动势. 解: 以向外磁通为正则(1) ]ln [lnπ2d π2d π2000dad b a b Ilr l r Ir l r Iab b ad d m +-+=-=⎰⎰++μμμΦ (2) tIb a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε题7-47-4 如题7-4图所示,长直导线通以电流I =5 A ,在其右方放一长方形线圈,两者共面.线圈长b =0.06 m ,宽a =0.04 m ,线圈以速度v =0.03 m/s 垂直于直线平移远离.求:d =0.05 m 时线圈中感应电动势的大小和方向.解: AB 、CD 运动速度v方向与磁力线平行,不产生感应电动势. DA 产生电动势⎰==⋅⨯=ADIvbvBb l B v d2d )(01πμεBC 产生电动势)(π2d )(02d a Ivbl B v CB+-=⋅⨯=⎰με∴回路中总感应电动势8021106.1)11(π2-⨯=+-=+=ad d Ibv μεεε V 方向沿顺时针.7-5 长度为l 的金属杆ab 以速率v 在导电轨道abcd 上平行移动.已知导轨处于均匀磁场B 中,B 的方向与回路的法线成60°角(如题7-5图所示),B 的大小为B =kt (k 为正常数).设t =0时杆位于cd 处,求:任一时刻t 导线回路中感应电动势的大小和方向.题7-5图解: ⎰==︒=⋅=22212160cos d klvt lv kt Blvt S B m Φ∴ klvt tm-=-=d d Φε即沿abcd 方向顺时针方向.题7-6图7-6 一矩形导线框以恒定的加速度向右穿过一均匀磁场区,B 的方向如题7-6图所示.取逆时针方向为电流正方向,画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0). 解: 如图逆时针为矩形导线框正向,则进入时0d d <Φt,0>ε; 题7-6图(a)题7-6图(b)在磁场中时0d d =tΦ,0=ε; 出场时0d d >tΦ,0<ε,故t I -曲线如题7-6图(b)所示.7-7 导线ab 长为l ,绕过O 点的垂直轴以匀角速ω转动.aO=3l,磁感应强度B 平行于转轴,如题7-7所示.试求:(1) ab 两端的电势差;(2) a ,b 两端哪一点电势高?题7-7图解: (1)在Ob 上取dr r r +→一小段 则 ⎰==320292d l Ob l B r rB ωωε 同理 ⎰==302181d l Oa l B r rB ωωε ∴ 2261)92181(l B l B Ob aO ab ωωεεε=+-=+= (2)∵ 0>ab ε 即0<-b a U U ∴b 点电势高.题7-8图7-8 一无限长直导线和一正方形的线圈如题7-8图所示放置(导线与线圈接触处绝缘).求:线圈与导线间的互感系数.解: 设长直电流为I ,其磁场通过正方形线圈的互感磁通为⎰==32300122ln π2d π2a a Iar rIaμμΦ∴ 2ln π2012aIM μΦ==7-9 两根平行长直导线,横截面的半径都是a ,中心相距为d ,两导线属于同一回路.设两导线内部的磁通可忽略不计,证明:这样一对导线长度为l 的一段自感为0L=Inl d aaμπ-.题7-9图解: 如题7-9图所示,取r l S d d = 则 ⎰⎰-----=--=-+=ad aad aad da a d Il r r r Ilr l r Ir πI)ln (ln 2πd )d 11(π2d ))d (π22(0000μμμμΦ aad Il-=lnπ0μ ∴ aad lIL -==lnπ0μΦ7-10 两线圈顺串联后总自感为1.0 H ,在它们的形状和位置都不变的情况下,反串联后总自感为0.4 H.试求:它们之间的互感. 解: ∵顺串时 M L L L 221++= 反串联时M L L L 221-+='∴ M L L 4='-15.04='-=L L M H题7-11图7-11 一矩形截面的螺绕环如题7-11图所示,共有N 匝.试求:(1)此螺绕环的自感系数;(2)若导线内通有电流I ,环内磁能为多少? 解:如题7-11图示 (1)通过横截面的磁通为 ⎰==baab NIhr h r NIlnπ2d π200μμΦ 磁链 ab IhN N lnπ220μΦψ== ∴ ab hN IL lnπ220μψ==(2)∵ 221LI W m = ∴ ab hI N W m ln π4220μ=7-12 一无限长圆柱形直导线,其截面各处的电流密度相等,总电流为I .求:导线内部单位长度上所储存的磁能. 解:在R r <时 20π2RI B rμ=∴ 4222002π82R r I B w m μμ== 取 r r V d π2d =(∵导线长1=l ) 则 ⎰⎰===RRm I R rr I r r w W 0204320π16π4d d 2μμπ7-13 圆柱形电容器内、外导体截面半径分别为R 1和R 2(R 1<R 2),中间充满介电常数为ε的电介质.当两极板间的电压随时间的变化为=k dUdt时(k 为常数),求介质内距圆柱轴线为r 处的位移电流密度. 解:圆柱形电容器电容 12ln 2R R lC πε=12ln 2R R lUCU q πε== 1212ln ln 22R R r U R R r lU S q D εππε===∴ 12ln R R r ktD j ε=∂∂=7-14 试证:平行板电容器的位移电流可写成d I =CdUdt.式中C 为电容器的电容,U 是电容器两极板的电势差.如果不是平板电容器,以上关系还适用吗? 解:∵ CU q =SCUD ==0σ ∴CU DS D ==Φ不是平板电容器时 0σ=D 仍成立 ∴ tUCI D d d =还适用.7-15 半径为R =0.10 m 的两块圆板构成平行板电容器,放在真空中.今对电容器匀速充电,使两极板间电场的变化率为13=1.010dEdt⨯V/(m·s).求两极板间的位移电流,并计算电容器内离两圆板中心联线r (r <R )处的磁感应强度B r 以及r =R 处的磁感应强度B R . 解: (1) tEt D j D ∂∂=∂∂=0ε 8.22≈==R j S j I D D D πAtUC t ID D d d d d ==Φ(2)∵ S j I l H SD ld d 0⋅+=⋅⎰∑⎰取平行于极板,以两板中心联线为圆心的圆周r l π2=,则22d d 2r tE r j r H D πεππ== ∴ tEr H d d 20ε=tEr H B r d d 2000εμμ== 当R r =时,600106.5d d 2-⨯==tER B R εμ T。
第七章 稳恒磁场习题7-1 一个半径为r 的半球面如图放在均匀磁场中,通过半球面的磁通量为多少?解:取平面S ’与半球面S 构成闭合曲面,根据高斯定理有 0m mS mS ΦΦΦ'=+=2cos mS mS r E ΦΦπα'=-=-球面外法线方向为其正方向7-2 如图所示,几种载流导线在平面内分布,电流均为I ,它们在点O 的磁感应强度各为多少?08IR μ垂直画面向外0022II RR μμπ-垂直画面向里 00+42I IR Rμμπ垂直画面向外 7-3 如图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连。
已知圆环的粗细均匀,求环中心O 的磁感应强度。
解: 如图所示,圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
且θ-πθ==21221R R I I 电阻电阻 1I 产生1B 方向⊥纸面向外πθπμ2)2(2101-=R I B2I 产生2B 方向⊥纸面向里πθμ22202R I B =∴1)2(2121=-=θθπI I B B 有0210=+=B B B7-4 如图所示,已知地球北极地磁场磁感强度B 的大小为6.0×10-5T 。
如设想此地磁场是由地球赤道上一圆电流所激发的,此电流有多大?流向如何?(已知圆电流轴线上北极点的磁感强度()R IRR IR B 24202/32220μμ=+=)解:9042 1.7310A RBI μ==⨯方向如图所示7-5 有一同轴电缆,其尺寸如题图所示.两导体中的电流均为I ,但电流的流向相反,导体的磁性可不考虑。
试计算以下各处的磁感应强度:(1)r<R 1;(2)R 1<r<R 2;(3)R 2<r<R 3;(4)r>R 3。
解:同轴电缆的电流分布具有轴对称性在电缆各区域中磁感应线是以电缆轴线为对称轴的同心圆。
习 题 77.1选择题(1) 容器中贮有一定量的理想气体,气体分子的质量为m ,当温度为T 时,根据理想气体的分子模型和统计假设,分子速度在x 方向的分量平方的平均值是:(A)2x υ=.(B) 2x υ= [ ](C) 23x kT m υ= . (D) 2x kT mυ=. [答案:D 。
2222x y z υυυυ=++, 222213x y z υυυυ===,23kT mυ=。
](2) 一瓶氦气和一瓶氮气的密度相同,分子平均平动动能相同,而且都处于平衡状态,则它们 [ ] (A) 温度相同、压强相同. (B) 温度、压强都不相同. (C) 温度相同,但氦气的压强大于氮气的压强. (D) 温度相同,但氦气的压强小于氮气的压强.[答案:C 。
由32w kT =,w w =氦氮,得T 氦=T 氮 ; 由molpM RTρ=,ρρ=氦氮,T 氦=T 氮 ,而M M <mol 氦mol 氮,故p p >氦氮。
](3) 在标准状态下,氧气和氦气体积比为V 1 /V 2=1/2,都视为刚性分子理想气体,则其内能之比E 1 / E 2为: [ ] (A) 3 / 10. (B) 1 / 2. (C) 5 / 6. (D) 5 / 3.[答案:C 。
由2mol M i E RT M =2ipV =,得111112222256E i pV i V E i pV i V ==⋅=。
](4) 一定质量的理想气体的内能E 随体积V 的变化关系为一直线,其延长线过E ~V 图的原点,题7.1图所示,则此直线表示的过程为: [ ] (A) 等温过程. (B) 等压过程. (C) 等体过程. (D) 绝热过程.[答案:B 。
由图得E =kV , 而2i E pV =,i 不变,2ik p =为一常数。
](5) 在恒定不变的压强下,气体分子的平均碰撞频率Z 与气体的热力学温度T 的关系为 [ ] (A) Z 与T 无关. (B).Z 与T 成正比 . (C) Z 与T 成反比. (D) Z 与T 成正比.[答案:C。
版权归原著所有 本答案仅供参考习题77-1.原长为m 5.0的弹簧,上端固定,下端挂一质量为kg 1.0的物体,当物体静止时,弹簧长为m 6.0.现将物体上推,使弹簧缩回到原长,然后放手,以放手时开始计时,取竖直向下为正向,写出振动式。
(g 取9.8)解:振动方程:cos()x A t ωϕ=+,在本题中,kx mg =,所以9.8k =;∴ω=== 取竖直向下为x 正向,弹簧伸长为0.1m 时为物体的平衡位置,所以如果使弹簧的初状态为原长,那么:A =0.1m ,当t =0时,x =-A ,那么就可以知道物体的初相位为π。
所以:0.1cos x π=+) 即:)x =-。
7-2.有一单摆,摆长m 0.1=l ,小球质量g 10=m ,0=t 时,小球正好经过rad 06.0-=θ处,并以角速度0.2rad/s θ=向平衡位置运动。
设小球的运动可看作简谐振动,试求:(1)角频率、频率、周期;(2)用余弦函数形式写出小球的振动式。
(g 取9.8)解:振动方程:cos()x A t ωϕ=+ 我们只要按照题意找到对应的各项就行了。
(1)角频率: 3.13/rad s ω===,频率:0.5Hz ν=== ,周期:22T s π===; (2)振动方程可表示为:cos 3.13A t θϕ=+(),∴ 3.13sin3.13A t θϕ=-+()根据初始条件,0t =时:cos Aθϕ=,0(12sin 0(343.13A θϕ>=-<,象限),象限)可解得:,-2.32rad 95.3227rad,108.802===⨯=-ϕA 所以得到振动方程: rad )32.213.3cos(108.82-⨯=-t θ。
7-3. 一竖直悬挂的弹簧下端挂一物体,最初用手将物体在弹簧原长处托住,然后放手,此系统便上下振动起来,已知物体最低位置是初始位置下方10.0cm 处,求:(1)振动频率;(2)物体在初始位置下方cm 0.8处的速度大小。
习题精解7-1一条无限长直导线在一处弯折成半径为R 的圆弧,如图所示,若已知导线中电流强度为I,试利用比奥—萨伐尔定律求:(1)当圆弧为半圆周时,圆心O 处的磁感应强度;(2)当圆弧为1/4圆周时,圆心O 处的磁感应强度。
解(1)如图所示,圆心O 处的磁感应强度可看作由3段载流导线的磁场叠加而成。
因为圆心O 位于直线电流AB 和DE 的延长线上,直线电流上的任一电流元在O 点产生的磁感应强度均为零,所以直线电流AB 和DE 段在O 点不产生磁场。
根据比奥—萨伐尔定律,半圆弧上任一电流元在O 点产生的磁感应强度为 024IdldB Rμπ=方向垂直纸面向内。
半圆弧在O 点产生的磁感应强度为 000220444RIIdl I B R R R Rπμμμπππ===⎰方向垂直纸面向里。
(2)如图(b )所示,同理,圆心O 处的磁感应强度可看作由3段载流导线的磁场叠加而成。
因为圆心O 位于电流AB 和DE 的延长线上,直线电流上的任一电流元在O 点产生的磁感应强度均为零,所以直线电流AB 和DE 段在O 点不产生磁场。
根据毕奥—萨伐尔定理,1/4圆弧上任一电流元在O 点产生的磁感应强度为 024IdldB R μπ=方向垂直纸面向内,1/4圆弧电流在O 点产生的磁感应强度为00022204428RIIdl I R B R R Rπμμμπππ===⎰方向垂直纸面向里。
如图所示,有一被折成直角的无限长直导线有20A 电流,P 点在折线的延长线上,设a 为,试求P 点磁感应强度。
解 P 点的磁感应强度可看作由两段载流直导线AB 和BC 所产生的磁场叠加而成。
AB 段在P 点所产生的磁感应强度为零,BC 段在P 点所产生的磁感应强度为 0120(cos cos )4IB r μθθπ=- 式中120,,2r a πθθπ=== 。
所以500(cos cos ) 4.010()42I B T a μπππ=-=⨯ 方向垂直纸面向里。