大学物理作业(二)答案
- 格式:doc
- 大小:169.50 KB
- 文档页数:3

《大学物理》作业 No.2波动方程班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、判断题[ F ] 1. 解:电磁波就可以在真空中传播。
[ F ] 2. 解:波动是振动的传播,沿着波的传播方向,振动相位依次落后。
[ F ] 3. 解:质元的振动速度和波速是两个概念,质元的振动速度是质元振动的真实运动速度,而波速是相位的传播速度,其大小取决于介质的性质。
[ F ] 4. 解:振动曲线描述的是一个质点离开平衡位置的位移随时间的变化关系;波形曲线是某一时刻,波线上各个质点离开平衡位置的情况。
[ F ] 5. 解:对于波动的介质元而言,其动能和势能同相变化,它们时时刻刻都有相同的数值。
二、选择题:1. 一平面简谐波表达式为)2(sin 05.0x t y --=π (SI) ,则该波的频率v (Hz)、波速u (m ⋅s -1)及波线上各点振动的振幅A (m)依次为:(A) 2/1,2/1,05.0- (B) 2/1,1,05.0-(C) 2/1,2/1,05.0 (D) 2 ,2,05.0[ C ]解:平面简谐波表达式可改写为(SI))22cos(05.0)2(sin 05.0ππππ+-=--=x t x t y与标准形式的波动方程 ])(2[cos ϕπ+-=u xt v A y 比较,可得 )s (m 21,(Hz)21,(m)05.01-⋅===u v A 。
故选C2. 一平面简谐波的波动方程为)3cos(1.0πππ+-=x t y (SI),t = 0时的波形曲线如图所示。
则:(A) O 点的振幅为-0.1 m(B) 波长为3 m (C) a 、b 两点位相差 π21(D) 波速为9 m ⋅s -1解:由波动方程可知(Hz),23(m),1.0==νA (m)2=λ,)s (m 32231-⋅=⨯==νλua 、b 两点间相位差为:2422πλλπλπϕ===∆ab故选C3. 一平面简谐波沿x 轴正向传播,t = T/4时的波形曲线如图所示。
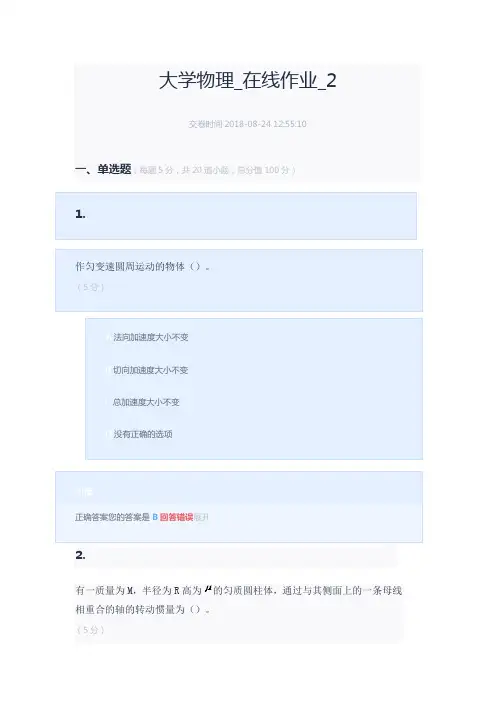
大学物理_在线作业_2交卷时间2018-08-24 12:55:10一、单选题(每题5分,共20道小题,总分值100分)2.有一质量为M,半径为R高为的匀质圆柱体,通过与其侧面上的一条母线相重合的轴的转动惯量为()。
(5分)A2/3B1/2C1/4D2/3正确答案您的答案是A回答错误展开3.物体不能出现下述哪种情况?()(5分)A运动中,瞬时速率和平均速率恒相等B曲线运动中,加速度不变,速率也不变C运动中,加速度不变速度时刻变化D曲线运动中,加速度越来越大曲率半径总不变正确答案您的答案是B回答正确展开4.质量为0.01kg的质点作简谐振动,振幅为0.1m,最大动能为0.02J。
如果开始时质点处于负的最大位移处,则质点的振动方程为()。
(5分)A x=0.1cos(0.2t+)B x=0.1cos(20t)C x=0.1cos(20t+)D x=0.1cos(200t+)正确答案您的答案是C回答正确展开5.两个质量相同飞行速度相同的球A和B,其中A球无转动,B球转动,假设要把它们接住所作的功分别为A1、A2,则()。
(5分)A无法判断B A1<A2C A1>A2D A1=A2正确答案您的答案是B回答正确展开6.根据高斯定理,下列说法中正确的是()。
(5分)A闭合曲面上各点的场强仅由面内的电荷决定B闭合曲面上各点的场强为零时,面内一定没有电荷C通过闭合曲面的电通量为正时面内比无负电荷D通过闭合曲面的电通量仅由面内电荷的代数和决定正确答案您的答案是D回答正确展开7.在单色光垂直入射的劈形膜干涉实验中,若慢慢地减小劈形膜夹角,则从入射光方向可以观察到干涉条纹的变化情况为()。
(5分)A条纹间距减小B给定区域内条纹数目增加C条纹间距增大D观察不到干涉条纹有什么变化正确答案您的答案是C回答正确展开8.冰上芭蕾舞运动员以一只脚为轴旋转时将两臂收拢,则()。
(5分)A转动角速度减小B转动惯性减小C转动动能不变D角速度增大正确答案您的答案是B回答正确展开9.质量相同的物块A、B用轻质弹簧连接后,再用细绳悬吊着,当系统平衡后,突然将细绳剪断,则剪断后瞬间()。








作业1 质点运动学(一)参考答案1. B ;2. D;3. 8m, 10m.4. 3, 3 6;5. 解:(1) 5.0/-==∆∆t x v m/s(2) v = d x /d t = 9t - 6t 2v (2) =-6 m/s(3) S = |x (1.5)-x (1)| + |x (2)-x (1.5)| = 2.25 m6. 答:矢径r是从坐标原点至质点所在位置的有向线段.而位移矢量是从某一个初始时刻质点所在位置到后一个时刻质点所在位置的有向线段.它们的一般关系为0r r r-=∆0r 为初始时刻的矢径, r 为末时刻的矢径,△r为位移矢量.若把坐标原点选在质点的初始位置,则0r =0,任意时刻质点对于此位置的位移为△r =r,即r既是矢径也是位移矢量.1. D ;2. -g /2 , ()g 3/322v3. 4t 3-3t 2 (rad/s), 12t 2-6t (m/s 2)4. 17.3 m/s, 20 m/s .5. 解: =a d v /d t 4=t , d v 4=t d t⎰⎰=vv 0d 4d tt tv 2=t 2v d =x /d t 2=t 2t t x txx d 2d 020⎰⎰=x 2= t 3 /3+x 0 (SI)6. 解:根据已知条件确定常量k()222/rad 4//s Rt t k ===v ω24t =ω, 24Rt R ==ωvt=1s 时, v = 4Rt 2 = 8 m/s2s /168/m Rt dt d a t ===v 22s /32/m R a n ==v()8.352/122=+=nt a a a m/s 21.D2.C3.4. l/cos 2θ5.如图所示,A ,B ,C 三物体,质量分别为M=0.8kg, m= m 0=0.1kg ,当他们如图a 放置时,物体正好做匀速运动。
(1)求物体A 与水平桌面的摩擦系数;(2)若按图b 放置时,求系统的加速度及绳的张力。
65. 如图所示,几种载流导线在平面内分布,电流均为I ,求:它们在O 点的磁感应强度。
1 RIB 80μ=方向 垂直纸面向外2 R I R I B πμμ2200-= 方向 垂直纸面向里 3 RI R I B 4200μπμ+= 方向 垂直纸面向外 66. 一半径为R 的均匀带电无限长直圆筒,电荷面密度为σ,该筒以角速度ω绕其轴线匀速旋转。
试求圆筒内部的磁感应强度。
解:如图所示,圆筒旋转时相当于圆筒上具有同向的面电流密度i , σωσωR R i =ππ=)2/(2作矩形有向闭合环路如图中所示.从电流分布的对称性分析可知,在ab 上各点B的大小和方向均相同,而且B 的方向平行于ab ,在bc 和fa 上各点B的方向与线元垂直,在de , cd fe ,上各点0=B.应用安培环路定理∑⎰⋅=I l B 0d μ可得 ab i ab B 0μ=σωμμR i B 00==圆筒内部为均匀磁场,磁感强度的大小为σωμR B 0=,方向平行于轴线朝右.67.在半径为R 的长直金属圆柱体内部挖去一个半径为r 的长直圆柱体,两柱体轴线平行,其间距为a (如图)。
今在此导体内通以电流I ,电流在截面上均匀分布,求:空心部分轴线上O ' 点的磁感应强度的大小。
解:)(22r R IJ -=π10121r J B ⨯=μ 20221r J B ⨯-=μJa O O J r r J B B 021********21)(21μμμ=⨯=-⨯=+=r R Ia)(2220-=πμ68.一无限长圆柱形铜导体,半径为R ,通以均匀分布的I 今取一矩形平面S (长为L ,宽为2R ),位置如图,求:通过该矩形平面的磁通量。
解:在圆柱体内部与导体中心轴线相距为r 处的磁感强度的大小,由安培环路定律可得:)(220R r rRIB ≤π=μ因而,穿过导体内画斜线部分平面的磁通1为⎰⎰⋅==S B S B d d 1 Φr rL RI Rd 2020⎰π=μπ=40LIμ在圆形导体外,与导体中心轴线相距r 处的磁感强度大小为 )(20R r rIB >π=μ因而,穿过导体外画斜线部分平面的磁通2为⎰⋅=S B d 2Φr r IL R Rd 220⎰π=μ2ln 20π=ILμ穿过整个矩形平面的磁通量 21ΦΦΦ+=π=40LIμ2ln 20π+ILμ69.如图所示,载有电流I 1和I 2的无限长直导线相互平行,相距3r ,今有载有电流I 3的导线MN = r 水平放置,其两端M 、N 分别与I 1、I 2距离均为r ,三导线共面,求:导线MN 所受的磁场力的大小与方向。
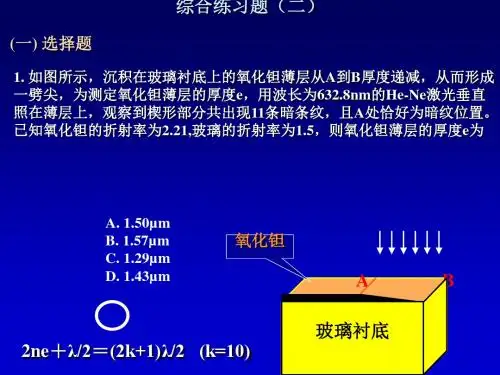
作业2 动量与角动量 功与能2-1一步枪在射击时,子弹在枪膛受到的推力满足 t F 51034400⨯-= 的规律,已知击发前子弹的速率为零,子弹出枪口时的速度为300 m/s ,受到的力变为零. 求: ⑴ 子弹受到的冲量? ⑵ 子弹的质量为多少克? 原题 3-32-2 一个质量m = 50 g ,以速率υ= 20 m/s 作匀速圆周运动的小球,在1/4周期向心力加给它的冲量是多大? 原题 3-42-3 有一运送砂子的皮带以恒定的速率υ水平运动,砂子经一静止的漏斗垂直落到皮带上,忽略机件各部位的摩擦及皮带另一端的其它影响,试问:⑴ 若每秒有质量为t M M d d ='的砂子落到皮带上,要维持皮带以恒定速率υ运动,需要多大的功率?⑵ 若='M 20 kg/s ,5.1=υm/s ,水平牵引力多大?所需功率多大? 解: ⑴ 设t 时刻落到皮带上的砂子质量为M , 速率为υ,t + d t 时刻,皮带上的砂子质量为 M + d M ,速率也是υ,根据动量定理,皮带作用在砂子上的外力 F 的冲量为:)0d ()d (d ⋅+-+=M M M M t F υυυ⋅=M d∴ M t M F '==υυ d d由第三定律,此力等于砂子对皮带的作用力F ',即F F ='. 由于皮带匀速运动,动力源对皮带的牵引力F F '='',因而,F F ='',F F ='',F ρ''与υρ同向,动力源所供给的功率为: t M F P d d υυυρρρρ⋅=⋅=t M d 2υ=M '=2υ⑵ 当t M M d d ='=20 kg/s ,5.1=υm/s ,时, 水平牵引力 M F '=''υ= 30N 所需功率 M P '=2υ=45W2-4 哈雷彗星绕太阳运动的轨道是一个非常扁的椭圆,它离太阳最近的距离是1011075.8⨯=r m ,此时它的速度是 411046.5⨯=υm/s ,它离太阳最远时的速率是221008.9⨯=υm/s ,这时它离太阳的距离r 2是多少? 原题 3-82-5 假设一个运动的质子P 只受某重核N 的有心排斥力的作用.已知质子的质量为m ,当它运动到与N 相距最近的A 点时,距离为a ,速度为A υρ,运动到某点B 时,速度为B υρ,求此时重核N 到速度B υρ的垂直距离b .(图左侧的长虚线为与B υρ方向平行的直线). 解:重核N 的质量 M >> m ,在质子P 从接近到远离重核N 的全过程中,重核 N 可视为静止. 质子P 只受重核N 的有心排斥力作用,P 对N 中心的角动量守恒.υρρρm r L ⨯= = 恒矢量 B B B A A A m r m r θυθυsin sin = a r A A =θsin , b r B B =θsin ∴ b m a m B A υυ= 得 a b BAυυ=2-6 一质量为 3102-⨯kg 的子弹,在枪膛中前进时受到的合力 x F 98000400-= (SI),子弹在枪口的速度为300 m/s .试计算枪筒的长度. 原题 4-1题2-5图2-7 一质量为m 的质点在指向圆心的平方反比力2--=kr F 的作用下,作半径为r 的势能零点,则其机械能为 )2(r k - .原题 4-32-8 有一劲度系数为 k 的轻弹簧,竖直放置,下端悬一质量为 m 的小球,先使弹簧为原长,而小球恰好与地接触,再将弹簧上端缓慢地提起,直到小球刚能脱离 地面为止.在此过程中外力所作的功为 )2(22k g m .原题 4-72-9 有一人造地球卫星,质量为m ,在地球表面上空 2 倍于地球半径 R 的高度沿圆轨道运行,用m ,R ,引力常数 G 和地球的质量 M 表示⑴ 卫星的动能 ;⑵ 卫星的引力势能为 . 原题 4-82-10 一长方体蓄水池,面积为S = 50 m 2,贮水深度为 h 1 = 1.5 m .假定水平面低于地面的高度是h 2 = 5 m ,问要将这池水全部抽到地面上来,抽水机需做功多少?若抽水机的功率为80%,输入功率为P = 35 kw ,则抽光这池水需要多长时间? 原题 4-22-11 某弹簧不遵守胡克定律,若施力F ,则相应伸长为x ,力与伸长的关系为: F = 52.8 x + 38.4 x 2(SI ),求:⑴ 将弹簧从伸长x 1 = 0.50 m 拉伸到伸长 x 2 = 1.00 m 时所需做的功; ⑵ 将弹簧横放在水平光滑桌面上,一端固定,另一端系一个质量为2.17 kg 的物体,然后将弹簧拉伸到伸长 x = 1.00 m ,再将物体由静止释放.求当弹簧回到伸长x 1 = 0.50 m 时,物体的速率. 原题 4-52-12 一质量为m 的质点在xOy 平面上运动,其位置矢量为j t q it p r ˆ sin ˆ cos ωω+=ρ (SI),式中p 、q 、ω是正值常数,且p > q .求:⑴ 求质点在点 P ( p , 0) 和点Q ( 0, q ) 处的动能; ⑵ 质点所受的作用力 F ρ,以及当质点从点 P 运动到点Q 的过程中的分力F x 和F y 分别作的功.解:⑴ 由位矢 j t q it p r ˆ sin ˆ cos ωω+=ρ 可知: cos t p x ω=, sin t q y ω= t x x d d =υ sin t p ωω-=, t y y d =υ cos t q ωω=点P ( p , 0 ) 处 1 cos =t ω, 0 sin =t ω, 22k 2121y xP mv mv E +=2221ωmq = 点Q ( 0, q ) 处 0 cos =t ω, 1 sin =t ω, 22k 2121y xQ mv mv E +=2221ωmp = ⑵ t a x x d υ= cos 2t p ωω-=, t a y y d υ= sin 2t q ωω-=)ˆˆ(ˆˆj a i a m j F i F F y x y x +=+=ρ)ˆ sin ˆ cos ( 2j t q it p m ωωω+-= 由点P →Q x F A p x x d 0⎰=x ma p x d 0⎰=x t mp p d cos 02⋅-=⎰ωωx x m p d 02⎰-=ω2221ωmp =y F A qy y d 0⎰=y ma qy d 0⎰=y t mq qd sin 02⋅-=⎰ωωy y m qd 02⎰-=ω2221ωmq -=作业4 气体动理论4-1 氧气钢瓶体积为5升,充氧气后在27℃时压强为20个大气压,试求瓶贮存有多少氧气?现高空中使用这些氧气,在高空空气的压强为0.67个大气压,温度为-27℃,试问这时钢瓶可提供在高空使用的氧气是多少升?0.13 kg ,117升;原题 8—14-2 在P-V图上的一点代表系统平衡状态;一条光滑的曲线代表气体的准静态过程.4-3 设想每秒有1023个氧分子以500 m/s的速度沿着与器壁法线成30°角的方向撞在面积为3 104m2的器壁上,求这群分子作用在器壁上的压强.原题 8—34-4 两瓶不同类型的理想气体,它们的温度和压强相同,但体积不同,则它们的分子数密度 相同 ;气体的质量密度 不同 ;单位体积气体分子的平均动能为 不同 .原题 8—44-5 若理想气体的体积为V ,压强为P ,温度为T ,一个分子的质量为m ,k 为玻耳解: kT VN nkT p == kT pVN = 4-6 质量相同的氢气和氦气,温度相同,则氢气和氦气的能之比为 10 : 3 ,氢分子与氦分子的平均动能之比为 5 : 3 ;氢分子与氦分子的平均平动动能之比为 1 : 1 .原题 8—64-7 试指出下列各量的物理意义⑴ kT /2; ⑵ 3kT /2; ⑶ ikT /2.答: ⑴ kT /2 ——理想气体分子任一自由度的平均动能; ⑵ 3kT /2 ——理想气体的分子的平均平动动能;⑶ ikT /2 ——理想气体的分子的平均总动能 4-8 将0.2mol 氧气从27℃加热到37℃,其能增加了多少?分子的平均平动动能变化了多少?解:氧气为双原子分子,5=i ,则能增量为55.411031.82.025)(212 =⨯⨯⨯=-=∆T T R i E νJ分子的平均平动动能为kT E K 23=,其增量为22231007.2101038.12323--⨯=⨯⨯⨯=∆=∆T k E K J4-9 一绝热密封容器的体积为102m 3,以100 m/s 的速度匀速直线运动,容器中有100g 的氢气,当容器突然停止时,氢气的温度、压强各增加多少?原题 8—74-10 容器有一摩尔的双原子分子理想气体,气体的摩尔质量为μ,能为E ,则气体的温度T = R E 52 ,分子的最可几速率 p υ= )5(2μE ,分子的平均速率 υ= )π5(4μE .原题 8—84-11 已知)(υf 为麦克斯韦速率分布函数,N 为分子总数, 则速率大于100 m/s 的分子数目的表达式 υυυd )(d 100⎰⎰∞=='f NN N ; 速率大于100 m/s 的分子数目占分子总数的百分比的表达式 υυd )(100⎰∞=f P ; 速率大于100 m/s 的分子的平均速率的表达式 υυυυυυd )(d )(100100⎰⎰∞∞=f f .∵d )(d υυυf NN =—— 速率区间 υυυd ~+的分子数占总分子数的百分比(几率)4-12 麦克斯韦速率分布曲线如图所示,图中A ,B 两部分面积相等,则该图表示[ ](A )0υ为最概然速率 (B )0υ为平均速率(C )0υ为方均根速率(D )速率大于和小于0υ的分子数各占一半 参考解:A 部分面积()N N f S AA Δd 00==⎰υυυ; B 部分面积 ()NN f S BB Δd 0==⎰∞υυυ B A S S = ∴B A N N ΔΔ= 答案为 [ D ]4-13 容积为33100.2m -⨯的容器中,有能为J 21075.6⨯的刚性双原子分子理想气体,求:⑴ 气体的压强;⑵ 设分子总数为22104.5⨯个,求分子的平均平动动能及气体的温度;解:(1) 由 RT i M m E 2•=和 RT Mm PV = 可得气体压强 5321035.1100.251075.622⨯=⨯⨯⨯⨯==-iV E P Pa (2)分子数密度V N n =,则该气体温度k .NkPV nk P T 210623⨯=== 气体分子的平均平动动能为 211049723-⨯==.kT k εJ4-14 真空管的线度为 210-m ,真空度为 310333.1-⨯Pa .设空气分子的有效直径为10103-⨯m ,摩尔质量为28.97310-⨯kg .求在27℃时真空管中空气的分子数密度、平均碰撞频率和平均自由程. 解:P301 12.26空气的分子数密度为 kTpn == …… = 3.2×1017 (m -3 )平均自由程为 nd 2π21=λ= …… = 7.8(m) 0(υf 题4-12图平均碰撞频率为 υn d z 2 π2=MRT nd π8 π22= = …… = 59.9 (s -1)*4-15 麦克斯韦速率分布律kTm kT m f 22322eπ2π4)(υυυ-⎪⎭⎫⎝⎛=,求速率倒数的平均值⎪⎭⎫⎝⎛υ1,并给出它与速率的平均值υ的关系. 解:P296 12.9由平均值的定义有υυυυd )(110f ⎰∞=⎪⎭⎫ ⎝⎛υυυd eπ2π4 22230kTm kT m -∞⎪⎭⎫ ⎝⎛=⎰⎝⎛-⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛=-∞⎰220232d eπ2π42υυkT m m kT kT m kTm ∵速率的平均值υkT m 8 π=∴*4-16 假定 N 个粒子的速率分布曲线如图示.⑴ 由 N 和0υ求a ;⑵ 求速率在1.50υ到2.00υ之间的粒子数 N ∆; ⑶ 求粒子的平均速率 υ 和方均根速率2υ. 解:P295 12.7 ⑴ 由归一化条件有υυd )(0⎰∞f 1d d 00 0200=+=⎰⎰υυυυυυυa a, 解之,得 032υ=a ⑵ υυυυd )(025.1⎰=∆f N N υυυd 025.1Na ⎰=)5.10.2(32000υυυ-=N N 31== 0.333 N ⑶ υυυυd )( 0⎰∞=f υυυυυυυυd d 00 02020a a⎰⎰+=03031υυυa =002221υυυa +0911υ== 1.220υυυυυd )(022⎰∞=f υυυυυυυυd d 220300 0a a⎰⎰+=004041υυυa =002331υυυa +301231υa =201831υ= 021831υυ=0662υ== 1.310υ 0题4-16图作业6 狭义相对论基础6-1 惯性系S 和S '的坐标在 0='=t t 时重合,有一事件发生在S '系中的时空坐标为()8108 ,0 ,10 ,60-⨯.若s '系相对于s 以速度u = 0.6c 沿x x '-轴正方向运动,则该事件在S 系中测量时空坐标为( , , , ). 原题 6-16-2 天津和相距120 km .在某日19时整有一工厂因过载而断电,在天津同日19时0分0.0003秒有人放了一响礼炮. 试求在以 c u 8.0= 速度沿到天津方向飞行的飞船中,观察者测量到这两个事件之间的时间间隔.哪一个事件发生在前.原题 6-36-3 长为4m 的棒静止在s 系中xOy 平面,并与x 轴成ο30角,s '系以速度0.5c 相对于s 系沿x x '-轴正向运动,0='=t t 时两坐标原点重合,求s '系中测得此棒的长度和它与x '轴的夹角.原题 6-46-4 中子静止时的平均寿命为15 min 30 s ,它能自发地衰变为三个粒子(质子、电子和中微子).已知地球到太阳的平均距离为1.4961110⨯m .有一个中子被太阳抛 向地球,它必须具有 1.418×108 = 0.473 c m/s 的速率,才能在衰变前到达地球.解: 0γττ=20)(1c u -=τ ♉ τu l =20)(1c u u -=τ ♉ 220)(c l lu +=τ6-5 一火箭静止在地面上测量时长度20 m ,当它以 0.8 c 在空间竖直向上匀速直线飞行时,地面上观察者测得其长度为 .若宇航员在飞船上举一次手用2.4 s ,则地面上测到其举手所用时间为 . 原题 6-66-6 以地球-月球作为参考系测得地-月之间的距离为 810844.3⨯m ,一火箭以0.8c 的速率沿着地球到月球的方向飞行,先经过地球(事件1),之后又经过月球(事件2).要求分别用:⑴ 洛仑兹变换公式,⑵ 长度收缩公式,⑶ 时间膨胀公式,求在地球-月球参考系和在火箭参考系中观测,火箭由地球飞向月球各需要多少时间? P369 15.4;P371 15.9解: 取地-月系为S 系,地-月距离=∆x 810844.3⨯m ,固定在火箭上的坐标系为S '系,其相对S 系的速率 u = 0.8 c ,则在S 系中火箭由地球飞向月球的时间为u x t ∆=∆= …= 1.6 s由已知 8.0=≡c uβ 35112=-≡βγ⑴ 由洛仑兹变换公式 )(x c t t βγ-=' )(x c t t ∆-∆='∆βγ可求得在火箭S '系中 t '∆= …= 0.96 s⑵ S '系中,测地-月距离为l ',是运动长度,由长度收缩公式 l l '= γ 有 l l =' 则 l t '='∆)(γu l t ='∆ =…= 0.96 s⑶ S '系中,两个事件在同一个地点发生,t '∆为固有时间0τ;S 系中两事件时间间隔t ∆为运动时间τ,由时间膨胀公式 0γττ=γττ=='∆0t γt ∆==…= 0.96 s6-7一匀质薄板静止时测得长、宽分别是a 、b ,质量为m ,假定该板沿长度方向以接近光速的速度υ作匀速直线运动,那么它的长度为 )(122c a υ- ,质量为面积密度(单位面积的质量).(原题6-8) 解:∵ 沿运动方向 0l l =,)(1 22c a a a υγ-=='∴;m m γ=')(122c mυ-=∵ b ⊥ 运动方向,b b ='∴ , b a m '''=∴σ )1(22c ab m υ-=6-8 一静止长度为 l 0 的火箭,相对于地面以速率 u 飞行,现从火箭的尾端发射一个光信号.试根据洛仑兹变换计算,在地面系中观测,光信号从火箭的尾端到前端所经历的位移、时间和速度. P370 15.6 解:取固定在地面上的坐标系为S 系,固定在火箭上的坐标系为S '系,自火箭尾端发射光信号为事件“1”, 光信号到达火箭前端为事件“2”,则有S 系中:事件1),(11t x ,事件2),(22t x , 12x x x -=∆, 12t t t -=∆S '系中:事件1),(11t x '',事件2),(22t x '', 012l x x x ='-'='∆, 12t t t '-'='∆c l c x 0='∆= S '系相对S 系运动速率为u ,由洛仑兹变换)( t c x x '+'=βγ,)(x c t t '+'=βγ可得位移 )( t c x x '∆+'∆=∆βγ200)(1)]([c u c l u l -+=cu c u l -+=110时间 )(x c t t '∆+'∆=∆βγ2200)(1)]([c u c l u c l -+=cu cu cl -+=110 速度 c t x =∆∆=υ6-9 设火箭的静止质量为100 t ,当它以第二宇宙速率 3102.11⨯=υm/s 飞行时,其质量增加了 0.7×10 kg . P374 15.13 解: c <<υ,2)(2020k υm c m m E =-=,)2()(2202k 0c m c E m m m υ==-=∆=… 6-10 电子静止质量 310101.9-⨯=m Kg ,当它具有2.6 ⨯ 105 eV 动能时,增加的质量与静止质量之比是 0.508 原题 6-9 解:2k mc E ∆=Θ,2kc E m =∆∴,20k 0 c m E m m =∆∴= 0.508 = 50.8% 6-11 α 粒子在加速器中被加速,当其质量为静止质量的5倍时,其动能为静止能量的 4 倍. (解:2k mc E ∆=Θ,020km m c m E ∆=∴005m m m -= = 4 ) 原题 6-106-12 设某微观粒子的总能量是它的静止能量的k 倍,求其运动速度的大小.(用c 表示真空中光速) 原题 6-11 解: 02020m m c m mc E E k ===γ=2211c υ-=, 1 2-=∴k k c υ,211 k c -=υ6-13 ⑴ 粒子以多大速度运动时,它的相对论动量是非相对论动量的两倍? ⑵ 如果粒子的动能与它的静能相等,粒子的速率是多少? 原题 6-12 解:⑴ Θγ=0p p2211c υ-== 2,c 23 =∴υ= 0.866 c ⑵ 202k c m mc E -=Θ2020 c m c m -=γ20c m =,2 =∴γ,c 23 =∴υ= 0.866 c6-14 要使电子的速率从1.2 ×108m/s 增加到2.4 ×108m/s ,需做多少功?P374 15.15解:做功等于电子动能的增量201202k )()(c m m c m m E ---=∆212)(c m m -=⎪⎪⎭⎫ ⎝⎛---=221222201111c c cm υυ = … = 4.7×10 J = 2.94×10 eV6-15 在氢的核聚变反应中,氢原子核聚变成质量较大的核,每用 1 g 氢约损失0.006 g 静止质量.而1 g 氢燃烧变成水释放出的能量为1.3 × 105J .氢的核聚变反应中 释放出来的能量与同质量的氢燃烧变成水释放出的能量之比为 4.1×106 . 解:每用1g 氢释放核能 21mc E ∆=∆=…= 5.4×1011 J ;1g 氢燃释放能量2E ∆= 1.3×105 J6-16 两个静止质量都是m 0的小球,其中一个静止,另一个以=υ0.8c 的速度运动,在它们作对心碰撞后粘在一起,求碰撞后合成小球的质量、速度及静止质量. 原题 6-13 m=2.67m 0,=υ0.5c ,0031.2m m =' 6-13 (没详解)*6-17 ⑴ 如果要把一个粒子的动能写作 220υm ,而误差不大于1%,试问这个粒子的最大速率等于多少?⑵ 以这个速率运动的电子动能是多少?(电子静止质量 31e 101.9-⨯=m Kg ) ⑶ 以这个速率运动的质子动能是多少?(质子静止质量 e 01840m m =) P377 15.21 解: c υβ=,211βγ-=⑴ 相对论动能 20k )(c m m E -=20)1(c m -=γ202][111 c m --=β 依题意有 %12k 20k ≤-E m E υ ♉ %1111 21222][≤---cβυ♉ 01.0111 21][22≤---ββ∵ 211βγ-=, 则 2211γβ-=,上式可写为01.01 112112≤--⋅-γγ ♉ 01.0)1(2112≤+-γγ♉ 0198.12≤--γγ 解方程 0198.12=--γγ ♉ 98.1298.1411⨯⨯+±=γγ取正值有 211βγ-=0067.1≤ ♉ 2211γβ-=115.0≤即 c 115.0≤υ(= 3.45×107 m) ∴ c 115.0m ax =υ⑵ 以速率c 116.0=υ时, β= 0.115,γ= 1.0067运动的电子动能 2e ke )(c m m E -=2e 2][111 c m --=β=…= 5.49×1016(J) = 3.43×103 eV(电子加速电压 V ≥3.5 kV 时,电子速率≥υ=3.5×107m 时,要用相对论公式!!)⑶∵ 质子的静止质量 e p 1840m m =∴以速率c 116.0=υ运动的质子动能 ke kp 1840E E == 6.31×106eV作业8 波 动8-1 一个余弦横波以速度u 沿x 轴正方向传播,t 时刻波形曲线如图所示.试在图中画出A ,B ,C ,D ,E ,F ,G 各质点在该时刻的运动方向.并画出(t + T /4)时刻的波形曲线.原题 20-18-2 地震波纵波和横波的速度分别为8000 m/s 和4450 m/s ,观测点测得这两种波到达的时间差=∆t 75.6 s ,则震中到观测点的距离 r = 7.58×105m . 解: t u r u r ∆=-)()(12 )(2121u u u u t r -⋅∆==…= 7.58×105m8-3 ⑴ 有一钢丝,长2.00 m ,质量20.0×103 kg ,拉紧后的力是1000 N ,则此钢丝上横波的传播速率为 316 m/s . ⑵钢棒中声速5200m/s ,钢的密度=ρ7.8g/cm 3, 钢的弹性模量为2.11×1011(N/m 2).8-4 已知一波的波函数为 )6.0π10sin(105 2x t y -⨯=-⑴ 求波长,频率,波速及传播方向;⑵ 说明x = 0时波函数的意义. 原题 20-3y8-5 一螺旋形长弹簧的一端系一频率为25 Hz 的波源,在弹簧上激起一连续的正弦纵波,弹簧中相邻的两个稀疏区之间的距离为24 cm .⑴ 试求该纵波的传播速度;⑵ 如果弹簧中质点的最大纵向位移为 0.30 cm ,而这个波沿x 轴的负向传播,设波源在 x = 0 处,而x = 0 处的质点在 t = 0 时恰好在平衡位置处,且向x 轴的正向运动,试写出该正弦波的波函数. 解:⑴ νλ=u = 24 ×25 = 600 cm/s⑵ 波源处⎭⎬⎫>-===0sin 0cos 00ϕωυϕA A y 初相位 2π-=ϕ,波源振动方程为 )π2cos(30.000ϕν+=t y )2ππ50cos(30.0-=t 波沿x 轴的负向传播的波函数为])(cos[ϕω-+=u x t A y ]2π)600π(50cos[30.0-+=x t )]24π(252sin[30.0x t +=即,该正弦波的波函数为 )]24π(252sin[30.0x t y += (cm)8-6 波源作谐振动,周期为0.01s ,经平衡位置向正方向运动时,作为时间起点,若此振动以υ= 400 ms 1的速度沿直线传播,求: ⑴ 距波源为8 m 处的振动方程和初相位;⑵ 距波源为9 m 和10 m 两点的相位差. 原题 20-58-7 一平面简谐波,沿x 轴正向传播,波速为4 m/s ,已知位于坐标原点处的波源的振动曲线如图(a)所示.⑴ 写出此波的波函数; ⑵ 在图(b)中画出t = 3 s 时刻的波形图(标明尺度). P317 13.16 解:⑴ 由图知,A = 4 cm = 4 × 102 m , T = 4 s ∴ T π2=ω2π=,uT =λ= 4 × 4 = 16 m 原点处 A A y ==ϕcos 0 初相位 0=ϕ 原点振动方程为 )cos(ϕω+=t A y t A ωcos = ∴ 波函数为 )(cos u x t A y -=ω即 )]4(2cos[1042x t y -⨯=-π⑵ 将t = 3 s 代入波函数,得波形曲线方程)]43(2cos[1042x y -⨯=-πt = 3 s 时刻的波形图见图(b).8-8 一正弦式空气波沿直径为0.14 m 的圆柱形管道传播,波的平均强度为1.8⨯10 2J/(sm 2),频率为300 Hz ,波速为300 m/s ,问波中的平均能量密度和最大能量密度各是多少?每两个相邻周相差为2π 的同相面之间的波段中包含有多少能量? 原题 20-78-9 频率为100 Hz ,传播速度为300 m/s 的平面简谐波,波线上两点振动的位相差为31π,则此两点距离为 0.5 m . 原题 20-11 解:νλu ==…= 3 m , x ∆=∆)π2(λϕ,))π2(λϕ∆=∆x =…= 0.5 m(b)u)cm (y 48O1216202444-)m (x 题8-7图(a))cm (y )s (t 12O 34564-(b)cm)(y O)m (x8-10 在弹性媒质中有一波动方程为)2ππ4cos(01.0--=x t y (SI )的平面波沿x 轴正向传播,若在x = 5.00处有一媒质分界面,且在分界面处相位突变 π,设反射后波的强度不变,试写出反射波的波函数. 原题 20-108-11 一平面简谐波某时刻的波形图如图所示,此波以速率u 沿x 轴正向传播,振幅为A ,频率为v .⑴ 若以图中B 点为坐标原点,并以此时刻为 t = 0 时刻,写出此波的波函数; ⑵ 图中D 点为反射点,且为波节,若以D 点为坐标原点,并以此时刻为 t = 0 时刻,写出入射波的波函数和反射波的波函数;⑶ 写出合成波的波函数,并定出波节和波腹的位置坐标.P326 13.29解:⑴ B 点为坐标原点,t = 0 时刻,A A y -==ϕcos 0 ♉ 初相位 π=ϕ 振动方程 )cos(ϕω+=t A y ♉ )ππ2cos(+=t A yB ν ∴ 波函数为 ]π)(π2cos[+-=u x t A y ν ⑵ D 点为坐标原点,t = 0 时刻,入射波: ⎭⎬⎫>'-=='=0sin 0cos 00ϕωυϕA A y ♉ 初相位 2π-='ϕ 反射波:∵D 点为波节,∴初相位 2ππ=+'=''ϕϕD 点振动方程 )2ππ2cos(-=t A y D ν入, )2ππ2cos(+=t A y D ν反∴波函数为 ]2π)(π2cos[--=x t A y ν入, ]2π)(π2cos[++=x t A y ν反 ⑶ 合成波的波函数 )π2cos()2ππ2cos(2t u x A y y y νν+=+=反入波节:由 π)21(2ππ2+=+k u x ν 得 νu k x ⋅=2 (k = 0, -1, -2, …)波腹:由 π2ππ2k x =+ν 得 νu k x )412(-= (k = 0, -1, -2, …)题8-11图8-12 入射波的波函数为)( π2cos 1λx T t A y +=,在x = 0处发生反射,反射点为自由端.⑴ 写出反射波的波函数;⑵ 写出驻波的波函数;⑶ 给出波节和波腹的位置. P327 13.30解:反射点为自由端,是波腹,无半波损失, ⑴ 反射波的波函数为 )( π2cos 2λx T t A y -=⑵ 驻波的波函数为 t Tx A y y y π2cos π2cos 221λ=+=⑶ 当1π2cos =x λ,即ππ2 k x =λ时,得波腹的位置为 2 λk x =,k = 0, 1, 2, …当0π2cos =x λ,即2π)12(π2 +=k x λ时,得波节的位置为4)2( λ+=k x ,k = 0, 1, 2, …*8-13 一平面简谐波沿x 轴正向传播,振幅为A = 10 cm ,角频率π7=ω rad/s ,当t = 1.0 s 时,x = 10 cm 处a 质点的振动状态为0=a y ,0)d d (<a t y ;同时x = 20cm 处b 质点的振动状态为0.5=b y cm ,0)d (>b t y .设波长10>λcm ,求该波的波函数.P315 13.13解:当t = 1.0s 时刻,a 质点 0cos ==a a A y ϕ,0sin )d d ( <-==a a a A t y ϕωυ, ♉ 2ππ2+=k a ϕ ①b 质点 2cos A A y a b ==ϕ,0sin )d d ( >-==a b b A t y ϕωυ,♉ 3ππ2-'=k b ϕ a 、b 两点相位差 b a ϕϕϕ-=∆65π)(π2+'-=k ka 、b 两点间距λ<=-=∆10b a x x x ,∴π2<∆ϕ,则ϕ∆的取值可分两种情况⑴ 当0='-k k 时,b a ϕϕϕ-=∆65π=,♉λϕ2π=∆∆x ,则 )(2πϕλ∆∆=x = 24 (cm)∵波沿x 轴正向传播,可设波函数为)π2cos(0ϕλω+-=x t A y )24π2π7cos(100ϕ+-=x t当t = 1.0 s ,x = 10 cm 时波函数的相位 a ϕϕ=+⨯-⨯01024π21.0π7 ②由式①、②求得: 317ππ20-=k ϕ, 不妨取 k = 0,则 17π0-=ϕ 波函数为 )π31712ππ7cos(10--=x t y (cm)⑵ 当1-='-k k 时,b a ϕϕϕ-=∆67π-= < 0,波将沿x 轴负向传播,故舍去.作业10 光的衍射10-1 如果单缝夫琅和费衍射的第一级暗纹发生在衍射角为︒=30θ的方位上,所用单色光波长为500=λnm ,则单缝宽度为: 1.0 μm . 解: 暗纹公式 λθk a =sin10-2 在单缝夫琅和费衍射装置中,设中央明纹衍射角围很小.若使单缝宽度a 变为原来的3/2,同时使入射单色光波长变为原来的3/4,则屏上单缝衍射条纹中央明纹的宽度2ρ将变为原来的 1/2 倍.解:由单缝衍射暗纹公式 λθk a =sin ,暗纹位置 θθsin tan f f x k ≈⋅=,∴中央明半纹宽a f x λρ==1;若43λλ=',23a a =' 代入上式得 2ρρ=' 10-3 在单缝夫琅和费衍射中,设第一级暗纹的衍射角很小.若纳黄光(≈1λ589.3 nm )中央明纹宽度为4.00 mm ,则=2λ442 nm 的兰紫色光的中央明纹宽度为 3 mm. 解:单缝衍射中央明纹半宽度a f x λρ==1,∴2121λλρρ=,1122)(22ρλρ== 3 mm 10-4 单缝夫琅和费衍射对应三级暗纹,单缝宽度所对应的波面可分为 6 个半波带.若缝宽缩小一半,原来第三级暗纹变为第 一级明 纹.(原题22-2)解:由单缝暗纹公式 263sin λλλθ⨯===k a ∴ 单缝面分为6个半波带.若缝宽缩小一半,单缝面分为3个半波带,所以原第三级暗纹为变第一级明纹. 10-5 波长分别为1λ和2λ的两束平面光波,通过单缝后形成衍射,1λ的第一极小和2λ的第二极小重合.问:⑴1λ与2λ之间关系如何?⑵ 图样中还有其他极小重合吗? 解:⑴ 由单缝极小条件 11sin λθ=a 222sin λθ=a而 21θθ= ∴ 212λλ=⑵ 由 111sin λθk a =与 222sin λθk a = ,如有其它级极小重合时,必有21θθ= ,于是 2211λλk k = ,而212λλ=∴ 212k k = 即只要符合级数间的这个关系时,还有其它级次的极小还会重合.10-6 如图所示,用波长为546 nm 的单色平行光垂直照射单缝,缝后透镜的焦距为40.0 cm ,测得透镜后焦平面上衍射中央明纹宽度为 1.50 mm ,求:⑴ 单缝的宽度;⑵ 若把此套实验装置浸入水中,保持透镜焦距不变,则衍射中央明条纹宽度将为多少?(水的折射率为1.33) 原题22-1⑴ a = 2.912×10-4m⑵ 中央明纹宽a f x λρ2221=== 1.13×10-3 m10-7 衍射光栅主极大公式λθk d =sin ,Λ,3 ,2 ,1 ,0±±±=k .在k = 2的方向上第一条缝与第六条缝对应点发出的两条衍射光的光程差δ λ10 . 解:光栅相邻缝对应点发出的衍射光在2=k 的方向上光程差为λ2,则1=N 与6=N 对应点发出的衍射光的光程差λλδ1052=⨯=.10-8 用波长为546.1 nm 的平行单色光垂直照射在一透射光栅上,在分光计上测得第一级光谱线的衍射角︒=30θ,则该光栅每一毫米上有 916 条刻痕.解:由光栅方程 λθk d =sin , 得 mm 91630sin 1条=︒==λd N10-9 用一毫米刻有500条刻痕的平面透射光栅观察钠光谱(3.589=λnm ),当光线垂直入射时,最多能看到第 3 级光谱.解:63102500101--⨯=⨯=d m ,光线垂直入射时,光栅衍射明纹条件λθk d =sin∵1sin <θ, 得 39.3=<λdk ,取整数 3max =k10-10 一束平行光垂直入射在平面透射光栅上,当光栅常数d /a = 3 时,k = 3, 6, 9级不出现. 解:由光栅缺级条件()k a d k '=,Λ,3,2,1±±±='k 时,Λ,9,6,3±±±=k 级缺级当k '取1时,3=k ,∴a d 3= 10-11 入射光波长一定时,当光线从垂直于光栅平面入射变为斜入射时,能观察到的光谱线最高级数max k 变大 (填“变小”或“变大”或“不变”). 解:正入射光栅方程λθk d =sin ;斜入射光栅方程λθk i d '=+)sin (sin ,…,∵︒<90θ,︒<≤︒900i ,∴1sin <θ,1sin 0<<i , ∴ m ax max k k >' 10-12 用波长围为400~760 nm 的白光照射到衍射光栅上,其衍射光谱的第二级和第三级重叠,则第三级光谱被重叠部分的波长围是 400 ~ 506.7 nm . 原题22-6 解:λλ''=k k ,2323λλ=,令 2λ= 760 nm ,得 3λ = 506.7 nm 10-13 从光源射出的光束垂直照射到衍射光栅上.若波长为3.6531=λnm 和2.4102=λnm 的两光线的最大值在︒=41θ处首次重合.问衍射光栅常数为何值?解:由光栅方程公式有 dk d k 2211sin λλθ==∴60.12.4103.6561212===λλk k 而1k 与 2k 必须是整数,又取尽量小的级数 ∴8,521==k k=︒⨯⨯==-41sin 103.6565sin 91θλk d 61000.5-⨯ m10-14 波长为500nm 的单色平行光垂直入射于光栅常数为3103-⨯=d mm 的光栅上,若光栅中的透光缝宽度3102-⨯=a mm ,问⑴ 哪些谱线缺级?⑵ 在光栅后面的整个衍射场中,能出现哪几条光谱线? 解:⑴ 根据缺级条件 k a dk '=(Λ,3,2,1±±±='k )则光栅的第k 级谱线缺级(k 为整数) 本题 k k k a d k '='⨯⨯='=--2310210333 当 ='k 2、4、6….时k = 3、6、…则第±3、±6,…谱线缺级根据光栅方程 λθk d =sin , λθsin d k = , 令 2/πθ<得 61050010103933=⨯⨯⨯=<---λdk ,再考虑到缺级.只能出现 0、±1、±2、±4、±5共9条光谱线.10-15 一双缝,缝距 d = 0.40 mm ,两缝的宽度都是a = 0.080 mm ,用波长为480=λnm 的平行光垂直照射双缝,在双缝后放一焦距为f = 2.0 m 的透镜,求:⑴ 在透镜焦平面处的屏上,双缝干涉条纹的间距∆x ;⑵ 在单缝衍射中央亮纹围的双缝干涉亮纹数目. 原题22-3⑴ ∆x = 2.4×10-3 m⑵ 在单缝衍射中央亮纹围有 9条 亮谱线:4 ,3 ,2 ,1 ,0±±±±级10-16 光学仪器的最小分辨角的大小[ C ](A) 与物镜直径成正比; (B) 与工作波长成反比(C) 取决于工作波长与物镜直径的比值;(D) 取决于物镜直径与工作波长的比值. 解:Dλϕ22.1δ=10-17 人眼瞳孔随光强大小而变,平均孔径约为3.0 mm ,设感光波长为550 nm ,眼睛可分辨的角距离约为 1 分. 解:取人眼孔径为3 mm ,入射光波长为550nm ,眼最小分辨角 122.1δ'≅=ΛDλϕ10-18 在夜间人眼的瞳孔直径约为5.0 mm ,在可见光中人眼最敏感的波长为550 nm ,此时人眼的最小分辨角为 27.6 秒,有迎面驶来的汽车,两盏前灯相距1.30 m ,当汽车离人的距离为 9.69×103m 时,人眼恰好可分辨这两盏灯.原题22-7 解:Λ==Dλϕ22.1δ; Λ=∆∆=θx l10-19 根据光学仪器分辨率的瑞利判据,要利用望远镜分辨遥远星系中的星体,可采用 增大透镜直径 或 用较短的波长 的方法.10-20 用一部照相机在距离地面20 km 的高空中拍摄地面上的物体,若要求它能分辨地面上相距为0.1m 的两点,问照相机镜头的直径至少要 13.4 cm .(设感光波长为550 nm )解:由 l s D ==λϕ22.1δ,得134.01.010*********.1 22.139=⨯⨯⨯⨯==-s l D λm = 13.4cm 10-21 以未知波长的X 射线掠入射于晶面间隔为10103-⨯=d m 的晶面上,测得第一级布喇格衍射角︒=51θ,则该X . 解:λϕk d =sin 2,k = 1,……10-22 一束波长围为0.095 ~ 0.140 nm 的X 射线照射到某晶体上,入射方向与某一晶面夹角为︒30,此晶面间的间距为0.275 nm ,求这束X 射线中能在此晶面上产生强反射的波长的大小. 原题22-8=λ0.1375 nm10-23 测量未知晶体晶格常数最有效的方法是X 射线衍射法.现用波长07126.0=λ nm (钼谱线)的X 射线照射到某未知晶体上,转动晶体,在三个相互正交的方位上各测得第2级布喇格衍射角分别为59561'''︒=ϕ、79132'''︒=ϕ、14943'''︒=ϕ,请分别求出这三个相互正交方位上的晶面间距. 解:晶体的衍射满足布喇格方程 λϕk d =sin 2 ϕλsin 2k d =已知 k = 2,︒=985.61ϕ、︒=319.32ϕ、︒=161.43ϕ解得:=1d 0.586 nm ,=2d 1.231 nm ,=3d 0.982 nm (该晶体为斜方晶系的无水芒硝)习题参考答案作业2 动量与角动量 功与能2-1 0.6 N·s; 2 g 2-2 1.41 Ns2-3 M P '=2υ;=''F 30N ,=P 45W 2-4 5.30 × 1012m 2-5 B A a b υυ= 2-6 0.45 m2-7 )(mr k ,)2(r k - 2-8 )2(22k g m2-9 )6(R GMm ,)3(R GMm - 2-10 4.23×106 J , 151 s 2-11 31 J ,5.345 m/s2-12 222k ωq m E P =,222k ωp m E Q =222ωp m A x =,222ωq m A y -=作业4 气体动理论4-1 0.13 kg ,117升4-2 平衡状态,气体的准静态过程 4-3 1.53 × 104 Pa 4-4 相同,不同,不同 4-5 kTpVN =4-6 10 : 3, 5 : 3, 1 : 1 4-7 略4-8 =∆E 41.55 J ,221007.2-⨯=∆K E 4-9 =∆T 0.481 K ,41000.2⨯=∆p Pa 4-10 R E 52,)5(2μE ,)π5(4μE4-11 υυυd )(d 100⎰⎰∞=='f NN N ,υυd )(100⎰∞=f P ,υυυυυυd )(d )(100100⎰⎰∞∞=f f4-12 D4-13 51035.1⨯=P Pa 4-14 n = 3.2×1017 m 3 ,=λ7.8 m ,=z 59.9 s 14-15 =⎪⎭⎫ ⎝⎛υ1kT m π2=, υυ1π41⋅=⎪⎭⎫ ⎝⎛4-16 )3(20υ=a ,=∆N 0.333 N ,=υ 1.220υ,=2υ 1.310υ作业6 狭义相对论基础6-1 93,10,0,2.5×107s 6-2 51033.3-⨯-s ,天津 6-3 3.61 m ,143369.33'︒=︒ 6-4 1.418×108 m/s = 0.473 c 6-5 12 m ,4 s6-6 =∆t 1.6 s ,='∆t 0.96 s 6-7 )(122c a υ-,)(122c mυ-,)1(22c ab mυ-6-8cu c u l x -+=∆110,c u c u cl t -+=∆110,c =υ 6-9 0.7×106-10 50.8% 6-11 46-12 211k c -=υ 6-13 0.866 c ,0.866 c 6-14 2.94×10 eV6-15 4.1×1066-16 m = 2.67m 0,=υ0.5c ,0031.2m m =' 6-17 c 115.0m ax =υ,=ke E 3.43×103eV ,==ke kp 1840E E 6.31×106eV作业8 波 动8-1 略8-2 7.58×105 m8-3 316, 2.11×10118-4 10.5m ,5Hz ,52.4m/s ,x 轴正方向x = 0处质元的振动方程 8-5 600 cm/s ,)]24π(252sin[30.0x t y +=(cm)8-6 2π9-=ϕ,2π=∆ϕ 8-7 )]4(2cos[1042x t y -⨯=-π,图略8-8 4106.0-⨯J/m 3,4102.1-⨯J/m 3;71024.9-⨯J 8-9 0.58-10 []2ππ4cos 01.0++=x t y 反 8-11 ]π)(π2cos[+-=u x t A y ν]2π)(π2cos[--=x t A y ν入]2π)(π2cos[++=u x t A y ν反波节:νu k x ⋅=2(k = 0, -1, -2, …),波腹:νu k x )412(-=(k = 0, -1,-2, …)8-12 )( π2cos 2λx T t A y -=,t Tx A y y y π2cos π2cos 221λ=+=波腹 2 λk x =,k = 0, 1, 2, …波节 4)2( λ+=k x ,k = 0, 1, 2, …8-13 )π31712ππ7cos(10--=x t y (cm)作业10 光的衍射10-1 1.0 10-2 1/2 10-3 310-4 6, 一级明10-5 212λλ=,1λ的第k 1极小和2λ的第k 2 = 2k 1极小重合. 10-6 a = 2.912×10-4m,=ρ2 1.13×10-3m 10-7 λ10 10-8 916 10-9 3 10-10 3 10-11 变大10-12 400 ~ 506.7 10-13 61000.5-⨯=d m10-14 第±3、±6,…谱线缺级,只出现0,±1,±2,±4,±5共9条光谱线. 10-15 2.4 mm , 9条亮纹10-16 C 10-17 110-18 27.6, 9.69×10310-19 增大透镜直径, 用较短的波长 10-20 13.4 10-21 111023.5-⨯ 10-22 =λ0.1375 nm10-23 =1d 0.586 nm ,=2d 1.231 nm ,=3d 0.982 nm。
第二次作业:静电场(二)一.选择题(答案填入下表)题号12345答案1.某电场的电力线分布情况,如图所示。
一负电荷从M 点移到N 点。
有人根据这个图作出下列几点结论,其中哪点是正确的?[答案填入上表](A)电场强度N M E E >;(B)电势N M U U >;(C)电势能N M W W <;(D)电场力的功0>A 。
2.半径为r 的均匀带电球面1,带电量为q ;其外有同心的半径为R 的均匀带电球面2,带电量为Q ,则此两球面之间的电势差U 1-U 2为:[答案填入上表](A)[q/(4πε0)][(1/r)-(1/R)];(B)[Q/(4πε0)][(1/R)-(1/r)];(C)[1/(4πε0)][(q/r)-(Q/R)];(D)q/(4πε0r).3.真空中有一点电荷Q ,在与它相距为r 的a 点处有一试验电荷q .现使试验电荷q 从a 点沿半圆弧轨道运动到b 点,如图所示,则电场力对q 做功为[答案填入上表](A)24220r rQq ππε⋅;(B)r r Qq 2420⋅πε;(C)204r Qq πε;(D)0.4.在静电场中,下列说法中哪一个是正确的?[答案填入上表](A)带正电荷的导体,其电势一定是正值。
(B)等势面上各点的场强一定相等。
(C)场强为零处,电势也一定为零。
(D)场强相等处,电势梯度矢量一定相等。
5.有四个等量点电荷在OXY平面上的四种不同组态,所有点电荷均与原点等距,设无穷远处电势为零,则原点O处电场强度和电势为零的组态是:[答案填入上表]二、填空题(答案填入下表)题号12-(1)2-(2)3答案题号4-(1)4-(2)4-(3)4-(4)答案题号567答案1.如图所示,一等边三角形边长为a,三个顶点上分别放置着电量为q、2q、3q的三个正点电荷。
设无穷远处为电势零点,则三角形中心处O的电势U0=[答案填入上表].2.一“无限长”均匀带电直导线沿Z轴放置,线外某区域的电势表达式为U=Aln(x2+y2),式中A为常数,该区域的场强的两个分量为: E[(1)答案填入上表]=z E[(2)答案填入上表] =x3.设在均匀电场中,场强E 与半径为R 的半球面的轴相平行,通过此半球面的电场强度通量为[答案填入上表].4.把一个均匀带电量为+Q 的球形肥皂泡由半径r 1吹到半径r 2,则半径为R (r 1<R <r 2)的高斯球面上任一点的场强大小E 由[(1)答案填入上表]变为[(2)答案填入上表];电势U 由[(3)答案填入上表]变为[(4)答案填入上表]。
习 题 十 三13-1 求各图中点P 处磁感应强度的大小和方向。
[解] (a) 因为长直导线对空间任一点产生的磁感应强度为:()210cos cos 4θθπμ-=aIB 对于导线1:01=θ,22πθ=,因此aI B πμ401=对于导线2:πθθ==21,因此02=BaIB B B πμ4021p =+= 方向垂直纸面向外。
(b) 因为长直导线对空间任一点产生的磁感应强度为:()210cos cos 4θθπμ-=aIB 对于导线1:01=θ,22πθ=,因此r I a I B πμπμ44001==,方向垂直纸面向内。
对于导线2:21πθ=,πθ=2,因此rI a I B πμπμ44002==,方向垂直纸面向内。
半圆形导线在P 点产生的磁场方向也是垂直纸面向内,大小为半径相同、电流相同的圆形导线在圆心处产生的磁感应强度的一半,即rIr I B 4221003μμ==,方向垂直纸面向内。
所以,rIr I r I r I r I B B B B 4244400000321p μπμμπμπμ+=++=++=(c) P 点到三角形每条边的距离都是a d 63=o 301=θ,o 1502=θ每条边上的电流在P 点产生的磁感应强度的方向都是垂直纸面向内,大小都是()aI d IB πμπμ23150cos 30cos 400000=-=故P 点总的磁感应强度大小为aIB B πμ29300== 方向垂直纸面向内。
13-2 有一螺线管长L =20cm ,半径r =2.0cm ,导线中通有强度为I =5.0A 的电流,若在螺线管轴线中点处产生的磁感应强度B =310166-⨯.T 的磁场,问该螺线管每单位长度应多少匝?[解] 已知载流螺线管轴线上场强公式为()120cos cos 2θθμ-=nIB由图知: 10410cos 2=θ,10410cos 1-=θ,所以,⎪⎪⎭⎫ ⎝⎛⨯=10410220nI B μ, 所以,匝=1000101040IBn μ=13-3 若输电线在地面上空25m 处,通以电流31081⨯.A 。
(单选题)1: 关于高斯定理的理解有下面几种说法,其中正确的是()A: 如果高斯面上电场强度处处为零,则该面内必无电荷B: 如果高斯面无电荷,则高斯面上电场强度处处为零C: 如果高斯面上电场强度处处不为零,则高斯面内必有电荷D: 如果高斯面内有净电荷,则通过高斯面的电通量必不为零正确答案: D(单选题)2: 一带电体可作为点电荷处理的条件是()A: 电荷必须呈球形分布B: 带电体的线度很小C: 带电体的线度与其它有关长度相比可忽略不计D: 电量很小正确答案: C(单选题)3: 一物体做斜抛运动(略去空气阻力),在由抛出到落地的过程中()A: 物体的加速度是不断变化的B: 物体在最高点处的速率为零C: 物体在任一点处的切向加速度均不为零D: 物体在最高点处的法向加速度最大正确答案: D(单选题)4: 关于电场强度与电势之间的关系,下列说法中,哪一种是正确的()A: 在电场中,场强为零的点,电势必为零B: 在电场中,电势为零的点,电场强度必为零C: 在电势不变的空间,场强处处为零D: 在场强不变的空间,电势处处相等正确答案: C(单选题)5: 质点作变速直线运动时,速度、加速度的关系为()A: 速度为零,加速度一定也为零B: 速度不为零,加速度一定也不为零C: 加速度很大,速度一定也很大D: 加速度减小,速度的变化率一定也减小正确答案: D(单选题)6: 物体作曲线运动时()有加速度。
A: 一定B: 不一定正确答案: A(单选题)7: 将一重物匀速推上一个斜坡,因其动能不变,所以()A: 推力不作功B: 推力功与摩擦力的功等值反号C: 推力功与重力的功等值反号。
班级___ ___学号____ ____姓名____ _____成绩______________ 一、选择题
1. m 与M 水平桌面间都是光滑接触,为维持m 与M 相对静止,则推动M 的水平力F 为:( B ) (A)(m +M )g ctg (B)(m +M )g tg (C)mg tg (D)Mg tg
2. 一质量为m 的质点,自半径为R 的光滑半球形碗口由静止下滑,质点在碗内某处的速率为v ,则质点对该处的压力数值为:( B )
(A)R mv 2 (B)R mv 232 (C)R mv 22 (D)R mv 252
3. 如图,作匀速圆周运动的物体,从A 运动到B 的过程中,物体所受合外力的冲量:( C ) (A) 大小为零
(B ) 大小不等于零,方向与v A 相同 (C) 大小不等于零,方向与v B 相同
(D) 大小不等于零,方向与物体在B 点所受合力相同
二、填空题
1. 已知m A =2kg ,m B =1kg ,m A 、m B 与桌面间的摩擦系数
=,(1)今用水平
力F =10N 推m B ,则m A 与m B 的摩擦力f =_______0______,m A 的加速度a A =_____0_______. (2)今用水平力F =20N 推m B ,则m A 与m B 的摩擦力
f =____5N____,m A 的加速度a A =. (
g =10m/s 2)
2. 设有三个质量完全相同的物体,在某时刻t 它们的速度分别为v 1、v 2、v 3,并且v 1=v 2=v 3 ,
v 1与v 2方向相反,v 3与v 1相垂直,设它们的质量全为m ,试问该时刻三物体组成的系统的总
动量为_______m v 3________.
3.两质量分别为m 1、m 2的物体用一倔强系数为K 的轻弹簧相连放在光滑水平桌面上(如图),当两物体相距为x 时,系统由静止释放,已知弹簧的自然长度为x 0,当两物体相距为x 0时,m 1的速度大小为
F
m A m B
m
M
F
θ
A O
B R v A
v B
x
m
1m 2
2
2
121
Km x m m m + . 4. 一弹簧变形量为x 时,其恢复力为F =2ax -3bx 2
,现让该弹簧由x =0变形到x =L ,其弹力的功为: 23
aL bL - .
5. 如图,质量为m 的小球,拴于不可伸长的轻绳上,在光滑水平桌面上作匀速圆周运动,其半径为R ,角速度为,绳的另一端通过光滑的竖直管用手拉住,如把绳向下拉R /2时角速度’
为
4 ,在此过程中,手对绳所作的功为 223
2
m R ω .
三、计算题:
1.一质量为m的物体,从质量为M的圆弧形槽顶端由静止滑下,设圆弧形槽的半径为R,张角为/2,如图所示,如所有摩擦都可忽略,求:(1)物体刚离开槽底时,物体和槽的速度各是多少(2)在物体从A滑到B的过程中,物体对槽做的功为多少
(3)物体到达B点时,对槽的压力(B点为槽的最底端).
解:(1)m 从M 上下滑的过程中,机械能守恒,以m ,M ,地球为系统,以最低点为重力势能零点,则有
222
1
21MV mv mgR +=
又下滑过程,动量守恒,以m ,M 为系统则在m 脱离M 瞬间,水平方向有 0=-MV mv 联立,以上两式,得 ()M m MgR v +=
2;2()
gR
V m M M m =+
(2)22
12m gR W MV M m
==+
(3)'v V v += 2'v F mg m R =+ 2(3)m
N mg M
=+
2.设N 67j i F -=合.(1) 当一质点从原点运动到m 1643k j i r
++-=时,求F 所作的
功.(2)如果质点到r 处时需,试求平均功率.(3)如果质点的质量为1kg ,试求动能的变化.
m
R
m
M
R
O
B
解: (1)由题知,合F
为恒力,(76)(3416)W F r i j i j k =⋅=-⋅-++合
J 452421-=--= (2) 4575w 0.6
W P t =
==∆ (3) 由动能定理,45J
k E W ∆==-
3. 质量m =的小球,拴在长度L =的轻绳的一端,构成摆,摆动时与竖直的最大夹角为60°. (1)小球通过竖直位置时的速度为多少此时绳的张力(2)在<60°的任一位置,求小球速度
v 与 的关系式,这时小球的加速度为何绳的张力为多大.
解: (1)0
2
1(cos60)02
mg l l mv -=
- 得 v gl ; 2
2v T mg m mg l
=+= (2)0
2
1(cos cos60)02
mg l l mv θ-=- 得(2cos 1)v gl θ=
-
20
53
cos(60)(cos 1)2v T mg m mg l θθθ=-+=+-
O B
m
A
θ 60o。