研究生高等光学-空间滤波与θ调制-原理及实验指导

实验一θ调制法空间假彩色编码【实验目的】1．掌握θ调制法假彩色编码的原理．巩固和加深对光栅衍射基本理论的理解；2．掌握用θ调制法进行空间假彩色编码的方法，并作出相应的实验结果，加深对阿贝二次成像理论和空间频率滤波的理解，为今后学习其他假彩色编码方法打下基础。

3．了解用计算机胶片输出简单的二维θ调制片的制作原理。

【实验光路】图1-1【实验原理】Ө调法假彩色编码是阿贝二次衍射成像理论的一种巧妙的应用。

它是先用不同的光栅分别调制图像的不同部分，制成Ө调制片（或称光栅调制片），然后将其置于4f系统的输入面上，并用白光照明。

在频谱面上进行适当的空间滤波处理，便可在输出面上得到假彩色图像。

在一透镜前方放置一块栅线平行等距的光栅，当用一束单色平行光垂直照明时，在透镜的后焦面（即频谱面）上会形成光栅衍射的离散频谱点，其排列方向垂直于光栅栅线的方向。

如果有一个二维图像，其不同部位受到方向不同的光栅的调制，则频谱面上频谱点的分布也对应于不同的方向。

若挡住任一方向的频谱点，则与其对应的那部分图像就会消失。

可见，输入图像中的各个部分的频谱，只存在于调制光栅的频谱点附近，这显然是由于各部分图像频谱与其对应的调制光栅的频谱卷积的结果。

如果用白光光源照明Ө调制片，则在频谱面上得到色散的彩色谱斑。

每个彩色谱斑的颜色分布都是从外向内按照红、橙、黄、绿、蓝、靛、紫的顺序变化。

这种现象是易于理解的，因为光栅衍射角的大小与入射角的波长有关。

红光的波长最长，故衍射角最大，分布在最外；而紫光的波长最短，故衍射角最小，分布在最里。

如果在频谱面上放置一个空间滤波器，让不同方位的谱斑通过不同的颜色，则在像面上可以得到彩色像。

由于这种方法是利用不同方位的光栅（彼此转动了θ角）对图像进行调制，因此称其为θ调制技术。

又因为它是将图像中不同空间部位编上不同的颜色，故又称空间假彩色编码。

θ调制空间假彩色编码就是通过θ调制的处理手段，“提取”白光中所包含的彩色，再“赋予”图像而形成的。

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==θ调制实验报告篇一：θ调制实验θ调制实验一、相关科目：光栅及光栅衍射，阿贝成像原理，空间频谱与空间滤波，假彩色编码二、实验原理：θ调制实验是对阿贝的二步成像理论的一个巧妙应用。

将一个物体用不同的光栅来进行编码，制作成θ片。

如本实验中的花朵、叶子和背景，分别是由三组取向成120度的光栅构成的。

将θ片置于白光照明中，在频谱面上进行适当的空间滤波处理，便可在输出面上得到一个假彩色的像。

我们知道，如果在一个透镜的前面放置一块光栅并用一束单色平行光垂直的照射它，在透镜的后焦面（即频谱面）上就会形成一串的衍射光斑，其方向将垂直于光栅的方向。

如果有一个二维的图形，其不同部分由取向不同光栅制成（调制），显而易见，他们的衍射光斑也将有不同的取向，即在透镜的后焦平面（频谱面）上，各部分的频谱分布也将有不同，如果我们挡住某一部分的频谱，在频谱面后的这部分图象将会消失，可见，输入图象中各部分的频谱，只存在于调制光栅的频谱点附近。

如果我们用白光照射θ片，则在频谱上可得到彩色的频谱斑（色散作用），每个彩色斑的颜色分布从外向里按赤、橙、黄、绿青、兰、紫的顺序排列，这是由于光栅的衍射角与光波长有关，波长越长衍射角越大。

如果我们在频谱面上，放置一个空间滤波器，这种滤波器可以让不同方位的光斑串，不同的颜色有选择地通过，则我们就可以得到一幅彩色的像。

如，在花朵图象的光斑方向上，我们让光斑中绿色的光通过；在背景图象的光斑方向上，让光斑中绿色的光通过；在背景图象的光斑方向上，让光斑中兰色的光通过，这样我们就会得到一幅红花、绿叶、蓝色背景的彩色图像，而实际上物体（θ片）是无色的，这就实现了假彩色编码。

三、实验方法：1、按下图摆放实验装置。

2、在频谱架上插入一张白纸（或纸板），前后移动频谱架观察θ片的频谱，体会θ片中各方向光栅的作用，使频谱尽量明亮清晰，固定好频谱架。

空间滤波实验实验目的1、加深傅立叶光学基本概念和理论的理解2、了解空间滤波实验系统3、验证阿贝二次成像理论 实验原理空间滤波实验也称阿贝—波特实验，属于采用滤波方法来处理光学信息的技术，其理论基础是阿贝二次成像原理。

阿贝（Ernst Abbe,1840-1905），德国科学家，曾在蔡司公司任职，1873年在研究如何提高显微镜的分辨本领时，他首次提出了一个与几何光学成像传统理论完全不同的成像概念。

后来，阿贝本人1893年和波特于1906年用实验验证了阿贝成像理论。

阿贝理论和上述两次实验可以看作是傅立越光学的开端。

阿贝成像理论的核心是：相干照明下成像过程可分做两步，首先是物面上发出的光波在物镜后焦面上发生夫琅和费衍射，得到第一次衍射像；然后，该衍射像作为新的相干波源，由它发出的次波在像面上干涉而构成物体的像，称为第二次衍射像。

因此，该理论也常被称为“阿贝二次衍射成像理论”。

后人称其为阿贝成像原理（Abbe’ Principle of image of formation ）。

图1是上述成像过程的示意图。

其中物面()11,y x ，用相干平行光照明，在透镜后焦面即频谱面()22,y x 得到物的频谱，这是第一次成像过程，实际上是经过了一次傅立叶变换；由频谱()22,y x 而到像面()33,y x ，也是完成了一次夫琅和费衍射过程，等于又经过一次傅立叶变换。

当像面取反射坐标时，后—次变换可视为傅立叶逆变换。

经上述两次变换，像面上形成的是物体的像。

A B CP P 'A 'B 'C (x 2,y 2)(x 3,y 3)图1 阿贝二次成像理论示意图用频谱语言表达阿贝成像原理，那就是，第一步发生夫琅和费衍射，起“分频”作用，第二步发生干涉，起“合成”作用。

这两个步骤本质上就是两次傅立叶变换。

第一步“分频”是把物面光场的空间分布()y x g ,变为频谱面上的空间频率分布),(y x f f G 。

姓名：学号：（实验五）空间滤波和θ调制一、实验目的1. 了解空间滤波概念、实现方法及其在光学信息处理中的作用；2. 初步了解简单的空间滤波在光学信息处理中的实际应用；3. 了解θ调制的原理；4. 学会利用光学原件组装θ调制光路。

二、实验原理1. 空间滤波根据阿贝成像理论，像是频谱面上各级频谱产生的子波相干叠加的结果（干涉合频）。

由此启发我们，可通过对频谱面的改造达到改造像的目的。

在频谱面上所作的光学处理就是空间滤波。

最简单的滤波器就是把一些特殊形式的光阑插到焦平面上，使一个或几个频率分量能通过，而挡住其他频率分量，从而使像平面上的图像只包括一种或几种频率分量。

2.θ调制θ调制是用不同取向的光栅对物平面的各部位进行调制（编码），通过特殊滤波器控制像平面相应部位的灰度（用单色光照明）或色彩（用白光照明）的方法。

对如图所示的θ调制板，图案各部分是有不同取向的光栅。

如果使用白光照射，每个光栅会在不同方向形成彩色频谱（零级除外）。

每个彩色谱斑的颜色分布都是从外向里按红、橙、黄、绿、蓝、靛、紫的顺序排列。

在频谱面上放置一个空间滤波器，让不同方向的谱斑通过不同的颜色，则在像面上得到彩色像。

这是利用不同方向的光栅对图像进行调制，因此称为θ调制法。

又因为它将图像中的不同部位“编”上不同的颜色，故又称空间假彩色编码。

三、实验内容1. 方向滤波按如图调节光路，物面上放置正交光栅，观察其频谱和像。

在频谱面上放置如图取向的单缝光阑，分别观察像的变化，作出必要的解释。

2. 低通滤波把一个带正交网格的透明字（透明的“光”字内有叠加的网格）置于物平面，观察其频谱和像。

把一个可变圆孔光阑放在频谱面上，使圆孔由大变小，观察像的变化，并作出解释。

3. 高通滤波将一个透光十字屏放在物平面上，从像平面观察放大像。

然后在频谱面上置一圆屏光阑，挡住频谱面的中部，再观察和记录像面变化，作出解释。

3. θ调制按如图所示调节光路，其中，L1和L2的焦距分别是190mm和225mm。

课程名称：大学物理实验（二）实验名称：阿贝成像原理和空间滤波
图2 透镜的低通滤波作用
特別当物的结构非常精细（例如很密的光栅），或物镜的孔径非常小时，有可能只有
则在像平面上只有光斑而完全不能形成图像。

根据上面讨论，我们可以看到显微镜中的物镜的孔径实际上起了高频滤波（即低通滤波）的作用。

这也启示我们，如果在谱平面上人为地插上一些滤波器以提取某些频段的光信息，从而使图像发生相应的变化，
图3空间滤波
图4 图像处理系统
2.4θ调制
将一幅透明画拆分成三部分：房子、草地、天空，将这三部分分别刻在三片不同取向的光栅上，将光栅叠在一起作为物，此物叫调制片，用白光照明调制片，光束发生衍射，衍射光束经透镜后在其焦平面成像形成衍射谱（彩色光斑），如在谱平面上放置频谱滤波器（即能让一部分光通过的挡板），在房子谱方向只让红色光谱通过，在草地谱方向只让绿色通过，在天空谱方向只让蓝色谱通过，在像平面上将看到图像被“着上”不同颜色
图4 实验现象图
图5 物镜孔径大小影响示意图。

θ调制与空间假彩色编码实验改进毛艺潜;齐怡;陶小平;张增明;孙腊珍【摘要】用曝光干涉法制作θ调制光栅物片对干涉场的质量要求很高，传统方法不能直接判断干涉场的质量。

利用CCD探测器实时采集干涉条纹，编写M atlab程序，计算干涉场参量。

该改进可以保证在干涉场较理想时曝光，提高了制作全息光栅的成功率。

%T raditional methods can not directly determine the quality of the interference field .A real‐time detection of the interference field was achieved using CCD detector ,and Matlab program was w rittento calculate the interference field parameters using acquired images ,thus the holographic im‐age could be taken when the interference field was good enoug h to increase the success rate of the pro‐duction of holographic gratings .【期刊名称】《物理实验》【年(卷),期】2015(000)007【总页数】4页(P6-9)【关键词】θ调制;全息光栅;干涉场【作者】毛艺潜;齐怡;陶小平;张增明;孙腊珍【作者单位】中国科学技术大学地球和空间科学学院，安徽合肥230026;中国科学技术大学地球和空间科学学院，安徽合肥230026;中国科学技术大学物理学院，安徽合肥230026;中国科学技术大学物理学院，安徽合肥230026;中国科学技术大学物理学院，安徽合肥230026【正文语种】中文【中图分类】O436.1“θ调制与空间假彩色编码”实验由于有搭建干涉光路和曝光等难度较高的步骤，在时间有限的教学中许多学生难以取得成功.本文采用的改进方案在搭建干涉光路和曝光之间插入了对干涉场进行质量检测的步骤，在保证搭建光路成功的基础上进行曝光操作，避免了因为光路没有调好导致无用的曝光.除此之外，本文采集干涉场图像后，还利用Matlab计算了干涉条纹宽度等信息，这有利于准确控制制成光栅物片的参量.1 实验原理θ调制是通过对图像的不同区域分别用取向不同的光栅进行调制，使其频谱在空间上发生分离.由于照明光源为白光，因而各级频谱是彩色谱带，同一级频谱从中心向外波长依次增大.采用只在特定部位打上小孔以透光的遮光板，使特定波长的光透过，即可实现特定的彩色输出.原理如图1所示[1].光栅由干涉法曝光得到，是正弦型光栅，透光率函数为其中：m是条纹对比度，ξ0是单位距离内的条纹数，l是光栅宽度.用单位振幅的单色平面光波垂直照明光栅，则距屏为z处观察平面上的夫朗禾费衍射为[2]要想提高衍射效率，需要增大m值，要求光栅透光率对比度足够高.实验最终得到的彩色还原像的效果取决于制作的全息光栅的质量.图1 θ调制实验原理图2 实验装置与实验方法2.1 马赫－曾德尔干涉采用光学方法制作光栅，利用干涉条纹使全息干板曝光，形成透光率的特定分布.具体光路图如图2所示.激光器为2.5mW氦氖激光器，全息干板采用氯化银干板. 图2 马赫－曾德尔干涉光路图2.2 CCD检测干涉场的光路干涉光路质量决定了光栅的衍射效率，也就决定了实验效果.而要想检查干涉光路是否有效，无论逐一元件检查或者试做光栅进行检验，花费时间都较多.这里采用更为直接有效的检查方式.如图3所示，在原光路布置全息干板处放置CCD(DMK －21AU04型)，调整高度和角度，接收干涉图像，传到计算机显示和分析.待实验者认为干涉场质量足够好，再将全息干板布置在CCD所在位置，进行曝光.2.3 实验方法图3 利用CCD检测干涉场质量光路图实验用的模板是1盆花的图案，有花瓣、茎叶、花盆3个部分.搭建加入CCD的马赫－曾德尔干涉光路(图3)，采集干涉场图像，若干涉场质量较差，则继续调节光路，直到干涉条纹宽度合适、足够清晰，再将CCD撤下，全息干板放回原处，进行曝光.将全息干板显影、定影，得到光栅物片.布置白光还原光路(图1).将光栅物片放在P1位置，调节各元件位置，使光栅物片的各部分都被照明，且频谱面P2上的衍射谱带清晰.分别在3个方向的1级衍射斑上选色打孔，为花、茎叶、花盆配上颜色，在光屏P3上观察还原像[3].具体实验过程参见文献[4].实验参量(如光路参量、曝光时间和显影时间)的控制不是本文讨论的重点，可参见文献[5].3 干涉图像的计算分析3.1 干涉条纹宽度计算实验中CCD采集的干涉条纹如图4所示.CCD采集的图像是灰度图，每个像素点对应1个灰度值，全黑时为0，全白时为255.图像存储为480×640的矩阵.由于条纹是周期性变化，故图像矩阵经傅里叶变换后，其对应条纹宽度的频率分量会是很明显的峰值.图4 干涉场图像(局部)为了进行频谱分析，定义灰度矩阵G[nx，ny]，(1≤nx≤640，1≤ny≤480)，它的第nx 行第ny列元素为图像对应点的像素值.矩阵的每行可以看作长度为640的序列，对特定的某行作离散傅里叶变换，可得频谱这里关心的是幅度谱，即它的模｜［k，ny0］｜．对于第200行像素（ny0＝200），｜［k，ny0］｜如图5所示．其峰值对应的频数k＝169，意义是在水平方向周期性条纹出现了169次．所以条纹宽度“水平分量”为图5 干涉条纹图像频域图对ny0＝1，2，…，480每行重复该过程，算出dx取平均得＝3.78pixel.类似地，对G[nx，ny]的每列做上述计算可得＝27.12pixel.由几何关系，条纹宽度为由CCD参量：1pixel＝6.73μm，故条纹宽度为25.2μm.3.2 干涉场对比度计算根据实验条件的不同，采集的干涉场图像质量也有变化.类似对干涉条纹的计算，同样可以通过计算机来计算干涉条纹的清晰程度，从而达到检测光路质量的目的.近似认为干涉条纹的光强分布为其中m为干涉条纹对比度.将光强替换为灰度值，则I0＝255.若采集的图像明条纹处灰度值为255，暗条纹处为0，则对比度为1.若采集的图像完全均匀，即每一点灰度值为相同值，则对比度为0.因此m可以反映干涉条纹清晰程度.为了计算m，首先将的本底去除.定义对ny0行作离散傅里叶变换：ny0＝200时，在k＝169处达到峰值，为2 478.作为对比，定义m＝1的理想情况下，则，与实际值对比，可得．对y［nx，ny］各行作上述计算，对m取平均，得＝0．062．这就是水平方向的对比度，一般来说正常的图像水平、竖直方向算出的对比度相差不大，采用水平对比度来衡量干涉场质量已经足够．4 实验结果与结论4.1 实验结果利用改进的方法进行实验.进行曝光的干涉场的参量已经在前面计算给出.在平行白光照射下，制作的全息光栅物片在频谱面上产生3个明亮的衍射斑，如图6所示. 图6 频谱面的白光衍射斑在3个方向的谱带上选色打洞，为花盆图案配色.在频谱面后方合适的位置放置光屏，看到花盆的还原像，如图7(b)，模板见图7(a).图7 图案模板及花盆的还原像4.2 结论1)实验结果说明：用对比度为0.062的干涉场进行曝光可以得到较好的效果，后续的实验可以将这个值作为参考，当对比度接近或超过0.062时曝光，会增大实验成功的把握.2)本文计算的干涉场对比度也依赖于某些实验条件，包括激光功率、CCD灵敏度.在一定的实验条件下，经过几次前期试验，可以定出符合该实验条件的最低对比度建议值，在后续实验中，只要不更改激光输出功率、不更换CCD，就可以一直沿用该建议值.【相关文献】[1]唐雄贵，李和平，廖进昆，等.θ调制实验的教学改进及其模拟实现[J].实验科学与技术，2009，7(1)：13－15.[2]卞松玲，刘木兴，刘良读，等.傅里叶光学[M].北京：兵器工业出版社，1989：133－136.[3]陆启图，刘永道，王德钊.漂白银盐干版的假彩色编码[J].物理实验，1988，8(6)：284－285.[4]欧振湖.θ调制和彩色像的产生[J].华南师范大学学报(自然科学版)，1995(2)：112.[5]何建瑜，赵荣涛，竺哲欣，等.全息光栅制作新发现[J].大学物理实验，2011，24(3)：48－50.。

实训报告题目：θ调制与伪彩色编码实验θ调制与伪彩色编码实验实验目的1.掌握用θ调制法进行空间假彩色编码的方法，并做出相应的实验结果，加深对阿贝二次成像理论和空间频率滤波的理解，为今后学习其他假彩色编码方法打下基础。

2.掌握θ调制法假彩色编码的原理．巩固和加深对光栅衍射基本理论的理解；3.巩固和加深对光栅衍射基本理论的理解；获得假彩色编码图像。

实验原理Ө调法假彩色编码是阿贝二次衍射成像理论的一种巧妙的应用。

它是先用不同的光栅分别调制图像的不同部分，制成Ө调制片（或称光栅调制片），然后将其置于4f系统的输入面上，并用白光照明。

在频谱面上进行适当的空间滤波处理，便可在输出面上得到假彩色图像。

对于一幅图像的不同区域分别用取向不同(方位角θ不同)的光栅预先进行调制，经多次曝光和显影、定影等处理后制成透明胶片，并将其放人光学信息处理系统中的输入面，用白光照明，则在其频谱面上，不同方位的频谱均呈彩虹颜色。

如果在频谱面上开一些小孔，则在不同的方位角上，小孔可选取不同颜色的谱，最后在信息处理系统的输出面上便得到所需的彩色图像。

由于这种编码方法是利用不同方位的光栅对图像不同空间部位进行调制来实现的，故称为θ调制空间假彩色编码。

具体编码过程如下：物的样品如图1所示。

若要使其中草地、天安门和天空3个区域呈现3种不同的颜色，则可在同一胶片上曝光3次，每次只曝光其中一个区域(其他区域被挡住)，并在其上覆盖某取向的光栅，3次曝光分别取3个不同取向的光栅，如图中线条所示。

将这样获得的调制片经显影、定影处理后，置于光学信息处理的输入平面。

用白光平行光照明，并进行适当的空间滤波处理。

图1 被调制物示意图由于物被不同取向的光栅所调制，所以在频谱面上得到的将是取向不同的带状谱(均与其光栅栅线垂直)，物的3个不同区域的信息分布在3个不同的方向上，互不干扰，当用白光照明时，各级频谱呈现出的是色散的彩带，由中心向外按波长从短到长的顺序排列。

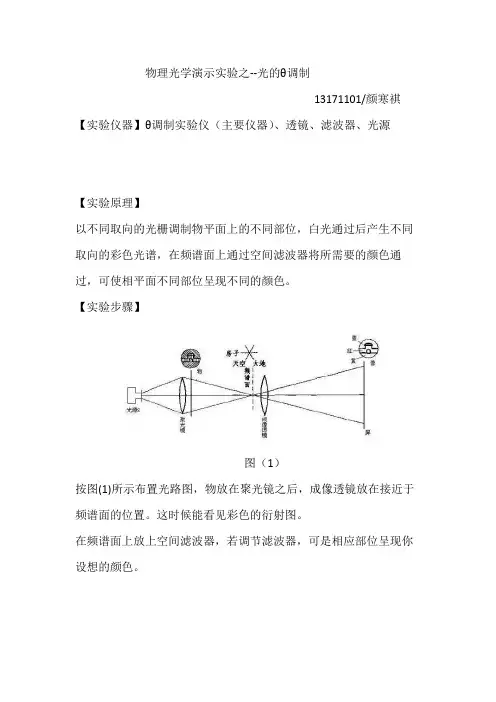
物理光学演示实验之--光的θ调制
13171101/颜寒祺【实验仪器】θ调制实验仪（主要仪器）、透镜、滤波器、光源
【实验原理】
以不同取向的光栅调制物平面上的不同部位，白光通过后产生不同取向的彩色光谱，在频谱面上通过空间滤波器将所需要的颜色通过，可使相平面不同部位呈现不同的颜色。

【实验步骤】
图（1）
按图(1)所示布置光路图，物放在聚光镜之后，成像透镜放在接近于频谱面的位置。

这时候能看见彩色的衍射图。

在频谱面上放上空间滤波器，若调节滤波器，可是相应部位呈现你设想的颜色。

【实际应用】
空间调制器可在随时间变化的电驱动信号或其他信号的控制下，改变空间上光分布的振幅或强度、相位、偏振态以及波长，或者把非相干光转化成相干光。

由于它的这种性质，可作为实时光学信息处理、光计算和光学神经网络等系统中构造单元或关键的器件。

在光信息处理系统中,它是系统和外界信息交换的接口。

它可以作为
系统的输入器件,也可在系统中用作变换或运算器件。

作为输入器件时,其功能主要是将待处理的原始信息处理成系统所要求的输入形式。

此时,空间光调制器作为输入传感器,可以实现电-光转换、串行-并行转换、非相干光-相干光转换、波长转换等。

另外,作为处理和运算器件时,可以实现光放大、矢量-矩阵或矩阵-矩阵间乘法、对比反转、波面形状控制等。

除此还有模拟图像存储的功能。

实验六 空间滤波与θ调制【实验目的】1、了解空间频率、阿贝成像原理以及θ调制的原理。

2、会利用光学原件组装θ调制光路。

【实验仪器】光源、透镜、光栅、θ调制板【实验原理】我们知道，一个通讯系统所接收或传递的信息（例如一个受调制的电压波形），通常具有随时间而变的性质。

而用来成象的光学系统，处理的对象是物平面和象平面上的光强分布。

如果借用通讯理论的观念，我们完全可以把物平面的光强分布视作输入信息，把象平面上的光强视作输出信息，这样，光学系统所扮演的角色相当于把输入信息转变为输出信息，只不过光学系统所传递和处理的信息是随空间变化的函数。

从数学的角度看，随空间变化的函数与随时间变化的函数，其数学变化规律并无实质性的差别。

也就是说，傅里叶变换应该可以帮助我们从更高的角度来研究光学中若干新的理论与实际问题。

傅里叶光学所讨论的物理内容，尽管仍然是学的传播，干涉，衍射和成象所遵循的规律，但由于傅里叶分析方法的引入，使我们有可能对于早已熟悉的许多光学现象的内在联系，从理论上及数学方法上获得更系统的理解，进行更深入的探讨。

尤其重要的是，由此引入的空间频率和频谱的概念，已成为目前迅速发展的光学信息处理、象质评价、成象理论等的基础，这些课题的前景是特别引人注目的。

1、 空间频率概念的引入我们知道，波动是一个时空过程，沿z 方向传播的单色平面光波的表达式为0cos 2()t z E A T πλ=- 或 0cos()E A t kz ω=-单色平面光波最显著的特点是它的时间周期性和空间周期性，它反映出单色光波是一种随时间t 无限延续、随空间z 无限延伸的波动。

为了描述单色光波的时间周期性，通常将周期T 称为单色光波的时间周期，它的倒数1υ=/T 称为时间频率，将2/T ωπ=称为时间角频率；与此类似，为了描述单色光波的空间周期性，通常将波长λ称为单色光波的空间周期，1/λ称为空间频率，将波数2/k πλ=称为空间角频率.因此,空间频率是在空间呈现正弦(或余弦)分布的几何图形或物理量在某个方向上单位长度内重复的次数,其单位为周/厘米.如果两个单色波沿其传播方向有着不同的空间频率,这就意味着它们有不同的波长,波的传播如图9-50所示.()a 为某一位置观察到的图象()E E t =,()b 为某一时刻观察到的图象()E E z =.E(t)T O t E(t)O λz (a )(b)（图1）图1()a 反映光波随时间变化的情况，图1()b 反映光波在空间传播的情况。

实验一傅里叶光学的空间频谱与空间滤波一、预备知识傅里叶光学是把通信理论,特别是傅里叶分析(频谱分析)方法引入到光学中来遂步形成的一个分支。

它是现代物理光学的重要组成部分。

光学系统和通信系统相似，不仅在于两者都是用来传递和交换信息，而且在于这两种系统都具有一些相同的基本性质，因而都可以用傅里叶分析(频谱分析)方法来加以描述。

通信理论中许多经典的概念和方法，如滤波、相关、卷积和深埋于噪声中的信号的提取等，被移植到光学中来，形成了光学传递函数、光学信息处理、全息术等现代光学发展的新领域。

阿贝成像理论是建立在傅里叶光学基础上的信息光学理论，阿贝——波特实验是阿贝成像理论的有力证明。

阿贝成像理论所揭示的物体成像过程中频谱的分解与综合，使得人们可以通过物理手段在谱面上改变物体频谱的组成和分布，从而达到处理和改造图像的目的，这就是空间滤波。

空间滤波的目的是通过有意识的改变像的频谱，使像产生所希望的变换。

光学信息处理是一个更为宽广的领域，它主要是用光学方法实现对输入信息的各种变换或处理。

空间滤波和光学信息处理可追溯到1873年阿贝(Abbe)提出二次成像理论，阿贝于1893年、波特(Porter)于1906年为验证这一理论所作的实验，科学的说明了成像质量与系统传递的空间频谱之间的关系。

20世纪六十年代由于激光的出现和全息术的重大发展，光学信息处理进入了蓬勃发展的新时期。

二、阿贝成像理论阿贝研究显微镜成像时，提出了一种不同于几何光学的新观点，即将物像看成是不同空间频率的集会，在相干光照明下，显微镜物镜的成像过程分两步完成，如下图所示：第一步是入射光经物平面P1发生夫琅禾费衍射，衍射光在物镜L后焦面P2上形成一系列的衍射斑(初级衍射图或称频谱图)；第二步是各种衍射斑作为新的次波源向前发出球面次波，在像面P3上干涉叠加，形成目镜焦面上的像。

将显微镜的成像过程看成是上述两步成像的过程，是波动光学的观点，后来人们称其为阿贝成像理论。

实验二 θ调制实验一、实验目的1．了解空间频率、阿贝成像原理以及θ调制的原理。

2．会利用光学原件组装θ调制光路。

二、实验原理1．阿贝成像原理阿贝认为在相干平行光照射下，显微镜的成像可分为两个步骤。

第一个步骤是通过物的衍射在物镜后焦面上形成一个初级干涉图；第二个步骤则为物镜后焦面上的初级干涉图复合为像(如图1所示)。

成像的这两个步骤本质上就是两次傅里叶变换。

物的复振幅分布是g(x,y)，可以证明在物镜的频谱面（后焦面）上的复振幅分布是g(x,y)的傅里叶变换(,)x y G f f 。

所以第一个步骤起的作用就是把光场分布变为空间频率分布。

而第二个步骤则是又一次傅里叶变换将(,)x y G f f 又还原到空间分布g’(x’,y’)。

物是空间不同频率的信息的集合,第一次付立叶变换是分频的过程,第二次付立叶逆变换是合频过程,形成新的不同频率的信息的集合—象.( 付立叶变换在物理上代表原函数—空间周期函数的频谱)。

如果这两次傅氏变换完全是理想的，信息在变换过程中没有损失，则像和物完全相似。

但由于透镜的孔径是有限的，总有一部分衍射角度较大的高次成分（高频信息）不能进入物 镜而被丢弃了。

所以物所包含的超过一定空间频率的成分就不能包含在像上。

如果高频信息没有到达像平面，则无论显微镜有多大的放大倍数，也不能在像平面上分辨这些细节。

这是显微镜分辨率受到限制的根本原因。

2．光学滤波在光学信息处理中，依据傅立叶逆变换公式，通过改变频谱函数，就可改变象函数。

在频谱面上人为地放置一些滤波器，以该变频谱面所需位置上的光振幅或位相，便可得到所需要的象函数。

这个改变频谱函数的过程就是空间滤波。

3．θ调制与空间彩色编码θ调制技术是阿贝原理的应用。

θ调制是白光照射透明物体,物体不同部分是取向不同的刻痕光栅,在接收面上形成彩色图像。

第一步入射光经物平面发生夫琅禾费衍射，在透镜的后焦面上形成一系列衍射斑（即物的频谱）这一步称―分频‖。

空间频率滤波与角度调制背景：空间频率滤波是在光学系统的空间频谱面上放置适当的滤波器，去掉（或有选择地通过）某些空间频率或改变它们的振幅和位相，使物体的图像按照人们的希望得到改善。

它是信息光学中最基本、最典型的基础实验，是相干光学信息处理中的一种最简单的情况。

一、实验目的1. 了解傅里叶光学基本理论的物理意义，加深对光学空间频率、空间频谱和空间频率滤波等概念的理解；2. 验证阿贝成像原理，理解成像过程的物理实质——“分频”与“合成”过程，了解透镜孔径对显微镜分辨率的影响；二、实验原理1. 傅里叶光学变换设有一个空间二维函数),(y x g ，其二维傅里叶变换为dxdy y x i y x g G )](2exp[),(),(ηξπηξ+-=⎰⎰∝∝- (1)式中ηξ,分别为x,y 方向的空间频率，而),(y x g 则为),(ηξG 的傅里叶逆变换，即ηξηξπηξd d y x i G y x g ⎰⎰+=∝∝-)](2exp[),(),( (2)式（2）表示，任意一个空间函数),(y x g 可表示为无穷多个基元函数)](2exp[y x i ηξπ+的线性迭加，),(ηξG 是相应于空间频率为ηξ,的基元函数的权重，),(ηξG 称为),(y x g 的空间频谱。

用光学的方法可以很方便地实现二维图像的傅里叶变换，获得它的空间频谱。

由透镜的傅里叶变换性质知，只要在傅里变换透镜的前焦面上放置一透率为),(y x g 的图像，并以相干平行光束垂直照明之，则在透镜后焦面上的光场分布就是),(y x g 的傅里叶变换),(ηξG ，即空间频谱),(f y f x G λ''。

其中λ为光波波长，f 为透镜的焦距，（y x '',）为后焦面（即频谱面）上任意一点的位置坐标。

显然，后焦面上任意一点（y x '',）对应的空间频率为2. 阿贝成像原理傅里叶变换光学在光学成像中的重要性，首先在显微镜的研究中显示出来。

实验48 光学信号的空间频谱与空间滤波一个光信号与它的频谱是同一事物在两个空间的表现，光信号分布于坐标空间),(y x ,而它的频谱存在于频率空间),(y x f f 。

由信号到频谱可以通过透镜(欲获得准确的变换，当然不是一般的透镜所能凑效的)来实现。

阿贝成像理论以及阿贝—波特实验告诉人类：可以通过对信号的频谱进行处理(滤波)来达到对信号本身作相应处理的目的。

这正是现代光学信息处理最基本的思想和内容。

阿贝—波特实验告诉我们，人类已迈进了光学信息处理的大门。

【实验目的】1．了解信号与频谱的关系以及透镜的傅立叶变换功能。

2．掌握现代成像原理和空间滤波的基本原理，理解成像过程中“分频”和“合成”的作用。

3．掌握光学滤波技术，观察各种光学滤波器产生的滤波效果，加深对光学信息处理基本思想的认识。

【实验原理】1． 光学信号的傅立叶频谱一个光学信号),(y x g 往往是空间变量y x ,的二维函数，其傅立叶变换被定义为⎰⎰+∞∞-∙+∙-=dxdy ey x g f f G y f x f j y x y x )(2),(),(π= )},({y x g FT(48-1)符号FT 表示傅立叶变换。

),(y x f f G 本身也是两个自变量y x f f ,的函数。

y x f f ,分别是与y x ,方向对应的空间频率变量。

),(y x f f G 被称为光信号),(y x g 的傅立叶频谱，亦称空间频谱。

一般地说，),(y x g 是非周期函数，),(y x f f G 应该是y x f f ,的连续函数。

式(48-1)的逆运算被称为逆傅立叶变换，即⎰⎰+∞∞-∙+∙=y x y f x f j y x df df ef f G y xg y x )(2),(),(π(48-2)上式可以理解为，一个复杂光学信号可以看作是由无穷多列平面波的干涉叠加组成，每列平面波的权重就是),(y x f f G 。

应该指出，式(48-1)、(48-2)所代表的傅立叶变换运算是通过透镜来完成的。

光学空间滤波实验研究1．阿贝成像原理1873年，阿贝(Abbe)在研究显微镜成像原理时提出了一个相干成像的新原理，这个原理为当今正在兴起的光学信息处理奠定了基础。

如图1-1所示，用一束平行光照明物体，按照传统的成像原理，物体上任一点都成了一次波源，辐射球面波，经透镜的会聚作用，各个发散的球面波转变为会聚的球面波，球面波的中心就是物体上某一点的像。

一个复杂的物体可以看成是无数个亮度不同的点构成，所有这些点经透镜的作用在像平面上形成像点，像点重新叠加构成物体的像。

这种传统的成像原理着眼于点的对应，物像之间是点点对应关系。

阿贝成像原理认为，透镜的成像过程可以分成两步：第一步是通过物的衍射光在透镜后焦面(即频谱面)上形成空间频谱，这是衍射所引起的“分频”作用；第二步是代表不同空间频率的各光束在像平面上相干叠加而形成物体的像，这是干涉所引起的“合成”作用。

成像过程的这两步本质上就是两次傅里叶变换。

如果这两次傅里叶变换是完全理想的，即信息没有任何损失，则像和物应完全相似。

如果在频谱面上设置各种空间滤波器，挡去频谱某一些空间频率成份，则将会使像发生变化。

空间滤波就是在光学系统的频谱面上放置各空间滤波器，去掉(或选择通过)某些空间频率或者改变它们的振幅和相位，使二维物体像按照要求得到改善。

这也是相干光学处理的实质所在。

以图l-l 为例，平面物体的图像可由一个二维函数g(x,y)描述，则其空间频谱G(f x ，f y )即为g(x ，y)的傅里叶变换：2(,)(,)(,)x y i f x f y x y G f f g x y edxdy π∞-∞-=⎰⎰ （1-1）设,x y ''为透镜后焦面上任一点的位置坐标，则式中为x x f F λ'=，y y f Fλ'= （1-2） 方向的空间频率，量纲为L -1, F 为透镜焦距，λ为入射平行光波波长。

再进行一次傅里叶变换，将(,)G fx fy 从频谱分布又还原到空间分布(,)g x y '''''。