阿贝成像与空间滤波实验汇总
- 格式:doc
- 大小:1.26 MB
- 文档页数:5

阿贝成像原理与空间滤波一个光信号与它的频谱是同一事物在两个空间的表现,光信号分布于坐标空间(x , y ),而它的频谱存在于频率空间(f x , f y )。
由信号到频谱可以通过透镜来实现。
1873年阿贝(E.Abbe ,1840-1905)在显微镜成像原理的研究中,首次提出了在相干光照明下显微镜两次成像的概念。
阿贝成像理论以及阿贝—波特实验告诉人类:可以通过对信号的频谱进行处理(滤波)来达到对信号本身作相应处理的目的。
这正是现代光学信息处理最基本的思想和内容。
本实验对加深傅里叶光学空间频率、空间频谱和空间滤波等概念的理解,熟悉阿贝成像原理,了解透镜孔径对成像分辨率的影响以及对研究现代光学信息处理均有十分重要的意义。
一、实验目的1. 了解信号与频谱的关系以及透镜的傅里叶变换功能。
2. 掌握现代成像原理和空间滤波的基本原理,理解成像过程中“分频”和“合成”的作用。
3. 掌握光学滤波技术,观察各种光学滤波器产生的滤波效果,加深对光学信息处理基本思想的认识。
二、实验原理1、光学傅里叶变换一个光学信号),(y x g 是空间变量y x ,的二维函数,其傅里叶变换被定义为:⎰⎰+∞∞-•+•-=dxdy ey x g f f G y f x f j y x y x )(2),(),(π= )},({y x g FT (1)符号FT 表示傅里叶变换。
),(y x f f G 本身也是两个自变量y x f f ,的函数。
y x f f ,分别是与y x ,方向对应的空间频率变量。
),(y x f f G 被称为光信号),(y x g 的傅里叶频谱,亦称空间频谱。
一般地说,),(y x g 是非周期函数,),(y x f f G 应该是y x f f ,的连续函数。
式(1)的逆运算被称为逆傅里叶变换,即⎰⎰+∞∞-•+•=y x y f x f j y x df df ef f G y xg y x )(2),(),(π(2)上式可以理解为,一个复杂光学信号可以看作是由无穷多列平面波的干涉叠加组成,每列平面波的权重就是),(y x f f G 。
实验十二 阿贝成像原理和空间滤波阿贝所提出的显微镜成像的原理以及随后的阿—波特实验在傅里叶光学早期发展历史上具有重要的地位。
这些实验简单而且漂亮,对相干光成像的机理、对频谱的分析和综合的原理做出了深刻的解释。
同时,这种用简单模板做滤波的方法,直到今天,在图像处理中仍然有广泛的应用价值。
一、实验目的1.通过实验,结合所学的傅里叶光学的理论, 加深对光学中空间频谱和空间滤波等概念的理解。
2.熟悉阿贝成像原理,进一步了解透镜孔径对显微镜分辨率的影响。
二、实验原理阿贝认为在相干平行光照射下,显微镜的成像可分为两个步骤。
第一个步骤是通过物的衍射在物镜后焦面上形成一个初级干涉图;第二个步骤则为物镜后焦面上的初级干涉图复合为像。
这就是通常所说的阿贝成像原理。
成像的这两个步骤本质上就是两次傅里叶变换。
如果物的复振幅分布是00g(x ,y ),可以证明在物镜的后焦面f f (x ,y )上的复振幅分布是00g(x ,y )的傅里叶变换f f G(x ,y )(只要令x f f f =x /λ,y f f f =y /λ;l 为光的波长,f 为物镜焦距)。
所以第一个步骤起的作用就是把光场分布变为空间频率分布。
而第二个步骤则是又一次傅里叶变换将f f G(x ,y )又还原到空间分布。
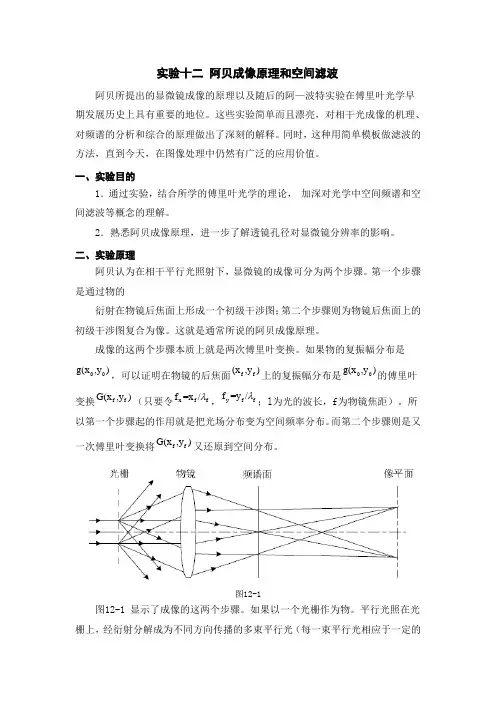
图12-1图12-1 显示了成像的这两个步骤。
如果以一个光栅作为物。
平行光照在光栅上,经衍射分解成为不同方向传播的多束平行光(每一束平行光相应于一定的空间频率)。
经过物镜分别聚焦在后焦面上形成点阵。
然后,代表不同空间频率的光束又重新在像平面上复合而成像。
如果这两次傅氏变换完全是理想的,信息在变换过程中没有损失,则像和物完全相似。
但由于透镜的孔径是有限的,总有一部分衍射角度较大的高次成分(高频信息)不能进入物镜而被丢弃了。
所以物所包含的超过一定空间频率的成分就不能包含在像上。
高频信息主要反映物的细节。
如果高频信息没有到达像平面,则无论显微镜有多大的放大倍数,也不能在像平面上分辨这些细节。

阿贝成像原理和空间滤波实验及计算机模拟
实验
1 阿贝成像原理
阿贝成像原理是显微镜中常用的成像原理之一,指的是利用波前衍射理论进行物体成像的原理。
根据这个原理,将光束通过电子透镜透射样品后,样品将会呈现出一定的衍射图样,这个衍射图样可以被传输函数所描述。
通过对传输函数的反取下,可以得到原始的样品图像。
2 空间滤波实验
空间滤波实验是显微镜实验中比较重要的一个部分,它指的是根据样品的空间图像,对样品进行处理的一种实验方法。
在空间滤波实验中,我们可以使用各种滤波算法来进行图像处理,如高通滤波、低通滤波等。
这些滤波算法可以使我们得到更为清晰的样品图像,缩小图像中的噪点并提高对比度。
3 计算机模拟实验
除了实际的显微镜实验外,计算机模拟实验也是很重要的一种方法。
计算机模拟实验可以帮助研究者更好地理解阿贝成像原理和空间滤波实验。
使用计算机模拟实验可以在短时间内模拟出实际实验的结果,尤其在进行显微镜实验前,通过计算机模拟实验,可以帮助研究者更好地规划实验的系列流程。
在计算机模拟实验中,我们可以针对
阿贝成像原理和空间滤波实验进行模拟,根据模拟实验的结果,对实
际的显微镜实验进行优化,提高实验的成功率和效率。
4 结束语
综上所述,阿贝成像原理和空间滤波实验是显微镜领域中比较重
要的一些实验方法,是我们进行研究的基础。
计算机模拟实验则是帮
助我们更好地理解和实践这些实验的重要工具。
我们需要不断探索和
学习这些实验方法,以便更好地利用显微镜技术研究物质的微观结构。

阿贝成像与空间滤波实验报告精品⽂档班级09级1班姓名巩⾠⽇期3⽉1⽇组别 1 组学号1090600004 指导教师【实验⽬的】1.了解透镜孔径对成像的影响和简单的空间滤波;2.掌握在相⼲光条件下调节多透镜系统的共轴;3.验证和演⽰阿贝成像原理,加深对傅⾥叶光学中空间频率、空间频谱和空间滤波概念的理解;4.初步了解简单的空间滤波在光信息处理中的实际应⽤【实验仪器与⽤具】GP-78光具座JSQ-250 氦氖激光器及电源物(光栅)透镜X3 (f=15mm f=70mm f=225mm) 光阑⽚【实验原理】1、关于傅⾥叶光学变换设有⼀个空间⼆维函数g x, y,其⼆维傅⾥叶变换为:G f x, f y Fgx,y gx,yexp i2 f x X f y ydxdy式中f x、f y分别为x、y⽅向的空间频率,g x,y是G f x, f y的逆傅⾥叶变换,即:g(x,y) F G f x,f y G f x, f y expi2 f x x f y y df x df y该式表⽰:任意⼀个空间函数g x, y可表⽰为⽆穷多个基元函数exp i2 f x x f y y的线性叠加。
G f x,f y df x df y是相应于空间频率为f x、f y的基元函数的权重,G f x, f y称为g x, y的空间频谱。
理论上可以证明,对在焦距为f的会聚透镜的前焦⾯上放⼀振幅透过率为g x, y的图像作为物,并⽤波长为的单⾊平⾯波垂直照明,则在透镜后焦⾯x , y上的复振幅分布就是g x,y的傅⾥叶变换G f x,f y,其中空间频率f x、f y与坐标x、y的关系为:【实验题⽬】阿贝成像原理和空间滤波f x专f y专故x , y⾯称为频谱⾯(或傅⽒⾯),由此可见,复杂的⼆维傅⾥叶变换可以⽤⼀透镜来实现,称为光学傅⾥叶变换,频谱⾯上的光强分布,也就是物的夫琅⽲费衍射图。
2、关于阿贝成像原理阿贝(E.Abbe )在1873年提出了相⼲光照明下显微镜的成像原理。

阿贝成像原理和空间滤波实验阿贝所提出的显微镜成像的原理以及随后的阿—波特实验在傅里叶光学早期发展历史上具有重要的地位。
这些实验简单而且漂亮,对相干光成像的机理、对频谱的分析和综合的原理做出了深刻的解释。
同时,这种用简单模板做滤波的方法,直到今天,在图像处理中仍然有广泛的应用价值。
一.实验目的1.通过实验,加强对傅里叶光学中有关空间频率、空间频谱和空间滤波等概念的理解。
2.熟悉空间滤波的光路及进行高通、低通和方向滤波的方法。
二.实验原理阿贝认为在相干平行光照射下,显微镜的成像可分为两个步骤。
第一个步骤是通过物的衍射在物镜后焦面上形成一个初级干涉图(频谱面);第二个步骤则为物镜后焦面上的初级干涉图复合为像。
这就是通常所说的阿贝成像原理。
成像的这两个步骤本质上就是两次傅里叶变换。
如果物的复振幅分布是g(x0,y0),可以证明在物镜的后焦面(xf,yf)上的复振幅分布是g(x0,y0)的傅里叶变换G(xf,yf)(只要令fx=xf/λf,fy=yf/λf;λ为光的波长,f 为物镜焦距)。
所以第一个步骤起的作用就是把光场分布变为空间频率分布。
而第二个步骤则是又一次傅里叶变换将G(xf,yf)又还原到空间分布。
图1显示了成像的这两个步骤。
如果以一个光栅作为物。
平行光照在光栅上,经衍射分解成为不同方向传播的多束平行光(每一束平行光相应于一定的空间频率)。
经过物镜分别聚焦在后焦面上形成点阵。
然后,代表不同空间频率的光束又重新在像平面上复合而成像。
如果这两次傅氏变换完全是理想的,信息在变换过程中没有损失,则像和物完全相似。
但由于透镜的孔径是有限的,总有一部分衍射角度较大的高次成分(高频信息)不能进入物镜而被丢弃了。
所以物所包含的超过一定空间频率的成分就不能包含在像上。
高频信息主要反映物的细节。
如果高频信息没有到达像平面,则无论显微镜有多大的放大倍数,也不能在像平面上分辨这些细节。
这是显微镜分辨率受到限制的根本原因。






阿贝成像原理和空间滤波1.引言:阿贝所提出的显微镜成像的原理以及随后的阿—波特实验在傅里叶光学早期发展历史上具有重要的地位。
这些实验简单而且漂亮,对相干光成像的机理、对频谱的分析和综合的原理做出了深刻的解释。
同时,这种用简单模板做滤波的方法,直到今天,在图像处理中仍然有广泛的应用价值。
2.实验目的:1). 加强对傅里叶光学中有关空间频率、空间频谱和空间滤波等概念的理解。
2). 于一个带有蓝天白云还有城楼的光栅的空间滤波和再现图像熟悉空间滤波的光路及空间滤波的原理。
3.实验原理:1). 二维傅里叶变换设有一个空间二维函数),(y x g ,其二维傅里叶变换为=),(y x f f G F [][]d xdy y f x f i y x g y x g y x ⎰⎰∞∞-+-=)(2exp ),(),(π (1)式中y x f f ,分别为x,y 方向的空间频率,其量纲为L -1,而),(y x g 又是),(y x f f G 的逆傅里叶变换,即=),(y x g F -1[]=),(y x f f G []y x y x y x df df y f x f i f f G ⎰⎰∞∞-+)(2exp ),(π (2) 式(2)表示任意一个空金函数),(y x g ,可以表示为无穷多个基元函数[])(2exp y f x f i y x +π的线性叠加,),(y x f f G y x df df 是相应于空间频率为y x f f ,的基元函数的权重,),(y x f f G 称为),(y x g 的空间频率。
当),(y x g 是一个空间周期性函数时,其空间频率是不连续的离散函数。
2). 光学傅里叶变换直理论证明,如果在焦距为F 的会聚透镜的前焦面上放一振幅透过率为),(y x g 的图象作为物,并以波长为λ的单色平面波垂照明图象,则在透镜后焦面(x’,y’)上的振幅分布就是),(y x g 的傅里叶变换),(y x f f G ,其中y x f f ,与坐标x’,y’的关系为FY f F x f Y x λλ','== (3) 故x’-y’面称为频谱面(或傅氏面),见图1,由此可见,复杂的二维傅里叶变换可以用一透镜来实现,称为光学傅里叶变换,频谱面上的光强分布则为2),(y x f f G ,称为频谱,也就是物的夫琅禾费衍射图。
阿贝成像原理与空间滤波实验内容:l.光路调节本实验基本光路图如图1所示,其中透镜L 1 (焦距f 1)、L 2 (焦距f 2)组成倒装置望远镜系统将激光扩展成具有较大截面的平行光束,L(焦距为f)则为成像透镜。
调节步骤如下:图1 空间滤波实验光路(1) 调节激光管的仰角及转角,使光束平行于光学平台水平面。
(2) 放上L 1和L 2,使产生一扩束的平行光并调节它们共轴。
怎样检验 L 2出来的光是否平行光?如L 1的焦距为 mm,L 2焦距为 mm,,则扩束多少倍? (3)放上物(带光栅的“光”字)及透镜L,调节它们共轴,调节L 位置,使大于4 m 距离的屏幕上得到清晰的图像。
固定物及透镜L 位置(调节成像时,可在物面前暂放一毛玻璃,以便在扩展光源照明下,找到成像的精确位置。
)(4)确定频谱面位置去掉物,用毛玻璃在L 后焦面附近移动,当毛玻璃散射产生的散斑达到最大线度时,毛玻璃上光点最小,此毛玻璃所在平面就是频谱面。
然后将滤波器支架放在此平而上。
2.阿贝成像原理实验(1) 在物平面放上一维光栅,像平面上看到沿铅垂方向的光栅条纹。
频谱面上出现0,±1,±2,±3,… ,一排清晰衍射光点,如图2中A 所示。
测量l,2,3级衍射点与光轴(0级衍射)的距离x′,由式(3)求出相应空间频率f x,并求光栅的基频。
图2 频谱面及光阑A.频谱面上的衍射光斑B.只通过0级C.只通过0级和±1级D.遮挡±1级E.遮挡0级(2)在傅氏面上放上可调狭缝及其他附加光阑,按图2中A,B,C,D,E 分别通过一定的空间频率成分,按表l 依次记录像面上成像的特点及条纹间距,特别注意观察D 和E 两条件下图像的差异,并对图像变化作出适当的解释。
表1像面成像特点条件 通过的衍射点 图像情况 简要解释 A 全部 B 0级 C 0,±1级 D 0,±2级 E ±1,±2级衍射次级位置 x′/mm间频空率 f x /mm -11 2 3(3)取下物向上的一维光栅,换上一个二维正交光栅则在频谱而上吖看到二维离散的光点阵(即止交光栅的频谱),像而上可以看到放大了的止交光栅的像测出像面上的网格间距。
光信息专业实验指导材料(试用)实验1-1 阿贝成像原理与空间滤波[实验目的]1、了解阿贝成像原理,并进行实验验证;2、加深对空间频谱和空间滤波概念的理解;3、利用空间滤波技术消除图像噪声;4、了解透镜的傅里叶变换作用。
[实验仪器]实验室提供:半导体激光器(带二维调节架),光具座导轨(1000mm ),滑块,傅里叶透镜(φ80,f 190),准直透镜(φ55,f 50),扩束镜(带二维调节架),放大镜,干板架,正交光栅2枚(空间频率分别为25 lp/mm 和100 lp/mm ),“光”字屏,毛玻璃屏,白屏,小孔屏,滤波器组件(带二维调节架),手电筒。
[实验原理]一、阿贝成像理论1873年阿贝首次提出了一个与几何光学传统成像理论完全不同的概念,它认为相干照明下透镜成像过程可分作两步:首先,物光波经透镜,在透镜后焦面上形成频谱,该频谱称为第一次衍射像;然后频谱成为新的次波源,由它发出的次波在像平面上干涉而形成物体的像,该像称为第二次衍射像。
上述过程即为“阿贝成像理论”。
根据这一理论,像的结构完全依赖于频谱的结构。
图1是上述成像过程的示意图。
设相干平行光照射复振幅为),(00y x g 的物面,由傅里叶光学可知,经透镜L 的傅里叶变换,在其后焦面(频谱平面)上可得到物的频谱,其数学表述为:物平面 频谱平面 像平面图1 阿贝成像理论示意图()()()[]0000002j exp,,dy dx vy ux πy x g v u G +-=⎰⎰∞∞- (1) 式中u ,v 为空间频率。
透镜L 则称为傅里叶变换透镜。
由频谱面到像平面,光波完成了一次夫朗和费衍射过程,相当于频谱又经过一次傅里叶变换,在像平面上综合成物体的像。
()()()[]dudv y v x u πu,v G y x g '+'=''⎰⎰∞∞-2j exp ,' (2) 由(1)、(2)式可见,物面与像面的复振幅之比是一个常数,所以像与物几何相似。
物 理 实 验 报 告班 级 09级1班组 别 1组 姓 名 巩辰 学 号 1090600004日 期 3月1日 指导教师 【实验题目】 阿贝成像原理和空间滤波【实验目的】1. 了解透镜孔径对成像的影响和简单的空间滤波;2. 掌握在相干光条件下调节多透镜系统的共轴;3. 验证和演示阿贝成像原理,加深对傅里叶光学中空间频率、空间频谱和空间滤波概念的理解;4. 初步了解简单的空间滤波在光信息处理中的实际应用.【实验仪器与用具】GP-78光具座 JSQ-250氦氖激光器及电源 物(光栅)透镜×3(f=15mm 、f=70mm 、f=225mm ) 光阑片【实验原理】1、关于傅里叶光学变换设有一个空间二维函数()y x g ,,其二维傅里叶变换为:式中x f 、y f 分别为x 、y 方向的空间频率,()y x g ,是()y x f f G ,的逆傅里叶变换,即:该式表示:任意一个空间函数()y x g ,可表示为无穷多个基元函数()[]y f x f i y x +π2exp 的线性叠加。
()y x y x df df f f G ,是相应于空间频率为x f 、y f 的基元函数的权重,()y x f f G ,称为()y x g ,的空间频谱。
理论上可以证明,对在焦距为f 的会聚透镜的前焦面上放一振幅透过率为()y x g ,的图像作为物,并用波长为λ的单色平面波垂直照明,则在透镜后焦面()y x '',上的复振幅分布就是()y x g ,的傅里叶变换()y x f f G ,,其中空间频率x f 、y f 与坐标x '、y '的关系为:故()y x '',面称为频谱面(或傅氏面),由此可见,复杂的二维傅里叶变换可以用一透镜来实现,称为光学傅里叶变换,频谱面上的光强分布,也就是物的夫琅禾费衍射图。
2、关于阿贝成像原理阿贝(E.Abbe )在1873年提出了相干光照明下显微镜的成像原理。
实验6-3 阿贝成像与空间滤波实验
【实验目的】
1、 通过实验了解空间频率、空间频谱的概念以及傅里叶光学的基本思想。
2、 了解阿贝成像的原理,理解透镜成像的物理过程。
3、 了解如何通过空间滤波的方法,实现对图象的改造。
【实验原理】
1、傅里叶光学变换
设有一个空间二维函数()y x g ,,其二维傅里叶变换为:
()()[]()()[]
dxdy y f x f i y x g y x g F f f G y x y x +-==⎰⎰∞π2exp ,,, (6-3-1)
式中x f 、y f 分别为x 、y 方向的空间频率,()y x g ,是()y x f f G ,的逆傅里叶变换,即:
()[]()()[]y x y x y
x y x df df y f x f i f f G f f G F y x g +==⎰⎰∞-π2exp ,,),(1 (6-3-2)
该式表示:任意一个空间函数()y x g ,可表示为无穷多个基元函数()[]y f x f i y x +π2exp 的线性叠加。
()y x y x df df f f G ,是相应于空间频率为x f 、y f 的基元函数的权重,()y x f f G ,称为()y x g ,的空间频谱。
理论上可以证明,对在焦距为f 的会聚透镜的前焦面上放一振幅透过率为()y x g ,的图像作为物,并用波长为λ的单色平面波垂直照明,则在透镜后焦面()y x '',上的复振幅分布就是()y x g ,的傅里叶变换()
y x f f G ,,其中空间频率x f 、y f 与坐标x '、y '的关系为: ⎪⎪⎩
⎪⎪⎨⎧'
='=f y f f x f y x λλ (6-3-3) 故()y x '',面称为频谱面(或傅氏面),由此可见,复杂的二维傅里叶变换可以用一透镜来实现,称为光学傅里叶变换,频谱面上的光强分布,也就是物的夫琅禾费衍射图。
2、阿贝成像原理
阿贝(E.Abbe )在1873年提出了相干光照明下显微镜的成像原理。
他认为,在相干光照明下,显微镜的成像可分为两个步骤:第一步是通过物的衍射光在物镜的后焦面上形成一个衍射图;第二步是物镜后焦面上的衍射图复合为(中间)像,这个像可以通过目镜观察到。
成像的这两个步骤本质上就是两次傅里叶变换。
第一步把物面光场的空间分布()y x g ,变为频谱面上空间频率分布()y x f f G ,,第二步则是再作一次变换,又将()
y x f f G ,还原到空间分布()y x g ,。
图6-3-1显示了成像的两个步骤。
我们假设物是一个一维光栅,单色平行光垂直照在光栅上,经衍射分解成为不同方向的很多束平行光(每一束平行光相应于一定的空间频率),经过物镜分别聚焦在后焦面上形成点阵。
然后代表不同空间频率的光束又重新在像面上复合而成像。
如果这两次变换完全是理想的,即信息没有任何损失,则像和物应完全相似(可能有放大或缩小),但一般说来像和物不可能完全相似,这是由于透镜的孔径是有限的,总有一部分衍射角度较大的高次成分(高频信息)不能进入到物镜而被丢弃了,所以像的信息总是比物的信息要少一些。
高频信息主要反映了物的细节,如果高频信息受到了孔径的限制而不能达到像平面,则无论显微镜有多大的放大倍数,也不可能在像平面上显示出这些高频信息所反映的细节,这是显微镜分辨率受到限制的根本原因。
特别是当物的结构非常精细(如很密的光栅)或物镜孔径非常小时,有可能只有0级衍射(空间频率为0)能通过,则在像平面上完全不能形成像.
3、空间滤波
根据上面讨论,透镜成像过程可看作是两次傅里叶变换,即从空间函数()y x g ,变为频谱函数
()y x f f G ,,再变回到空间函数()y x g ,(忽略放大率)。
显然如果我们在频谱面(即透镜的后焦面)上放一些不同结构的光阑,以提取(或摒弃)某些频段的物信息,则必然使像面上的图像发生相应的变化,这样的图像处理称为空间滤波,频谱面上这种光阑称为滤波器。
滤波器使频谱面上一个或一部分频率分量通过,而挡住其它频率分量,从而改变了像面上图像的频率成分。
例如光轴上的圆孔光栏可以作为一个低通滤波器,而圆屏就可以用作为高通滤波器。
【实验仪器及光路】
实验仪器包括:光学平台或光具座、氦氖激光器、针孔滤波器、透镜、作为物的光栅、滤波器、白色像屏等。
实验光路如图6-3-2所示,扩束镜0L 与准直透镜c L 共焦,使c L 输出平行光束.在公共焦点上安置针孔滤波器SF,以使光斑亮度均匀。
依次放上物(12~15条/mm的一维光栅)和焦距为f 的透镜L ,调共轴。
调节透镜位置,使光栅清晰的成像在4m以外的白屏上,此时物的位置接近于透镜L 的前焦平面。
【实验内容】
1、观测一维光栅的频谱
(1)在透镜L后缓慢移动白屏,寻找光束会聚点,即透镜L 的后焦平面(频谱面),可看到0级、±1级、±2级、±3级……一排清晰的衍射光点。
衍射角越大,衍射级次越高,空间频率也越高。
(2)将白纸放在频谱面上,通过放大镜观察频谱,并用针尖分别扎透0级、±1级、±2级、±3级衍射点的中心。
然后,将有扎孔的纸拿到读数显微镜下测出各级衍射点与零级衍射点的距离
1x '±、2x '±、3x '±,求出相应的空间频率 1x f 、 2x f 、3x f ,并由基频1x f (d
f x 11=,d 为光栅常数)求出光栅常数d 。
2、阿贝成像原理实验
频谱面上的衍射点如图6-3-3(a )所示。
在频谱面上放上可调狭缝或滤波模板,使通过的衍射点如图6-3-3所示:(a )全部;(b )零级;(c )零和±1级;(d )零和±2级;(e )除零级外。
分别记录像面特点和条纹间距,并做出定性解释。
3、阿贝一波特实验(方向滤波)
(1)光路不变,将一维光栅的物换成二维正交光栅,在频谱面上可以观察到二维分立的光点阵(频谱),像面上可以看到放大了的正交光栅像,测出像面上的网格间距。
(2)在频谱面放上可旋转狭缝光阑(方向滤波器),在下述情况:(a )只让光轴上水平的一行频谱分量通过;(b )只让光轴上垂直的一行频谱分量通过;(c )只让光轴上45°的一行频谱分量通过。
记录像面上的图像变化、像面上条纹间距,并做出适当的解释。
将所观测的现象、数据添入表6-3-1中。
方向滤波可去除某些方向的频谱或仅让某些方向的频谱通过,以突出图像的某些特征。
4.高低通滤波
图6-3-4中,(a )为低通滤波器,(b )为高通滤波器,(c )为带通滤波器。
低通滤波器的作用是滤掉高频成分,仅让靠近零级的低频成分通过。
它可以用来滤掉高频噪声,例如滤去有网格照片中的网状结构。
高通滤波器是一个中心部分不透光的小光屏,它能滤去低频成分而允许高频成分通过,可用于突出像的边沿部分或者实现像的衬度反转。
带通滤波器可以让某些需要的频谱分量通过,其余的被滤掉,可用于消除噪音。
图6-3-3一维光栅频谱与滤波器
表6-3-1
(1)低通滤波
将正交光栅与一个透明的“光”字重叠放在物平面上,光栅为12~15条/mm,而字的笔划粗细为毫米数量级,放大像如图6-3-5(a)所示。
通过透镜L成像在像平面上。
由于网格为一周期性的空间函数,它的频谱是有规律排列的分立点阵,而字迹是一个非周期性的低频信号,它的频谱是连续的.
将一个可变圆孔光阑放在频谱面上,逐步缩小光阑,直到像上不再有网格,但字迹仍然保留下来。
(2)高通滤波
将一漏光“+”字板作为物,可在像面上观察到物的像,见图6-3-5(b)。
在频谱面上放一圆屏光阑挡住谱面的中心部分,观察并记录像面上的图像变化。
【思考题】
1、透镜前焦面上是50条/mm的一维光栅,其频谱面上的空间频率各是多少?相邻两衍射点间距离是多少?已知f=5.0cm, =632.8nm。
2、在低通滤波中,如果想滤掉字而保留光栅,应怎么办?
【参考资料】
1、张成英,光学实验,北京:电子工业出版社,1989.
2、朱自强,现代光学教程,成都:四川大学出版社,1990.
3、王秉超等,大学物理实验(下册),北京:高等教育出版社,2003.
4、李志超等,大学物理实验(第三册),北京:高等教育出版社,2001.。