六年级下册小升初专题练习:立体图形及答案-人教版
- 格式:docx
- 大小:75.90 KB
- 文档页数:7

2024学年人教版六年级下册数学小升初专题训练:立体图形一、单选题1.把一个圆柱体的底面分成许多相等的扇形,切开后拼成一个近似的长方体。
这个长方体与原来的圆柱体相比较()A.表面积和体积都没变B.表面积和体积都变了C.表面积没变,体积变了D.表面积变了,体积没变2.一个圆柱的侧面展开图是正方形,则这个圆柱的高是底面直径的()倍。
A.πB.2πC.14πD.12π3.把下图的展开图围成正方体后,与E相对的面是()。
A.A B.B C.C D.D4.在一个注满水的水缸中,放入两个完全相同的铁块,溢出了60mL的水,那么一个铁块的体积是()立方厘米。
A.20B.30C.60D.1205.一个圆柱与圆锥体积相等,底面积之比为1:2,圆柱的高为6厘米,圆锥的高()。
A.3厘米B.6厘米C.9厘米D.18厘米6.如下图,一个长方体的长、宽、高分别为adm、bdm、hdm。
如果它的高增加5dm,那么它的表面积比原来增加()dm2。
A.5ab B.5a+5bC.10a+10b D.2(5a+5b+ab)二、判断题7.用两张同样的长方形纸卷成两个不同的圆柱,它们的体积相等。
(接缝处忽略不计)()8.把28L水倒入一个从里面量长40cm、宽25cm、高40cm的长方体玻璃水槽中,这时水面距水槽口28cm。
()9.当正方体的棱长是6cm时,它的表面积和体积相等。
()10.正方体的棱长扩大到原来的2倍,体积就扩大到原来的6倍。
()11.两个高相等的圆柱体底面半径之比是3:2,那么体积之比也是3:2。
()12.一个圆柱体木料削去12立方分米后,正好是一个与它等底等高的圆锥体。
原来这个圆柱体的体积是18立方分米。
()三、填空题13.正方体的棱长扩大到原来的3倍,棱长总和扩大到原来的倍,表面积扩大到原来的倍,体积扩大到原来的倍。
14.一个正方体木块的棱长是2dm,现在把它削成一个最大的圆柱。
削成的圆柱侧面积是dm2,削成的圆柱的体积占原来正方体体积的%。
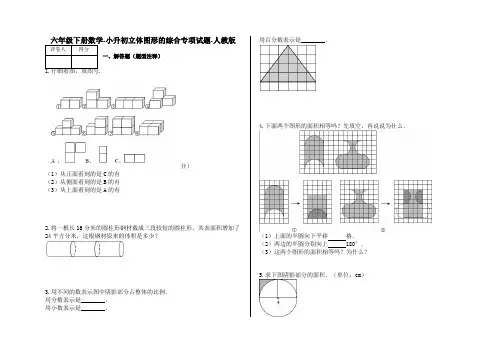
-小升初立体图形的综合专项试题-人教版一、解答题(题型注释).分)(1)从正面看到的是C的有(2)从侧面看到的是B的有(3)从上面看到的是A的有2.将一根长16分米的圆柱形钢材截成三段较短的圆柱形,其表面积增加了24平方分米,这根钢材原来的体积是多少?3.用不同的数表示图中阴影部分占整体的比例.用分数表示是________,用小数表示是________,用百分数表示是________.4.下面两个图形的面积相等吗?先填空,再说说为什么.(1)上面的半圆向下平移格.(2)两边的半圆分别向上180°.(3)这两个图形的面积相等吗?为什么?5.求下图阴影部分的面积.(单位:cm)6.如图中,在长方形内画了一些直线,已知边上有三块面积分别是13,35,49.那么图中阴影部分的面积是多少?7.按要求操作与解答.(1)①画一个边长为4厘米的正方形.②在正方形内画一个最大的圆.(2)假如把正方形内的圆外部分称为“阴影部分”,求阴影部分面积与圆面积的比.8.小鸽子从半空中低头往下一看,正好看见一辆小轿车,它看到的是哪一幅图呢?在( )里画“△”。
9.用哪些立体图形可以画出右面的图形?圈一圈10.沿着图中的虚线旋转一周,可以得到一个立体图形,请回答下列问题。
(1)这个立体图形的名称:(2)求这个立体图形的体积。
参数答案1.(1)①⑧(2)②⑤⑥⑦(3)④【解析】1.从正面看到是C的有:①⑧,从侧面看到是B的有:②⑤⑥⑦,从上面看到是A的有:④。
2.解:圆柱的底面积:24÷4=6(平方分米)圆柱的体积:6×16=96(立方分米)答:这根钢材的体积是96立方分米.【解析】2.由题意可知:一根16分米长的圆柱形钢材,锯成3段后,增加了4个面,增加的面积已知,从而可以求出1个面的面积,也就是钢材的底面积,进而利用圆锥的体积公式就可以求出圆柱形钢材的体积.3.25, 0.4,40%【解析】3.解:(6×4÷2)÷(6×5)=12÷30= 252 5=2÷5=0.40.4=40%所以答案是:25,0.4,40%.4.(1)5(2)平移3格再旋转(3)解:两个图形的面积相等,因为经过平移、旋转后得到的两个长方形,图形一:长方形的宽占4格,长占5格,那么面积就占了:4×5=20(格),图形二:长方形的宽占4格,长占6格,面积就占了:4×6=24(格),图形一的面积小于图形二的面积,答:平移3格再旋转180°;图形一的面积小于图形二的面积,因为经过平移、旋转后得到的两个长方形,根据长方形的面积公式可计算出图形一的面积占20格,图形二的面积占24格,所以图形一的面积小于图形二的面【解析】4.根据图可知,①上面的半圆向下平移5格,就可得到一个长方形,长方形的宽占4格,长占5格,那么根据长方形的面积公式可计算出这个图形的面积占(4×5)格;②将图形中的第二个图两边的半圆分别向上平移3格再旋转180°,也可得到一个长方形,长方形的宽占4格,长占6格,面积就占(4×6)格;这两个图形经过平移、旋转后得到的图形都是长方形,根据长方形的面积公式进行计算然后再进行比较即可得到答案.解答此题的关键是将图形进行平移、旋转,将图形转化我们学过的图形,再根据图形的面积公式进行计算、比较即可.5.解:(4÷2)×(4÷2)﹣3.14×(4÷2)2× ,=2×2﹣3.14×4× ,=4﹣3.14,=0.86(平方厘米);答:图中阴影部分的面积是0.86平方厘米【解析】5.已知圆的直径是4厘米,正方形的边长等于圆的半径,用正方形的面积减去圆面积的14,由此解答.此题求图中阴影部分的面积,采用去空求差法,即用正方形的面积减去圆心角是90°的扇形的面积,由此解决问题.6.解:因为长方形的面积等于△ABC与△ECD的面积和,所以△ABC与△ECD重叠部分的面积等于长方形未被这两个三角形盖住部分的面积和,即:S=49+35+13=97.答:图中阴影部分的面积是97【解析】6.所求的影阴部分,恰好是三角形ABC与三角形CDE的公共部分,而面积为13,49,35这三块是长方形中没有被三角形ABC与三角形CDE盖住的部分.因此,△ABC面积+△CDE面积+(13+49+35)=长方形面积+阴影部分面积.而△ABC的底是长方形的长,高是长方形的宽;△CDE的底是长方形的宽,高是长方形的长.因此,三角形ABC面积与三角形CDE面积,都是长方形面积的一半.本题主要考查对三角形和长方形面积的计算及其之间关系的掌握,以及观察分析能力.7.(1)解:如图所示(2)解:圆的面积:3.14×(4÷2)2=12.56(平方厘米),阴影部分的面积=16﹣12.56,=3.44(平方厘米);3.44:12.56=43:157答:阴影部分的面积与圆面积的比是43:157.【解析】7.(1)①先画一条4厘米的线段,再分别过这条线段的两个端点,作这条线段的4厘米垂线段连接两条垂线段的另外一个端点,所形成的图形就是边长为4厘米的正方形.②所画的最大圆的直径应该等于正方形的边长,正方形的边长已知,于是可以画出这个圆.(2)正方形的边长是4厘米,则圆的半径可以求出,进而利用圆的面积公式就可以求出这个圆的面积.阴影部分的面积=正方形的面积﹣圆的面积8.解:【解析】8. 9.解:【解析】9.10.(1)圆锥(2)×3.14×32×4=37.68(立方厘米)答:这个立体图形的体积是37. 68立方厘米。
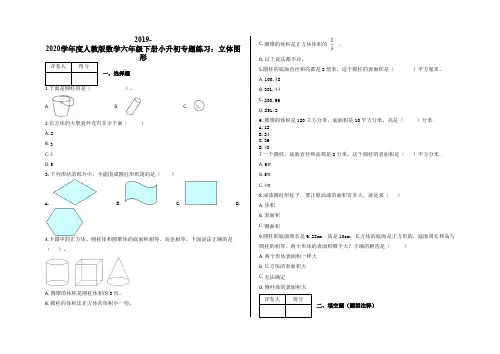
2019-2020学年度人教版数学六年级下册小升初专题练习:立体图形一、选择题)。
A. B. C.2.长方体的火柴盒外壳有多少个面()A. 2B. 3C. 4D. 53.下列形状的纸片中,不能围成圆柱形纸筒的是()A. B. C. D.4.下图中的正方体、圆柱体和圆锥体的底面积相等,高也相等。
下面说法正确的是()。
A. 圆锥的体积是圆柱体积的3倍。
B. 圆柱的体积比正方体的体积小一些。
C. 圆锥的体积是正方体体积的。
D. 以上说法都不对。
5.圆柱的底面直径和高都是8厘米,这个圆柱的表面积是()平方厘米。
A. 100.48B. 301.44C. 200.96D. 251.26.圆锥的体积是120立方分米,底面积是10平方分米,高是()分米.A.12B.24C.36D.487.一个圆柱,底面直径和高都是2分米,这个圆柱的表面积是()平方分米.A. 6πB. 5πC. 4π8.油漆圆柱形柱子,要计算油漆的面积有多大,就是求()A. 体积B. 表面积C. 侧面积9.圆柱的底面周长是6.28cm,高是10cm;长方体的底面是正方形的,底面周长和高与圆柱的相等.两个形体的表面积哪个大?正确的解答是()A. 两个形体表面积一样大B. 长方体的表面积大C. 无法确定D. 圆柱体的表面积大二、填空题(题型注释)10.如图的四个正方体堆放在墙角处,露在外面的有( )个面。
A. 6 B. 9 C. 15 D. 2411.两个长方体的表面积相等,它们的形状一定相同. .12.正方体的棱长扩大到原来的3倍,那么它的表面积扩大到原来的6倍,体积扩大到原来的9倍. .13.如果把圆柱的侧面展开可以得到一个长方形,这个长方形的长等于圆柱的底面 ,宽等于圆柱的 .14.把一个高为9分米的圆锥体钢坏,经熔铸后,成为一个与它等底的圆柱体,这个圆柱体的高是 .15.正方体的棱长扩大4倍,它的体积也扩大4倍. .16.这个长方体的前面与________面是完全相同的长方形,每个面的面积都是________平方分米;右面与________面完全相同,每个面的面积都是________平方分米;还有________面与________面完全相同,每个面的面积都是________平方分米.17.一个高6cm 的圆锥形容器盛满了水,倒入和它等底等高的圆柱形容器内,这时水面的高是(_______)cm 。
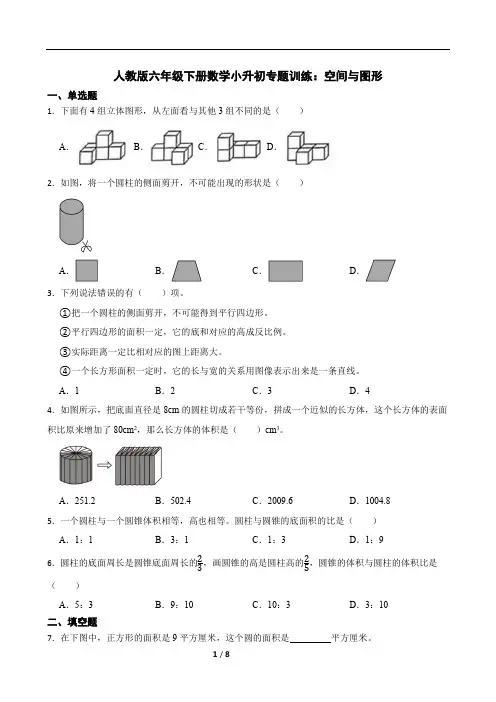
人教版六年级下册数学小升初专题训练:空间与图形一、单选题1.下面有4组立体图形,从左面看与其他3组不同的是( )A .B .C .D .2.如图,将一个圆柱的侧面剪开,不可能出现的形状是( )A .B .C .D .3.下列说法错误的有( )项。
①把一个圆柱的侧面剪开,不可能得到平行四边形。
②平行四边形的面积一定,它的底和对应的高成反比例。
③实际距离一定比相对应的图上距离大。
④一个长方形面积一定时,它的长与宽的关系用图像表示出来是一条直线。
A .1B .2C .3D .44.如图所示,把底面直径是8cm 的圆柱切成若干等份,拼成一个近似的长方体,这个长方体的表面积比原来增加了80cm 2,那么长方体的体积是( )cm 3。
A .251.2B .502.4C .2009.6D .1004.85.一个圆柱与一个圆锥体积相等,高也相等。
圆柱与圆锥的底面积的比是( )A .1:1B .3:1C .1:3D .1:96.圆柱的底面周长是圆锥底面周长的23,画圆锥的高是圆柱高的25,圆锥的体积与圆柱的体积比是( )A .5:3B .9:10C .10:3D .3:10二、填空题7.在下图中,正方形的面积是9平方厘米,这个圆的面积是 平方厘米。
8.做一个棱长50厘米的无盖正方体鱼缸,至少需要 平方厘米玻璃。
9.如图,将圆柱形纸筒沿虚线剪开得到一个长方形,这个长方形的长是 厘米,宽是 厘米。
(π取3.14)10.将一个底面半径是2cm,高是15cm的铁制圆锥放入盛满水的桶里(圆锥完全浸没),将有 cm3的水溢出。
11.一个等腰三角形的顶角是50°,这个三角形的一个底角是 。
12.如图,小聪在小明的 偏 的 方向上。
13.如下图是一个圆柱的展开图,圆柱的底面半径是 cm,表面积是 cm2,体积是 cm3。
14.把一个圆柱削成一个最大的圆锥,削去的体积是80cm3,则圆锥的体积是 cm3,圆柱的体积是 cm3。
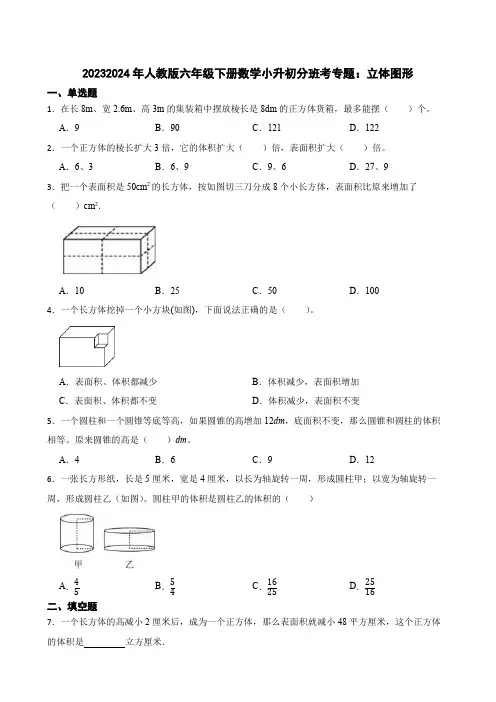
20232024年人教版六年级下册数学小升初分班考专题:立体图形一、单选题1.在长8m、宽2.6m、高3m的集装箱中摆放棱长是8dm的正方体货箱,最多能摆()个。
A.9B.90C.121D.1222.一个正方体的棱长扩大3倍,它的体积扩大()倍,表面积扩大()倍。
A.6、3B.6、9C.9、6D.27、93.把一个表面积是50cm2的长方体,按如图切三刀分成8个小长方体,表面积比原来增加了()cm2.A.10B.25C.50D.1004.一个长方体挖掉一个小方块(如图),下面说法正确的是()。
A.表面积、体积都减少B.体积减少,表面积增加C.表面积、体积都不变D.体积减少,表面积不变5.一个圆柱和一个圆锥等底等高,如果圆锥的高增加12dm,底面积不变,那么圆锥和圆柱的体积相等。
原来圆锥的高是()dm。
A.4B.6C.9D.126.一张长方形纸,长是5厘米,宽是4厘米,以长为轴旋转一周,形成圆柱甲;以宽为轴旋转一周,形成圆柱乙(如图)。
圆柱甲的体积是圆柱乙的体积的()A.45B.54C.1625D.2516二、填空题7.一个长方体的高减小2厘米后,成为一个正方体,那么表面积就减小48平方厘米,这个正方体的体积是立方厘米.8.家用卫生纸的宽度一般是10cm,中间硬卷轴的直径是3.5cm。
制作中间的纸轴需要cm2的硬纸板。
9.把一个长12分米的圆柱体木料,锯成3个小圆柱体,表面积增加了32平万分米,这根圆柱体木料的体积是立方分米。
10.把个底面半径是3厘米、高18厘米的圆锥形橡皮泥捏成个底面与圆锥相等的圆柱。
圆柱的高是厘米。
11.一个圆柱形罐头盒的侧面贴着商标纸,圆柱底面半径是5cm,高是20cm。
如果这张商标纸展开后是一个长方形,则它的长是cm,宽是cm,面积是cm2.12.小雪的学校叫实验小学,一进校门,就能看到大厅的8根一样大小的圆柱形大理石柱,每根柱子的半径是5分米,高6米,如果要清洗这些柱子,清洗的面积是平方米。

2023-2024学年人教版六年级下册数学小升初专题训练:立体图形一、单选题1.一个长方体正好可以切成3个一样的正方体,切开后每个正方体的表面积是12平方厘米,那么原来这个长方体的表面积是( )平方厘米。
A.36B.30C.28D.242.图中呈现的是一瓶已经喝了一些的果汁和一个圆锥形玻璃杯,如果瓶中的果汁倒入这种圆锥形玻璃杯,最多可以倒满( )。
(容器厚度忽略不计)A.2杯B.3杯C.4杯D.6杯3.小明买了一瓶水喝掉了一部分后还有剩余(如图所示),已知这个饮料瓶的内直径是6cm。
根据如图中标出的数据,小明用算式“3.14×(6÷2)2×(18+7)”计算的是( )A.喝掉的水的体积。
B.瓶子的容积。
C.剩余水的体积。
D.喝掉的水和剩余的水相差的体积。
4.一个圆柱体和一个圆锥体的底面周长之比是1:3,它们的体积比是1:3,圆柱体和圆锥体高的比是( )。
A.3:1B.1:9C.1:1D.3:25.一个长方体的长、宽、高分别扩大到原来的2倍,则它的表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
此题选( )。
A.2;4B.4;8C.6;8D.8;46.下面( )图形是圆柱的展开图。
(单位:cm)A.B.C.D.二、填空题7.长方体和正方体都有6个面, 条棱, 个顶点8.西游记中的孙悟空正直勇敢、嫉恶如仇,他有一件神奇的兵器叫如意金箍棒,可以任意缩小或放大。
如果孙悟空把如意金箍棒变化成底面周长是6.28分米,那么此时,它的体积是 立方分米。
9.如先图,把一个直径为4cm,高为8cm的圆柱,表面积增加了 平方厘米。
10.把64升水倒入一个长8分米、宽2.5分米、高4分米的长方体水箱内,这时水面距箱口 分米。
11.一根长1米,横截面直径是2分米的木头浮在水面上,小明发现它正好是一半露出水面,这根木头露出水面部分的体积是 立方分米。
12.用一根48分米长的铁丝做成一个正方体框架,这个正方体框架的表面积 平方分米,体积是 立方分米。

2024年人教版六年级下册数学小升初专题训练:立体图形一、单选题1.把一支新的圆柱形铅笔削尖,笔尖(圆锥部分)的体积是削去部分的( )。
A.13B.23C.12D.2倍2.比较等底等高的圆柱、正方体、长方体的体积的大小,结果是()A.长方体体积大B.正方体体积大C.圆柱体积大D.一样大3.把一个长、宽、高分别是6cm、2cm和2cm的长方体锯成三个大小完全相等的小正方体,表面积比原来增加了( )cm2。
A.8B.16C.24D.364.如图,两个圆柱形容器盛有相同体积的水,①号容器原来水面高是8cm,放入小球后水面的高是10cm;②号容器放入同样大的小球和一个小长方体后水面的高是26cm,小球的体积与小长方体的体积比是( )A.3:11B.3:5C.3:2D.9:75.两个圆柱的体积相等,底面积之比为3:4。
则这两个圆柱的高的比是( )。
A.4:3B.3:4C.9:16D.16:96.一个圆柱的底面半径是1cm,高是4cm,它的表面积是( )cm2。
A.12.56B.25.12C.31.4D.56.52二、判断题7.一个正方体的棱长是6厘米,它的表面积和体积相等。
( )8.如果两个圆柱的侧面积相等,那么它们的体积也一定相等。
( )9.把一个圆柱削成一个最大的圆锥,削去部分的体积是圆柱体积的23。
( )10.圆柱和圆锥都有无数条高。
11.长方体中,高不变,底面积越大,体积也越大。
( )12.一个圆锥的底面半径和高都是3cm,它的体积是28.26cm3。
( )三、填空题13.把一个圆柱形木料加工成一个最大的圆锥体,需要削去30立方分米的木料,则原来这根木料的体积是 立方分米。
14.一个圆锥,底面半径是4厘米,高是12厘米,从圆锥的顶点沿高将它切成相同的两半后,表面积比原来圆锥的表面积增加了 平方厘米。
15.一个圆柱,沿底面直径和高竖直切开得到两个半圆柱,切面是边长为4厘米的正方形。
原来这个圆柱的表面积是 平方厘米,体积是 立方厘米。

2024年人教版六年级下册数学小升初分班考必刷专题:立体图形一、选择题1.小华用6个同样大小的正方体摆成一个物体.从正面和上面看到的都是从右侧面看摆成的物体,看到的是第()号图形.A.B.C.D.2.一个直角三角形两条直角边分别是4厘米和6厘米,如果以较长的直角边所在的直线为轴,将三角形旋转一周形成的立体图形的体积是()立方厘米.A.301.44B.452.16C.100.48D.150.723.一个正方体的底面积是25平方厘米,它的体积是()立方厘米。
A.25B.125C.225D.5504.把两个表面积分别是24cm2的正方体拼成一个长方体,该长方体的表面积是()。
A.48cm2B.40cm2C.36cm2D.24cm25.一个圆柱和一个圆锥的底面积相等,圆柱和圆锥的体积比是3:2,圆柱和圆锥的高的比是()。
A.1∶3B.3:1C.1:2D.2:16.一个棱长10cm的正方体容器中装有一些水,将一个高8cm的长方体铁块竖直着放入水中(铁块底面与容器底面平行),铁块还没有完全浸没时,水就满了(如下图)。
这个铁块的体积是()3cm。
A.300B.400C.600D.800二、填空题7.南山湖音乐喷泉是由48个内直径为2厘米的出水管围成的一个圆形。
打开音乐喷泉时,水喷涌的速度是5米/秒,如果不实行水循环系统,那么一分钟会浪费( )吨水。
(每立方米水的质量是1吨)8.一个棱长是5分米的正方体水箱内,水面的高度为3分米,水的体积是( )升.9.如图,以长方形3厘米的边所在直线为轴旋转,可以得到一个( ),它的底面直径是( )厘米,侧面积是( )平方厘米。
10.长方体纸盒的长为acm,宽和高都是bcm,用含有字母的式子表示这个纸盒的体积是( )cm3。
11.一个立体图形,从左面看到的形状是,从上面看到的形状是,搭成这样的立体图形,最少需要( )个小正方体。
12.如图所示,把底面半径为4分米的圆柱切成若干等份,拼成一个近似的长方体,这个长方体的表面积比原来增加40平方分米,这个圆柱的高是( )分米,圆柱的体积是( )立方分米。

通用版小升初专项复习:立体图形一、填空题1.下面图形以红色线为轴旋转后会得到圆锥吗,如果是说出圆锥的高和底面半径。
2.至少用个棱长1cm的小正方体可以拼成一个较大的正方体。
拼成这个大正方体的体积是,表面积是。
3.把一块长8dm、宽6dm、高5dm的长方体分割成两个完全相同的小长方体,则它的表面积最多增加dm2,最少增加dm2。
4.绕着一个圆锥形状的碎石堆的外边缘走一圈,要走18.84米.如果这堆碎石的高是2.4米,它的体积是立方米?5.一个底面半径是20cm、高是15cm的圆柱形铁块,可以熔铸成个底面直径是20cm、高是15cm的圆锥形铁块。
(损耗不计)6.一个圆柱的底面周长是6.28厘米,高5厘米,它的侧面积是,表面积是,体积是。
7.把一个底面直径为3厘米、高是5厘米的圆柱体沿直径切割成两个半圆柱,表面积增加了。
8.把一个棱长是3dm的正方体,切削成最大的圆柱,这个圆柱的侧面积是dm2。
9.5x=4y,那么x∶y=∶.二、单选题10.下面图形中,折叠后能围成正方体的是()。
A.B.C.D.11.一个圆锥的体积是141.3cm3,与它等底等高的圆柱的体积是()cm3。
A.47.1B.141.3C.282.6D.423.912.有一堆小麦如下图,从上面及侧面看,形状大致会是()A.三角形,圆形B.梯形,圆形C.圆形,长方形D.圆形,三角形13.如下图,这块石头的体积约是()cm3。
A.500B.1000C.5000D.6000 14.一个圆锥的体积是100立方厘米,底面积是50平方厘米,它的高是()厘米。
A.2B.23C.6D.1015.奇奇将圆柱内的水倒入()圆锥内,正好倒满。
A.B.C.D.16.学校买来420本课外书,按照人数的比分配给六年级3个班。
六(1)班42人,六(2)班50人,六(3)班48人。
六(3)班可分得()本。
A.126B.140C.144D.15017.如图所示的展开图中是左边的正方体的展开图的是()A.B.C.D.18.用一块长56.52cm、宽31.4cm的长方形铁皮,配上一块直径()cm的圆形铁皮可以做成一个容积最大的水桶。

2023-2024学年人教版六年级下册数学小升初专题训练:立体图形一、单选题1.一个底面是正方形的长方体铁箱,如果把它的侧面展开,正好得到一个边长是40厘米的正方形,这个铁箱的容积是() 升。
A.400B.4000C.4D.402.小明在一个底面积为48 cm2的长方体水槽中放入了一块石头(完全浸没,水未溢出)。
水面上升了2cm.这块石头的体积是() cm3.A.24B.50C.96D.1923.一块长是3分米,宽是2分米,体积是25.2立方分米的长方体木料,()完全放入一个长是3.1分米,宽是2.1分米,高是4分米的长方体纸箱内(纸箱厚度忽略不计)。
A.能B.不能C.不一定能D.条件不足,无法确定4.张华想将四个完全相同的小正方体纸箱堆放在墙角,()露在外面的面积最小。
A.B.C.D.5.一个长方体的长、宽、高分别扩大到原来的2倍,它的表面积扩大到原来的()倍。
A.2B.4C.6D.86.下面图()可以围成一个圆柱。
A.B.C.D.二、判断题7.等底等高的正方体、长方体,圆柱和圆锥的体积都相等。
()8.把28L水倒入一个从里面量长40cm、宽25cm、高40cm的长方体玻璃水槽中,这时水面距水槽口28cm。
()9.一个圆柱的侧面展开图是一个正方形,这个圆柱的底面直径与高的比是1:π。
()10.一个圆柱和一个圆锥的底面半径的比为2:1,高的比为1:1,那么圆柱和圆锥的体积比是4:1。
()11.8 个小正方体拼成的大正方体,拿走一个小正方体,如图,它的表面积和体积都变小了。
()12.一个圆柱的高不变,它的底面半径扩大到原来的2倍,体积扩大到原来的8倍。
()三、填空题13.在一个长10厘米、宽8厘米、高7厘米的长方体盒子里面最多能放个棱长为2厘米的小正方体。
(小正方体不外露)14.把两个底面直径为6cm,高为5cm 的圆柱拼成一个大圆柱,表面积(填“增加”或“减少”)cm2。
15.如图,把底面直径为6cm 的圆柱沿直径切成若干等份,拼成一个近似的长方体,这个长方体的表面积比原来增加60cm2,那么长方体的体积是cm3。

人教版六年级下册数学小升初分班考必刷专题:立体图形一、单选题1.有一块棱长是6分米的正方体木料,把它加工成一个圆锥,这个圆锥的体积最大是()立方分米。
A.216πB.54πC.72πD.18π2.一个直角三角形的两条直角边长分别为3cm和4cm,以较短直角边为轴旋转一周得到一个圆锥,这个圆锥的体积是()cm3。
A.12πB.16πC.36πD.48π3.如果正方体、圆柱、圆锥的底面积相等,高也相等。
下面说法正确的是()。
A.圆柱的体积比正方体的体积小B.圆柱和正方体的表面积相同C.圆柱的体积是圆锥的13D.圆锥的体积是正方体的134.一块长方体肥皂的长是15厘米,宽是8厘米,高是8厘米。
这块肥皂的表面积是()平方厘米。
A.62B.608C.960D.1445.下面各图形中,()是圆柱的展开图。
(单位:cm)A.B.C.D.6.底面积相等的圆柱和圆锥,它们的体积比是2:1,圆锥的高是9cm,圆柱的高是()。
A.3cm B.6cm C.9cm D.18cm二、填空题7.一个长方体和一个正方体的棱长总和相等,已知长方体的长、宽、高分别是3dm、2dm、4dm,那么正方体的体积是dm3。
8.等底等高的一个圆柱和一个圆锥,体积相差60立方厘米,圆柱体的体积是立方厘米,圆锥体的体积是立方厘米。
9.一个圆柱形油桶,从里面量底面直径是4分米,高是5分米。
它的容积是升。
10.做一个棱长50厘米的无盖正方体鱼缸,至少需要平方厘米玻璃。
11.如图,将圆柱形纸筒沿虚线剪开得到一个长方形,这个长方形的长是厘米,宽是厘米。
(π取3.14)12.一个正方体木块的棱长是6cm,把它削成一个最大的圆柱体。
圆柱体的体积是cm3。
再把这个圆柱体削成一个最大的圆锥体,圆锥体的体积是cm3。
13.一个直角三角形,两条直角边分别是9厘米和6厘米,绕着其中一条直角边旋转一周可以得到一个立体图形,这个立体图形的体积是立方厘米。
14.如图是圆柱的侧面展开图,侧面积是cm2,体积是cm3。
第6节:立体图形拓展【例1】用棱长为1的小正方体木块摆成一个长20,宽15,高10的长方体,然后将所摆成的长方体表面喷上颜色。
则没有喷到颜色的木块共有( )个。
【例2】一个长方体木块,锯掉5厘米后,得到一个正方体木块,表面积比原来减少100平方厘米,求原来长方体木块的表面积。
【例3】一个棱长是3厘米的正方体木块,各面中心凿出一孔面边长是1厘米的正方形柱孔,它余下的体积是多少立方厘米?表面积是多少平方厘米?1.将1立方米的大正方体锯成体积是1立方厘米的小正方体,然后将它们一个一个连成一排,其总长度是 千米。
2. 一个正方体木块,棱长4 厘米,把它的外表涂成绿色,然后切割成棱长为1 厘米的小正方体。
小正方体中,只有一面是绿色的有( )块,没有一面是绿色的有( )块。
3.已知一个正方体的体积是729立方厘米,现在要在它的8个角上分别截去8个大小相同的小正方体,使得截去后余下的体积是665立方厘米,则截去的每个小正方体的棱长是 。
形状不规则的物体可以用排水法求体积,形状规则的物体可以用公式直接求体积。
排水法的公式:V 物体 =V 现在-V 原来也可以 V 物体 =S 底面×(h 现在- h 原来) V 物体 =S 底面×h 升高模块一:正方体题型举例模块二:液体浸物【例1】一个圆柱形容器中有足够量的水,在水中放入一个圆锥形铅锤后,水面上升了3厘米,已知容器内部底面的半径是铅锤底面半径的2倍,这个铅锤的高为多少厘米?【例2】一个圆柱形的容器的底部放着一块正方体铅块,现在向容器内匀速注水,20秒时水恰好没过铅块的上表面,又过了1.5分钟,水注满了容器。
若容器高度是24厘米,铅块高是6厘米,则容器底面积是多少平方厘米?【例3】如图,在底面是边长为60厘米的正方体容器里,直立放着一个高100厘米,底面边长为18厘米的正方形的铁块,这时容器里的水深是50厘米,现在把铁块提出容器之后,水面下降()厘米1.一瓶装满的矿泉水,小亮喝了一些,把瓶盖拧紧后倒置放好在水平的桌面上,无水部分是高3cm,内直径是6cm的圆柱体,那么小亮喝了()cm3水。
【小升初】人教版2023-2024学年六年级下册数学专项练习(立体图形)一、单选题1.用一根长48cm的铁丝制作棱长都是整厘米数的长方体框架,这个长方体框架的长、宽、高可能是( )。
A.7cm 2cm 1cm B.20cm 18cm 10cmC.5cm 5cm 6cm D.5cm 4cm 3cm2.一团橡皮泥,妙想第一次把它捏成一个长方体,第二次把它捏成一个正方体。
捏成的两个物体的体积相比较,( )。
A.长方体大B.正方体大C.一样大D.无法确定3.一个底面是正方形的长方体铁箱,如果把它的侧面展开,正好得到一个边长是40厘米的正方形,这个铁箱的容积是( ) 升。
A.400B.4000C.4D.404.小明在一个底面积为48 cm2的长方体水槽中放入了一块石头(完全浸没,水未溢出)。
水面上升了2cm.这块石头的体积是( ) cm3.A.24B.50C.96D.192 5.有两个底面积相等的圆柱,一个圆柱的高是24cm,体积是1200cm3;另一个圆柱的高是35cm,它的体积是( )cm3。
A.50B.1200C.1750D.2950 6.一个圆柱的侧面展开图是正方形,这个圆柱的底面直径的长度和高的比( )。
A.2π:1B.π:1C.2:1D.1:π二、填空题7.圆柱的两个底面圆心之间的距离叫作 。
8.一个圆柱的体积是48dm3,与它等底等高的圆锥的体积是 。
9.在一个长10厘米、宽8厘米、高7厘米的长方体盒子里面最多能放 个棱长为2厘米的小正方体。
(小正方体不外露)10.如图,把底面直径为6cm 的圆柱沿直径切成若干等份,拼成一个近似的长方体,这个长方体的表面积比原来增加60cm2,那么长方体的体积是 cm3。
11.一个圆柱的底面半径是6cm,高是10cm,它的侧面积是 cm2,表面积是 cm2,体积是 cm3。
12.一个圆锥和它等底等高的圆柱的体积相差9.6立方厘米,圆柱的体积是 立方厘米,圆锥的体积是 立方厘米。
绝密★启用前小升初分班考重点专题:立体图形-数学六年级下册人教版学校:___________姓名:___________班级:___________考号:___________注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上一、选择题1.由十个小正方体木块堆积而成的几何体如图所示,且紧挨着的两个木块颜色不同,那么从下往上看该几何体,得到的图形是( )。
A .B .C .D .2.一种长方体饼干盒,长3cm 、宽2cm 、高1cm 的(如图),买3盒这样的饼干包装成一件礼品,用最节约纸的方式包装,需要包装纸( )。
(接口处不计)A .238cmB .242cmC .254cmD .258cm3.由一个正方体木块加工成最大的圆柱,它的底面直径是10厘米,这个正方体的体积是( )立方厘米。
A .8000B .4000C .1000D .3144.已知两个圆柱体的底面半径之比是1∶3,高之比是6∶1,那么它们的体积之比是( )。
A .2∶1B .1∶3C .1∶1D .2∶35.1包饼干包装后为圆柱形,将12包这种饼干放入一个长24cm ,宽18cm 的长方体纸盒内(如图)。
每包饼干的底面直径是( )cm 。
A .4B .6C .9D .126.如图,一个凉亭有8根柱子,每根柱子高约3米,直径约0.5米,如果给这些柱子涂上红色油漆,正确表述涂色面积是多少平方米的算式是( )。
A .3.140.538⨯⨯⨯B .()23.140.53 3.140.258⨯⨯+⨯⨯C .()23.140.53 3.140.2528⨯⨯+⨯⨯⨯D .23.140.58⨯⨯二、填空题7.在一个棱长是4dm 的正方体水箱中盛满水,再将水全部倒入一个底面积是20dm 2,高是4dm 的圆柱形水桶中,水深( )dm 。
8.一个小正方体与一个大正方体的棱长比是2∶5,它们的表面积之比是( ),它们的体积比是( )。
小升初真题特训:立体图形-小学数学六年级下册人教版学校:___________姓名:___________班级:___________考号:___________....二、填空题7.(2022·河北廊坊·统考小升初真题)一个圆柱的底面直径是2cm,高是3cm,它的体积是()cm3;一个圆锥与这个圆柱等底等体积,那这个圆锥的高是()cm。
8.(2022·浙江温州·统考小升初真题)如图,正方体一个角上画一个三角形,三边长度分别是3cm、4cm和5cm。
按角分类这个三角形属于()三角形,它的面积是()cm2。
9.(2021·统考小升初真题)如图,(单位:厘米)一个立体图形,从正面看得到的是图形①,从上面看得到的是图形②,这个图形的体积是()立方厘米。
如果用一个长方体或正方体盒子包装它,这个盒子的容积至少是()立方厘米。
10.(2022·浙江杭州·校考小升初真题)冬冬用棱长1厘米的小正方体摆成一个物体,从前面、右面、上面三个方向看到的形状如下图所示,这个物体的体积是()立方厘米。
11.(2021·天津南开·统考小升初真题)一个圆柱和一个圆锥等底等高,圆柱体积与圆锥的体积比是()。
12.(2022·广东深圳·统考小升初真题)下图是一个正方体六个面的展开图,这六个面分别是A、B、C、D、E、F,三组对应的面中,C对();E对()。
13.(2020·广东揭阳·小升初真题)把一张长12.56分米,宽6.28分米的长方形铁皮圈成一个圆柱铁皮桶,这个铁皮桶的底面积是()或()平方分米。
(接头处忽略不计)14.(2022·山东菏泽·统考小升初真题)一个长方体和一个正方体的棱长总和相等,已知长方体的长、宽、高分别是3分米、2分米、4分米,那么正方体的体积是()立方分米。
-小升初立体图形的综合专项试题-人教版评卷人得分一、解答题(题型注释)2.请你计算出这个图形的总面积.(单位:米)3.列式解答:如图是一盒巧克力,如果将这样的三盒巧克力包装成一个礼包,怎样包装才能最节省包装纸?(重叠处不计)(图:一个长20厘米、宽15厘米、高6厘米的长方体)(1)用这种包装方法包装成的礼包长厘米、宽厘米、高厘米.(2)用这种包装方法包装成的礼包至少要用多少包装纸?4.如图,半圆的直径BC=12厘米,AB=AC,D为AC的中点,求阴影部分的面积.5.如图三角形ABC是直角三角形,边AB长12厘米,BC长4厘米,求阴影部分面积6.有一张长方形的纸,把纸的一角像如图那样折叠,求图中阴影部分的面积.(单位:cm)7.计算下面各图形的面积。
(单位:厘米)(1)(2)8.小明星期天请6名同学来家做客,他选用一盒用长方体(如图(1))包装的饮料招待同学,给每名同学倒上一满杯(如图(2))后,他自己还有喝的饮料吗?(写出主要过程)9.计算下列图形中阴影部分的面积。
(单位:厘米) (1) 10.如图,有甲、乙两个立体图形,从正面、左面和上面看这两个立体图形,哪些面看到的图形是一样的?甲乙参数答案1.解:图(1)4个;图(2)5个;图(3)4个;图(4)5个【解析】1.此问题的解决主要在于对被遮挡的小正方体的计数,四个小问题中只有第一个在第2行、第1列、第1层有一个小正方体被遮挡住了,其余三题均无遮挡问题,可直接计数。
所以图(1)是由4个正方体摆成,图(2)是由5个正方体摆成,图(3)是由4个正方体摆成,图(4)是由5个正方体摆成.考查目的:通过立体图形的计数,考查学生对遮挡的认识,发展学生的空间观念。
2.解:12×6÷2+12×4=36+48=84(平方米)答:这个图形的面积是84平方米【解析】2.这个图形由一个三角形和一个平行四边形组成,利用S= ah 和S=ah即可求解.此题主要考查三角形和平行四边形的面积公式的灵活应用.3.(1)20;15;18(2)解:(20×15+20×18+15×18)×2,=(300+360+270)×2,=930×2,=1860(平方厘米),答:将20×15的面相连接,组成一个长为20厘米,宽15厘米,高18厘米的长方体表面积最小,所以这样包装才能最省包装纸,至少需要包装纸1860平方厘米.【解析】3.解:(1)将20×15的面相连接,组成一个长为20厘米,宽15厘米,高为6×3=18厘米的长方体表面积最小,所以这样包装才能最省包装纸.所以答案是:20;15;18.4.解:S阴=S扇形AOB= ×3.14×(12÷2)2=3.14×9=28.26(平方厘米)答:阴影部分的面积是28.26平方厘米【解析】4.如图所示,连接AO,则AO就是三角形ABC的高,因为三角形ABD的面积等于三角形AOB的面积,所以阴影部分的面积=S扇形AOB= 14圆的面积,将数据代入此等式即可求解.解答此题的关键是做出合适的辅助线,将阴影转化成圆面积的四分之一.5.解:设半圆的半径为x厘米,则(12﹣x):12=x:412x=4(12﹣x)12x=48﹣4x16x=4816x÷16=48÷16x=312×4÷2﹣3.14×32÷2=24﹣3.14×9÷2=24﹣14.13=9.87(平方厘米)答:阴影部分面积是9.87平方厘米【解析】5.首先根据相似三角形的性质得到半圆的半径,再根据阴影部分面积=三角形的面积﹣半圆的面积,代入数据计算即可求解.考查了组合图形的面积,本题关键是理解阴影部分面积=三角形的面积﹣半圆的面积,难点是得到半圆的半径.6.解:7×4﹣×(7﹣4)×4×2=28﹣×3×4×2=28﹣12=16(cm2)答:图中阴影部分的面积是16cm2【解析】6.图中阴影部分面积是原长方形的面积减去2倍的三角形的面积(三角形下面覆盖一个同样的三角形).图中三角形的底一条直角边是(7﹣4)cm,一条是4cm,原长方形的面积和三角形的面积的条件都已具备.本题是考查简单图形的折叠问题,关键明白三角形下面覆盖一个同样的三角形,因此用长方形的面积减去2倍的三角形的面积.7.(1)(18×8.5)÷2 = 76.5(平方厘米)(2)11×7+11×4 = 121(平方厘米)【解析】7.(1)根据三角形的面积=12×底×高,可求得图1的面积,为(18×8.5)÷2 = 76.5(平方厘米);(2)根据组合图形的面积等于各图形的面积之和,图二的面积为平行四边形的面积+长方形的面积,再根据平行四边形的面积=底×高,长方形的面积=长×宽,可求得图2的面积,为11×7+11×4 = 121(平方厘米)8.15×12×6=1080(立方厘米) 20×8×6=960(立方厘米)1080立方厘米﹥960立方厘米答:他自己还有喝的饮料。
2019-2020学年度人教版数学六年级下册小升初专题练习:立体图形一、选择题)。
A. B. C.2.长方体的火柴盒外壳有多少个面()A. 2B. 3C. 4D. 53.下列形状的纸片中,不能围成圆柱形纸筒的是()A. B. C. D.4.下图中的正方体、圆柱体和圆锥体的底面积相等,高也相等。
下面说法正确的是()。
A. 圆锥的体积是圆柱体积的3倍。
B. 圆柱的体积比正方体的体积小一些。
C. 圆锥的体积是正方体体积的。
D. 以上说法都不对。
5.圆柱的底面直径和高都是8厘米,这个圆柱的表面积是()平方厘米。
A. 100.48B. 301.44C. 200.96D. 251.26.圆锥的体积是120立方分米,底面积是10平方分米,高是()分米.A.12B.24C.36D.487.一个圆柱,底面直径和高都是2分米,这个圆柱的表面积是()平方分米.A. 6πB. 5πC. 4π8.油漆圆柱形柱子,要计算油漆的面积有多大,就是求()A. 体积B. 表面积C. 侧面积9.圆柱的底面周长是6.28cm,高是10cm;长方体的底面是正方形的,底面周长和高与圆柱的相等.两个形体的表面积哪个大?正确的解答是()A. 两个形体表面积一样大B. 长方体的表面积大C. 无法确定D. 圆柱体的表面积大二、填空题(题型注释)10.如图的四个正方体堆放在墙角处,露在外面的有( )个面。
A. 6 B. 9 C. 15 D. 2411.两个长方体的表面积相等,它们的形状一定相同. .12.正方体的棱长扩大到原来的3倍,那么它的表面积扩大到原来的6倍,体积扩大到原来的9倍. .13.如果把圆柱的侧面展开可以得到一个长方形,这个长方形的长等于圆柱的底面 ,宽等于圆柱的 .14.把一个高为9分米的圆锥体钢坏,经熔铸后,成为一个与它等底的圆柱体,这个圆柱体的高是 .15.正方体的棱长扩大4倍,它的体积也扩大4倍. .16.这个长方体的前面与________面是完全相同的长方形,每个面的面积都是________平方分米;右面与________面完全相同,每个面的面积都是________平方分米;还有________面与________面完全相同,每个面的面积都是________平方分米.17.一个高6cm 的圆锥形容器盛满了水,倒入和它等底等高的圆柱形容器内,这时水面的高是(_______)cm 。
18.一条200米长的拦河大坝的横截面是梯形,它的上底是8米,下底是32米,高是4.2米.修这条拦河大坝一共需要土石________立方米。
19.圆柱一共有________个面,有________条高。
上下两个面是________形,侧面是一个________面。
20.一个长方体的长是5dm ,宽是4dm ,高是3dm 。
这个长方体的棱长总和是________dm ,前面的面积是________dm 2 , 上面的面积是________dm 2。
21.把两个同样大小的正方体粘合成一个长方体,粘合成的长方体比原来的两个正方体少掉________个面.如果正方体的边长是2分米,那么粘合成的长方体的长是________分米,宽是________分米,高是________分米.22.动动手,折折看,下面________几幅图形可以折成圆圈中的图形。
23.长方体的高锯掉2厘米后成了棱长为6厘米的正方体,原长方体的表面积是________体积是________三、解答题(题型注释)1米,高为4.5分米,用这堆沙在5米宽的公路上铺2厘米厚的路面,可以铺几米?25.一个长方体的汽油桶,底面积是35dm²,高是5dm 。
如果1升汽油重0.73千克,这个油桶可以装汽油多少千克?26.一个工程队要挖一个长60m ,宽40m ,深150cm 的长方体水池。
这个工程队挖出多少方的沙土?27.如图,观察这个长方体,数一数它有几个面?几条棱?几个顶点?每个面的面积是多少?四、作图题2厘米,高2厘米的圆柱体展开图。
五、判断题______)30.长方体的长、宽、高都扩大2倍,则棱长之和也扩大2倍.(_____)参数答案1.B【解析】1.长方体是长长方方的,有平平的面,有尖尖的点,无法滚动。
正方体是四四方方的,有平平的面,有尖尖的点,正方体也无法滚动。
圆柱是直直的,上下一样粗细,两头圆圆的,平平的;圆柱如果“躺”在桌子上,它能够滚动,如果立在桌子上,它就不能滚动。
球是圆圆的,它没有平平的面,放在桌子上可以任意地滚动。
所以图中B是圆柱。
故选:B。
2.C【解析】2.根据实际情况火柴盒外壳没有底面,去掉两个底面,还剩4个面。
故答案为:C.3.D【解析】3.试题分析:根据圆柱的侧面展开图的特点,将圆柱的侧面的几种展开方法与展开后的图形列举出来,利用排除法即可进行选择.解:(1)如果圆柱的底面周长与高相等,把圆柱的侧面展开有两种情况:①沿高线剪开:此时圆柱的侧面展开是一个正方形;②不沿高线剪:斜着剪开将会得到一个平行四边形;(2)如果圆柱的底面周长与高不相等,把圆柱的侧面展开有两种情况:①沿高线剪开:此时圆柱的侧面展开是一个长方形;②不沿高线剪:斜着剪开将会得到一个平行四边形或菱形;根据上述圆柱的展开图的特点可得:题干的四个图形中只有正六边形不能围成圆柱形;故选:D.4.C【解析】4.略5.B 【解析】5.圆柱的底面直径和高都是8厘米,求这个圆柱的表面积是多少平方厘米,要用它的侧面积加上两个底面积,列式为3.14×8×8+3.14×(8÷2)²×2=301.44平方厘米。
6.C【解析】6.解:120×3÷10 =360÷10=36(分米)答:它的高是36分米.故选:C.7.A【解析】7.π×2×2+π×()2×2,=π×4+π×2,=6π(平方分米);故选A8.C【解析】8.油漆圆柱形柱子,要计算油漆的面积有多大,就是求圆柱的侧面积。
故选:C9.D【解析】9.圆柱和长方体的底面周长和高都是相等的,那么它们的侧面积是相等的,圆柱的底面周长等于长方体的底面正方形的周长,所以圆的面积大于正方形的面积,所以圆柱的表面积大于长方体的表面积。
这道题考查的是表面积的知识,解答此题要明确周长相等的情况下,圆的面积大于正方形的面积,据此分析即可。
10.B【解析】10.略11.×【解析】11.试题分析:长方体的表面积大小是由长、宽、高的数值决定的,若两个长方体的表面积相等,则它们的长、宽、高不一定相等,这两个长方体的形状就不一定相同,据此即可做出判断.解:因为长方体的表面积大小是由长、宽、高的数值决定的,若两个长方体的表面积相等,则它们的长、宽、高不一定相等,这两个长方体的形状就不一定相同;故答案为:×.12.错误【解析】12.试题分析:根据正方体的表面积公式:s=6a2,体积公式:v=a3,再根据积的变化规律,积扩大的倍数等于因数扩大倍数的乘积.由此解答.解:正方体的棱长扩大到原来的3倍,那么它的表面积扩大到原来的3×3=9倍,体积扩大到原来的3×3×3=27倍.所以,正方体的棱长扩大到原来的3倍,那么它的表面积扩大到原来的6倍,体积扩大到原来的9倍.此说法是错误的.故答案为:错误.13.周长,高.【解析】13.试题分析:联系实际操作可知,圆柱的侧面展开会得到一个长方形,这个长方形的长与圆柱的底面周长完全重合,宽就是圆柱的高来进行解答.解答:解:把一个圆柱的侧面展开得到一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高.故答案为:周长,高.14.3分米【解析】14.试题分析:因为熔铸前后的体积不变,所以圆柱与圆锥的体积相等,底面积相等,据此先利用圆柱与圆锥的体积公式求出它们的高的比,再利用圆锥的高是9分米,即可求出圆柱的高.解:解设圆柱与圆锥的体积是V,底面积是S,所以圆柱的高:圆锥的高=:=1:3;又因为圆锥的高是9分米,所以圆柱的高是9÷3=3(分米),答:圆柱的高是3分米.故答案为:3分米.15.错误【解析】15.试题分析:根据正方体的体积公式:v=a3,再根据积的变化规律:积扩大的倍数等于因数扩大倍数的乘积.由此解答.解:根据分析:正方体的棱长扩大4倍,它的体积就扩大4×4×4=64倍.因此,正方体的棱长扩大4倍,它的体积也扩大4倍.此说法错误.故答案为:错误.16.后18左24上下12【解析】16.长方体的6个面都是长方形,相对的两个面的面积相等,上面或下面的面积=长×宽,前面或后面的面积=长×高,左面或右面的面积=宽×高,据此列式解答.17.2【解析】17.略18.16800【解析】18.略19.3无数圆曲【解析】19.略20.481520【解析】20.棱长总和:(5+4+3)×4=12×4=48(dm),前面的面积:5×3=15(dm²),上面的面积:5×4=20(dm²)。
故答案为:48;15;2021.6422【解析】21.略22.A,E,F【解析】22.略23.264平方厘米288立方厘米【解析】23.略24.4.71m【解析】24.4.5dm=0.45m 2cm=0.02m 3.14×1²×0.45×13÷(0.02×5)=4.71(m)25.127.75千克【解析】25.35×5×0.73=127.75(千克)答:这个油桶可以装汽油127.75千克。
26.3600方【解析】26.150厘米=1.5米60×40×1.5=3600(立方米)=3600(方)答:这个工程队挖出3600方的沙土。
27.6个面、12条棱、8个顶点。
前后面的面积各是 72平方厘米;左右面的面积各是24平方厘米;上下面的面积各是48平方厘米。
【解析】27.这个长方体有6个面、12条棱、8个顶点。
前后面的面积各是:12×6=72(平方厘米);左右面的面积各是:4×6=24(平方厘米);上下面的面积各是:12×4=48(平方厘米)。
28.【解析】28.略29.×【解析】29.长方体的6个面都是长方形,有时有两个相对的面是正方形。
30.正确【解析】30. 略。