空间中的垂直关系(带答案)教学提纲

《空间中的垂直关系》教学设计
一、教学目标
1、掌握直线与平面垂直的定义、断定定理和性质定理，并能运用它们进展论证和解决有关的问题；
2、掌握平面与平面垂直的概念和断定定理、性质定理，并能运用它们进展推理论证和解决有关问题；
二、教学重点、难点
在研究垂直问题时，要擅长应用“转化〞和“降维〞的思想，通过线线、线面、面面平行与垂直关系的转化，从而使问题获得解决。

三、教学过程
环节一：思维构建
环节二：线线垂直
【21年全国甲卷第19题】如图，直三棱柱111ABC A B C -中，侧面11AA BB 为正方形，2AB BC ==,,E F 分别是1,AC CC 的中点，D 为棱11A B 上的点
11BF A B ⊥.
证明：BF DE ⊥
环节三：线面垂直
【20年山东卷第20题】如图，四棱锥P ABCD -的底面为正方形，PD ⊥底面ABCD .设平面PAD 与平面PBC 的交线为l . 证明：l ⊥平面PDC
环节四：面面垂直
【17年全国Ⅲ卷第19题】如图，四面体ABCD 中，ABC ∆是正三角形，ACD ∆是直角三角形，AB BD =. 证明：平面ACD ⊥平面ABC。

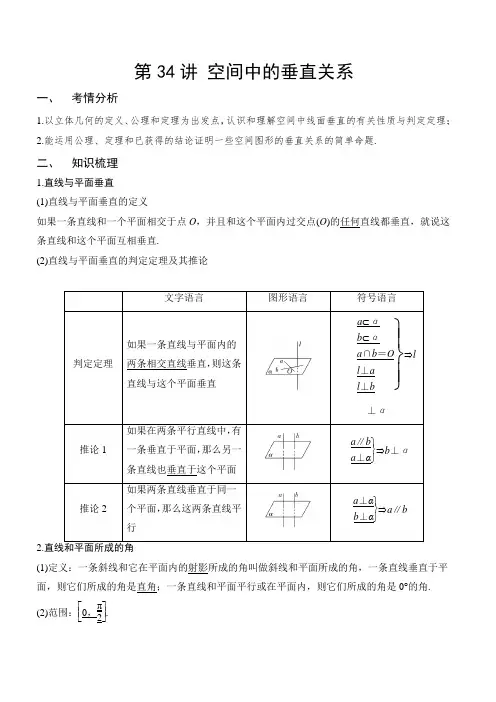
第34讲 空间中的垂直关系一、 考情分析1.以立体几何的定义、公理和定理为出发点，认识和理解空间中线面垂直的有关性质与判定定理；2.能运用公理、定理和已获得的结论证明一些空间图形的垂直关系的简单命题.二、 知识梳理1.直线与平面垂直 (1)直线与平面垂直的定义如果一条直线和一个平面相交于点O ，并且和这个平面内过交点(O )的任何直线都垂直，就说这条直线和这个平面互相垂直.(2)直线与平面垂直的判定定理及其推论文字语言图形语言符号语言判定定理如果一条直线与平面内的两条相交直线垂直，则这条直线与这个平面垂直⎭⎪⎬⎪⎫a ⊂αb ⊂αa ∩b ＝O l ⊥al ⊥b⇒l ⊥α推论1如果在两条平行直线中，有一条垂直于平面，那么另一条直线也垂直于这个平面⎭⎬⎫a ∥b a ⊥α⇒b ⊥α 推论2如果两条直线垂直于同一个平面，那么这两条直线平行⎭⎬⎫a ⊥αb ⊥α⇒a ∥b 2.(1)定义：一条斜线和它在平面内的射影所成的角叫做斜线和平面所成的角，一条直线垂直于平面，则它们所成的角是直角；一条直线和平面平行或在平面内，则它们所成的角是0°的角. (2)范围：⎣⎢⎡⎦⎥⎤0，π2.3.二面角(1)定义：从一条直线出发的两个半平面所组成的图形叫做二面角；(2)二面角的平面角：在二面角的棱上任取一点，以该点为垂足，在两个半平面内分别作垂直于棱的两条射线，这两条射线所构成的角叫做二面角的平面角.(3)二面角的范围：[0，π].4.平面与平面垂直(1)平面与平面垂直的定义如果两个相交平面的交线与第三个平面垂直，又这两个平面与第三个平面相交所得两条交线互相垂直，就称这两个平面互相垂直.(2)平面与平面垂直的判定定理与性质定理文字语言图形语言符号语言判定定理如果一个平面过另一个平面的一条垂线，则这两个平面互相垂直⎭⎬⎫l⊥αl⊂β⇒α⊥β性质定理如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面⎭⎬⎫α⊥βl⊂βα∩β＝al⊥a⇒l⊥α[微点提醒]1.两个重要结论(1)若两平行线中的一条垂直于一个平面，则另一条也垂直于这个平面.(2)若一条直线垂直于一个平面，则它垂直于这个平面内的任何一条直线(证明线线垂直的一个重要方法).2.使用线面垂直的定义和线面垂直的判定定理，不要误解为“如果一条直线垂直于平面内的无数条直线，就垂直于这个平面”.三、经典例题考点一线面垂直的判定与性质【例1】如图，在三棱锥P－ABC中，AB＝BC＝22，P A＝PB＝PC＝AC＝4，O为AC的中点.(1)证明：PO⊥平面ABC；(2)若点M在棱BC上，且MC＝2MB，求点C到平面POM的距离.(1)证明因为AP＝CP＝AC＝4，O为AC的中点，所以OP⊥AC，且OP＝2 3.连接OB.因为AB＝BC＝22AC，所以△ABC为等腰直角三角形，且OB⊥AC，OB＝12AC＝2.由OP2＋OB2＝PB2知，OP⊥OB.由OP⊥OB，OP⊥AC且OB∩AC＝O，知PO⊥平面ABC.(2)解作CH⊥OM，垂足为H.又由(1)可得OP⊥CH，所以CH⊥平面POM.故CH的长为点C到平面POM的距离.由题设可知OC＝12AC＝2，CM＝23BC＝423，∠ACB＝45°.所以OM＝25 3，CH＝OC·MC·sin∠ACBOM＝455.所以点C到平面POM的距离为45 5.规律方法 1.证明直线和平面垂直的常用方法有：(1)判定定理；(2)垂直于平面的传递性(a∥b，a⊥α⇒b⊥α)；(3)面面平行的性质(a⊥α，α∥β⇒a ⊥β)；(4)面面垂直的性质(α⊥β，α∩β＝a，l⊥a，l⊂β⇒l⊥α).2.证明线面垂直的核心是证线线垂直，而证明线线垂直则需借助线面垂直的性质.因此，判定定理与性质定理的合理转化是证明线面垂直的基本思想.考点二面面垂直的判定与性质【例2】如图，在四棱锥P－ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面P AD⊥底面ABCD，P A⊥AD，E和F分别是CD和PC的中点，求证：(1)P A⊥底面ABCD；(2)BE∥平面P AD；(3)平面BEF⊥平面PCD.证明(1)∵平面P AD⊥底面ABCD，且P A垂直于这两个平面的交线AD，P A⊂平面P AD，∴P A⊥底面ABCD.(2)∵AB∥CD，CD＝2AB，E为CD的中点，∴AB∥DE，且AB＝DE.∴四边形ABED为平行四边形.∴BE∥AD.又∵BE⊄平面P AD，AD⊂平面P AD，∴BE∥平面P AD.(3)∵AB⊥AD，而且ABED为平行四边形.∴BE⊥CD，AD⊥CD，由(1)知P A⊥底面ABCD，CD⊂平面ABCD，∴P A⊥CD，且P A∩AD＝A，P A，AD⊂平面P AD，∴CD⊥平面P AD，又PD⊂平面P AD，∴CD⊥PD.∵E和F分别是CD和PC的中点，∴PD∥EF.∴CD⊥EF，又BE⊥CD且EF∩BE＝E，∴CD⊥平面BEF，又CD⊂平面PCD，∴平面BEF⊥平面PCD.规律方法 1.证明平面和平面垂直的方法：(1)面面垂直的定义；(2)面面垂直的判定定理.2.已知两平面垂直时，一般要用性质定理进行转化，在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直.考点三平行与垂直的综合问题角度1多面体中平行与垂直关系的证明【例3－1】如图，在四棱锥P－ABCD中，底面ABCD为矩形，平面P AD⊥平面ABCD，P A⊥PD，P A＝PD，E，F分别为AD，PB的中点.(1)求证：PE⊥BC；(2)求证：平面P AB⊥平面PCD；(3)求证：EF∥平面PCD.证明(1)因为P A＝PD，E为AD的中点，所以PE⊥AD.因为底面ABCD为矩形，所以BC∥AD.所以PE⊥BC.(2)因为底面ABCD为矩形，所以AB⊥AD.又因为平面P AD⊥平面ABCD，平面P AD∩平面ABCD＝AD，所以AB⊥平面P AD.所以AB⊥PD.又因为P A⊥PD，且P A∩AB＝A，所以PD⊥平面P AB.又PD⊂平面PCD，所以平面P AB⊥平面PCD.(3)如图，取PC中点G，连接FG，DG.因为F，G分别为PB，PC的中点，所以FG∥BC，FG＝12BC.因为ABCD为矩形，且E为AD的中点，所以DE∥BC，DE＝12BC.所以DE∥FG，DE＝FG.所以四边形DEFG为平行四边形.所以EF∥DG.又因为EF⊄平面PCD，DG⊂平面PCD，所以EF∥平面PCD.规律方法 1.三种垂直的综合问题，一般通过作辅助线进行线线、线面、面面垂直间的转化. 2.垂直与平行的结合问题，求解时应注意平行、垂直的性质及判定的综合应用.角度2平行与垂直关系中的探索性问题【例3－2】如图，三棱锥P－ABC中，P A⊥平面ABC，P A＝1，AB＝1，AC＝2，∠BAC＝60°.(1)求三棱锥P－ABC的体积；(2)在线段PC上是否存在点M，使得AC⊥BM，若存在点M，求出PMMC的值；若不存在，请说明理由.解(1)由题知AB＝1，AC＝2，∠BAC＝60°，可得S△ABC ＝12·AB·AC·sin 60°＝32，由P A⊥平面ABC，可知P A是三棱锥P－ABC的高.又P A＝1，所以三棱锥P－ABC的体积V＝13·S△ABC·P A＝36.(2)在平面ABC 内，过点B 作BN ⊥AC ，垂足为N .在平面P AC 内，过点N 作MN ∥P A 交PC 于点M ，连接BM .由P A ⊥平面ABC 知P A ⊥AC ，所以MN ⊥AC . 由于BN ∩MN ＝N ，故AC ⊥平面MBN . 又BM ⊂平面MBN ，所以AC ⊥BM . 在Rt △BAN 中，AN ＝AB ·cos ∠BAC ＝12， 从而NC ＝AC －AN ＝32. 由MN ∥P A ，得PM MC ＝AN NC ＝13. 故存在满足条件的点M ，且PM MC ＝13.规律方法 1.求条件探索性问题的主要途径：(1)先猜后证，即先观察与尝试给出条件再证明；(2)先通过命题成立的必要条件探索出命题成立的条件，再证明充分性.2.涉及点的位置探索性问题一般是先根据条件猜测点的位置再给出证明，探索点存在问题，点多为中点或三等分点中某一个，也可以根据相似知识建点. 角度3 空间位置关系与几何体的度量计算【例3－3】 如图，在四棱锥P －ABCD 中，AD ⊥平面PDC ，AD ∥BC ，PD ⊥PB ，AD ＝1，BC ＝3，CD ＝4，PD ＝2.(1)求异面直线AP 与BC 所成角的余弦值； (2)求证：PD ⊥平面PBC ；(3)求直线AB 与平面PBC 所成角的正弦值.(1)解 如图，由已知AD ∥BC ，故∠DAP 或其补角即为异面直线AP 与BC 所成的角.因为AD⊥平面PDC，PD⊂平面PDC，所以AD⊥PD.在Rt△PDA中，由已知，得AP＝AD2＋PD2＝5，故cos∠DAP＝ADAP＝55.所以，异面直线AP与BC所成角的余弦值为5 5.(2)证明由(1)知AD⊥PD，又因为BC∥AD，所以PD⊥BC.又PD⊥PB，BC∩PB＝B，所以PD⊥平面PBC.(3)解过点D作DF∥AB，交BC于点F，连接PF，则DF与平面PBC所成的角等于AB与平面PBC所成的角.因PD⊥平面PBC，故PF为DF在平面PBC上的射影，所以∠DFP为直线DF和平面PBC所成的角.由于AD∥BC，DF∥AB，故BF＝AD＝1.由已知，得CF＝BC－BF＝2.又AD⊥DC，故BC⊥DC.在Rt△DCF中，可得DF＝CD2＋CF2＝2 5.在Rt△DPF中，可得sin∠DFP＝PDDF＝55.所以直线AB与平面PBC所成角的正弦值为5 5.规律方法 1.本题证明的关键是垂直与平行的转化，如由AD∥BC，AD⊥PD，得PD⊥BC，进而利用线面垂直的判定定理证明PD⊥平面PBC.2.利用综合法求空间线线角、线面角、二面角一定注意“作角、证明、计算”是完整统一过程，缺一不可.(1)线面角的求法：找出斜线在平面上的射影，关键是作垂线，找垂足，要把线面角转化到一个三角形中求解.(2)二面角的大小用它的平面角来度量.平面角的作法常见的有：①定义法；②垂面法.注意利用等腰、等边三角形的性质.[方法技巧]1.证明线面垂直的方法：(1)线面垂直的定义：a 与α内任何直线都垂直⇒a ⊥α； (2)判定定理1：⎭⎬⎫m ，n ⊂α，m ∩n ＝A l ⊥m ，l ⊥n ⇒l ⊥α； (3)判定定理2：a ∥b ，a ⊥α⇒b ⊥α；(4)面面垂直的性质：α⊥β，α∩β＝l ，a ⊂α，a ⊥l ⇒a ⊥β； 2.证明面面垂直的方法(1)利用定义：两个平面相交，所成的二面角是直二面角； (2)判定定理：a ⊂α，a ⊥β⇒α⊥β. 3.转化思想：三种垂直关系之间的转化4.证明线面垂直时，易忽视面内两条线为相交线这一条件.5.面面垂直的判定定理中，直线在面内且垂直于另一平面易忽视.6.面面垂直的性质定理在使用时易忘面内一线垂直于交线而盲目套用造成失误.7.在解决直线与平面垂直的问题过程中，要注意直线与平面垂直的定义、判定定理和性质定理的联合交替使用，即注意线线垂直和线面垂直的相互转化.四、 课时作业1．（2020·陕西高三其他（文））已知m ，n 表示两条不同的直线，α表示平面．下列说法正确的是（ ） A ．若m ∥α，n ∥α，则m ∥n B ．若m ⊥α，n ⊥α，则m ∥n C ．若m ⊥α，m ⊥n ，则n ∥α D ．若m ∥α，m ⊥n ，则n ⊥α【答案】B【解析】对于A ，若m ∥α，n ∥α，则m ∥n 或m 与n 相交或m 与n 异面，故A 不正确； 对于B ，根据垂直于同一个平面的两条直线平行可知，B 正确； 对于C ，若m ⊥α，m ⊥n ，则n ∥α或n ⊂α，故C 不正确；对于D ，若m ∥α，m ⊥n ，则n ⊥α或//n α或n ⊂α或n 与α相交但不垂直，故D 不正确.2．（2020·甘肃城关�兰州一中高三一模（理））如图，在正方体ABCD -A 1B 1C 1D 1中，M ､N 分别为AC ，A 1B 的中点，则下列说法错误的是（ ）A ．MN ∥平面ADD 1A 1B ．MN ⊥ABC ．直线MN 与平面ABCD 所成角为45° D ．异面直线MN 与DD 1所成角为60° 【答案】D【解析】如图，连结BD ，1A D ，由M ，N 分别为AC ，1A B 的中点知 1//MN A D ， 对A ，由1//MN A D ，从而MN ∥平面ADD 1A 1，A 正确；对B ，由AB ⊥面11ADD A ，可得AB ⊥1A D ，又1//MN A D ，得MN AB ⊥，B 正确； 对C ，由1//MN A D ，直线MN 与平面ABCD 所成角为145A DA ∠=︒，C 正确； 对D ，由1//MN A D ，直线MN 与DD 1所成角为11A DD ∠45=︒，D 错误；3．（2020·辽宁沈河�沈阳二中高三其他（理））已知m ，n 为两条不同的直线，α，β为两个不同的平面，则下列为真命题的是（ ） A ．若//m α，//n α，则//m nB ．若//n m ，n α⊥，则m α⊥C ．若//m α，//n β，m n ⊥，则αβ⊥D ．若//m α，n β⊥，//m n ，则//αβ 【答案】B【解析】解：对于选项A ，若//m α，//n α，则m 与n 平行，相交或者异面，故A 错误； 对于选项B ，若//n m ，n α⊥，则m α⊥，故B 正确；对于选项C ，若//m α，//n β，m n ⊥，则α与β也可以平行，故C 错误；对于选项D ，若n β⊥，//m n ，所以m β⊥，因为//m α，则α与β垂直，故D 错误.4．（2020·乌鲁木齐市第四中学高一期末）如图，空间四边形ABCD 中，平面ABD ⊥平面BCD ，90BAD ∠=︒，且AB ＝AD ，则AD 与平面BCD 所成的角是（ ）A ．30°B ．45°C ．60°D ．90°【答案】B【解析】如图，过点A 作AE BD ⊥,垂足为E .因为平面ABD ⊥平面BCD ，AE BD ⊥，平面ABD ⋂平面BCD BD =,所以AE ⊥平面BCD ,所以AD 与平面BCD 所成的角是ADE ∠,因为90BAD ∠=︒，且AB ＝AD ，所以45ADE =∠.所以AD 与平面BCD 所成的角是45.5．（2020·全国高三（理））在三棱锥A BCD -中,AC ⊥底面，，BD DC =，，，则点C 到平面ABD 的距离是（ ）A ．55aB ．155aC ．35aD ．153a 【答案】B6．（2020·全国高一课时练习）如图，设平面PQ αβ⋂=，EG ⊥平面α，FH ⊥平面α，垂足分别为,G H .为使PQ GH ⊥，则需增加的一个条件是（ ）A ．EF ⊥平面αB ．EF ⊥平面βC ．PQ GE ⊥D ．PQ FH ⊥【答案】B 【解析】因为EG ⊥平面α，PQ ⊂平面α，所以EG PQ ⊥.若EF ⊥平面β，则由PQ ⊂平面β，得EF PQ ⊥.又EG 与EF 为相交直线，且EG ⊥平面α，FH ⊥平面α，则EG FH ，∴,,,E F H G 四点共面，所以PQ ⊥平面EFHG ，所以PQ GH ⊥，7．（2019·陕西武功�高三月考（理））已知直线l ⊥平面α，直线m ∥平面β，若αβ⊥，则下列结论正确的是A ．l β∥或l β⊂B ．//l mC ．m α⊥D ．l m ⊥ 【答案】A【解析】对于A ，直线l ⊥平面α，αβ⊥，则l β//或l β⊂，A 正确；对于B ，直线l ⊥平面α，直线//m 平面β，且αβ⊥，则//l m 或l 与m 相交或l 与m 异面，∴B 错误； 对于C ，直线l ⊥平面α，直线//m 平面β，且αβ⊥，则m α⊥或m 与α相交或m α⊂或//m α，∴C 错误；对于D ，直线l ⊥平面α，直线//m 平面β，且αβ⊥，则//l m 或l 与m 相交或l 与m 异面，∴D 错误． 8．（2019·营口市第二高级中学高一月考）在棱长为a 的正方体ABCD －A 1B 1C 1D 1中，M 为AB 的中点， 则点C 到平面A 1DM 的距离为 ( )A ．3aB ．6aC ．2aD ．12a 【答案】A【解析】画出图形如下图所示,设C 到平面1A DM 的距离为h ,则根据等体积法有11A CDM C A DM V V --=,即11113232a a a h ⋅⋅⋅⋅=⋅⋅,解得3h a =,故选A .9．（2020·四川雨城�雅安中学高二月考（理））已知正方形ABCD 的边长为4，E ､F 分别是AB ､AD 的中点，GC ⊥平面ABCD ，且2GC =，则点B 到平面EFG 的距离为（ ）A 211B 311C 210D 310 【答案】A【解析】设B 到平面EFG 的距离为h .1111422232323G BEF V BE AF CG -=⨯⨯⨯⨯=⨯⨯⨯⨯=. 2222422426GE GF ==++==2222822EF =+==. 所以22112222211222GEF EF S EF GE ∆⎛⎫=⨯-=⨯= ⎪⎝⎭由G BEF B EFG V V --=得1421121133h h ⨯=⇒=. 故选：A10．（2020·山东芝罘�烟台二中高一月考）如图，ABCD ﹣A 1B 1C 1D 1为正方体，则以下结论：①BD ∥平面CB 1D 1；②AC 1⊥BD ；③AC 1⊥平面CB 1D 1其中正确结论的个数是（ ）A ．0B ．1C ．2D ．3【答案】D 【解析】解：由正方体的性质得BD ∥11B D ，所以结合线面平行的判定定理可得：BD ∥平面11CB D ；所以①正确.由正方体的性质得 AC ⊥BD ，1C C ⊥BD ，可得BD ⊥平面1CC A ，所以1AC ⊥BD ，所以②正确.由正方体的性质得 BD ∥11B D ，由②可得1AC ⊥BD ，所以1AC ⊥11B D ，同理可得11AC CB ，进而结合线面垂直的判定定理得到：1AC ⊥平面11CB D ，所以③正确.故选：D. 11．（2018·安徽花山�马鞍山二中高三月考（文））已知a ，b 是平面α内的两条直线，l 是空间中的一条直线.则“直线l a ⊥且l b ⊥”是“l α⊥”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件【答案】B【解析】解：,,,l a b l a l b αα''''⊥⊂⇒⊥⊥，反之不一定成立，例如//a b 时．“直线l a ⊥且l b ⊥”是“l α⊥”的必要而不充分条件．12．（2020·全国高一课时练习）已知长方体1111ABCD A B C D -，在平面11AA B B 上任取点M ，作ME AB ⊥于点E ，则（ ）A ．ME ⊥平面ABCDB ．ME ⊂平面ABCDC ．ME 平面ABCD D ．以上都有可能【答案】A【解析】∵ME ⊂平面11AA B B ，平面11AA B B 平面ABCD AB =，且平面11AA B B ⊥平面,ABCD ME AB ，∴ME ⊥平面ABCD .13．（2020·全国高一课时练习）已知直线l ⊥平面α，直线m α⊂，则（ ）A ．l m ⊥B ．l mC ．,l m 异面D ．,l m 相交而不垂直 【答案】A【解析】根据线面垂直的定义，若直线与平面垂直，则直线垂直与该平面内的任意一条直线，因此 l m ⊥，故选A14．（2020·七台河市第一中学高一期末（理））已知m ，n 是空间中两条不同的直线，α，β为空间中两个互相垂直的平面，则下列命题正确的是（ ）A ．若m α⊂，则m β⊥B ．若m α⊂，n β⊂，则m n ⊥C ．若m α⊄，m β⊥，则//m aD ．若m αβ=，n m ⊥，则n a ⊥【答案】C【解析】对于A ，直线m 与平面β可能垂直，也可能平行或m 在平面β内，故A 不正确；对于B ，直线m 与n 平行、异面或相交，故B 不正确；对于C ，m β⊥，则//m a 或m α⊂，又m α⊄，所以//m a ，故C 正确；对于D ，缺少条件n β⊂，故D 不正确；15．（2020·北京通州�高一期末）已知直线a ⊂平面α，直线b ⊂平面α，则“直线m α⊥”是“m a ⊥，且m b ⊥”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件 【答案】A【解析】直线a ⊂平面α，直线b ⊂平面α，则“直线m α⊥”能推出“m a ⊥，且m b ⊥”，是充分条件，反之“m a ⊥，且m b ⊥”，直线m 与平面α不一定垂直，不是必要条件，16．（2020·浙江高三其他）一个几何体的三视图如图所示，则该几何体两两垂直的平面共有（ ）A ．4对B ．5对C ．6对D ．7对【答案】D 【解析】由三视图可知，该几何体为如图所示的四棱锥P ABCD -，其中ABCD 为边长为1的正方形，PA ⊥平面ABCD ，所以平面PAB ⊥平面ABCD ,平面PAD ⊥平面ABCD ,平面PAC ⊥平面ABCD ,又,,AD AB PA AD AB PA A ⊥⊥⋂=,所以AD ⊥平面PAB ,平面PAD ⊥平面PAB ,又AC BD ⊥,,PA BD PA AC A ⊥⋂=,所以BD ⊥平面PAC ,平面PBD ⊥平面PAC ,同理可证：CD ⊥平面PAD ，CB ⊥PAB ，故平面PBC ⊥平面PAB ，平面PCD ⊥平面PAD ，故该几何体两两垂直的平面共有7对.17．（2019·重庆高三三模（文））下列命题错误的是（ ）A ．若平面α⊥平面β，则平面α内所有直线都垂直于平面βB ．若平面α⊥平面β，则平面α内一定存在直线垂直于平面βC ．若平面α不垂直于平面β，则平面α内一定不存在直线垂直于平面βD ．若平面α⊥平面γ，平面β⊥平面γ，l αβ=则l γ⊥ 【答案】A【解析】对于选项A ．若平面α⊥平面β，则平面α内存在直线不垂直于平面β，命题错误；B ．若平面α⊥平面β，则平面α内一定存在直线垂直于平面β，如平面α内垂直于两平面交线的直线，命题正确；C ．若平面α内存在直线垂直于平面β，根据面面垂直的判定有平面α垂直于平面β，与平面α不垂直于平面β矛盾，所以若平面α不垂直于平面β，则平面α内一定不存在直线垂直于平面β，命题正确；D ．若平面α⊥平面γ，平面β⊥平面γ，l αβ=，如图，，设,a b αγβγ⋂=⋂=，在γ内直线a 、b 外任取一点O ，作OA a ⊥，交点为A ，作OB b ⊥，交点为B ， 因为平面α⊥平面γ，所以OA α⊥，又l α⊂，所以OA l ⊥，同理可得OB l ⊥，因为OA OB O =，且OA γ⊂,OB γ⊂，所以l γ⊥，D 选项正确.18．（2020·广东汕头�高三二模（文））在立体几何中，以下命题中假命题的个数为（ ）①若直线//a b ，b ⊂平面α，则//a α.②若平面α⊥平面γ，平面β⊥平面γ，l αβ=，则l γ⊥.③有3个角是直角的四边形是矩形.④若平面α⊥平面β，a ⊂平面α，b ⊂平面β，且a b ⊥，则a β⊥.A ．0个B ．1个C ．2个D ．3个 【答案】D【解析】①若直线//a b ，b ⊂平面α，则//a α或a α⊂，所以不正确.②若平面α⊥平面γ，平面β⊥平面γ，l αβ=,则l γ⊥，正确,证明如下. 如图设a αγ⋂=，b γβ=，在β内，直线,a b 外任取一点O ，作OA a ⊥，交点为A ，因为平面α⊥平面γ,则OA α⊥，所以OA l ⊥。

空间中的垂直关系教案 -回复适用对象：中小学老师课时：1课时教学目标：1. 学生能够理解垂直关系的概念，并能准确使用相关的术语描述和解释。

2. 学生能够观察和辨别常见的垂直关系，并能在日常生活中找到实际的例子。

3. 学生能够通过小组合作，运用所学知识绘制和解读简单的垂直结构图。

教学准备：1. 黑板/白板和可擦笔2. 教学图片或实物，如墙壁、门、书架、长方体积木等3. 垂直结构图的示例教学过程：一、导入（5分钟）1. 引入垂直关系的概念：让学生观察教室中的物体，例如桌子、椅子、黑板等，提问学生这些物体之间有什么关系。

2. 引导学生回答：这些物体之间存在一种特殊的关系，即垂直关系。

并解释垂直关系是指两个物体或平面相互正交或垂直交叉的关系。

二、学习和实践（15分钟）1. 呈现垂直关系的实例图片或实物，让学生观察并描述垂直关系。

2. 导入垂直术语：上下、左右、垂直、水平、垂直交叉等。

解释这些术语的意义和使用方法。

3. 学生小组活动：让学生分成小组，依次观察教室中的物体，找出并描述它们之间的垂直关系。

鼓励学生找到尽可能多的例子，并将其描述出来。

1. 引入垂直结构图：教师示范绘制一张简单的垂直结构图，解释结构图中的线段代表垂直关系。

然后让学生跟随示范练习绘图，并描述图中物体之间的垂直关系。

2. 学生个人活动：让学生自选一个日常生活场景，绘制一个垂直结构图，并描述图中物体之间的垂直关系。

3. 学生展示：让学生展示自己绘制的垂直结构图，并向同学们解释图中的垂直关系。

四、归纳总结（5分钟）1. 教师引导学生回顾本节课所学内容，包括垂直关系的定义、相关术语和结构图的绘制。

2. 教师总结学生对垂直关系的理解和应用能力，并强调其在日常生活中的重要性。

五、课堂作业（5分钟）布置课后作业：让学生观察并记录家庭或学校中的垂直关系，了解更多的实际例子，并在下节课上分享。

教学反思与延伸：本节课通过观察、描述、绘图等多种方式帮助学生理解和运用空间中的垂直关系。

βαm la αaα 1.2.3 直线与平面垂直教学目的：1.理解直线与平面垂直的定义；2.掌握直线与平面垂直的判定、性质定理内容及其应用；3.应用直线与平面垂直的判定、性质定理解决问题 .教学重点：直线与平面垂直的判定、性质定理内容及其应用. 教学难点：直线与平面垂直的判定、性质定理内容及论证过程教学过程：一、复习引入：1.直线和平面的位置关系是什么?观察空间直线和平面可知它们的位置关系有：（1）直线在平面内（无数个公共点）；（2）直线和平面相交（有且只有一个公共点）；（3）直线和平面平行（没有公共点）它们的图形分别可表示为如下，符号分别可表示为a ⊂α，a ⋂α=A ，a//α.2.线面平行的判定定理：如果不在一个平面内的一条直线和平面内的一条直线平行，那么这条直线和这个平面平行.推理模式：,,////l m l m l ααα⊄⊂⇒ 3.线面平行的性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行.推理模式：//,,//l l m l αβαβ⊂⋂=⇒ 引入新课:在直线和平面相交的位置关系中,有一种相交是很特殊的,我们把它叫做垂直相交,这节课我们重点来探究这种形式的相交----引出课题.二、研探新知1.观察实例,发现新知现实生活中线面垂直的实例:旗杆与地面的关系，大桥的桥柱与水面的位置关系，房屋的屋柱与地面的关系，都给人以直线与平面垂直的形象。

2.实例研探,定义新知探究:什么叫做直线和平面垂直呢?当直线与平面垂直时，此直线与平面内的所有直线的关系又怎样呢?变换时间观察现实生活中线面垂直的实例:在阳光下观察直立于地面的旗杆及它在地面的影子，随着时间的变化，尽管影子的位置在移动，但是旗杆所在的直线始终与影子所在的直线垂直，就是说，旗杆AB所在直线与地面上任意一条过点B的直线垂直（如图），事实上，旗杆AB所在直线与地面内任意一条不过点B的直线也是垂直的。

人教版高中必修2(B版)1.2.3空间中的垂直关系教学设计一、教学目标1.了解空间中垂直关系的概念和性质，掌握相关的基本概念和定义；2.能够运用垂直关系的定义，判断两条直线、两个平面、线段和直线、线段和平面等是否垂直，解决与垂直相关的简单问题；3.通过垂直关系的学习，增强学生的空间想象能力和数学思维水平。

二、教学重点和难点1.垂直关系的定义和应用；2.掌握判断两条直线、两个平面、线段和直线、线段和平面等是否垂直的方法；3.解决与垂直相关的简单问题。

三、教学方法本课采用讲授、讨论和练习相结合的教学方法，倡导“启发式”教学，让学生在教师的引导下自主思考，发掘规律和方法，并通过课堂讨论和解决问题的过程中加深对知识的理解和记忆。

四、教学步骤1. 引入（10分钟）通过一个有趣的例子，激发学生对垂直关系的兴趣，引导学生了解垂直关系的概念和性质。

举例：小明在修建房屋时，需要确定柱子是否和地面垂直。

那么，垂直现象出现在我们生活中的哪些场合呢？2. 讲解垂直关系的基本概念和定义（20分钟）通过演示、讲解等方式，介绍垂直关系的定义和性质，如“两条直线垂直的条件是什么？两个平面垂直的条件是什么？”等等。

3. 探究垂直关系的应用（30分钟）带领学生探究判断两条直线、两个平面、线段和直线、线段和平面等是否垂直的方法和步骤，并通过练习，帮助学生巩固相关知识，增强应用能力。

4. 实际应用（30分钟）分组或个人作业，设计一些实际问题，让学生通过运用垂直关系的知识，解决实际问题。

举例：如何确定大型建筑物的每根柱子是否与地面垂直？5. 总结（10分钟）对本节课的重点知识、难点问题进行总结，并对学生问题进行答疑解惑，解决学生的困惑。

五、教学工具黑板、粉笔、几何模型、PPT等。

六、教学评价1.通过课堂练习，检验学生对垂直关系的掌握程度；2.通过实际应用的作业，检验学生对垂直关系的应用能力；3.通过教师观察、记录等方式，评价学生的表现和进步情况。

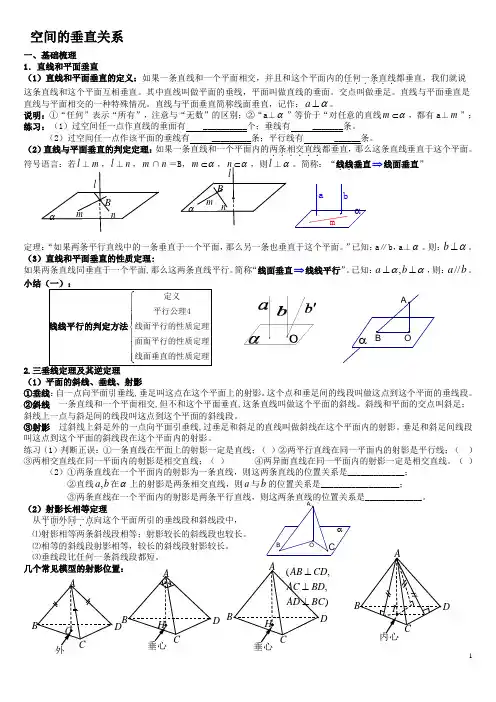
空间的垂直关系一、基础梳理1．直线和平面垂直（1）直线和平面垂直的定义：如果一条直线和一个平面相交，并且和这个平面内的任何一条直线．．．．．．都垂直，我们就说这条直线和这个平面互相垂直。

其中直线叫做平面的垂线，平面叫做直线的垂面。

交点叫做垂足。

直线与平面垂直是直线与平面相交的一种特殊情况。

直线与平面垂直简称线面垂直，记作：aα⊥。

说明：①“任何”表示“所有”，注意与“无数”的区别；②“a⊥α”等价于“对任意的直线m⊂α，都有a⊥m”；练习：（1）过空间任一点作直线的垂面有 __________个；垂线有 _______条。

（2）过空间任一点作该平面的垂线有 _________条；平行线有 ______条。

（2）直线与平面垂直的判定定理：如果一条直线和一个平面内的两条相交直线．．．．．．都垂直，那么这条直线垂直于这个平面。

符号语言：若l⊥m，l⊥n，m∩n＝。

简称：“线线．．垂直⇒线面垂直”定理：“如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于这个平面。

”已知：a∥b，a⊥α。

则：bα⊥。

（3）直线和平面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行。

简称“线面垂直⇒线线平行”。

已知：,a bαα⊥⊥，则：//ab。

2.（1）平面的斜线、垂线、射影①垂线：自一点向平面引垂线,垂足叫这点在这个平面上的射影。

这个点和垂足间的线段叫做这点到这个平面的垂线段。

②斜线一条直线和一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线。

斜线和平面的交点叫斜足；斜线上一点与斜足间的线段叫这点到这个平面的斜线段。

③射影过斜线上斜足外的一点向平面引垂线,过垂足和斜足的直线叫做斜线在这个平面内的射影。

垂足和斜足间线段叫这点到这个平面的斜线段在这个平面内的射影。

练习（1）判断正误：①一条直线在平面上的射影一定是直线；（）②两平行直线在同一平面内的射影是平行线；（）③两相交直线在同一平面内的射影是相交直线；（）④两异面直线在同一平面内的射影一定是相交直线。

1.6空间中的垂直关系（优质课）教案教学目标：理解空间中三种垂直关系的定义；掌握空间中三种垂直关系判定及性质；用空间中三种垂直关系的定义、判定及性质解决垂直问题．教学过程：一、直线与平面垂直1.如果两条直线相交于一点或经过平移后相交于一点，并且交角为直角，则称这两条直线互垂直．2.如果一条直线(AB)和一个平面(α)相交于点O，并且和这个平面内过点O的任何直线都垂直，我们就说这条直线和这个平面互相垂直，记作AB⊥α，直线叫做平面的垂线，平面叫做直线的垂面，交点叫做垂足．垂线上任一点到垂足间的线段，叫做这点到这个平面的垂线段．垂线段的长度叫做这点到平面的距离3.直线和平面垂直的判定4.(1)判定定理：如果一条直线和一个平面内的任何两条相交直线都垂直，那么这条直线垂直于这个平面．符号语言：l⊥a，l⊥b，a∩b＝A，a⊂α，b⊂α⇒l⊥α，如图：(2)如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于同一个平面．符号语言：a∥b，a⊥α⇒b⊥α，如图：5．直线与平面垂直的性质(1)性质定理：如果两条直线同垂直于一个平面，那么这两条直线平行．符号语言：a⊥α，b⊥α⇒a∥b，如图：(2)一条直线垂直于一个平面，它就和平面内的任意一条直线垂直．符号语言：a⊥α，b⊂α⇒a⊥b，如图：6．设P是三角形ABC所在平面α外一点，O是P在α内的射影(1)若PA＝PB＝PC，则O为△ABC的外心．特别地当∠C＝90°时，O为斜边AB中点．(2)若PA、PB、PC两两垂直，则O为△ABC的垂心．(3)若P到△ABC三边距离相等，则O为△ABC的内心．7．(1)过一点有且只有一条直线与已知平面垂直．(2)过一点有且只有一个平面与已知直线垂直．二、直线和平面平行1．平面与平面垂直的定义：如果两个相交平面的交线与第三个平面垂直，又这两个平面与第三个平面相交所得的两条交线互相垂直，就称这两个平面互相垂直．平面α、β互相垂直，记作α⊥β.2．两个平面垂直的判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直．符号表示：a⊥α，a⊂β⇒α⊥β，如图：3．两个平面垂直的性质定理：如果两个平面垂直，那么在一个平面内垂直于它们交线的直线，垂直于另一个平面．符号表示：α⊥β，α∩β＝CD，BA⊂α，BA⊥CD，B为垂足⇒BA⊥β，如图：推论：如果两个平面垂直，那么过第一个平面内的一点垂直于第二个平面的直线，在第一个平面内．类型一线面垂直例1：如图，直角△ABC 所在平面外一点S ，且SA ＝SB ＝SC ，点D 为斜边AC 的中点． (1)求证：SD ⊥平面ABC ；(2)若AB ＝BC ，求证：BD ⊥平面SAC.解析：由于D 是AC 中点，SA ＝SC ，∴SD 是△SAC 的高，连接BD ，可证△SDB ≌△SDA .由AB ＝BC ，则Rt △ABC 是等腰直角三角形，则BD ⊥AC ，利用线面垂直的判定定理即可得证． 答案：(1)∵SA ＝SC ，D 为AC 的中点， ∴SD ⊥AC .在Rt △ABC 中，连接BD ，则AD ＝DC ＝BD ，又∵SB ＝SA ，SD ＝SD ， ∴△ADS ≌△BDS .∴SD ⊥BD .又AC ∩BD ＝D ， ∴SD ⊥面ABC .(2)∵BA ＝BC ，D 为AC 中点，∴BD ⊥AC . 又由(1)知SD ⊥面ABC ，∴SD ⊥BD .于是BD 垂直于平面SAC 内的两条相交直线， ∴BD ⊥平面SAC . 练习1：((2014·河南南阳一中高一月考)如图所示，在四棱锥P －ABCD 中， 底面ABCD 是矩形，侧棱P A ⊥平面ABCD ，E 、F 分别是AB 、PC 的中点， P A ＝AD .求证：EF ⊥平面PCD .答案：如图，取PD 的中点H ，连接AH 、HF .∴FH12CD ， ∴FH AE ，∴四边形AEFH 是平行四边形，∴AH ∥EF . ∵底面ABCD 是矩形，∴CD ⊥AD . 又∵PA ⊥底面ABCD ， ∴PA ⊥CD ，PA ∩AD ＝A ， ∴CD ⊥平面PAD .又∵AH ⊂平面PAD ，∴CD ⊥AH .又∵PA ＝AD ，∴AH ⊥PD ，PD ∩CD ＝D ， ∴AH ⊥平面PCD ，又∵AH ∥EF ，∴EF ⊥平面PCD .练习2：如右图，在正方体1111ABCD A B C D -中，P 为1DD 的中点，O 为ABCD 的中心， 求证：1B O ⊥平面PAC 答案：连结111,,PO PB B D ,OP D 1C 1B 1A 1D CA由正方体的性质可知，1,AC BD AC BB ⊥⊥,且1BD BB B =∴AC ⊥面11BDD B 又∵BO ⊂面11BDD B ∴1B O AC ⊥ 设AB a =，则11121,2,2OB OD a B D a PD PD a ===== ∵2222222222221113113,22424OB OB BB a a a OP PD DO a a a =+=+==+=+= 222222111119244PB B D PD a a a =+=+=∴2221OB PO PB += ∴1B O PO ⊥ ∵PO AC O =∴1B O ⊥平面PAC练习3：在如右图，在空间四边形ABCD 中，,AB AD BC CD ==, 求证：AC BD ⊥答案：设E 为BD 的中点，连结,AE EC∵AB AD = ∴BD AE ⊥ 同理可证：BD EC ⊥ 又∵AEEC E = ∴BD ⊥面AEC∵AE ⊂面AEC ∴BD AC ⊥例2：如图在△ABC 中，∠B ＝90°，SA ⊥平面ABC ， 点A 在SB 和SC 上的射影分别是N 、M ，求证：MN ⊥SC . 解析：根据直线平面垂直的性质，找到所求垂直的线段中的 一条与另一条所在的平面垂直，即可证明这两条线段互相垂直． 答案：证明：∵SA ⊥平面ABC ， ∴SA ⊥BC ，又∠ABC ＝90°， ∴BC ⊥AB ，∴BC ⊥平面SAB ， ∴AN ⊥BC ，又AN ⊥SB ，∴AN ⊥平面SBC ， ∴AN ⊥SC ，又AM ⊥SC ， ∴SC ⊥平面AMN ， ∴MN ⊥SC .练习1：如图，在正方体ABCD －A 1B 1C 1D 1中，E 、F 分别为A 1D 、AC 上的点，且EF ⊥A 1D ，EF ⊥AC .求证：EF ∥BD 1. 答案：如图所示，连接A 1C 1、C 1D 、BD 、B 1D 1. 由于AC ∥A 1C 1，EF ⊥AC ，∴EF ⊥A 1C 1. 又EF ⊥A 1D ，A 1D ∩A 1C 1＝A 1， ∴EF ⊥平面A 1C 1D .①E ABCD∵BB 1⊥平面A 1B 1C 1D 1，A 1C 1⊂平面A 1B 1C 1D 1， ∴BB 1⊥A 1C 1.又∵四边形A 1B 1C 1D 1为正方形，∴A 1C 1⊥B 1D 1. ∵BB 1∩B 1D 1＝B 1，∴A 1C 1⊥平面BB 1D 1D . 而BD 1⊂平面BB 1D 1D ，∴BD 1⊥A 1C 1. 同理，DC 1⊥BD 1，DC 1∩A 1C 1＝C 1， ∴BD 1⊥平面A 1C 1D .②由①②可知EF ∥BD 1.练习2：在空间中，下列命题：①平行于同一条直线的两条直线平行；②垂直与同一直线的两条直线平行；③平行与同一平面的两条直线平行；④垂直于同一平面的两条直线平行．其中正确的由___ ． 答案：①④练习3：已知,,a b c 及平面β，则下列命题正确的是（ ）A 、////a a b b ββ⎫⇒⎬⊂⎭B 、a a b b ββ⊥⎫⇒⊥⎬⊥⎭C 、//a c a b b c ⊥⎫⇒⎬⊥⎭D 、//a a b b ββ⊂⎫⇒⎬⊂⎭ 答案：B例3：如图，在底面为直角梯形的四棱锥P －ABCD 中，AD ∥BC ， ∠ABC ＝90°，PA ⊥平面ABCD ，PA ＝3，AD ＝2，AB ＝23，BC ＝6.求证：BD ⊥平面PAC .解析：通过计算得到直角，进而得到垂直． 答案：∵PA ⊥平面ABCD ，BD ⊂平面ABCD ，∴BD ⊥PA .∵∠BAD 和∠ABC 都是直角，∴tan ∠ABD ＝AD AB ＝33，tan ∠BAC ＝BCAB＝3， ∴∠ABD ＝30°，∠BAC ＝60°.∴∠AEB ＝90°，即BD ⊥AC ， 又PA ∩AC ＝A ，∴BD ⊥平面PAC .练习1：在正方体中ABCD －A 1B 1C 1D 1中，P 为DD 1的中点， O 为底面ABCD 的中心．求证：B 1O ⊥平面PAC . 答案：如图所示，连接AB 1、CB 1、B 1D 1、PB 1、PO .设AB ＝a ，则AB 1＝CB 1＝B 1D 1＝2a ，AO ＝OC ＝22a ， ∴B 1O ⊥AC .∵B 1O 2＝OB 2＋BB 21＝⎝⎛⎭⎪⎫22a 2＋a 2＝32a 2，PB 21＝PD 21＋B 1D 21＝⎝ ⎛⎭⎪⎫12a 2＋(2a )2＝94a 2，OP 2＝PD 2＋DO 2＝⎝ ⎛⎭⎪⎫12a ＋⎝⎛⎭⎪⎫22a 2＝34a 2，∴B 1O 2＋OP 2＝PB 21，∴B 1O ⊥OP . 又PO ∩AC ＝O ，∴B 1O ⊥平面PAC .练习2: 如图，若测得旗杆PO ＝4，P A ＝PB ＝5，OA ＝OB ＝3，则旗杆PO 和地面α的关系是________．答案：∵PO ＝4，OA ＝OB ＝3，P A ＝PB ＝5，∴PO 2＋AO 2＝P A 2，PO 2＋OB 2＝PB 2， ∴PO ⊥OA ，PO ⊥OB .又OA ∩OB ＝O ，∴PO ⊥平面AOB ，∴PO ⊥地面α.类型二 平面与平面垂直例4：(2014·山东临沂高一期末测试)如图，在底面为正三角形的直三棱柱ABC －A 1B 1C 1中，点D 是BC的中点，求证：平面AC 1D ⊥平面BCC 1B 1. 解析：运用平面垂直的判定．答案：∵△ABC 为正三角形，D 为BC 的中点，∴AD ⊥BC .又∵CC 1⊥底面ABC ，AD ⊂平面ABC ， ∴CC 1⊥AD .又BC ∩CC 1＝C ， ∴AD ⊥平面BCC 1B 1. 又AD ⊂平面AC 1D ，∴平面AC 1D ⊥平面BCC 1B 1.练习1：三棱锥S －ABC 中，∠BSC ＝90°，∠ASB ＝60°，∠ASC ＝60°，SA ＝SB ＝SC . 求证：平面ABC ⊥平面SBC .答案：解法一：取BC 的中点D ，连接AD 、SD .由题意知△ASB 与△ASC 是等边三角形，则AB ＝AC . ∴AD ⊥BC ，SD ⊥BC .令SA ＝a ，在△SBC 中，SD ＝22a ， 又∵AD ＝AC 2－CD 2＝22a ，∴AD 2＋SD 2＝SA 2. 即AD ⊥SD .又∵AD ⊥BC ，∴AD ⊥平面SBC . ∵AD ⊂平面ABC ，∴平面ABC ⊥平面SBC .解法二：∵SA ＝SB ＝SC ＝a ， 又∵∠ASB ＝∠ASC ＝60°，∴△ASB 、△ASC 都是等边三角形． ∴AB ＝AC ＝a .作AD ⊥平面SBC 于点D ，∵AB ＝AC ＝AS ，∴D 为△SBC 的外心． 又∵△BSC 是以BC 为斜边的直角三角形， ∴D 为BC 的中点，故AD ⊂平面ABC . ∴平面ABC ⊥平面SBC .练习2：如右图,在四面体ABCD 中，2,BD a AB AD CB CD a =====．求证：平面ABD ⊥平面BCD ． 答案：取BD 的中点E ，连结,AE EC∵AB AD = ∴AE BD ⊥ 同理CE BD ⊥ 在△ABD 中，12,2AB a BE BD a === ∴2222AE AB BE a =-=同理22CE a = 在△AEC 中，2,2AE CE a AC a === ∴222AC AE CE =+ ∴AE CE ⊥ ∵BDCE E = ∴AE ⊥平面BCD ∵AE ⊂平面ABD ∴平面ABD ⊥平面BCD练习3：空间四边形ABCD 中，若,AD BC BD AD ⊥⊥，那么有（ ） A 、平面ABC ⊥平面ADC B 、平面ABC ⊥平面ADBC 、平面ABC ⊥平面DBCD 、平面ADC ⊥平面DBC 答案：D例5：已知P 是△ABC 所在平面外的一点，且P A ⊥平面ABC ，平面P AC ⊥平面PBC ，求证：BC ⊥AC .解析：已知条件是线面垂直和面面垂直，要证明两条直线垂直，应将两条直线中的一条放入一平面中，使另一条直线与该平面垂直，即由线面垂直得到线线垂直．在空间图形中，高一级的垂直关系蕴含着低一级的垂直关系，通过本题可以看到：面面垂直⇒线面垂直⇒线线垂直． 答案：如图，在平面P AC 内作AD ⊥PC 于点D ，∵平面P AC ⊥平面PBC ，AD ⊂平面P AC ，且AD ⊥PC ， ∴AD ⊥平面PBC ，又BC ⊂平面PBC ，∴AD ⊥BC .∵P A ⊥平面ABC ，BC ⊂平面ABC ， ∴P A ⊥BC ，∵AD ∩P A ＝A ，∴BC ⊥平面P AC ， 又AC ⊂平面P AC ，∴BC ⊥AC .练习1：已知三棱锥P －ABC 中，侧面PAC 与底面ABC 垂直，PA ＝PB ＝PC . (1)求证：AB ⊥BC ；(2)若AB ＝BC ，过点A 作AF ⊥PB 于点F ，连接CF ，求证：平面PBD ⊥平面AFC . 答案：如图所示：(1)取AC 的中点D ，连接PD 、BD ， ∵PA ＝PC ，∴PD ⊥AC ，又平面PAC ⊥平面ABC ，且平面PAC ∩平面ABC ＝AC ， ∴PD ⊥平面ABC ，D 为垂足． ∵PA ＝PB ＝PC ， ∴DA ＝DB ＝DC ，∴AC 为△ABC 的外接圆的直径，故AB ⊥BC . (2)∵PA ＝PC ，AB ＝BC ，PB ＝PB ， ∴△ABP ≌△CBP .ABCDE∵AF⊥PB，∴CF⊥PB，又AF∩CF＝F，∴PB⊥平面AFC，又PB⊂平面PBD，∴平面PBD⊥平面AFC.练习2：已知平面P AB⊥平面ABC，平面P AC⊥平面ABC，如图所示．求证：P A⊥平面ABC.答案：如图所示，在平面ABC内任取一点D，作DF⊥AC于点F，作DG⊥AB于点G，∵平面PAC⊥平面ABC，平面PAC∩平面ABC＝AC，∴DF⊥平面PAC，又∵PA⊂平面PAC，∴PA⊥DF，同理可证：DG⊥PA，∵DF∩DG＝D，且DF⊂平面ABC，DG⊂平面ABC，∴PA⊥平面ABC.1．一条直线和三角形的两边同时垂直，则这条直线和三角形的第三边的位置关系是( ) A．平行B．垂直C．相交不垂直D．不确定答案：B2．若一条直线l上有两个点到平面α的距离相等，则l与α的关系是( )A．平行B．相交C．垂直D．不确定答案：D3．已知直线l⊥平面α，直线m⊂平面β，给出下列四个命题：①α∥β，l⊄β⇒l⊥m②α⊥β⇒l∥m③l∥m⇒α⊥β④l⊥m⇒α∥β其中正确的两个命题是( )A．①②B．③④C．②④D．①③答案：D4．如图，四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A－BCD，则在三棱锥A－BCD中，下列命题正确的是( )A．平面ABD⊥平面ABCB．平面ADC⊥平面BDCC．平面ABC⊥平面BDCD．平面ADC⊥平面ABC答案：D5．若有直线m、n和平面α、β，下列四个命题中，正确的是( )A．若m∥α，n∥α，则m∥nB．若m⊂α，n⊂α，m∥β，n∥β，则α∥βC．若α⊥β，m⊂α，则m⊥βD．若α⊥β，m⊥β，m⊄α，则m∥α答案：D6. Rt △ABC 所在平面α外一点P 到直角顶点的距离为24，到两直角边的距离都是610，那么点P 到平面α的距离等于__________．答案： 12_________________________________________________________________________________ _________________________________________________________________________________基础巩固1．已知一平面平行于两条异面直线，一直线与两异面直线都垂直，那么这个平面与这条直线的位置关系是( )A ．平行B ．垂直C ．斜交D ．不能确定 答案：B2．直线a ⊥直线b ，a ⊥平面β，则b 与β的位置关系是( )A ．b ⊥βB ．b ∥βC ．b ⊂βD ．b ⊂β或b ∥β 答案：D 3．下列命题①⎭⎪⎬⎪⎫a ⊥αb ⊂α⇒a ⊥b ； ②⎭⎪⎬⎪⎫a ⊥αa ∥b ⇒b ⊥α； ③⎭⎪⎬⎪⎫a ⊥αb ∥α⇒a ⊥b; ④⎭⎪⎬⎪⎫a ⊥ba ⊥b b ⊂αc ⊂α⇒a ⊥α； ⑤⎭⎪⎬⎪⎫a ∥αa ⊥b ⇒b ⊥α； ⑥⎭⎪⎬⎪⎫a ⊥αb ⊥a ⇒b ∥α. 其中正确命题的个数是( )A ．3B ．4C ．5D ．6 答案：A4.．若平面α∥平面β，直线a ⊂α，直线b ⊂β，那么a 、b 的位置关系是( )A ．无公共点B ．平行C ．既不平行也不相交D ．相交答案：A5．直线a 与平面α内的两条直线都垂直，则a 与α的位置关系是( )A ．垂直B ．平行C ．a 在平面α内D ．不确定 答案：D6．若平面α⊥平面β，且平面α内的一条直线a 垂直于平面β内的一条直线b ，则( )A ．直线a 必垂直于平面βB ．直线b 必垂直于平面αC ．直线a 不一定垂直于平面βD．过a的平面与过b的平面垂直答案：C7．长方体ABCD－A1B1C1D1中，MN在平面BCC1B1内，MN⊥BC于M，则MN与AB的位置关系为____________________．答案：MN⊥AB8．如图所示，已知正三棱柱ABC－A1B1C1的面对角线A1B⊥B1C，求证B1C⊥C1A.答案：如图所示，连接A1C，交AC1于点D，则点D是A1C的中点．取BC的中点N，连接AN、DN，则DN∥A1B.又A1B⊥B1C，∴B1C⊥DN.又△ABC是正三角形，∴AN⊥BC.又平面ABC⊥平面BB1C1C，平面ABCD∩平面BB1C1C＝BC，AN⊂平面ABC，∴AN⊥平面BB1C1C.又B1C⊂平面BB1C1C，∴B1C⊥AN.又AN⊂平面AND，DN⊂平面AND，AN∩DN＝N，∴B1C⊥平面AND.又C1A⊂平面AND，∴B1C⊥AC1.能力提升9．若两直线a与b异面，则过a且与b垂直的平面()A．有且只有一个B．至多有一个C．有无数多个D．一定不存在答案：B10.已知三棱锥S－ABC的各顶点都在一个半径为r的球面上，球心O在AB上，SO⊥底面ABC，AC＝2r，则球的体积与三棱锥体积之比是()A．πB．2πC．3πD．4π答案：D11. (2014·浙江文，6)设m，n是两条不同的直线，α、β是两个不同的平面()A．若m⊥n，n∥α，则m⊥αB．若m∥β，β⊥α，则m⊥αC．若m⊥β，n⊥β，n⊥α，则m⊥αD．若m⊥n，n⊥β，β⊥α，则m⊥α答案：C12.已知平面ABC外一点P，且PH⊥平面ABC于H.给出下列4个命题：①若P A⊥BC，PB⊥AC，则H是△ABC的垂心；②若P A、PB、PC两两互相垂直，则H是△ABC的垂心；③若∠ABC＝90°，H是AC的中点，则P A＝PB＝PC；④若P A＝PB＝PC，则H是△ABC的外心．其中正确命题的个数为()A．1B．2C．3D．4答案：D13. 平面α的斜线AB 交α于点B ，过定点A 的动直线l 与AB 垂直，且交α于点C ，则动点C 的轨迹为________．(填直线、圆、其它曲线)答案：直线14. 如图所示，已知矩形ABCD 中，AB ＝1，BC ＝a ，P A ⊥平面ABCD ，若在BC 上只有一个点Q 满足PQ ⊥QD ，则a 的值等于________．答案：215. 如图所示，在四棱锥P －ABCD 中，P A ⊥底面ABCD .底面各边都相等，M 是PC 上的一动点，当点M 满足________________时，平面MBD ⊥平面PCD .(注：只要填写一个你认为正确的即可)答案：BM ⊥PC （其它合理答案亦可）16. 如图所示，△ABC 为正三角形，CE ⊥平面ABC ，BD ∥CE ，且CE ＝AC ＝2BD ，M 是AE 的中点．(1)求证：DE ＝DA ；(2)求证：平面BDM ⊥平面ECA ；(3)求证：平面DEA ⊥平面ECA .答案：(1)取EC 的中点F ，连接DF .∵CE ⊥平面ABC ，∴CE ⊥BC .易知DF ∥BC ，∴CE ⊥DF .∵BD ∥CE ，∴BD ⊥平面ABC .在Rt △EFD 和Rt △DBA 中，EF ＝12CE ＝DB ，DF ＝BC ＝AB ， ∴Rt △EFD ≌Rt △DBA .故DE ＝DA .(2)取AC 的中点N ，连接MN 、BN ，则MN CF .∵BD CF ，∴MN BD ，∴N ∈平面BDM .∵EC ⊥平面ABC ，∴EC ⊥BN .又∵AC ⊥BN ，EC ∩AC ＝C ，∴BN ⊥平面ECA .又∵BN ⊂平面BDM ，∴平面BDM ⊥平面ECA .(3)∵DM ∥BN ，BN ⊥平面ECA ，∴DM ⊥平面ECA .又∵DM ⊂平面DEA ，∴平面DEA ⊥平面ECA .。

空间中的垂直关系教案空间中的垂直关系一. 教学内容：空间中的垂直关系二、学习目标1、掌握直线与平面垂直的定义、判定定理和性质定理，并能运用它们进行论证和解决有关的问题；2、掌握平面与平面垂直的概念和判定定理、性质定理，并能运用它们进行推理论证和解决有关问题；3、在研究垂直问题时，要善于应用“转化”和“降维”的思想，通过线线、线面、面面平行与垂直关系的转化，从而使问题获得解决。

三、知识要点1、直线与平面垂直的定义：如果一条直线和一个平面内的任何一条直线都垂直，那么就称这条直线和这个平面垂直。

2、直线与平面垂直的判定：常用方法有：①判定定理： .② b⊥α, a∥ba⊥α；（线面垂直性质定理）③α∥β,a⊥βa⊥α（面面平行性质定理）④α⊥β，α∩β=l，a⊥l，a a⊥α（面面垂直性质定理）3、直线与平面垂直的性质定理：①如果两条直线同垂直于一个平面，那么这两条直线平行。

（a⊥α，b⊥α⇒a∥b）②直线和平面垂直时，那么该直线就垂直于这个平面内的任何直线（）4、点到平面的距离的定义：从平面外一点引这个平面的垂线，这个点和垂足间的线段的长度叫做这个点到平面的距离。

特别注意：点到面的距离可直接向面作垂线，但要考虑垂足的位置，如果垂足的位置不能确定，往往采取由点向面上某一条线作垂线，再证明此垂足即为面的垂足。

5、平面与平面垂直的定义及判定定理：（1）定义：如果两个相交平面的交线与第三个平面垂直，又这两个平面与第三个平面相交所得的两条交线互相垂直，就说这两个平面互相垂直。

记作：平面α⊥平面β（2）判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。

（简称：线面垂直，面面垂直）6、两个平面垂直的性质定理：如果两个平面垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。

（简称：面面垂直，线面垂直。

）思维方式：判定两相交平面垂直的常用方法是：线面垂直，面面垂直；有时用定义也是一种办法。

专题17 空间垂直关系空间异面直线垂直、直线与平面垂直、平面与平面垂直等垂直关系在复杂的空间图形中隐藏得比较深,不易发现或作出,若再渗透折叠,则容易产生思维痛点.证明空间垂直关系是高考数学命题中的必选项,垂直关系中,直线与平面垂直的定义、直线与平面垂直的判定定理、平面与平面垂直的判定定理、勾股定理的逆定理等是最基本的知识,不论是空间位置关系判定还是度量关系计算,基础都是人的空间概念与空间想象能力,没有在脑海中建立正确的空间概念是导致立体几何题求解失败的根本原因,看不清位置关系,卡壳点自然产生.一、巧连线寻找线面垂直关系二、问题1:如图1,已知三棱柱ABC−A1B1C1,平面A1ACC1⟂平面ABC,∠ABC=90∘,∠BAC=30∘,A1A=A1C=AC,E,F分别是AC,A1B1的中点.证明:EF⟂BC.【解析】卡壳点:不会寻找证明垂直关系的途径.应对策略1:把证明线线垂直关系转化为证明线面垂直关系.问题解答:连接A1E,因为A1A=A1C,E是AC的中点,所以A1E⟂AC.又平面A1ACC1⟂平面ABC,A1E⊂平面A1ACC1,平面A1ACC1∩平面ABC=AC, 所以A1E⟂平面ABC,则A1E⟂BC.又因为A1F//AB,∠ABC=90∘,故BC⟂A1F.所以BC⟂平面A1EF.因此EF⟂BC.应对策略2:发现三线垂直关系,利用空间向量运算证明垂直关系.问题解答:连接A1E,因为A1A=A1C,E是AC的中点,所以A1E⟂AC.又平面A1ACC1⟂平面ABC,A1E⊂平面A1ACC1,平面A1ACC1∩平面ABC=AC,所以A1E⟂平面ABC.如图2,以点E为原点,分别以射线EC,EA 1为y 轴、z 轴的正半轴,建立空间直角坐标系E −xyz . 不妨设AC =4,则A 1(0,0,2√3),B(√3,1,0),B 1(√3,3,2√3),F (√32,32,2√3),C (0,2,0)因此EF ⃗⃗⃗⃗⃗ =(√32,32,2√3),BC ⃗⃗⃗⃗⃗ =(−√3,1,0). 由EF⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =0得EF⟂BC . 【反思】证明空间位置关系时,寻找或添加关键的辅助线是一个智慧点.二、勾股定理促线线位置关系分析问题2:已知等边ΔABC 的边长为3,点D,E 分别是边AB,AC 上的点,且满足AD DB =CE EA=12(如图3).将ΔADE 沿DE 折起到ΔA 1DE 的位置,使二面角A 1−DE −B 成直二面角,连接A 1B,A 1C (如图4).求证:A 1D⟂平面BCED .【解析】卡壳点:折叠前后对线线位朢关系的分析不到位.应对策略：结合勾股定理的逆定理,由计算结果来验证垂直关系.问题解答:因为等边ΔABC 的边长为3,且AD DB =CE EA =12,所以AD =1,AE =2. 在ΔADE 中,∠DAE =60∘,由余弦定理得DE =√12+22−2×1×2×cos60∘=√3.因为AD 2+DE 2=AE 2,所以AD⟂DE ,折叠后有A 1D⟂DE .因为二面角A 1−DE −B 是直二面角,所以平面A 1DE⟂平面BCED .又平面A 1DE ∩平面BCED =DE,A 1D ⊂平面A 1DE,A 1D⟂DE ,所以A 1D⟂平面BCED .【反思】(1)题设信息中隐藏着AD⟂DE ,需要用勾股定理的逆定理来证明,这是解决问题的一个关键点,必须识破.(2)题设给定的面面垂直与目标要证的线面垂直之间只需证明直线垂直于棱即可.三、逆向存在性问题顺向思考问题3:如图5,三棱柱ABC −A 1B 1C 1的各棱长均为2,侧面BCC 1B 1⟂底面ABC ,侧棱BB 1与底面ABC 所成的角为60∘,在线段A 1C 1上是否存在点P ,使得平面B 1CP⟂平面ACC 1A 1?若存在,求出C 1P 的长;若不存在,请说明理由.【解析】卡壳点:存在性命题的顺向思考方法韩失.应对策略:若空间位置关系复杂,可将逆向设计的存在性问题顺向思考. 问题解答:过点B 1作B 1O⟂BC 于点O ,因为侧面BCC 1B 1⟂底面ABC ,所以B 1O⟂底面ABC,∠B 1BC =60∘,所以O 为BC 的中点.以O 为原点,以AO,OC,OB 1分别为x 轴,y 轴,z 轴正方向建立如图6所示的坐标系, 则A(−√3,0,0),B (0,−1,0),C (0,1,0),B 1(0,0,√3),A 1(−√3,1,√3),C 1(0,2,√3). 假设在线段A 1C 1上存在点P ,使得平面B 1CP⟂平面ACC 1A 1.设C 1P ⃗⃗⃗⃗⃗⃗⃗ =λC 1A 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ,则C 1P ⃗⃗⃗⃗⃗⃗⃗ =λ(−√3,−1,0),CP ⃗⃗⃗⃗⃗ =CC 1⃗⃗⃗⃗⃗⃗⃗ +C 1P ⃗⃗⃗⃗⃗⃗⃗ =(−√3λ,1−λ,√3),B 1C ⃗⃗⃗⃗⃗⃗⃗ =(0,1,−√3).设平面B 1CP 的法向量为m =(x 1,y 1,z 1),则{m ⋅B 1C ⃗⃗⃗⃗⃗⃗⃗ =y 1−√3z 1=0,m ⋅CP ⃗⃗⃗⃗⃗ =−√3λx 1+(1−λ)y 1+√3z 1=0. 取z 1=1,则y 1=√3,x 1=2−λλ.故m =(x 1,y 1,z 1)=(2−λλ,√3,1).设平面ACC 1A 1的法向量为n =(x 2,y 2,z 2),则{n⋅AC⃗⃗⃗⃗⃗ =√3x2+y2=0,n⋅C1C⃗⃗⃗⃗⃗⃗⃗ =−y2−√3z2=0.取z2=1,则y2=−√3,x2=1.n=(x2,y2,z2)=(1,−√3,1).m⋅n=(2−λλ,√3,1)⋅(1,−√3,1)=2−λλ−2=0,解得λ=23.所以|C1P⃗⃗⃗⃗⃗⃗⃗ |=43.【反思】(1)建立空间直角坐标系时,要对位置关系进行证明,这一点很重要,然后根据已证明的位置关系去建立坐标系.(2)用坐标法时,确定点的坐标非常重要,不能有一点错误,否则前功尽弃.四、学云动态研究空间垂直关系问题4:如图7,已知边长为1的菱形ABCD,设∠ABC=120∘,沿AC折叠后,取AC 的中点E,连接DE,BE,BD.(I)当平面ABC⟂平面ACD时(如图8)或(II)当平面ABC与平面ACD所成二面角的平面角为α时(如图9),分别探究以下各题.(1)AC与BD,AD与BC的位置关系.(2)AD与BC所成角大小(或余弦值).(3)BC与平面ADC所成角大小(或正弦值).(4)求二面角A−BD−C大小(或余弦值).(5)在此问题情境下,请你提出一个新的问题并探究之.【解析】卡壳点:面对开放性问题,创新思维准备不足.应对策略:面对两平面垂直关系时,较容易;面对一般情形时,要善于用抽象符号来表达.问题解答:(I)当平面ABC⟂平面ACD时.(1)由于AC⟂平面BDE,所以AC⟂BD,AD与BC为异面直线.(2)取AB的中点F,BD的中点G,连接EF,EG,FG,则∠EFG为AD与BC所成的角,EF=12,EG=√24,FG=12,cos∠EFG=14+14−182×12×12=34.(3)BE⟂平面ADC,∠BCE为BC与平面ADC所成角为π6.(4)(4)见（II)(4),令α=π2即可.(5)（5）见（II）(5),令α=π2即可.(6)(II)当平面ABC与平面ACD所成二面角的平面角为α时.(7)(1)由于AC⟂平面BDE,所以AC⟂BD,AD与BC为异面直线.(8)(2)取AB的中点F,BD的中点G,AD与BC所成的角为∠EFG,EF=FG=1 2,BD=√14+14−2×14cosα=sinα2,EG=cosα22,(9)所以cos∠EFG=14+14−14cos2α22×12×12=1−12cos2α2.(10)(3)如图10,在平面BDE中,过点B作BH⟂DE,易知BH⟂平面ACD,于是∠BCH为BC与平面ADC所成的角,BH=12sinα,sin∠BCH=BHBC=12sinα.(11)(4)如图11,过AC作BD的垂面,交BD于点G,则∠AGC为所求二面角的平面角.(12)由于ΔABD为等腰三角形,所以G为BD的中点,故AG=√1−DG2=√1−(12sinα2)2=CG,cos∠AGC=AG2+CG2−AC22AG⋅CG =2−12sin2α2−42−12sin2α2.(13)(5)提出的新问题如下.层次一求证:当α=π2时,平面BDE⟂平面ABC,或平面BDE⟂平面ADC.层次二求证:不论α为何值,平面BDE⟂平面ABC,或平面BDE⟂平面ADC,层次三在折叠过程中,是否存在α,使得平面ABD⟂平面CBD?【反思】空间位置关系与度量关系,从特殊到一般的探究,对于学生是一次重要体验.五、驾㲼经典模型中的垂直关系问题5:如图12,AC为圆O的直径,B为圆周上不与点A,C重合的点,PA垂直于圆O 所在的平面,连接PB,PC,AB,BC.(I)图12中直角三角形的个数为,异面垂直的直线有对;(II)若在图12中添加AN⟂PB,AS⟂PC,连接SN,如图13,则图13中直角三角形个数为异面垂直的直线有对;(III)图12中直线垂直平面的对数为对,图13中直线垂直平面的对数为(IV)图12中互相垂直的平面对数为对;(V)证明:平面ANS⟂平面PBC.【解析】卡壳点:空间概念弱导致数不清檚符合要求的直线与平面数.应对策略:对照空间图形,分类思考或数数.问题解答:(I)观察可知直角三角形有4个,异面垂直的直线只有1对,即PA⟂BC.(II)若在图12中添加AN⟂PB,AS⟂PC,连接SN,如图13,则图13中直角三角形个数为异面垂直的直线有对;(III)图12中直线垂直平面的对数为对,图13中直线垂直平面的对数为(IV)图12中互相垂直的平面对数为对;(V)证明:平面ANS⟂平面PBC.【解析】卡壳点:空间概念弱导致数不清檚符合要求的直线与平面数.应对策略:对照空间图形,分类思考或数数.问题解答:(I)观察可知直角三角形有4个,异面垂直的直线只有1对,即PA⟂BC.(II)在图12中添加了AN,AS,SN后,增加6个直角三角形,共有10个直角三角形;异面垂直的直线有3对,增加了AN⟂BC,AN⟂PC.(III)图12中有2对直线垂直平面:PA⟂平面ABC,BC⟂平面PAB;图13中增加2对:PC⟂平面ANS,AN⟂平面PBC.图13中共有4对直线与平面垂直.(IV)图12中有3对互相垂直的平面:平面PAB⟂平面ABC,平面PAC⟂平面ABC,平面PAB⟂平面PBC;图13中有5对互相垂直的平面,增加2对:平面ANS⟂平面PBC,平面ANS⟂平面PAC.(V)因为PA⟂平面ABC,BC⊂平面ABC,所以PA⟂BC.又AC为圆O的直径,所以AB⟂BC.因为AB∩PA=A,所以BC⟂平面PAB.又AN⊂平面PAB,所以AN⟂BC.因为AN⟂PB,PB∩BC=B,所以AN⟂平面PBC.又PC⊂平面PBC,所以AN⟂PC.因为PC⟂AS,AS∩AN=A,所以PC⟂平面ANS.又PC⊂平面PBC,所以平面ANS⟂平面PBC.【反思】(1)此空间经典模型可以将立体几何的所有问题融人其中,且对于训练学生的空间概念与空间想象能力非常有利.(2)此空间经典模型中的线线位置关系、线面位置关系、面面位置关系非常丰富,尤其是垂直关系.(3)学生在思考上述问题时,一是空间概念要清楚,二是观察要细致,三是思考要全面,四是证明的逻辑推理要有序.六、静态分析运动中的空间图形问题6:如图14,一个棱长为2的正四面体O−ABC的顶点O在平面α上,底面ABC 平行于平面α,平面OBC与平面α的交线为l.(I)当平面OBC绕l顺时针旋转时,求证:l⟂AO;(II)在上述旋转过程中,设ΔOBC在平面α上的投影为ΔOB1C1,如图15,若B1C1的中点为O1,当AO⟂平面α时,在OA上是否存在一点P,使O1P⟂平面OBC?【解析】卡壳点:面对几何体旋转的情境时不知所措.应对策略:面对运动的几何体,进行浯态分析.问题解答:(I)证明:因为平面ABC//平面α,平面ABC ∩平面COB =BC ,平面α∩平面COB =l ,所以BC//l .取BC 的中点E ,连接AE,EO ,则BC⟂AE,BC⟂EO .所以l⟂AE,l⟂EO,AE ∩EO =E,AE ⊂平面AOE,EO ⊂平面AOE ,所以l⟂平面AOE . 又AO ⊂平面AOE ,所以l⟂AO .(II)解法1当点P 与点A 重合时,O 1P⟂平面OBC ,如图16,因为BC⟂AE,BC⟂EO 1,所以BC⟂面AEO 1,BC⟂AO 1.在图中,作AS//OE,ES//OA ,由AS 2+O 1A 2=O 1S 2知∠SAO 为直角,OE⟂AO 1,AO 1⟂平面OBC .解法2易得AE =OE =√3,OA =2OE 1. 设点A 在平面OBC 上的射影为点G ,若O 1P⟂平面OBC ,则O 1P//AG,O 1E =1.所以OO 1=√2.设PO 1交OE 于点H,OH:OO 1=OO 1:OE,OH =2√33. 又OG =2√33,所以点P 与点A 重合. 解法3以O 1为原点,O 1C 1所在直线为x 轴,O 1O 所在直线为y 轴,O 1E 所在直线为z 轴建立平面直角坐标系,则O(0,√2,0),C (1,0,1),B (−1,0,1),A(0,√2,2).设P(0,√2,z),则OC ⃗⃗⃗⃗⃗ =(1,−√2,1),O 1P ⃗⃗⃗⃗⃗⃗⃗ =(0,√2,z).由于BC ⃗⃗⃗⃗⃗ ⟂O 1P ⃗⃗⃗⃗⃗⃗⃗ ,OC ⃗⃗⃗⃗⃗ ⟂O 1P ⃗⃗⃗⃗⃗⃗⃗ ,所以z =2,即点A 与点P 重合时,O 1P⟂平面OBC .【反思】高考数学命题中关于空间图形的问题情景主要是静态的、规则的图形中的点、线、面位置关系及度量关系,其中出现比较多的是平面图形翻折成空间图形或由规则图形截取得到不规则图形后的点、线、面位置关系及度量关系.强化练习1.已知三棱锥P−ABC的底面ABC是边长为2√3的正三角形,点A在侧面PBC内的射影H为ΔPBC的垂心,二面角P−AB−C的平面角的大小为60∘,则AP的长为A.3 B.3√2 C.√7 D.4【解析】如答图所示,连接并延长BH,交PC于点E,连接AE,设点P在底面ABC内的射影为点O,则PO⊥平面ABC,连接CO并延长,交AB于点F.因为点A在侧面PBC内的射影H为△PBC的垂心,所以AH⊥平面PBC,BE⊥PC,所以AH⊥PC.因为BE∩AH=H,BE⊂平面ABE,AH⊂平面ABE,所以PC⊥平面ABE,所以PC⊥AB.因为CB⊂平面ABC,PO⊥平面AC,所以PO⊥AB.因为PO∩PC=P,PO⊂平面PFC,PC⊂平面PFC,所以AB⊥平面PFC.因为CO⊂平面PFC,所以AB⊥CO.同理可证AC⊥BO.所以O是△ABC的垂心,所以三棱雉P−ABC为正三棱雉.因为三棱雉P−ABC的底面ABC是边长为2√3的正三角形,所以BF=√3,CF=3,则PO=1.因为二面角P−AB−C的平面角的大小为60∘,所以∠PFC为二面角P−AB−C的平面角.在Rt△POF中,∠PFC=60∘,FO=1,所以PF=2.在Rt△PFA中,PF=2,AF=√3,所以AP=√22+(√3)2=√7.故选C.第1题答图【反思】先判断三棱锥P−ABC为正三棱锥,然后根据异面直线所成的角的定义可得∠PFC为二面角P−AB−C的平面角,解直角三角形即可得解.2.如图,棱雉P−ABCD的底面是菱形,∠DAB=π,且ΔPAB是正三角形,求3证:PD⟂AB.【解析】取AB的中点O,连接OD,OP,由题意得△DAB为正三角形,所以AB⊥OD. 因为△PAB是正三角形,所以AB⊥OP.又OP∩OB=O,所以AB⊥平面POD且PD⊂平面POD,所以PD⊥AB.【反思】(1)立体几何命题的证明讲究逻辑,符合基本定理前提,此几何背景中有许多特殊的三角形,关键是找准一个点,即AB的中点.(2)为证线线垂直,转而证明线面垂直,而证线面垂直,线面垂直的判断是基础.3.如图,长方体ABCD−A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⟂EC1.求证:BE⟂平面EB1C1.【解析】由已知得B1C1⊥平面ABB1A1,BE⊂平面ABB1A1,故B1C1⊥BE.又BE⊥EC1,所以BE⊥平面EB1C1.【反思】根据线面垂直的判定定理,在复杂空间图形中寻找需要的条件.4.图1是由矩形ADEB、RtΔABC和菱形BFGC组成的一个平面图形,其中AB= 1,BE=BF=2,∠FBC=60∘,将其沿AB,BC折起,使得BE与BF重合,连接DG,如图2,证明:图2中的A,C,G,D四点共面,且平面ABC⟂平面BCGE.5.【解析】由已知得AD//BE,CG//BE,所以AD//CG,故AD和CG确定一个平面,从而A,C,G,D四点共面.由已知得AB⊥BE,AB⊥BC,故AB⊥平面BCGE.又因为AB⊂平面ABC,所以平面ABC⊥平面BCGE.【反思】翻折前后线线、线面位置关系的变与不变是思考的基础.6.已知在边长为1的菱形ABCD中,∠ABC=60∘,沿AC折叠后,设平面ABC与平面ACD所成角为α,折叠过程中,是否存在α,使得平面ABD⟂平面CBD?7.【解析】由对称性且△ABD与△CBD为等腰三角形,取BD的中点G,则∠AGC为平面ABD与平面CBD所成二面角的平面角.在△BDE中,由余弦定理得BD2=34+34−2×34cos⁡α=3sin2⁡α2,或由三角函数定义可得BD=√3sin⁡α2,于是AG2=1−34sin2⁡α2=CG2.当AG2+CG2=AC2时,平面ABD⊥平面ADC,即当2(1−34sin2⁡α4)=1,也即sin⁡α2=√63时,平面ABD⊥平面ADC.由于12<69<34,所以π4<α2<π3.故存在α,使得平面ABD⊥平面CBD.【反思】(1)用最简单的平面图形创设问题情境,检测学生的空间想象能力与创新能力.面对新的数学问题,需要对问题情境有比较深入的理解,才能达到较高层次的认知,层次一属千找到一个;层次二不仅找到而且发现更一般的情形;层次三向更深的地方思考并探索,提出了存在性命题.这样一个开放性命题给不同数学认知水平的学生提供了一个平台,有利于培养学生创新意识.(2)在证明过程中,还可以逆向思考,要使∠AGC 为直角,只要AG =CG =√22,只要DG =√22,或BD =√2,只要sin⁡α2=√638. 如图,在矩形ABCD 中,点E 在线段CD 上,AB =3,BC =CE =2,沿直线BE 将ΔBCE 翻折成ΔBC ′E ,使点C ′在平面ABED 上的射影F 落在直线BD 上.求证:直线BE⟂平面CFC ′.9.【解析】(I)如答图所示,在线段AB 上取点G ,使BG =2,连接CG ,交BE 于点H .因为在正方形BCEG 中,BE ⊥CG ,所以翻折后,BE ⊥C ′H,BE ⊥GH .又C ′H ∩GH =H ,所以BE ⊥平面C ′HG .又BE ⊂平面ABED ,所以平面ABED ⊥平面C ′HG .又平面ABED ∩平面C ′HG =GC ,所以点C ′在平面ABED 上的射影F 落在直线GC 上.又点C ′在平面ABED 上的射影F 落在直线BD 上,所以F 为直线BD 与GC 的交点,所以平面CFC ′即平面C ′HG ,所以直线BE ⊥平面CFC ′.第6题答图【反思】按照直线与平面垂直判定的逻辑推理方式进行规范的叙述.7.如图,在四棱锥P−ABCD中,PC⟂平面ABCD,AB⟂AD,AB//CD,PD=AB=2AD=2CD=2,E为PB的中点.证明:平面EAC⟂平面PBC.【解析】证明:PC⊥平面ABCD,故PC⊥AC.又AB=2,CD=1,AD⊥AB,所以AC=BC=√2.故AC2+BC2=AB2,即AC⊥BC.所以AC⊥平面PBC,所以平面ACE⊥平面PBC.【反思】面对大量线段时,巧用勾股定理的逆定理判断位置关系.8如图,在三棱锥P−ABC中,PA⟂平面ABC,2AC=PC=2,AC⟂BC,D,E,F分别为AC,AB,AP的中点,M,N分别为线段PC,PB上的动点,且有MN//BC.(I)求证:MN⟂平面PAC;(II)探究:是否存在这样的动点M,使得二面角E−MN−F为直二面角?若存在,求CM的长;若不存在,说明理由.【解析】因为PA⊥平面ABC,所以PA⊥BC.又AC⊥BC,所以BC⊥平面PAC.又因为MN//BC,所以MN⊥平面PAC.（II)由条件可得,∠FMD即为二面角E−MN−F的平面角. 若二面角E−MN−F为直二面角,则∠FMD=90∘.在Rt△PCA中,设CM=t(0⩽t⩽2),则PM=2−t.在△MDC中,由余弦定理可得，DM2=CM2+CD2−2CM⋅CDcos⁡60∘=t2+14−12t.同理可得,FM2=PM2+PF2−2PM⋅PFcos⁡30∘=(2−t)2+34−32(2−t)又由FD2=FM2+MD2,得2t2−3t+1=0,解得t=1,或t=12.所以存在直二面角E−MN−F,且CM的长度为1或12.【反思】求是否存在点的位置可以转化为求是否存在一定长度的线段,把对“形”的研究转化到对“数”的分析上.。

人教版高二数学必修第四册《空间中的垂直关系》说课稿一、引言《空间中的垂直关系》是人教版高二数学必修第四册的一章内容，本章主要介绍了三维空间中的垂直关系的概念、性质以及应用，并通过丰富的例题让学生深入理解垂直关系的几何特征和运用方法。

本说课稿将重点介绍该章节的教学目标、教学重点和难点、教学方法和教学过程的设计。

二、教学目标1.理解垂直关系的概念，掌握判断两条直线或两个平面是否垂直的方法；2.掌握垂直关系的性质和判定定理，并能运用定理解决问题；3.在三维空间中，能够熟练应用垂直关系的概念和性质，分析解决相关几何问题。

三、教学重点和难点3.1 教学重点1.垂直关系的定义和性质；2.垂直关系的判定定理。

3.2 教学难点1.理解垂直关系的几何特征，能准确判断两直线或两平面是否垂直；2.运用垂直关系的判定定理解决实际问题。

四、教学内容和安排4.1 教学内容1.垂直关系的概念和性质；2.垂直关系的判定定理；3.垂直关系在三维空间中的应用。

4.2 教学安排1.师生互动，通过引导问题引发学生对垂直关系的思考；2.展示垂直关系的定义和性质，以图例和实例帮助学生理解；3.通过演示和讨论，引入垂直关系的判定定理；4.练习和实践，通过例题和习题的讲解，巩固学生对垂直关系的理解和应用；5.总结与反思，让学生回顾本节课的重要内容和自己的学习体会。

五、教学方法本节课将采用多种教学方法来促进学生的主动参与和深入理解垂直关系的概念和运用方法。

具体教学方法包括：1.启发式教学法：通过提出问题、让学生自主发现、分析和总结，引导学生理解垂直关系的几何特征和性质；2.归纳法：通过示例与练习，让学生掌握垂直关系的判定定理，培养学生逻辑思维和推理能力；3.演示法：用图表和实例展示垂直关系的概念和运用方法，加深学生对知识点的理解；4.口头解答和板书：通过口头解答来激发学生思考和讨论，同时将关键内容通过板书方式呈现，方便学生复习和记忆。

六、教学过程设计6.1 Step 1 引入通过举例引发学生对垂直关系的思考，比如问“墙面上两个相交的直线之间是否存在垂直关系？”等问题。

第07讲、空间中的垂直关系（讲义）在这一讲中，我们讨论空间中的垂直关系. 主线依旧是从线线关系到线面、面面关系，并且将后者转化为前者来解决.一、线线垂直我们还是从平面几何谈起. 下面列出了平面几何中与垂线概念相关的一些重要信息： ① 定义：交角为直角（即平角的一半）的两条直线互相垂直；② 存在唯一性定理：过（直线上或者直线外）一点有且仅有一条直线与已知直线垂直； 如何将两直线的垂直关系推广到空间呢？一个预备性的定理，角的平移不变性，保证了这一推广的有效性. 事实上，角的平移不变性可以使我们谈论更为一般的空间中直线位置关系，即两条异面直线的夹角问题.定义：如果两条直线相交于一点，或者经过平移后相交于一点，并且交角为直角，则称这两条直线互相垂直.二、线面垂直先来看一种基于平面图形的直观构造，如下图，直线l 是线段AB 的垂直平分线，并且它们在同一平面内；如何由此产生一个与线段AB 垂直的平面呢？一种自然的想法是令直线l 绕垂足旋转一周，从而产生出一个平面. 就直觉而言，直线l 转过的每个位置都是线段AB 的垂直平分线，反过来说，如果有一条直线稍稍偏离了垂直平分线的位置，那它也就不会被包含于这个平面之中.也许你会奇怪为什么要令AB 是线段，其实这只是为了便于讨论了引入的一种简化处理，我们知道直线上任意一点都是其对称点，相应地也可以在该点两侧截取等长线段，因此前述图景中并未包含任何可能丧失一般性的限制. 相反，它提示我们可以从直线上对称地截取等长线段，从而构造出有限图形而更便于深入讨论.定义：如果一条直线（AB ）与一个平面α相交于点O ，并且与这个平面内所有过交点O 的直线都垂直，则称这条直线和这个平面互相垂直，这条直线叫做平面的垂线，这个平面叫做直线的垂面，交点叫做垂足. 垂线上任意一点到垂足间的线段叫做这个点到这个平面的垂线段. 垂线段的长度叫做这个点到平面的距离.从这个定义出发，我们很自然地会追问一些问题. 例如，平面α内的直线并不都是经过垂足O 的，那些不过O 点的直线也与垂线垂直吗？线面垂直性质定理：如果一条直线垂直于一个平面，那么它就和平面内任意一条直线垂直.已知：如图①，αα⊂⊥m l ,；证明：m l ⊥.证：若直线m 经过垂足，则根据线面垂直定义有m l ⊥；若m 不过垂足，则可过垂足作m 的平行线a ，线面垂直定义保证a l ⊥，而根据线线垂直定义，此时仍有m l ⊥. 综合两种情况，原命题得证.接下来我们看看判定问题，线面垂直的定义其实不具有可用性，因为“与所有过交点的直线都垂直”是难以实现的，因此，我们要找到一种通过有限次操作就能确认的方法. 很显① 画图提示：画线面垂直时，通常把直线化成和表示平面的平行四边形的一边垂直.然，只与一条过交点的直线垂直是不能保证线面垂直的（你能举出反例吗？），而两条相交直线可以唯一确定一个平面，因此我们将希望寄托于此.线面垂直的判定定理：如果一条直线与平面内的两条相交直线都垂直，则这条直线与这个平面垂直.分析：我们的目标是由“与平面内的两条相交直线都垂直”推出“与平面内所有过交点的直线都垂直”，从而符合线面垂直定义. 为了进一步的讨论我们做两点处理，同时要注意不失一般性（请你自己确认一下理由）. 第一个处理是将平面内直线n m ,平移到使其交点与线面交点重合，第二个处理是在直线与平面的交点两侧截取等长的线段.已知：如上中图，线段F AB =α 且FB AF =，过F 点的直线n m ,均与AB 垂直，l 是经过F 点的任一直线；证明：l 是线段AB 的垂直平分线.证：任取点l E ∈，过E 作直线分别交n m ,于点D C ,，连接BE AE BD AD BC AC ,,,,,； 为便于识别将ACD ∆和BCD ∆置于同一平面内，由SSS 全等判据得BCD ACD ∆∆≌，从而BCD ACD ∠=∠，接着BCE ACE ∆∆≌，所以BE AE =. 结合BE AE BF AF ==,可知l 是线段AB 的垂直平分线（理由是什么？）.现在我们证明了“过线面交点的任一直线都与该直线垂直”，根据定义可以知道，该直线与平面垂直. 这样，我们就将判定线面垂直的问题转化为判定线线垂直问题.接着我们来看该判据的两条推论.推论1、两条平行直线中，如果有一条垂直于平面，那么另一条也垂直于这个平面.已知：α⊥l m l ,∥；求证：α⊥m证：根据线面垂直性质定理，α⊥l 意味着可以在α内找到两条相交直线，例如b a ,，使得b l a l ⊥⊥,. 空间中线线垂直的定义表明垂直关系在平移变换下保持不变，因此由m l ∥我们有b m a m ⊥⊥,，由线面垂直判定定理可知α⊥m . 推论2、如果两条直线垂直于同一平面，那么这两条直线平行.已知：αα⊥⊥m l ,；求证：m l ∥.证：反证. 设l m ,不平行，则由平行公理，过m 与α的交点存在唯一直线l m ∥'，根据推论1可知α⊥'m . 接着，考由相交直线m m ',所决定的平面β，记βα =a ，α m m B '=，则a B =∈βα ，于是，在平面β内，过直线a 上一点B 存在两条垂线m 和m '，与平面内（这个限制条件很重要！）垂线的存在唯一性矛盾. 因此假设不成立，即必有m l ∥.点评：（1）上述两条推论可以看做是哪两条平面几何定理向空间的推广？请你对比一下.（2）在证明推论2时，我们实际上证明了“过平面内一点有且仅有一条垂线”，再补充上“过平面外一点有且仅有一条垂线”，就完成了将“过点作垂线的存在唯一性”的空间定理的证明. 现在我们来具体看看.如图，假设过平面外一点P 可以作两条平面的垂线，垂足分别为点B A ,；则在点B A P ,,所决定的平面内，由直线AB 外一点P 可以向它引两条垂线（线面垂直性质定理！），与平面内垂线存在唯一性矛盾.综合上述两种情况，我们有：空间中，过一点与已知平面垂直的直线有且仅有一条.例1、一根旗杆AB 高8米，它的顶端A 挂着两根长10米的绳子.拉紧绳子，并把它的下端放在地面上的C B ,两点（和旗杆脚不在同一直线上），并且这两点都与旗杆脚的距离是6米.解答：依题意6,10,8=====BD BC AD AC AB ，由勾股定理逆定理AD AB AC AB ⊥⊥，，根据线面垂直的判定定理可知BCD AB ⊥.点评：（1）这是“由线段度量确定角度关系”的一个空间版的呈现，也许你还记得，古代埃及人用长绳构造直角的方法是在绳子上标记12个等长的段，接着拉出一个边长为()5,4,3的三角形从而得到直角. 这个问题提示我们：在确定足量的线段长度之后，就可以确定角度.（2）如果你听到诸如“求三棱锥BCD A -的体积”这样的问题时，会不会觉得奇怪？事实上你应该记得，在定义直棱柱和锥、台等立体的高时，我们都明确用到了线面垂直概念.例2、已知：如图，l AP l A l ⊥=⊥,,αα求证：α⊂AP .证：反证，设α⊄AP ，则设相交直线AP l ,所决定的平面为β，由βα ∈A ，设βα =AM . 根据线面垂直性质定理，αα⊂⊥AM l ,，得到AM l ⊥，但同时有AP l ⊥，于是在平面β内，过直线l 上点A 有两条垂线AP AM ,，导致矛盾. 因此必有α⊂AP .点评：线面垂直保证了“平面内过交点的每条直线都与该直线垂直”，现在我们证明了“过交点的每条垂线都在平面内”，这是对于前述直观感觉“垂面是由过交点的全体垂线构成的”的精确化表述. 公理化论证模式并不是要推翻直观，而是不断努力将直观精确化，提出其中的谬误，使剩余部分更准确也更有力.例3、正方体中的线面垂直（1）证明：11B BDD AC ⊥；（2）证明：BD A AC 11⊥；分析：证明线面垂直的关键就是在面内找到两条相交垂线，而寻找线线垂直的方法有两种，平面内的相关证明，或者是作为线面垂直的性质.解答：仅给出思路，请自己补充细节；（1）在平面ABCD 内证明BD AC ⊥，由线面垂直关系得到1BB AC ⊥；（2）由（1）中结论同理得11A ACC BD ⊥，从而有BD AC ⊥1；同理可得B A AC 11⊥.三、面面垂直从直观上看，我们之前建立的印象“包含平面的一条垂线的面与该平面垂直”（如下左图）是简明清晰而合乎直觉的，但是如果把它作为面面垂直的定义会有什么不足呢？关键在于可推广性. 在平面几何中，我们是把“垂直”作为相交的特例来处理的，也就是说，一般地，两条直线可以有一个交角，而垂直不过是交角恰为直角的情况. 这样，在定义面面垂直时，我们其实真正希望做的是先定义“面面交角”，然后把垂直作为特例.定义：如果两个相交平面的交线与第三个平面垂直，并且这两个平面与第三个平面相交所得的两条交线互相垂直，就称这两个平面互相垂直②.至于我们最初的那个简明清晰的直觉，它就成为判定定理；或者更一般地说，判定定理总要具有相对简单、好用的形式.面面垂直判定定理：若一个平面经过另一个平面的一条垂线，则这两个平面互相垂直.已知：βα⊂⊥l l ,；求证：αβ⊥.证明：如右图，记P a l a == ,βα，在平面α内过P 点作a 的垂线m ，记相交直线m l ,所决定的平面为γ；由线面垂直性质定理可知m l a l ⊥⊥,，结合a m ⊥可知γ⊥a （第三个面与两面交线垂直），注意到m l m l ⊥==,,γαγβ ，符合面面垂直定义，因此有αβ⊥.这次的性质定理指向性比较明确，它与判定定理在逻辑上很密切.② 从这个定义中，你是否看到了一般的“两平面交角”（即“二面角”）的推广定义？或者更具体地，如果我们要定义“两个相交平面的交角为α”，该如何修改上述定义？面面垂直性质定理：若两个平面互相垂直，则在一个平面内垂直于交线的直线也垂直于另一平面.已知：a l l a ⊥⊂=⊥,,,ββααβ ；求证：β⊥m .证：如右图，记P a l = ，在平面α内过P 点作a 的垂线m ，记相交直线m l ,所决定的平面为γ；由线面垂直判定定理可知γ⊥a ，且γαγβ ==m l ,，根据面面垂直的定义可知m l ⊥. 由l m a m a l P ⊥⊥=,, ，根据线面垂直判定定理得β⊥m .上述两个命题的证明过程具有高度的相关性（甚至连图都差不多！），这是因为证明的核心在于构造出定义所要求的“第三个平面与交线垂直且两条交线彼此垂直”，并且将面面关系转化为线面关系问题.例4、如图，平面βα⊥，在两面交线上取线段4=AB ，BD AC ,分别在平面α和β内，它们都垂直于交线AB ，且3=AC ，12=BD ，求CD 的长.解答：由于AB DB AB ⊥=⊥,,βαβα ，根据面面垂直性质定理可知α⊥DB ，而α⊂CB ，由线面垂直性质定理得BC DB ⊥；在ABC Rt ∆中，4,3==AB AC ，因此5=BC ；在BCD Rt ∆中，12,5==BD BC ，因此13=CD .点评：事实上，题中利用线面关系的语言描述了一个三棱锥的构造过程，例如，根据题中信息，你能画出三棱锥ABD C -的三视图吗？例5、已知ABC Rt ∆中，a AC AB ==，AD 是斜边BC 上的高，以AD 为折痕使BDC ∠成直角.（1）证明：BDC ACD BDC ABD ⊥⊥,；（2）︒=∠60BAC ；解答：（1）根据线面垂直判定定理，CD AD BD AD ⊥⊥,，因此有BCD AD ⊥；再根据面面垂直判定定理，经过垂线AD 的平面ACD ABD ,都与底面BCD 垂直；（2）对BCD Rt ∆使用勾股定理得a BC =，从而有正ABC ∆.点评：实际上，对于三棱锥BCD A -，我们该问的是“还有什么是不能知道的”. 有兴趣的同学不妨在这里尝试一下你前面推广得到的“二面角”的概念，看能否计算出平面ABD 与ABC 的夹角？作为对本讲的总结，让我们回顾一下多面体：请你试着用空间中线面关系的语言，重新定义常见的多面体.。

示范教案错误!教学分析本节教材给出了两直线垂直和直线与平面垂直的定义，并讨论了判定定理和性质．在教学过程中，要注意调动学生的学习积极性,留出足够思考时间，培养学生的思维能力．值得注意的是尽量使用信息技术，以便突破难点．对于判定定理的证明不作要求，仅供学习有余力的同学参考．三维目标1．掌握两直线垂直和直线与平面垂直的定义，培养学生的空间想象能力．2．掌握直线与平面垂直的判定定理及其推论，提高学生的应用能力．重点难点教学重点:直线与平面垂直的判定定理及其推论．教学难点：归纳判定定理,证明推论2。

课时安排1课时错误!导入新课设计1.(情境导入)日常生活中，我们对直线与平面垂直有很多感性认识,比如,旗杆与地面的位置关系，大桥的桥柱与水面的位置关系等，都给我们以直线与平面垂直的印象．在阳光下观察直立于地面的旗杆及它在地面的影子．随着时间的变化，尽管影子BC的位置在移动，但是旗杆AB所在直线始终与BC所在直线垂直．也就是说，旗杆AB所在直线与地面内任意一条不过点B的直线B′C′也是垂直的．设计2。

（实例导入）如果一条直线垂直于一个平面的无数条直线，那么这条直线是否与这个平面垂直?举例说明．如下图，直线AC1与直线BD、EF、GH等无数条直线垂直，但直线AC1与平面ABCD不垂直．推进新课错误!错误!(1）阅读教材，说说空间中两直线垂直的定义．（2)想想看，如果A,B是空间中的两点，那么在空间中线段AB 的垂直平分线有多少条？AB的这些垂直平分线构成的集合是怎样的图形（如下图)?固定线段AB，让l保持与AB垂直并绕直线AB在空间旋转，l的轨迹是怎样的图形?（3)归纳空间直线与平面垂直的定义．（4）直线l⊥平面α,直线m α，则l与m垂直吗?讨论结果：（1）如果两条直线相交于一点或经过平移后相交于一点,并且交角为直角，则称这两条直线互相垂直．（2)容易发现，空间中线段AB的所有垂直平分线构成的集合是一个平面．(3）如果一条直线(AB）和一个平面(α）相交于点O，并且和这个平面内过交点（O）的任何直线都垂直，我们就说这条直线和这个平面互相垂直，这条直线叫做平面的垂线，这个平面叫做直线的垂面,交点叫做垂足．垂线上任意一点到垂足间的线段,叫做这个点到这个平面的垂线段．垂线段的长度叫做这个点到平面的距离．(4)如下图，如果l⊥a,垂足为O，直线m是平面α内不过点O 的任意一条直线，那么在α内过点O，可引直线m∥a,根据空间直线与平面垂直的定义，由l⊥a可得l⊥m.这就是说：如果一条直线垂直于一个平面,那么它就和平面内的任意一条直线垂直．画直线和平面垂直时,通常要把直线画成和表示平面的平行四边形的一边垂直，如上下图所示．直线l和平面α互相垂直,记作l⊥α。

空间中的垂直关系【知识导图】近年来，立体几何高考命题形式比较稳定，题目难易适中，常常立足于棱柱、棱锥和正方体，复习是要以多面体为依托，始终把直线与直线、直线与平面、平面与平面垂直的性质和判定作为考察重点.在难度上也始终以中等偏难为主，在新课标教材中将立体几何要求进行了降低，重点在对图形及几何体的认识上，实现平面到空间的转化，示知识深化和拓展的重点，因而在这部分知识点上命题，将是重中之重.知识讲解知识点1 线线垂直1、判断线线垂直的方法：所成的角是直角，两直线垂直；垂直于平行线中的一条，必垂直于另一条.2、三垂线定理：在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直.3、三垂线定理的逆定理：在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直.推理模式：,,PO O PA A a AO a a AP αααα⊥∈⎫⎪=⇒⊥⎬⎪⊂⊥⎭.⑴三垂线指PA ，PO ，AO 都垂直α内的直线a 其实质是：斜线和平面内一条直线垂直的判定和性质定理⑵要考虑a 的位置，并注意两定理交替使用.知识点2 线面垂直定义：如果一条直线l和一个平面α相交，并且和平面α内的任意一条直线都垂直，我们就说直线l和平面α互相垂直其中直线l叫做平面的垂线，平面α叫做直线l的垂面,直线与平面的交点叫做垂足.直线l与平面α垂直记作：l⊥α.直线与平面垂直的判定定理：如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面.直线和平面垂直的性质定理：如果两条直线同垂直于一个平面,那么这两条直线平行.知识点3 面面垂直两个平面垂直的定义：相交成直二面角的两个平面叫做互相垂直的平面.两平面垂直的判定定理：（线面垂直⇒面面垂直）如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直.两平面垂直的性质定理：（面面垂直⇒线面垂直）若两个平面互相垂直，那么在一个平面内垂直于它们的交线的直线垂直于另一个平面.例题讲解类型一线线垂直【例题1】如图1所示，已知正方体ABCD—A1B1C1D1中，E、F、G、H、L、M、N分别为A1D1，A1B1，BC，CD，DA，DE，CL的中点，求证：EF⊥GF.【解析】证明：如图2，作GQ ⊥B 1C 1于Q ，连接FQ ，则GQ ⊥平面A 1B 1C 1D 1，且Q 为B 1C 1的中点.在正方形A 1B 1C 1D 1中，由E 、F 、Q 分别为A 1D 1、A 1B 1、B 1C 1的中点可证明EF ⊥FQ ，由三垂线定理得EF ⊥GF .【例题2】如图所示，四面体ABCD 中，ABC △是正三角形，AD CD =．证明：AC BD ⊥；【答案】详见证明【解析】设AC 中点为F ，联结FD ，FB ，AD CD FD AC =⇒⊥，AB AC FB AC =⇒⊥，FD FB F =AD ⇒⊥平面DFB AD BD ⇒⊥. 类型二 线面垂直【例题1】（1）如图，ABCD —A 1B 1C 1D 1是正四棱柱，求证：BD ⊥平面ACC 1A 1. （2）如图，在五面体ABCDEF 中，点O 是矩形ABCD 的对角线的交点，面CDE 是等边三角形，棱12EF BC ∥.（I ）证明FO ∥平面;CDE ； （II）设,BC=证明EO ⊥平面.【解析】证明：（1）∵ABCD —A 1B 1C 1D 1是正四棱柱， ∴CC 1⊥平面ADCD , ∴BD ⊥CC 1B1∵ABCD 是正方形，∴BD ⊥AC又∵AC ，CC 1⊂平面ACC 1A 1,且AC ∩CC 1=C , ∴BD ⊥平面ACC 1A 1. （2）证明：（I ）取CD 中点M ，连结OM .在矩形ABCD 中，1,2OM BC ∥又1,2EF BC ∥则.EF OM ∥连结EM ，于是四边形EFOM 为平行四边形.FO ∴∥EM. 又FO ⊂平面CDE ，且EM ⊂平面CDE ，FO ∴∥平面CDE .（II ）连结FM .由（I ）和已知条件，在等边CDE ∆中，,CM DM = EM CD ⊥且1.22EM BC EF === 因此平行四边形EFOM 为菱形，从而EO FM ⊥.,,CD OM CD EM CD ⊥⊥∴⊥平面EOM ，从而.CD EO ⊥而,FMCD M =所以EO ⊥平面.CDF【例题2】【2019全国2卷理17】长方体1111ABCD A B C D -的底面ABCD 是正方形，点E 在棱上，BE ⊥1EC . 证明：BE ⊥平面11EB C ； 【答案】：见解析【解析】（1）平面ABCD -1111A B C D 是长方体 111C B ABB A ∴⊥平面又11BE ABB A ⊂平面 11C B BF ∴⊥又1BE EC ⊥ 1111EC B C C ⋂=11BE EB C ∴⊥平面【总结与反思】考查直线与平面垂直等基础知识，考查空间想象能力和推理论证能力.DCABEOFM【例题3】如图，直三棱柱ABC—A1B1C1中，AC＝BC＝1，∠ACB＝90°，AA1＝2，D是A1B1中点．（1）求证C1D⊥平面A1B；（2）当点F在BB1上什么位置时，会使得AB1⊥平面C1DF？并证明你的结论.【解析】（1）证明：如图，∵ABC—A1B1C1是直三棱柱，∴A1C1＝B1C1＝1，且∠A1C1B1＝90°.又D是A1B1的中点，∴C1D⊥A1B1.∵AA1⊥平面A1B1C1，C1D⊂平面A1B1C1，∴AA1⊥C1D，∴C1D⊥平面AA1B1B.（2）解：作DE⊥AB1交AB1于E，延长DE交BB1于F，连结C1F，则AB1⊥平面C1DF，点F即为所求.事实上，∵C1D⊥平面AA1BB，AB1⊂平面AA1B1B，∴C1D⊥AB1．又AB1⊥DF，DF C1D＝D，∴AB1⊥平面C1DF.【总结与反思】本题（1）的证明中，证得C1D⊥A1B1后，由ABC—A1B1C1是直三棱柱知平面C1A1B1⊥平面AA1B1B，立得C1D⊥平面AA1B1B.（2）是开放性探索问题，注意采用逆向思维的方法分析问题.类型三面面垂直【例题1】如图，△ABC为正三角形，EC⊥平面ABC，BD∥CE，CE＝CA＝2BD，M 是EA的中点，求证：（1）DE＝DA；（2）平面BDM⊥平面ECA；（3）平面DEA⊥平面ECA.【解析】证明：（1）如图，取EC 中点F ，连结DF .∵EC ⊥平面ABC ，BD ∥CE ，得DB ⊥平面ABC . ∴DB ⊥AB ，EC ⊥BC . ∵BD ∥CE ，BD ＝21CE ＝21FC ，则四边形FCBD 是矩形，DF ⊥EC . 又BA ＝BC ＝DF ，∴Rt △DEF ≌Rt △ABD ，所以DE ＝DA . （2）取AC 中点N ，连结MN 、NB ， ∵M 是EA 的中点，∴MN 21EC . 由BD21EC ，且BD ⊥平面ABC ，可得四边形MNBD 是矩形，于是DM ⊥MN . ∵DE ＝DA ，M 是EA 的中点，∴DM ⊥EA ．又EA MN ＝M ，∴DM ⊥平面ECA ，而DM ⊂平面BDM ，则平面ECA ⊥平面BDM .（3）∵DM ⊥平面ECA ，DM ⊂平面DEA ，∴平面DEA ⊥平面ECA .【例题2】【2018全国1卷理18】如图，四边形ABCD 为正方形,E ,F 分别为AD ,BC 的中点,以DF 为折痕把△DFC 折起,使点C 到达点P 的位置,且PF ⊥BF . 证明:平面PEF ⊥平面ABFD ;【答案】证明略【解析】证明：（1）因为四边形ABCD 为正方形，且E ，F 分别为AD ，BC 的中点，所以EF BF ⊥，又因为,,,PF BF EF PF PEF EF PF F ⊂⋂=⊥面，所以BF ⊥面PEF ，而BF ABFD ⊂面，所以平面PEF ⊥平面ABFD .【总结与反思】（1）证明DE ＝DA ，可以通过图形分割，证明△DEF ≌△DBA .（2）证明面面垂直的关键在于寻找平面内一直线垂直于另一平面.由（1）知DM ⊥EA ，取AC 中点N ，连结MN 、NB ，易得四边形MNBD 是矩形.从而证明DM ⊥平面ECA .面面垂直的问题常常转化为线面垂直、线线垂直的问题解决课堂练习【基础】1、下列命题中正确的个数是( )①如果直线l 与平面α内的无数条直线垂直，则l ⊥α； ②如果直线l 与平面α内的一条直线垂直，则l ⊥α； ③如果直线l 不垂直于α，则α内没有与l 垂直的直线；④如果直线l 不垂直于α，则α内也可以有无数条直线与l 垂直． A ．0 B ．1 C ．2 D ．32、已知m ，n 是不同的直线，α，β是不重合的平面，则下列命题中正确的是( ) A ．若m ∥α，m ∥n ，则n ∥α B ．若m ⊥α，n ⊥α，则n ⊥m C ．若m ⊥α，m ∥β，则α⊥β D ．若α⊥β，m ⊂α，则m ⊥β3、如图所示，PA ⊥平面ABC ，△ABC 中BC ⊥AC ，则图中直角三角形的个数为( )A ．4B ．3C ．2D ．14、如图所示，在正方体ABCD —A 1B 1C 1D 1中，E 、F 分别是棱B 1C 1、B 1B 的中点． 求证：CF ⊥平面EAB ．5.【2018全国1卷文18】如图,在平行四边形ABCM 中, AB =AC =3,∠ACM =90°.以AC 为折痕将△ACM 折起,使点M 到达点D 的位置,且AB ⊥DA . 证明:平面ACD ⊥平面ABC ;答案与解析 1、【答案】B【解析】只有④正确． 2、【答案】C【解析】A 中还有可能n ⊂α；B 中n ∥m ；D 中还有可能m ∥β或m ⊂β或相交不垂直；C 中，由于m ∥β，设过m 的平面γ与β交于b ，则m ∥b ，又m ⊥α，则b ⊥α，又b ⊂β，则α⊥β，所以C 正确． 3、【答案】A 【解析】⎭⎬⎫PA ⊥平面ABC BC ⊂平面ABC ⇒⎭⎬⎫PA ⊥BC AC ⊥BC ⇒BC ⊥平面PAC ⇒BC ⊥PC ，∴直角三角形有△PAB 、△PAC 、△ABC 、△PBC ．4、【答案】证明 在平面B 1BCC 1中，∵E 、F 分别是B 1C 1、B 1B 的中点， ∴△BB 1E ≌△CBF ， ∴∠B 1BE ＝∠BCF ，∴∠BCF ＋∠EBC ＝90°，∴CF ⊥BE ， 又AB ⊥平面B 1BCC 1，CF ⊂平面B 1BCC 1， ∴AB ⊥CF ，AB ∩BE ＝B ，∴CF ⊥平面EAB ． 【解析】利用全等三角形的性质证明垂直. 5.【答案】（1）详见解析 【解析】解：（1）四边形ABCD 是平行四边形//CM AB ∴,又90ACM ∠=,即AC CM ⊥AB DA ∴⊥又,AB DA AC DA A ⊥=AB ∴⊥平面ADCAB ⊂平面ABC∴平面ACD ⊥平面ABC 【巩固】1、从平面外一点P 向平面引一条垂线和三条斜线，斜足分别为A ，B ，C ，如果PA ＝PB ＝PC ，有如下命题：①△ABC 是正三角形；②垂足是△ABC 的内心； ③垂足是△ABC 的外心；④垂足是△ABC 的垂心． 其中正确命题的个数是( )A ．1B ．2C ．3D ．42、如图所示，在正方体ABCD —A 1B 1C 1D 1中，若E 是A 1C 1的中点，则直线CE 垂直于( )A ．ACB ．BDC ．A 1D D ．A 1D 1 3、如图，四棱锥P -ABCD 中，AP ⊥平面PCD ，AD ∥BC ，AB =BC =21AD ,E ,F 分别为线段AD ，PC 的中点.（Ⅰ）求证：AP ∥平面BEF （Ⅱ）求证：BE ⊥平面PAC4、如图，PA ⊥平面ABCD ，四边形ABCD 是矩形，PA =AD =a ，M 、N 分别是AB 、PC 的中点．求证：平面MND ⊥平面PCD5.【2016全国1卷理18】如图，在以F E D C B A ,,,,,为顶点的五面体中，面ABEF 为正方形，FD AF 2=,︒=∠90AFD ,且二面角E AF D --与二面角F BE C --都是︒60 证明：EFDC ABEF 平面平面⊥:答案与解析 1、【答案】A【解析】PO ⊥面ABC ．则由已知可得，△PAO 、△PBO 、△PCO 全等，OA ＝OB ＝OC ， O 为△ABC 外心． 只有③正确2、【答案】B【解析】证BD ⊥面CC 1E ，则BD ⊥CE ．3、【答案】（Ⅰ）连接AC 交BE 于点O ，连接OF ，不妨设AB =BC =1,则AD =2,//,BC AD BC AB =∴四边形ABCE 为菱形AP OF PC AC F O //,,∴中点，分别为又BEF AP BEF OF 平面，平面//∴⊂（Ⅱ）CD AP PCD CD PCD AP ⊥∴⊂⊥,平面，平面CD BE BCDE ED BC ED BC //,,//∴∴=为平行四边形， ,PA BE ⊥∴AC BE ABCE ⊥∴为菱形，又PAC AC PA A AC PA 平面、又⊂=⋂, ,PAC BE 平面⊥∴【解析】通过线线垂直证明线面垂直，利用了菱形的性质.4、【答案】取PD 中点E ，连结EN ，EA ，则EN CDAM ，∴四边形ENMA 是平行四边形， ∴EA ∥MN ．∵AE ⊥PD ，AE ⊥CD ， ∴AE ⊥平面PCD ， 从而MN ⊥平面PCD ， ∵MN 平面MND ，∴平面MND ⊥平面PCD ．【解析】通过线线垂直证明线面垂直，又利用线面垂直证明面面垂直. 5.【答案】：（Ⅰ）见解析： 【解析】：（Ⅰ）∵ABEF 为正方形∴AF EF ⊥ ∵90AFD ∠=︒ ∴AF DF ⊥ ∵=DF EF F ∴AF ⊥面EFDC AF ⊥面ABEF∴平面ABEF ⊥平面EFDC【拔高】1、α、β、γ为不同的平面，m ，n ，l 为不同的直线，则m ⊥β的一个充分条件是( ) A ．n ⊥α，n ⊥β，m ⊥α B ．α∩γ＝m ，α⊥γ，β⊥γ C ．α⊥γ，β⊥γ，m ⊥α D ．α⊥β，α∩β＝l ，m ⊥l2、(2014·聊城堂邑中学模拟)若a ，b ，c 是空间三条不同的直线，α，β是空间中不同的平面，则下列命题中不正确的是( )A ．若c ⊥α，c ⊥β，则α∥βB ．若b ⊂α，b ⊥β，则α⊥βC ．若b ⊂α，a ⊄α且c 是a 在α内的射影，若b ⊥c ，则a ⊥bD ．当b ⊂α且c ⊄α时，若c ∥α，则b ∥c3、如图，PA ⊥正方形ABCD ，下列结论中不正确的是( )21⊂A．PB⊥BC B．PD⊥CD C．PD⊥BD D．PA⊥BD4、如图，直四棱柱ABCD－A1B1C1D1中，AB∥CD，AD⊥AB，AB＝2，AD＝2，E为CD 上一点，DE＝1，EC＝3.证明：BE⊥平面BB1C1C；5.【2019全国2卷文17】如图，长方体ABCD-A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.证明：BE⊥平面EB1C答案与解析1、【答案】A【解析】由n⊥α，n⊥β知α∥β，又m⊥α，∴m⊥β，但当m⊥β时，n⊥α，n⊥β不一定成立，故选A.2、【答案】D【解析】对于A，若c⊥α，c⊥β，则α∥β，根据一条直线同时垂直于两个不同的平面，则可知结论成立．对于B，若b⊂α，b⊥β，则α⊥β，符合面面垂直的判定定理，成立．对于C，当b⊂α，a⊄α且c是a在α内的射影，若b⊥c，则a⊥b符合三垂线定理，成立．对于D，当b⊂α且c⊄α时，若c∥a，则b∥c，线面平行，不代表直线平行于平面内的所有的直线，故错误．选D3、【答案】C【解析】由CB ⊥BA ，CB ⊥PA ，PA ∩BA ＝A ，知CB ⊥平面PAB ，故CB ⊥PB ，即A 正确；同理B 正确；由条件易知D 正确，故选C .4、【答案】如图，过点B 作CD 的垂线交CD 于点F ，则BF ＝AD ＝2，EF ＝AB －DE ＝1，FC ＝2.在Rt △BFE 中，BE ＝BF 2＋EF 2＝ 3. 在Rt △CFB 中，BC ＝BF 2＋CF 2＝ 6.在△BEC 中，因为BE 2＋BC 2＝9＝EC 2，故BE ⊥BC . 由BB 1⊥平面ABCD ，得BE ⊥BB 1， 又BC ∩BB 1＝B ，所以BE ⊥平面BB 1C 1C . 【解析】利用勾股定理证明垂直5.【答案】：（1）见解析；【知识点】：空间位置关系的推导，空间几何体的体积； 【考察能力】：空间想象能力，运算分析能力；【解析】：（1）证明：由长方体性质，⊥11C B 平面B B AA 11，所以⊥11C B BE ；又1EC BE ⊥，1111C EC C B = ，所以⊥BE 平面11C EB课堂小结本节讲了2个重要内容： 1、空间垂直关系的判定方法： (1)判定线线垂直的方法有：①计算所成的角为90°(包括平面角和异面直线所成的角)； ②线面垂直的性质(若a ⊥α，b ⊂α，则a ⊥b )；③面面垂直的定义：两平面相交形成的二面角的平面角为90°． (2)判定线面垂直的方法有：①线面垂直定义(一般不易验证任意性)；②线面垂直的判定定理(a⊥b，a⊥c，b⊂α，c⊂α，b∩c＝M⇒a⊥α)；③平行线垂直平面的传递性质(a∥b，b⊥α⇒a⊥α)；④面面垂直的性质(α⊥β，α∩β＝l，a⊂β，a⊥l⇒a⊥α)；⑤面面平行的性质(a⊥α，α∥β⇒a⊥β)；⑥面面垂直的性质(α∩β＝l，α⊥γ，β⊥γ⇒l⊥γ)．(3)面面垂直的判定方法有：①根据定义；②面面垂直的判定定理(a⊥β，a⊂α⇒α⊥β)．2．垂直关系的转化是：课后练习【基础】1、下列命题中：①平行于同一直线的两个平面平行；②平行于同一平面的两个平面平行；③垂直于同一直线的两直线平行；④垂直于同一平面的两直线平行．其中正确命题的个数有( )A．4个B．1个C．2个D．3个2、已知三条相交于一点的线段PA、PB、PC两两垂直，点P在平面ABC外，PH⊥面ABC 于H，则垂足H是△ABC的( )A．外心B．内心C．垂心D．重心3、如图所示，在正方体ABCD—A1B1C1D1中，若E是A1C1的中点，则直线CE垂直于( )A．AC B．BD C．A1D D．A1D14、如图所示，正方体ABCD－A1B1C1D1中，点P在侧面BCC1B1及其边界上运动，并且总是保持AP⊥BD1，则动点P的轨迹是( )A．线段B1C B．线段BC1C．BB1的中点与CC1的中点连成的线段D．BC的中点与B1C1的中点连成的线段5.【2018全国2卷文19】如图，在三棱柱P-ABC中，AB=BC=2√2,PA=PB=PC=AC=4,O为AC的中点.证明：PO⊥平面ABC答案与解析1.【答案】C【解析】②和④对2.【答案】C如图所示，由已知可得PA⊥面PBC，PA⊥BC，又PH⊥BC，∴BC⊥面APH，BC⊥AH．同理证得CH⊥AB，∴H为垂心．【解析】利用线面垂直的性质3．【答案】B【解析】证BD⊥面CC1E，则BD⊥CE．4．【答案】A【解析】连接AC，AB1，B1C，∵BD ⊥AC ，AC ⊥DD 1， BD ∩DD 1＝D ， ∴AC ⊥面BDD 1， ∴AC ⊥BD 1， 同理可证BD 1⊥B 1C ， ∴BD 1⊥面AB 1C ．∴P ∈B 1C 时，始终AP ⊥BD 1，选A ．5.【答案】（1）连接OB ，证明,PO AC ⊥利用勾股定理证明,PO OB ⊥即可证明 【解析】（1）连接OB ,由PAC ∆为等边三角形PO AC ∴⊥,且PO =在ABC ∆中，4AB BC AC ===,ABC ∴∆是等腰直角三角形，122BO AC ∴== 又222PO OB PB +=,PO OB ∴⊥,,AC OB O AC OB =⊂平面ABC PO ∴⊥平面ABC【巩固】1.如图所示，在四棱锥P —ABCD 中，PA ⊥底面ABCD ，且底面各边都相等，M 是PC 上的一动点，当点M 满足________时，平面MBD ⊥平面PCD .(只要填写一个你认为是正确的条件即可)2.某几何体的三视图如图所示，P 是正方形ABCD 对角线的交点，G 是PB 的中点．(1)根据三视图，画出该几何体的直观图； (2)在直观图中，①证明：PD ∥面AGC ； ②证明：面PBD ⊥面AGC ．3.如图所示，四棱锥P—ABCD的底面是边长为a的菱形，∠BCD＝120°，平面PCD⊥平面ABCD，PC＝a，PD＝2a，E为PA的中点．求证：平面EDB⊥平面ABCD．4. 如图１所示，ABCD为正方形，SA⊥平面ABCD，过A且垂直于SC的平面分别交，，．求证：AE SB，，于E F GSB SC SD⊥，AG SD⊥．5.【2019全国3卷文19】图1是由矩形ADEB、Rt△ABC和菱形BFGC组成的一个平面图形，其中AB=1，BE=BF=2，∠FBC=60°.将其沿AB，BC折起使得BE与BF重合，连结DG ，如图2.（1）证明图2中的A ，C ，G ，D 四点共面，且平面ABC ⊥平面BCGE ； （2）求图2中的四边形ACGD 的面积.图1 图2 答案与解析1．【答案】DM ⊥PC (答案不唯一) 【解析】由定理可知，BD ⊥PC .∴当DM ⊥PC 时， 即有PC ⊥平面MBD ， 而PC ⊂平面PCD ， ∴平面MBD ⊥平面PCD .2. 【答案】(1)解 该几何体的直观图如图所示(2)①证明 连接AC ，BD 交于点O ，连接OG ，因为G 为PB 的中点，O 为BD 的中点，所以OG ∥PD ．又OG ⊂面AGC ，PD ⊄面AGC ，所以PD ∥面AGC ．②证明 连接PO ，由三视图，PO ⊥面ABCD ， 所以AO ⊥PO ． 又AO ⊥BO ， 所以AO ⊥面PBD ． 因为AO ⊂面AGC ， 所以面PBD ⊥面AGC ．A【解析】通过三视图证明垂直3.【答案】证明设AC∩BD＝O，连接EO，则EO∥PC．∵PC＝CD＝a，PD＝2a，∴PC2＋CD2＝PD2，∴PC⊥CD．∵平面PCD⊥平面ABCD，CD为交线，∴PC⊥平面ABCD，∴EO⊥平面ABCD．又EO⊂平面EDB，∴平面EDB⊥平面ABCD．【解析】通过线面垂直证明面面垂直4.【答案】∵SA⊥平面ABCD，⊥．∴SA BC⊥，∵AB BC∴BC⊥平面SAB．又∵AE⊂平面SAB，⊥．∴BC AE∵SC⊥平面AEFG，⊥．∴SC AE∴AE⊥平面SBC．⊥．∴AE SB⊥同理可证AG SD【解析】通过线面垂直证明线线垂直5.【答案】（Ⅰ）见解析（Ⅱ）4【知识点】面面垂直判定，面积计算；【考查能力】运算求解能力，推理论证能力，空间想象能力【解析】解：（1）由已知得AD BE ，CG BE ，所以AD CG ，故AD ，CG 确定一个平面，从而A ，C ，G ，D 四点共面．由已知得AB ⊥BE ，AB ⊥BC ，故AB ⊥平面BCGE ． 又因为AB 平面ABC ，所以平面ABC ⊥平面BCGE ． （2）取CG 的中点M ，连结EM ，DM .因为AB //DE ，AB ⊥平面BCGE ，所以DE ⊥平面BCGE ，故DE ⊥CG . 由已知，四边形BCGE 是菱形，且∠EBC =60°得EM ⊥CG ，故CG ⊥平面DEM .因此DM ⊥CG .在Rt △DEM 中，DE =1，EM =√3，故DM =2. 所以四边形ACGD 的面积为4.【拔高】1. 如图所示，四边形ABCD 中，AD ∥BC ，AD ＝AB ，∠BCD ＝45°，∠BAD ＝90°.将△ADB 沿BD 折起，使平面ABD ⊥平面BCD ，构成三棱锥A —BCD ，则在三棱锥A —BCD 中，下列结论正确的是( )A ．平面ABD ⊥平面ABCB ．平面ADC ⊥平面BDC C ．平面ABC ⊥平面BDC D.平面ADC ⊥平面ABC 2.如图，PA ⊥正方形ABCD ，下列结论中不正确的是( )A ．PB ⊥BC B ．PD ⊥CD C ．PD ⊥BD D ．PA ⊥BD 3. 直线a ⊥直线b ，b ⊥平面β，则a 与β的关系是( )A ．a ⊥βB ．a ∥βC ．a ⊂βD ．a ⊂β或a ∥β4. 如图，四棱锥P —ABCD 中，AB ⊥AC ，AB ⊥PA ，AB ∥CD ，AB ＝2CD ，E ，F ，G ，M ，N分别为PB，AB，BC，PD，PC的中点．(1)求证：CE∥平面PAD；(2)求证：平面EFG⊥平面EMN.5. 【2019全国3卷文理8】如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则( )A．BM=EN，且直线BM、EN是相交直线B．BM≠EN，且直线BM，EN是相交直线C．BM=EN，且直线BM、EN是异面直线D．BM≠EN，且直线BM，EN是异面直线答案与解析1.【答案】D【解析】∵在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，∴BD⊥CD.又平面ABD⊥平面BCD，且平面ABD∩平面BCD＝BD，故CD⊥平面ABD，则CD⊥AB.又AD⊥AB，AD∩CD＝D，故AB⊥平面ADC，又AB⊂平面ABC，∴平面ABC ⊥平面ADC .2.【答案】C【解析】由CB ⊥BA ，CB ⊥PA ，PA ∩BA ＝A ，知CB ⊥平面PAB ，故CB ⊥PB ，即A 正确；同理B 正确；由条件易知D 正确3．【答案】D【解析】略4.【答案】 证法一 如图(1)，取PA 的中点H ，连接EH ，DH .图(1)因为E 为PB 的中点，所以EH ∥AB ，EH ＝12AB . 又AB ∥CD ，CD ＝12AB ， 所以EH ∥CD ，EH ＝CD .所以四边形DCEH 是平行四边形．所以CE ∥DH .又DH ⊂平面PAD ，CE ⊄平面PAD ，所以CE ∥平面PAD .图(2)证法二 如图(2)，连接CF .因为F 为AB 的中点，所以AF ＝12AB . 又CD ＝12AB ，所以AF ＝CD . 又AF ∥CD ，所以四边形AFCD为平行四边形．所以CF∥AD.又CF⊄平面PAD，所以CF∥平面PAD.因为E，F分别为PB，AB的中点，所以EF∥PA.又EF⊄平面PAD，所以EF∥平面PAD.因为CF∩EF＝F，故平面CEF∥平面PAD.又CE⊂平面CEF，所以CE∥平面PAD.(2)证明因为E，F分别为PB，AB的中点，所以EF∥PA.又AB⊥PA，所以AB⊥EF.同理可证AB⊥FG.又EF∩FG＝F，EF⊂平面EFG，FG⊂平面EFG，因此AB⊥平面EFG.又M，N分别为PD，PC的中点，所以MN∥DC.又AB∥DC，所以MN∥AB，所以MN⊥平面EFG.又MN⊂平面EMN，所以平面EFG⊥平面EMN.5.【答案】B【知识点】空间几何体的计算和空间中两直线位置关系【考查能力】空间想象能力，运算求解能力【解析】如图，过E，F做CD的垂线交于F、G两点连接FN，GB，设正方形边长为4，由题知三角形EFN和三角形BMG都是直角三角形.所以BM EN.又因为，，分别是DE BDDE BD=D M N、相交，中点，BM EN.。

典例解析考点一：直线与平面垂直的判定【例1】如图所示，已知PA⊥矩形ABCD所在平面，M，N分别是AB，PC的中点.（1）求证：MN⊥CD；（2）若∠PDA=45°.求证：MN⊥平面PCD.变式：如图，正方形ABCD和四边形ACEF所在的平面互相垂直，CE⊥AC，EF//AC，AB=2,CE=EF=1，求证：CF⊥平面BDE。

考点二：直线与平面垂直的性质PA平面ABC，点C在以AB为直径的⊙O上，【例2】如图所示，⊥CBA，2∠30︒=PA AB，点E为线段PB的中点，点M在AB上，且OM∥AC．求证：平面PAC⊥平面PCB；变式：如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，AB//DC，ΔPAD4.设M是PC上的一点，证是等边三角形，已知BD=2AD=8，AB=2DC=5明：平面MBD⊥平面PAD；考点三：平面与平面垂直的判定【例3】如图所示，在三棱锥P—ABC中，PA⊥底面ABC，△ABC为正三角形，D、E分别是BC、CA的中点.证明：平面PBE⊥平面PAC；P FEABCQFA 1CP BE变式：如图，在四棱锥中，底面是正方形，其他四个侧面都是等边三角形，与的交点为O. （1）求证：平面；（2）已知为侧棱上一个动点. 试问对于上任意一点，平面与平面是否垂直？若垂直，请加以证明；若不垂直，请说明理由.考点四：平面与平面垂直的性质及应用【例4】如图1，在边长为3的正三角形ABC 中，E ，F ，P 分别为AB ，AC ，BC 上的点，且满足1AE FC CP ===.将△AEF 沿EF 折起到△1A EF 的位置，使平面1A EF ⊥平面EFB ，连结1A B ，1A P .（如图2）求证：1A E ⊥EP .图1 图2S ABCD -ABCD AC BD SO ⊥ABCD E SC SC E BDE SAC OSABCDE-的底面是边长为1的正方形，侧棱PA⊥变式：如图，四棱锥P ABCDPA=，E是侧棱PA上的动点.是否不论点E在侧棱底面ABCD，且2⊥？证明你的结论．PA的任何位置，都有BD CE考点五：垂直的应用例5.设m，n是两条不同的直线，α、β、γ是三个不同的平面，给出下列命题：①若m⊂β，α⊥β，则m⊥α；②若m∥α，m⊥β，则α⊥β；③若α⊥β，α⊥γ，则β⊥γ；④若α∩γ＝m，β∩γ＝n，m∥n，则α∥β.上面命题中，真命题的序号是________(写出所有真命题的序号)．变式.关于直线m，n和平面α，β，有以下四个命题：①若m∥α，n∥β，α∥β，则m∥n；②若m∥n，m⊂α，n⊥β，则α⊥β；③若α∩β＝m，m∥n，则n∥α且n∥β；④若m⊥n，α∩β＝m，则n⊥α或n⊥β.其中假命题的序号是________．巩固练习1.设l，m是两条不同的直线，α是一个平面，则下列命题正确的有________．①若l⊥m，m⊂α，则l⊥α；②若l⊥α，l∥m，则m⊥α；③若l∥α，m⊂α，则l∥m；④若l∥α，m∥α，则l∥m.2.设b，c表示两条直线，α，β表示两个平面，现给出下列命题：①若b⊂α，c∥α，则b∥c; ②若b⊂α，b∥c，则c∥α；③若c∥α，α⊥β，则c⊥β；④若c∥α，c⊥β，则α⊥β.其中正确的命题是________．(写出所有正确命题的序号)3. 已知直线a，b与平面α，β，γ，能使α⊥β的条件是________．(填序号)①α⊥γ，β⊥γ；②α∩β＝a，b⊥a，b⊂β；③a∥α，a∥β；④a⊥β，a∥α.4. 在各个面都是正三角形的四面体PABC中，D，E，F分别是AB，BC，CA的中点，下面四个结论中成立的是________(填序号)．①BC∥平面PDF；②DF⊥平面PAE；③平面PDF⊥平面ABC；④平面PAE⊥平面ABC.5. 如图所示，PA⊥平面ABCD，四边形ABCD为矩形，那么以P、A、B、C、D五个点中的三点为顶点的直角三角形的个数是________．（第5题图） （第6题图）6.如图所示，矩形ABCD 中，AB ＝1，BC ＝2，PA ⊥平面ABCD ，且PA ＝1，则在BC 上存在________个点使PQ ⊥QD.7.称四个面均为直角三角形的三棱锥为“四直角三棱锥”，若在四直角三棱锥SABC 中，∠SAB ＝∠SAC ＝∠SBC ＝90°，则第四个面中的直角为________．8. 如图所示，四棱锥PABCD 的底面ABCD 是边长为1的正方形，侧棱PA ＝1，PB ＝PD ＝2，则它的5个面中，互相垂直的面有________对．9. 如图，在四棱锥P -ABCD 中，PA ⊥底面ABCD ，底面各边都相等，M 是PC 上的一动点，当点M 满足________时，平面MBD ⊥平面PCD.10.如图，棱柱ABCA1B1C1的侧面BCC1B1是菱形，B A C B 11 .求证：平面C AB 1⊥平面11BC A .11.如图，AB 为圆O 的直径，点E 在圆O 上，矩形ABCD 所在的平面和圆O 所在的平面互相垂直． 求证：AE ⊥平面CBE.12.如图，在四棱锥PABCD 中， PD ⊥平面ABCD ，AD ＝CD ，DB 平分∠ADC ，E 为PC 的中点． 证明：平面PAC ⊥平面PDB.13.如图，在正方体1111D C B A ABCD -中．求证：平面⊥D BC 1平面11ACC A ；11.4空间中的垂直关系答案典例解析例1：略 变式：略例2：删变式：略例3：略变式：略例4：略变式：略例5：（2）变式：（1）（3）（4）巩固练习1.B2.（4）3.（4）4.（1）（2）（4）5.96.1∠7ABC8.5BM⊥9.PC10. 略11.略12.略13.略。

8.5空间中的垂直关系1．直线与平面垂直 (1)直线和平面垂直的定义直线l 与平面α内的任意一条直线都垂直，就说直线l 与平面α互相垂直． (2)直线与平面垂直的判定定理及性质定理文字语言 图形语言符号语言判定定理一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直⎭⎪⎬⎪⎫a ，b ⊂αa ∩b ＝Ol ⊥a l ⊥b⇒l ⊥α 性质定理垂直于同一个平面的两条直线平行⎭⎪⎬⎪⎫a ⊥αb ⊥α⇒a ∥b ．平面与平面垂直的判定定理与性质定理 文字语言图形语言符号语言判定定理一个平面过另一个平面的垂线，则这两个平面互相垂直⎭⎪⎬⎪⎫l ⊂βl ⊥α⇒α⊥β 性质定理两个平面互相垂直，则一个平面内垂直于交线的直线垂直于另一个平面⎭⎪⎬⎪⎫α⊥βl ⊂βα∩β＝a l ⊥a ⇒l ⊥α1．证明线面垂直时，易忽视面内两条线为相交线这一条件． 2．面面垂直的判定定理中，直线在面内且垂直于另一平面易忽视．3．面面垂直的性质定理在使用时易忘面内一线垂直于交线而盲目套用造成失误． [试一试]1．“直线a 与平面M 内的无数条直线都垂直”是“直线a 与平面M 垂直”的________条件(填“充分不必要”，“必要不充分”，“充要”或“既不充分也不必要”)．【解析】根据直线与平面垂直的定义知“直线a 与平面M 的无数条直线都垂直”不能推出“直线a与平面M垂直”，反之可以，所以应该是必要不充分条件．【答案】必要不充分2．(2014·盐城摸底)设m，n是两条不同的直线，α是一个平面，有下列四个命题：(1)若m⊥n，m⊂α，则n⊥α；(2)若m⊥α，n∥m，则n⊥α；(3)若n∥α，m⊂α，则n∥m；(4)若m∥α，n∥α，则m∥n.其中真命题是________(填序号)．【解析】对于(1)，n⊂α，n与α相交，n⊥α都有可能；对于(3)，n与m异面，n∥m都有可能；对于(4)，m与n相交，平行，异面都有可能．【答案】(2)3．(2014·常州模拟)给出下列命题：(1)若一个平面经过另一个平面的垂线，则这两个平面相互垂直；(2)若一个平面内的两条直线与另一个平面都平行，则这两个平面相互平行；(3)若两条平行直线中的一条垂直于直线m，则另一条直线也与直线m垂直；(4)若两个平面垂直，则一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中所有真命题的序号为________．【解析】由判定定理可知(1)正确；(2)中没有明确这两条直线是否相交，故(2)错误；由等角定理可知(3)正确；(4)中若与交线不垂直的直线与另一个平面垂直，可在该平面内作一条与交线垂直的线，则该直线必定垂直于另一个平面，这样与交线垂直的直线和不垂直的直线相互平行，这在同一平面内相互矛盾，故(4)正确．【答案】(1)(3)(4)1．转化与化归思想——垂直关系2．判定线面垂直的常用方法(1)利用线面垂直的判定定理．(2)利用“两平行线中的一条与平面垂直，则另一条也与这个平面垂直”．(3)利用“一条直线垂直于两平行平面中的一个，则与另一个也垂直”．(4)利用面面垂直的性质．3．判定线线垂直的方法：(1)平面几何中证明线线垂直的方法；(2)线面垂直的性质：a ⊥α，b ⊂α⇒a ⊥b ； (3)线面垂直的性质：a ⊥α，b ∥α⇒a ⊥b . 4．判断面面垂直的方法(1)利用定义：两个平面相交，所成的二面角是直二面角； (2)判定定理：a ⊂α，a ⊥β⇒α⊥β. [练一练]1．(2014·南通期末)已知直线l ⊥平面α，直线m ⊂平面β.给出下列命题： (1)α∥β⇒l ⊥m ；(2)α⊥β⇒l ∥m ；(3)l ∥m ⇒α⊥β；(4)l ⊥m ⇒α∥β. 其中正确的命题是________(填序号)．【解析】(1)正确；(2)中l 与m 还可以是异面或相交的位置关系，(2)不正确；(3)正确；(4)中α与β可能相交，(4)不正确．【答案】(1)(3)2．已知平面α，β和直线m ，给出条件：①m ∥α；②m ⊥α；③m ⊂α；④α∥β.当满足条件________时，有m ⊥β.(填所选条件的序号)【解析】若m ⊥α，α∥β，则m ⊥β.故填②④. 【答案】②④考点一垂直关系的基本问题1．(2014·，β分别为两个不同的平面，直线l ⊂α，则“l ⊥β”是“α⊥β”成立的________条件(填“充分不必要”“必要不充分”“充要”或“既不充分也不必要”)．【解析】依题意，由l ⊥β，l ⊂α可以推出α⊥β；反过来，由α⊥β，l ⊂α不能推出l ⊥β.因此“l ⊥β”是“α⊥β”成立的充分不必要条件．【答案】充分不必要2．(2014·合肥模拟)设m ，n 是两条不同的直线，α，β，γ是三个不同的平面，有以下四个命题①⎭⎪⎬⎪⎫α∥βα∥γ⇒β∥γ ②⎭⎪⎬⎪⎫α⊥βm ∥α⇒m ⊥β ③⎭⎪⎬⎪⎫m ⊥αm ∥β⇒α⊥β ④⎭⎪⎬⎪⎫m ∥n n ⊂α⇒m ∥α 其中正确的命题是________(填写序号)．【解析】对于②，直线m 与平面β可能平行或相交；对于④，直线m 可能也在平面α内．而①③都是正确的命题．【答案】①③3．如图，P A ⊥⊙O 所在平面，AB 是⊙O 的直径，C 是⊙O 上一点，AE ⊥PC ，AF ⊥PB ，给出下列结论：①AE ⊥BC ；②EF ⊥PB ；③AF ⊥BC ；④AE ⊥平面PBC ，其中真命题的序号是________．【解析】①AE ⊂平面P AC ，BC ⊥AC ，BC ⊥P A ⇒AE ⊥BC ，故①正确，②AE ⊥PB ，AF ⊥PB ⇒EF ⊥PB ，故②正确，③若AF ⊥BC ⇒AF ⊥平面PBC ，则AF ∥AE 与已知矛盾，故③错误，由①可知④正确．【答案】①②④[备课札记] [类题通法]解决此类问题常用的方法有(1)依据定理条件才能得出结论的，可结合符合题意的图形作出判断； (2)否定命题时只需举一个反例；(3)寻找恰当的特殊模型(如构造长方体)进行筛选．考点二线面垂直的判定与性质[典例] (2013·重庆高考)如图，四棱锥P ­ABCD 中，P A ⊥底面ABCD ，P A ＝23，BC ＝CD ＝2，∠ACB ＝∠ACD ＝π3.(1)求证：BD ⊥平面P AC ；(2)若侧棱PC 上的点F 满足PF ＝7FC ，求三棱锥P ­BDF 的体积． [解] (1)证明：因为BC ＝CD ，所以△BCD 为等腰三角形． 又∠ACB ＝∠ACD ，故BD ⊥AC . 因为P A ⊥底面ABCD ，所以P A ⊥BD .从而BD 与平面P AC 内两条相交直线P A ，AC 都垂直，所以BD ⊥平面P AC .(2)三棱锥P ­BCD 的底面BCD 的面积S △BCD ＝12BC ·CD ·sin ∠BCD ＝12×2×2×sin 2π3＝ 3.由P A ⊥底面ABCD ，得V P ­BCD ＝13·S △BCD ·P A ＝13×3×23＝2.由PF ＝7FC ，得三棱锥F ­BCD 的高为18P A ，故V F­BCD＝13·S△BCD·18P A＝13×3×18×23＝14.所以V P­BDF＝V P­BCD－V F­BCD＝2－14＝74.[备课札记][类题通法]1．解答此类问题的关键在于熟练把握空间垂直关系的判定与性质，注意平面图形中的一些线线垂直关系的灵活利用，这是证明空间垂直关系的基础．2．由于“线线垂直”“线面垂直”“面面垂直”之间可以相互转化，因此整个证明过程围绕着线面垂直这个核心而展开，这是化解空间垂直关系难点的技巧所在．[针对训练]如图，在正方体ABCD­A1B1C1D1中，E为棱C1D1的中点，F为棱BC的中点．(1)求证：直线AE⊥直线DA1；(2)在线段AA1上求一点G，使得直线AE⊥平面DFG.【解】(1)证明：连结AD1，BC1，由正方体的性质可知，DA1⊥AD1，DA1⊥AB，又AB∩AD1＝A，∴DA1⊥平面ABC1D1，又AE⊂平面ABC1D1，∴DA1⊥AE.(2)所示G点即为A1点，证明如下：由(1)可知AE⊥DA1，取CD的中点H，连结AH，EH，由DF⊥AH，DF⊥EH，AH∩EH＝H，可证DF⊥平面AHE，∵AE⊂平面AHE，∴DF⊥AE.又DF∩A1D＝D，∴AE⊥平面DF A1，即AE⊥平面DFG.考点三面面垂直的判定与性质[典例](2014·连云港期末)如图，在直三棱柱ABC­A1B1C1中，AB＝AC，D为BC的中点，E为BD的中点，F在AC1上，且AC1＝4AF.求证：(1)平面ADF⊥平面BCC1B1；(2)EF∥平面ABB1A1.[证明](1)在直三棱柱ABC­A1B1C1中，CC1⊥平面ABC，而AD⊂平面ABC，所以CC1⊥AD.又AB＝AC，D为BC的中点，所以AD⊥BC.因为BC∩CC1＝C，BC⊂平面BCC1B1，CC1⊂平面BCC1B1，所以AD⊥平面BCC1B1，又AD⊂平面ADF，所以平面ADF⊥平面BCC1B1.(2)连结CF并延长交AA1于点G，连结GB.因为AC1＝4AF，AA1∥CC1，所以CF＝3FG.因为D为BC的中点，E为BD的中点，所以CE＝3EB，所以EF∥GB.又EF⊄平面ABB1A1，GB⊂平面ABB1A1，所以EF∥平面ABB1A1.[备课札记][类题通法]1．两个平面互相垂直是两个平面相交的特殊情形．2．由平面和平面垂直的判定定理可知，要证明平面与平面垂直，可转化为从现有直线中寻找平面的垂线，即证明线面垂直．3．平面和平面垂直的判定定理的两个条件：l⊂α，l⊥β，缺一不可．[针对训练](2013·徐州、宿迁三检)如图，AB，CD均为圆O的直径，CE垂直圆O所在的平面，BF∥CE.求证：(1)平面BCEF⊥平面ACE；(2)直线DF∥平面ACE.证明：(1)因为CE垂直圆O所在的平面，BC⊂圆O所在的平面，所以CE⊥BC.因为AB为圆O的直径，点C在圆O上，所以AC⊥BC.因为AC∩CE＝C，AC，CE⊂平面ACE，所以BC⊥平面ACE.因为BC⊂平面BCEF，所以平面BCEF⊥平面ACE.(2)由(1)知AC⊥BC，又因为CD为圆O的直径，所以BD⊥BC.因为AC，BC，BD在同一平面内，所以AC∥BD.因为BD⊄平面ACE，AC⊂平面ACE，所以BD∥平面ACE.因为BF∥CE，同理可证BF∥平面ACE.因为BD∩BF＝B，BD，BF⊂平面BDF，所以平面BDF∥平面ACE.因为DF⊂平面BDF，所以直线DF∥平面ACE.考点四平行与垂直的综合问题空间线、面的平行与垂直的综合考查一直是高考必考热点，归纳起来常见的命题角度有：1平行与垂直关系的证明.2探索性问题中的平行与垂直关系.3折叠问题中的平行与垂直关系.角度一平行与垂直关系的证明1．如图所示，在棱长为2的正方体ABCD­A1B1C1D1中，E，F分别为DD1，DB的中点．(1)求证：EF∥平面ABC1D1；(2)求证：CF⊥B1E.证明：(1)如图，连结BD1，在△DD1B中，E，F分别为D1D，DB的中点，∴EF为△DD1B的中位线，∴EF∥D1B，而D1B⊂平面ABC1D1，EF⊄平面ABC1D1，∴EF∥平面ABC1D1.(2)在等腰直角三角形BCD中，∵F为BD的中点，∴CF⊥BD，①在正方体ABCD­A1B1C1D1中，DD1⊥平面ABCD，∵CF⊂平面ABCD，∴DD1⊥CF，②综合①②，且DD1∩BD＝D，DD1，BD⊂平面BDD1B1，∴CF⊥平面BDD1B1，而B1E⊂平面BDD1B1，∴CF⊥B1E.角度二探索性问题中的平行与垂直关系2.如图，在四棱锥S­ABCD中，平面SAD⊥平面ABCD，四边形ABCD为正方形，且P为AD的中点，Q为SB的中点，M为BC的中点．(1)求证：CD⊥平面SAD；(2)求证：PQ∥平面SCD；(3)若SA＝SD，在棱SC上是否存在点N，使得平面DMN⊥平面ABCD？并证明你的结论．【解】(1)证明：因为四边形ABCD为正方形，所以CD⊥AD.又平面SAD⊥平面ABCD，且平面SAD∩平面ABCD＝AD，所以CD⊥平面SAD.(2)证明：连结PM，QM.因为Q，P，M分别为SB，AD，BC的中点．所以QM∥SC，PM∥DC.因为QM∩PM＝M，QM，PM⊂平面PQM，SC∩DC＝C，所以平面PQM∥平面SCD，又PQ⊂平面PQM，所以PQ∥平面SCD.(3)存在点N，使得平面DMN⊥平面ABCD.连结PC，DM交于点O，连结SP.因为SA＝SD，P为AD的中点，所以SP⊥AD.因为平面SAD⊥平面ABCD，所以SP⊥平面ABCD，SP⊥PC.在△SPC中，过O点作NO⊥PC交SC于点N，此时N为SC的中点则SP∥NO，则NO⊥平面ABCD，因为NO⊂平面DMN，所以平面DMN⊥平面ABCD，所以存在满足条件的点N.角度三折叠问题中的平行与垂直关系3．如图1，在等腰梯形CDEF中，DE＝CD＝2，EF＝2＋2，将它沿着两条高AD，CB折叠成如图2所示的四棱锥E­ABCD(E，F重合)．(1)求证：BE⊥DE；(2)设点M为线段AB的中点，试在线段CE上确定一点N，使得MN∥平面DAE.【解】(1)证明：∵AD⊥EF，∴AD⊥AE，AD⊥AB.又∵AB∩AE＝A，∴AD⊥平面ABE，∴AD⊥BE.由图1和题中所给条件知，AE＝BE＝1，AB＝CD＝2，∴AE2＋BE2＝AB2，即AE⊥BE.又∵AE∩AD＝A，∴BE⊥平面ADE，∴BE⊥DE.(2)取EC的中点G，BE的中点P，连结PM，PG，MG.则MP∥AE，GP∥CB∥DA，∴MP∥平面DAE，GP∥平面DAE.∵MP∩GP＝P，∴平面MPG∥平面DAE.∵MG⊂平面MPG，∴MG∥平面DAE，即存在点N与G重合满足条件．[备课札记][类题通法]平行与垂直的综合应用问题的处理策略(1)探索性问题一般是先根据条件猜测点的位置再给出证明，探索点存在问题，点多为中点或三等分点中某一个，也可以根据相似知识建点．(2)折叠问题中的平行与垂直关系的处理关键是结合图形弄清折叠前后变与不变的数量关系，尤其是隐含着的垂直关系．[课堂练通考点]1．(2014·扬州期末)设a，b是两条不同的直线，α，β是两个不同的平面，则下列四个命题：(1)若a⊥b，a⊥α，则b∥α；(2)若a⊥β，α⊥β，则a∥α；(3)若a∥α，a⊥β，则α⊥β；(4)若a⊥b，a⊥α，b⊥β，则α⊥β.其中正确命题的序号是________．【解析】(1)中，b可能在平面α内；(2)中，a可能在平面α内；(3)中，因为a∥α，a ⊥β，所以α内必存在一条直线b与a平行，从而得到b⊥β，故(3)正确；(4)中，因为a⊥b，a⊥α，所以b∥α或b⊂α，故α内必有一条直线c与b平行，又b⊥β，所以c⊥β，故α⊥β，所以(4)正确．【答案】(3)(4)2．已知l，m，n为两两垂直的三条异面直线，过l作平面α与直线m垂直，则直线n 与平面α的关系是________．【解析】∵l⊂α，且l与n异面，∴n⊄α，又∵m⊥α，n⊥m，∴n∥α.【答案】n∥α3．设a，b为不重合的两条直线，α，β为不重合的两个平面，给出下列命题：(1)若a∥α且b∥α，则a∥b；(2)若a⊥α且a⊥β，则α∥β；(3)若α⊥β，则一定存在平面γ，使得γ⊥α，γ⊥β；(4)若α⊥β，则一定存在直线l，使得l⊥α，l∥β.上面命题中，所有真命题的序号是________．【解析】(1)中a与b可能相交或异面，故不正确．(2)垂直于同一直线的两平面平行，正确．(3)中存在γ，使得γ与α，β都垂直．(4)中只需直线l⊥α且lβ就可以．【答案】(2)(3)(4)4．如图，三棱柱ABC­A1B1C1中，侧棱垂直于底面，∠ACB＝90°，2AC＝AA1，D，M分别是棱AA1，BC的中点，证明：(1)AM∥平面BDC1；(2)DC1⊥平面BDC.证明：(1)取BC 1的中点N ，连结DN ，MN ，则MN 綊12CC 1. 又AD 綊12CC 1， ∴AD ∥MN ，且AD ＝MN ，∴四边形ADNM 为平行四边形， ∴DN ∥AM ，又DN ⊂平面BDC 1，AM ⊄平面BDC 1， ∴AM ∥平面BDC 1.(2)由题设知BC ⊥CC 1，BC ⊥AC ，又CC 1∩AC ＝C ， ∴BC ⊥平面ACC 1A 1.又DC 1⊂平面ACC 1A 1，∴DC 1⊥BC ， 又由题设知∠A 1DC 1＝∠ADC ＝45°， ∴∠CDC 1＝90°，∴DC 1⊥DC .又DC ∩BC ＝C ， ∴DC 1⊥平面BDC .。